Abstract
Magnéli phases exhibit significant potential for applications in electronic materials in energy conversion due to their high electrical conductivity and excellent thermal stability. In this study, single-phase TinO2n−1 (n = 4, 5, 6) bulk materials were successfully prepared by a combination of the carbothermal reduction of nano-sized rutile TiO2 and hot-press sintering methods. The relationships between the phase evolution, microstructural features, and thermoelectric performance were investigated systematically. Synchrotron X-ray diffraction (SXRD) and scanning electron microscopy (SEM) analyses revealed that the Ti4O7 and Ti5O9 materials had single-phase structures with high densities (relative density > 97%) and no obvious grain boundary holes or microcracks. We tested the thermoelectric properties of the Magnéli phases in the temperature range of 300–1100 K. The Magnéli phases exhibited a significant temperature dependence, with peak zT values of 0.17, 0.18, and 0.14 for Ti4O7, Ti5O9, and Ti6O11, respectively, at 1100 K. This variation in thermoelectric performance was mainly attributed to the synergistic effect of the oxygen vacancy concentration and the shear surface density on the carrier concentration and lattice thermal conductivity. Furthermore, the Fermi energy levels and electronic thermal conductivity of the Magnéli phases were calculated using the single parabolic band (SPB) model.
1. Introduction
In recent years, significant advancements have been achieved in the research of thermoelectric materials, driven by the global energy transition and the development of green technology. Conventional thermoelectric materials, such as SnSe, Bi2Te3, PbTe, and SiGe [1,2,3,4,5,6], exhibit a relatively high thermoelectric figure of merit (zT values). However, they face critical limitations, including environmental toxicity, degradations in high-temperature performance, and prohibitive manufacturing costs, which severely restrict their large-scale applications. For instance, PbTe tends to decompose at elevated temperatures, releasing toxic lead vapors, while the synthesis of SiGe alloys requires high-purity inert atmospheres, resulting in complex and costly processes. In response to these challenges, metal oxide thermoelectric materials, which combine environmental compatibility with excellent chemical stability, have emerged as a research focus. Taking perovskite-type SrTiO3 as an example, aliovalent doping with La3+ or Nb5+ enables precise carrier concentration control, demonstrating breakthrough potential, with zT values exceeding 0.3, and establishing a paradigm for oxide thermoelectric systems [7,8].
As another representative metal oxide, titanium dioxide (TiO2) has attracted considerable attention due to its exceptional chemical stability, low ecological toxicity, and abundant natural reserves [9]. However, the wide bandgap (~3.0 eV for rutile and ~3.2 eV for anatase) and ultralow electrical conductivity (<10−3 S·cm−1) of intrinsic TiO2 severely limit its thermoelectric performance [10,11,12,13,14]. To address these limitations, researchers have adopted dual optimization strategies: on the one hand, aliovalent doping with Nb5+ or Ta5+ enhances carrier concentration, boosting electrical conductivity to the order of 10² S·cm⁻¹ and achieving a zT value of 0.2 at 800 K [15,16,17,18]; on the other hand, constructing oxygen-vacancy-ordered Magnéli-phase titanium oxides (TiₙO2n−1 ) through periodic oxygen vacancy arrangements within shear planes simultaneously increases carrier concentration (~1021 cm−3) and reduces lattice thermal conductivity (κl < 1.8 W·m−1·K−1), revealing unique potential for thermoelectric regulation. Portehault et al. synthesized nanostructured Ti₄O₇ via sol–gel combined with spark plasma sintering (SPS), reducing κl to 1.0 W·m−1·K−1 through grain boundary scattering. However, the maximum zT value reached was only 0.08 at 1073 K [19]. Ti5O9, prepared by Pandey’s team using solid-state reaction and hot-pressing sintering, achieved a zT value of 0.3 at 1076 K [20]. Fan et al. reported a zT value of 0.16 at 764 K for Ti9O17 [21], while Wang et al. obtained zT = 0.32 at 973 K through a Ti6O11/Ti7O13 mixed-phase structure. Nevertheless [22], current research remains fragmented, lacking systematic analysis of the structure–property relationships in TinO2n−1 systems.
In this work, high-purity TinO2n−1 (n = 4, 5, 6) materials were synthesized through controlled titanium oxide reduction, and single-phase, high-density bulk samples (with relative densities of greater than 97%) were fabricated by using hot-pressure sintering. The electrical conductivity (σ), Seebeck coefficient (S), and thermal conductivity (κ) of these samples were characterized systematically over a wide temperature range (300–1100 K), and the zT values were calculated to evaluate the thermoelectric properties. Notably, we correlated and analyzed the measurement data using a single parabolic band model. This study aims to elucidate the quantitative correlation between oxygen vacancy ordering and thermoelectric parameters, providing an experimental basis for the rational design of Magnéli-phase materials.
2. Experimental Section
2.1. Preparation
High-purity titanium dioxide powder with a nano-size rutile structure was subjected to a reduction reaction, and pure powder of Magnéli-phase TinO2n−1 (n = 4, 5, 6) was obtained. The powder was formed into high-densification bulks using a hot-press sintering method. A total of 120 g of powder was loaded into a graphite mold with a diameter of 60 mm and placed in a hot-press furnace. Before heating, the chamber was evacuated down to a pressure of 5 Pa, followed by purging with high-purity argon (99.999%). The above process was repeated three times to minimize the oxygen content in the chamber. The sample was sintered under a pressure of 30 MPa for 30 min at a heating rate of 10 °C per minute in a flowing argon atmosphere at 1200 °C. After cooling down to ambient temperature, the as-prepared samples were mechanically ground with SiC sandpapers to remove adhering graphite paper and then polished to obtain a bright surface (as shown in Figure 1). Finally, the samples were cut into two different sizes using a diamond wire cutter (STX-202A, KEJING, Shenyang, China): 3 × 3 × 10 mm (thermoelectric system test) and 10 × 10 × 1 mm (thermal conducting test).
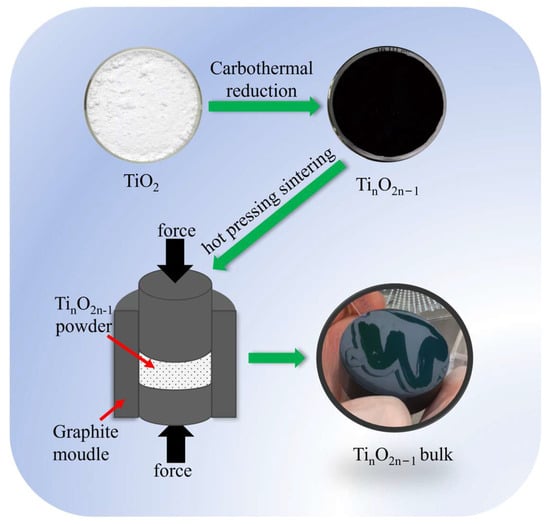
Figure 1.
Schematic of the preparation of bulk Magnéli-phase TinO2n−1.
2.2. Characterization
The crystal structure of the initial powder of the Magnéli-phase TinO2n−1 was characterized by synchrotron radiation diffraction measurement at the BL14B1 beamline of the Shanghai Synchrotron Radiation Facility with an incident X-ray wavelength of 0.6199 Å, and the hot-pressed bulk material was measured using a Rigaku (Tokyo, Japan) Miniflex-600 X-ray diffractor (copper target wavelength of 1.5169 Å). The microstructure was observed using scanning electron microscopy (SEM, ThermoFisher, Verios 5UC, Waltham, MA, USA) with electron backscatter diffraction (EBSD), respectively. The Seebeck coefficient and electrical conductivity were measured with commercial equipment (CTA3S/1150, Cryoall, Beijing, China) under a helium atmosphere. The thermal diffusivity of the TinO2n−1 was measured using a laser flash method (LFA 500, Linseis, Selb, Germany), and the heat capacity (Cp) of the samples was calculated by the Dulong–Petit law. The density was measured by the Archimedean method (SQP, Sartorius, Göttingen, Germany).
3. Results and Discussion
3.1. Characterization of Structure
The crystal structure of Magnéli-phase titanium oxides is derived from the rutile-type TiO2 lattice, with oxygen octahedra coordinated around titanium atoms as the fundamental building blocks. As shown in Figure 2a, these TiO6 octahedra extend in three-dimensional space through corner-sharing or edge-sharing configurations. Crystallographic analysis revealed that the unit cell composition of the TinO2n−1 can be rationalized as a combination of n intact TiO2 units and one oxygen-deficient TiO unit. This structural reconstruction is achieved through periodic planar oxygen vacancy defects—specifically, an oxygen vacancy plane is generated every n layers of rutile-type structural units. The ordered arrangement of these defects reduces the crystal symmetry from the parent tetragonal system (P42/mnm) to triclinic (P ) [23,24,25]. The introduction of oxygen vacancies induces fundamental alterations in the polyhedral connectivity (Figure 2b). Within the defect layers, adjacent TiO6 octahedra couple via face-sharing mechanisms, forming crystallographic shear planes that structurally compensate for lattice distortion caused by oxygen substoichiometry. The periodic arrangement of these shear planes significantly reduces the bandgap (Eg~0.1 eV), while the enhanced carrier mobility (μ ≈ 10−2 cm2 V⁻1 s⁻1) contributes to high intrinsic conductivity (σ~103 S/cm). With an increasing Magnéli index n (Ti4O7 → Ti6O11), the system demonstrates distinct structure–property evolution: the planar oxygen vacancy density decreases linearly from 0.25 O/nm2 (n = 4) to 0.17 O/nm2 (n = 6), accompanied by shear plane spacing expansion from 1.2 nm to 1.8 nm. This structural progression induces two competing effects: The carrier concentration undergoes decay with reduced oxygen defects, leading to a decrease in conductivity by approximately two orders of magnitude. Concurrently, the increased shear plane spacing effectively suppresses active oxygen migration in the lattice, enhancing chemical stability and improving durability in oxidative and corrosive environments.
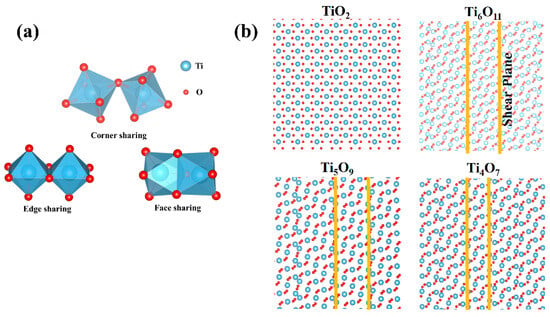
Figure 2.
(a) Coordination modes of TiO6 octahedra: corner-sharing, edge-sharing, face-sharing. (b) The crystal presents a periodic layered stacking: alternating n layers of complete TiO2 units and 1 layer of anoxic TiO layers.
As shown in Figure 3a, XRD characterization of the precursor TinO2n−1 (n = 4, 5, 6) powders revealed distinct Magnéli-phase features. The diffraction peaks of Ti4O7, Ti5O9, and Ti6O11 precisely matched their respective standard PDF cards, with no detectable impurity phases, confirming the high-purity single-phase nature of the TiO2-derived powders. In this study, we aimed to detect superlattice diffraction peaks (e.g., (121)rutile) along the 1/2 [011]rutile crystallographic orientation using synchrotron radiation in order to validate the long-range ordered arrangement of oxygen vacancies within shear planes and provide direct evidence for the periodic crystallographic shear plane model in TinO2n−1 crystals [21,26,27]. However, under the current experimental conditions and sample characteristics, conclusive evidence of superlattice diffraction signals was not obtained due to the weak X-ray scattering of oxygen. Further characterization by conventional XRD of the hot-pressed bulk samples (Figure 3b) demonstrated that the Ti4O7 and Ti5O9 retained their single-phase structures, whereas the Ti6O11 bulk contained trace Ti5O9 impurities (>5 wt%). This phenomenon was attributed to excessive oxygen loss during hot-pressing under high-vacuum conditions (<10−3 Pa) with graphite dies, leading to partial reduction of Ti6O11 to Ti5O9. These results suggest the need for optimizing oxygen stoichiometry control through sintering atmosphere regulation (e.g., Ar/H2 mixtures) or interface passivation techniques.
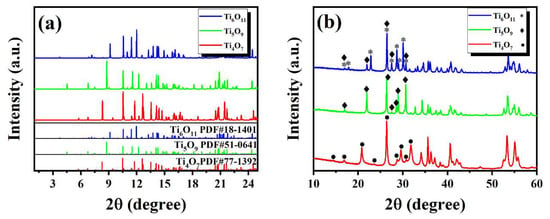
Figure 3.
XRD patterns of TinO2n−1 samples as (a) initial powder (λ = 0.6199 Å) and (b) hot-press-sintered bulks (λ = 1.5169 Å).
3.2. Microstructure
As shown in Figure 4(a1–c1), the Magnéli-phase TinO2n−1 (n = 4, 5, 6) single-phase powders prepared using the carbothermal reduction method were all nano-sized. In order to systematically evaluate the thermoelectric properties of the Magnéli-phase structures, hot-press sintering was employed for powder densification. This process requires precise control to maintain single-phase integrity while achieving optimal densification. Previous investigations revealed that excessive densification temperatures lead to uncontrollable oxygen vacancy concentrations and secondary phase formation, while pressure optimization critically determines the final density. These combined factors significantly influence the accuracy of electrical and thermal conductivity measurements, ultimately affecting the reliability of thermoelectric performance characterization. SEM analysis (Figure 4(a2–c2)) demonstrated defect-free surfaces without observable voids, confirming excellent densification and structural homogeneity. The Archimedes method measurements (Table 1) corroborated these findings, showing relative densities exceeding 97% for all bulk materials. Electron backscatter diffraction (EBSD)-based grain size analysis (Figure 4(a3–c3)) revealed average dimensions of 2.4 (±0.1) μm for Ti4O7, 3.8 (±0.1) μm for Ti5O9, and 2.0 (±0.1) μm for Ti6O11. Notably, EBSD pole figure analysis confirmed the absence of a crystallographic texture in all three materials, providing direct evidence of isotropic grain growth mechanisms during the hot-press sintering process.

Figure 4.
SEM images of TinO2n−1 samples as initial powder (a1–c1) and hot-press-sintered bulks (a2–c2), and EBSD IPF maps of the TinO2n−1 bulks (a3–c3).

Table 1.
Grain size, density, relative density, and conductivity of the Ti4O7, Ti5O9, and Ti6O11 at room temperature.
3.3. Electrical Properties
As shown in Figure 5a, all Magnéli phases exhibited negative Seebeck coefficients (S = −30~−135 μV·K⁻¹), confirming the n-type semiconductor transport mechanism. The absolute value of the Seebeck coefficient increased as the oxygen content increased over the whole temperature range investigated, and it increased with the temperature for TinO2n−1 (n = 4, 5, 6). We used the single parabolic band model combined with the Seebeck coefficient inversion technique to obtain the represented reduced Fermi (η) and Fermi level (Ef) [30]. Based on the Boltzmann transport theory, the following expressions were derived:
With the scattering parameter λ = −1/2 (acoustic phonon scattering dominance), Equation (1) simplifies to:
where kB is Boltzmann’s constant, e is the elementary charge, and division of the two gives a constant of 86.1733 μV/K, where η represents the reduced Fermi level:
Fi denotes the Fermi–Dirac integrals:
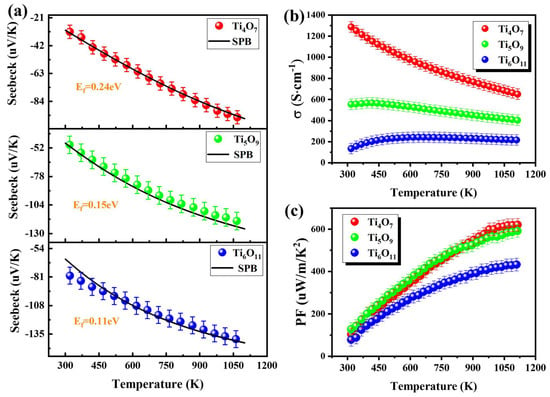
Figure 5.
Temperature dependence of the Seebeck coefficient (spheres are test results; black solid line lines are the SPB model fits) (a), electrical conductivity (b), and thermoelectric power factor (c) for TinO2n−1.
Through the experimental Seebeck coefficient inversion for η determination (Figure 6a), subsequent calculations of Ef via Equation (3) were carried out (Figure 6b). The Ef values for the Magnéli phases were averaged separately, yielding values of 0.24 eV for Ti4O7, 0.15 eV for Ti5O9, and 0.11 eV for Ti6O11. The black solid line in Figure 5a shows the fitted curves obtained from the SPB model, indicating that the SPB model is highly effective for evaluating thermoelectric properties.
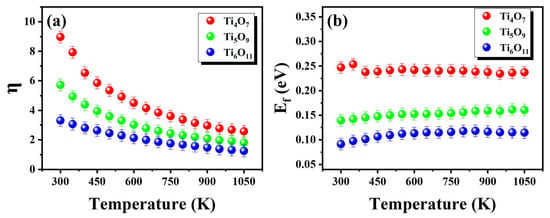
Figure 6.
Relationship between (a) η, (b) Ef, and temperature in the SPB model.
The temperature-dependent conductivity in Figure 5b reveals that Ti4O7 possessed the highest intrinsic conductivity (~1287 S·cm−1) at room temperature, outperforming Ti5O9 (558 S·cm−1) and Ti6O11 (134 S·cm−1) while maintaining a five-order advantage over pristine TiO2 (σ < 10−3 S·cm−1) [11]. Over the whole temperature range investigated, Ti4O7 showed negative temperature coefficient behavior, indicating metalloid-like conduction [31]; Ti5O9 maintained quasi-steady conductivity (Δσ < 5%) below 450 K but exhibited a metal-like thermal response at medium–high temperatures (T > 450 K); and Ti6O11 followed typical semiconductor behavior, with increasing conductivity [32]. This divergence originated from structural differences: The density of oxygen-vacancy-induced face-sharing TiO6 octahedral shear planes decreased with increasing the n-value. The high-density shear planes in the Ti4O7 enhanced electron delocalization, resulting in superior conductivity, but they compromised the absolute Seebeck coefficient (|S| < 30 μV·K−1). The power factor (PF = S2σ) evolution in Figure 5c shows that the Ti4O7 and Ti5O9 reached peak PF values of 618 μW·m−1·K−2 and 591 μW·m−1·K−2 at T = 1100 K (error overlapping bars), representing 43% and 36% enhancements over Ti6O11 (432 μW·m−1·K−2). This suggests that moderate modulation of the oxygen vacancy concentration (n = 4 ⟶ 5) can optimize the carrier effective mass while preserving high conductivity, leading to significant breakthroughs in thermoelectric performance at the Pareto frontier.
3.4. Thermal Conductivity
As shown in Figure 7a, the total thermal conductivity (K = κe + κl) of the Magnéli-phase TinO2n−1 systems exhibited a systematic decrease with increasing the n-value, which aligns well with previous studies [33,34]. In the temperature range of RT-1100 K, the measured total thermal conductivities for Ti4O7, Ti5O9, and Ti6O11 were 2.7–3.8 W·m−1·K−1, 2.6–3.4 W·m−1·K−1, and 2.3–3.4 W·m−1·K−1, respectively. The lower value of the thermal conductivity of the hot-pressed Magnéli-phase TinO2n−1 compared to the rutile single-crystal TiO2 (6–8 Wm/K) [35] was attributed to phonon scattering at grain boundaries. The increasing oxygen vacancy concentration induced two regulatory mechanisms on the thermal transport properties: the enhanced carrier concentration significantly improved the electronic thermal conductivity (Figure 7b), while shear-plane induced lattice distortion intensified the phonon scattering, thereby suppressing the lattice thermal conductivity. To quantitatively analyze the electron–phonon coupling mechanism, we employed the Wiedemann–Franz approximation to establish an electronic thermal conductivity model (Equation (5)), with electronic and lattice thermal conductivity derived through differential analysis.
where σ denotes the electrical conductivity, T is the absolute temperature, and L represents the Lorenz number. Considering theoretical discrepancies between degenerate (2.45 × 10−8 W·Ω·K−2) and non-degenerate limits (1.5 × 10−8 W·Ω·K−2), we obtained a precise computational framework for L-values using a single parabolic band model combined with the Seebeck coefficient inversion technique [30]. Based on the Boltzmann transport theory (Equation (1)), the following expressions were derived:
With a scattering parameter of λ = −1/2, Equation (6) simplifies to:
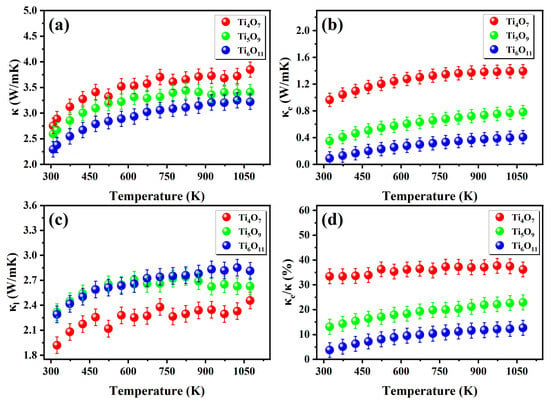
Figure 7.
Thermal conductivity as a function of temperature for TinO2n−1: (a) total thermal conductivity κ, (b) electronic thermal conductivity κe, and (c) lattice thermal conductivity κe, (d) as a percentage of κe/κ.
Through experimental Seebeck coefficient inversion for η determination, subsequent calculations of L via Equations (2) and (4) enabled the precise determination of κe using Equation (5).
Figure 7b reveals a strong positive correlation between κe and the electrical conductivity in the Magnéli phases. At room temperature, the κe contributions to the total thermal conductivity were 33.4%, 13.1%, and 3.8% for Ti4O7, Ti5O9, and Ti6O11, respectively (as shown in Figure 5c). These results demonstrate distinct thermal transport regimes: (1) electron-dominated transport in high-conductivity Ti4O7, (2) electron–phonon mixed conduction in Ti5O9, and (3) phonon-dominated thermal transport in Ti6O11. Theoretically, the lattice thermal conductivity should exhibit an inverse correlation with the shear plane density (reciprocal of shear plane spacing) due to enhanced phonon scattering at the shear planes. However, the experimental results show nearly identical κl values between Ti6O11 and Ti5O9 (Δκl < 0.2 W·m−1·K−1) [25], which can be attributed to two concurrent mechanisms: phase purity effects and grain size effects. XRD analysis revealed that the Ti6O11 bulk contained above 5 wt% Ti5O9 as a secondary phase (Figure 3b). The lower shear plane density (n = 5) of this impurity phase likely counteracted the expected κl reduction. We attempted to achieve single-phase Magnéli structures under different sintering temperatures, resulting in a decreased average grain size from 3.8 μm to 2.0 μm (Figure 4(b2,c2)). According to the Callaway model, larger grains extend the phonon mean free path, systematically elevating κl.
Systematic analysis based on experimental data revealed that the evolution of the thermoelectric figure of merit in the Magnéli-phase titanium oxides (TiₙO2n−1) exhibited significant temperature dependence but a non-monotonic correlation with the n-value (Figure 8). Notably, the zT trajectories of the Ti4O7 and Ti5O9 showed substantial overlap within the RT-1100 K range, suggesting potential similarities in their electron–phonon coupling mechanisms. Specifically, the zT value of the Ti4O7 increased linearly from 0.015 at room temperature to 0.17 at 1100 K, with performance limitations primarily attributed to the dominant contribution of electronic thermal conductivity (κe/κ > 33%), closely linked to its metallic-like electronic structure and strong electron–phonon scattering. When n increased to 5, the reduced oxygen vacancy concentration in the Ti5O9 lowers its electronic thermal conductivity to κe/κ = 13–22%. Through synergistic optimization of the carrier concentration and Seebeck coefficient, the Ti5O9 achieved a zT value of 0.18 at 1100 K. In contrast, the Ti6O11 exhibited the lowest total thermal conductivity (κ~2.3 W·m−1·K−1), and its diminished electrical conductivity resulted in an insufficient power factor, ultimately restricting its zT value to 0.14 at 1100 K. This phenomenon highlights an inherent competition between thermal conductivity reduction and electrical transport maintenance in Magnéli-phase systems, necessitating atomic-scale defect engineering to achieve the cooperative optimization of both properties.
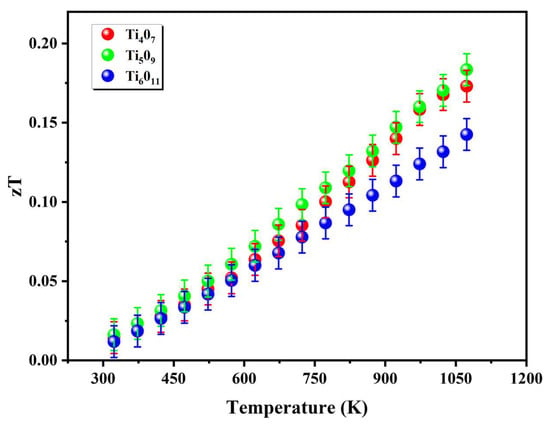
Figure 8.
Figure of merit (zT) as a function of temperature.
4. Conclusions
In this work, high-density (>97% relative density) single-phase Magnéli-phase titanium oxide (TiₙO2n−1, n = 4–6) bulk materials were successfully synthesized via carbothermal reduction combined with hot-pressing sintering. The structure–property relationships among the phase evolution, microstructural characteristics, and thermoelectric performance were systematically investigated. The absolute Seebeck coefficient decreased with increasing the oxygen vacancy concentration (lower n-values). Both the electrical conductivity and total thermal conductivity were negatively correlated with the oxygen vacancy concentration. Ti4O7 demonstrated κ = 3.2 W·m−1·K−1 with a dominant electronic contribution (κe/κ = 33%), whereas Ti5O9 exhibited a reduced κ = 2.8 W·m−1·K−1 (κe/κ = 13–22%). The thermoelectric figure of merit (zT) showed pronounced temperature dependence but a non-monotonic correlation with the n-values. At 1100 K, the peak zT values reached 0.17, 0.18, and 0.14 for Ti4O7, Ti5O9, and Ti6O11, respectively. The performance limitation of Ti4O7 stemmed from strong electron–phonon scattering (Lorenz number L = 2.1 × 10−8 W·Ω·K−2) induced by its metallic-like electronic structure (high density of states near the Fermi level). In contrast, Ti5O9 achieved superior high-temperature zT stability (>900 K) through optimized oxygen vacancy concentration and enhanced carrier mobility. Our study provides critical experimental insights for designing high-performance oxide thermoelectric materials via oxygen vacancy ordering and stoichiometric control. In addition, future investigations could systematically explore advanced doping strategies and nano-structuring to optimize the carrier concentration and phonon scattering synergistically, thereby pushing the thermoelectric figure of merit (zT) beyond current limitations.
Author Contributions
Data curation, Z.G., C.F. and H.S.; Funding acquisition, F.Z.; Investigation, Z.G., L.Y., X.W., J.Z., and F.W.; Methodology, Z.G. and H.L.; Validation, X.Y., H.Y. and Y.T.; Writing—original draft, Z.G. and C.F.; Writing—review & editing, F.Z. and H.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was financially supported by the National Natural Science Foundation of China under contract numbers of 52173226 and 52130108, the National Key R&D Program of China (No. 2022YFA1603800), and the Guangdong Basic and Applied Basic Research Foundation (No. 2023A1515140089). F.X. Zhang appreciates the support received from the Pearl River Talent Recruitment Program, as outlined in contract 2021CX02C058.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author(s).
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Chen, Z.G.; Shi, X.; Zhao, L.D.; Zou, J. High-Performance SnSe Thermoelectric Materials: Progress and Future Challenge. Prog. Mater. Sci. 2018, 97, 283–346. [Google Scholar] [CrossRef]
- Cho, H.; Yun, J.H.; Back, S.Y.; Lee, J.S.; Kang, N.; Jang, Y.I.; Lim, J.; Son, J.H.; Park, J.Y.; Kim, J.; et al. Superior Thermoelectric Cooling Performance by Suppressing Bipolar Diffusion Effect and Enhancing Anisotropic Texture in P-/n-Type Bi2Te3 Based Compounds. J. Alloys Compd. 2021, 888, 161572. [Google Scholar] [CrossRef]
- Hsieh, H.C.; Wang, C.H.; Lan, T.W.; Lee, T.H.; Chen, Y.Y.; Chu, H.S.; Wu, A.T. Joint Properties Enhancement for PbTe Thermoelectric Materials by Addition of Diffusion Barrier. Mater. Chem. Phys. 2020, 246, 122848. [Google Scholar] [CrossRef]
- Basu, R.; Singh, A. High Temperature Si–Ge Alloy towards Thermoelectric Applications: A Comprehensive Review. Mater. Today Phys. 2021, 21, 100468. [Google Scholar] [CrossRef]
- Ghafoor, F.; Ghafoor, B.; Kim, D.k.; Khan, M.F.; Anis-ur-Rehman, M. Enhancement in Figure of Merit in N-Type Bi(R)-Te Thermoelectric Nanomaterials. J. Mater. Res. Technol. 2023, 23, 3617–3625. [Google Scholar] [CrossRef]
- Chen, W.Y.; Shi, X.L.; Yang, Q.; Li, M.; Lyu, W.; Liu, T.; Cao, T.; Hu, B.; Liu, W.; Sun, S.; et al. Solvothermally Silver Doping Boosting the Thermoelectric Performance of Polycrystalline Bi2Te3. Chem. Eng. J. 2023, 475, 146428. [Google Scholar] [CrossRef]
- Zhang, L.; Cao, Z.; Fu, Q.Q.; Li, C.Y.; Du, Y.Q.; Li, Y.N.; La, T.; Zhang, D.B.; Wang, J. Thermoelectric Properties of Yb-La-Nb-Doped SrTiO3. J. Eur. Ceram. Soc. 2024, 44, 1647–1653. [Google Scholar] [CrossRef]
- Wang, K.X.; Wang, J.; Li, Y.; Zou, T.; Wang, X.H.; Li, J.B.; Cao, Z.; Shi, W.J.; Yaer, X. Enhancement of Thermoelectric Properties of SrTiO3/LaNb-SrTiO3 Composite by Different Doping Levels. Chin. Phys. B 2018, 27, 048401. [Google Scholar] [CrossRef]
- Liu, H.J.; Luo, M.Q.; Yang, L.X.; Zeng, C.L.; Fu, C. A High Strength and Conductivity Bulk Magnéli Phase Ti4O7 with Superior Electrochemical Performance. Ceram. Int. 2022, 48, 25538–25546. [Google Scholar] [CrossRef]
- He, Q.; Hao, Q.; Chen, G.; Poudel, B.; Wang, X.; Wang, D.; Ren, Z. Thermoelectric Property Studies on Bulk TiOx with x from 1 to 2. Appl. Phys. Lett. 2007, 91, 052505. [Google Scholar] [CrossRef]
- Thébaud, S.; Adessi, C.; Bouzerar, G. Investigating the Higherature Thermoelectric Properties of N-Type Rutile TiO2. Phys. Rev. B 2019, 100, 195202. [Google Scholar] [CrossRef]
- Tao, J.; Luttrell, T.; Batzill, M. A Two-Dimensional Phase of TiO2 with a Reduced Bandgap. Nat. Chem. 2011, 3, 296–300. [Google Scholar] [CrossRef]
- Eddy, D.R.; Permana, M.D.; Sakti, L.K.; Sheha, G.A.N.; Solihudin, G.A.N.; Hidayat, S.; Takei, T.; Kumada, N.; Rahayu, I. Heterophase Polymorph of TiO2 (Anatase, Rutile, Brookite, TiO2 (B)) for Efficient Photocatalyst: Fabrication and Activity. Nanomaterials 2023, 13, 704. [Google Scholar] [CrossRef]
- Luttrell, T.; Halpegamage, S.; Tao, J.; Kramer, A.; Sutter, E.; Batzill, M. Why Is Anatase a Better Photocatalyst than Rutile?—Model Studies on Epitaxial TiO2 Films. Sci. Rep. 2015, 4, 4043. [Google Scholar] [CrossRef]
- Liu, X.; Yu, J.; Wang, B.; Maji, K.; Alvarez-Ruiz, D.T.; Guilmeau, E.; Freer, R. Enhancing the Thermoelectric Properties of Nb-Doped TiO2-Based Ceramics through in-Situ Synthesis of β-Sn Inclusions at Grain Boundaries. J. Eur. Ceram. Soc. 2023, 43, 2523–2533. [Google Scholar] [CrossRef]
- Alim, M.A.; Bak, T.; Atanacio, A.; Plessis, J.D.; Zhou, M.; Davis, J.; Nowotny, J. Electrical Conductivity and Defect Disorder of Tantalum-Doped TiO2. J. Am. Ceram. Soc. 2017, 100, 4088–4100. [Google Scholar] [CrossRef]
- Liu, H.; Ma, H.; Wang, F.; Liu, B.; Liu, B.; Chen, J.; Jia, X. Further Insights into Thermoelectric Properties of Nonstoichiometric Titanium Oxide Fabricated by High Pressure and High Temperature. Ceram. Int. 2018, 44, 8043–8047. [Google Scholar] [CrossRef]
- Jaćimović, J.; Gaál, R.; Magrez, A.; Piatek, J.; Forró, L.; Nakao, S.; Hirose, Y.; Hasegawa, T. Low Temperature Resistivity, Thermoelectricity, and Power Factor of Nb Doped Anatase TiO2. Appl. Phys. Lett. 2013, 102, 10–13. [Google Scholar] [CrossRef]
- Portehault, D.; Maneeratana, V.; Candolfi, C.; Oeschler, N.; Veremchuk, I.; Grin, Y.; Sanchez, C.; Antonietti, M. Facile General Route toward Tunable Magnéli Nanostructures and Their Use as Thermoelectric Metal Oxide/Carbon Nanocomposites. ACS Nano 2011, 5, 9052–9061. [Google Scholar] [CrossRef]
- Pandey, S.J.; Joshi, G.; Wang, S.; Curtarolo, S.; Gaume, R.M. Modeling the Thermoelectric Properties of Ti5O9 Magnéli Phase Ceramics. J. Electron. Mater. 2016, 45, 5526–5532. [Google Scholar] [CrossRef]
- Fan, Y.; Feng, X.; Zhou, W.; Murakami, S.; Kikuchi, K.; Nomura, N.; Wang, L.; Jiang, W.; Kawasaki, A. Preparation of Monophasic Titanium Sub-Oxides of Magnéli Phase with Enhanced Thermoelectric Performance. J. Eur. Ceram. Soc. 2018, 38, 507–513. [Google Scholar] [CrossRef]
- Wang, L.; Li, Z.; Hao, L.; Ohira, S.; Itoi, T.; Yoshida, H.; Lu, Y. Thermoelectric Performance Enhancement of Magnéli Phase TinO2n−1 Compacts by In Situ Reduction of TiO2 with Charcoal Powder via Spark Plasma Sintering. J. Electron. Mater. 2022, 51, 7078–7084. [Google Scholar] [CrossRef]
- Walsh, F.C.; Wills, R.G.A. The Continuing Development of Magnéli Phase Titanium Sub-Oxides and Ebonex® Electrodes. Electrochim. Acta 2010, 55, 6342–6351. [Google Scholar] [CrossRef]
- Malik, H.; Sarkar, S.; Mohanty, S.; Carlson, K. Modelling and Synthesis of Magnéli Phases in Ordered Titanium Oxide Nanotubes with Preserved Morphology. Sci. Rep. 2020, 10, 8050. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, J.; Liu, Y.; Zheng, J.; Lee, W.; Shi, J.; Horlyck, J.; Xie, J.; Tay, Y.Y.; Tan, T.T.; et al. Manipulation of Planar Oxygen Defect Arrangements in Multifunctional Magnèli Titanium Oxide Hybrid Systems: From Energy Conversion to Water Treatment. Energy Environ. Sci. 2020, 13, 5080–5096. [Google Scholar] [CrossRef]
- Harada, S.; Tanaka, K.; Inui, H. Thermoelectric Properties and Crystallographic Shear Structures in Titanium Oxides of the Magǹli Phases. J. Appl. Phys. 2010, 108, 6–11. [Google Scholar] [CrossRef]
- Acha, C.; Monteverde, M.; Núñez-Regueiro, M.; Kuhn, A.; Alario Franco, M.A. Electrical Resistivity of the Ti4O7 Magneli Phase under High Pressure. Eur. Phys. J. B 2003, 34, 421–428. [Google Scholar] [CrossRef]
- Wei, W.; Yuan, T.; Ye, J. Recent Progress in Electrochemical Application of Magnéli Phase Ti4O7-Based Materials: A Review. J. Mater. Sci. 2023, 58, 14911–14944. [Google Scholar] [CrossRef]
- Ying, H.; Tian, H.; Meng, Z.; Han, W. TinO2n-1 Series Compounds-Properties, Preparation Methods and Applications. Prog. Chem. 2015, 27, 361–372. [Google Scholar] [CrossRef]
- Zhu, J.; Zhang, X.; Guo, M.; Li, J.; Hu, J.; Cai, S.; Cai, W.; Zhang, Y.; Sui, J. Restructured Single Parabolic Band Model for Quick Analysis in Thermoelectricity. npj Comput. Mater. 2021, 7, 116. [Google Scholar] [CrossRef]
- Li, X.; Zhu, A.L.; Qu, W.; Wang, H.; Hui, R.; Zhang, L.; Zhang, J. Magneli Phase Ti4O7 Electrode for Oxygen Reduction Reaction and Its Implication for Zinc-Air Rechargeable Batteries. Electrochim. Acta 2010, 55, 5891–5898. [Google Scholar] [CrossRef]
- Watanabe, M. Raman Spectroscopy of Charge-Ordered States in Magnéli Titanium Oxides. Phys. Status Solidi C Curr. Top. Solid State Phys. 2009, 6, 260–263. [Google Scholar] [CrossRef]
- Wang, G.; Liu, Y.; Ye, J. Thermoelectric Properties of Non-Stoichiometric Magnéli Phase TinO2n−1 (n = 4, 5, 8, 9) Monoliths. Sci. Adv. Mater. 2018, 10, 39–45. [Google Scholar] [CrossRef]
- Hao, L.; Kikuchi, Y.; Yoshida, H.; Jin, Y.; Lu, Y. Magnèli Phase TinO2n-1 Bulks Prepared by SPS Followed by Carbon Reduction and Their Thermoelectric Performance. J. Alloys Compd. 2017, 722, 846–851. [Google Scholar] [CrossRef]
- Torres, P.; Rurali, R. Thermal Conductivity of Rutile and Anatase TiO2 from First-Principles. J. Phys. Chem. C 2019, 123, 30851–30855. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).