Segmental Mobility, Interfacial Polymer, Crystallization and Conductivity Study in Polylactides Filled with Hybrid Lignin-CNT Particles
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
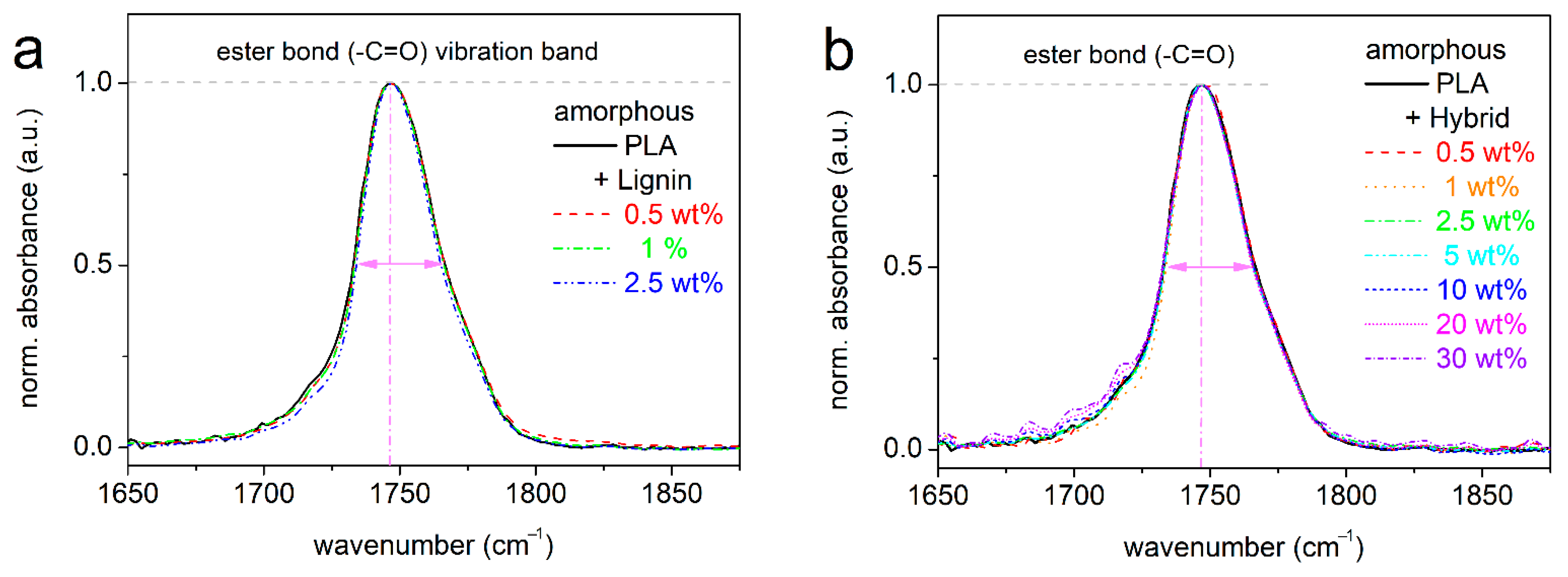
2.2. Infrared Spectroscopy
2.3. Scanning Electron Microscopy (SEM)
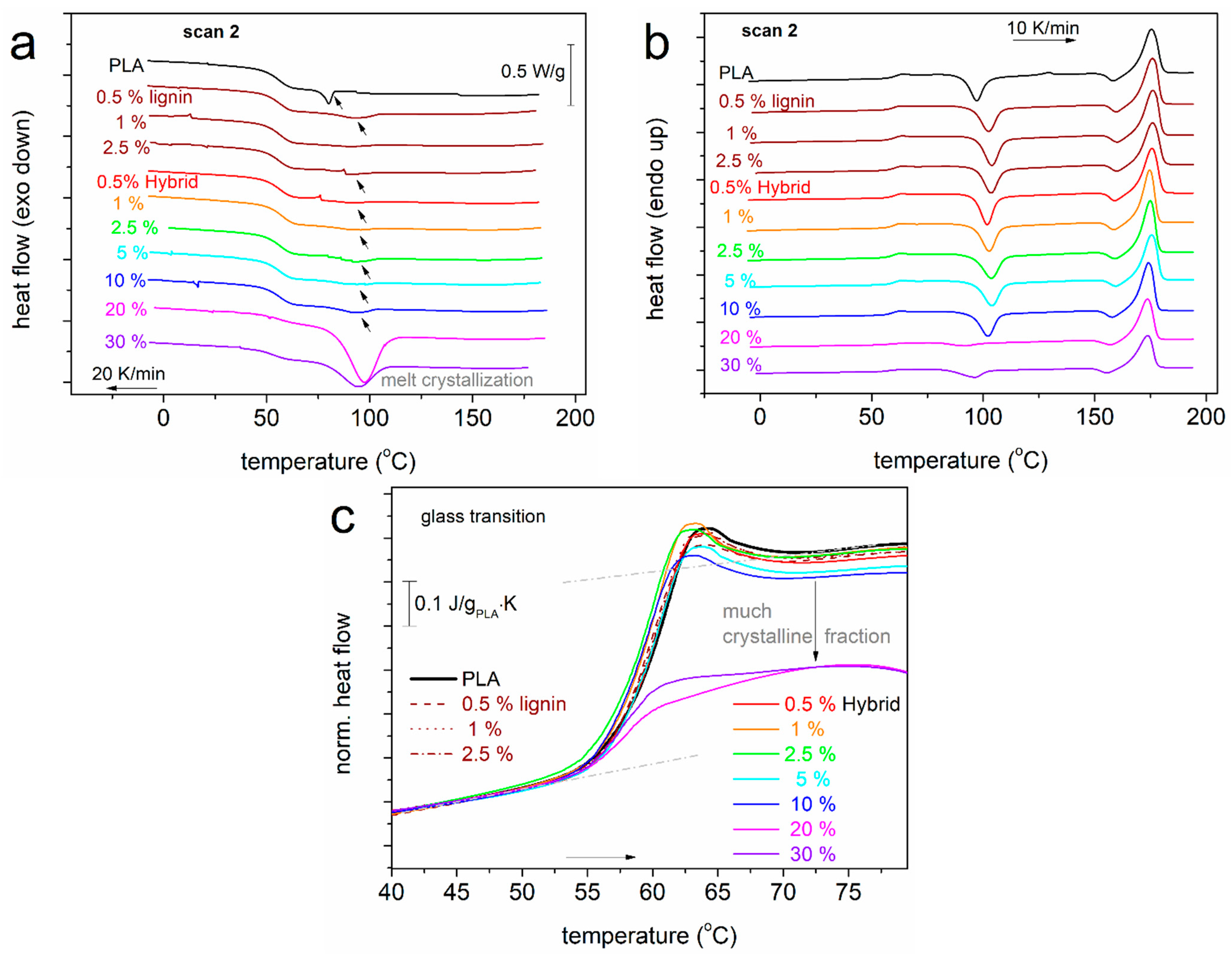
2.4. Differential Scanning Calorimetry (DSC)
2.5. Broadband Dielectric Spectroscopy (BDS)
3. Results and Discussion
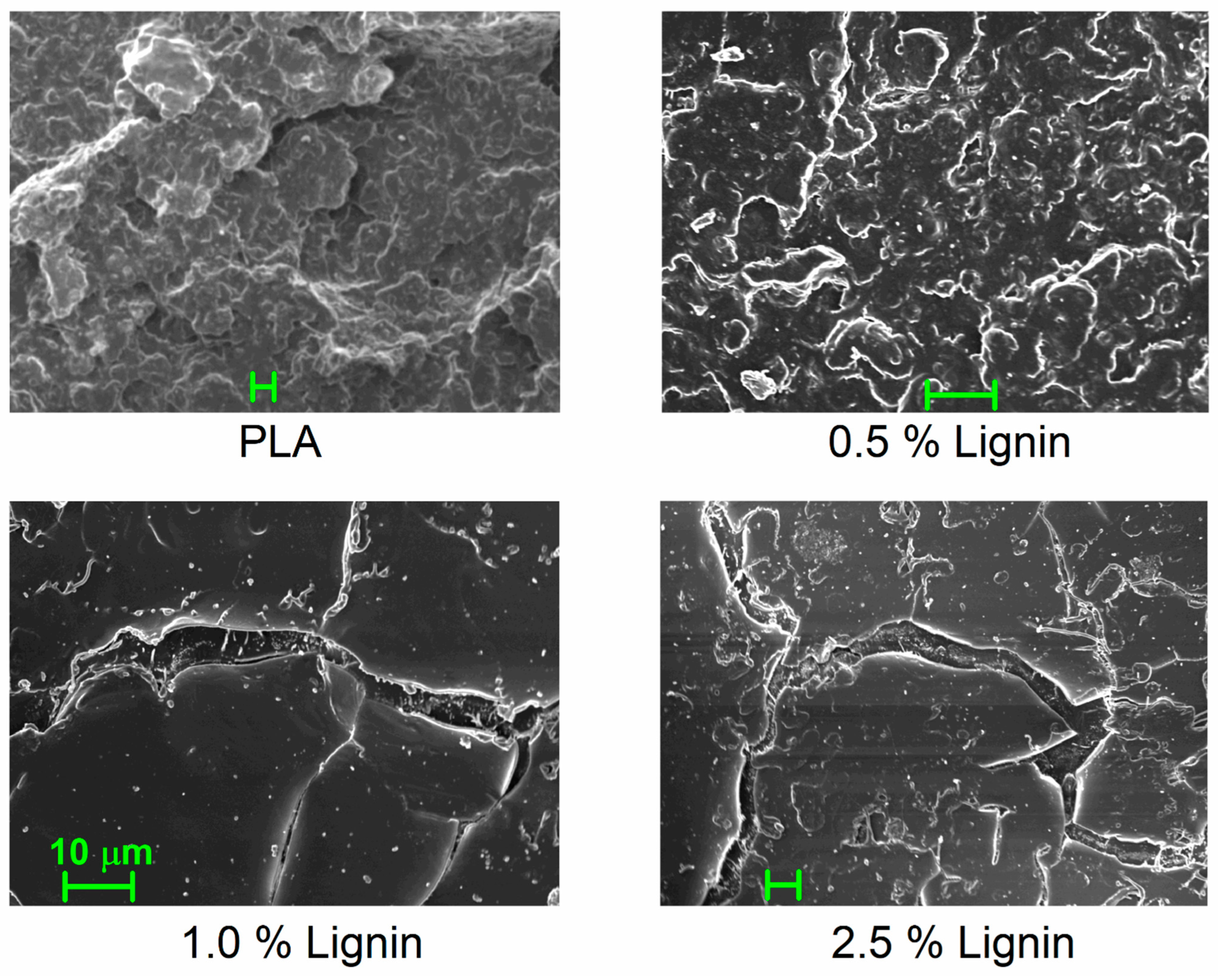
3.1. Structure—Dispersion of Particles
3.2. Glass Transition and Interfacial Adhesion
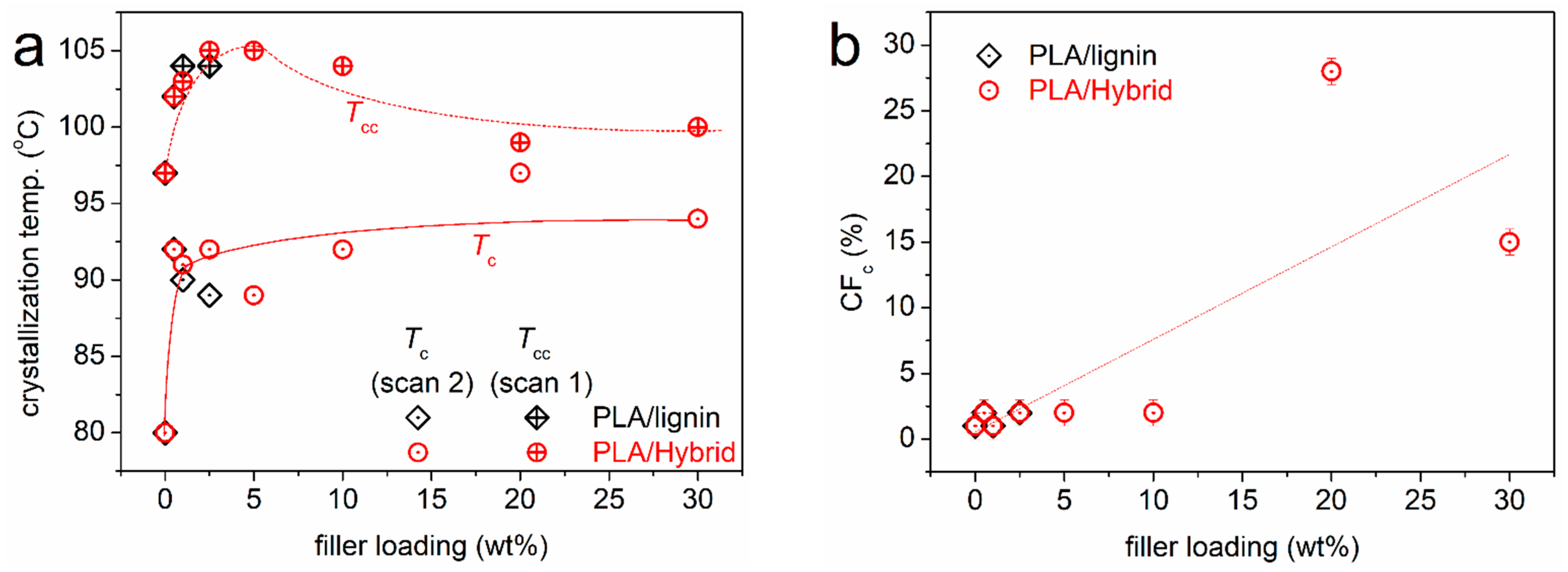
3.3. Effects on the Polymer Crystallization
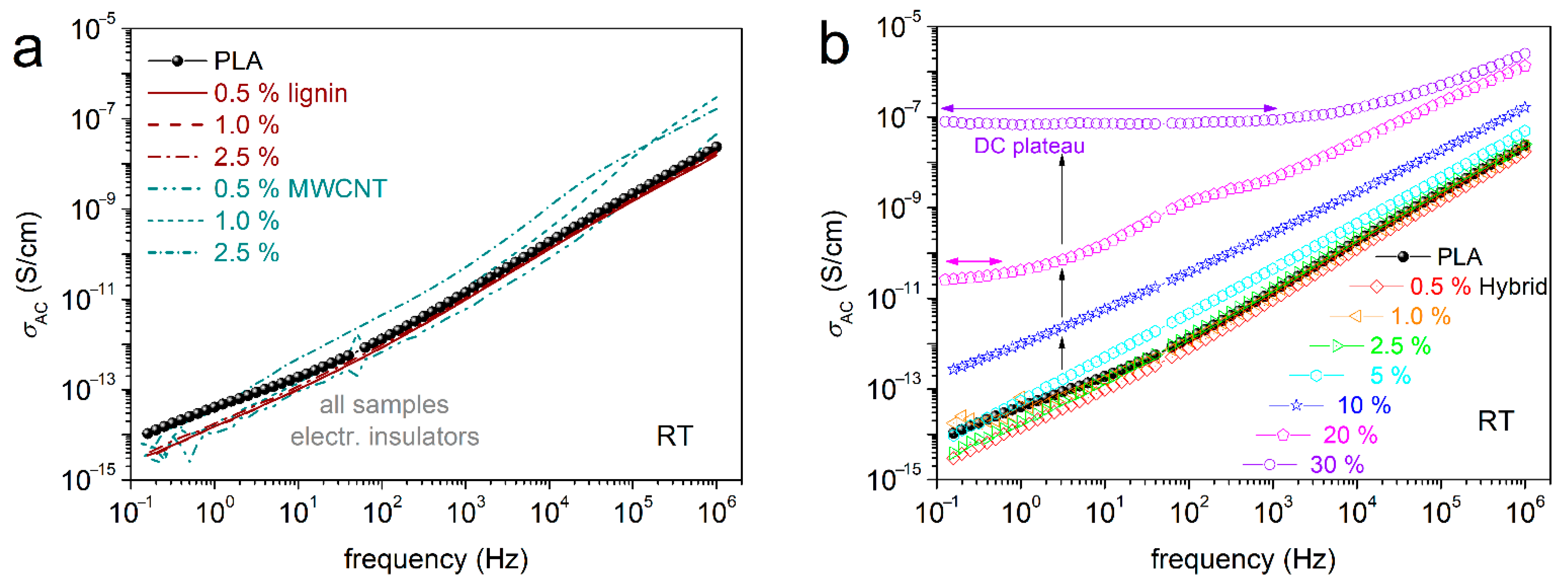
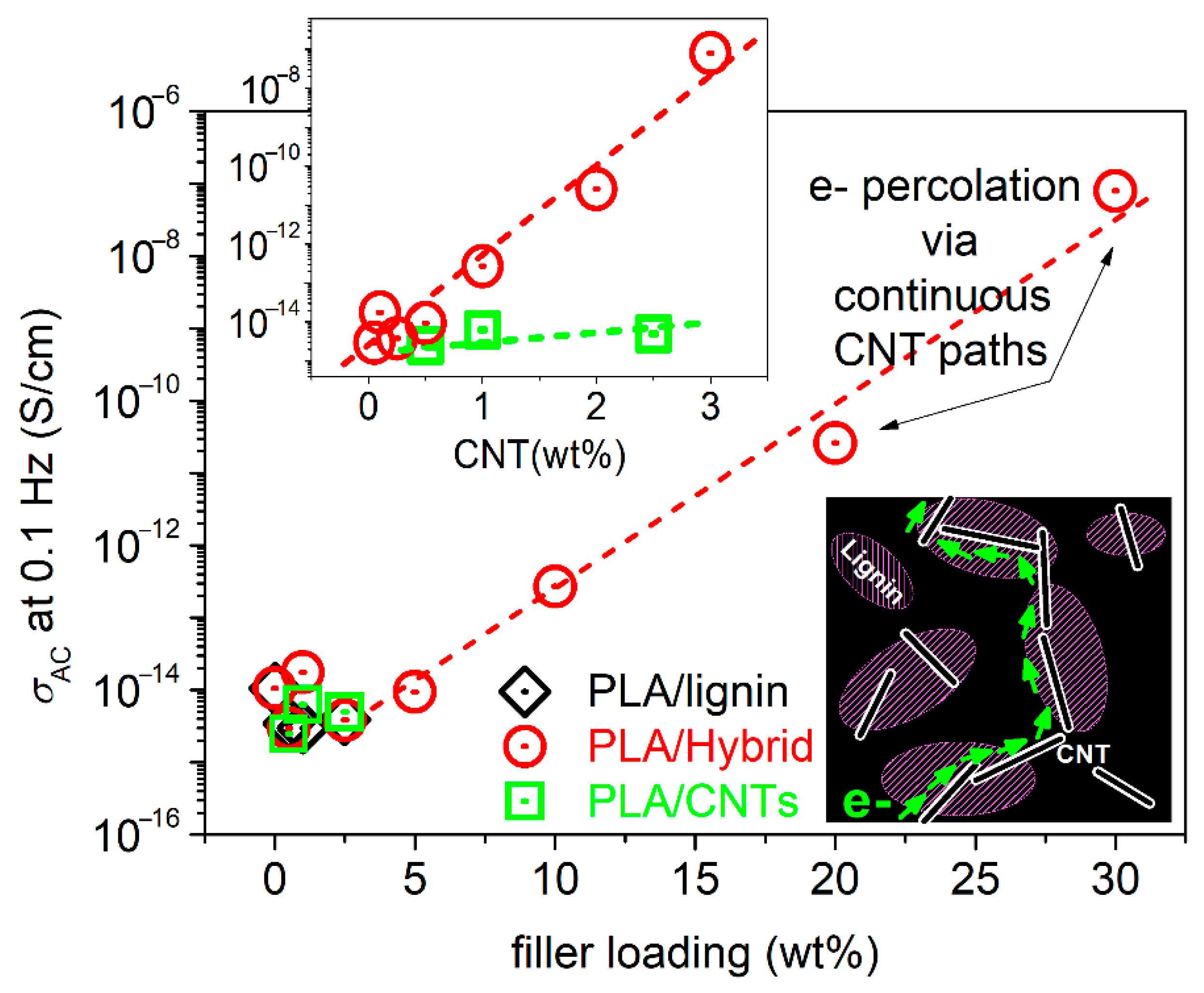
3.4. Electrical Conductivity Aspects
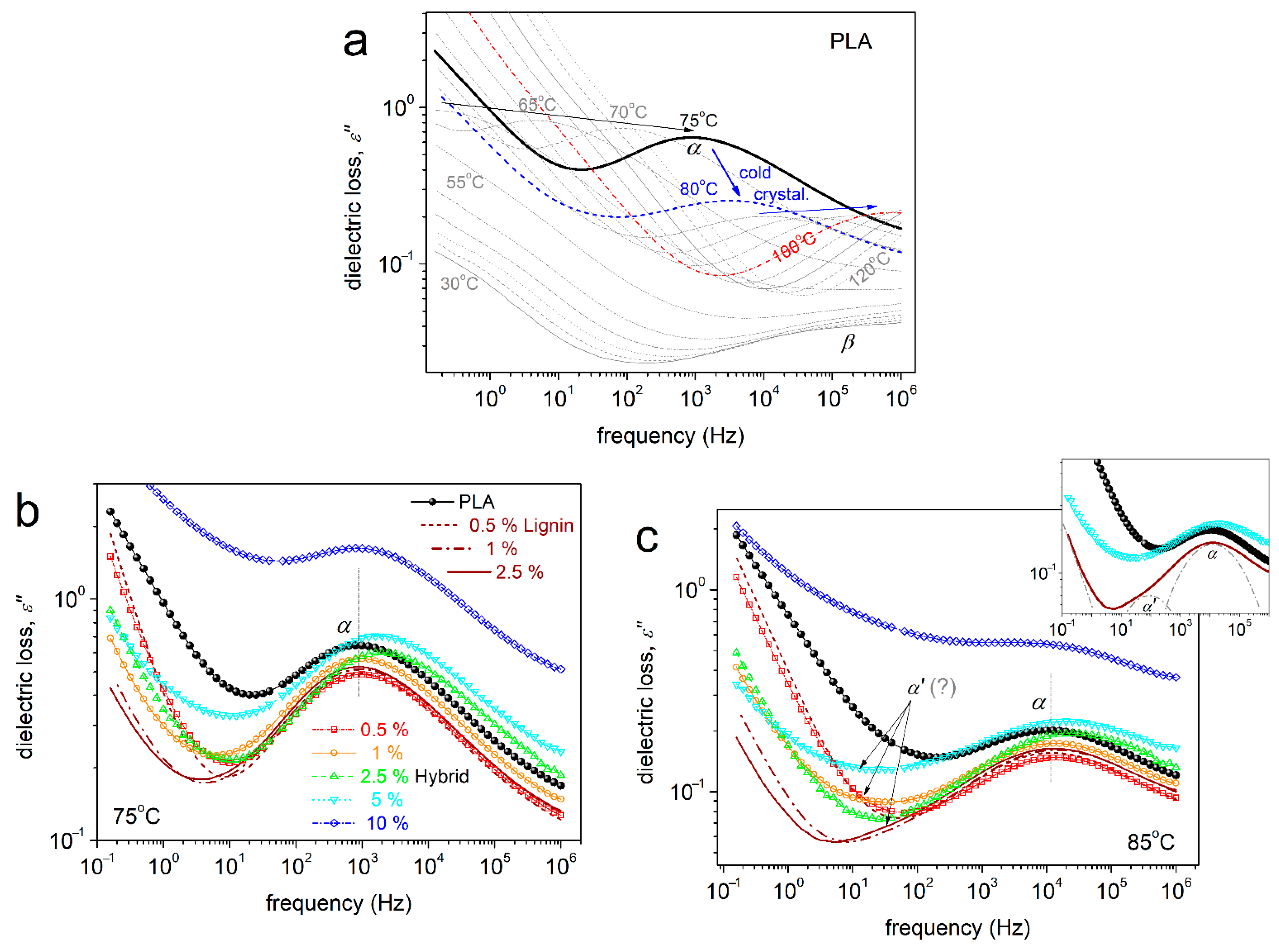
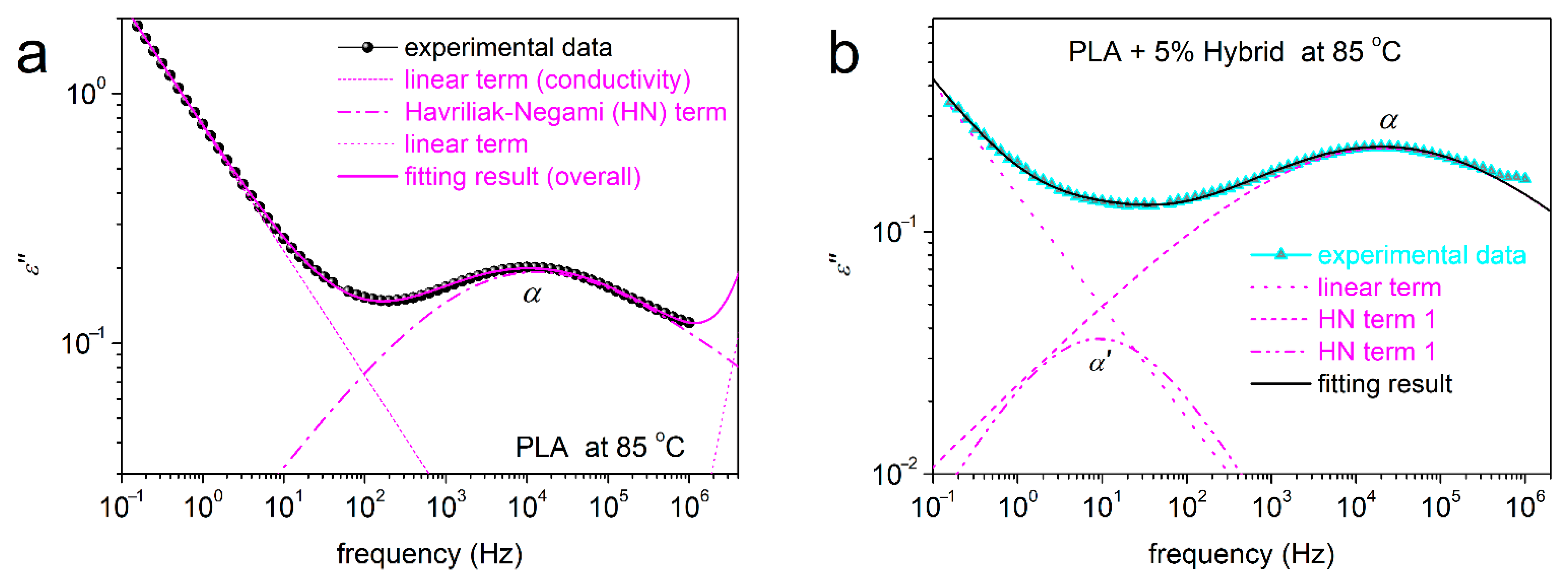
3.5. Segmental Dynamics
4. Conclusions
- PLA and lignin are electrical insulators due to the absence of free electrons. The conducting character (DC conductivity plateau) of the composites was offered by the addition of >2% CNTs. Interestingly, this was found true only in the case of hybrid particles, and not by the addition of neat CNTs in PLA at similar amounts.
- The result suggests an additional effect of lignin in the sense of facilitating the formation of CNT continuous paths (electronic percolation), which is, interestingly, compatible with the recorded microscopic view by SEM.
- For the composites, we obtained proofs for the formation of an interfacial polymer layer around the particles, without the implementation of strong polymer–particles interactions.
- A mild drop in the Tg of PLA (60 °C), by 1–2 K, was recorded in the presence of the fillers, suggesting the formation of, in general, softer composites, compared with neat PLA.
- The latter is accompanied by the almost unchanged Tm of PLA, which remains relatively low (174–176 °C).
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Armentano, I.; Bitinis, N.; Fortunati, E.; Mattioli, S.; Rescignano, N.; Verdejo, R.; Lopez-Manchado, M.A.; Kenny, J.M. Multifunctional nanostructured PLA materials for packaging and tissue engineering. Prog. Polym. Sci. 2013, 38, 1720–1747. [Google Scholar] [CrossRef]
- Auras, R.; Harte, B.; Selke, S. An overview of polylactides as packaging materials. Macrom. Biosci. 2004, 4, 835–864. [Google Scholar] [CrossRef]
- Naser, A.Z.; Deiab, I.; Darras, B.M. Poly(lactic acid) (PLA) and polyhydroxyalkanoates (PHAs), green alternatives to petroleum-based plastics: A review. RSC Adv. 2021, 11, 17151–17196. [Google Scholar] [CrossRef]
- Chanda, M.; Roy, S.K. Industrial Polymers, Specialty Polymers, and Their Applications; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Rowan, S.J. 100th Anniversary of macromolecular science viewpoints. ACS Macro Lett. 2021, 10, 466–468. [Google Scholar] [CrossRef] [PubMed]
- Sheldon, R.A.; Norton, M. Green chemistry and the plastic pollution challenge: Towards a circular economy. Green Chem. 2020, 22, 6310–6322. [Google Scholar] [CrossRef]
- Bikiaris, N.D.; Koumentakou, I.; Samiotaki, C.; Meimaroglou, D.; Varytimidou, D.; Karatza, A.; Kalantzis, Z.; Roussou, M.; Bikiaris, R.D.; Papageorgiou, G.Z. Recent Advances in the Investigation of Poly(lactic acid) (PLA) Nanocomposites: Incorporation of Various Nanofillers and their Properties and Applications. Polymers 2023, 15, 1196. [Google Scholar] [CrossRef]
- Garlotta, D. A literature review of poly(lactic acid). J. Polym. Environ. 2001, 9, 63–84. [Google Scholar] [CrossRef]
- Saini, P.; Arora, M.; Kumar, M.N.V.R. Poly(lactic acid) blends in biomedical applications. Adv. Drug Deliv. Rev. 2016, 107, 47–59. [Google Scholar] [CrossRef]
- Balla, E.; Daniilidis, V.; Karlioti, G.; Kalamas, T.; Stefanidou, M.; Bikiaris, N.D.; Vlachopoulos, A.; Koumentakou, I.; Bikiaris, D.N. Poly(lactic acid) a versatile biobased polymer of next decades with multifunctional properties. From monomer synthesis, polymerization techniques and molecular weight increase to PLA applications. Polymers 2021, 13, 1822. [Google Scholar] [CrossRef]
- Ahmed, J.; Varshney, S.K. Polylactides-chemistry, properties and green packaging technology: A review. Int. J. Food. Prop. 2011, 14, 37–58. [Google Scholar] [CrossRef]
- Lafraya, A.; Prieto, C.; Pardo-Figuerez, M.; Chiva, A.; Lagaron, J.M. Super-repellent paper coated with electrospun biopolymers and electrosprayed silica of interest in food packaging applications. Nanomaterials 2021, 11, 3354. [Google Scholar] [CrossRef] [PubMed]
- Ngo, T.D.; Kashani, A.; Imbalzano, G.; Nquyen, K.T.Q.; Hui, D. Additive manufacturing (3D printing): A review of materials, methods, applications and challenges. Compos. Part B Eng. 2018, 143, 172–196. [Google Scholar] [CrossRef]
- Constanzo, A.; Spotorno, R.; Candal, M.V.; Fernández, M.M.; Müller, A.J.; Graham, R.S.; Cavallo, D.; McIlroy, C. Residual alignment and its effect on weld strength in material-extrusion 3D-printing of polylactic acid. Addit. Manuf. 2020, 36, 101415. [Google Scholar]
- Dominguez-Robles, J.; Martin, N.K.; Fong, M.L.; Stewart, S.A.; Irwin, N.J.; Rial-Hermida, M.I.; Donnelly, R.F.; Larrañeta, E. Antioxidant PLA composites containing lignin for 3D printing applications: A potential material for healthcare applications. Pharmaceutics 2019, 11, 165. [Google Scholar] [CrossRef]
- Wang, B.; Wen, T.; Zhang, X.; Tercjak, A.; Dong, X.; Müller, A.J.; Wang, D.; Cavallo, D. Nucleation of poly(lactide) on the surface of different fibers. Macromolecules 2019, 52, 6274–6284. [Google Scholar] [CrossRef]
- Casalini, T.; Rossi, F.; Castrovinci, A.; Perale, G. A perspective on polylactic acid-based polymers use for nanoparticles synthesis and applications. Front. Bioeng. Biotechnol. 2019, 7, 259. [Google Scholar] [CrossRef] [PubMed]
- Sha, L.; Chen, Z.; Chen, Z.; Zhang, A.; Yang, Z. Polylactic acid based nanocomposites: Promising safe and biodegradable materials in biomedical field. Int. J. Polym. Sci. 2016, 2016, 6869154. [Google Scholar] [CrossRef]
- Saeidlou, S.; Huneault, M.A.; Li, H.; Park, C.B. Poly(lactic acid) crystallization. Prog. Polym. Sci. 2012, 37, 1657–1667. [Google Scholar] [CrossRef]
- Zhang, R.; Du, F.; Jariyavidyanont, K.; Zhuravlev, E.; Schick, C.; Androsch, R. Glass transition temperature of poly(d,l-lactic acid) of different molar mass. Thermochim. Acta 2022, 718, 179387. [Google Scholar] [CrossRef]
- Klonos, P.A.; Bikiaris, N.D.; Barmpalexis, P.; Kyritsis, A. Segmental mobility in linear polylactides of various molecular weights. Polymer 2024, 305, 127177. [Google Scholar] [CrossRef]
- Klonos, P.A.; Chronaki, K.; Vouyiouka, S.; Kyritsis, A. Effects of high crystallinity on the molecular mobility in poly(lactic acid)-based microcapsules. ACS Appl. Polym. Mat. 2024, 6, 1573–1583. [Google Scholar] [CrossRef]
- Zhou, T.; Guo, Y.T.; Yang, C.; Meng, X.B.; Du, F.S.; Li, Z.C. High-Tg PLA copolymers via base-catalyzed transesterification of PLA with 2,5,7-trioxabicyclo[2.2.2]octan-6-one. Polymer Chem. 2024, 15, 156–165. [Google Scholar] [CrossRef]
- Klonos, P.A.; Bikiaris, N.D.; Zamboulis, A.; Valera, M.A.; Mangas, A.; Kyritsis, A.; Terzopoulou, Z. Segmental mobility in sustainable copolymers based on poly(lactic acid) blocks built onto poly(butylene succinate) in situ. Soft Matter 2023, 19, 7846–7858. [Google Scholar] [CrossRef] [PubMed]
- Androsch, R.; Zhang, R.; Schick, C. Melt-recrystallization of poly (l-lactic acid) initially containing α′-crystals. Polymer 2019, 176, 227–235. [Google Scholar] [CrossRef]
- Toda, A.; Androsch, R.; Schick, C. Insights into polymer crystallization and melting from fast chip calorimetry. Polymer 2016, 91, 239–263. [Google Scholar] [CrossRef]
- Rahmanifard, M.; Khademi, S.M.H.; Asheghi-Oskooee, R.; Farizeh, T.; Hemmati, F. Reactive processing-microstructure-mechanical performance correlations in biodegradable poly(lactic acid)/expanded graphite nanocomposites. RSC Adv. 2024, 14, 794–807. [Google Scholar] [CrossRef]
- Klonos, P.; Terzopoulou, Z.; Koutsoumpis, S.; Zidropoulos, S.; Kripotou, S.; Papageorgiou, G.Z.; Bikiaris, D.; Kyritsis, A.; Pissis, P. Rigid amorphous fraction and segmental dynamics in nanocomposites based on poly(L-lactic acid) and nano-inclusions of 1-3D geometry studied by thermal and dielectric techniques. Eur. Polym. J. 2016, 82, 16–34. [Google Scholar] [CrossRef]
- Georgiopoulos, P.; Kontou, E.; Meristoudi, A.; Pispas, S.; Chatzinikolaidou, M. Τhe effect of silica nanoparticles on the thermomechanical properties and degradation behavior of polylactic acid. J. Biomat. Appl. 2014, 29, 662–674. [Google Scholar] [CrossRef]
- Lin, J.; Shenogin, S.; Nazarenko, S. Oxygen solubility and specific volume of rigid amorphous fraction in semicrystalline poly(ethylene terephthalate). Polymer 2002, 43, 4733–4743. [Google Scholar] [CrossRef]
- Safandowska, M.; Makarewicz, C.; Rozanski, A.; Idczak, R. Barrier properties of semicrystalline polylactide: The role of the density of the amorphous regions. Macromolecules 2022, 55, 10077–10089. [Google Scholar] [CrossRef]
- Klonos, P.A.; Peoglos, V.; Bikiaris, D.N.; Kyritsis, A. Rigid amorphous fraction and thermal diffusivity in nanocomposites based on poly(L-lactic acid) filled with carbon nanotubes and graphene oxide. J. Phys. Chem. C 2020, 123, 5469–5479. [Google Scholar] [CrossRef]
- Klonos, P.A.; Bikiaris, R.D.; Terzopoulou, Z.; Mouchlianiti, K.; Tsachouridis, K.; Anastasiou, A.D.; Kyritsis, A.; Kyzas, G.Z. Structure-properties relationships in new polymer nanocomposites based on the renewable poly(butylene succinate) filled with low amounts of nanoparticles of 1-3D geometries. Polymer 2024, 296, 126841. [Google Scholar] [CrossRef]
- Ainali, N.M.; Kalaronis, D.; Evgenidou, E.; Kyzas, G.Z.; Bobori, D.C.; Kaloyianni, M.; Yang, X.; Bikiaris, D.N.; Lambropoulou, D.A. Do poly(lactic acid) microplastics instigate a threat? A perception for their dynamic towards environmental pollution and toxicity. Sci. Tot. Environ. 2022, 832, 155014. [Google Scholar] [CrossRef]
- Naddeo, M.; Viscusi, G.; Gorrasi, G.; Pappalardo, D. Degradable elastomers: Is there a future in tyre compound formulation? Molecules 2021, 26, 4454. [Google Scholar] [CrossRef]
- Stauffer, D.; Aharony, A. Introduction to Percolation Theory; Taylor and Francis: London, UK, 1985. [Google Scholar]
- Logakis, E.; Pollatos, E.; Pandis, C.; Peoglos, V.; Zuburtikudis, I.; Delidis, C.G.; Vatalis, A.; Gjoka, M.; Syskakis, E.; Viras, K. Structure-property relationships in isotactic polypropylene/multi-walled carbon nanotubes nanocomposites. Compos. Sci. Technol. 2010, 70, 328–335. [Google Scholar] [CrossRef]
- Sandler, J.K.W.; Kirk, J.E.; Kinloch, I.A.; Shaffer, M.S.P.; Windle, A.H. Ultra-low electrical percolation threshold in carbon-nanotube-epoxy composites. Polymer 2003, 44, 5893–5899. [Google Scholar] [CrossRef]
- Sam-Daliri, O.; Faller, L.M.; Farahani, M.; Roshanghias, A.; Araee, A.; Baniassadi, M.; Oberlercher, H.; Zangl, H. Impedance analysis for condition monitoring of single lap CNT-epoxy adhesive joint. Int. J. Adhes. Adhes. 2019, 88, 59–65. [Google Scholar] [CrossRef]
- Zhang, H.; Bilotti, E.; Peijs, T. The use of carbon nanotubes for damage sensing and structural health monitoring in laminated composites: A review. Nanocomposites 2015, 1, 167–184. [Google Scholar] [CrossRef]
- Sam-Daliri, O.; Faller, L.M.; Farahani, M.; Zangl, H. Structural health monitoring of adhesive joints under pure mode I loading using the electrical impedance measurement. Eng. Fract. Mech. 2021, 245, 107585. [Google Scholar] [CrossRef]
- Bie, Z.; Liu, X.; Deng, Y.; Shi, X.; He, X. Study on crack resistance mechanism of helical carbon nanotubes in nanocomposites. Nanomaterials 2025, 15, 119. [Google Scholar] [CrossRef]
- Meegan, J. Some of the challenges faced by the Composites Industry in its bid to become more sustainable. RSC Sustain. 2023, 1, 1737–1742. [Google Scholar] [CrossRef]
- Terzopoulou, Z.; Bikiaris, D.N. Biobased plastics for the transition to a circular economy. Mater. Lett. 2024, 362, 136174. [Google Scholar] [CrossRef]
- Sternberg, J.; Sequerth, O.; Pilla, S. Green chemistry design in polymers derived from lignin: Review and perspective. Prog. Polym. Sci. 2021, 113, 101344. [Google Scholar] [CrossRef]
- Mohanty, A.K.; Wu, F.; Micheva, R.; Hakkarainen, M.; Raquez, J.-M.; Mielewski, D.H.; Narayan, R.; Netravali, A.N.; Misra, M. Sustainable polymers. Nat. Rev. Methods Primers 2022, 2, 46. [Google Scholar] [CrossRef]
- Ma, C.; Kim, T.H.; Liu, K.; Ma, M.G.; Choi, S.E.; Si, C. Multifunctional lignin-based composite materials for emerging applications. Front. Bioeng. Biotechnol. 2021, 9, 708976. [Google Scholar] [CrossRef]
- Gordobil, O.; Delucis, R.; Egüés, I.; Labidi, J. Kraft lignin as filler in PLA to improve ductility and thermal properties. Ind. Crops Prod. 2015, 72, 46–53. [Google Scholar] [CrossRef]
- Zhang, Y.; Naebe, M. Lignin: A review on structure, properties, and applications as a light-colored UV absorber. ACS Sustain. Chem. Eng. 2021, 9, 1427–1442. [Google Scholar] [CrossRef]
- Li, J.; Liu, W.; Qiu, X.; Zhao, X.; Chen, Z.; Yan, M.; Fang, Z.; Li, Z.; Tu, Z.; Huang, J. Lignin: A sustainable photothermal block for smart elastomers. Green Chem. 2022, 24, 823–836. [Google Scholar] [CrossRef]
- Domínguez-Robles, J.; Larrañeta, E.; Fong, M.L.; Martin, N.K.; Irwin, N.J.; Mutjé, P.; Tarrés, Q.; Delgado-Aguilar, M. Lignin/poly(butylene succinate) composites with antioxidant and antibacterial properties for potential biomedical applications. Int. J. Biol. Macrom. 2020, 145, 92–99. [Google Scholar] [CrossRef]
- Ullah, I.; Chen, Z.; Xie, Y.; Khan, S.S.; Singh, S.; Yu, C.; Cheng, G. Recent advances in biological activities of lignin and emerging biomedical applications: A short review. Int. J. Biol. Macrom. 2022, 208, 819–832. [Google Scholar] [CrossRef]
- Domenek, S.; Louaifi, A.; Guinault, A.; Baumberger, S. Potential of lignins as antioxidant additive in active biodegradable packaging materials. J. Polym. Environ. 2013, 21, 692–701. [Google Scholar] [CrossRef]
- Makri, S.P.; Xanthopoulou, E.; Valera, M.Á.; Mangas, A.; Marra, G.; Ruiz, V.; Koltsakidis, S.; Tzetzis, D.; Zoikis Karathanasis, A.; Deligkiozi, I.; et al. Poly(lactic acid) composites with lignin and nanolignin synthesized by in situ reactive processing. Polymers 2023, 15, 2386. [Google Scholar] [CrossRef] [PubMed]
- Shi, K.; Liu, G.; Sun, H.; Weng, Y. Polylactic acid/lignin composites: A review. Polymers 2023, 15, 2807. [Google Scholar] [CrossRef] [PubMed]
- Gordobil, O.; Eques, I.; Llano-Ponte, R.; Labidi, J. Physicochemical properties of PLA lignin blends. Polym. Degrad. Stab. 2014, 108, 330–338. [Google Scholar] [CrossRef]
- Makri, S.P.; Klonos, P.A.; Marra, G.; Zoikis Karathanasis, A.; Deligkiozi, I.; Valera, M.Á.; Mangas, A.; Nikolaidis, N.; Terzopoulou, Z.; Kyritsis, A.; et al. Structure–property relationships in renewable composites of poly(lactic acid) reinforced by low amounts of micro- and nano-kraft-lignin. Soft Matter 2024, 20, 5014–5027. [Google Scholar] [CrossRef]
- Makri, S.; Grigoropoulos, A.; Bikiaris, D.; Geligkiozi, I.; Zoikis-Karathanasis, A. assignee Creative Nano P.C. Ultrasound-AsSisted Process for the Production of Lignin Nanoparticles, p. European Patent Office. EP4471093A1, 4 December 2024. [Google Scholar]
- Kremer, F.; Schönhals, A. (Eds.) Broadband Dielectric Spectroscopy; Springer: New York, NY, USA, 2003. [Google Scholar] [CrossRef]
- Leng, J.; Kang, N.; Wang, D.Y.; Wurm, A.; Schick, C.; Schönhals, A. Crystallization behavior of nanocomposites based on poly(l-lactide) and MgAl layered double hydroxides–Unbiased determination of the rigid amorphous phases due to the crystals and the nanofiller. Polymer 2017, 108, 257–264. [Google Scholar] [CrossRef]
- Righetti, M.C.; Gazzano, M.; Delpouve, N.; Saiter, A. Contribution of the rigid amorphous fraction to physical ageing of semi-crystalline PLLA. Polymer 2017, 125, 241–253. [Google Scholar] [CrossRef]
- De Bortoli, L.S.; de Farias, R.; Mezalira, D.Z.; Schabbach, L.M.; Fredel, M.C. Functionalized carbon nanotubes for 3D-printed PLA-nanocomposites: Effects on thermal and mechanical properties. Mat. Tod. Commun. 2022, 31, 103402. [Google Scholar] [CrossRef]
- Lage-Rivera, S.; Ares-Pernas, A.; Becerra Permuy, J.C.; Gosset, A.; Abad, M.J. Enhancement of 3D printability by FDM and electrical conductivity of PLA/MWCNT filaments using lignin as bio-dispersant. Polymers 2023, 15, 999. [Google Scholar] [CrossRef]
- Sargsyan, A.; Tonoyan, A.; Davtyan, S.; Schick, C. The amount of immobilized polymer in PMMA SiO2 nanocomposites determined from calorimetric data. Eur. Polym. J. 2007, 43, 3113–3127. [Google Scholar] [CrossRef]
- Wurm, A.; Ismail, M.; Kretzschmar, B.; Pospiech, D.; Schick, C. Retarded crystallization in polyamide/layered silicates nanocomposites caused by an immobilized interphase. Macromolecules 2010, 43, 1480–1487. [Google Scholar] [CrossRef]
- Klonos, P.; Kulyk, K.; Borysenko, M.V.; Gun’ko, V.M.; Kyritsis, A.; Pissis, P. Effects of molecular weight below the entanglement threshold on interfacial nanoparticles/polymer dynamics. Macromolecules 2016, 49, 9457–9473. [Google Scholar] [CrossRef]
- Leng, J.; Szymoniak, P.; Kang, N.J.; Wang, D.Y.; Wurm, A.; Schick, C.; Schönhals, A. Influence of interfaces on the crystallization behavior and the rigid amorphous phase of poly(L-lactide)-based nanocomposites with different layered double hydroxides as nanofiller. Polymer 2019, 184, 121929. [Google Scholar] [CrossRef]
- Fragiadakis, D.; Pissis, P.; Bokobza, L. Glass transition and molecular dynamics in poly(dimethylsiloxane)/silica nanocomposites. Polymer 2005, 46, 6001–6008. [Google Scholar] [CrossRef]
- Füllbrandt, M.; Purohit, P.J.; Schönhals, A. Combined FTIR and dielectric investigation of poly(vinyl acetate) adsorbed on silica particles. Macromolecules 2013, 46, 4626–4632. [Google Scholar] [CrossRef]
- Holt, A.P.; Griffin, P.J.; Bocharova, V.; Agapov, A.L.; Imel, A.E.; Dadmun, M.D.; Sangoro, J.R.; Sokolov, A.P. Dynamics at the polymer/nanoparticle interface in poly(2-vinylpyridine)/silica nanocomposites. Macromolecules 2014, 47, 1837–1843. [Google Scholar] [CrossRef]
- Androsch, R.; Di Lorenzo, M.L.; Schick, C.; Wunderlich, B. Mesophases in polyethylene polypropylene, and poly(1-butene). Polymer 2010, 51, 4639–4662. [Google Scholar] [CrossRef]
- Purohit, P.J.; Wang, D.Y.; Wurm, A.; Schick, C.; Schönhals, A. Comparison of thermal and dielectric spectroscopy for nanocomposites based on polypropylene and layered double hydroxide–proof of interfaces. Eur. Polym. J. 2014, 55, 48–56. [Google Scholar] [CrossRef]
- Fragiadakis, D.; Bokobza, L.; Pissis, P. Dynamics near the filler surface in natural rubber-silica nanocomposites. Polymer 2011, 52, 3175–3182. [Google Scholar] [CrossRef]
- Kim, Y.G.; Thérien-Aubin, H. Impact of the solvent quality on the local dynamics of soft and swollen polymer nanoparticles functionalized with polymer chains. Macromolecules 2020, 53, 7561–7569. [Google Scholar] [CrossRef]
- Beigbeder, A.; Linares, M.; Devalckenaere, M.; Degée, P.; Claes, M.; Beljonne, D.; Lazzaroni, R.; Dubois, P. CH-π interactions as the driving force for silicone-based nanocomposites with exceptional properties. Adv. Mater. 2008, 20, 1003–1007. [Google Scholar] [CrossRef]
- Tadiello, L.; D’Arienzo, M.; Di Credico, B.; Hanel, T.; Matejka, L.; Mauri, M.; Morazzoni, F.; Simonutti, R.; Spirkova, M.; Scotti, R. The filler–rubber interface in styrene butadiene nanocomposites with anisotropic silica particles: Morphology and dynamic properties. Soft Matter 2015, 11, 4022–4033. [Google Scholar] [CrossRef]
- Fischer, E.W.; Sterzel, H.J.; Wegner, G. Investigation of the structure of solution grown crystals of lactide copolymers by means of chemical reactions. Kolloid-Z. Z. Polym. 1973, 251, 980–990. [Google Scholar] [CrossRef]
- Logakis, E.; Pissis, P.; Pospiech, D.; Korwitz, A.; Krause, B.; Reuter, U.; Pötschke, P. Low electrical percolation threshold in poly(ethylene terephthalate)/multi-walled carbon nanotube nanocomposites. Eur. Polym. J. 2010, 46, 928–936. [Google Scholar] [CrossRef]
- Qu, F.; Sun, W.; Li, B.; Li, F.; Gao, Y.; Zhao, X.; Zhang, L. Synergistic effect in improving the electrical conductivity in polymer nanocomposites by mixing spherical and rod-shaped fillers. Soft Matter 2020, 16, 10454–10462. [Google Scholar] [CrossRef] [PubMed]
- Ren, J.; Urakawa, O.; Adachi, K. Dielectric study on dynamics and conformations of poly(D,L-lactic acid) in dilute and semi-dilute solutions. Polymer 2003, 44, 847–855. [Google Scholar] [CrossRef]
- Brás, A.R.; Viciosa, M.T.; Wang, Y.; Dionisio, M.; Mano, J.F. Crystallization of poly(L–lactic acid) probed with dielectric relaxation spectroscopy. Macromolecules 2006, 39, 6513–6520. [Google Scholar] [CrossRef]
- Lin, Y.; Liu, L.; Xu, G.; Zhang, D.; Guan, A.; Wu, G. Interfacial interactions and segmental dynamics of poly(vinyl acetate)/silica nanocomposites. J. Phys. Chem. C 2015, 119, 12956–12966. [Google Scholar] [CrossRef]
- Böhmer, R.; Ngai, K.; Angell, C.A.; Plazek, D.J. Nonexponential relaxations in strong and fragile glass formers. J. Chem. Phys. 1993, 99, 4201–4209. [Google Scholar] [CrossRef]
- Adam, G.; Gibbs, J.H. On the temperature dependence of cooperative relaxation properties in glass-forming liquids. J. Chem. Phys. 1965, 43, 139–146. [Google Scholar] [CrossRef]
- Delpouve, N.; Saiter, A.; Dargent, E. Cooperativity length evolution during crystallization of poly(lactic acid). Eur. Polym. J. 2011, 47, 2414–2423. [Google Scholar] [CrossRef]
- Schönhals, A.; Szymoniak, P. (Eds.) Dynamics of Composite Materials; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Madkour, S.; Yin, H.; Füllbrandt, M.; Schönhals, A. Calorimetric evidence for a mobile surface layer in ultrathin polymeric films: Poly(2-vinyl pyridine). Soft Matter 2015, 11, 7942–7958. [Google Scholar] [CrossRef] [PubMed]
- Koutsoumpis, S.; Raftopoulos, K.N.; Oguz, O.; Papadakis, C.M.; Menceloglu, Y.Z.; Pissis, P. Dynamic glass transition of the rigid amorphous fraction in polyurethane-urea/SiO2 nanocomposites. Soft Matter 2017, 13, 4580–4590. [Google Scholar] [CrossRef] [PubMed]
- Monnier, X.; Cangialosi, D. Thermodynamic ultrastability of a polymer glass confined at the micrometer length Scale. Phys. Rev. Lett. 2018, 121, 137801. [Google Scholar] [CrossRef]



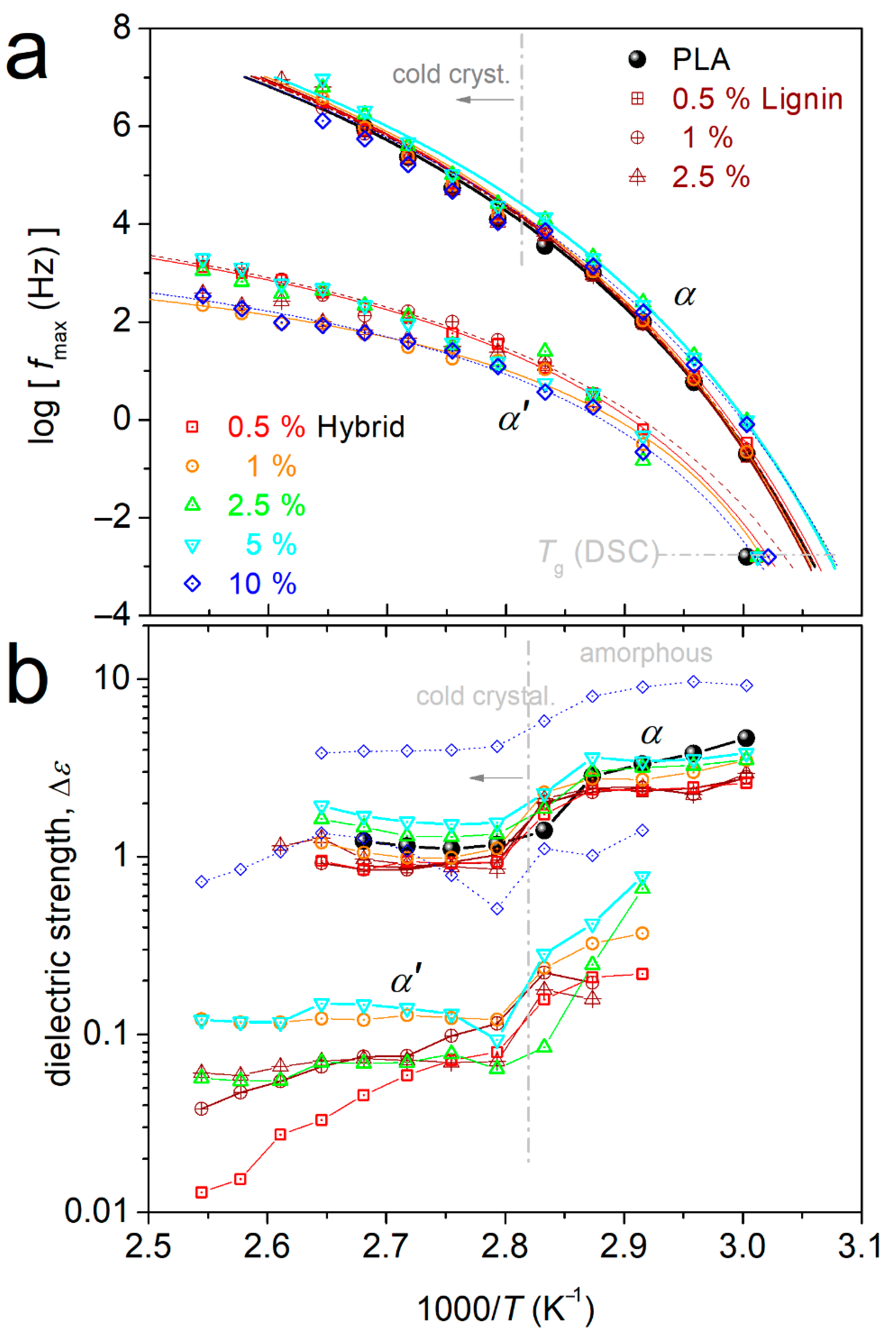

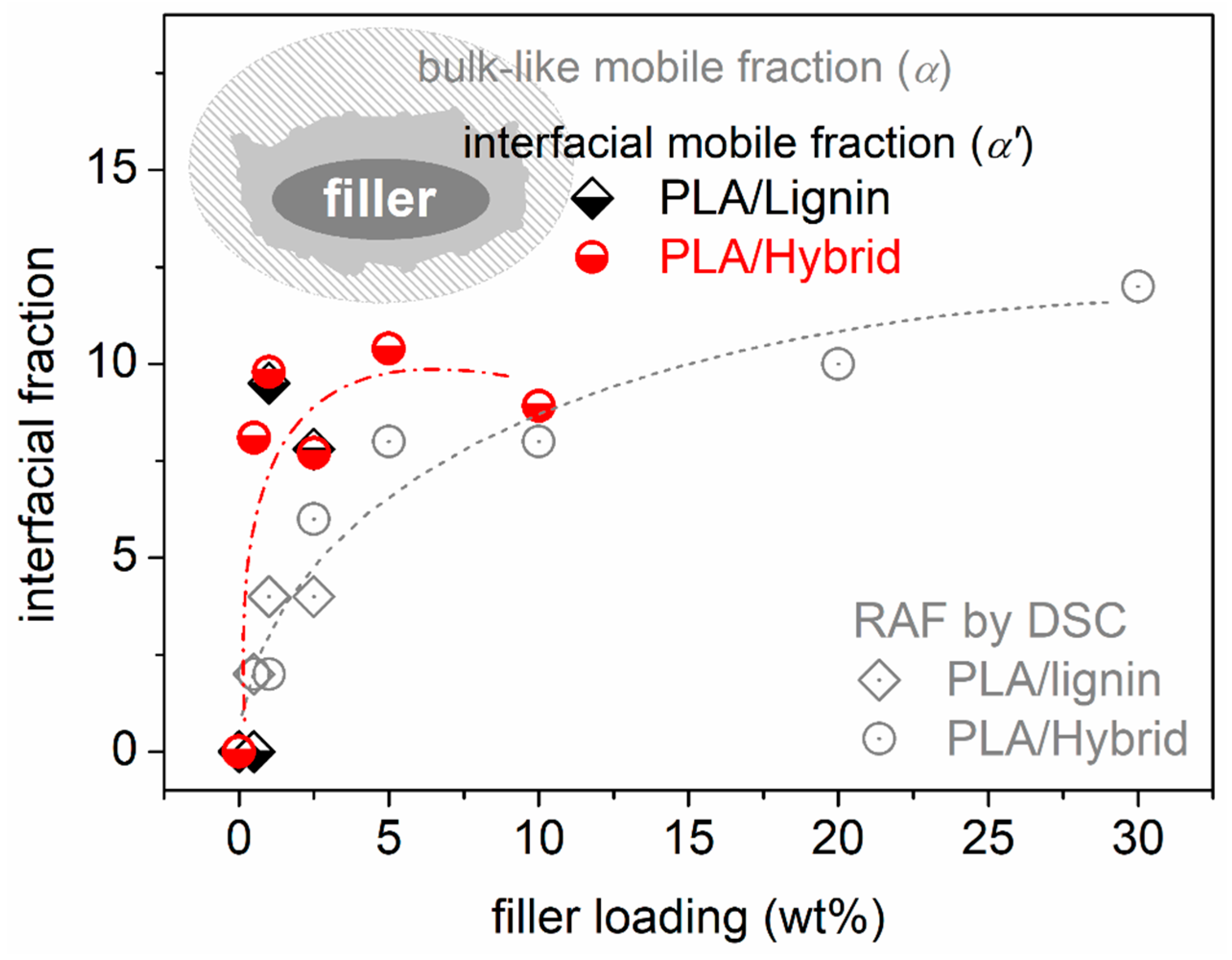
| Sample | Lignin (wt%) | CNT (wt%) | DSC (Fast Cooled, Amorphous) | DSC (Cooled at 20 K/min) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Tg (°C) | Δcp,norm (J/gPLA∙K) | RAF (%) | Tcc1 (°C) | Tc (°C) | ΔHc,norm (J/gPLA) | CFc (%) | Tg (°C) | Tm (°C) | |||
| PLA (neat) | 0 | 0 | 60 | 0.50 | 0 | 97 | 80 | 1.3 | 1 | 60 | 175 |
| PLA + 0.5% lignin | 0.5 | 0 | 59 | 0.49 | 2 | 102 | 92 | 2.3 | 2 | 59 | 176 |
| PLA + 1.0% lignin | 1.0 | 0 | 59 | 0.48 | 4 | 104 | 90 | 1.0 | 1 | 59 | 176 |
| PLA + 2.5% lignin | 2.5 | 0 | 59 | 0.48 | 4 | 104 | 89 | 1.8 | 2 | 59 | 176 |
| PLA + 0.5% hybrid | 0.45 | 0.05 | 59 | 0.49 | 2 | 102 | 92 | 1.5 | 2 | 59 | 176 |
| PLA + 1.0% hybrid | 0.9 | 0.1 | 59 | 0.49 | 2 | 103 | 91 | 1.3 | 1 | 59 | 175 |
| PLA + 2.5% hybrid | 2.25 | 0.25 | 59 | 0.47 | 6 | 105 | 92 | 1.8 | 2 | 58 | 175 |
| PLA + 5.0% hybrid | 4.5 | 0.5 | 59 | 0.46 | 8 | 105 | 89 | 1.4 | 2 | 59 | 175 |
| PLA + 10.0% hybrid | 9 | 1 | 58 | 0.46 | 8 | 104 | 92 | 2.0 | 2 | 61 | 174 |
| PLA + 20.0% hybrid | 18 | 2 | 58 | 0.45 | 10 | 99 | 97 | 26 | 28 | 57 | 174 |
| PLA + 30.0% hybrid | 27 | 3 | 58 | 0.44 | 12 | 100 | 94 | 14 | 15 | 57 | 174 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klonos, P.A.; Ioannidis, R.O.; Pitsavas, A.; Bikiaris, N.D.; Makri, S.P.; Koutsourea, S.; Grigoropoulos, A.; Deligkiozi, I.; Zoikis-Karathanasis, A.; Kyritsis, A.; et al. Segmental Mobility, Interfacial Polymer, Crystallization and Conductivity Study in Polylactides Filled with Hybrid Lignin-CNT Particles. Nanomaterials 2025, 15, 660. https://doi.org/10.3390/nano15090660
Klonos PA, Ioannidis RO, Pitsavas A, Bikiaris ND, Makri SP, Koutsourea S, Grigoropoulos A, Deligkiozi I, Zoikis-Karathanasis A, Kyritsis A, et al. Segmental Mobility, Interfacial Polymer, Crystallization and Conductivity Study in Polylactides Filled with Hybrid Lignin-CNT Particles. Nanomaterials. 2025; 15(9):660. https://doi.org/10.3390/nano15090660
Chicago/Turabian StyleKlonos, Panagiotis A., Rafail O. Ioannidis, Andreas Pitsavas, Nikolaos D. Bikiaris, Sofia P. Makri, Stefania Koutsourea, Alexios Grigoropoulos, Ioanna Deligkiozi, Alexandros Zoikis-Karathanasis, Apostolos Kyritsis, and et al. 2025. "Segmental Mobility, Interfacial Polymer, Crystallization and Conductivity Study in Polylactides Filled with Hybrid Lignin-CNT Particles" Nanomaterials 15, no. 9: 660. https://doi.org/10.3390/nano15090660
APA StyleKlonos, P. A., Ioannidis, R. O., Pitsavas, A., Bikiaris, N. D., Makri, S. P., Koutsourea, S., Grigoropoulos, A., Deligkiozi, I., Zoikis-Karathanasis, A., Kyritsis, A., & Bikiaris, D. N. (2025). Segmental Mobility, Interfacial Polymer, Crystallization and Conductivity Study in Polylactides Filled with Hybrid Lignin-CNT Particles. Nanomaterials, 15(9), 660. https://doi.org/10.3390/nano15090660












