Dynamical Properties of Plasmon Polaritons in Nanorings Driven by Cassini-Ordered Emitters
Abstract
1. Introduction
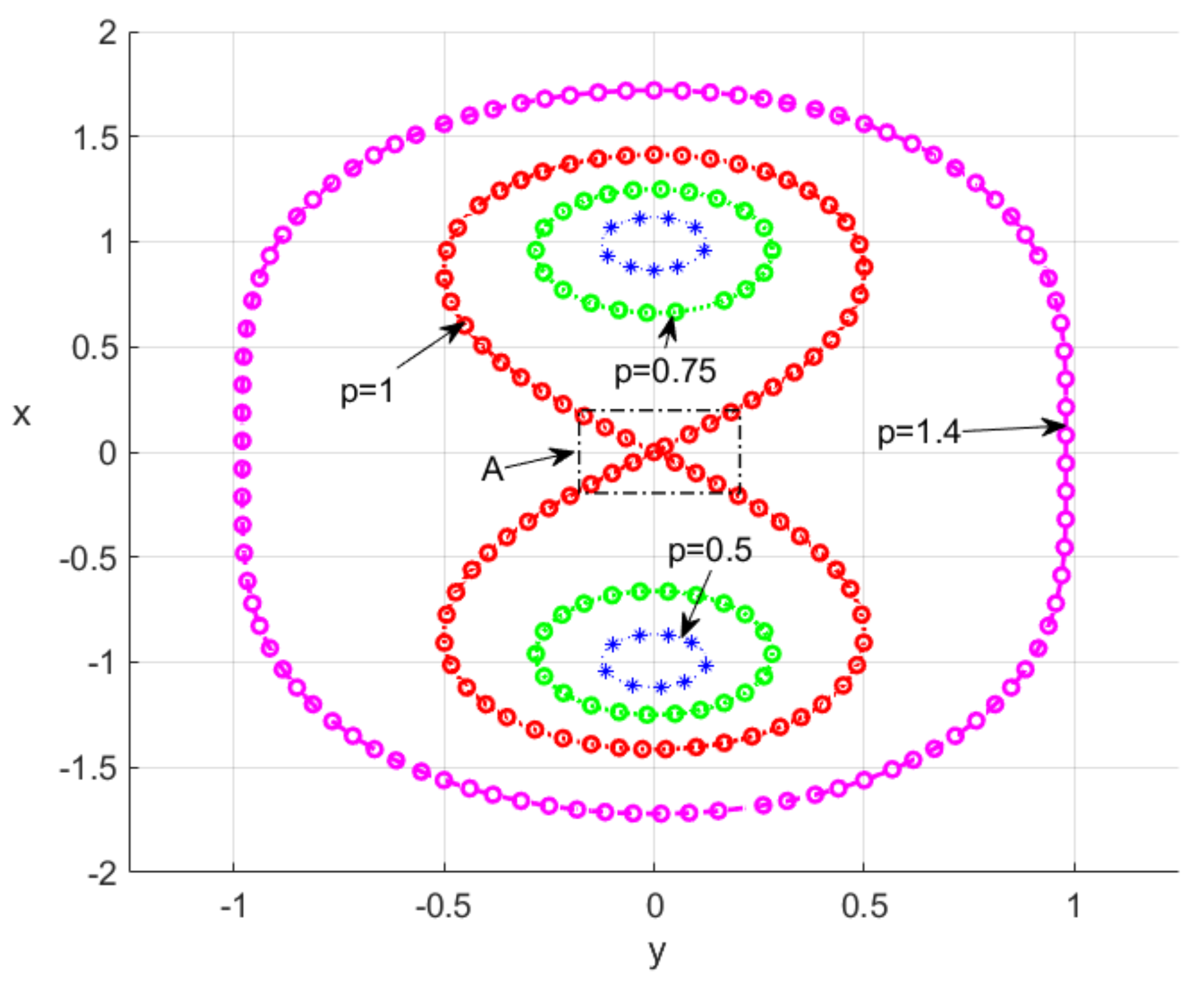
2. Basic Equations
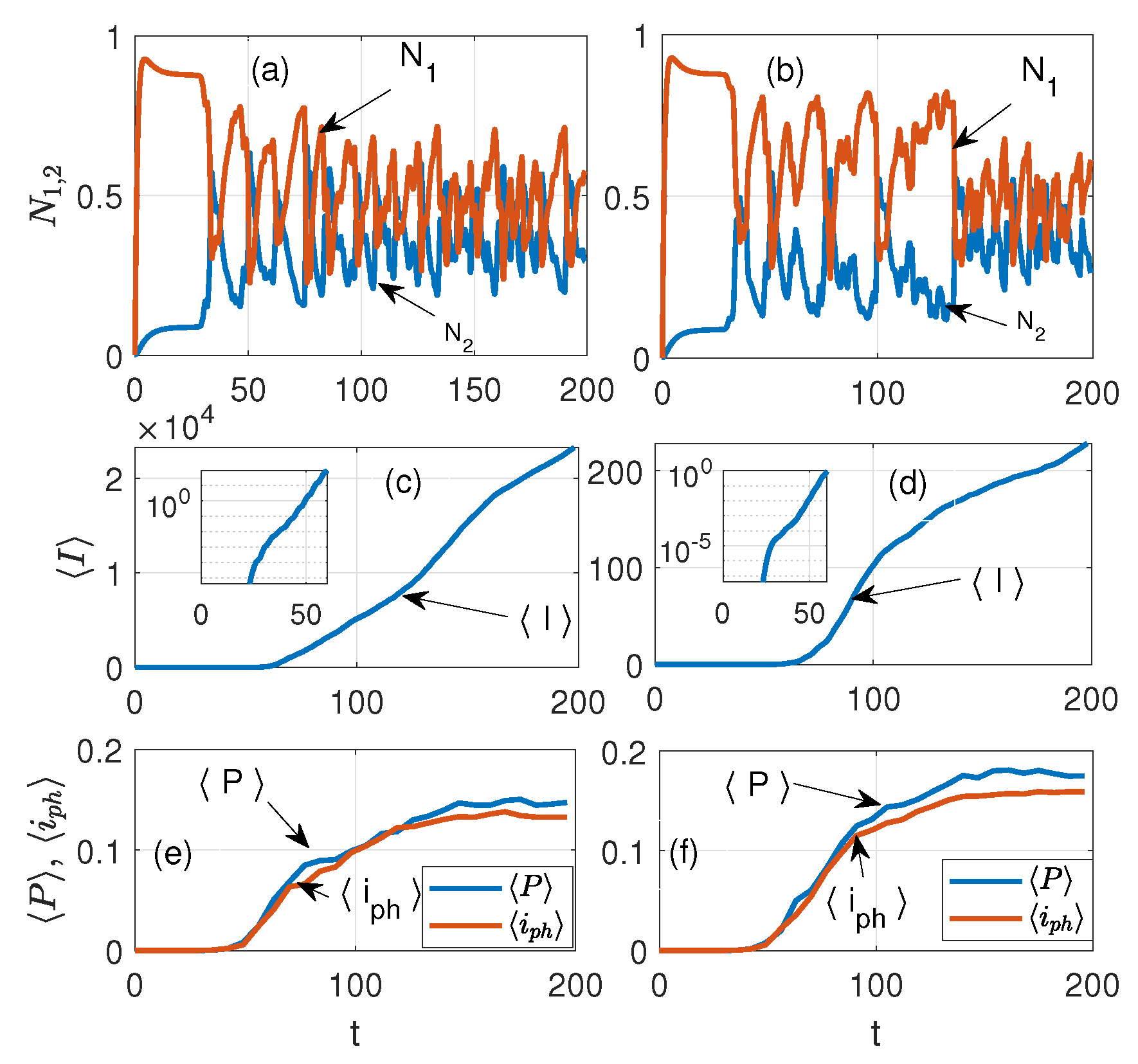
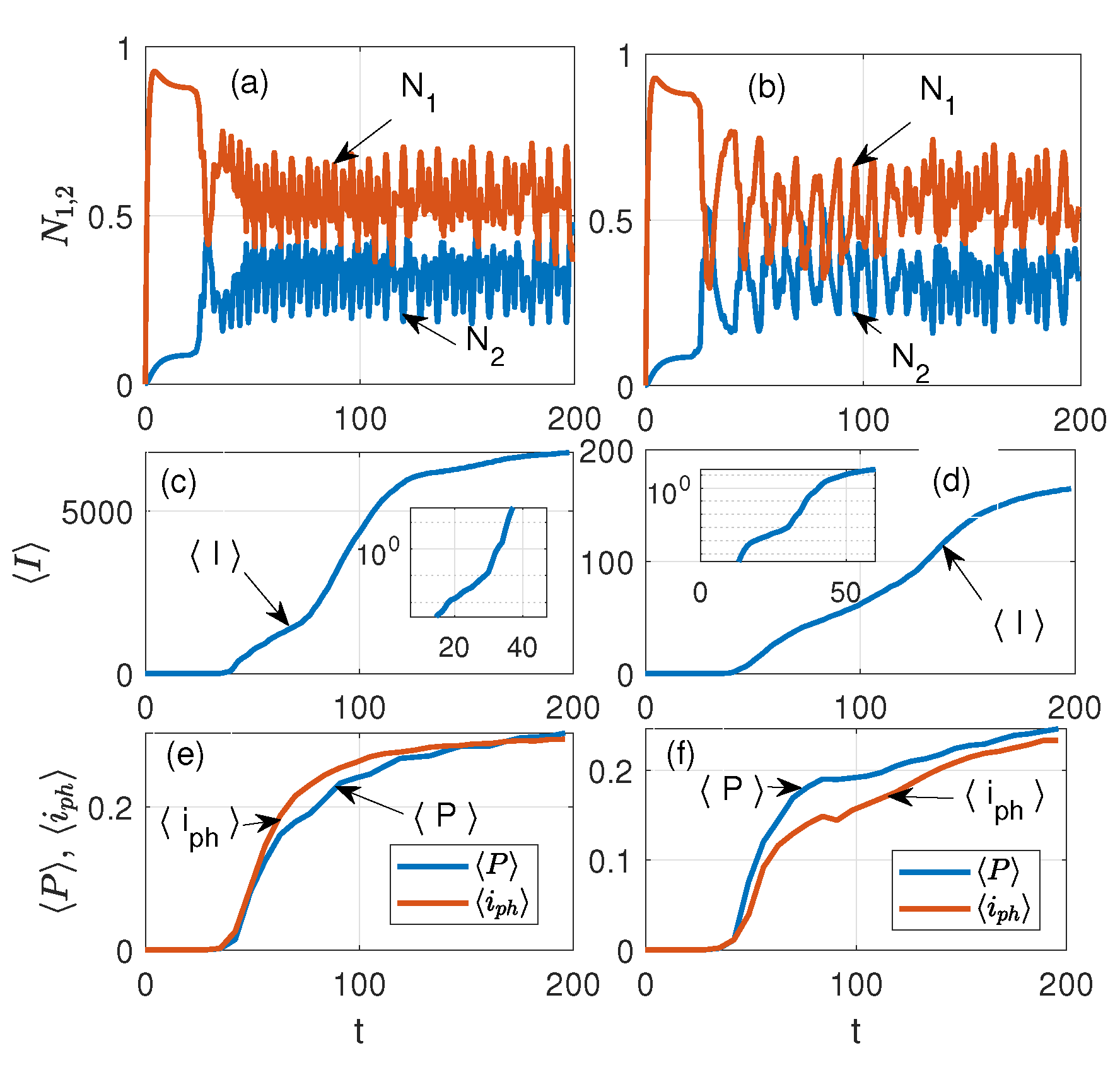
3. Lasing of Nanoemitters in the System with Nanorings
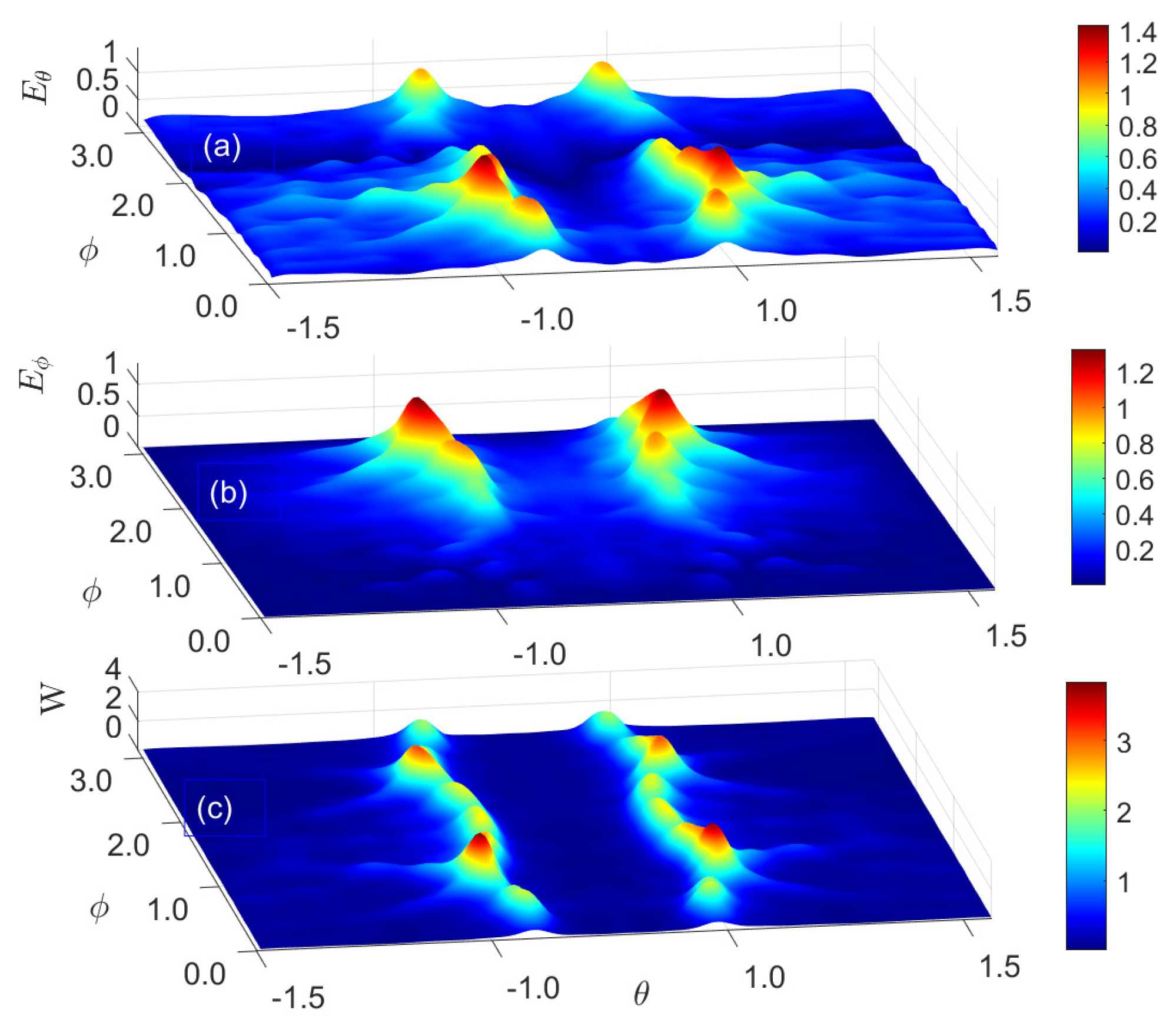
4. Near-Field-to-Far-Field Transformation
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guo, J.; Black, K.; Hu, J.; Singh, M. Study of plasmonics in hybrids made from a quantum emitter and double metallic nanoshell dimer. J. Phys. Condens. Matter 2018, 30, 185301. [Google Scholar] [CrossRef] [PubMed]
- Habisreutinger, S.N.; Blackburn, J.L. Carbon nanotubes in high-performance perovskite photovoltaics and other emerging optoelectronic applications. J. Appl. Phys. 2021, 129, 010903. [Google Scholar] [CrossRef]
- Martinez-Castro, J.; Bolat, R.; Fan, Q.; Werner, S.; Arefi, H.H.; Esat, T.; Sundermeyer, J.; Wagner, C.; Michael Gottfried, J.; Temirov, R.; et al. Disentangling the electronic structure of an adsorbed graphene nanoring by scanning tunneling microscopy. Commun. Mater. 2022, 3, 57. [Google Scholar]
- Hao, F.; Nordlander, P.; Burnett, M.T.; Maier, S.A. Enhanced tunability and linewidth sharpening of plasmon resonances in hybridized metallic ring/disk nanocavities. Phys. Rev. B 2007, 76, 245417. [Google Scholar] [CrossRef]
- Im, H.; Bantz, K.C.; Lee, S.H.; Johnson, T.W.; Haynes, C.L.; Oh, S.H. Self-Assembled Plasmonic Nanoring Cavity Arrays for SERS and LSPR Biosensing. Adv. Mater. 2013, 25, 2678–2685. [Google Scholar] [CrossRef] [PubMed]
- Shen, Z.; Du, M. High-performance refractive index sensing system based on multiple Fano resonances in polarization-insensitive metasurface with nanorings. Opt. Express 2021, 29, 28287–28296. [Google Scholar] [CrossRef] [PubMed]
- Forcherio, G.T.; Blake, P.; DeJarnette, D.; Roper, D.K. Nanoring structure, spacing, and local dielectric sensitivity for plasmonic resonances in Fano resonant square lattices. Opt. Express 2014, 22, 17791–17804. [Google Scholar] [CrossRef]
- Mu, S.; Chen, H.; Shi, C.; Zhang, J.; Yang, B. Au nanoring arrays with tunable morphological features and plasmonic resonances. Nano Res. 2021, 14, 4674–4679. [Google Scholar] [CrossRef]
- Wu, P.C.; Sun, G.; Chen, W.T.; Yang, K.Y.; Huang, Y.W.; Chen, Y.H.; Huang, H.L.; Hsu, W.L.; Chiang, H.P.; Tsai, D.P. Vertical split-ring resonator based nanoplasmonic sensor. Appl. Phys. Lett. 2014, 105, 033105. [Google Scholar] [CrossRef]
- Mirzaei-Ghormish, S.; Shahabadi, M.; Smalley, D.E. Body-of-revolution finite-difference time-domain modeling of hybrid-plasmonic ring resonators. Opt. Express 2022, 30, 36332–36342. [Google Scholar] [CrossRef]
- Wu, P.C.; Hsu, W.L.; Chen, W.T.; Huang, Y.W.; Liao, C.Y.; Liu, A.Q.; Zheludev, N.I.; Sun, G.; Tsai, D.P. Plasmon coupling in vertical split-ring resonator metamolecules. Sci. Rep. 2015, 5, 9726. [Google Scholar]
- Ren, P.; Zheng, A.; Xiao, J.; Pan, X.; Bao, X. Exploring the ring current of carbon nanotubes by first-principles calculations. Chem. Sci. 2015, 6, 902–908. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Amoosoltani, N.; Mehrabi, K.; Zarifkar, A.; Farmani, A.; Yasrebi, N. Double-ring resonator plasmonic refractive index sensor utilizing dual-band unidirectional reflectionless propagation effect. Plasmonics 2021, 16, 1277–1285. [Google Scholar]
- Eatemadi, A.; Daraee, H.; Karimkhanloo, H.; Kouhi, M.; Zarghami, N.; Akbarzadeh, A.; Abasi, M.; Hanifehpour, Y.; Joo, S.W. Carbon nanotubes: Properties, synthesis, purification, and medical applications. Nanoscale Res. Lett. 2014, 9, 393. [Google Scholar] [CrossRef] [PubMed]
- AlAloul, M.; Rasras, M. Plasmon-enhanced graphene photodetector with CMOS-compatible titanium nitride. J. Opt. Soc. Am. B 2021, 38, 602–610. [Google Scholar] [CrossRef]
- Angelis, F.D.; Das, G.; Candeloro, P.; Patrini, M.; Galli, M.; Bek, A.; Lazzarino, M.; Maksymov, I.; Liberale, C.; Andreani, L.C.; et al. Nanoscale chemical mapping using three-dimensional adiabatic compression of surface plasmon polaritons. Nat. Nanotechnol. 2010, 5, 67–72. [Google Scholar] [CrossRef]
- Pitarke, J.M.; Silkin, V.M.; Chulkov, E.V.; Echenique, P.M. Theory of surface plasmons and surface-plasmon. Rep. Prog. Phys. 2007, 70, 1–87. [Google Scholar] [CrossRef]
- Muchuweni, E.; Mombeshora, E.T.; Martincigh, B.S.; Nyamori, V.O. Recent Applications of Carbon Nanotubes in Organic Solar Cells. Front. Chem. 2022, 9, 733552. [Google Scholar] [CrossRef]
- Moore, K.; Wei, W. Applications of carbon nanomaterials in perovskite solar cells for solar energy conversion. Nano Mater. Sci. 2021, 3, 276–290. [Google Scholar] [CrossRef]
- Tian, F.; Sumikura, H.; Kuramochi, E.; Takiguchi, M.; Ono, M.; Shinya, A.; Notomi, M. All-optical dynamic modulation of spontaneous emission rate in hybrid optomechanical emitter-cavity systems. Optica 2022, 9, 309–316. [Google Scholar] [CrossRef]
- Burlak, G.; Medina-Ángel, G. Structure of optical Cherenkov radiation in a three-dimensional compound medium with carbon nanotubes. J. Opt. Soc. Am. B 2019, 36, 187–193. [Google Scholar] [CrossRef]
- Burlak, G.; Cuevas-Arteaga, C.; Medina-Ángel, G.; Martínez-Sánchez, E.; Calderón-Segura, Y.Y. Plasmon-polariton oscillations in three-dimensional disordered nanotubes excited by a moving charge. J. Appl. Phys. 2019, 126, 013101. [Google Scholar] [CrossRef]
- Burlak, G.; Medina-Ángel, G.; Martínez-Sánchez, E. Condensation of plasmon-polaritons in dispersive carbon nanotubes assisted by a fast charge. Phys. Scr. 2021, 96, 125515. [Google Scholar] [CrossRef]
- Yanagi, K.; Okada, R.; Ichinose, Y.; Yomogida, Y.; Katsutani, F.; Gao, W.; Kono, J. Intersubband plasmons in the quantum limit in gated and aligned carbon nanotubes. Nat. Commun. 2018, 9, 1121. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Zeng, Y.; Bai, Y.; Li, Z.; Tian, Y.; Li, R. Coherent surface plasmon polariton amplification via free-electron pumping. Nature 2022, 611, 55–60. [Google Scholar] [CrossRef]
- Singh, M.R.; Schindel, D.G.; Hatef, A. Dipole-dipole interaction in a quantum dot and metallic nanorod hybrid system. Appl. Phys. Lett. 2011, 99, 181106. [Google Scholar] [CrossRef]
- Terzis, A.; Kosionis, S.; Boviatsis, J.; Paspalakis, E. Nonlinear optical susceptibilities of semiconductor quantum dot-metal nanoparticle hybrids. J. Mod. Opt. 2015, 63, 451–461. [Google Scholar] [CrossRef]
- Singh, M.R.; Davieau, K.; Carson, J.J. Effect of quantum interference on absorption of light in metamaterial hybrids. J. Phys. D Appl. Phys. 2016, 49, 445103. [Google Scholar] [CrossRef]
- Yannopapas, V.; Paspalakis, E. Optical properties of hybrid spherical nanoclusters containing quantum emitters and metallic nanoparticles. Phys. Rev. B 2018, 97, 205433. [Google Scholar] [CrossRef]
- Singh, M.R. Theory of all-optical switching based on the Kerr nonlinearity in metallic nanohybrids. Phys. Rev. A 2020, 102, 013708. [Google Scholar] [CrossRef]
- Burlak, G.; Medina-Ángel, G. Extended dynamics and lasing of nanoemitters enhanced by dispersing single-walled carbon nanotubes. J. Quant. Spectrosc. Radiat. Transf. 2023, 296, 108463. [Google Scholar] [CrossRef]
- Downing, C.A.; Weick, G. Plasmonic modes in cylindrical nanoparticles and dimers. Proc. R. Soc. A Math. Phys. Eng. Sci. 2020, 476, 20200530. [Google Scholar] [CrossRef]
- Siegman, A.E. Lasers; University Science Books: Sausalito, CA, USA, 1986. [Google Scholar]
- Taflove, A.; Hagness, S.C. Computational Electrodynamics: The Finite-Difference Time-Domain Method, 3rd ed.; Artech House: Norwood, MA, USA, 2005. [Google Scholar]
- Jiang, X.; Soukoulis, C.M. Time Dependent Theory for Random Lasers. Phys. Rev. Lett. 2000, 85, 70–73. [Google Scholar] [CrossRef] [PubMed]
- Burlak, G.; Rubo, Y.G. Mirrorless lasing from light emitters in percolating clusters. Phys. Rev. A 2015, 92, 013812. [Google Scholar] [CrossRef]
- Cao, H.; Zhao, Y.G.; Ho, S.T.; Seelig, E.W.; Wang, Q.H.; Chang, R.P.H. Random Laser Action in Semiconductor Powder. Phys. Rev. Lett. 1999, 82, 2278. [Google Scholar] [CrossRef]
- Burlak, G.; Medina-Ángel, G. Property of Plasmon-Polaritons in Nanorings Assisted by Lemniscate Ordered Emitters. In Proceedings of the 14th International Conference Series on Laser-Light and Interactions with Particles (LIP 2024), Xi’an, China, 18–22 September 2024; p. 3. Available online: https://lip-conference.org/abstracts/Book_of_Abstracts_LIP2024.pdf (accessed on 1 September 2024).
- Balanis, C.A. Antenna Theory: Analysis and Design, 4th ed.; Wiley: London, UK, 2016. [Google Scholar]
- Omar, N.A.S.; Fen, Y.W.; Saleviter, S.; Daniyal, W.M.E.M.M.; Anas, N.A.A.; Ramdzan, N.S.M.; Roshidi, M.D.A. Development of a Graphene-Based Surface Plasmon Resonance Optical Sensor Chip for Potential Biomedical Application. Materials 2019, 12, 1928. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Burlak, G.; Medina-Ángel, G. Dynamical Properties of Plasmon Polaritons in Nanorings Driven by Cassini-Ordered Emitters. Nanomaterials 2025, 15, 576. https://doi.org/10.3390/nano15080576
Burlak G, Medina-Ángel G. Dynamical Properties of Plasmon Polaritons in Nanorings Driven by Cassini-Ordered Emitters. Nanomaterials. 2025; 15(8):576. https://doi.org/10.3390/nano15080576
Chicago/Turabian StyleBurlak, Gennadiy, and Gustavo Medina-Ángel. 2025. "Dynamical Properties of Plasmon Polaritons in Nanorings Driven by Cassini-Ordered Emitters" Nanomaterials 15, no. 8: 576. https://doi.org/10.3390/nano15080576
APA StyleBurlak, G., & Medina-Ángel, G. (2025). Dynamical Properties of Plasmon Polaritons in Nanorings Driven by Cassini-Ordered Emitters. Nanomaterials, 15(8), 576. https://doi.org/10.3390/nano15080576