Abstract
By leveraging machine learning insights from prior perovskite studies and employing the sol–gel method, we successfully synthesized two novel perovskite nanoceramics—M0.5 Ca0.25Mg0.25MnO3 (M = La, Pr)—as multifunctional nanomaterials. X-ray diffraction (XRD) confirmed their orthorhombic Pnma crystal structure. The Williamson–Hall method estimated average particle sizes of 59.5 nm for PCMMO and 21.8 nm for LCMMO, while the Scherrer method provided corresponding values of 32.59 nm and 20.43 nm. SEM, UV-Vis, and FTIR analyses validated the chemical composition, homogeneity, and optical properties of the synthesized compounds, revealing band gaps of 3.25 eV (LCMMO) and 3.71 eV (PCMMO) with Urbach energies of 0.29 eV and 0.26 eV, respectively. These findings provide valuable insights into the structural and optical properties of LCMMO and PCMMO, highlighting their potential as multifunctional materials for advanced device applications.
Keywords:
nanomanganites; perovskite; Mg doping; sol–gel; SEM; gap energy; multifunctional materials 1. Introduction
The development of materials is a fundamental pillar of scientific and technological progress. With the advancement in machine learning (ML) techniques, these tools have become an effective means for analyzing and designing materials in innovative ways. Machine learning is distinguished by its ability to extract relationships from data without relying on traditional physical mechanisms, enabling the prediction of virtual material properties and their evaluation to discover high-performance materials. In light of our research team’s recent focus on machine learning [1,2,3], particularly the latest work by Soundous [4] and two other related studies in this field [5,6], inspiring ideas have emerged regarding ABX3 perovskite materials. The results of these studies drew our attention to the fascinating properties of manganite perovskite compounds, including magnetic properties, insulating properties, and other intriguing characteristics, making them a central focus for scientific research and technological applications.
Perovskite manganites with the general formula R1−xAxMnO3 (where R is a trivalent rare-earth ion and A is a divalent alkaline-earth) have attracted the attention of researchers and scientists due to the intricate interplay between spin, charge, orbital, and lattice degrees of freedom, which gives rise to their remarkable properties [7,8]. These materials exhibit a wide range of phenomena, including colossal magnetoresistance (CMR) [9,10], metal–insulator transitions, charge/orbital ordering [11,12], and various magnetic phases such as paramagnetism, super-paramagnetism, ferromagnetism, antiferromagnetism, and spin-glass behavior. The parent compounds, RMnO3, are antiferromagnetic insulators [13,14], but doping with divalent cations like Mg2+, Ca2+, Sr2+, or Ba2+ at the R-site induces mixed Mn3+/Mn4+ valence states, which dramatically affects their magnetic and related transport properties. The double-exchange mechanism, initially proposed by Zener [11,15] and later refined by others [16,17], provides insight into the correlation between ferromagnetic ordering and conductivity observed in these systems. According to this mechanism, the mobility of electrons is maximized when neighboring Mn3+/Mn4+ spins align in parallel, promoting ferromagnetic ordering and metallic behavior. The exceptional properties of perovskite manganites make them promising for various technological applications, including random-access memories [18,19], colossal magnetoresistance (CMR) [9,20], the magnetocaloric effect (MCE) [21,22], photocatalysis [23], magnetic refrigeration [24], electric field sensors [25], spintronics [26], and photovoltaic materials [27]. Additionally, some compositions show multiferroic behavior [28,29], combining ferroelectric and ferromagnetic order, which enables multifunctional device applications. Extensive research on La1−xCaxMnO3 (LCMO) systems has revealed complex phase diagrams characterized by diverse magnetic and electronic phases. Phases such as ferromagnetic metallic (FM-M), charge-ordered (CO) antiferromagnetic insulating, and canted antiferromagnetic (CAF) emerge based on Ca doping levels and temperature. Strong electron correlations in these systems complicate a detailed microscopic understanding of their properties. Notably, a significant phase transition occurs from a low-temperature FM-M phase to a high-temperature paramagnetic insulating (PM-I) phase for doping levels between 0.2 < x < 0.5 [30].
In recent years, considerable attention has focused on the effects of finite size and surface modifications in nanoscale perovskite manganites [31,32]. Studies have shown that reducing particle size can significantly impact magnetism and transport characteristics by destabilizing charge and orbital order, leading to notable differences from bulk counterparts. This phenomenon, especially relevant at the nanoscale, has sparked substantial interest. Two primary hypotheses aim to explain these size-dependent effects: modifications to bulk strain and changes in surface electronic structure [33,34,35,36]. Further studies are needed to clarify the competing factors influencing nanoscale materials. Perovskite manganite nanoparticles exhibit unique properties, including super-paramagnetism with potential applications in magnetic hyperthermia [37,38,39], surface spin-glass behavior, large coercivities, reduced Curie temperatures, and low-field saturation magnetization compared to their bulk counterparts [40,41]. Ongoing research explores the effects of different synthesis methods, doping strategies, and nanostructuring on the physical properties of these manganites [42,43,44,45].
Although extensive research has focused on the magnetic and transport properties of manganites, their optical properties have received less attention, primarily due to their insulating (large bandgap) or metallic (no bandgap) behavior [46]. However, if these systems could be induced to exhibit semiconducting characteristics along with strong magnetic moments, they could become promising candidates for magnetic semiconducting devices.
While there is substantial research on LCMO (La1−xSrxMnO3) and LSMO (La1-xSrxMnO3) systems, other compositions within the R1−xAxMnO3 family, such as Pr1−xCaxMnO3 (PCMO) [47,48,49] and Pr1−xSrxMnO3 (PSMO) [50,51], have received comparatively less attention. These systems have distinct phase diagrams and physical properties that warrant further investigation, particularly in the high doping regime (x > 0.5) where charge ordering and canted antiferromagnetism are expected to play significant roles.
Although numerous studies on the doping of LaMnO3 with magnesium have been conducted, firstly by X. Z. Zhou [52] and Li [53] and recently by Selmi [54]. However, no similar investigations have been made to explore the effects of magnesium on the La1−xCaxMnO3 and Pr1−xCaxMnO3 compounds. The existing literature in this area is limited to a single study by L. Liu et al. [55], who employed oxides and carbonates (La2O3, CaCO3, MgO, and MnCO3) as reactants and used the chemical composition La2/3(Ca1−xMgx)1/3MnO3 (with x ranging from 0 to 0.5). In contrast, Garcia et al. [56] demonstrated that doping LaMnO3 with magnesium could enhance its semiconducting properties, with the structure of all the samples belonging to space group R-3c. Similar results are observed in other systems such as ZnO [57,58]. For this purpose, studying the substitution of magnesium in La1−xCaxMnO3 and Pr1−xCaxMnO3 is essential for evaluating its potential to induce significant changes in the structural and functional properties of LCMMO and PCMMO materials, they possess significant potential to serve as exceptional materials for advanced magnetic semiconductor technologies.
Based on the findings from machine learning studies related to perovskites and the unique properties of the La1−xCaxMnO3 compound, such as magnetism, colossal magnetoresistance (CMR), and their importance in spintronic and insulating applications, along with Garcia’s study that indicated magnesium doping could enhance semiconductor properties, and our semi-comprehensive research (see Table S1), we select to prepare and characterize two new nanomaterials: La0.5Ca0.25Mg0.25MnO3 (LCMMO) and Pr0.5Ca0.25Mg0.25MnO3 (PCMMO). The innovation lies in substituting magnesium into the chemical composition to explore its effect on their physical properties. The study also included a systematic comparison of the impact of lanthanum (La) and praseodymium (Pr) substitution to gain a deeper understanding of these modification effects. This study aims to leverage machine learning results along with experimental observations to prepare innovative materials that enhance semiconductor properties while maintaining the well-known magnetic properties, contributing to a broader understanding of these materials’ behavior and opening new avenues for advanced technological applications.
2. Exploring Materials: Advanced Research Techniques
The reactants were sourced from Sigma–Aldrich (St. Louis, MO, USA)with high purity, including Manganese (II) nitrate tetrahydrate (Mn(NO3)2·4H2O 99.9%), lanthanum nitrate hexahydrate (La(NO3)3·6H2O 99.99%), praseodymium (III) nitrate hexahydrate (Pr(NO3)3·6H2O 99.9%), calcium nitrate tetrahydrate (Ca(NO3)2·4H2O 99%), and magnesium nitrate anhydrous (Mg(NO3)2 99%). Powder X-ray diffraction (XRD) patterns of the final products were obtained using a Panalytical EMPYREAN (Malvern, UK) powder diffractometer (CuK 1, 40 mA, 30 kV) with a step size of 0.01° and an acquisition time of 6 s/step in the 15–70° 2θ range under room temperature conditions. The nanoparticle size distribution and chemical composition were examined using scanning electron microscopy (SEM) with a TESCAN VEGA3 SBU EasyProbe electron microscope system (Brno, Czech Republic) coupled with a Bruker detector (Billerica, MA, USA) for energy-dispersive X-ray (EDX) analysis. The molar concentrations of lanthanum, praseodymium, calcium, and magnesium were determined using the ESPRIT Microanalysis Software (v2.5) from Bruker. Secondary electron images were acquired using primary electron beams at energies of 5 keV and 25 keV. The elemental samples were analyzed using an X-ray fluorescence (XRF) spectrometer (S2PUMA-BRUKER, Karlsruhe, Germany) with energy-dispersive X-ray fluorescence (EDXRF) capabilities. This spectrometer employs a Pd source for generating X-rays and can automatically adjust its focus points between 0.3 and 10 mm in diameter using a silicon drift detector. The sample chamber can operate in air, helium (He), nitrogen (N2), or vacuum environments. The voltage applied can go up to 40 kV. The optical properties, the band gap and Urbach energies of the samples, were explored by ultraviolet-visible spectroscopic analysis (UV-VIS) using a Shimadzu UV1800 (Kyoto, Japan) spectrophotometer. The FTIR measurements were conducted using a Jasco FT/IR-4200 instrument (Easton, MD, USA), the FTIR spectrum was recorded in transmission mode over the range of 2500–400 cm−1, utilizing a KBr pellet as the sample matrix.
3. Strategic Insights into Prepared Samples Selection
Recent machine learning studies on perovskite materials [4,5] have identified manganese perovskite compounds as among the most promising due to their diverse applications and technological potential. Given the increasing interest in these materials, we conducted research to select and characterize new nanomaterials, focusing on addressing research gaps and enhancing their fundamental properties for broader applications. Substitutions at the A-site in these compounds play a crucial role in determining their structural, chemical, and physical properties. By incorporating alkaline-earth and rare-earth elements, the average ionic radius of the A-site can be modified, leading to structural changes that influence their optical and dielectric properties [46,55,59]. As shown in Table S1, this table serves as a key reference for the samples prepared and characterized based on prior research. It presents three scenarios for synthesizing new predicted materials, focusing on variations in the A-site element position. The first scenario, shown in column 1, involves combining one rare-earth element with one alkaline-earth element. Columns 2 and 3 outline two additional scenarios: the second uses two alkaline-earth elements with one rare-earth element, while the third uses two rare-earth elements with one alkaline-earth element. In Table S1, the green highlights indicate materials that have not been synthesized or characterized yet, representing 66.67% (40 out of 60) of the total. The orange highlights correspond to materials with limited research, accounting for 13.33% (8 out of 60), while red signifies materials that have been extensively studied, making up 20% (12 out of 60) of the materials.
Leveraging the ionic radii of selected elements from Table S2, derived from Shannon’s ionic radius table, and utilizing Goldschmidt’s equation (Equation (S1)), alongside Equations (S2) and (S3) for the calculation of the average ionic radius of the A-site cations, we determined the tolerance factors for 60 perovskite manganite solid solution compounds. These tolerance factors enabled the prediction of the crystal structures for each compound, as presented in Table S3. The tolerance factor serves as a pivotal parameter for assessing the stability of perovskite crystal structures, with values approaching unity denoting enhanced structural stability. The computed tolerance factors for the compounds span from 0.85 to 0.98, highlighting diverse structural preferences. Specifically, compounds with tolerance factors between 0.95 and 0.99 are predisposed to adopting rhombohedral phases, whereas those with factors below 0.95 exhibit a tendency toward orthorhombic phases. Noteworthy is the incorporation of Barium (Ba), whose larger ionic radius relative to calcium (Ca) and magnesium (Mg) induces rhombohedral distortion, thereby significantly influencing the crystal structure and broadening the applicability of these materials in various technological contexts. The analysis further indicates that orthorhombic structures are the predominant predicted phase, comprising 70% of the materials, while rhombohedral phases account for the remaining 30%, as depicted in Figure S1.
In light of this, we focused on the synthesis and characterization of two novel nanomaterials: La0.5Ca0.25Mg0.25MnO3 (LCMMO) and Pr0.5Ca0.25Mg0.25MnO3 (PCMMO). Our investigation prioritized their optical properties to evaluate their potential for semiconductor applications.
4. Results and Discussion
4.1. Preparation
New nanocrystalline samples with targeted compositions of La0.5Ca0.25Mg0.25MnO3 (LCMMO) and Pr0.5Ca0.25Mg0.25MnO3 (PCMMO) were prepared using the sol–gel technique. In the first step, the reagents including Mn(NO3)2·4H2O (2.07 mmole), Ca(NO3)2·4H2O (0.5 mmole), and Mg(NO3)2 (0.5 mmole) were dissolved in methanol (MeOH) solvent using a magnetic stirrer for 10 min. Then, La(NO3)3·6H2O (1 mmole) and Pr(NO3)3·6H2O (1 mmole) were added separately using a magnetic stirrer for 10 min for the second time in sol preparation (A) and (B), respectively. A citric acid (C6H8O7) solution (0.6 g in MeOH) was added to the mixture. The key roles of citric acid in the sol–gel process are (i) as a chelating agent for metal ions, (ii) as a viscosity-controlling agent of the medium, and (iii) as an organic fuel during the calcination process. In the second step, the resulting solutions were heated to 70 °C until gel formation occurred in 27 min (LCMMO preparation) and 21 min (PCMMO preparation), respectively. Finally, the gels were dried at 80 °C in a drying cabinet for 24 h to produce precursor powders. The obtained powders were milled and annealed at 800 °C for 2.5 h under ambient air conditions (Figure 1).
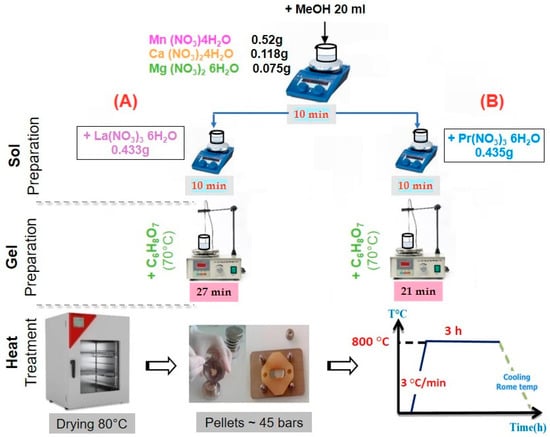
Figure 1.
Sample experimental protocol: (A) LCMMO; (B) PCMMO.
4.2. Morphology and Elemental Composition
Figure 2 presents SEM micrographs of (a) LCMMO and (b) PCMMO. Although the resolution limitations of the SEM prevented detailed imaging at the nanoscale, it effectively revealed the aggregated morphology of the nanoparticles. Both samples exhibit a uniform polycrystalline and porous structure composed of densely packed grains—a typical microstructural trait of perovskites synthesized via the sol–gel method followed by thermal treatment. The powders were successfully characterized in terms of chemical composition and homogeneity. The SEM images reveal micron-sized spherical agglomerates composed of finer nanoparticles, with some aggregates measuring below 100 nm, as highlighted in the insets of Figure 2a,b. Energy-dispersive X-ray spectroscopy (EDX) analysis confirmed the elemental composition, phase purity, and stoichiometry of the samples, closely aligning with the intended molar ratio of 0.5:0.25:0.25:1 for La (or Pr), Ca, Mg, and Mn, respectively. These results were averaged over multiple zones to ensure consistency and representativeness. No notable impurities were observed in either sample. The apparent Fe peak observed in Figure 3a is attributed to the software limitations of the EDX detector, where closely overlapping signals from Mn and Fe can lead to erroneous peak identification. Minor unidentified signals are attributed to the sample substrate. Furthermore, the X-ray fluorescence (XRF) analysis corroborated the expected stoichiometry and elemental distribution, as summarized in Table 1.

Figure 2.
SEM images for (a) LCMMO and (b) PCMMO nano powders.
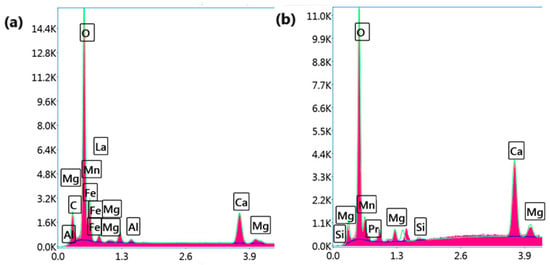
Figure 3.
EDX mappings and spectra for (a) LCMMO and (b) PCMMO nanoparticles.

Table 1.
Atomic Percentages (At. %) from XRF analysis.
4.3. XRD Characterization
A. L. Liu et al. [55] studied a variant composition of (La2/3(Ca1−xMgx)1/3MnO3) emphasizing the enhanced durability of the orthorhombic perovskite lattice when subjected to compositional alterations. The parent compounds of our study are La0.5Ca0.5MnO3 [60] and Pr0.5Ca0.5MnO3 [61,62], both of which are isostructural and characterized by the same crystal structure. Their powder diffraction profiles are identified in the ICDD Cards No. 01-089-0793 and No. 01-089-0795, respectively.
To delve into the nuances of structural variations induced by changes in composition, we meticulously examined the phase purity and crystal structure of our nano manganite powders, which boast distinct particle sizes. This scrutiny was accomplished through an X-ray diffraction (XRD) analysis conducted at room temperature. The XRD findings, as depicted in Figure 4a and Figure 5a, underscored the presence of a pristine orthorhombic perovskite crystalline structure in both LCMMO and PCMMO, corroborating their conformity to the Pnma space group (experimental profile). Despite the doping of Mg, there was no discernible alteration in the appearance or disappearance of diffraction peaks (simulated profile). The powder XRD patterns of the investigated manganite perovskites LCMMO and PCMMO reveal well-crystallized nanoparticle phases and showcase particle size uniformity through Williamson–Hall plots in Figure 4b and Figure 5b. The shapes of peaks were modeled using a pseudo-Voigt function and a Caglioti model [63] and Scherrer’s formula using X’Pert HighScore Plus. The XRD patterns were originally generated using the HighScore software (version 5.0). For the Williamson–Hall (W–H) analysis and Caglioti curve fitting, 12 diffraction peaks within the 20–60° 2θ range were selected for LCMMO (Figure 4c), and 11 peaks for PCMMO (Figure 5c).
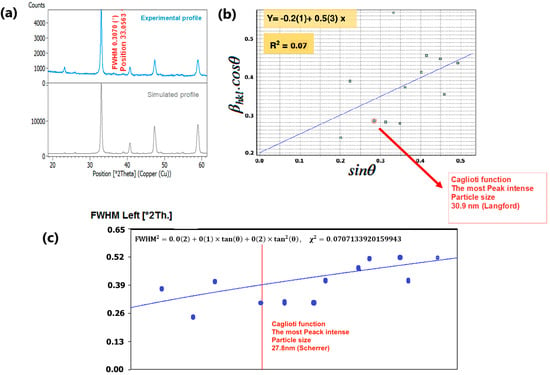
Figure 4.
(a) XRD spectrum of LCMMO, (b) Williamson–Hall plot, and (c) FWHM Caglioti function.
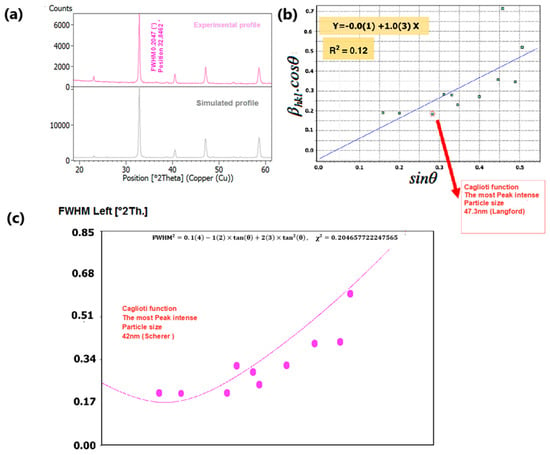
Figure 5.
(a) XRD spectrum of PCMMO, (b) Williamson–Hall plot, and (c) FWHM Caglioti function.
Regarding the dependence of crystallite size on the annealing process, it is important to note that the final annealing temperature plays a significant role in grain growth. Higher annealing temperatures typically enhance atomic diffusion, which in turn leads to an increase in crystallite size.
The Caglioti equation is given by FWHM2 = U·tan2θ + V·tanθ + W, where U, V, and W are empirical fitting parameters, and θ is the Bragg angle.
The difference in the linearity of the plots in Figure 4c (linear) and Figure 5c (non-linear) stems from variations in these parameters. These discrepancies reflect underlying microstructural differences and strain variations between the two materials. Figure 4c and Figure 5c). No significant crystallized impurities are detected, as demonstrated by the homogeneity of particle sizes in the Williamson–Hall plots for both PCMMO and LCMMO nanoparticles. In this work, the average particle size of PCMMO was determined to be 59.5 ± 3 nm using the Williamson–Hall (W–H) size–strain analysis (Langford method), with a corresponding strain of 0.2%. This strain value, which falls within the typical range of 0.1–0.5%, suggests the presence of lattice distortions and intrinsic defects. The crystallite size estimated by the Scherrer formula was 32.59 ± 2 nm, which is significantly smaller than that obtained by the W–H method. Since the Scherrer method often underestimates particle size due to its neglect of strain effects, we propose that the W–H result is closer to the true particle size. For LCMMO, the average particle size estimated using the W–H method was 21.8 ± 2 nm, while the Scherrer method yielded a crystallite size of 20.43 ± 1.5 nm. The strain calculated in this case was only 0.02%, indicating high crystallinity and low defect density. This behavior is consistent with the findings in oxide nanoparticles such as TiO2 and CeO2, where it has been shown that synthesis methods significantly influence structural properties, including crystallinity and strain [64]. These results suggest that the sol–gel synthesis route is particularly effective for preparing highly crystalline LCMMO nanoparticles. The average particle sizes are 59.5 ± 3 nm for PCMMO and 21.8 ± 2 nm for LCMMO compared to crystallite sizes of 32.59 ± 2 nm and 20.43 ± 1.5 nm, respectively, as summarized in Table 2.

Table 2.
Crystallite size (D), diffraction angle (θ), and full width at half maximum (FWHM (β)) of both LCMMO and PCMMO nanoparticles.
4.4. Exploring Optical Characteristics
4.4.1. Fourier Transform Infrared Spectroscopy
Also known as vibrational spectroscopy (IR), involves a meticulous examination of how infrared light interacts with molecules. In the literature, FIR spectra have been documented for various compounds, including ABX3 perovskite titanates [65], niobates [66], fluorides [67], zirconates [68], chromites, ferrites [69], and silicates [70], consistently revealing three absorption bands (around 200 cm−1, 400 cm−1, and 600 cm−1), which are called “external,” “bending,” or “stretching” modes [71], irrespective of stoichiometry and structural variations. Different studies have described the order of these bands in varying ways. The crystal structure of rare-earth manganites typically adopts a distorted GdFeO3-type structure, featuring a central Mn atom surrounded by six oxygen ions arranged in an octahedral configuration. While the MnO6 octahedron theoretically harbors six vibrating modes, only two exhibit infrared activity. The FTIR spectra depicted in Figure 6 enable the identification of frequency band peaks for both the LCMMO and PCMMO nano powders. Notably, a distinct band around 604 cm−1 for LCMMO and 607 cm−1 for PCMMO is attributed to the stretching vibration of the O–Mn–O bond within the MnO6 octahedron [68]. This indicates that each sample contains a significant presence of the Mn–O bond, and variations in the Mn–O–Mn bond length, driven by internal motion, are responsible for the formation of this band. The confirmation of the O–Mn–O bond presence around 600 cm−1 serves to validate the formation of nanocrystallites, consistent with previous research findings. The prominent broad peak observed in nano samples aids in discerning localized distortion within the MnO6 octahedral structure in perovskite samples, a critical determinant of their transport. Throughout the synthesis of nano perovskites, various physical effects, including atomic disorder, contamination, and grain boundary dislocations, may significantly influence the structural characteristics and material properties.
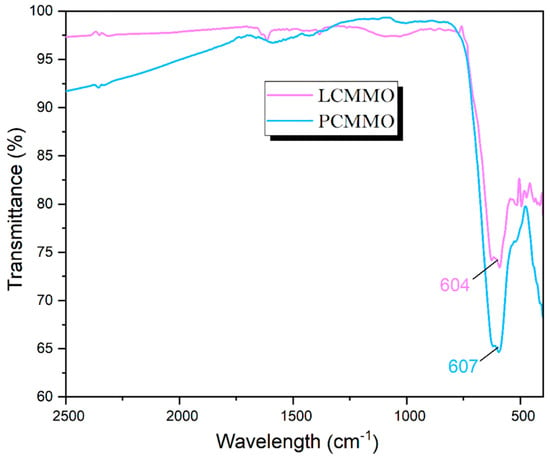
Figure 6.
Standard FTIR spectra analysis of LCMMO and PCMMO.
4.4.2. UV–Vis Absorbance Spectroscopy
To thoroughly investigate the optical properties of the samples, UV-Vis spectroscopy was employed, a widely used analytical technique that aids in determining absorbance and energy gaps in synthesized nanoparticles. Figure 7 illustrates the UV-Vis absorption intensity of the samples within the 300–800 nm wavelength range. Due to the high concentration of the solid solution, the absorption intensity is notably high. The peak absorption for the LCMMO and PCMMO nanoparticles occurs around 300 nm, indicating that both pure nanoceramics absorb in the UV range. This absorption peak is likely due to a p-d charge transfer transition [O(2p)→Mn(3d)] within the MnO6 octahedral centers in both perovskites. The optical bandgaps of the LCMMO and PCMMO nanoparticles were derived using Tauc’s equation:
where
is the absorption coefficient;
represents the energy of the incident light;
is the absorption edge width;
is the optical bandgap of the material;
is an index related to different electronic transitions.
By extrapolating the linear portion of the Tauc plot (Figure 7, inset), the optical bandgaps for the LCMMO and PCMMO nanoparticles were estimated at 3.25 ± 0.04 eV and 3.71 ± 0.07 eV, respectively. These values are significantly higher than similar half-doped manganites such as Pr0.5Sr0.5MnO3 (~1.17 eV) [72] and Nd0.5Sr0.5MnO3 (~0.47 eV) [73], highlighting their distinct optical properties. The smaller ionic radius of Mg2+ (0.89 Å) compared to Ca2+ (1.18 Å) and Sr2+ (1.31 Å) induces lattice contraction, which modifies the average A-site cationic radius ❬rA❭ and alters the Mn–O–Mn bond angles. This structural distortion enhances crystal field effects and Jahn–Teller distortions, reducing the orbital overlap and decreasing the electronic bandwidth (W). The resulting distortion of the MnO6 octahedra further disrupts the electronic structure, influencing charge carrier dynamics and orbital hybridization. Consequently, these effects shift electronic states, increase carrier localization, and significantly widen the bandgap (3.25 eV for LCMMO, 3.71 eV for PCMMO) compared to Ca/Sr-doped systems. These characteristics suggest potential applicability in magnetic semiconductor devices [46]. These materials exhibit wide optical energy gaps (Eg > 3 eV), indicating potential suitability for various optoelectronic applications, such as gas sensors [74], solar cells [75], optoelectronic devices [76,77,78], liquid crystal displays (LCDs), and organic light-emitting diodes (OLEDs) [79,80,81,82]. However, further electrical conductivity measurements are necessary to fully assess their viability as transparent conductive oxides (TCOs), which will be explored in future studies. In these synthesized perovskite LCMMO and PCMMO nanoparticles, Mn cations exhibit a mixed valence state (Mn3⁺ and Mn4⁺), each surrounded by six oxygen anions forming MnO6 octahedral structures. Under the octahedral crystal field, the five 3d orbitals of the Mn cation split into low-lying triplet and high-lying doublet sub-bands. For the Mn4⁺ ion (3d3 configuration), the orbitals remain empty, whereas for Mn3⁺ (3d4 configuration), these orbitals contain one electron with spin aligned parallel to the core spin. Due to exchange interactions, the sub-bands split further into up-spin and down-spin bands. The observed optical bandgaps are attributed to electronic transitions from the up-spin band of Mn3⁺ (split by the Jahn–Teller effect) to the down-spin band of a neighboring Mn4⁺ ion. The energy gap between these two bands correspond to Hund’s coupling energy (EJ), as similarly reported for (La0.6Pr0.4)0.65Ca0.35MnO3 nanocrystals [46,80]. Given the wide distribution of the up-spin and down-spin bands, excitation energy can extend into higher photon energy ranges.
Determining the Urbach tail energy (Eu) is essential for identifying the structural defects and vacancies that introduce localized states within the bandgap, especially in disordered or amorphous materials. Known as the band tail energy, Eu is critical for assessing crystallinity, structural disorder, and material imperfections [80]. Eu values are extracted from UV-Vis diffuse reflectance data, with higher Eu values indicating reduced crystallinity and increased disorder, leading to localized states extending into the bandgap. Eu quantifies the extent of localized states near the conduction band edge, revealing imperfections often arising from oxygen and magnetic ions as well as phonon-related disorder. Practically, Eu can be determined using the Urbach–Martienssen law [82]. For this study, Eu was determined by plotting ln(α) against hν and calculating its value through linear fitting, as shown in Figure 8a,b for LCMMO and PCMMO, respectively. The resulting slopes, approximately 3.4 and 3.8, correspond to the Urbach energies of Eu = 0.29 eV for LCMMO and Eu = 0.26 eV for PCMMO nanoceramics. These relatively low Urbach energy values suggest minimal structural disorder, consistent with high-quality perovskite oxides such as LSNMT ceramics (0.227 eV) [83], and LYCMO (0.2 eV) [79], which exhibit similar defect-suppressed behavior.
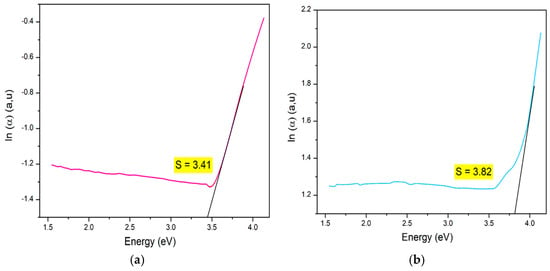
Figure 8.
Urbach energy of (a) LCMMO and (b) PCMMO.
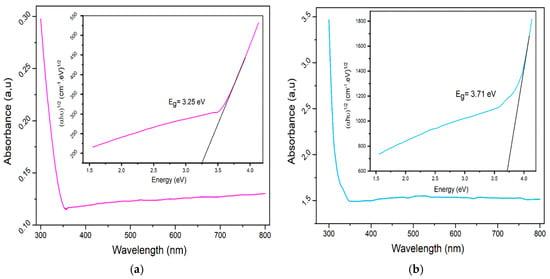
Figure 7.
Uv-v absorbance spectra (insert gap energy with Tauc plot) of (a) LCMMO and (b) PCMMO.
While the direct bandgaps of LCMMO and PCMMO suggest promise for ultraviolet (UV)-selective applications, the significant Urbach energies (3.41 eV and 3.82 eV) point to high defect densities and substantial structural disorder. These features likely limit the performance of the materials in applications such as high-efficiency optoelectronic devices or solar absorbers. For practical implementation, further optimization of synthesis to reduce disorder is essential. Therefore, the proposed applications must be considered with caution, and the current results are more appropriate for fundamental characterization or proof-of-concept systems.
5. Conclusions
In conclusion, this study successfully synthesized two novel perovskite nanoceramics, La0.5Ca0.25Mg0.25MnO3 (LCMMO) and Pr0.5Ca0.25Mg0.25MnO3 (PCMMO) using an environmentally friendly sol–gel method. This approach proved highly effective, yielding 100% of the desired nanoparticles. Comprehensive characterization of these materials was performed using a variety of techniques. Particle size analysis employed both the Williamson–Hall and Scherrer methods, providing complementary insights into the nanostructure. The chemical composition, homogeneity, and optical properties were confirmed through a combination of scanning electron microscopy (SEM), UV-vis absorbance spectroscopy, and Fourier-transform infrared (FTIR) spectroscopy. Notably, LCMMO and PCMMO exhibited distinct optical band gaps of 3.25 eV and 3.71 eV, respectively, highlighting their unique optical properties, potentially suitable for optoelectronics, like advanced materials [75,76]. The low Urbach energy values observed suggest minimal disorder or imperfections within the samples, indicating high-quality synthesis. The successful synthesis and thorough characterization of these novel nanoceramics not only expand our understanding of doped manganite perovskites but also pave the way for their potential applications in advanced materials science and technology. Future research could explore the performance of these materials in specific device configurations and investigate potential enhancements through further compositional tuning or processing optimizations.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/nano15070561/s1, Figure S1: Predicted crystalline structure distribution of perovskite manganites; Table S1: Previous studies on A-site-substituted perovskite manganites: comprehensive table. Table S2: Ionic radii of selected elements for perovskite manganites tolerance factor calculations (Shannon’s 9-Coordination Data). Table S3. Predicting crystal structure and tolerance factor in A-site-substituted perovskite manganites using Shannon’s ionic radius table.
Author Contributions
Conceptualization, C.L.B.M. and Z.H.; methodology, I.K.L.; software, A.D.; validation, A.L.B.K., S.G.-S. and M.B.K.; formal analysis, I.K.L.; investigation, A.D.; resources, A.L.B.K.; data curation, Z.H.; writing—original draft preparation, Z.H.; writing—review and editing, M.B.K.; visualization, R.S.S.J.; supervision, J.A.A.; project administration, S.L.; funding acquisition, Z.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are available upon reasonable request from the corresponding author.
Acknowledgments
The research team from Université Amar Telidji Laghouat expresses their deep gratitude for the outstanding support from the Technical Platform of Physico-Chemical Analysis at Université Amar Telidji Laghouat, Algeria, the Technical Platform of Physico-Chemical Analysis at USTHB University, Bab Ezzouar, Algeria, and the Department of General, Organic, and Biomedical Chemistry, NMR and Molecular Imaging Laboratory at the University of Mons, Belgium, under the leadership of Sophie Laurent. This work is supported by the Algerian Ministry of Higher Education and Scientific Research through Projects de Recherche Formation-Universitaire PRFU under grant B00L01UN030120220002. S. Goumri-Said thanks the office of research at Alfaisal University in Saudi Arabia for funding this research work through internal project number 24407. M.B.K would like to thank Prince Sultan University for its support.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ben Kamri, A.L.; Fadla, M.A.; Lefkaier, I.K.; Messaoud, C.L.B.; Kanoun, M.B.; Goumri-Said, S. AI-driven ensemble learning for accurate Seebeck coefficient prediction in half-Heusler compounds based on chemical formulas. Comput. Condens. Matter 2024, 40, e00923. [Google Scholar] [CrossRef]
- Touati, S.; Benghia, A.; Hebboul, Z.; Lefkaier, I.K.; Kanoun, M.B.; Goumri-Said, S. Predictive machine learning approaches for perovskites properties using their chemical formula: Towards the discovery of stable solar cells materials. Neural Comput. Appl. 2024, 36, 16319–16329. [Google Scholar] [CrossRef]
- Benghia, A.; Mechraoui, B.K.; Ferchane, S.; Lefkaier, I.K.; Fadla, M.A.; Hebboul, Z.; Arar, R.; Kanoun, M.B.; Goumri-Said, S. Data driven enhancement of mid-infrared non-linear optical properties of quaternary and ternary chalcogenides. Optik 2023, 293, 171432. [Google Scholar] [CrossRef]
- Touati, S.; Benghia, A.; Hebboul, Z.; Lefkaier, I.K.; Kanoun, M.B.; Goumri-Said, S. Machine Learning Models for Efficient Property Prediction of ABX3 Materials: A High-Throughput Approach. ACS Omega 2024, 9, 47519–47531. [Google Scholar] [CrossRef]
- Tao, Q.; Xu, P.; Li, M.; Lu, W. Machine learning for perovskite materials design and discovery. Npj Comput. Mater. 2021, 7, 23. [Google Scholar] [CrossRef]
- Zeng, Z.; Xu, Y.; Zhang, Z.; Gao, Z.; Luo, M.; Yin, Z.; Zhang, C.; Xu, J.; Huang, B.; Luo, F.; et al. Rare-earth-containing perovskite nanomaterials: Design, synthesis, properties and applications. Chem. Soc. Rev. 2020, 49, 1109–1143. [Google Scholar] [CrossRef]
- Jonker, G.H.; Van Santen, J.H. Ferromagnetic compounds of manganese with perovskite structure. Physica 1950, 16, 337–349. [Google Scholar] [CrossRef]
- Tian, H.; Zheng, W.; Zhao, Z.; Ding, T.; Yu, S.; Zheng, B.; Li, X.; Meng, F.; Jiang, Q. Magnetic properties and electron spin resonance of charge ordering manganite Y0.5Ca0.5MnO3. Chem. Phys. Lett. 2005, 401, 585–589. [Google Scholar] [CrossRef]
- Von Helmolt, R.; Wecker, J.; Holzapfel, B.; Schultz, L.; Samwer, K. Giant negative magnetoresistance in perovskitelike La 2/3 Ba 1/3 MnO x ferromagnetic films. Phys. Rev. Lett. 1993, 71, 2331–2333. [Google Scholar] [CrossRef]
- Salamon, M.B.; Jaime, M. The physics of manganites: Structure and transport. Rev. Mod. Phys. 2001, 73, 583–628. [Google Scholar] [CrossRef]
- Zener, C. Interaction Between the d Shells in the Transition Metals. Phys. Rev. 1951, 81, 440–444. [Google Scholar] [CrossRef]
- Shankar, U.; Singh, A.K. Origin of Suppression of Charge Ordering Transition in Nanocrystalline Ln 0.5 Ca 0.5 MnO 3 (Ln = La, Nd, Pr) Ceramics. J. Phys. Chem. C 2015, 119, 28620–28630. [Google Scholar] [CrossRef]
- Koriba, I.; Lagoun, B.; Guibadj, A.; Belhadj, S.; Ameur, A.; Cheriet, A. Structural, electronic, magnetic and mechanical properties of three LaMnO3 phases: Theoretical investigations. Comput. Condens. Matter 2021, 29, e00592. [Google Scholar] [CrossRef]
- De Gennes, P.-G. Effects of Double Exchange in Magnetic Crystals. Phys. Rev. 1960, 118, 141–154. [Google Scholar] [CrossRef]
- Zener, C. Interaction between the d -Shells in the Transition Metals. II. Ferromagnetic Compounds of Manganese with Perovskite Structure. Phys. Rev. 1951, 82, 403–405. [Google Scholar] [CrossRef]
- Millis, A.J.; Littlewood, P.B.; Shraiman, B.I. Double Exchange Alone Does Not Explain the Resistivity of La1-xSrxMnO3. Phys. Rev. Lett. 1995, 74, 5144–5147. [Google Scholar] [CrossRef]
- Millis, A.J.; Mueller, R.; Shraiman, B.I. Fermi-liquid-to-polaron crossover. II. Double exchange and the physics of colossal magnetoresistance. Phys. Rev. B 1996, 54, 5405–5417. [Google Scholar] [CrossRef]
- Cheng, S.; Xu, C.; Deng, S.; Han, M.-G.; Bao, S.; Ma, J.; Nan, C.; Duan, W.; Bellaiche, L.; Zhu, Y.; et al. Interface reconstruction with emerging charge ordering in hexagonal manganite. Sci. Adv. 2018, 4, eaar4298. [Google Scholar] [CrossRef]
- Jaiswar, S.; Mandal, K.D. Evidence of Enhanced Oxygen Vacancy Defects Inducing Ferromagnetism in Multiferroic CaMn 7 O 12 Manganite with Sintering Time. J. Phys. Chem. C 2017, 121, 19586–19601. [Google Scholar] [CrossRef]
- Morelli, D.T.; Mance, A.M.; Mantese, J.V.; Micheli, A.L. Magnetocaloric properties of doped lanthanum manganite films. J. Appl. Phys. 1996, 79, 373–375. [Google Scholar]
- Gschneidner, K.A.; Pecharsky, V.K.; Tsokol, A.O. Recent developments in magnetocaloric materials. Rep. Prog. Phys. 2005, 68, 1479–1539. [Google Scholar] [CrossRef]
- Phan, M.-H.; Yu, S.-C. Review of the magnetocaloric effect in manganite materials. J. Magn. Magn. Mater. 2007, 308, 325–340. [Google Scholar]
- Abuova, A.U.; Mastrikov, Y.A.; Kotomin, E.A.; Piskunov, S.N.; Inerbaev, T.M.; Akilbekov, A.T. First-Principles Modeling of Oxygen Adsorption on Ag-Doped LaMnO3 (001) Surface. J. Elec Mater. 2020, 49, 1421–1434. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, X. Predicting AsxSe1-x Glass Transition Onset Temperature. Int. J. Thermo phys. 2020, 41, 149. [Google Scholar] [CrossRef]
- Ito, D.; Fujimura, N.; Yoshimura, T.; Ito, T. Ferroelectric properties of YMnO3 epitaxial films for ferroelectric-gate field-effect transistors. J. Appl. Phys. 2003, 93, 5563–5567. [Google Scholar] [CrossRef]
- Bowen, M.; Maurice, J.L.; Barthélémy, A.; Bibes, M.; Imhoff, D.; Bellini, V.; Bertacco, R.; Wortmann, D.; Seneor, P.; Jacquet, E. Using half-metallic manganite interfaces to reveal insights into spintronicsnics. J. Phys. Condens. Matter 2007, 19, 315208. [Google Scholar] [CrossRef]
- Han, H.; Song, S.; Lee, J.H.; Kim, K.J.; Kim, G.W.; Park, T.; Jang, H.M. Switchable Photovoltaic Effects in Hexagonal Manganite Thin Films Having Narrow Band Gaps. Chem. Mater. 2015, 27, 7425–7432. [Google Scholar] [CrossRef]
- Lonkai, T.; Hohlwein, D.; Ihringer, J.; Prandl, W. The magnetic structures of YMnO3-δ and HoMnO3. Appl. Phys. A 2002, 74, s843–s845. [Google Scholar] [CrossRef]
- Chadli, A.; Halit, M.; Lagoun, B.; Mohamedi, F.; Maabed, S.; Cheriet, A.; Hlil, E.; Farh, H. Structural and Anisotropic Elastic Properties of Hexagonal YMnO3 in Low Symmetry Determined by First-Principles Calculations. Solid State Phenom. 2019, 297, 120–130. [Google Scholar] [CrossRef]
- Schiffer, P.; Ramirez, A.P.; Bao, W.; Cheong, S.-W. Low Temperature Magnetoresistance and the Magnetic Phase Diagram of La1-xCaxMnO3. Phys. Rev. Lett. 1995, 75, 3336–3339. [Google Scholar] [CrossRef]
- Mahesh, R.; Mahendiran, R.; Raychaudhuri, A.K.; Rao, C.N.R. Effect of particle size on the giant magnetoresistance of La0.7Ca0.3MnO3. Appl. Phys. Lett. 1996, 68, 2291–2293. [Google Scholar] [CrossRef]
- Siwach, P.K.; Goutam, U.K.; Srivastava, P.; Singh, H.K.; Tiwari, R.S.; Srivastava, O.N. Colossal magnetoresistance study in nanophasic La0.7Ca0.3MnO3 manganite. J. Phys. D Appl. Phys. 2005, 39, 14. [Google Scholar] [CrossRef][Green Version]
- Dey, P.; Nath, T.K. Effect of grain size modulation on the magneto- and electronic-transport properties of La0.7Ca0.3MnO3 nanoparticles: The role of spin-polarized tunneling at the enhanced grain surface. Phys. Rev. B 2006, 73, 214425. [Google Scholar] [CrossRef]
- López-Quintela, M.A.; Hueso, L.E.; Rivas, J.; Rivadulla, F. Intergranular magnetoresistance in nanomanganites. Nanotechnology 2003, 14, 212–219. [Google Scholar] [CrossRef]
- Venkataiah, G.; Krishna, D.C.; Vithal, M.; Rao, S.S.; Bhat, S.V.; Prasad, V.; Subramanyam, S.V.; Reddy, P.V. Effect of sintering temperature on electrical transport properties of La0.67Ca0.33MnO3. Phys. B Condens. Matter 2005, 357, 370–379. [Google Scholar] [CrossRef]
- Shankar, K.S.; Kar, S.; Subbanna, G.N.; Raychaudhuri, A.K. Enhanced ferromagnetic transition temperature in nanocrystalline lanthanum calcium manganese oxide (La0.67Ca0.33MnO3). Solid State Commun. 2004, 129, 479–483. [Google Scholar] [CrossRef]
- Ferreira, M.C.; Pimentel, B.; Andrade, V.; Zverev, V.; Gimaev, R.R.; Pomorov, A.S.; Pyatakov, A.; Alekhina, Y.; Komlev, A.; Makarova, L.; et al. Understanding the Dependence of Nanoparticles Magnetothermal Properties on Their Size for Hyperthermia Applications: A Case Study for La-Sr Manganites. Nanomaterials 2021, 11, 1826. [Google Scholar] [CrossRef]
- Pashchenko, A.V.; Liedienov, N.A.; Fesych, I.V.; Li, Q.; Pitsyuga, V.G.; Turchenko, V.A.; Pogrebnyak, V.G.; Liu, B.; Levchenko, G.G. Smart magnetic nanopowder based on the manganite perovskite for local hyperthermia. RSC Adv. 2020, 10, 30907–30916. [Google Scholar] [CrossRef]
- Ahmad, A.; Akbar, H.; Zada, I.; Anjum, F.; Afzal, A.M.; Javed, S.; Muneeb, M.; Ali, A.; Choi, J.R. Improvement of the Self-Controlled Hyperthermia Applications by Varying Gadolinium Doping in Lanthanum Strontium Manganite Nanoparticles. Molecules 2023, 28, 7860. [Google Scholar] [CrossRef]
- Sánchez, R.D.; Rivas, J.; Vázquez-Vázquez, C.; López-Quintela, A.; Causa, M.T.; Tovar, M.; Oseroff, S. Giant magnetoresistance in fine particle of La0.67Ca0.33MnO3 synthesized at low temperatures. Appl. Phys. Lett. 1996, 68, 134–136. [Google Scholar] [CrossRef]
- Siwach, P.K.; Singh, H.K.; Srivastava, O.N. Low field magnetotransport in manganites. J. Phys. Condens. Matter 2008, 20, 273201. [Google Scholar] [CrossRef]
- Yang, H.; Zhu, Y.H.; Xian, T.; Jiang, J.L. Synthesis and magnetocaloric properties of La0.7Ca0.3MnO3 nanoparticles with different sizes. J. Alloys Compd. 2013, 555, 150–155. [Google Scholar] [CrossRef]
- Hueso, L.E.; Sande, P.; Miguéns, D.R.; Rivas, J.; Rivadulla, F.; López-Quintela, M.A. Tuning of the magnetocaloric effect in δ nanoparticles synthesized by sol–gel techniques. J. Appl. Phys. 2002, 91, 9943–9947. [Google Scholar] [CrossRef]
- Lampen, P.; Puri, A.; Phan, M.-H.; Srikanth, H. Structure, magnetic, and magnetocaloric properties of amorphous and crystalline La0.4Ca0.6MnO3+δ nanoparticles. J. Alloys Compd. 2012, 512, 94–99. [Google Scholar] [CrossRef]
- Siwach, P.K.; Prasad, R.; Gaur, A.; Singh, H.K.; Varma, G.D.; Srivastava, O.N. Microstructure-magnetotransport correlation in La0.7Ca0.3MnO3. J. Alloys Compd. 2007, 443, 26–31. [Google Scholar] [CrossRef]
- Kumar, S.; Dwivedi, G.D.; Kumar, S.; Mathur, R.B.; Saxena, U.; Ghosh, A.K.; Joshi, A.G.; Yang, H.D.; Chatterjee, S. Structural, transport and optical properties of (La0.6Pr0.4)0.65Ca0.35MnO3 nanocrystals: A wide band-gap magnetic semiconductor. Dalton Trans. 2015, 44, 3109–3117. [Google Scholar] [CrossRef]
- Karikar, A.; Ahmed, A.; Das, K.; Das, I. Magnetic and magnetocaloric properties of polycrystalline Pr1− xCaxMnO3 (x= 0.85, 0.90, 0.95) compounds: Emergence of large inverse and conventional magnetocaloric effects. J. Magn. Magn. Mater. 2023, 587, 171334. [Google Scholar] [CrossRef]
- Jammalamadaka, S.N.; Rao, S.S.; Bhat, S.V.; Vanacken, J.; Moshchalkov, V.V. Magnetocaloric effect and nature of magnetic transition in nanoscale Pr0.5Ca0.5MnO3. J. Appl. Phys. 2012, 112, 083917. [Google Scholar] [CrossRef]
- Rao, S.S.; Bhat, S.V. Probing the existing magnetic phases in Pr0.5Ca0.5MnO3 (PCMO) nanowires and nanoparticles: Magnetization and magneto-transport investigations. J. Phys. Condens. Matter 2010, 22, 116004. Available online: https://www.osti.gov/etdeweb/biblio/21375830 (accessed on 3 June 2024).
- Li, Q.; Wang, H.S.; Hu, Y.F.; Wertz, E. Anomalous anisotropic magnetoresistance in Pr0.67Sr0.33MnO3 thin films. J. Appl. Phys. 2000, 87, 5573–5575. [Google Scholar] [CrossRef]
- Liu, J.-M.; Yuan, G.L.; Sang, H.; Wu, Z.C.; Chen, X.Y.; Liu, Z.G.; Du, Y.W.; Huang, Q.; Ong, C.K. Low-field magnetoresistance in nanosized La 0.7 Sr 0.3 MnO 3/Pr 0.5 Sr 0.5 MnO 3 composites. Appl. Phys. Lett. 2001, 78, 1110–1112. [Google Scholar] [CrossRef]
- Zhou, X.Z.; Kunkel, H.P.; Zhao, J.H.; Stampe, P.A.; Williams, G. Evidence for an enhanced magnetoresistance accompanying a continuous phase transition in semiconducting La 0.67 Mg 0.33 MnO 3. Phys. Rev. B 1997, 56, R12714–R12717. [Google Scholar] [CrossRef]
- Li, Y.; Duan, X.F.; Zhang, J.H.; Wang, H.R.; Qian, Y.T.; Huang, Z.; Zhou, J.; Yuan, S.L.; Liu, W.; Zhu, C.F. Giant magnetoresistance in bulk La0.6Mg0.4MnO3. J. Mater. Res. 1997, 12, 2648–2650. Available online: https://www.osti.gov/biblio/554347 (accessed on 3 June 2024). [CrossRef]
- Selmi, R.; Cherif, W.; Sarabando, A.R.; Ferreira, N.M.; Ktari, L. Enhanced relative cooling power of lanthanum-deficiency manganites La0.77−xMg0.23MnO3 (0 ≤ x ≤ 0.2): Structural, magnetic and magnetocaloric properties. J. Mater. Sci. Mater. Electron. 2022, 33, 1703–1723. [Google Scholar] [CrossRef]
- Liu, L.; Xia, Z.C.; Yuan, S.L. Effect of Mg doping on the transport properties and magnetoresistance of La2/3Ca1/3MnO3 prepared in low temperature. Mater. Sci. Eng. B 2006, 128, 50–52. [Google Scholar] [CrossRef]
- Supelano, G.I.; Barón-González, A.J.; Santos, A.S.; Ortíz, C.; Gómez, J.A.M.; Vargas, C.A.P. Effect of Mg addition on LaMnO3 ceramic system. J. Mater. Res. Technol. 2018, 7, 77–81. [Google Scholar] [CrossRef]
- Tian, C.-S.; Chen, X.-L.; Ni, J.; Liu, J.-M.; Zhang, D.-K.; Huang, Q.; Zhao, Y.; Zhang, X.-D. Transparent conductive Mg and Ga co-doped ZnO thin films for solar cells grown by magnetron sputtering: H2 induced changes. Sol. Energy Mater. Sol. Cells 2014, 125, 59–65. [Google Scholar] [CrossRef]
- Kang, H.; Lu, Z.; Zhong, Z.; Gu, J. Structural, optical and electrical characterization of Ga-Mg co-doped ZnO transparent conductive films. Mater. Lett. 2018, 215, 102–105. [Google Scholar] [CrossRef]
- Panda, B.; Routray, K.L.; Behera, D. Studies on conduction mechanism and dielectric properties of the nano-sized La0.7Ca0.3MnO3 (LCMO) grains in the paramagnetic state. Phys. B Condens. Matter 2020, 583, 411967. [Google Scholar] [CrossRef]
- Wang, Y.X.; Du, Y.; Qin, R.W.; Han, B.; Du, J.; Lin, J.H. Phase equilibrium of the La–Ca–Mn–O system. J. Solid State Chem. 2001, 156, 237–241. [Google Scholar]
- Jirák, Z.; Krupička, S.; Šimša, Z.; Dlouhá, M.; Vratislav, S. Neutron diffraction study of Pr1- xCaxMnO3 perovskites. J. Magn. Magn. Mater. 1985, 53, 153–166. [Google Scholar] [CrossRef]
- Jirak, Z.; Krupička, S.; Nekvasil, V.; Pollert, E.; Villeneuve, G.; Zounova, F. Structural and magnetization study of Pr1- xCaxMnO3. J. Magn. Magn. Mater. 1980, 15, 519–520. [Google Scholar]
- Kaduk, J.A. A Rietveld tutorial—Mullite. Powder Diffr. 2009, 24, 351–361. [Google Scholar] [CrossRef]
- Canchanya-Huaman, Y.; Mayta-Armas, A.F.; Pomalaya-Velasco, J.; Bendezú-Roca, Y.; Guerra, J.A.; Ramos-Guivar, J.A. Strain and Grain Size Determination of CeO2 and TiO2 Nanoparticles: Comparing Integral Breadth Methods versus Rietveld, ?-Raman, and TEM. Nanomaterials 2021, 11, 2311. [Google Scholar] [CrossRef]
- Last, J.T. Infrared-Absorption Studies on Barium Titanate and Related Materials. Phys. Rev. 1957, 105, 1740–1750. [Google Scholar] [CrossRef]
- Perry, C.H. Far infrared reflectance spectra and dielectric dispersion of a variety of materials having the perovskite and related structures. Jpn. J. Appl. Phys. 1964, 3, 564. [Google Scholar] [CrossRef]
- Hunt, G.R.; Perry, C.H.; Ferguson, J. Far-Infrared Reflectance and Transmittance of Potassium Magnesium Fluoride and Magnesium Fluoride. Phys. Rev. 1964, 134, A688–A691. [Google Scholar] [CrossRef]
- Gao, F.; Lewis, R.A.; Wang, X.L.; Dou, S.X. Far-infrared reflection and transmission of La1- xCaxMnO3. J. Alloys Compd. 2002, 347, 314–318. [Google Scholar] [CrossRef]
- Lewis, R.A. Phonon modes in CMR manganites at elevated temperatures. J. Supercond. Inc. Nov. Magn. 2001, 14, 143–148. [Google Scholar] [CrossRef]
- Williams, Q.; Jeanloz, R. Melting relations in the iron-sulfur system at ultra-high pressures: Implications for the thermal state of the Earth. J. Geophys. Res. 1990, 95, 19299–19310. [Google Scholar] [CrossRef]
- Kim, K.H.; Gu, J.Y.; Choi, H.S.; Park, G.W.; Noh, T.W. Frequency Shifts of the Internal Phonon Modes in La 0.7 Ca 0.3 Mn O 3. Phys. Rev. Lett. 1996, 77, 1877–1880. [Google Scholar] [CrossRef]
- Kusuma, A.K.; Kumar, K.V.; Raghavender, A.T. Optical and Magnetic Properties of Chromium Doped Pr0.5Sr0.5MnO3 System. Int. J. Mech. Eng. 2022, 13, 290–299. [Google Scholar]
- Kusuma, A.K. Tunable Optical Bandgap of Chromium Doped Nd0. 5sr0. 5mno3 System Ashok Kumar Kusuma, Katrapally Vijaya Kumar* and At Raghavender. Stochastic Modeling. Available online: https://www.researchgate.net/profile/Jhansi-Rani-M-R-2/publication/382643050_Overconfidence_Bias_Finance_Risk_Taking_Attitude_and_Mutual_Fund_Investment_Decision/links/66a786c9de060e4c7e671254/Overconfidence-Bias-Finance-Risk-Taking-Attitude-and-Mutual-Fund-Investment-Decision.pdf#page=124 (accessed on 7 December 2024).
- Mishra, S.K.; Kumari, D.; Gupta, B.D. Surface plasmon resonance-based fiber optic ammonia gas sensor using ITO and polyaniline. Sens. Actuators B Chem. 2012, 171–172, 976–983. [Google Scholar] [CrossRef]
- Wu, X. High-efficiency polycrystalline CdTe thin-film solar cells. Sol. Energy 2004, 77, 803–814. [Google Scholar] [CrossRef]
- Mishra, B.; Nanda, J.; Munisha, B.; Parida, C. Transition metal ion doped Mg-Zn manganites for optoelectronic device applications. Mater. Lett. 2024, 369, 136741. [Google Scholar] [CrossRef]
- H-e, M.M.S.; Alsobhi, B.O. Consequences of Tuning Rare-Earth RE3+-Site and Exchange–Correlation Energy U on the Optoelectronic, Mechanical, and Thermoelectronic Properties of Cubic Manganite Perovskites REMnO3 for Spintronics and Optoelectronics Applications. ACS Omega 2022, 7, 27903–27917. [Google Scholar] [CrossRef]
- Yoo, J.; Lee, J.; Kim, S.; Yoon, K.; Park, I.J.; Dhungel, S.; Karunagaran, B.; Mangalaraj, D.; Yi, J. High transmittance and low resistive ZnO: Al films for thin film solar cells. Thin Solid Film. 2005, 480, 213–217. [Google Scholar] [CrossRef]
- Arshad, M.; Abushad, M.; Husain, S.; Khan, W. Investigation of Structural, Optical and Electrical Transport Properties of Yttrium Doped La0.7Ca0.3MnO3 Perovskites. Electron. Mater. Lett. 2020, 16, 321–331. [Google Scholar] [CrossRef]
- Kharrat, A.B.J.; Khirouni, K.; Boujelben, W. Electrical and optical analysis of Pr0.5−xGdxSr0.5MnO3 (x = 0, 0.05, and 0.1) manganite compounds prepared via solid-state process. Ionics 2024, 30, 1209–1222. [Google Scholar] [CrossRef]
- Hassanien, A.S.; Akl, A.A. Effect of Se addition on optical and electrical properties of chalcogenide CdSSe thin films. Superlattices Microstruct. 2016, 89, 153–169. [Google Scholar] [CrossRef]
- Kesavulu, C.; Kim, H.; Lee, S.; Kaewkhao, J.; Wantana, N.; Kaewnuam, E.; Kothan, S.; Kaewjaeng, S. Spectroscopic investigations of Nd3+ doped gadolinium calcium silica borate glasses for the NIR emission at 1059 nm. J. Alloys Compd. 2017, 695, 590–598. [Google Scholar] [CrossRef]
- Raddaoui, Z.; El Kossi, S.; Smiri, B.; Al-Shahrani, T.; Dhahri, J.; Belmabrouk, H. Raman scattering and red emission of Mn4+ in La0.7Sr0.25Na0.05Mn0.7Ti0.3O3 manganite phosphor for LED applications. RSC Adv. 2020, 10, 23615–23623. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).