Borophene-Based Anisotropic Metamaterial Perfect Absorber for Refractive Index Sensing
Abstract
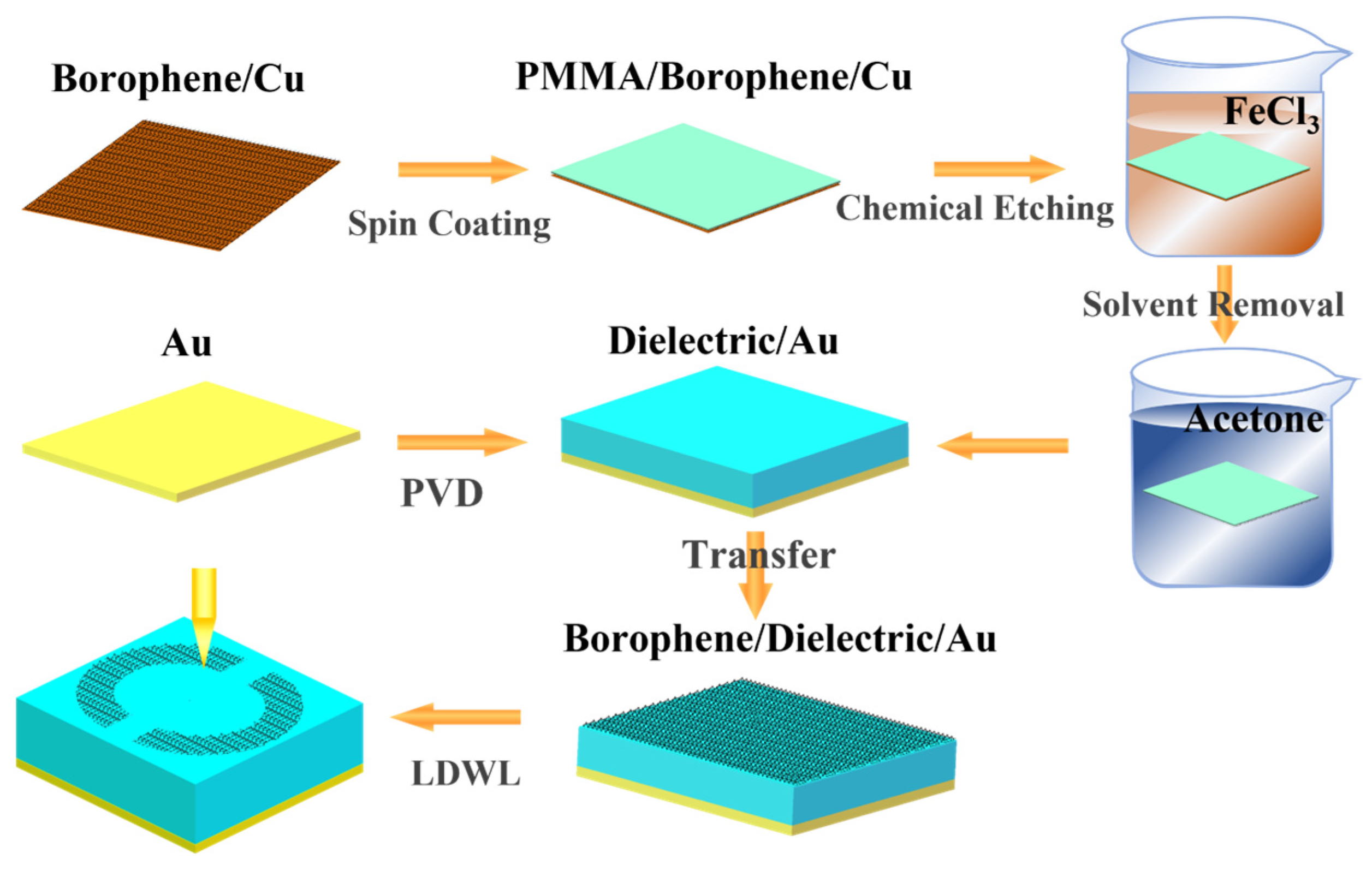
1. Introduction
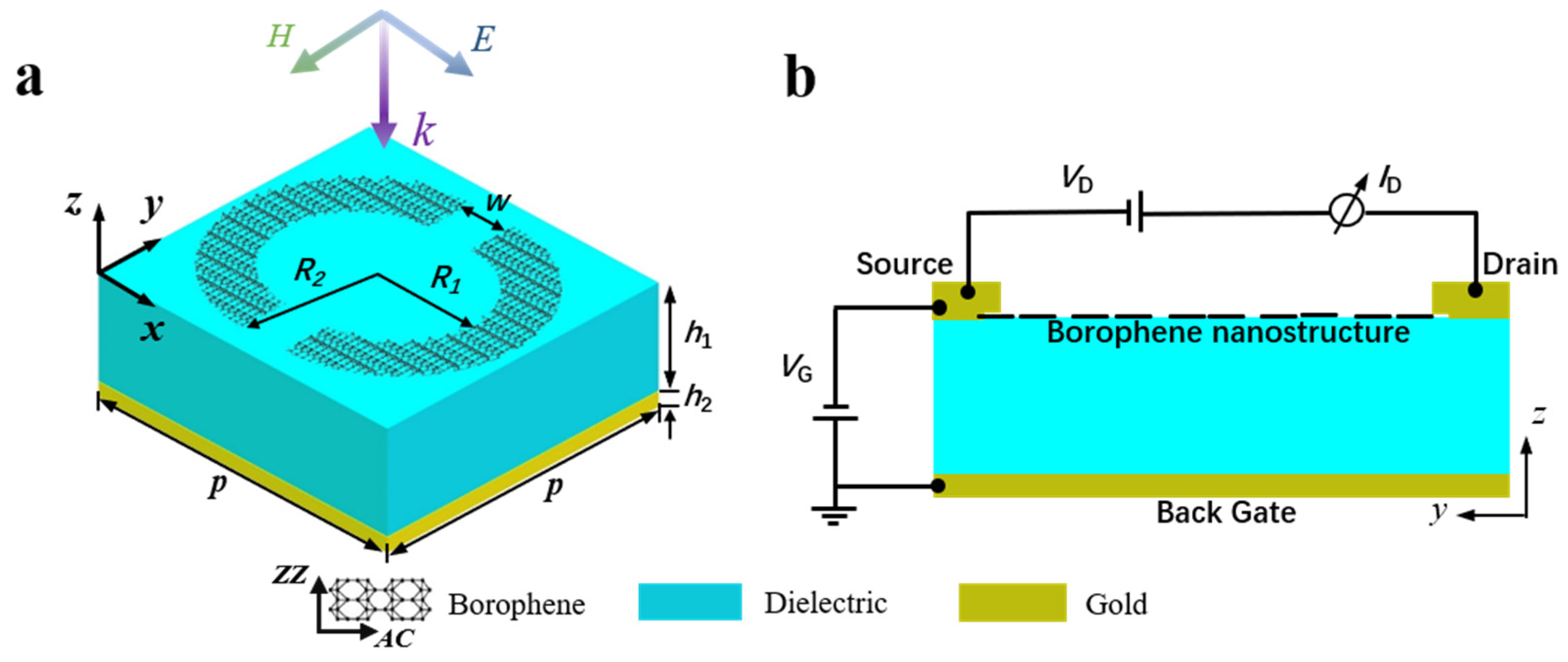
2. Structure and Methods
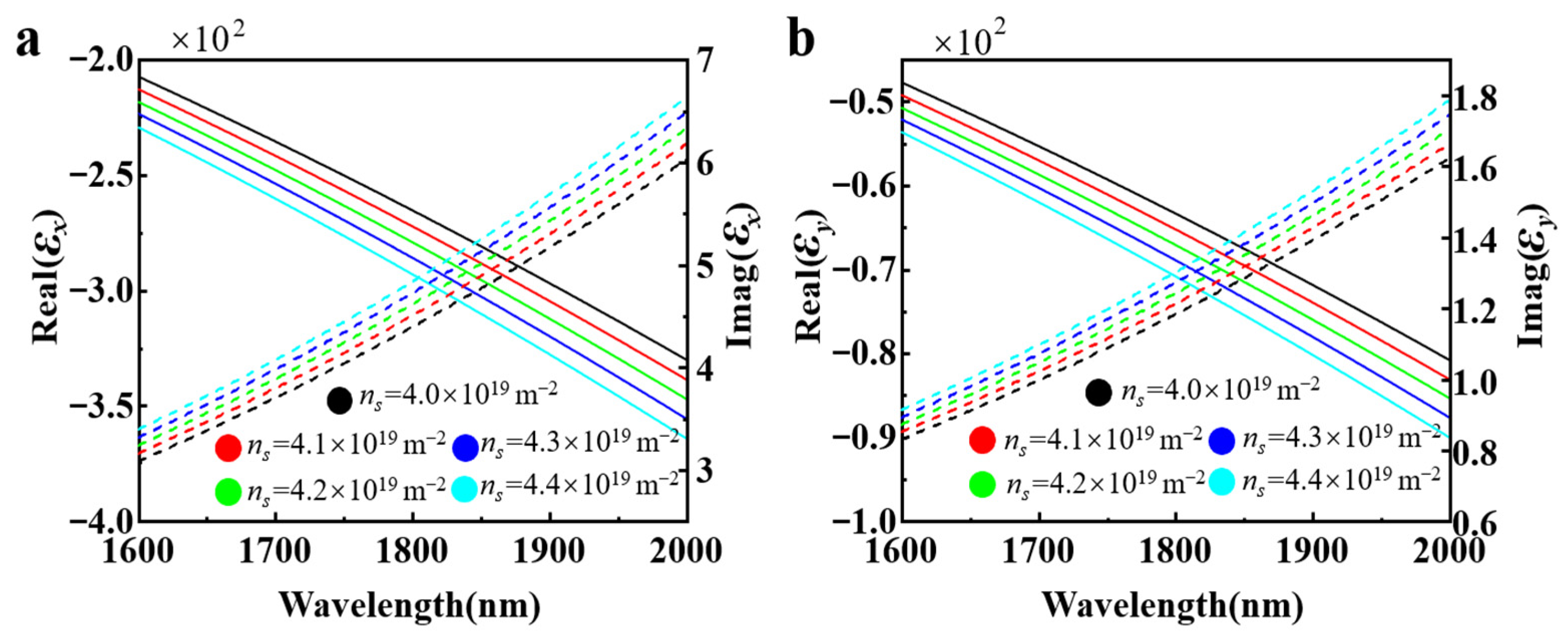
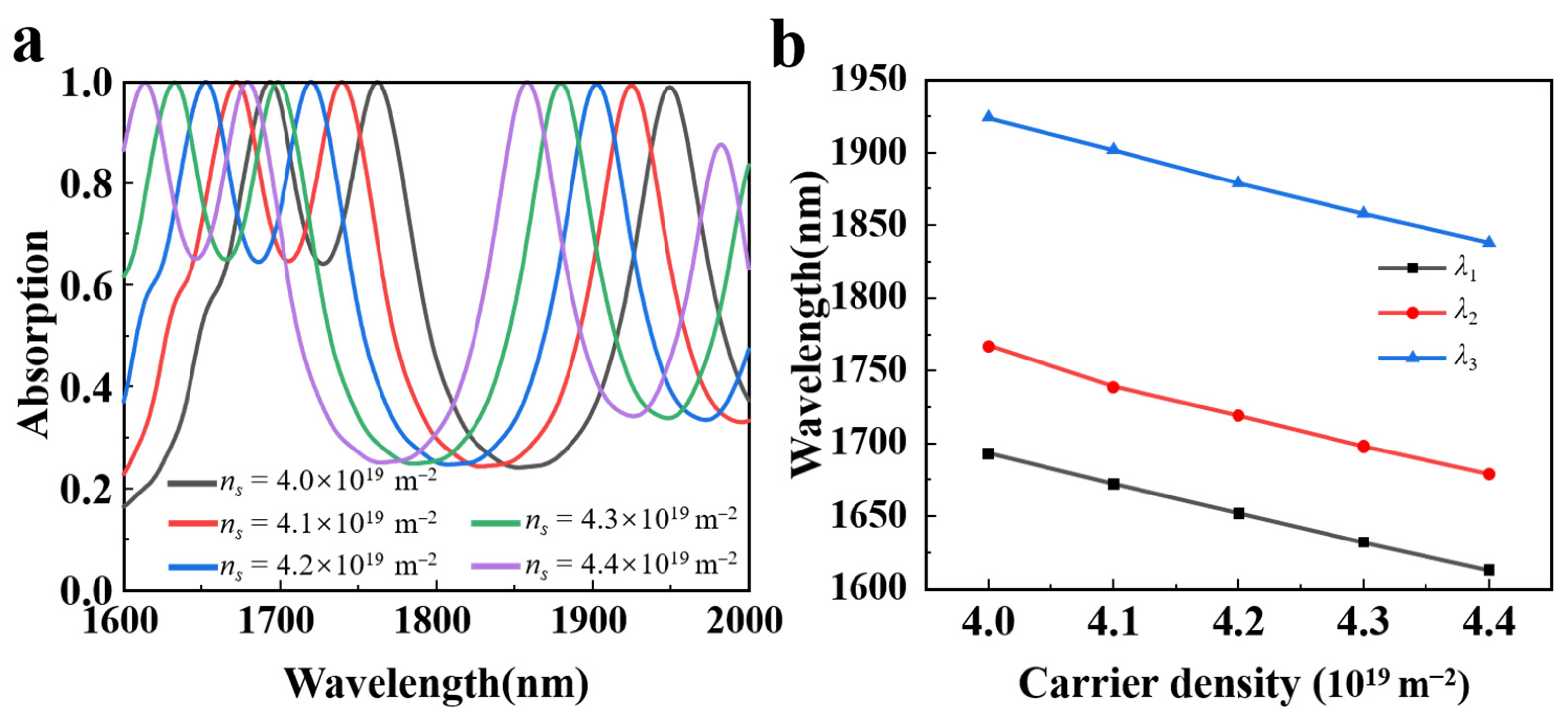
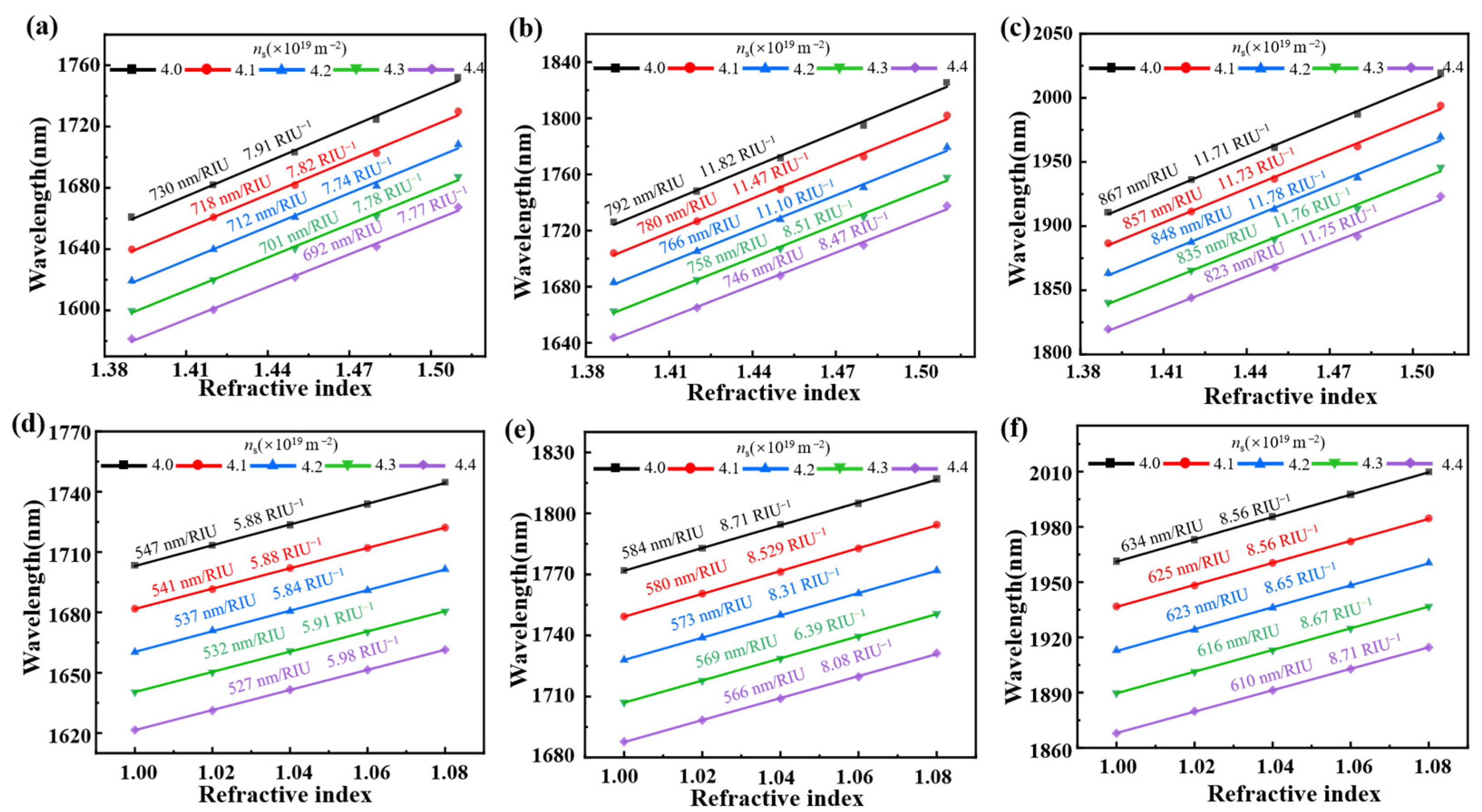
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, T.; Agrawal, A.; Abashin, M.; Chau, K.J.; Lezec, H.J. All-angle negative refraction and active flat lensing of ultraviolet light. Nature 2013, 497, 470–474. [Google Scholar] [CrossRef] [PubMed]
- Zhai, S.; Zhao, X.; Liu, S.; Shen, F.; Li, L.; Luo, C. Inverse doppler effects in broadband acoustic metamaterials. Sci. Rep. 2016, 6, 32388. [Google Scholar] [CrossRef] [PubMed]
- Duan, Z.; Tang, X.; Wang, Z.; Zhang, Y.; Chen, X.; Chen, M.; Gong, Y. Observation of the reversed Cherenkov radiation. Nat. Commun. 2017, 8, 14901. [Google Scholar] [CrossRef]
- Wu, J.; Yuan, T.; Liu, J.; Qin, J.; Hong, Z.; Li, J.; Du, Y. Terahertz metamaterial sensor with ultra-high sensitivity and tunability based on photosensitive semiconductor GaAs. IEEE Sens. J. 2022, 22, 15961–15966. [Google Scholar] [CrossRef]
- Chen, J.; Qi, H.; Liu, R.; Tang, B. Switchable large-angle beam splitter based on a continuous metasurface in the near-infrared region. Opt. Commun. 2024, 559, 130397. [Google Scholar] [CrossRef]
- Liu, Z.; Zhou, T.; Jin, G.; Su, J.; Tang, B. Switchable asymmetric transmission with broadband polarization conversion in vanadium dioxide-assisted terahertz metamaterials. Phys. Chem. Chem. Phys. 2024, 26, 1017–1022. [Google Scholar] [CrossRef]
- Landy, N.I.; Sajuyigbe, S.; Mock, J.J.; Smith, D.R.; Padilla, W.J. Perfect metamaterial absorber. Phys. Rev. Lett. 2008, 100, 207402. [Google Scholar] [CrossRef]
- Wang, B.X.; Xu, C.; Duan, G.; Xu, W.; Pi, F. Review of broadband metamaterial absorbers: From principles, design strategies, and tunable properties to functional applications. Adv. Funct. Mater. 2023, 33, 2213818. [Google Scholar] [CrossRef]
- Xiao, S.; Wang, T.; Liu, T.; Zhou, C.; Jiang, X.; Zhang, J. Active metamaterials and metadevices: A review. J. Phys. D-Appl. Phys. 2020, 53, 503002. [Google Scholar] [CrossRef]
- Gui, B.; Wang, J.; Zhu, Y.; Zhang, L.; Feng, M.; Wang, J.; Ma, H.; Qu, S. High temperature infrared-radar compatible stealthy metamaterial based on an ultrathin high-entropy alloy. Opt. Express 2022, 30, 45426–45435. [Google Scholar] [CrossRef]
- Chen, C.; Huang, Y.; Wu, K.; Bifano, T.G.; Anderson, S.W.; Zhao, X.; Zhang, X. Polarization insensitive, metamaterial absorber-enhanced long-wave infrared detector. Opt. Express 2020, 28, 28843–28857. [Google Scholar]
- Zhou, J.; Liu, X.; Zhang, H.; Liu, M.; Yi, Q.; Liu, Z.; Wang, J. Cross-shaped titanium resonators based metasurface for ultra-broadband solar absorption. IEEE Photonics J. 2021, 13, 4800108. [Google Scholar]
- Li, Z.; Butun, S.; Aydin, K. Large-area, lithography-free super absorbers and color filters at visible frequencies using ultrathin metallic films. ACS Photonics 2015, 2, 183–188. [Google Scholar] [CrossRef]
- Wang, G.; Chen, X.; Liu, S.; Wong, C.; Chu, S. Mechanical chameleon through dynamic real-time plasmonic tuning. ACS Nano 2016, 10, 1788–1794. [Google Scholar] [PubMed]
- Liu, X.; Fan, K.; Shadrivov, I.V.; Padilla, W.J. Experimental realization of a terahertz all-dielectric metasurface absorber. Opt. Express 2017, 25, 191–201. [Google Scholar]
- Zhu, Z.; Guo, C.; Liu, K.; Ye, W.; Yuan, X.; Yang, B.; Ma, T. Metallic nanofilm half-wave plate based on magnetic plasmon resonance. Opt. Lett. 2012, 37, 698–700. [Google Scholar]
- Khan, K.; Tareen, A.K.; Aslam, M.; Wang, R.; Zhang, Y.; Mahmood, A.; Ouyang, Z.; Zhang, H.; Guo, Z. Recent developments in emerging two-dimensional materials and their applications. J. Mater. Chem. C 2020, 8, 387–440. [Google Scholar]
- Xiao, S.; Liu, T.; Wang, X.; Liu, X.; Zhou, C. Tailoring the absorption bandwidth of graphene at critical coupling. Phys. Rev. B 2020, 102, 085410. [Google Scholar] [CrossRef]
- Chen, Z.; Cai, P.; Wen, Q.; Chen, H.; Tang, Y.; Yi, Z.; Wei, K.; Li, G.; Tang, B.; Yi, Y. Graphene Multi-Frequency Broadband and Ultra-Broadband Terahertz Absorber Based on Surface Plasmon Resonance. Electronics 2023, 12, 2655. [Google Scholar] [CrossRef]
- Zheng, R.; Liu, Y.; Ling, L.; Sheng, Z.; Yi, Z.; Song, Q.; Tang, B.; Zeng, Q.; Chen, J.; Sun, T. Ultra wideband tunable terahertz metamaterial absorber based on single-layer graphene strip. Diam. Relat. Mat. 2024, 141, 110713. [Google Scholar]
- Tang, B.; Guo, Z.; Jin, G. Polarization-controlled and symmetry-dependent multiple plasmon-induced transparency in graphene-based metasurfaces. Opt. Express 2022, 30, 35554–35566. [Google Scholar] [PubMed]
- Zhu, Y.; Tang, B.; Jiang, C. Tunable ultra-broadband anisotropic absorbers based on multi-layer black phosphorus ribbons. Appl. Phys. Express 2019, 12, 032009. [Google Scholar]
- Tang, B.; Yang, N.; Huang, L.; Su, J.; Jiang, C. Tunable anisotropic perfect enhancement absorption in black phosphorus-based metasurfaces. IEEE Photonics J. 2020, 12, 4500209. [Google Scholar]
- Tang, B.; Yang, N.; Song, X.; Jin, G.; Su, J. Triple-band anisotropic perfect absorbers based on α-phase MoO3 metamaterials in visible frequencies. Nanomaterials 2021, 11, 2061. [Google Scholar] [CrossRef]
- Jin, G.; Zhou, T.; Tang, B. Ultra-narrowband anisotropic perfect absorber based on α-MoO3 metamaterials in the visible light region. Nanomaterials 2022, 12, 1375. [Google Scholar] [CrossRef] [PubMed]
- Mannix, A.J.; Zhou, X.-F.; Kiraly, B.; Wood, J.D.; Alducin, D.; Myers, B.D.; Liu, X.; Fisher, B.L.; Santiago, U.; Guest, J.R. Synthesis of borophenes: Anisotropic, two-dimensional boron polymorphs. Science 2015, 350, 1513–1516. [Google Scholar]
- Feng, B.; Zhang, J.; Zhong, Q.; Li, W.; Li, S.; Li, H.; Cheng, P.; Meng, S.; Chen, L.; Wu, K. Experimental realization of two-dimensional boron sheets. Nat. Chem. 2016, 8, 563–568. [Google Scholar]
- Hafez, H.A.; Kovalev, S.; Deinert, J.-C.; Mics, Z.; Green, B.; Awari, N.; Chen, M.; Germanskiy, S.; Lehnert, U.; Teichert, J. Extremely efficient terahertz high-harmonic generation in graphene by hot Dirac fermions. Nature 2018, 561, 507–511. [Google Scholar] [PubMed]
- Kaneti, Y.V.; Benu, D.P.; Xu, X.; Yuliarto, B.; Yamauchi, Y.; Golberg, D. Borophene: Two-dimensional boron monolayer: Synthesis, properties, and potential applications. Chem. Rev. 2021, 122, 1000–1051. [Google Scholar]
- Mannix, A.J.; Zhang, Z.; Guisinger, N.P.; Yakobson, B.I.; Hersam, M.C. Borophene as a prototype for synthetic 2D materials development. Nat. Nanotechnol. 2018, 13, 444–450. [Google Scholar]
- Nong, J.; Feng, F.; Min, C.; Yuan, X.; Somekh, M. Effective transmission modulation at telecommunication wavelengths through continuous metal films using coupling between borophene plasmons and magnetic polaritons. Adv. Opt. Mater. 2021, 9, 2001809. [Google Scholar] [CrossRef]
- Nong, J.; Feng, F.; Min, C.; Yuan, X.; Somekh, M. Controllable hybridization between localized and delocalized anisotropic borophene plasmons in the near-infrared region. Opt. Lett. 2021, 46, 725–728. [Google Scholar]
- Jian, R.; Wu, S.; Zhao, B.; Xiong, G. Tunable multi-peak perfect absorbers based on borophene for high-performance near-infrared refractive index sensing. Opt. Mater. 2022, 131, 112751. [Google Scholar]
- Zhang, J.; Zhang, Z.; Song, X.; Zhang, H.; Yang, J. Infrared plasmonic sensing with anisotropic two-dimensional material borophene. Nanomaterials 2021, 11, 1165. [Google Scholar] [CrossRef]
- Liu, T.; Zhou, C.; Xiao, S. Tailoring anisotropic absorption in a borophene-based structure via critical coupling. Opt. Express 2021, 29, 8941–8950. [Google Scholar] [CrossRef]
- Liu, J.; Liu, Y. Perfect Narrow-Band Absorber of Monolayer Borophene in All-Dielectric Grating Based on Quasi-Bound State in the Continuum. Ann. Phys. 2023, 535, 2200500. [Google Scholar]
- Yang, C.; Lin, Q.; Du, W.-J.; Wang, L.-L.; Liu, G.-D. Bi-tunable absorber based on borophene and VO2 in the optical telecommunication band. J. Opt. Soc. Am. B 2022, 39, 2969–2974. [Google Scholar] [CrossRef]
- Vafapour, Z.; Ghahraloud, H.; Keshavarz, A.; Islam, M.S.; Rashidi, A.; Dutta, M.; Stroscio, M.A. The potential of refractive index nanobiosensing using a multi-band optically tuned perfect light metamaterial absorber. IEEE Sens. J. 2021, 21, 13786–13793. [Google Scholar] [CrossRef]
- Dereshgi, S.A.; Liu, Z.; Aydin, K. Anisotropic localized surface plasmons in borophene. Opt. Express 2020, 28, 16725–16739. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [PubMed]
- Guo, S.; Wang, Y.; Qu, H.; Zhou, W.; Ang, Y.S.; Zhang, S.; Zeng, H. Theoretical dissection of the electronic anisotropy and quantum transport of ultrascaled halogenated borophene MOSFETs. Phys. Rev. Appl. 2024, 21, 054016. [Google Scholar]
- Saeidi, A.; Jazaeri, F.; Stolichnov, I.; Enz, C.C.; Ionescu, A.M. Negative capacitance as universal digital and analog performance booster for complementary MOS transistors. Sci. Rep. 2019, 9, 9105. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Kong, L.; Chen, C.; Gou, J.; Sheng, S.; Zhang, W.; Li, H.; Chen, L.; Cheng, P.; Wu, K. Experimental realization of honeycomb borophene. Sci. Bull. 2018, 63, 282–286. [Google Scholar]
- Palik, E.D. Handbook of Optical Constants of Solids; Academic Press: Cambridge, MA, USA, 1998. [Google Scholar]
- He, L.; Yi, Y.; Zhang, J.; Xu, X.; Tang, B.; Li, G.; Zeng, L.; Chen, J.; Sun, T.; Yi, Z. A four-narrowband terahertz tunable absorber with perfect absorption and high sensitivity. Mater. Res. Bull. 2024, 170, 112572. [Google Scholar]
- Meng, B.; Booske, J.; Cooper, R. Extended cavity perturbation technique to determine the complex permittivity of dielectric materials. IEEE Trans. Microw. Theory Tech. 1995, 43, 2633–2636. [Google Scholar]
- Choi, W.J.; Jeon, D.I.; Ahn, S.-G.; Yoon, J.-H.; Kim, S.; Lee, B.H. Full-field optical coherence microscopy for identifying live cancer cells by quantitative measurement of refractive index distribution. Opt. Express 2010, 18, 23285–23295. [Google Scholar]
- Guo, T.; Zhong, Y.; Yan, Z.; Pu, X.; Du, W.; Gao, F.; Tang, C. Temperature Tunable Multiple Ultraviolet to near-Infrared Perfect Absorption as Highly Sensitive Metamaterial Biosensor. IEEE Sens. J. 2024, 24, 9909–9915. [Google Scholar]
- Peng, W.; Zhang, G.; Lv, Y.; Qin, L.; Qi, K. Ultra-narrowband absorption filter based on a multilayer waveguide structure. Opt. Express 2021, 29, 14582–14600. [Google Scholar] [CrossRef]
- Wan, Y.; An, Y.; Tao, Z.; Deng, L. Manipulation of surface plasmon resonance of a graphene-based Au aperture antenna in visible and near-infrared regions. Opt. Commun. 2018, 410, 733–739. [Google Scholar]
- Li, B.; Wei, Y.; Zeng, L.; Liu, M.; Wen, R.; Zhang, X.; Deng, C. A tunable perfect absorber based on a black phosphorus/bowtie shaped cavity hybrid metasurface. Phys. Chem. Chem. Phys. 2023, 25, 18109–18120. [Google Scholar]
- Yin, X.; Sang, T.; Qi, H.; Li, G.; Wang, X.; Wang, J.; Wang, Y. Symmetry-broken square silicon patches for ultra-narrowband light absorption. Sci. Rep. 2019, 9, 17477. [Google Scholar]
- Wu, P.; Chen, Z.; Jile, H.; Zhang, C.; Xu, D.; Lv, L. An infrared perfect absorber based on metal-dielectric-metal multi-layer films with nanocircle holes arrays. Results Phys. 2020, 16, 102952. [Google Scholar]
- Wu, R.; Drozdov, I.K.; Eltinge, S.; Zahl, P.; Ismail-Beigi, S.; Božović, I.; Gozar, A. Large-area single-crystal sheets of borophene on Cu (111) surfaces. Nat. Nanotechnol. 2019, 14, 44–49. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Z.; Yang, H.; Jin, G.; Zhu, Y.; Tang, B. Borophene-Based Anisotropic Metamaterial Perfect Absorber for Refractive Index Sensing. Nanomaterials 2025, 15, 509. https://doi.org/10.3390/nano15070509
Lin Z, Yang H, Jin G, Zhu Y, Tang B. Borophene-Based Anisotropic Metamaterial Perfect Absorber for Refractive Index Sensing. Nanomaterials. 2025; 15(7):509. https://doi.org/10.3390/nano15070509
Chicago/Turabian StyleLin, Zichen, Haorui Yang, Gui Jin, Ying Zhu, and Bin Tang. 2025. "Borophene-Based Anisotropic Metamaterial Perfect Absorber for Refractive Index Sensing" Nanomaterials 15, no. 7: 509. https://doi.org/10.3390/nano15070509
APA StyleLin, Z., Yang, H., Jin, G., Zhu, Y., & Tang, B. (2025). Borophene-Based Anisotropic Metamaterial Perfect Absorber for Refractive Index Sensing. Nanomaterials, 15(7), 509. https://doi.org/10.3390/nano15070509








