Study on Vacuum Breakdown Properties of Surface-Modified 304 Stainless Steel Electrodes Based on Fractal Theory
Abstract
1. Introduction
2. Experimental Details
2.1. Materials and Preparation
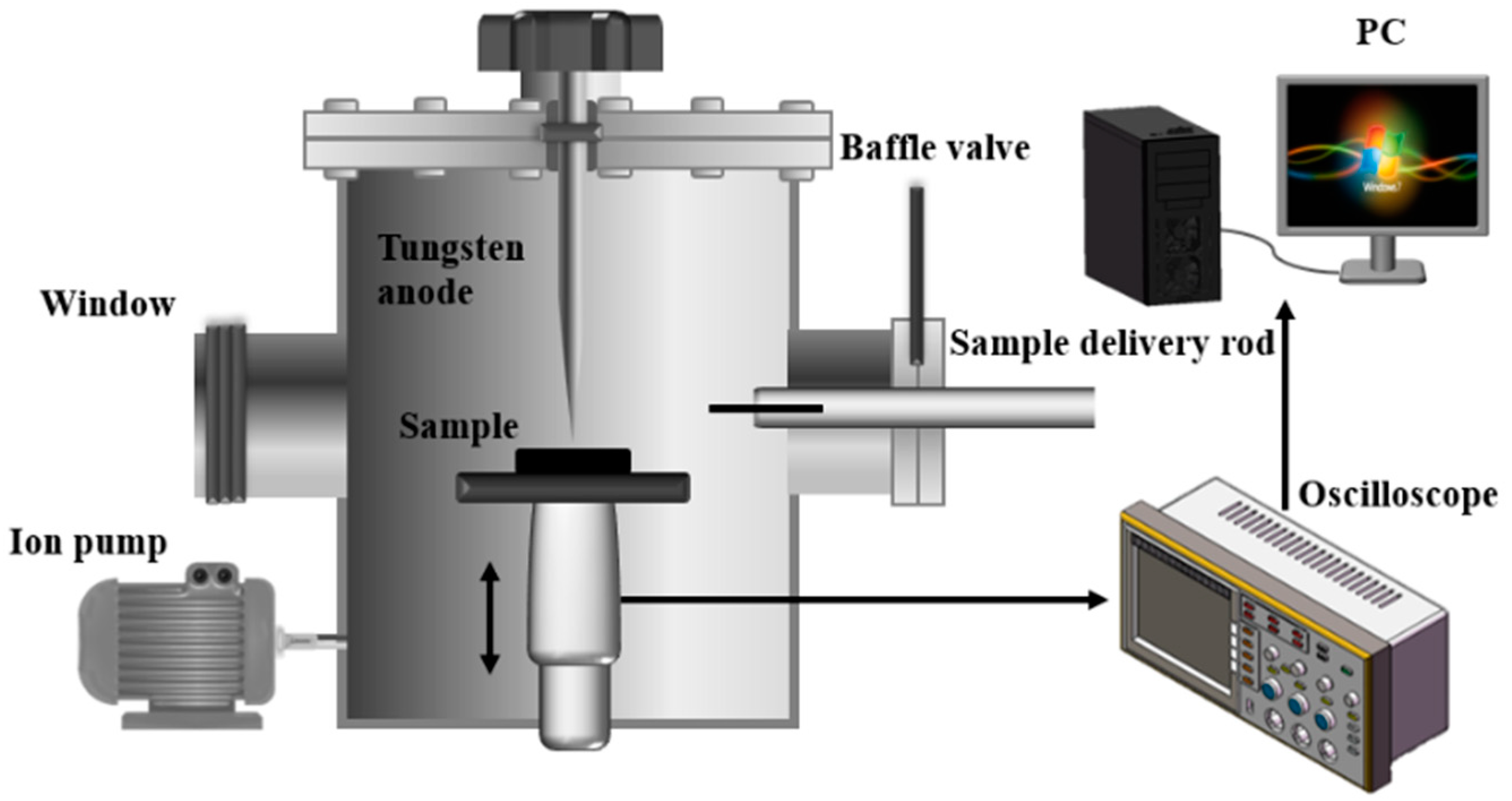
2.2. Characterization Equipment
2.3. Breakdown Characteristic Test
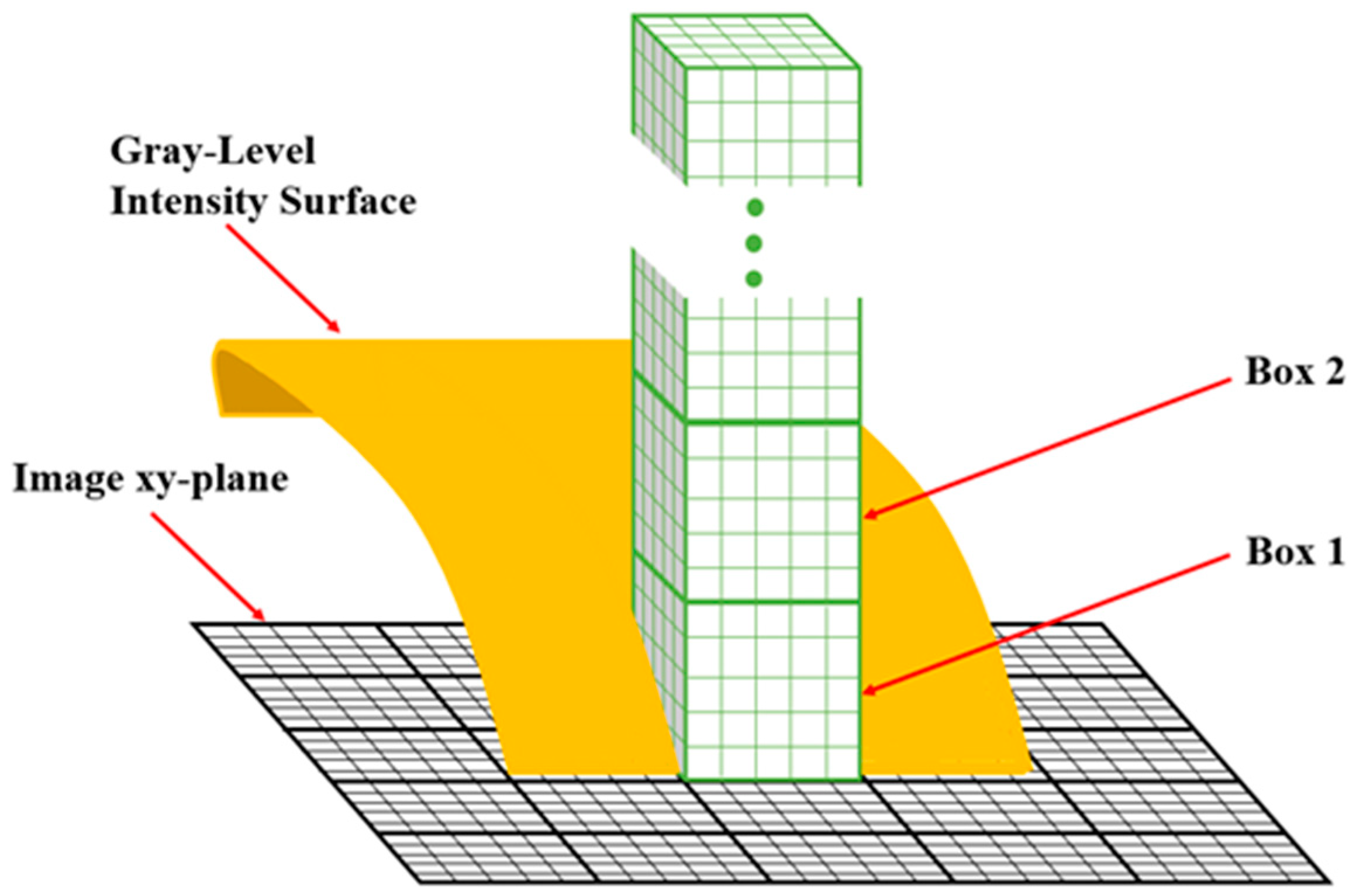
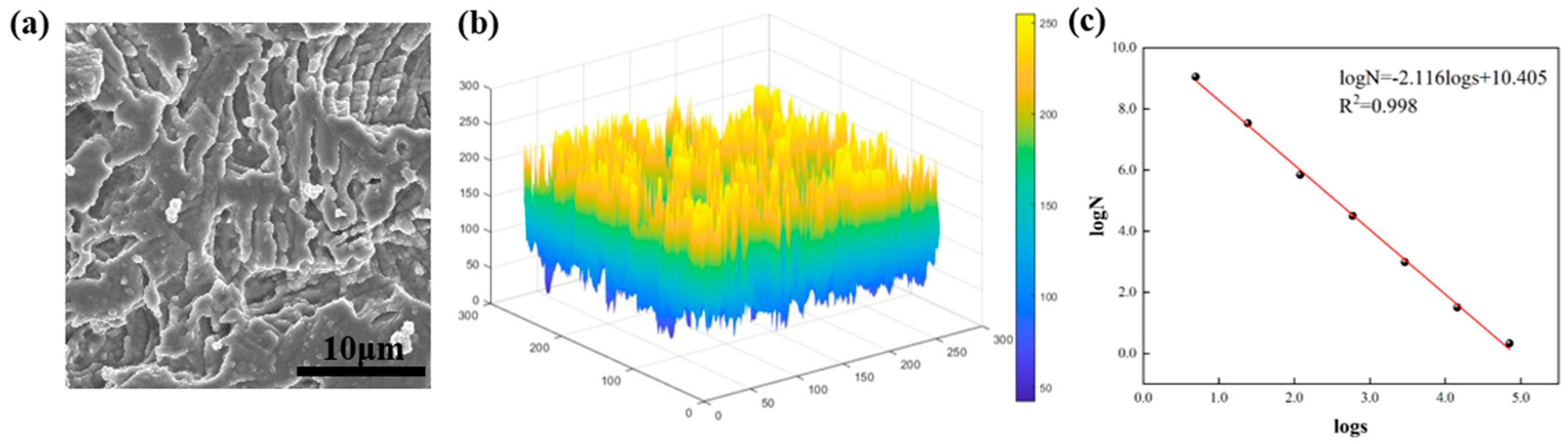
2.4. Box-Counting Method
3. Result and Discussion
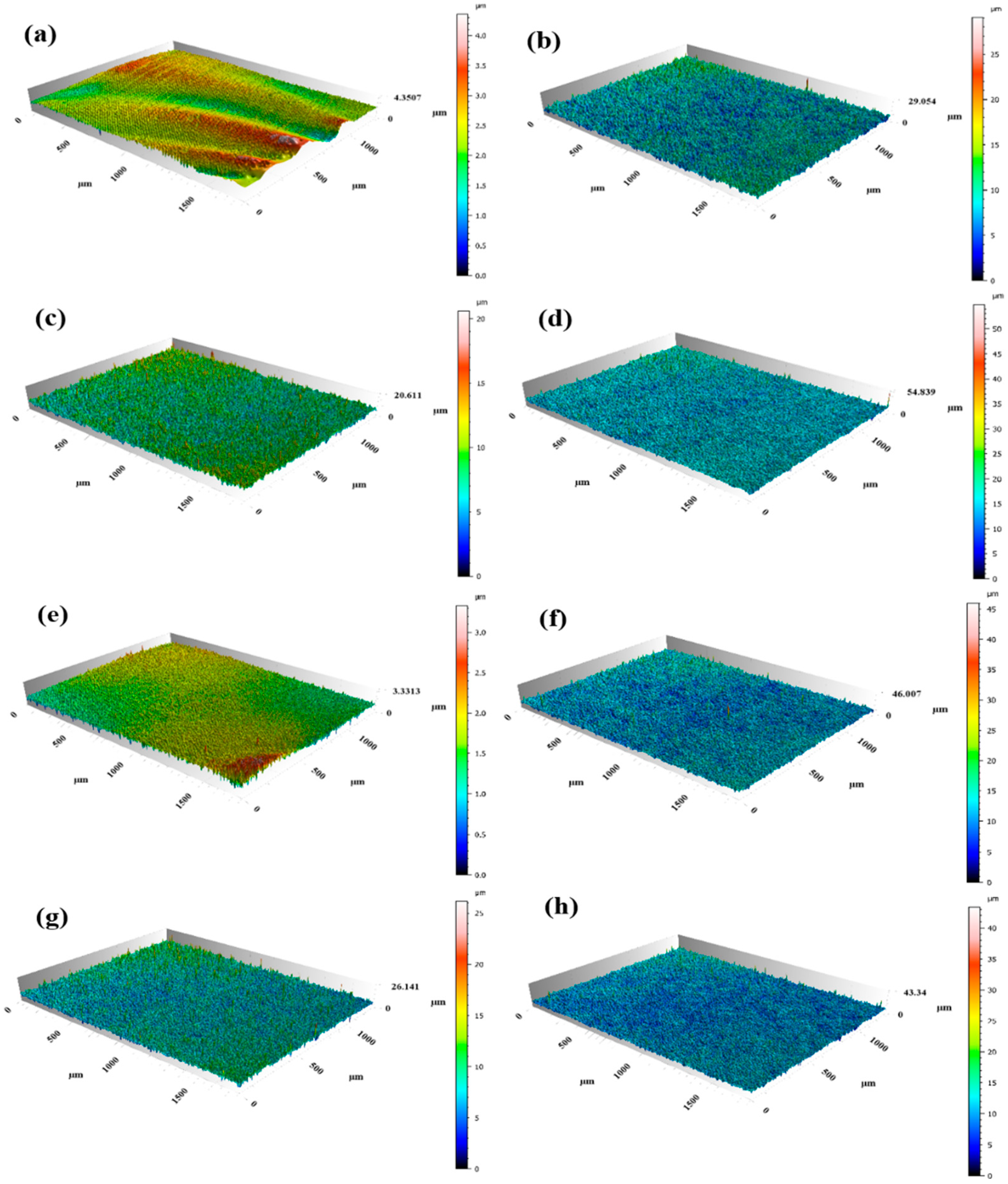
3.1. Morphological Characteristics of the Electrode Surface After Different Modification Treatments
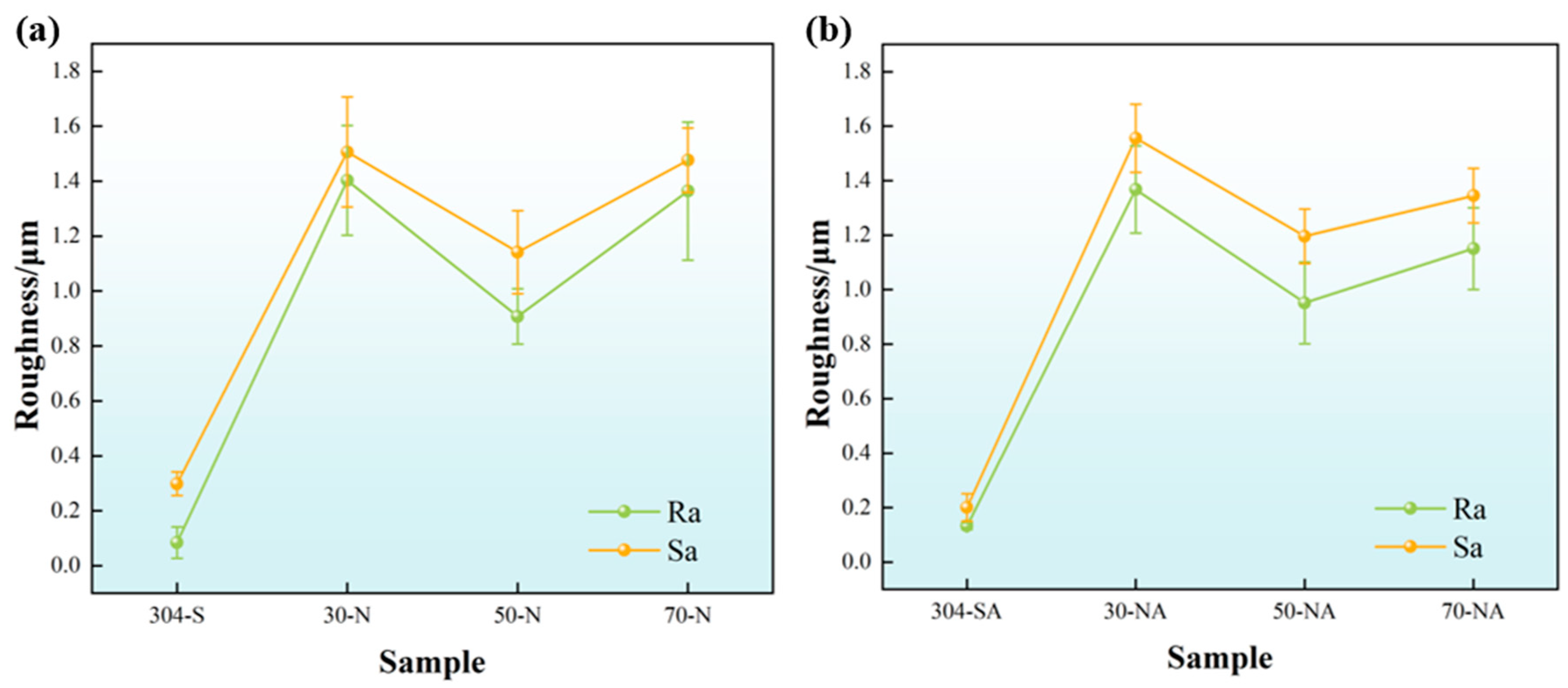
3.2. Fractal Dimension of Electrode Surface After Different Modification Treatments
3.3. Relationship Between Fractal Dimension and Surface Morphology of Electrodes After Modification Treatment
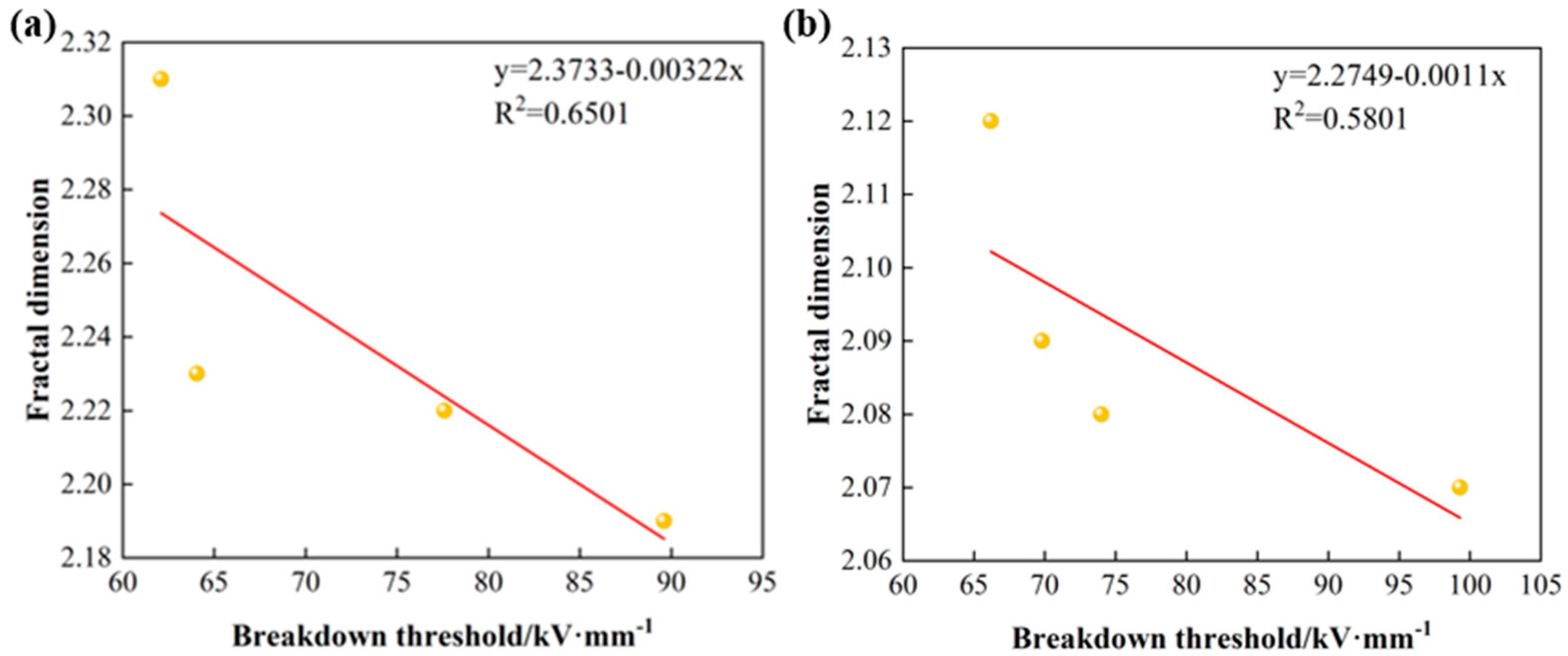
3.4. Relationship Between Fractal Dimension and Breakdown Threshold of Modified Electrodes
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kishek, R.; Lau, Y.Y. A novel phase focusing mechanism in multipactor discharge. Phys. Plasmas 1996, 3, 1481–1483. [Google Scholar] [CrossRef]
- Zhu, F.; Proch, D.; Hao, J.-K. Multipacting phenomenon at high electric fields of superconducting cavities. Chin. Phys. 2005, 14, 494. [Google Scholar]
- Huang, J.; Liu, G.; Wang, Z.; Jiang, L.; Yuan, X.; Liu, Y.; Deng, J.; Yi, Z. High voltage breakdown induced by outgassing of space materials. AIP Adv. 2015, 5, 037119. [Google Scholar] [CrossRef]
- Barengolts, S.A.; Mesyats, V.G.; Oreshkin, V.I.; Oreshkin, E.V.; Khishchenko, K.V.; Uimanov, I.V.; Tsventoukh, M.M. Mechanism of vacuum breakdown in radio-frequency accelerating structures. Phys. Rev. Accel. Beams 2018, 21, 061004. [Google Scholar] [CrossRef]
- Radmilovic-Radjenovic, D.M.; Radjenovic, M.B. Simulation study of direct current vacuum breakdown and its application to high-gradient accelerating structures. Nucl. Technol. Radiat. Prot. 2020, 35, 30–35. [Google Scholar] [CrossRef]
- Lauer, E.J.; Lauer, C.J. Electron avalanche on a dielectric-vacuum interface. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 1295–1299. [Google Scholar] [CrossRef]
- Cuneo, M.E. The effect of electrode contamination, cleaning and conditioning on high-energy pulsed-power device performance. IEEE Trans. Dielectr. Electr. Insul. 1999, 6, 469–485. [Google Scholar] [CrossRef]
- Li, L.; Liu, L.; Wen, J. Microstructure changes of cathodes after electron emission in high power diodes. J. Phys. D Appl. Phys. 2007, 40, 5338. [Google Scholar] [CrossRef]
- Simakov, E.I.; Dolgashev, V.A.; Tantawi, S.G. Advances in high gradient normal conducting accelerator structures. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2018, 907, 221–230. [Google Scholar] [CrossRef]
- Yan, W.; Wang, Z.; Cao, Z.; Li, H.; Sun, L.; Wang, J.; Generation, P. Their Behavior and Effect on Post-Arc Breakdowns After Capacitive-Current Vacuum Arc Interruption. IEEE Trans. Power Deliv. 2022, 37, 4303–4314. [Google Scholar] [CrossRef]
- Mayberry, C.S.; Wroblewski, B.; Schamiloglu, E.; Fleddermann, C.B. Suppression of vacuum breakdown using thin-film coatings. J. Appl. Phys. 1994, 76, 4448–4450. [Google Scholar] [CrossRef]
- Zhang, Y.; Su, J.; Qiu, X.; Li, R.; Zhao, L.; Cheng, J.; Zeng, B. Micro-effects of surface polishing treatment on microscopic field enhancement and long vacuum gap breakdown. AIP Adv. 2016, 6, 095103. [Google Scholar] [CrossRef]
- Zhang, T.; Lei, Y.; Yin, J.; Du, J.; Yu, P. Effects of pores on dielectric breakdown of alumina ceramics under AC electric field. Ceram. Int. 2019, 45, 13951–13957. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Stochastic models for the Earth’s relief, the shape and the fractal dimension of the coastlines, and the number-area rule for islands. Proc. Natl. Acad. Sci. USA 1975, 72, 3825–3828. [Google Scholar] [CrossRef] [PubMed]
- Dong, L. Mechanical response of Ti–6Al–4V hierarchical architected metamaterials. Acta Mater. 2019, 175, 90–106. [Google Scholar] [CrossRef]
- Jiang, Z.-Q.; Xie, W.-J.; Zhou, W.-X.; Sornette, D. Multifractal analysis of financial markets: A review. Rep. Prog. Phys. 2019, 82, 125901. [Google Scholar] [CrossRef]
- Yadav, R.P.; Kumar, T.; Baranwal, V.; Vandana; Kumar, M.; Priya, P.K.; Pandey, S.N.; Mittal, A.K. Fractal characterization and wettability of ion treated silicon surfaces. J. Appl. Phys. 2017, 121, 055301. [Google Scholar] [CrossRef]
- Jain, R.; Pitchumani, R. Fractal Model for Wettability of Rough Surfaces. Langmuir 2017, 33, 7181–7190. [Google Scholar] [CrossRef]
- Chen, Z.; Pan, D.; Zhao, B.; Ding, G.; Jiao, Z.; Wu, M.; Shek, C.-H.; Wu, L.C.M.; Lai, J.K.L. Insight on Fractal Assessment Strategies for Tin Dioxide Thin Films. ACS Nano 2010, 4, 1202–1208. [Google Scholar] [CrossRef]
- Othman, M.R.; Mustafa, N.N.N.; Ahmad, A.L. Effect of thermal treatment on the microstructure of sol–gel derived porous alumina modified platinum. Microporous Mesoporous Mater. 2006, 91, 268–275. [Google Scholar] [CrossRef]
- Chaudhuri, B.B.; Sarkar, N. Texture Segmentation Using Fractal Dimension. IEEE Trans. Pattern Anal. Mach. Intell. 1995, 17, 72–77. [Google Scholar] [CrossRef]
- Chen, S.S.; Keller, J.M.; Crownover, R.M. On the Calculation of Fractal Features from Images. IEEE Trans. Pattern Anal. Mach. Intell. 1993, 15, 1087–1090. [Google Scholar] [CrossRef]
- Cremers, V.; Puurunen, R.L.; Dendooven, J. Conformality in atomic layer deposition: Current status overview of analysis and modelling. Appl. Phys. Rev. 2019, 6, 021302. [Google Scholar] [CrossRef]
- Schmaljohann, F.; Hagedorn, D.; Löffler, F. Electrical insulation performance of aluminum oxide layers on metallic substrates—HiPIMS compared to RF-MS. Surf. Coat. Technol. 2019, 361, 119–122. [Google Scholar] [CrossRef]
- Richey, N.E.; de Paula, C.; Bent, S.F. Understanding chemical and physical mechanisms in atomic layer deposition. J. Chem. Phys. 2020, 152, 040902. [Google Scholar] [CrossRef]






| Sample | Pickling Passivation | ALD Cycle/Time | ||
|---|---|---|---|---|
| Solution | Temperature/°C | Time/min | ||
| 304-S | - | - | - | - |
| 30-N | 10%HNO3 + 5%HCl | 60 | 30 | - |
| 50-N | 10%HNO3 + 5%HCl | 60 | 50 | - |
| 70-N | 10%HNO3 + 5%HCl | 60 | 70 | - |
| 304-SA | - | - | - | 2000 |
| 30-NA | 10%HNO3 + 5%HCl | 60 | 30 | 2000 |
| 50-NA | 10%HNO3 + 5%HCl | 60 | 50 | 2000 |
| 70-NA | 10%HNO3 + 5%HCl | 60 | 70 | 2000 |
| Composition | Precursor | Precursor Temperature/°C | Oxygen Source | Deposition Temperature/°C | t1~t4/Time |
|---|---|---|---|---|---|
| Al2O3 | TMA | 200 | H2O2 | 25 | 0.5-17-0.1-16 |
| Sample | Size of Small Lamellae Within the Island Structure/μm | Continuous Island Size/μm | Covered Area/% | ||||
|---|---|---|---|---|---|---|---|
| Average | Maximum | Minimum | Average | Maximum | Minimum | ||
| 304-S | (Bulges) 2.61 | 4.00 | 1.28 | - | - | - | 57.273 |
| 30-N | 5.03 | 7.74 | 2.08 | 2.87 | 3.72 | 2.01 | 51.314 |
| 50-N | 7.90 | 14.35 | 4.59 | 12.21 | 23.81 | 3.92 | 56.683 |
| 70-N | (Granulate) 2.12 | 7.01 | 0.4 | 9.57 | 21.59 | 4.31 | 52.755 |
| 304-SA | (Granulate) 0.7 | 1.54 | 0.3 | - | - | - | 87.379 |
| 30-NA | 7.62 | 13.27 | 4.01 | 30.72 | 44.11 | 17.6 | 75.777 |
| 50-NA | 6.47 | 11.65 | 3.31 | 10.2 | 20.72 | 4.28 | 67.203 |
| 70-NA | (Granulate) 1.48 | 3.56 | 0.73 | Continuous island | - | - | 67.131 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Zhao, S.; Liu, B.; Shan, W.; Wei, H.; Ma, D.; Wang, H. Study on Vacuum Breakdown Properties of Surface-Modified 304 Stainless Steel Electrodes Based on Fractal Theory. Nanomaterials 2025, 15, 340. https://doi.org/10.3390/nano15050340
Wang S, Zhao S, Liu B, Shan W, Wei H, Ma D, Wang H. Study on Vacuum Breakdown Properties of Surface-Modified 304 Stainless Steel Electrodes Based on Fractal Theory. Nanomaterials. 2025; 15(5):340. https://doi.org/10.3390/nano15050340
Chicago/Turabian StyleWang, Shiqing, Shenming Zhao, Bo Liu, Weihong Shan, Hao Wei, Dayan Ma, and Hongbo Wang. 2025. "Study on Vacuum Breakdown Properties of Surface-Modified 304 Stainless Steel Electrodes Based on Fractal Theory" Nanomaterials 15, no. 5: 340. https://doi.org/10.3390/nano15050340
APA StyleWang, S., Zhao, S., Liu, B., Shan, W., Wei, H., Ma, D., & Wang, H. (2025). Study on Vacuum Breakdown Properties of Surface-Modified 304 Stainless Steel Electrodes Based on Fractal Theory. Nanomaterials, 15(5), 340. https://doi.org/10.3390/nano15050340






