Next Article in Journal
Green Synthesis of Highly Luminescent Carbon Quantum Dots from Asafoetida and Their Antibacterial Properties
Previous Article in Journal
Synthesis of Nanoparticles of Different Morphology in a DC Discharge
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Nanomaterials
Volume 15
Issue 23
10.3390/nano15231803
nanomaterials-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Designing 2D Wide Bandgap Semiconductor B12X2H6 (X=O, S) Based on Aromatic Icosahedral B12

by
Pei Gong
1,
Jun-Hui Yuan
2,*,
Gen-Ping Wu
3,
Zhi-Hong Liu
3,
Hao Wang
3,* and
Jiafu Wang
2
1
School of Mathematics and Physics, Nanyang Institute of Technology, Nanyang 473004, China
2
School of Physics and Mechanics, Wuhan University of Technology, Wuhan 430070, China
3
Wuhan Second Ship Design and Research Institute, Wuhan 430205, China
*
Authors to whom correspondence should be addressed.
Nanomaterials 2025, 15(23), 1803; https://doi.org/10.3390/nano15231803 (registering DOI)
Submission received: 3 November 2025 / Revised: 27 November 2025 / Accepted: 27 November 2025 / Published: 29 November 2025
(This article belongs to the Special Issue Analysis of 2D Semiconductor: Materials, Devices and Applications)
Browse Figures
Versions Notes

Abstract

Constructing two-dimensional (2D) novel materials using superatoms as building blocks is currently a highly promising research field. In this study, by employing an oxidation strategy and based on first-principles calculations, we successfully predicted two types of 2D borides, namely B12X2H6 (X=O, S), with icosahedral B12 serving as their core structural unit. Ab initio molecular dynamics simulations demonstrated that these two borides exhibit exceptionally high structural stability, retaining their original structural characteristics even under extreme temperature conditions as high as 2200 K. Electronic structure calculations revealed that B12O2H6 and B12S2H6 are both wide-bandgap indirect semiconductors, with bandgap widths reaching 4.92 eV and 5.25 eV, respectively. Analysis via deformation potential theory showed that the phonon-limited carrier mobilities of B12X2H6 can reach up to 1469 cm2V−1s−1 (for B12O2H6) and 635 cm2V−1s−1 (for B12S2H6). Notably, the surfaces of B12X2H6 demonstrate excellent migration performance for alkali metal ions, with migration barriers as low as 0.15 eV (for B12O2H6) and 0.033 eV (for B12S2H6). This study not only expands the family of 2D materials based on B12 superatoms but also provides a solid theoretical foundation for the potential application of B12X2H6 in the field of low-dimensional materials.

1. Introduction

Boron, as a unique element located at the junction of metals and non-metals in the periodic table, possesses electronic structural characteristics akin to a magical key, opening a gateway for boron-based materials to a realm of physicochemical diversity far surpassing that of traditional two-dimensional (2D) materials. In 2015, the teams of Tai et al. [1] and Mannix et al. [2] successfully synthesized 2D boron monolayers on copper foil and silver substrates, respectively. This milestone achievement not only robustly confirmed the stable existence of boron atomic layers at room temperature but also heralded a new era in 2D borophene research, guiding researchers into this field full of unknowns and surprises [3].
Boron’s electron-deficient nature renders it akin to a masterful architect, inclined to construct multicenter bonding networks. This characteristic blossoms brilliantly at the 2D scale, giving rise to a rich array of structural polymorphisms [4,5,6]. Theoretical calculations, like a precise prophet, have unveiled that borophene may exist in over 20 stable configurations, including α-, β-, and γ-phase [7,8,9]. Among them, the γ-phase boron monolayer, through the synergistic interplay of B12 and B2 units, exhibits remarkable mechanical strength with a Young’s modulus of up to 398 GPa and exceptional thermal stability, maintaining structural integrity even at 1000 °C [10]. However, the non-layered structure of bulk boron poses a formidable barrier, rendering traditional mechanical exfoliation methods ineffective. To overcome this challenge, researchers have continuously developed novel preparation techniques, such as chemical vapor deposition (CVD) and molecular beam epitaxy (MBE) [11,12]. Nevertheless, constrained by substrate dependency, the path to large-scale preparation remains fraught with challenges.
Leveraging its flexibly adjustable electronic properties, boron can give rise to numerous superatoms. Among them, the experimentally known most stable superatom, the icosahedral borane B12H122−, stands as one of its outstanding masterpieces [13]. A growing body of experimental and theoretical evidence supports that in the “bottom-up” approach, cluster superatoms, akin to exquisite building blocks, can serve as construction units to erect the grand edifice of self-assembled compounds and nanomaterials [14,15,16]. It is widely recognized that all 17 experimentally observed bulk boron allotropes to date contain icosahedral B12 structural units. In most cases, these units are accompanied by a certain number of boron atoms located outside the cage as interstitial atoms [17,18]. Therefore, constructing 2D borophene based on icosahedral B12 undoubtedly represents a field of immense research value and potential. Recently, Yan et al., utilizing aromatic icosahedral superatoms Ih B12H122− and D5d 1,12-C2B10H12 as construction units, predicted a series of core–shell polyhedral boranes and carboranes through a clever “bottom-up” approach with the aid of density functional theory calculations [19]. These findings can be further extended to form 1D and 2D boranes, injecting new vitality into borophene and borane research and significantly enriching the research landscape in this field.
Among the materials proposed by Yan et al., the 2D B12H6 monolayer has attracted our particular attention. As illustrated in Figure 1a, B12H6 forms a stable 2D network through inter-unit B-B bonds. However, our analysis revealed a critical detail: the B-B bond length connecting adjacent B12H6 units is 2.004 Å, notably longer than the typical B-B bond lengths observed in conventional borophene. This longer bond indicates relatively weaker structural stability but also presents a valuable opportunity for material modification. For instance, introducing oxidation at the B-containing triangular sites at the center of the B12H6 unit (marked by light red and light blue solid circles in Figure 1a) could yield a new class of borane-derived materials (Figure 1b). This work is precisely based on the aforementioned design rationale, systematically investigating the stability, electronic structure, and surface ion migration characteristics of the B12H6 oxidation-derived system B12X2H6 (X=O, S). The detailed findings of this study are presented in Section 3.

2. Methods

The calculations in this study were carried out utilizing the projector augmented-wave (PAW) method [20,21] as implemented in the VASP [22,23]. The valence electron configuration of H, B, O, S, Li, Na and K were configured as 1s1, 2s22p1, 2s22p4, 3s23p4, 2s1, 3s1 and 3p64s1. The plane wave cutoff energy was fixed at 500 eV. For the exchange-correlation energy, the generalized gradient approximation (GGA) in the Perdew-Burke-Ernzerhof (PBE) formulation [24] was adopted. Considering the well-known issue of band gap underestimation inherent in GGA [25,26], the screened hybrid functional HSE06 was further employed for electronic band structure calculations [27]. During structural optimization, stringent criteria were applied, including a force threshold of 0.005 eV/Å in any direction, an energy criterion of 10−7 eV, and a dense k-mesh (13 × 13 × 1, Γ-centered). To prevent interactions between adjacent layers, a vacuum slab of up to 20 Å was introduced along the z-direction for 2D B12X2H6. To assess the thermodynamic stability of 2D B12X2H6, ab initio molecular dynamics (AIMD) simulations [28] were conducted using a 3 × 3 × 1 supercell (comprising a total of 180 atoms for each 2D B12X2H6 structure) over a duration of 5 ps at various temperatures. Phonon dispersion calculations, based on density functional perturbation theory, were performed using Phonopy [29]. The correction for van der Waals forces between adsorbed ions and the substrate during ion migration was implemented using DFT-D3 [30]. For data analysis, the VASPKIT [31] and VESTA [32] software packages were utilized.

3. Results and Discussion

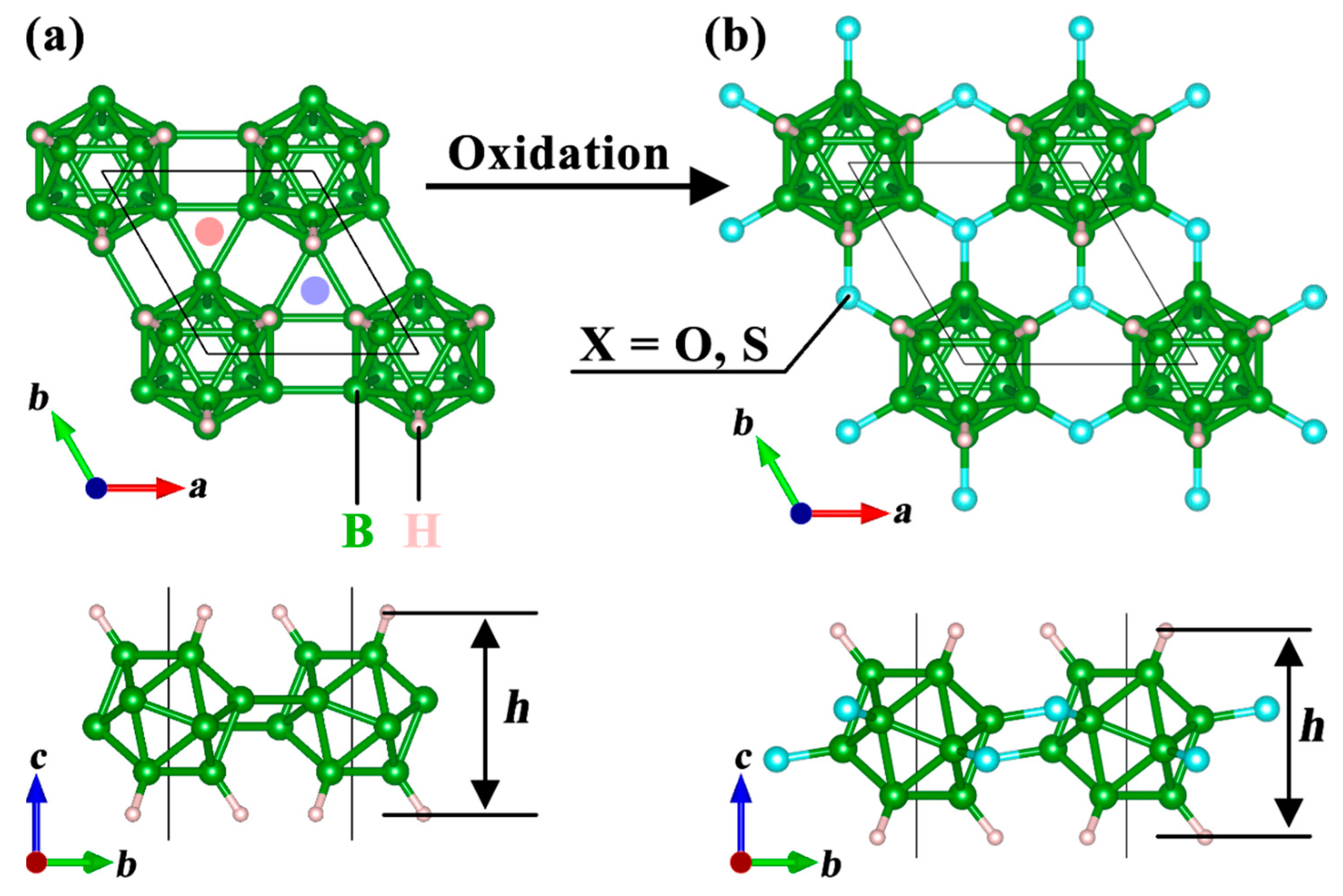
3.1. Structure and Stability

Figure 1 presents the top and side views of the crystal structures of B12H6 (Figure 1a) and its derivative material, B12X2H6 (Figure 1b). The crystal symmetry of B12X2H6 remains consistent with that of B12H6; however, the introduction of the X element induces lattice expansion. Specifically, the lattice constant increases from 4.898 Å in B12H6 to 5.409 Å in B12O2H6 and 5.950 Å in B12S2H6, with detailed data provided in Table 1. During this structural evolution, the bond lengths of B-H exhibit minimal variation (1.181 Å in B12H6, 1.189 Å in B12O2H6, and 1.192 Å in B12S2H6), while the bond lengths of B-B within the boron icosahedron also remain relatively stable (1.745–1.793 Å in B12H6, 1.764–1.776 Å in B12O2H6, and 1.777–1.797 Å in B12S2H6). In contrast, the bond lengths of B-O and B-S in B12O2H6 and B12S2H6 stabilize at 1.497 Å and 1.894 Å, respectively. Another notable structural change is observed in the layer thickness (h), where the layer thickness of B12X2H6 is consistently smaller than that of B12H6 (4.674 Å), and the layer thicknesses of B12O2H6 and B12S2H6 are nearly identical (4.609 Å and 4.604 Å, respectively). Overall, except for the significant lattice expansion, the changes in other structural parameters before and after oxidation are relatively limited.
From a design strategy perspective, two novel derivatives (B12O2H6 and B12S2H6) can be successfully obtained via the oxidation of B12H6. Nevertheless, to verify their experimental feasibility, a systematic evaluation of their stability remains necessary. The primary focus is on kinetic stability, as shown in Figure 2a,b. Phonon spectrum analysis results, based on DFPT, show no imaginary frequencies for either material, which indicates excellent kinetic stability. Meanwhile, the frequencies of the phonon spectra are primarily distributed in two regions: one ranging from 0 to 35 THz, where the phonon density of states (DOS) is jointly contributed by B, X, and H elements; the other is near 80 THz, where the phonon DOS is mainly contributed by B and H elements. The phonon spectrum results further confirm the high strength of the B-H bond. Subsequently, we systematically simulated the thermal stability of B12X2H6 at different temperatures, as presented in Figure 2c,d. The simulation results show minimal total energy fluctuations in B12X2H6 under low-temperature conditions, which demonstrates its excellent resistance to thermal perturbations. As the simulation temperature increases, the fluctuations in total energy gradually intensify. Combined with the analysis of the crystal structure at the end of the simulation, it is found that even at a high temperature of 2200 K, B12X2H6 can still maintain a stable structure (without structural collapse), which fully proves its excellent high-temperature stability and lays a solid foundation for the application of B12X2H6 in high-temperature fields. Moreover, we further conducted an in-depth assessment of the stability of B12X2H6 in O2 and H2O environments under both room temperature (300 K) and high temperature (1000 K) conditions. The relevant assessment results are presented in Figure 2e,f and Figure S1, respectively. The findings show that at room temperature, neither O2 nor H2O chemically reacts with the surface of B12X2H6—a phenomenon that fully confirms the material’s excellent environmental stability. However, when the temperature increases to 1000 K, the scenario changes: B12X2H6 undergoes dehydrogenation when exposed to an H2O environment (Figure S1), yet it still maintains excellent structural stability in an O2 environment. Based on this, in practical application scenarios, no additional protective measures are required under low-temperature conditions; but under high-temperature conditions, effective control of environmental humidity is still necessary. Subsequently, the mechanical stability of B12X2H6 was evaluated based on independent elastic constants, and the specific results are listed in Table 2. The evaluation results show that B12X2H6 fully meets the Born-Huang criteria [33], indicating good mechanical stability. The aforementioned stability analysis results fully confirm that B12X2H6 exhibits excellent performance in terms of kinetic, thermal, environmental, and mechanical stability, which undoubtedly provides a solid theoretical foundation for its experimental synthesis and potential applications. Regarding experimental preparation, some superatomic systems can currently be synthesized via CVD and MBE techniques [34]. Based on this, and following scientific reasoning, we tentatively propose that the two borides designed in this work are also highly likely to be compatible with these two preparation methods
Furthermore, based on the obtained independent elastic constants, we calculated the angle-dependent Young’s modulus (Y) and Poisson’s ratio (v) of B12X2H6. As shown in Figure 3, both the Young’s modulus and Poisson’s ratio of B12H6 and B12X2H6 exhibit isotropic behavior. Among these materials, B12O2H6 has the highest Young’s modulus (207.45 N m−1), followed by B12H6 (168.13 N m−1), while B12S2H6 has the lowest Young’s modulus at 130.31 N m−1. As a direct indicator of material stiffness, Young’s modulus show that among the three materials, B12O2H6 has the highest stiffness, whereas B12S2H6 has the lowest. This also indirectly reflects differences in the strength of chemical bonds within the materials. In terms of Poisson’s ratio, both B12O2H6 (0.234) and B12S2H6 (0.213) are smaller than the their parent material B12H6 (0.286) and are comparable to that of MoS2 (0.21) [4]. Furthermore, the Young’s modulus of B12X2H6 is lower than that of graphene (~340 N m−1) [35] and is comparable to or slightly lower than that of MoS2 (~200 N m−1) [36].

3.2. Electronic Properties

Subsequently, we focused our research on the electronic structure of B12X2H6, with relevant details illustrated in Figure 4. As clearly observed from Figure 4a,b, both B12O2H6 and B12S2H6 are wide-bandgap indirect semiconductors. Specifically, at the GGA-PBE level, the bandgap value of B12O2H6 is 3.74 eV, while that of B12S2H6 is even larger, reaching 4.19 eV. After hybrid functional correction (HSE06), the bandgaps of both compounds further increase: B12O2H6 and B12S2H6 exhibit bandgaps of 4.92 eV and 5.25 eV, respectively. These values are comparable to those of well-studied wide-bandgap semiconductors such as Ga2O3 (~4.9 eV) [37,38]. Compared to the parent material B12H6 (1.552 eV at the GGA-PBE level and 2.210 eV at the HSE06 level), the bandgaps of B12X2H6 are significantly larger. This phenomenon indicates that the introduction of O and S elements further enhances the localization of electrons within the system, thereby increasing the bandgap.
Further analysis shows that the conduction band minima (CBMs) of both B12O2H6 and B12S2H6 are located at the Γ point, while the positions of their valence band maxima (VBMs) differ. Specifically, the VBM of B12O2H6 is approximately centered between the K and M points while that of B12S2H6 is located at the M point. Furthermore, compared to the conduction band, the valence band of B12X2H6 near the Fermi level shows weaker dispersion, implying larger electron density of states (DOS) or carrier effective masses. Figure 4e,f display the partial density of states (PDOS) of B12O2H6 and B12S2H6, respectively, calculated using the HSE06 functional. Consistent with the band structure characteristics, the electron density of states of B12X2H6 in the valence band region is relatively high near the Fermi level, and to some extent, it approaches the DOS characteristics of the “Mexican hat”-type band structure. A high valence band DOS is beneficial for carrier accumulation, which in turn enhances the performance of electronic devices. Further analysis indicates that valence band DOS is mainly contributed by the B-2p and X-2p/3p (O-2p, S-3p) orbitals, highlighting the significant impact of X element (O/S) introduction on the system’s electronic structure. Finally, we also present the spatial charge distributions corresponding to the VBM and CBM of B12O2H6 and B12S2H6, as shown in Figure 4g,h. The results demonstrate that in B12X2H6, the charge corresponding to the VBM is primarily localized on the X atoms and the B atoms bonded to the X atoms. For the CBM, in addition to the charge localized on the X atoms and the B atoms bonded to the X atoms, there is also some charge localized on the H atoms.
For wide-bandgap semiconductors like B12X2H6, carrier mobility is another key parameter of interest. Based on deformation potential theory [39], we used the orthorhombic cells of B12X2H6 to calculate their electronic structures, in-plane elastic constants, and deformation potential constants. The relevant results are shown in Figure 5. By fitting the band structures, we obtained the effective masses of electrons and holes for B12X2H6 along the a and b directions. The specific data are presented in Table 3. For B12O2H6, the effective masses of electrons and holes along the a direction differ significantly. The electron effective mass is as high as 11.05 m0, while the hole effective mass is only 0.58 m0, indicating obvious anisotropy. This anisotropy is mainly attributed to the relatively weak valence band dispersion along the a direction. In contrast, B12O2H6 shows a smaller difference in effective masses along the b direction: the hole effective mass is 0.72 m0, and the electron effective mass is 2.00 m0. In B12S2H6, the effective masses of holes and electrons along the a and b directions are 1.99 m0 and 1.55 m0, respectively, while those along the b direction are 1.51 m0 and 0.46 m0, respectively. Thus, B12S2H6 exhibits less anisotropy than B12O2H6.
Finally, we combined the deformation potential constants and in-plane elastic constants to calculate the carrier mobilities of B12O2H6 and B12S2H6, with specific data presented in Table 3. The hole and electron mobilities of B12O2H6 along the a direction are 20.71 and 672.99 cm2V−1s−1, respectively, while those along the b direction are extremely high (197,818.31 cm2V−1s−1 for holes and 340.61 cm2V−1s−1 for electrons). The extremely high hole mobility of B12O2H6 along the b direction is mainly attributed to its extremely small fitted deformation potential constant (0.10 eV). However, such a large anisotropy is clearly inconsistent with physical reality. Thus, we re-estimated the hole mobility of B12O2H6 using the anisotropy correction method for carrier mobility in 2D materials proposed by Lang et al. [40] (see the underlined and bolded results in Table 3). After correction, the hole mobility of B12O2H6 along the b direction is 1469.41 cm2V−1s−1. For B12S2H6, the hole mobility is approximately 50 cm2V−1s−1, while the electron mobility is higher (up to 450 cm2V−1s−1). According to Lang et al.’s [40] method, the electron mobility ranges from 250 to 630 cm2V−1s−1. In summary, the carrier mobility of B12X2H6 is not outstanding among 2D materials, being much lower than that of 2D materials with ultra-high carrier mobilities (e.g., black phosphorus [41]). However, their carrier mobility is comparable to or even higher than that of MoS2 (~200 cm2V−1s−1) [42]. Additionally, it should be noted that in this work, we did not consider the influence of defects or impurities on the electronic structure and carrier mobility of the B12X2H6 monolayer. However, these factors play a non-negligible role in practical applications. Thus, when applying these findings to practical scenarios, these factors need to be comprehensively considered.

3.3. Alkali Ions Migration

Last but not least, we investigated the migration behavior of alkali metal ions (Li, Na and K) on the surface of B12X2H6. Figure 6a illustrates the supercell of the orthorhombic structure of B12X2H6. Based on symmetry analysis, four inequivalent adsorption sites exist on its surface, namely above the upper-layer X atoms (denoted as S1), above the lower-layer X atoms (S2), above the B12 cluster (S3), and at the hollow sites between adjacent B12X2H6 units (S4). After optimizing the adsorption structures of alkali metal ions at these four sites, we found that the alkali metal ions at the S1 and S4 sites eventually overlapped, with the final position closer to the S1 site (marked by the red dashed box in Figure 6a). Therefore, only the three sites, S1, S2, and S3, were considered in subsequent studies. Subsequently, we calculated the adsorption energies of alkali metal ions at these three sites (Figure 6b). The results showed that, except for Na on the B12S2H6 surface (where the lowest adsorption energy site was S2), the lowest adsorption energy site for all other adsorption system is S1. Furthermore, the adsorption energies of alkali metal ions on the B12O2H6 surface were significantly higher than those on the B12S2H6 surface: the former ranges from −0.99 to −0.57 eV/atom, and the latter ranges from −0.35 to −0.25 eV/atom. Lower adsorption energies correspond to weaker interactions, which significantly influence the surface migration behavior of ions. Based on the adsorption sites calculation results, we designed five migration pathways: path1 (S1→S1), path2 (S2→S2), path3 (S3→S3), path4 (S1→S3), and path5 (S1→S2). The migration energy barriers were calculated using the CI-NEB method [43], with the results presented in Figure 6d–m.
The migration energy barrier calculations for alkali metal ions on the B12O2H6 surface reveal that the strong adsorption interaction between alkali metal ions and the B12O2H6 surface results in relatively high migration energy barriers. Specifically, the migration energy barriers for K ions on the B12O2H6 are relatively high (0.31 to 0.45 eV), while those for Na ions are the lowest among the three ions (0.15 to 0.31 eV); and those for Li ions ranges from 0.24 to 0.43 eV. In contrast, the migration energy barriers for alkali metal ions on B12S2H6 are significantly lower than those on B12O2H6, which is attributable to the lower adsorption energies of alkali metal ions on B12S2H6. The specific values are as follows: 0.04 to 0.23 eV for Li ions, 0.033 to 0.15 eV for Na ions, and 0.05 to 0.15 eV for K ions. These results indicated that alkali metal ions exhibited relatively fast migration rates on B12O2H6, with migration energy barriers comparable to those of materials such as graphene (0.277 eV) [44], MoS2 (0.21 eV) [45], and β-B12 (0.3 eV) [46]. On B12S2H6, the migration rates are even faster, with minimum migration energy barriers comparable to those of materials such as Si3C (0.18 eV) [47], C3N (0.07 eV) [48], and PdI2 (0.08 eV) [49]. The excellent alkali ion migration performance of B12X2H6 suggests its potential applications in fields such as energy storage and chemical sensing.

4. Conclusions

In summary, using first-principles calculations and an oxidation strategy, we have successfully designed two novel two-dimensional (2D) borides, B12X2H6 (X=O, S). The core structural unit of these two borides is icosahedral boranes with partial hydrogen deficiency, and both materials exhibit exceptional kinetic, thermal, mechanical, and environmental stability. Notably, they can maintain excellent structural integrity even when exposed to an extreme high temperature of 2200 K. Hybrid functional calculations reveal that both B12O2H6 and B12S2H6 are wide-bandgap indirect semiconductors, with bandgap of 4.92 eV and 5.25 eV, respectively. Further calculations using the modified deformation potential theory indicate that the mobility of B12O2H6 ranges from 44 to 1469 cm2V−1s−1, while that of B12S2H6 ranges from 47 to 635 cm2V−1s−1. In-depth analysis shows that the relatively low carrier mobility of B12X2H6 is mainly attributed to the large effective masses and deformation potential constant of the carriers. Moreover, due to the low adsorption energy of alkali metal ions on the B12X2H6 surface, B12X2H6 exhibits excellent alkali metal ion transport performance, with migration energy barriers ranging from 0.15 to 0.45 eV (for B12O2H6) and from 0.033 to 0.23 eV (for B12S2H6). The findings of this study lay a solid theoretical foundation for the potential application of B12X2H6, and provide guidance for subsequent research on B12-based 2D materials.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/nano15231803/s1, Figure S1: The AIMD results of B12X2H6 under O2 and H2O environment at 1000 K.

Author Contributions

P.G.: Formal analysis, Investigation, Methodology, Software, Writing—original draft. J.-H.Y.: Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Writing—original draft, Writing—review and editing. G.-P.W.: Formal analysis, Resources. Z.-H.L.: Formal analysis, Resources. H.W.: Formal analysis, Funding acquisition, Resources, Software, Supervision, Writing—review and editing. J.W.: Formal analysis, Resources, Software. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

All data needed to evaluate the conclusions in the paper are present in the paper.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Tai, G.; Hu, T.; Zhou, Y.; Wang, X.; Kong, J.; Zeng, T.; You, Y.; Wang, Q. Synthesis of Atomically Thin Boron Films on Copper Foils. Angew. Chem. Int. Ed. 2015, 127, 15693–15697. [Google Scholar] [CrossRef]
  2. Mannix, A.J.; Zhou, X.-F.; Kiraly, B.; Wood, J.D.; Alducin, D.; Myers, B.D.; Liu, X.; Fisher, B.L.; Santiago, U.; Guest, J.R.; et al. Synthesis of Borophenes: Anisotropic, Two-Dimensional Boron Polymorphs. Science 2015, 350, 1513–1516. [Google Scholar] [CrossRef] [PubMed]
  3. Mannix, A.J.; Zhang, Z.; Guisinger, N.P.; Yakobson, B.I.; Hersam, M.C. Borophene as a Prototype for Synthetic 2D Materials Development. Nature Nanotechnol. 2018, 13, 444–450. [Google Scholar] [CrossRef] [PubMed]
  4. Yuan, J.; Yu, N.; Xue, K.; Miao, X. Ideal Strength and Elastic Instability in Single-Layer 8-Pmmn Borophene. RSC Adv. 2017, 7, 8654–8660. [Google Scholar] [CrossRef]
  5. Wu, X.; Dai, J.; Zhao, Y.; Zhuo, Z.; Yang, J.; Zeng, X.C. Two-Dimensional Boron Monolayer Sheets. ACS Nano 2012, 6, 7443–7453. [Google Scholar] [CrossRef]
  6. Zhou, X.-F.; Dong, X.; Oganov, A.R.; Zhu, Q.; Tian, Y.; Wang, H.-T. Semimetallic Two-Dimensional Boron Allotrope with Massless Dirac Fermions. Phys. Rev. Lett. 2014, 112, 085502. [Google Scholar] [CrossRef]
  7. Li, W.-L.; Chen, X.; Jian, T.; Chen, T.-T.; Li, J.; Wang, L.-S. From Planar Boron Clusters to Borophenes and Metalloborophenes. Nat. Rev. Chem. 2017, 1, 0071. [Google Scholar] [CrossRef]
  8. Wang, Z.-Q.; Lü, T.-Y.; Wang, H.-Q.; Feng, Y.P.; Zheng, J.-C. Review of Borophene and Its Potential Applications. Front. Phys. 2019, 14, 33403. [Google Scholar] [CrossRef]
  9. Wang, Y.; Park, Y.; Qiu, L.; Mitchell, I.; Ding, F. Borophene with Large Holes. J. Phys. Chem. Lett. 2020, 11, 6235–6241. [Google Scholar] [CrossRef]
  10. Ou, M.; Wang, X.; Yu, L.; Liu, C.; Tao, W.; Ji, X.; Mei, L. The Emergence and Evolution of Borophene. Adv. Sci. 2021, 8, 2001801. [Google Scholar] [CrossRef]
  11. Chen, C.; Lv, H.; Zhang, P.; Zhuo, Z.; Wang, Y.; Ma, C.; Li, W.; Wang, X.; Feng, B.; Cheng, P.; et al. Synthesis of Bilayer Borophene. Nat. Chem. 2022, 14, 25–31. [Google Scholar] [CrossRef]
  12. Innis, N.R.; Marichy, C.; Journet, C.; Bousige, C. Borophene Bottom-up Syntheses: A Critical Review. 2D Mater. 2025, 12, 022005. [Google Scholar] [CrossRef]
  13. Sivaev, I.B.; Bregadze, V.I.; Sjöberg, S. Chemistry of Closo-Dodecaborate Anion [B12H12]2−: A Review. Collect. Czech. Chem. Commun. 2002, 67, 679–727. [Google Scholar] [CrossRef]
  14. Reber, A.C.; Khanna, S.N.; Castleman, A.W. Superatom Compounds, Clusters, and Assemblies: Ultra Alkali Motifs and Architectures. J. Am. Chem. Soc. 2007, 129, 10189–10194. [Google Scholar] [CrossRef]
  15. Castleman, A.W.; Khanna, S.N. Clusters, Superatoms, and Building Blocks of New Materials. J. Phys. Chem. C 2009, 113, 2664–2675. [Google Scholar] [CrossRef]
  16. Jia, Y.; Luo, Z. Thirteen-Atom Metal Clusters for Genetic Materials. Coord. Chem. Rev. 2019, 400, 213053. [Google Scholar] [CrossRef]
  17. Oganov, A.R.; Chen, J.; Gatti, C.; Ma, Y.; Ma, Y.; Glass, C.W.; Liu, Z.; Yu, T.; Kurakevych, O.O.; Solozhenko, V.L. Ionic High-Pressure Form of Elemental Boron. Nature 2009, 457, 863–867. [Google Scholar] [CrossRef] [PubMed]
  18. Albert, B.; Hillebrecht, H. Boron: Elementary Challenge for Experimenters and Theoreticians. Angew. Chem. Int. Ed. 2009, 48, 8640–8668. [Google Scholar] [CrossRef] [PubMed]
  19. Yan, Q.-Q.; Wei, Y.-F.; Chen, Q.; Mu, Y.-W.; Li, S.-D. Superatom-Assembled Boranes, Carboranes, and Low-Dimensional Boron Nanomaterials Based on Aromatic Icosahedral B12 and C2B10. Nano Res. 2024, 17, 6734–6740. [Google Scholar] [CrossRef]
  20. Blöchl, P.E. Projector Augmented-Wave Method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
  21. Kresse, G.; Joubert, D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
  22. Kresse, G.; Furthmüller, J. Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
  23. Kresse, G.; Furthmüller, J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
  24. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
  25. Xue, K.-H.; Yuan, J.-H.; Fonseca, L.R.C.; Miao, X.-S. Improved LDA-1/2 Method for Band Structure Calculations in Covalent Semiconductors. Comput. Mater. Sci. 2018, 153, 493–505. [Google Scholar] [CrossRef]
  26. Yuan, J.-H.; Chen, Q.; Fonseca, L.R.C.; Xu, M.; Xue, K.-H.; Miao, X.-S. GGA-1/2 Self-Energy Correction for Accurate Band Structure Calculations: The Case of Resistive Switching Oxides. J. Phys. Commun. 2018, 2, 105005. [Google Scholar] [CrossRef]
  27. Krukau, A.V.; Vydrov, O.A.; Izmaylov, A.F.; Scuseria, G.E. Influence of the Exchange Screening Parameter on the Performance of Screened Hybrid Functionals. J. Chem. Phys. 2006, 125, 224106. [Google Scholar] [CrossRef]
  28. Lundgren, C.; Kakanakova-Georgieva, A.; Gueorguiev, G.K. A Perspective on Thermal Stability and Mechanical Properties of 2D Indium Bismide from Ab Initio Molecular Dynamics. Nanotechnology 2022, 33, 335706. [Google Scholar] [CrossRef] [PubMed]
  29. Togo, A.; Tanaka, I. First Principles Phonon Calculations in Materials Science. Scripta Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef]
  30. Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
  31. Wang, V.; Xu, N.; Liu, J.-C.; Tang, G.; Geng, W.-T. VASPKIT: A User-Friendly Interface Facilitating High-Throughput Computing and Analysis Using VASP Code. Computer Phys. Commun. 2021, 267, 108033. [Google Scholar] [CrossRef]
  32. Momma, K.; Izumi, F. VESTA3 for Three-Dimensional Visualization of Crystal, Volumetric and Morphology Data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
  33. Born, M.; Huang, K. Dynamical Theory of Crystal Lattices; Oxford University Press: New York, NY, USA, 1996; ISBN 978-0-19-267008-3. [Google Scholar]
  34. Doud, E.A.; Voevodin, A.; Hochuli, T.J.; Champsaur, A.M.; Nuckolls, C.; Roy, X. Superatoms in Materials Science. Nat. Rev. Mater. 2020, 5, 371–387. [Google Scholar] [CrossRef]
  35. Liu, F.; Ming, P.; Li, J. Ab Initio Calculation of Ideal Strength and Phonon Instability of Graphene under Tension. Phys. Rev. B 2007, 76, 064120. [Google Scholar] [CrossRef]
  36. Li, T. Ideal Strength and Phonon Instability in Single-Layer MoS2. Phys. Rev. B 2012, 85, 235407. [Google Scholar] [CrossRef]
  37. Qin, Y.; Li, L.; Zhao, X.; Tompa, G.S.; Dong, H.; Jian, G.; He, Q.; Tan, P.; Hou, X.; Zhang, Z.; et al. Metal–Semiconductor–Metal ε-Ga2O3 Solar-Blind Photodetectors with a Record-High Responsivity Rejection Ratio and Their Gain Mechanism. ACS Photonics 2020, 7, 812–820. [Google Scholar] [CrossRef]
  38. Qin, Y.; Li, L.; Yu, Z.; Wu, F.; Dong, D.; Guo, W.; Zhang, Z.; Yuan, J.; Xue, K.; Miao, X.; et al. Ultra-High Performance Amorphous Ga2O3 Photodetector Arrays for Solar-Blind Imaging. Adv. Sci. 2021, 8, 2101106. [Google Scholar] [CrossRef]
  39. Bardeen, J.; Shockley, W. Deformation Potentials and Mobilities in Non-Polar Crystals. Phys. Rev. 1950, 80, 72–80. [Google Scholar] [CrossRef]
  40. Lang, H.; Zhang, S.; Liu, Z. Mobility Anisotropy of Two-Dimensional Semiconductors. Phys. Rev. B 2016, 94, 235306. [Google Scholar] [CrossRef]
  41. Qiao, J.; Kong, X.; Hu, Z.-X.; Yang, F.; Ji, W. High-Mobility Transport Anisotropy and Linear Dichroism in Few-Layer Black Phosphorus. Nat. Commun. 2014, 5, 4475. [Google Scholar] [CrossRef]
  42. Cai, Y.; Zhang, G.; Zhang, Y.-W. Polarity-Reversed Robust Carrier Mobility in Monolayer MoS2 Nanoribbons. J. Am. Chem. Soc. 2014, 136, 6269–6275. [Google Scholar] [CrossRef] [PubMed]
  43. Henkelman, G.; Uberuaga, B.P.; Jónsson, H. A Climbing Image Nudged Elastic Band Method for Finding Saddle Points and Minimum Energy Paths. J. Chem. Phys. 2000, 113, 9901–9904. [Google Scholar] [CrossRef]
  44. Zhou, L.-J.; Hou, Z.F.; Wu, L.-M. First-Principles Study of Lithium Adsorption and Diffusion on Graphene with Point Defects. J. Phys. Chem. C 2012, 116, 21780–21787. [Google Scholar] [CrossRef]
  45. Li, Y.; Wu, D.; Zhou, Z.; Cabrera, C.R.; Chen, Z. Enhanced Li Adsorption and Diffusion on MoS2 Zigzag Nanoribbons by Edge Effects: A Computational Study. J. Phys. Chem. Lett. 2012, 3, 2221–2227. [Google Scholar] [CrossRef]
  46. Zhang, X.; Hu, J.; Cheng, Y.; Yang, H.Y.; Yao, Y.; Yang, S.A. Borophene as an Extremely High Capacity Electrode Material for Li-Ion and Na-Ion Batteries. Nanoscale 2016, 8, 15340–15347. [Google Scholar] [CrossRef]
  47. Wang, Y.; Li, Y. Ab Initio Prediction of Two-Dimensional Si3C Enabling High Specific Capacity as an Anode Material for Li/Na/K-Ion Batteries. J. Mater. Chem. A 2020, 8, 4274–4282. [Google Scholar] [CrossRef]
  48. Bhauriyal, P.; Mahata, A.; Pathak, B. Graphene-like Carbon–Nitride Monolayer: A Potential Anode Material for Na- and K-Ion Batteries. J. Phys. Chem. C 2018, 122, 2481–2489. [Google Scholar] [CrossRef]
  49. Zhang, P.; Yuan, J.-H.; Fang, W.-Y.; Li, G.; Wang, J. Two-Dimensional V-Shaped PdI2: Auxetic Semiconductor with Ultralow Lattice Thermal Conductivity and Ultrafast Alkali Ion Mobility. Appl. Surf. Sci. 2022, 601, 154176. [Google Scholar] [CrossRef]
Nanomaterials 15 01803 g001
Figure 1. Crystal structure of monolayer (a) B12H6 and (b) B12X2H6 (X=O, S). The light red and light blue solid circles represent the oxidation sites corresponding to the bottom surface and the top surface of B12H6, respectively.
Figure 1. Crystal structure of monolayer (a) B12H6 and (b) B12X2H6 (X=O, S). The light red and light blue solid circles represent the oxidation sites corresponding to the bottom surface and the top surface of B12H6, respectively.
Nanomaterials 15 01803 g001
Nanomaterials 15 01803 g002
Figure 2. Phonon dispersion and density of states of (a) B12O2H6 and (b) B12S2H6. The AIMD results of (c) B12O2H6 and (d) B12S2H6 under various simulation temperatures, respectively. The AIMD results of (e) B12O2H6 and (f) B12S2H6 under O2 and H2O environment at 300 K. The insert is the final crystal structure of B12X2H6 at 2200 K and 300 K (for O2 and H2O) at the end of simulation time.
Figure 2. Phonon dispersion and density of states of (a) B12O2H6 and (b) B12S2H6. The AIMD results of (c) B12O2H6 and (d) B12S2H6 under various simulation temperatures, respectively. The AIMD results of (e) B12O2H6 and (f) B12S2H6 under O2 and H2O environment at 300 K. The insert is the final crystal structure of B12X2H6 at 2200 K and 300 K (for O2 and H2O) at the end of simulation time.
Nanomaterials 15 01803 g002
Nanomaterials 15 01803 g003
Figure 3. The calculated angle-dependent (a) Young’s modulus and (b) Poisson ratio of B12H6 and B12X2H6.
Figure 3. The calculated angle-dependent (a) Young’s modulus and (b) Poisson ratio of B12H6 and B12X2H6.
Nanomaterials 15 01803 g003
Nanomaterials 15 01803 g004
Figure 4. Calculated electronic band structures of (a,c) B12O2H6 and (b,d) B12S2H6 at GGA-PBE and HSE06 level. Projected density of states of (e) B12O2H6 and (f) B12S2H6 at HSE06 level. The corresponding VBM and CBM of (g) B12O2H6 and (h) B12S2H6. The isosurface is set to 0.04 e Å−3.
Figure 4. Calculated electronic band structures of (a,c) B12O2H6 and (b,d) B12S2H6 at GGA-PBE and HSE06 level. Projected density of states of (e) B12O2H6 and (f) B12S2H6 at HSE06 level. The corresponding VBM and CBM of (g) B12O2H6 and (h) B12S2H6. The isosurface is set to 0.04 e Å−3.
Nanomaterials 15 01803 g004
Nanomaterials 15 01803 g005
Figure 5. (a) The orthorhombic cell and (b) its energy band corresponding to B12O2H6. The fitting curves of (c) the in-plane elastic modulus C2D and (d) the deformation potential constant E1 of B12O2H6 along a and b directions, respectively. (e) The orthorhombic cell and (f) its energy band corresponding to B12S2H6. The fitting curves of (g) the in-plane elastic modulus C2D and (h) the deformation potential constant E1 of B12S2H6 along a and b directions, respectively.
Figure 5. (a) The orthorhombic cell and (b) its energy band corresponding to B12O2H6. The fitting curves of (c) the in-plane elastic modulus C2D and (d) the deformation potential constant E1 of B12O2H6 along a and b directions, respectively. (e) The orthorhombic cell and (f) its energy band corresponding to B12S2H6. The fitting curves of (g) the in-plane elastic modulus C2D and (h) the deformation potential constant E1 of B12S2H6 along a and b directions, respectively.
Nanomaterials 15 01803 g005
Nanomaterials 15 01803 g006
Figure 6. (a) Schematic diagram of ion adsorption sites on B12X2H6. The X atoms in the upper layer (light purple) and the lower layer (red) are marked with different colors, respectively. (b) The adsorption energy of alkali metal ions on B12X2H6. The solid circles and diamonds represent the corresponding results for B12O2H6 and B12S2H6, respectively. (c) Schematic representation of the ion migration paths of ions on B12X2H6. Calculated migration energy barrier of Li/Na/K ions on B12O2H6 along (d) path 1, (e) path 2, (f) path 3, (g) path 4, and (h) path 5. Calculated migration energy barrier of Li/Na/K ions on B12S2H6 along (i) path 1, (j) path 2, (k) path 3, (l) path 4, and (m) path 5.
Figure 6. (a) Schematic diagram of ion adsorption sites on B12X2H6. The X atoms in the upper layer (light purple) and the lower layer (red) are marked with different colors, respectively. (b) The adsorption energy of alkali metal ions on B12X2H6. The solid circles and diamonds represent the corresponding results for B12O2H6 and B12S2H6, respectively. (c) Schematic representation of the ion migration paths of ions on B12X2H6. Calculated migration energy barrier of Li/Na/K ions on B12O2H6 along (d) path 1, (e) path 2, (f) path 3, (g) path 4, and (h) path 5. Calculated migration energy barrier of Li/Na/K ions on B12S2H6 along (i) path 1, (j) path 2, (k) path 3, (l) path 4, and (m) path 5.
Nanomaterials 15 01803 g006
Table 1. Calculated lattice constants a/b (Å), bond length l (Å), layer thickness h (Å), and band gaps (at GGA-PBE and HSE06 level, eV) of B12H6 and B12X2H6.
Table 1. Calculated lattice constants a/b (Å), bond length l (Å), layer thickness h (Å), and band gaps (at GGA-PBE and HSE06 level, eV) of B12H6 and B12X2H6.
Materialsa/blB-HlB-BlB-B/Xh E g P B E E g H S E
B12H64.8981.1811.745~1.7932.0044.6741.5522.210
B12O2H65.4091.1891.764~1.7761.4974.6093.7464.927
B12S2H65.9501.1921.777~1.7971.8944.6044.1965.257
Table 2. Calculated elastic constant C11, C22, C12, C66 (N m−1), axis Young’s modulus (Y11/Y22) and Poisson’s ratio (v11/v22) of B12O2H6 and B12S2H6.
Table 2. Calculated elastic constant C11, C22, C12, C66 (N m−1), axis Young’s modulus (Y11/Y22) and Poisson’s ratio (v11/v22) of B12O2H6 and B12S2H6.
MaterialsC11/C22C12C66Y11/Y22v11/v22
B12H6183.0952.3465.38168.130.286
B12O2H6219.4151.2384.09207.450.234
B12S2H6136.5129.0853.71130.310.213
Table 3. The calculated effective mass (m*, m0) of electron (e) and hole (h), in-plane elastic modulus C2D (N m−1), deformation potential constant (E1, eV) and corresponding carrier mobility (μ, cm2V−1s−1) of B12O2H6 and B12S2H6 monolayers. The carrier mobility results based on the BS method and Lang et al.’s [40] correction method (bold and underlined) are provided separately.
Table 3. The calculated effective mass (m*, m0) of electron (e) and hole (h), in-plane elastic modulus C2D (N m−1), deformation potential constant (E1, eV) and corresponding carrier mobility (μ, cm2V−1s−1) of B12O2H6 and B12S2H6 monolayers. The carrier mobility results based on the BS method and Lang et al.’s [40] correction method (bold and underlined) are provided separately.
MaterialsCarrier Typex-Axisy-Axis
ma* | E 1 a | C2Dμxmb* | E 1 b | C2Dμy
B12O2H6h11.052.51190.9220.71
/44.40		0.720.10188.63197,818.31
/1469.41
e0.583.11190.92672.99/
810.54		2.002.34188.63340.61
/269.75
B12S2H6h1.993.45127.1649.24/
57.49		1.552.71123.9757.12
/47.29
e1.512.18127.16452.82
/258.41		0.463.94123.97 443.64
/635.46
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Gong, P.; Yuan, J.-H.; Wu, G.-P.; Liu, Z.-H.; Wang, H.; Wang, J. Designing 2D Wide Bandgap Semiconductor B12X2H6 (X=O, S) Based on Aromatic Icosahedral B12. Nanomaterials 2025, 15, 1803. https://doi.org/10.3390/nano15231803

AMA Style

Gong P, Yuan J-H, Wu G-P, Liu Z-H, Wang H, Wang J. Designing 2D Wide Bandgap Semiconductor B12X2H6 (X=O, S) Based on Aromatic Icosahedral B12. Nanomaterials. 2025; 15(23):1803. https://doi.org/10.3390/nano15231803

Chicago/Turabian Style

Gong, Pei, Jun-Hui Yuan, Gen-Ping Wu, Zhi-Hong Liu, Hao Wang, and Jiafu Wang. 2025. "Designing 2D Wide Bandgap Semiconductor B12X2H6 (X=O, S) Based on Aromatic Icosahedral B12" Nanomaterials 15, no. 23: 1803. https://doi.org/10.3390/nano15231803

APA Style

Gong, P., Yuan, J.-H., Wu, G.-P., Liu, Z.-H., Wang, H., & Wang, J. (2025). Designing 2D Wide Bandgap Semiconductor B12X2H6 (X=O, S) Based on Aromatic Icosahedral B12. Nanomaterials, 15(23), 1803. https://doi.org/10.3390/nano15231803

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop