Gas–Solid Phase Separation of Active Brownian Particles Under Confinement of Hard Walls
Abstract
1. Introduction
2. Materials and Methods
2.1. ABP Model
2.2. Péclet Number
2.3. Identification of Crystallization
2.4. Numerical Simulations
3. Results and Discussion
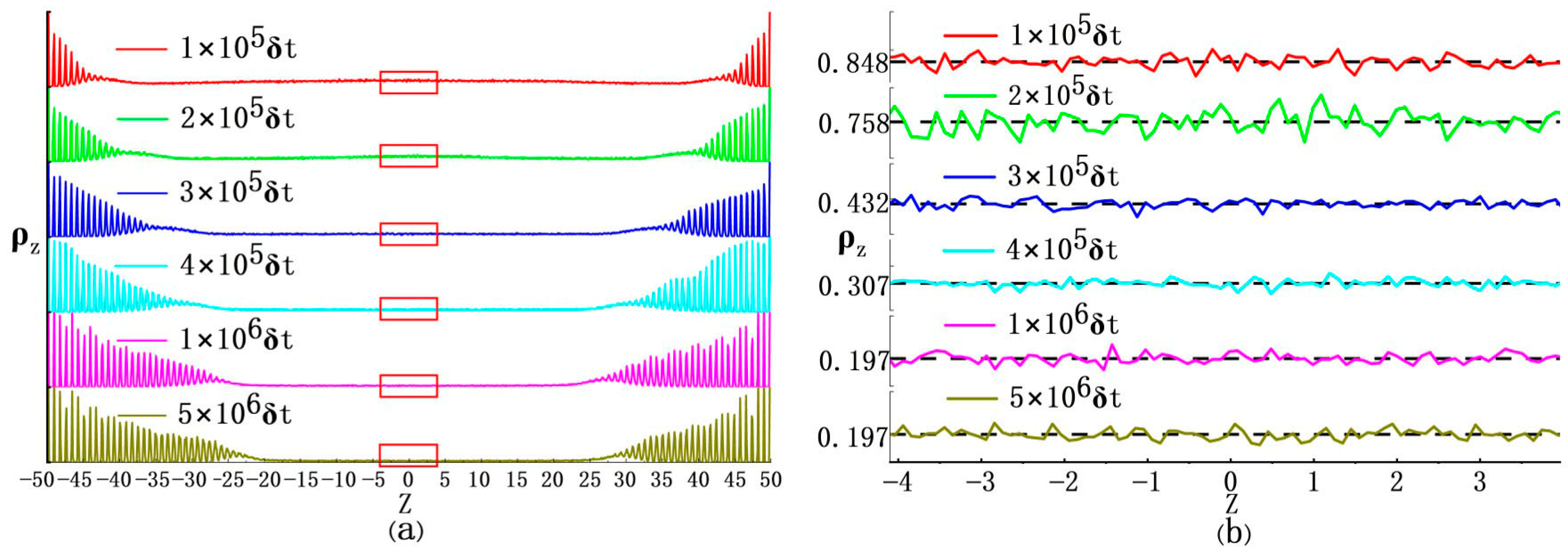
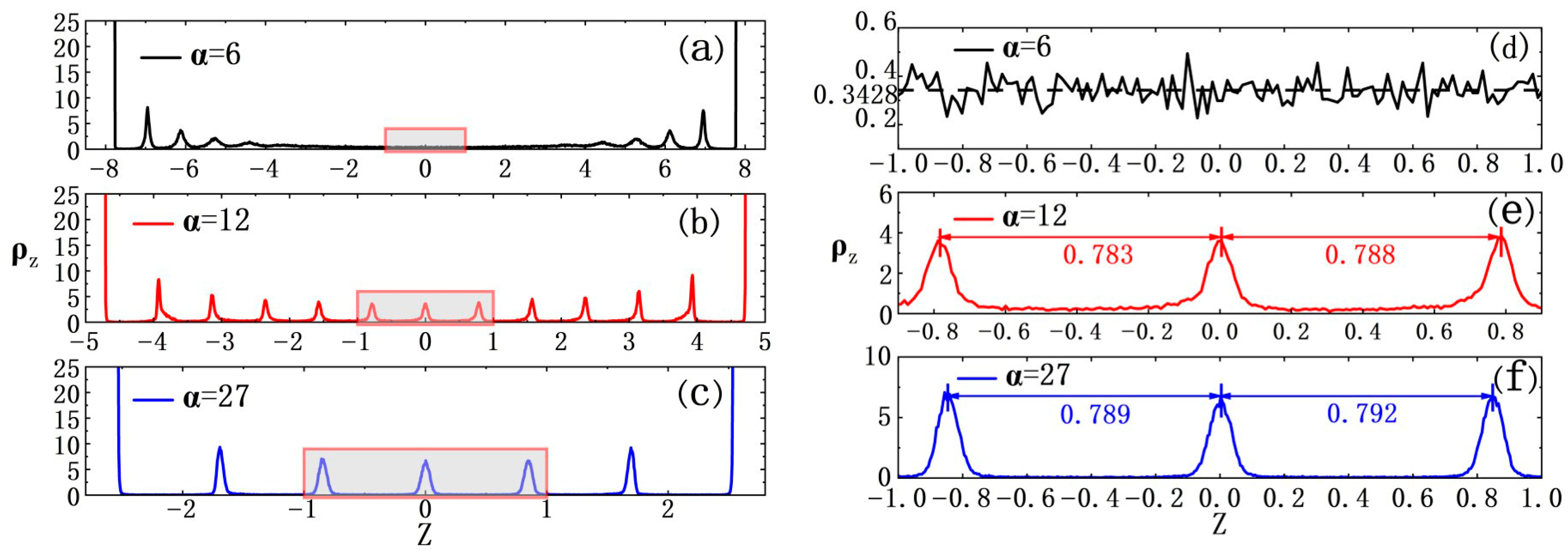
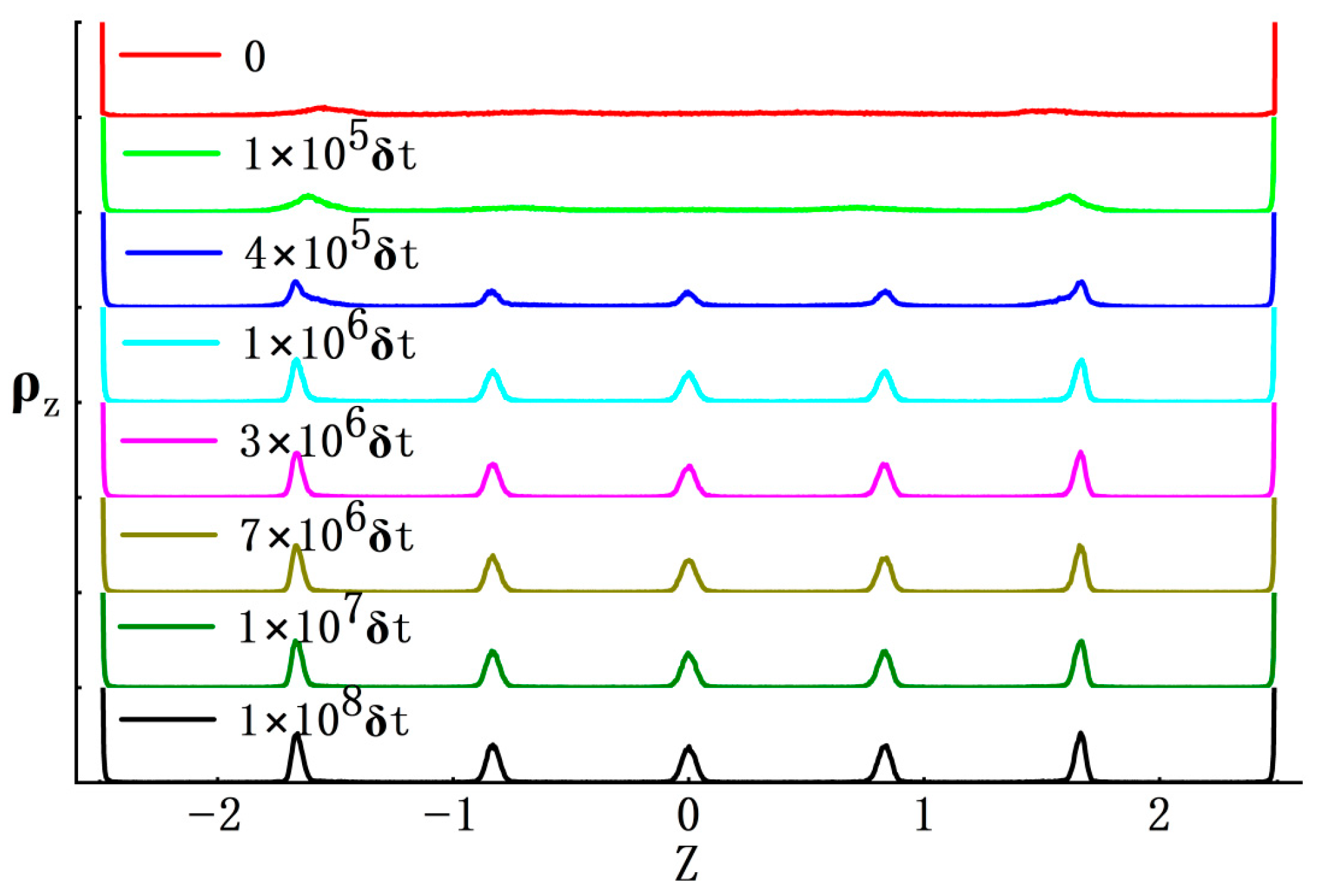
3.1. Gas–Solid Phase Separation
3.2. Inner Surface Effects on ABPs
3.3. Confinement of Hard Walls
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ABP | Active Brownian Particle |
| MIPS | motility-induced phase separation |
| ODLD | over-damped Langevin dynamics |
| WCA | Weeks-Chandler-Anderson |
| RDF | radial distribution function |
| GPU | Graphics Processing Unit |
| CUDA | Compute Unified Device Architecture |
| FCC | face-centered cubic |
| FM | Frank-van der Merwe |
References
- Ma, Z.; Yang, M.; Ni, R. Dynamic Assembly of Active Colloids: Theory and Simulation. Adv. Theor. Simul. 2020, 3, 2000021. [Google Scholar] [CrossRef]
- Redner, G.S.; Hagan, M.F.; Baskaran, A. Structure and dynamics of a phase-separating active colloidal fluid. Phys. Rev. Lett. 2013, 110, 055701. [Google Scholar] [CrossRef] [PubMed]
- Cavagna, A.; Cimarelli, A.; Giardina, I.; Parisi, G.; Santagati, R.; Stefanini, F.; Viale, M. Scale-free correlations in starling flocks. Proc. Natl. Acad. Sci. USA 2010, 107, 11865–11870. [Google Scholar] [CrossRef] [PubMed]
- Peruani, F.; Starruss, J.; Jakovljevic, V.; Sogaard-Andersen, L.; Deutsch, A.; Bar, M. Collective motion and nonequilibrium cluster formation in colonies of gliding bacteria. Phys. Rev. Lett. 2012, 108, 098102. [Google Scholar] [CrossRef] [PubMed]
- Recktenwald, S.M.; Graessel, K.; Maurer, F.M.; John, T.; Gekle, S.; Wagner, C. Red blood cell shape transitions and dynamics in time-dependent capillary flows. Biophys. J. 2022, 121, 23–36. [Google Scholar] [CrossRef]
- Aranson, I.S. Bacterial active matter. Rep. Prog. Phys. 2022, 85, 076601. [Google Scholar] [CrossRef]
- Dominguez, R.; Holmes, K.C. Actin structure and function. Annu. Rev. Biophys. 2011, 40, 169–186. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Zhou, C.; Zhang, H. Individual behaviors and dynamic self-assembly of active colloids. Chin. Sci. Bull. 2016, 62, 194–208. [Google Scholar] [CrossRef]
- Weninger, W.; Biro, M.; Jain, R. Leukocyte migration in the interstitial space of non-lymphoid organs. Nat. Rev. Immunol. 2014, 14, 232–246. [Google Scholar] [CrossRef]
- Ren, J.; Hu, P.; Ma, E.; Zhou, X.; Wang, W.; Zheng, S.; Wang, H. Enzyme-powered nanomotors with enhanced cell uptake and lysosomal escape for combined therapy of cancer. Appl. Mater. Today 2022, 27, 101445. [Google Scholar] [CrossRef]
- Liu, H.; Long, Y.; Liang, F. Interfacial Activity of Janus Particle: Unity of Molecular Surfactant and Homogeneous Particle. Chem.-Asian J. 2024, 19, e202301078. [Google Scholar] [CrossRef]
- Ye, J.; Fan, Y.; She, Y.; Shi, J.; Yang, Y.; Yuan, X.; Li, R.; Han, J.; Liu, L.; Kang, Y.; et al. Biomimetic Self-Propelled Asymmetric Nanomotors for Cascade-Targeted Treatment of Neurological Inflammation. Adv. Sci. 2024, 11, 2310211. [Google Scholar] [CrossRef]
- Turci, F.; Wilding, N.B. Phase Separation and Multibody Effects in Three-Dimensional Active Brownian Particles. Phys. Rev. Lett. 2021, 126, 038002. [Google Scholar] [CrossRef]
- Bricard, A.; Caussin, J.B.; Desreumaux, N.; Dauchot, O.; Bartolo, D. Emergence of macroscopic directed motion in populations of motile colloids. Nature 2013, 503, 95–98. [Google Scholar] [CrossRef] [PubMed]
- Shao, Y.; Zhao, Y.; Luo, M.; Zhao, G.; Xu, D.; Liu, Z.; Ma, L. Effect of Environmental Conditions on Strontium Adsorption by Red Soil Colloids in Southern China. Processes 2023, 11, 379. [Google Scholar] [CrossRef]
- Ye, Z.; Xu, D.; Zhong, J.; Gao, S.; Wang, J.; Zhang, Y.; Xu, H.; Li, Y.; Li, W. Influence of Soil Colloids on the Transport of Cd2+ and Pb2+ under Different pH and Ionic Strength Conditions. Agron. J. 2024, 14, 352. [Google Scholar] [CrossRef]
- Yildiz, A. Mechanism and regulation of kinesin motors. Nat. Rev. Mol. Cell Biol. 2025, 26, 86–103. [Google Scholar] [CrossRef]
- Sindelka, K.; Gadermeteva, A.; Lisal, M. Confined active particles: Wall accumulation and correspondence between active and fluid systems. Soft Matter 2025, 21, 7544–7564. [Google Scholar] [CrossRef] [PubMed]
- Elgeti, J.; Gompper, G. Wall accumulation of self-propelled spheres. Europhys. Lett. 2013, 101, 48003. [Google Scholar] [CrossRef]
- Becton, M.; Hou, J.; Zhao, Y.; Wang, X. Dynamic Clustering and Scaling Behavior of Active Particles under Confinement. Nanomaterials 2024, 14, 144. [Google Scholar] [CrossRef]
- Liu, P.; Zhu, H.; Zeng, Y.; Du, G.; Ning, L.; Wang, D.; Chen, K.; Lu, Y.; Zheng, N.; Ye, F.; et al. Oscillating collective motion of active rotors in confinement. Proc. Natl. Acad. Sci. USA 2020, 117, 11901–11907. [Google Scholar] [CrossRef]
- Lei, T.; Zhao, C.; Yan, R.; Zhao, N. Collective behavior of chiral active particles with anisotropic interactions in a confined space. Soft Matter 2023, 19, 1312–1329. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.; Misko, V.R.; Tempere, J.; Kong, M.; Peeters, F.M. Artificial living crystals in confined environment. Phys. Rev. E 2017, 95, 062602. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, Y.; Marchesoni, F.; Ghosh, P.K. Colloidal clustering and diffusion in a convection cell array. Soft Matter 2022, 18, 4778–4785. [Google Scholar] [CrossRef]
- Ghosh, P.K.; Zhou, Y.; Li, Y.; Marchesoni, F.; Nori, F. Binary Mixtures in Linear Convection Arrays. ChemPhysChem 2023, 24, e202200471. [Google Scholar] [CrossRef]
- Pieranski, P.; Małecki, J.; Wojciechowski, K. A hard disc system; Solid-solid phase transition in a thin layer. Mol. Phys. 1980, 40, 225–229. [Google Scholar] [CrossRef]
- Wojciechowski, K.W.; Pieranski, P.; Malecki, J. An instability in a hard-disc system in a narrow box (Helmholtz free energy). J. Phys. A Math. Gen. 1983, 16, 2197. [Google Scholar] [CrossRef]
- Stenhammar, J.; Marenduzzo, D.; Allen, R.J.; Cates, M.E. Phase behaviour of active Brownian particles: The role of dimensionality. Soft Matter 2014, 10, 1489–1499. [Google Scholar] [CrossRef]
- Hermann, S.; de Las Heras, D.; Schmidt, M. Non-negative Interfacial Tension in Phase-Separated Active Brownian Particles. Phys. Rev. Lett. 2019, 123, 268002. [Google Scholar] [CrossRef] [PubMed]
- Das, S.; Gompper, G.; Winkler, R.G. Confined active Brownian particles: Theoretical description of propulsion-induced accumulation. New J. Phys. 2018, 20, 015001. [Google Scholar] [CrossRef]
- Soto, R.; Pinto, M.; Brito, R. Kinetic Theory of Motility Induced Phase Separation for Active Brownian Particles. Phys. Rev. Lett. 2024, 132, 208301. [Google Scholar] [CrossRef]
- Rein ten Wolde, P.; Ruiz-Montero, M.J.; Frenkel, D. Numerical calculation of the rate of crystal nucleation in a Lennard-Jones system at moderate undercooling. J. Chem. Phys. 1996, 104, 9932–9947. [Google Scholar] [CrossRef]
- ten Wolde, P.R.; Ruiz-Montero, M.J.; Frenkel, D. Numerical Evidence for bcc Ordering at the Surface of a Critical fcc Nucleus. Phys. Rev. Lett. 1995, 75, 2714–2717. [Google Scholar] [CrossRef]
- Steinhardt, P.J.; Nelson, D.R.; Ronchetti, M. Bond-orientational order in liquids and glasses. Phys. Rev. B 1983, 28, 784–805. [Google Scholar] [CrossRef]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation: From Algorithms to Applications, 2nd ed.; Academic Press: San Diego, CA, USA, 2002. [Google Scholar]
- Sanders, J.; Kandrot, E. CUDA by Example: An Introduction to General-Purpose GPU Programming; Addison-Wesley: San Francisco, CA, USA, 2011. [Google Scholar]
- Caporusso, C.B.; Digregorio, P.; Levis, D.; Cugliandolo, L.F.; Gonnella, G. Motility-Induced Microphase and Macrophase Separation in a Two-Dimensional Active Brownian Particle System. Phys. Rev. Lett. 2020, 125, 178004. [Google Scholar] [CrossRef]
- van der Linden, M.N.; Alexander, L.C.; Aarts, D.G.A.L.; Dauchot, O. Interrupted Motility Induced Phase Separation in Aligning Active Colloids. Phys. Rev. Lett. 2019, 123, 098001. [Google Scholar] [CrossRef] [PubMed]
- Partridge, B.; Lee, C.F. Critical Motility-Induced Phase Separation Belongs to the Ising Universality Class. Phys. Rev. Lett. 2019, 123, 068002. [Google Scholar] [CrossRef]
- Digregorio, P.; Levis, D.; Suma, A.; Cugliandolo, L.F.; Gonnella, G.; Pagonabarraga, I. Full Phase Diagram of Active Brownian Disks: From Melting to Motility-Induced Phase Separation. Phys. Rev. Lett. 2018, 121, 098003. [Google Scholar] [CrossRef] [PubMed]
- Torres-Carbajal, A.; Sevilla, F.J. Motility-induced phase separation of soft active Brownian particles. Phys. Fluids 2024, 36, 027129. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- van Blaaderen, A.; Ruel, R.; Wiltzius, P. Template-directed colloidal crystallization. Nature 1997, 385, 321–324. [Google Scholar] [CrossRef]
- Xu, W.S.; Sun, Z.Y.; An, L.J. Heterogeneous crystallization of hard spheres on patterned substrates. J. Chem. Phys. 2010, 132, 144506. [Google Scholar] [CrossRef]
- Dasgupta, T.; Edison, J.R.; Dijkstra, M. Growth of defect-free colloidal hard-sphere crystals using colloidal epitaxy. J. Chem. Phys. 2017, 146, 074903. [Google Scholar] [CrossRef]
- Ouyang, W.; Zou, S.; Zhong, J.; Xu, S. Template-induced crystallization of charged colloids: A molecular dynamics study. Soft Matter 2023, 19, 6329–6340. [Google Scholar] [CrossRef]
- Zöttl, A.; Stark, H. Hydrodynamics Determines Collective Motion and Phase Behavior of Active Colloids in Quasi-Two-Dimensional Confinement. Phys. Rev. Lett. 2014, 112, 118101. [Google Scholar] [CrossRef] [PubMed]
- Buttinoni, I.; Bialké, J.; Kümmel, F.; Löwen, H.; Bechinger, C.; Speck, T. Dynamical Clustering and Phase Separation in Suspensions of Self-Propelled Colloidal Particles. Phys. Rev. Lett. 2013, 110, 238301. [Google Scholar] [CrossRef] [PubMed]
- Palacci, J.; Sacanna, S.; Steinberg, A.P.; Pine, D.J.; Chaikin, P.M. Living Crystals of Light-Activated Colloidal Surfers. Science 2013, 339, 936–940. [Google Scholar] [CrossRef]
- Auer, S.; Frenkel, D. Line tension controls wall-induced crystal nucleation in hard-sphere colloids. Phys. Rev. Lett. 2003, 91, 015703. [Google Scholar] [CrossRef] [PubMed]
- Hermann, S.; Krinninger, P.; de las Heras, D.; Schmidt, M. Phase coexistence of active Brownian particles. Phys. Rev. E 2019, 100, 052604. [Google Scholar] [CrossRef]
- Ni, R.; Cohen Stuart, M.A.; Bolhuis, P.G. Tunable Long Range Forces Mediated by Self-Propelled Colloidal Hard Spheres. Phys. Rev. Lett. 2015, 114, 018302. [Google Scholar] [CrossRef]
- Das, S.; Chelakkot, R. Morphological transitions of active Brownian particle aggregates on porous walls. Soft Matter 2020, 16, 7250–7255. [Google Scholar] [CrossRef] [PubMed]
- Qian, B.S.; Tian, W.D.; Chen, K. Absorption of self-propelled particles into a dense porous medium. Phys. Chem. Chem. Phys. 2021, 23, 20388–20397. [Google Scholar] [CrossRef] [PubMed]
- Marian, A.; Herman, W.R.; Helmut, S. Epitaxy: Physical Principles and Technical Implementation; Springer: Berlin, Germany, 2004. [Google Scholar]
- Menzel, A.M.; Löwen, H. Traveling and Resting Crystals in Active Systems. Phys. Rev. Lett. 2013, 110, 055702. [Google Scholar] [CrossRef] [PubMed]
- Menzel, A.M.; Ohta, T.; Löwen, H. Active crystals and their stability. Phys. Rev. E 2014, 89, 022301. [Google Scholar] [CrossRef]
- Kaiser, A.; Wensink, H.H.; Löwen, H. How to Capture Active Particles. Phys. Rev. Lett. 2012, 108, 268307. [Google Scholar] [CrossRef]
- Salim, S.A.; Mohan, M.S.; Ranganathan, S.; Parasuraman, P.; Lee, J.K.; Ramatchandirane, M.; Suchiang, K.; Busi, S. Derrisisoflavone-B interferes with AHL-mediated quorum sensing of Pseudomonas aeruginosa and decreased pathogenicity in Caenorhabditis elegans infection model. Microb. Pathog. 2025, 206, 107738. [Google Scholar] [CrossRef]
- Yi, J.; Xiao, S.; Yin, M.; Su, M.; Gao, C.; Tang, R. The Self-Adaptive Nanosystem for Implant-Related Infections Theranostics via Phase-Change Driven Anti-Biofilm and the Enhancement of Immune Memory. Adv. Funct. Mater. 2023, 33, 2302322. [Google Scholar] [CrossRef]
- Fodor, E.; Nardini, C.; Cates, M.E.; Tailleur, J.; Visco, P.; van Wijland, F. How Far from Equilibrium Is Active Matter? Phys. Rev. Lett. 2016, 117, 038103. [Google Scholar] [CrossRef]
- Broker, S.; Te Vrugt, M.; Jeggle, J.; Stenhammar, J.; Wittkowski, R. Pair-distribution function of active Brownian spheres in three spatial dimensions: Simulation results and analytical representation. Soft Matter 2023, 20, 224–244. [Google Scholar] [CrossRef]
- Moore, F.; Russo, J.; Liverpool, T.B.; Royall, C.P. Active Brownian particles in random and porous environments. J. Chem. Phys. 2023, 158, 104907. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Xu, S.; Zou, S.; Zhou, H.; Ouyang, W.; Zhong, J. Gas–Solid Phase Separation of Active Brownian Particles Under Confinement of Hard Walls. Nanomaterials 2025, 15, 1746. https://doi.org/10.3390/nano15221746
Zhang H, Xu S, Zou S, Zhou H, Ouyang W, Zhong J. Gas–Solid Phase Separation of Active Brownian Particles Under Confinement of Hard Walls. Nanomaterials. 2025; 15(22):1746. https://doi.org/10.3390/nano15221746
Chicago/Turabian StyleZhang, Hao, Shenghua Xu, Shuangyang Zou, Hongwei Zhou, Wenze Ouyang, and Jun Zhong. 2025. "Gas–Solid Phase Separation of Active Brownian Particles Under Confinement of Hard Walls" Nanomaterials 15, no. 22: 1746. https://doi.org/10.3390/nano15221746
APA StyleZhang, H., Xu, S., Zou, S., Zhou, H., Ouyang, W., & Zhong, J. (2025). Gas–Solid Phase Separation of Active Brownian Particles Under Confinement of Hard Walls. Nanomaterials, 15(22), 1746. https://doi.org/10.3390/nano15221746






