Enhancing CaV0.5Fe0.5O3-Based Lead-Free Perovskite Solar Cell Efficiency by over 23% via Transport Layer Engineering
Abstract
1. Introduction
- (i)
- Novel study: First thorough study of CaV0.5Fe0.5O3 as a novel perovskite solar cell material.
- (ii)
- Material integration innovation: CaV0.5Fe0.5O3 is abundant and non-toxic, with enhanced TiO2/Cu2O charge transport layers.
- (iii)
- Efficiency Record: Lead-free perovskite-inspired solar cells converted 23.28% electricity.
- (iv)
- Exceptional stability: Showed thermal stability of up to 100 °C.
- (v)
- Ideal band alignment: Ensured energy-level correlation between transport layers and CaV0.5Fe0.5O3 (~3.7 eV conduction band minimum/~5.5 eV valence band maximum).
2. Materials and Methods
2.1. Device Inverted Configuration
2.2. Simulation Software
2.3. Simulation Device Models
- (2)
- (3)
- (4)
- The optical absorption coefficient equation is used to model the interaction with light. For the optical absorption model, we choose the established classic model from SCAPS-1D’s selection. Here we can define the optical absorption coefficient “α” as α(λ) in the conventional paradigm, where “λ” is the optical wavelength and “hυ” is the energy. “Eg” represents the energy bandgap of the associated thin-film layer, while “A” and “B” are specified as arbitrary constants in this model according to Equation (7). The classic optical model is expressed as [37,38,39,40,41]
2.4. Energy Level Band Alignment
2.5. Device Simulation Parameters
2.6. Simulation Flow Chart
- Phase 3: Recommend (initial guess) the thickness range and doping density for each layer for initialization of the simulation.
- Phase 4: Optimization of ETL Thickness: Determine the ideal thickness of ETL (SnO2, ZnO, and TiO2) for each device with a fixed HTL (such as spiro OMeTAD as the hole transport layer), using a series of simulations that provide the greatest power conversion efficiency. Subsequently, update the running parameters of simulations using the ideal thickness of each ETL for further simulations.
- Phase 5: Evaluation of photovoltaic characteristics in relation to varying ETL thicknesses: assess the photovoltaic metrics, including open-circuit voltage, short-circuit current, fill factor, and power conversion efficiency of each device as a function of each ETL.
- Phase 6: Evaluation of photovoltaic characteristics in relation to varying ETL doping density: assess the photovoltaic metrics, including open-circuit voltage, short-circuit current, fill factor, and power conversion efficiency of each device as a function of each ETL’s doping density.
- Phase 7: Identify the most efficient electron transport layer among SnO2, ZnO, and TiO2 via the evaluation of power conversion efficiency, and thereafter use the optimal electron transport layer, together with its ideal thickness and doping density, for further optimization of the hole transport layer.
- Phase 8: Optimization of HTL Thickness: Determine the ideal thickness of HTL (PEDOT:PSS, Spiro OMeTAD, Cu2O) for each device with a fixed ETL (optimum electron transport layer determined from step 7), using a series of simulations that provide the greatest power conversion efficiency. Subsequently, update the running parameters of simulations using the ideal thickness of each HTL for further simulations.
- Phase 9: Evaluation of photovoltaic characteristics in relation to varying HTL thicknesses: Assess the photovoltaic metrics, including open-circuit voltage, short-circuit current, fill factor, and power conversion efficiency of each device as a function of each HTL.
- Phase 10: Evaluation of photovoltaic characteristics in relation to varying HTL doping density: assess the photovoltaic metrics, including open-circuit voltage, short-circuit current, fill factor, and power conversion efficiency of each device as a function of each HTL’s doping density.
- Phase 11: Identify the most efficient hole transport layer among S PEDOT:PSS, Spiro OMeTAD, and Cu2O via the evaluation of power conversion efficiency, and thereafter use the optimal HTL, together with its ideal thickness and doping density, for further optimization of the absorber layer.
- Phase 12: Optimization of absorber layer (CaV0.5Fe0.5O3) thickness: determine the ideal thickness of for the absorber layer where both ETL and HTL are the most efficient transport layers as determined in phase 7 and phase 11, respectively.
- Phase 13: Simulate the current-voltage (J–V) characteristics of the optimized electron transport layer, hole transport layer, and absorber CaV0.5Fe0.5O3 layer under AM1.5G illumination to extract essential photovoltaic parameters: short-circuit current density, open-circuit voltage, fill factor, and maximum possible power conversion efficiency.
- Phase 14: Assess the quantum efficiency (QE) spectra for both the original unoptimized and fully optimized device configurations to measure performance improvement across the absorption spectrum.
- Phase 15: Examine the influence of interface defect (or trap) density at the Perovskite/ETL and Perovskite/HTL interfaces on the performance metrics (Voc, Jsc, FF, PCE) of a highly optimized device.
- Phase 16: Assess the temperature-dependent photovoltaic efficacy of the highly optimized device throughout a spectrum of operating temperatures (up to 400 K).
- Phase 17: Examine the impact of series (RS) and shunt (RSH) resistances on the photovoltaic performance of the highly optimized device.
- Phase 18: End of simulation.
3. Results and Discussion
3.1. Thickness Optimization of Electron Transport Layer
3.2. Doping-Density Optimization of Electron Transport Layer
3.3. Thickness Optimization of Hole Transport Layer
3.4. Doping-Density Optimization of Hole Transport Layer
3.5. Thickness Optimization of Absorber Layer
3.6. Final Optimized Device Parameters
3.7. Optimized Photovoltaic and Quantum Efficiency Responses
3.8. Interface Trapped Density Responses Between Perovskite and Transport Layer
3.9. Temperature Effects on Proposed Perovskite Solar Cell
3.10. Series Resistance and Shunt Resistance Effects on Proposed Perovskite Solar Cell
3.11. Shunt Resistance Effects on Proposed Perovskite Solar Cell
3.12. Photovoltaic Comparison of the Proposed Perovskite Solar Cell
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Franco, A.C.; Franco, L.S. Photovoltaic solar energy and environmental impacts in the industrial sector: A critical overview of barriers and opportunities. Energy Sources Part A Recovery Util. Environ. Eff. 2025, 47, 10083–10095. [Google Scholar] [CrossRef]
- Seyisi, T.; Fouda-Mbanga, B.G.; Mnyango, J.I.; Nthwane, Y.B.; Nyoni, B.; Mhlanga, S.; Tywabi-Ngeva, Z. Major challenges for commercialization of perovskite solar cells: A critical review. Energy Rep. 2025, 13, 1400–1415. [Google Scholar] [CrossRef]
- Adewumi, A.; Olu-lawal, K.A.; Okoli, C.E.; Usman, F.O.; Usiagu, G.S. Sustainable energy solutions and climate change: A policy review of emerging trends and global responses. World J. Adv. Res. Rev. 2024, 21, 408–420. [Google Scholar]
- Herz, L.M. Charge-carrier dynamics in organic-inorganic metal halide perovskites. Annu. Rev. Phys. Chem. 2016, 67, 65–89. [Google Scholar] [CrossRef]
- Asensio, Y.; Olano-Vegas, L.; Mattioni, S.; Gobbi, M.; Casanova, F.; Hueso, L.E.; Martin-Garcia, B. Engineering magnetism in hybrid organic-inorganic metal halide perovskites. Mater. Horiz. 2025, 12, 2414–2435. [Google Scholar] [CrossRef]
- Liu, Z.; Lin, R.; Wei, M.; Yin, M.; Wu, P.; Li, M.; Tan, H. All-perovskite tandem solar cells achieving >29% efficiency with improved (100) orientation in wide-bandgap perovskites. Nat. Mater. 2025, 24, 252–259. [Google Scholar] [CrossRef]
- Yang, T.; Gao, L.; Lu, J.; Ma, C.; Du, Y.; Wang, P.; Zhao, K. One-stone-for-two-birds strategy to attain beyond 25% perovskite solar cells. Nat. Commun. 2023, 14, 839. [Google Scholar] [CrossRef]
- Chen, C.H.; Cheng, S.N.; Cheng, L.; Wang, Z.K.; Liao, L.S. Toxicity, leakage, and recycling of lead in perovskite photovoltaics. Adv. Energy Mater. 2023, 13, 2204144. [Google Scholar] [CrossRef]
- Needleman, H. Lead poisoning. Annu. Rev. Med. 2004, 55, 209–222. [Google Scholar] [CrossRef]
- Ara, A.; Usmani, J.A. Lead toxicity: A review. Interdiscip. Toxicol. 2015, 8, 55. [Google Scholar] [CrossRef]
- Ke, W.; Kanatzidis, M.G. Prospects for low-toxicity lead-free perovskite solar cells. Nat. Commun. 2019, 10, 965. [Google Scholar] [CrossRef] [PubMed]
- Giustino, F.; Snaith, H.J. Toward lead-free perovskite solar cells. ACS Energy Lett. 2016, 1, 1233–1240. [Google Scholar] [CrossRef]
- Moiz, S.A.; Alahmadi, A.N.M.; Alshaikh, M.S. Lead-Free FACsSnI3 Based Perovskite Solar Cell: Designing Hole and Electron-Transport Layer. Nanomaterials 2023, 13, 1524. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.; Zhang, Q.; Liu, Y.; Luo, W.; Guo, X.; Huang, Z.; Xiao, L. The dawn of lead-free perovskite solar cell: Highly stable double perovskite Cs2AgBiBr6 film. Adv. Sci. 2018, 5, 1700759. [Google Scholar] [CrossRef]
- Uddin, A.; Upama, M.B.; Yi, H.; Duan, L. Encapsulation of organic and perovskite solar cells: A review. Coatings 2019, 9, 65. [Google Scholar] [CrossRef]
- Rolston, N.; Watson, B.L.; Bailie, C.D.; McGehee, M.D.; Bastos, J.P.; Gehlhaar, R.; Dauskardt, R.H. Mechanical integrity of solution-processed perovskite solar cells. Extrem. Mech. Lett. 2016, 9, 353–358. [Google Scholar] [CrossRef]
- Yang, S.Y.; Seidel, J.; Byrnes, S.J.; Shafer, P.; Yang, C.H.; Rossell, M.D.; Ramesh, R. Above-bandgap voltages from ferroelectric photovoltaic devices. Nat. Nanotechnol. 2010, 5, 143–147. [Google Scholar] [CrossRef]
- Elkezaini, F.E.; ElKhou, A.; Drissi, L.B.; Chrafih, Y. Novel perovskite CaV0.5Fe0.5O3 a promising candidate for next-generation photovoltaic applications. J. Phys. Chem. Solids 2025, 207, 112938. [Google Scholar] [CrossRef]
- Sun, Z.; Wei, J.; Yuanfeng, Y.; Cao, A.; Zhang, J.; Shen, X. Employment of Charge Transport Layers in Bismuth Ferrite Ferroelectric Photovoltaic Cells for Achieving High Power Conversion Efficiency. ACS Sustain. Chem. Eng. 2025, 13, 14037–14048. [Google Scholar] [CrossRef]
- King, R.R.; Bhusari, D.; Larrabee, D.; Liu, X.Q.; Rehder, E.; Edmondson, K.; Karam, N.H. Solar cell generations over 40% efficiency. Prog. Photovolt. Res. Appl. 2012, 20, 801–815. [Google Scholar] [CrossRef]
- Kirchartz, T.; Rau, U. What makes a good solar cell? Adv. Energy Mater. 2018, 8, 1703385. [Google Scholar] [CrossRef]
- Jayanthi, G.; Sumathi, S.; Kannan, K.; Andal, V.; Murugan, S. A Review on Synthesis, Properties, and Environmental Application of Fe-Based Perovskite. Adv. Mater. Sci. Eng. 2022, 2022, 6607683. [Google Scholar] [CrossRef]
- Zhen, C.; Wu, T.; Chen, R.; Wang, L.; Liu, G.; Cheng, H.M. Strategies for modifying TiO2 based electron transport layers to boost perovskite solar cells. ACS Sustain. Chem. Eng. 2019, 7, 4586–4618. [Google Scholar] [CrossRef]
- Xiong, L.; Guo, Y.; Wen, J.; Liu, H.; Yang, G.; Qin, P.; Fang, G. Review on the application of SnO2 in perovskite solar cells. Adv. Funct. Mater. 2018, 28, 1802757. [Google Scholar] [CrossRef]
- Zhang, P.; Wu, J.; Zhang, T.; Wang, Y.; Liu, D.; Chen, H.; Li, S. Perovskite solar cells with ZnO electron-transporting materials. Adv. Mater. 2018, 30, 1703737. [Google Scholar] [CrossRef]
- Han, W.; Ren, G.; Liu, J.; Li, Z.; Bao, H.; Liu, C.; Guo, W. Recent progress of inverted perovskite solar cells with a modified PEDOT:PSS hole transport layer. ACS Appl. Mater. Interfaces 2020, 12, 49297–49322. [Google Scholar] [CrossRef]
- Moiz, S.A.; Alshaikh, M.S.; Alahmadi, A.N. Organic Bioelectronics: Diversity of Electronics Along with Biosciences. Biosensors 2025, 15, 587. [Google Scholar] [CrossRef]
- Juarez-Perez, E.J.; Leyden, M.R.; Wang, S.; Ono, L.K.; Hawash, Z.; Qi, Y. Role of the dopants on the morphological and transport properties of spiro-MeOTAD hole transport layer. Chem. Mater. 2016, 28, 5702–5709. [Google Scholar] [CrossRef]
- Li, J.; Liang, H.; Xiao, C.; Jia, X.; Guo, R.; Chen, J.; Guo, X.; Luo, R.; Wang, X.; Li, M.; et al. Enhancing the efficiency and longevity of inverted perovskite solar cells with antimony-doped tin oxides. Nat. Energy 2024, 9, 308–315. [Google Scholar] [CrossRef]
- Burgelman, M.; Decock, K.; Khelifi, S.; Abass, A. Advanced electrical simulation of thin film solar cells. Thin Solid Film. 2013, 535, 296–301. [Google Scholar] [CrossRef]
- Burgelman, M.; Verschraegen, J.; Degrave, S.; Nollet, P. Modeling thin-film PV devices. Prog. Photovolt. Res. Appl. 2004, 12, 143–153. [Google Scholar] [CrossRef]
- Verschraegen, J.; Burgelman, M. Numerical modeling of intra-band tunneling for heterojunction solar cells in scaps. Thin Solid Film. 2007, 515, 6276–6279. [Google Scholar] [CrossRef]
- Husainat, A.; Ali, W.; Cofie, P.; Attia, J.; Fuller, J. Simulation and analysis of methylammonium lead iodide (CH3NH3PbI3) perovskite solar cell with Au contact using SCAPS 1D simulator. Am. J. Opt. Photonics 2019, 7, 33. [Google Scholar] [CrossRef]
- Moulebhar, S.; Bendenia, C.; Bendenia, S.; Merad-Dib, H.; Khantar, S.A.; Merabet, S. High-efficiency design and optimization of 2 T monolithic polymer/polymer tandem solar cells using SCAPS-1D simulations. Phys. Scr. 2025, 100, 045108. [Google Scholar] [CrossRef]
- Nie, K.; Liang, Y.; Chen, X.; Zhang, Y.; Wang, J.; Zhou, C.; Zhang, Q. Numerical simulation and buffer layer optimization for Cd-free Cu (In, Ga) Se2 solar cells using SCAPS-1D. Opt. Quantum Electron. 2025, 57, 495. [Google Scholar] [CrossRef]
- Ashfaq, A.; Shokralla, E.A.; Alghamdi, S.M.; Rehman, U.U.; Albalawi, H.; Bayhan, Z.; Alsalhi, S.A. High-efficiency selenium and sulfur-based p-Sb2Se3/n-BaZrS3 heterostructure solar cells: A SCAPS-1D simulation study. J. Phys. Chem. Solids 2025, 199, 112490. [Google Scholar] [CrossRef]
- Gray, J.L. The physics of the solar cell. In Handbook of Photovoltaic Science and Engineering; Wiley: Hoboken, NJ, USA, 2011; Volume 2, pp. 82–128. [Google Scholar]
- Fonash, S.J. Solar Cell Device Physics; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Chin, V.J.; Salam, Z.; Ishaque, K. Cell modelling and model parameters estimation techniques for photovoltaic simulator application: A review. Appl. Energy 2015, 154, 500–519. [Google Scholar] [CrossRef]
- Burgelman, M.; Decock, K.; Niemegeers, A.; Verschraegen, J.; Degrave, S. SCAPS Manual; University of Ghent: Ghent, Belgium, 2016. [Google Scholar]
- Zeman, M.; Krc, J. Optical and electrical modeling of thin-film silicon solar cells. J. Mater. Res. 2008, 23, 889–898. [Google Scholar] [CrossRef]
- Klein, A. Energy band alignment at interfaces of semiconducting oxides: A review of experimental determination using photoelectron spectroscopy and comparison with theoretical predictions by the electron affinity rule, charge neutrality levels, and the common anion rule. Thin Solid Film. 2012, 520, 3721–3728. [Google Scholar]
- Wang, S.; Sakurai, T.; Wen, W.; Qi, Y. Energy level alignment at interfaces in metal halide perovskite solar cells. Adv. Mater. Interfaces 2018, 5, 1800260. [Google Scholar] [CrossRef]
- Rassol, R.A.; Hasan, R.F.; Ahmed, S.M. Numerical analysis of SnO2/Zn2SnO4/n-CdS/p-CdTe solar cell using the SCAPS-1D simulation software. Iraqi J. Sci. 2021, 62, 505–516. [Google Scholar] [CrossRef]
- Biswas, S.K.; Sumon, M.S.; Sarker, K.; Orthe, M.F.; Ahmed, M.M. A Numerical Approach to Analysis of an Environment-Friendly Sn-Based Perovskite Solar Cell with SnO2 Buffer Layer Using SCAPS-1D. Adv. Mater. Sci. Eng. 2023, 2023, 4154962. [Google Scholar] [CrossRef]
- Talukdar, A.; Sarkar, J.; Debnath, P.; Subba, S.; Chatterjee, S. Synthesizing solution processed W doped SnO2 as an effective ETL for all inorganic Cs (Ge0.5Sn0.5) I3 perovskite based solar cells: A combined experimental and simulation approach. Phys. B Condens. Matter. 2025, 715, 417650. [Google Scholar] [CrossRef]
- El Arfaoui, Y.; Khenfouch, M.; Habiballah, N. DFT and SCAPS-1D calculations of FASnI3-based perovskite solar cell using ZnO as an electron transport layer. Eur. Phys. J. Appl. Phys. 2023, 98, 60. [Google Scholar] [CrossRef]
- Moiz, S.A.; Alzahrani, M.S.; Alahmadi, A.N. Electron transport layer optimization for efficient PTB7: PC70BM bulk-heterojunction solar cells. Polymers 2022, 14, 3610. [Google Scholar] [CrossRef]
- Ait-Wahmane, Y.; Mouhib, H.; Ydir, B.; Ait Hssi, A.; Atourki, L.; Ihlal, A.; Bouabid, K. Comparison study between ZnO and TiO2 in CuO based solar cell using SCAPS-1D. Mater. Today Proc. 2022, 52, 166–171. [Google Scholar] [CrossRef]
- Lotfy, L.A.; Abdelfatah, M.; Sharshir, S.W.; El-Naggar, A.A.; Ismail, W.; El-Shaer, A. Numerical simulation and optimization of FTO/TiO2/CZTS/CuO/Au solar cell using SCAPS-1D. Sci. Rep. 2025, 15, 28022. [Google Scholar] [CrossRef]
- Ahmad, O.; Rashid, A.; Ahmed, M.W.; Nasir, M.F.; Qasim, I. Performance evaluation of Au/p-CdTe/Cs2TiI6/n-TiO2/ITO solar cell using SCAPS-1D. Opt. Mater. 2021, 117, 111105. [Google Scholar] [CrossRef]
- Moiz, S.A.; Alahmadi, A.N.M.; Aljohani, A.J. Design of a novel lead-free perovskite solar cell for 17.83% efficiency. IEEE Access 2021, 9, 54254–54263. [Google Scholar] [CrossRef]
- Abdel-Khalek, E.K.; Motawea, M.A.; Aboelnasr, M.A.; El-Bahnasawy, H.H. Study the oxygen vacancies and Fe oxidation states in CaFeO3-δ perovskite nanomaterial. Phys. B Condens. Matter. 2022, 624, 413415. [Google Scholar] [CrossRef]
- Shin, S. Oxygen stoichiometry in the system (CaxSr1−x) FeO3−y. Its effect on crystallographic and thermodynamic properties. Mater. Res. Bull. 1981, 16, 299–312. [Google Scholar] [CrossRef]
- Alipour, H.; Ghadimi, A. Optimization of lead-free perovskite solar cells in normal-structure with WO3 and water-free PEDOT: PSS composite for hole transport layer by SCAPS-1D simulation. Opt. Mater. 2021, 120, 111432. [Google Scholar] [CrossRef]
- Moiz, S.A.; Alshaikh, M.S.; Alahmadi, A.N. Simulation design of novel non-fluorine polymers as electron transport layer for lead-free Perovskite solar cells. Polymers 2023, 15, 4387. [Google Scholar] [CrossRef] [PubMed]
- Reyes-Molina, R.; Carrillo-Sendejas, J.C.; Mansurova, S.; Cosme, I. Effect of PEDOT: PSS optical properties at the frontal interface on electrical performance in MAPbI3 perovskite solar cells. Opt. Mater. 2024, 150, 115299. [Google Scholar] [CrossRef]
- Bouazizi, S.; Tlili, W.; Bouich, A.; Soucase, B.M.; Omri, A. Design and efficiency enhancement of FTO/PC60BM/CsSn0.5Ge0.5I3/Spiro-OMeTAD/Au perovskite solar cell utilizing SCAPS-1D Simulator. Mater. Res. Express 2022, 9, 096402. [Google Scholar] [CrossRef]
- Ren, G.; Han, W.; Deng, Y.; Wu, W.; Li, Z.; Guo, J.; Guo, W. Strategies of modifying spiro-OMeTAD materials for perovskite solar cells: A review. J. Mater. Chem. A 2021, 9, 4589–4625. [Google Scholar] [CrossRef]
- Moiz, S.A.; Alahmadi, A.N.; Alshaikh, M.S. Design Optimization of Cesium Contents for Mixed Cation MA1−xCsxPbI3-Based Efficient Perovskite Solar Cell. Nanomaterials 2025, 15, 1085. [Google Scholar] [CrossRef]
- Owolabi, J.A.; Onimisi, M.Y.; Ukwenya, J.A.; Bature, A.B.; Ushiekpan, U.R. Investigating the effect of ZnSe (ETM) and Cu2O (HTM) on absorber layer on the performance of pervoskite solar cell using SCAPS-1D. Am. J. Phys. Appl. 2020, 8, 8–18. [Google Scholar]
- Lam, N.D. Modelling and numerical analysis of ZnO/CuO/Cu2O heterojunction solar cell using SCAPS. Eng. Res. Express 2020, 2, 025033. [Google Scholar] [CrossRef]
- Sajid, M.; Ali, K.; Shah, H.S.; Shahid, A.; Bakar, S.A.; Yousaf, M.; Lee, S.L. Boosting solar cell performance: Optimization of WS2 absorber with Cu2O HTL ZnSe ETL using SCAPS-1D simulation. J. Opt. 2024, 1–12. [Google Scholar] [CrossRef]
- Lee, D.G.; Kim, M.C.; Kim, B.J.; Kim, D.H.; Lee, S.M.; Choi, M.; Jung, H.S. Effect of TiO2 particle size and layer thickness on mesoscopic perovskite solar cells. Appl. Surf. Sci. 2019, 477, 131–136. [Google Scholar] [CrossRef]
- Sławek, A.; Starowicz, Z.; Lipiński, M. The influence of the thickness of compact TiO2 electron transport layer on the performance of planar CH3NH3PbI3 perovskite solar cells. Materials 2021, 14, 3295. [Google Scholar] [CrossRef] [PubMed]
- Zaleska, A. Doped-TiO2: A review. Recent Pat. Eng. 2008, 2, 157–164. [Google Scholar] [CrossRef]
- Malati, M.A.; Wong, W.K. Doping TiO2 for solar energy applications. Surf. Technol. 1984, 22, 305–322. [Google Scholar] [CrossRef]
- Kim, G.W.; Shinde, D.V.; Park, T. Thickness of the hole transport layer in perovskite solar cells: Performance versus reproducibility. RSC Adv. 2015, 5, 99356–99360. [Google Scholar] [CrossRef]
- Wang, Q.; Bi, C.; Huang, J. Doped hole transport layer for efficiency enhancement in planar heterojunction organolead trihalide perovskite solar cells. Nano Energy 2015, 15, 275–280. [Google Scholar] [CrossRef]
- Prasad, D.; Anitha, G.; Leo, L.M.; Kumar, A. Theoretical analysis of earth-abundant solar cell based on green absorber CuFeO2. Opt. Quantum Electron. 2023, 55, 1262. [Google Scholar] [CrossRef]
- Akin, S.; Sadegh, F.; Turan, S.; Sonmezoglu, S. Inorganic CuFeO2 delafossite nanoparticles as effective hole transport materials for highly efficient and long-term stable perovskite solar cells. ACS Appl. Mater. Interfaces 2019, 11, 45142–45149. [Google Scholar] [CrossRef]
- Panigrahi, R.; Mallik, B.S. Ionic conduction and cathodic properties of CaMO3 (M = Fe and Mn) electrode materials via molecular dynamics and first-principles simulations. J. Phys. Chem. Solids 2025, 196, 112384. [Google Scholar] [CrossRef]
- Karimov, K.; Ahmed, M.M.; Noshin, F.; Saleem, M.; Mahroof-Tahir, M.; Moiz, S.A.; Rashid, A. Nickel phthalocyanine based organic photo transistor: Effect of semiconductor film thickness. Eur. Phys. J. Appl. Phys. 2015, 72, 20202. [Google Scholar] [CrossRef]
- Lin, K.; Xing, J.; Quan, L.N.; de Arquer, F.P.G.; Gong, X.; Lu, J.; Wei, Z. Perovskite light-emitting diodes with external quantum efficiency exceeding 20 per cent. Nature 2018, 562, 245–248. [Google Scholar] [CrossRef]
- Calado, P.; Burkitt, D.; Yao, J.; Troughton, J.; Watson, T.M.; Carnie, M.J.; Barnes, P.R. Identifying dominant recombination mechanisms in perovskite solar cells by measuring the transient ideality factor. Phys. Rev. Appl. 2019, 11, 044005. [Google Scholar] [CrossRef]
- Moiz, S.A.; Imran, S.M.; Nahhas, A.M.; Rehman, F.; Ahmed, M.M.; Kim, H.T.; Lee, J.H. Polaron Hopping Mechanism of Conducting Polymer. In Proceedings of the 2012 International Conference on Emerging Technologies, Islamabad, Pakistan, 8–9 October 2012; IEEE: New York, NY, USA, 2012; pp. 1–6. [Google Scholar]
- Karimov, K.S.; Saeed, M.T.; Khalid, F.A.; Moiz, S.A. Effect of displacement on resistance and capacitance of polyaniline film. Chin. Phys. B 2011, 20, 040601. [Google Scholar] [CrossRef]
- Meneses-Rodríguez, D.; Horley, P.P.; Gonzalez-Hernandez, J.; Vorobiev, Y.V.; Gorley, P.N. Photovoltaic solar cells performance at elevated temperatures. Sol. Energy 2005, 78, 243–250. [Google Scholar] [CrossRef]
- Moiz, S.A.; Khan, I.A.; Younis, W.A.; Masud, M.I.; Ismail, Y.; Khawaja, Y.M. Solvent induced charge transport mechanism for conducting polymer at higher temperature. Mater. Res. Express 2020, 7, 095304. [Google Scholar] [CrossRef]
- Singh, P.; Ravindra, N.M. Temperature dependence of solar cell performance—An analysis. Sol. Energy Mater. Sol. Cells 2012, 101, 36–45. [Google Scholar] [CrossRef]
- Todinova, A.; Contreras-Bernal, L.; Salado, M.; Ahmad, S.; Morillo, N.; Idígoras, J.; Anta, J.A. Towards a universal approach for the analysis of impedance spectra of perovskite solar cells: Equivalent circuits and empirical analysis. ChemElectroChem 2017, 4, 2891–2901. [Google Scholar] [CrossRef]
- Han, L.; Koide, N.; Chiba, Y.; Mitate, T. Modeling of an equivalent circuit for dye-sensitized solar cells. Appl. Phys. Lett. 2004, 84, 2433–2435. [Google Scholar] [CrossRef]
- Wolf, M.; Rauschenbach, H. Series resistance effects on solar cell measurements. Adv. Energy Convers. 1963, 3, 455–479. [Google Scholar] [CrossRef]
- Da, Y.; Xuan, Y.; Li, Q. Quantifying energy losses in planar perovskite solar cells. Sol. Energy Mater. Sol. Cells 2018, 174, 206–213. [Google Scholar] [CrossRef]
- Lopez-Varo, P.; Jiménez-Tejada, J.A.; García-Rosell, M.; Ravishankar, S.; Garcia-Belmonte, G.; Bisquert, J.; Almora, O. Device physics of hybrid perovskite solar cells: Theory and experiment. Adv. Energy Mater. 2018, 8, 1702772. [Google Scholar] [CrossRef]
- Sardar, R.H.; Bera, A.; Chattopadhyay, S.; Ali, S.I.; Pramanik, S.; Mandal, A.C. The impact of series (Rs) and shunt resistances (Rsh) on solar cell parameters to enhance the photovoltaic performance of f-PSCs. Opt. Mater. 2024, 155, 115818. [Google Scholar] [CrossRef]
- Cai, Q.; Li, H.; Jiang, Y.; Tu, L.; Ma, L.; Wu, X.; Chen, Y. High-efficiency perovskite solar cells based on MAI (PbI2)1−x (FeCl2)x absorber layers. Sol. Energy 2018, 159, 786–793. [Google Scholar] [CrossRef]
- Bandara, T.M.W.J.; Knee, C.S.; Furlani, M.; Albinsson, I.; Mellander, B.E. Novel photo-voltaic device based on Bi1−xLaxFeO3 perovskite films with higher efficiency. J. Mater. Sci. Mater. Electron. 2019, 30, 1654–1662. [Google Scholar] [CrossRef]
- Tiwari, D.; Fermin, D.J.; Chaudhuri, T.K.; Ray, A. Solution processed bismuth ferrite thin films for all-oxide solar photovoltaics. J. Phys. Chem. C 2015, 119, 5872–5877. [Google Scholar] [CrossRef]
- Kozlov, S.S.; Alexeeva, O.V.; Nikolskaia, A.B.; Shevaleevskiy, O.I.; Averkiev, D.D.; Kozhuhovskaya, P.V.; Almjasheva, O.V.; Larina, L.L. Double perovskite oxides La2NiMnO6 and La2Ni0.8Fe0.2MnO6 for inorganic perovskite solar cells. Nanosyst. Phys. Chem. Math. 2022, 13, 314–319. [Google Scholar] [CrossRef]



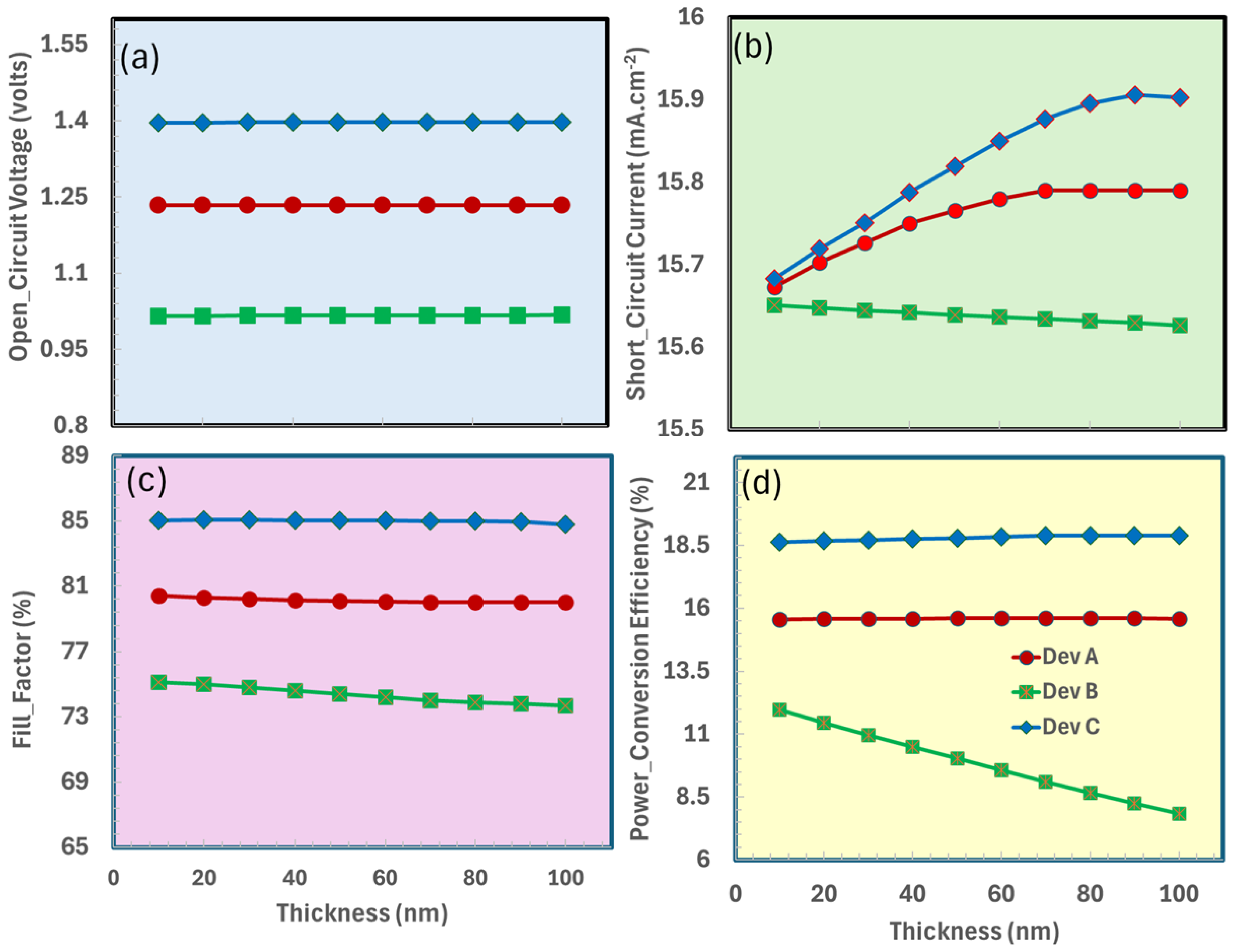
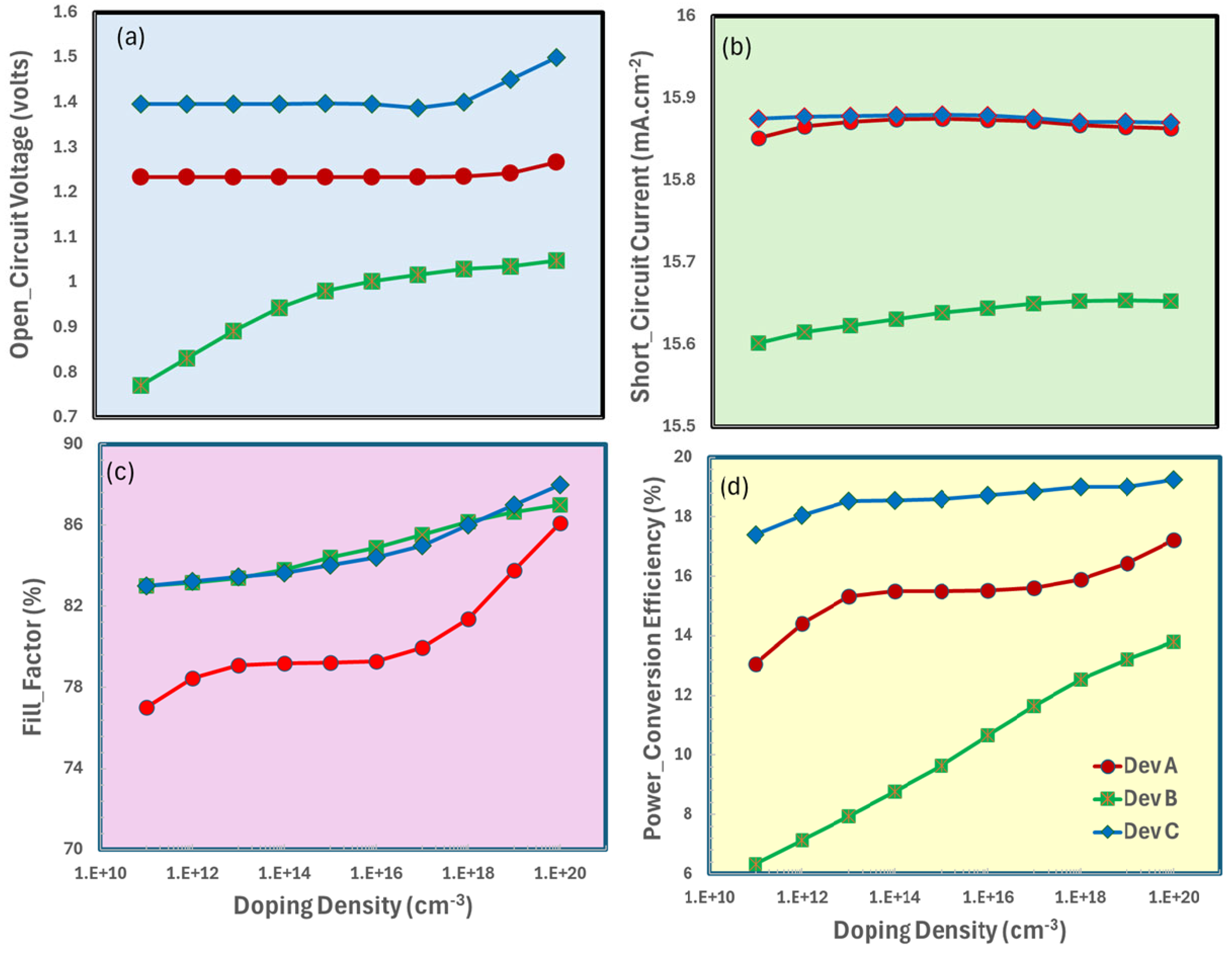
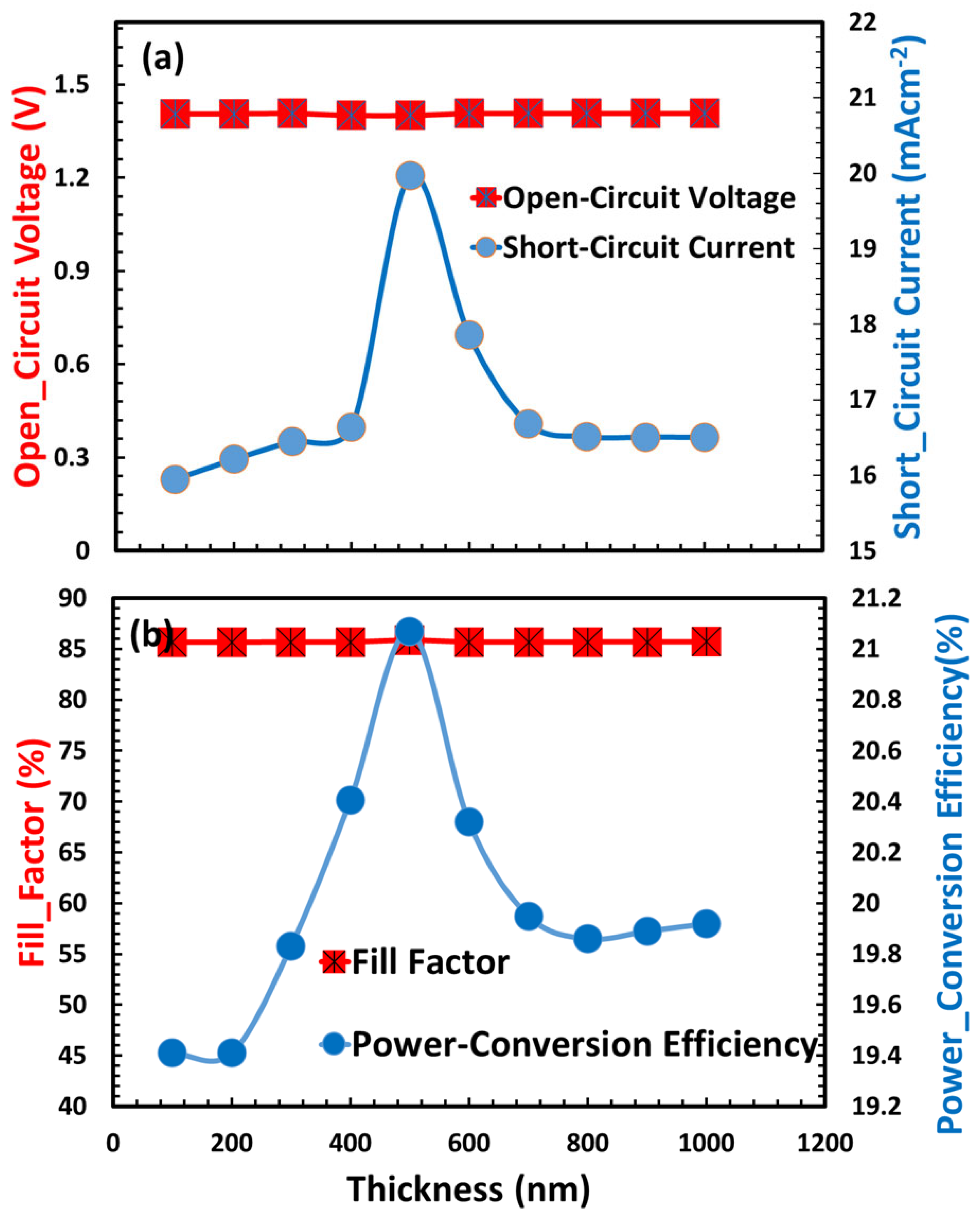
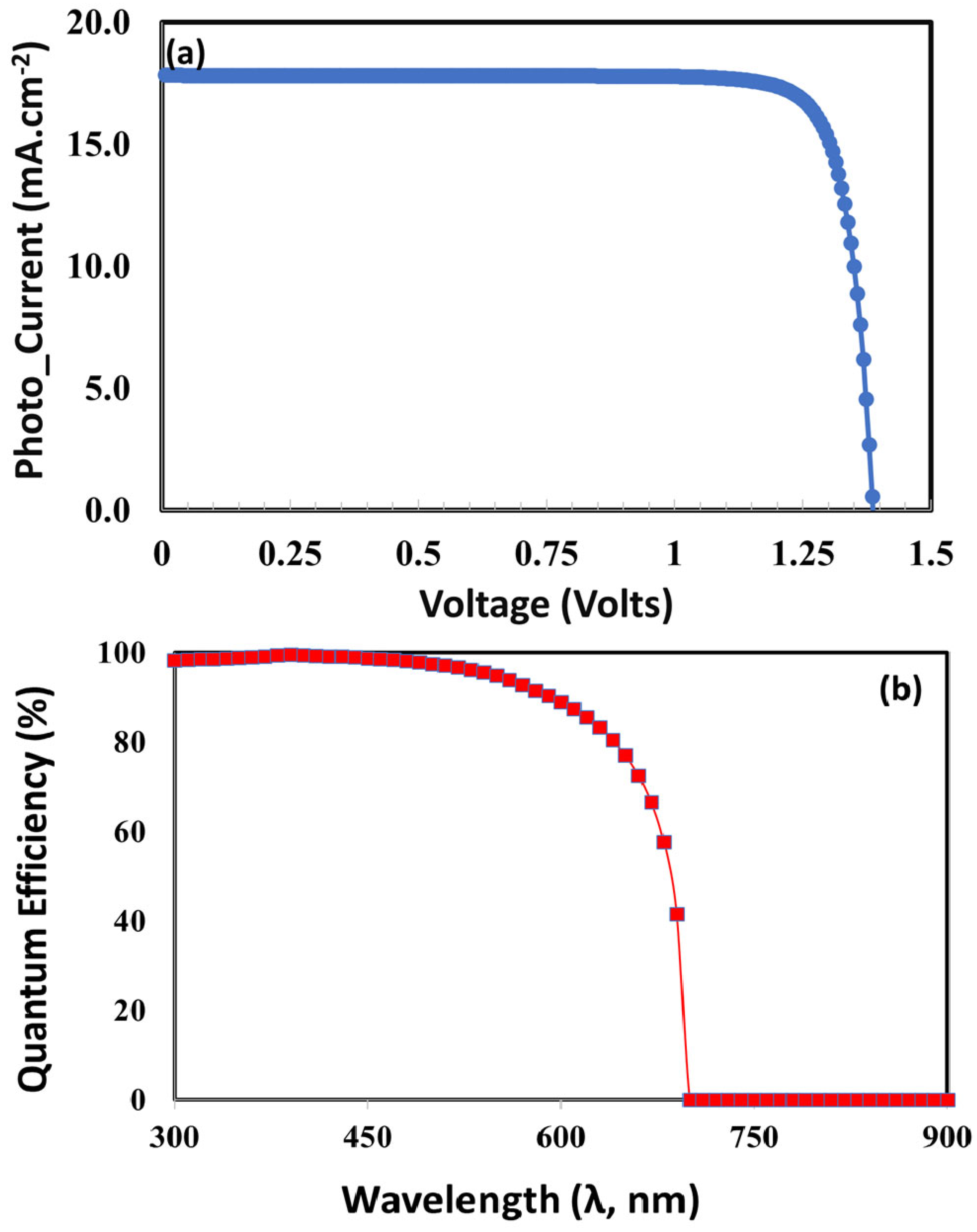
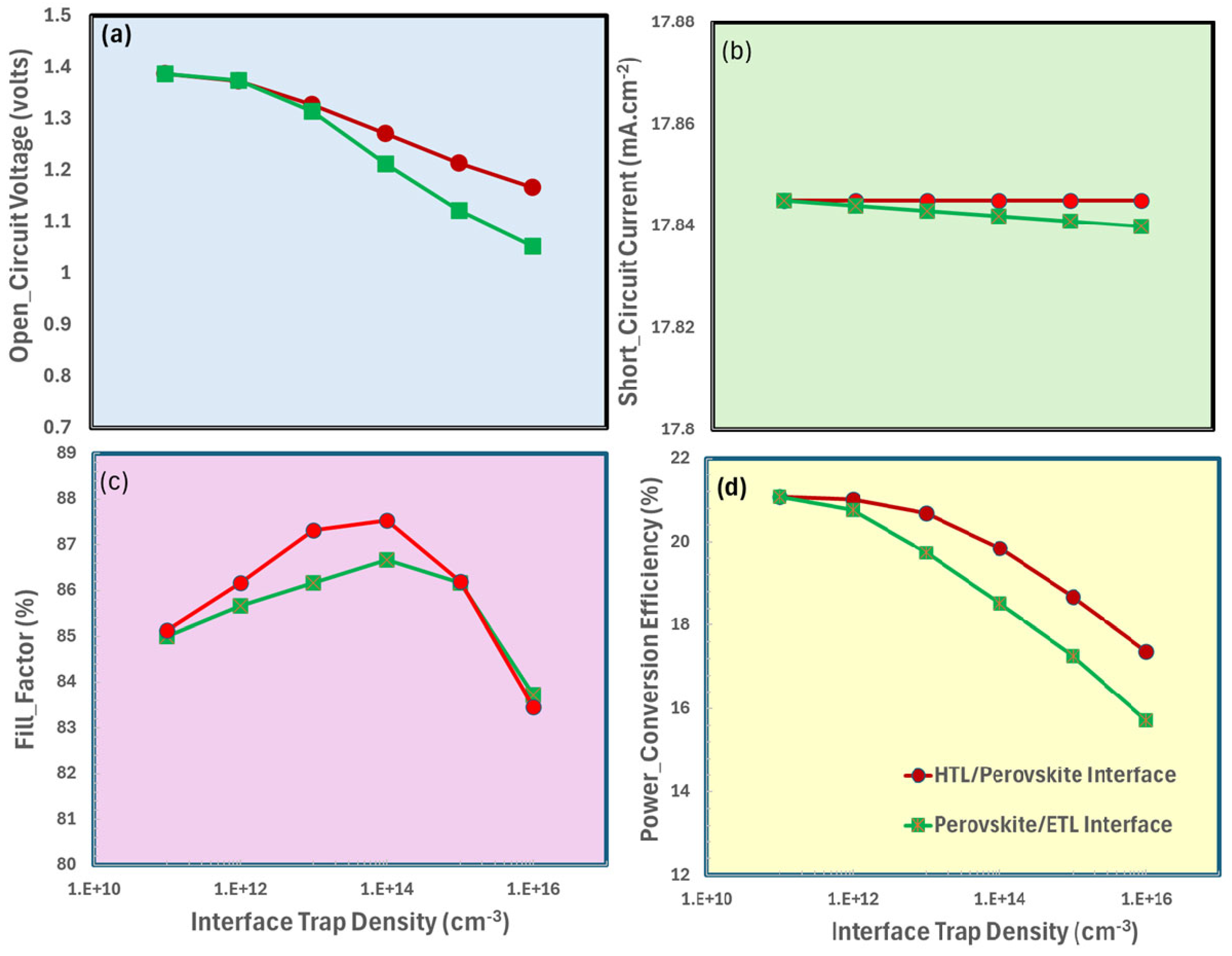

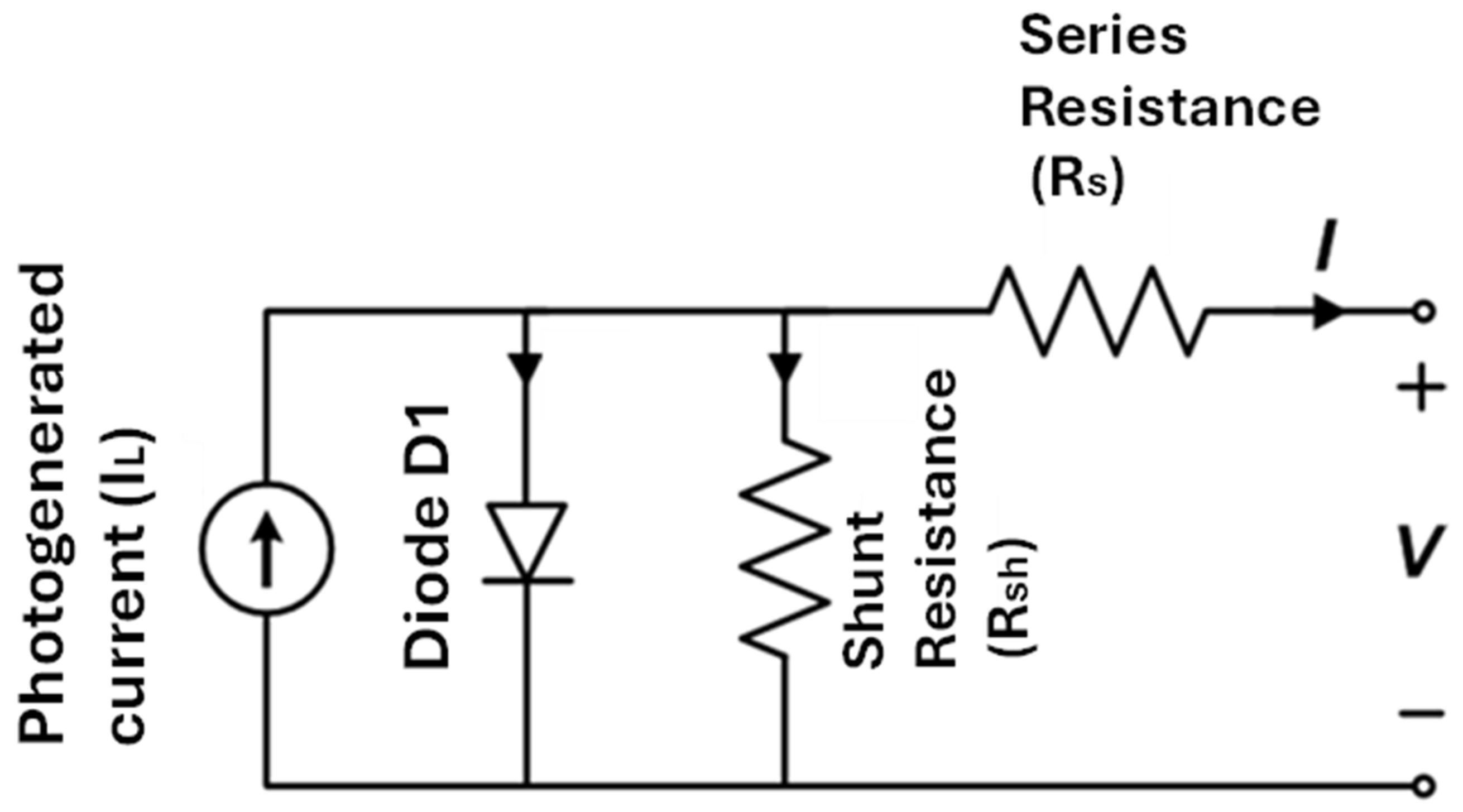
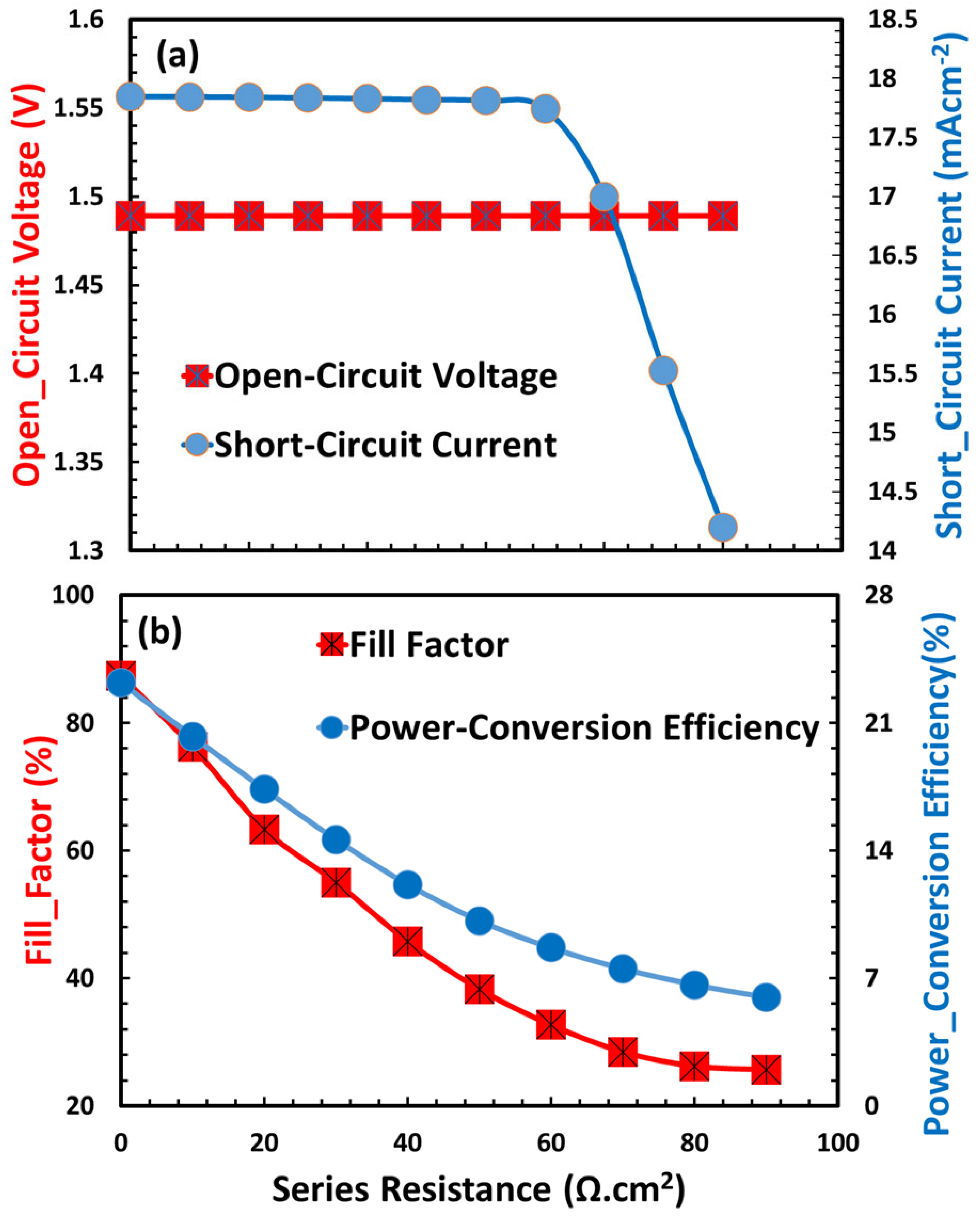
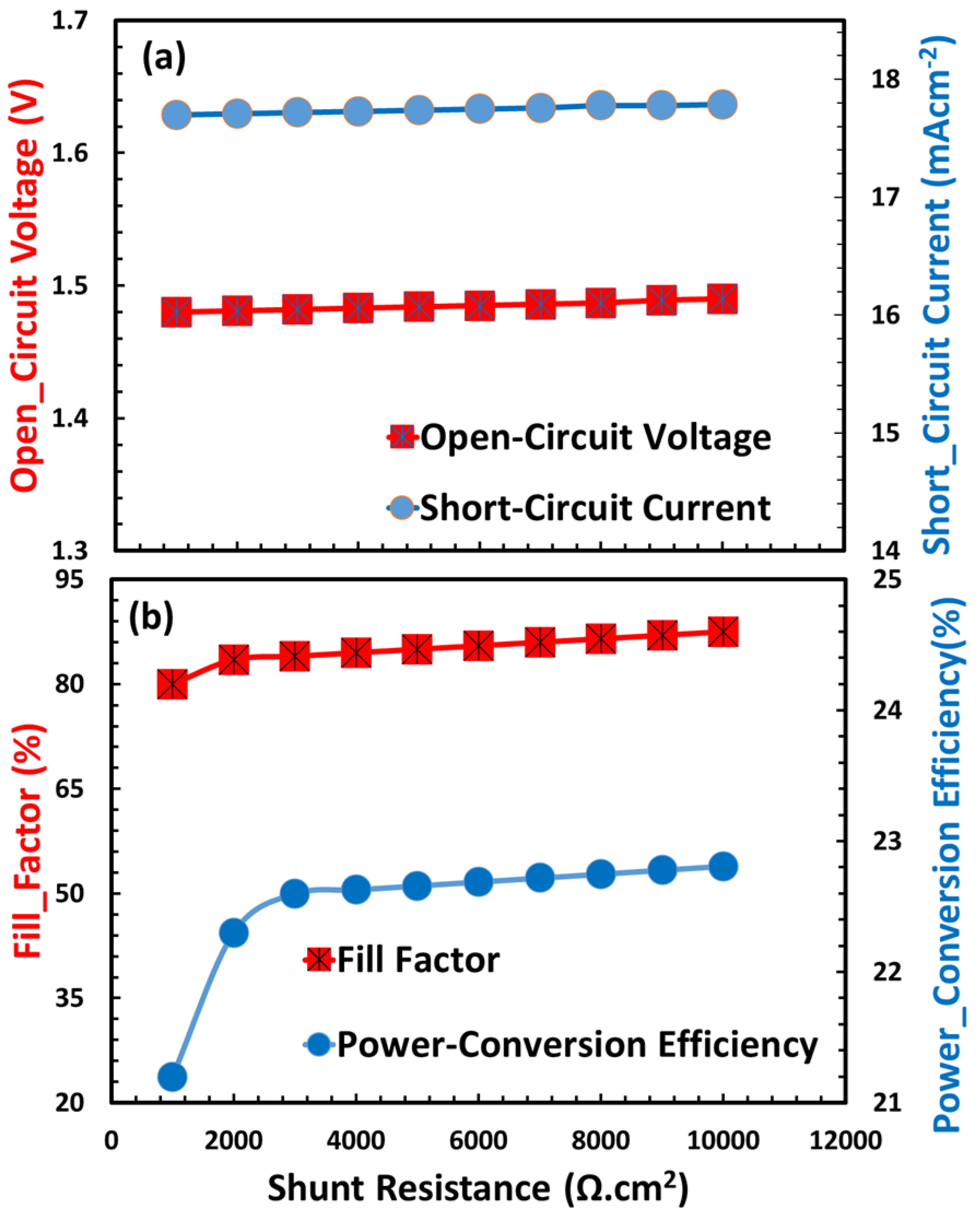
| Photovoltaic Parameters | Unit | Symbol | SnO2 | ZnO | TiO2 | CaV0.5Fe0.5O3 |
|---|---|---|---|---|---|---|
| Thickness | nm | Th | 350 | 350 | 350 | 350 |
| Energy Band Gap | eV | Eg | 3.5 | 2.2 | 3.3 | 1.78 |
| Electron Affinity | eV | χ | 4.2 | 4.5 | 4 | 3.9 |
| Dielectric Permittivity (Relative) | ε | 9 | 9 | 10 | 19 | |
| Effective Density of States at Conduction Band | cm−3 | NC | 2.2 × 1018 | 2.2 × 1018 | 2.2 × 1018 | 1 × 1019 |
| Effective Density of States at Valence Band | cm−3 | NV | 1.8 × 1019 | 1.8 × 1019 | 1.8 × 1019 | 1 × 1019 |
| Hole Thermal Velocity | cm/s | Vh | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 |
| Electron Thermal Velocity | cm/s | Ve | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 |
| Electron Mobility | cm−2/V·s | µe | 20 | 100 | 400 | 20 |
| Hole Mobility | cm−2/V·s | µh | 10 | 25 | 110 | 10 |
| Uniform Shallow Donor Doping | cm−3 | ND | 1 × 1017 | 1 × 1017 | 1 × 1017 | 1 × 1017 |
| Uniform Shallow Acceptor Doping | cm−3 | NA | 0 | 0 | 0 | 0 |
| Defect Density | cm−3 | NT | 1 × 1015 | 1 × 1015 | 1 × 1015 | 1 × 1015 |
| Photovoltaic Parameters | Unit | Symbol | PEDOT:PSS | Spiro OMeTAD | Cu2O |
|---|---|---|---|---|---|
| Thickness | nm | Th | 350 | 350 | 350 |
| Energy Band Gap | eV | Eg | 2.2 | 2.9 | 2.17 |
| Electron Affinity | eV | χ | 2.9 | 2.2 | 3.2 |
| Dielectric Permittivity | ε | 3 | 3.5 | 7.11 | |
| Effective Density of States at Con-duction Band | cm−3 | NC | 2.2 × 1018 | 2.2 × 1018 | 2.5 × 1017 |
| Effective Density of States at Valence Band | cm−3 | NV | 1.8 × 1019 | 1.8 × 1018 | 2.5 × 1019 |
| Hole Thermal Velocity | cm/s | Vh | 1 × 107 | 1 × 107 | 1 × 107 |
| Electron Thermal Velocity | cm/s | Ve | 1 × 107 | 1 × 107 | 1 × 107 |
| Electron Mobility | cm−2/V·s | µe | 10 | 1 × 10−4 | 200.00 |
| Hole Mobility | cm−2/V·s | µh | 10 | 1 × 10−1 | 80.00 |
| Uniform Shallow Donor Doping | cm−3 | ND | 0 | 0 | 0 |
| Uniform Shallow Acceptor Doping | cm−3 | NA | 1 × 1017 | 1 × 1017 | 1 × 1017 |
| Defect Density | cm−3 | NT | 1 × 1015 | 1 × 1015 | 1 × 1015 |
| References | [18,51,55,56] | [57,58,59] | [60,61,62] |
| Transport Layer | Optimization Parameters | Unit | Voc (V) | JSC mA·cm−2 | FF (%) | PCE (%) | |
|---|---|---|---|---|---|---|---|
| Electron Transport Layer (TiO2) | Thickness | 40 | nm | 1.38 | 19.8 | 85.2 | 23.28 |
| Doping Density | 1 × 1020 | cm−3 | |||||
| Hole Transport Layer (Cu2O) | Thickness | 50 | nm | ||||
| Doping Density | 1 × 1020 | cm−3 | |||||
| Perovskite Absorber Layer CaV0.5Fe0.5O3 | Thickness | 550 | nm | ||||
| Doping Density | - | cm−3 | |||||
| Perovskite Absorber | Hole Transport Layer | Electron Transport Layer | Open-Circuit Voltage | Short-Circuit Current | Fill-Factor | Power-Conversion Efficiency | Reference |
|---|---|---|---|---|---|---|---|
| MAI | Spiro OMeTAD | TiO2 | 1.07 | 20.19 | 67.92 | 14.67 | [87] |
| (MAI)0.991(FeCl2)0.009 | Spiro OMeTAD | TiO2 | 1.08 | 21.91 | 69.12 | 16.35 | [87] |
| (MAI)0.982(FeCl2)0.018 | Spiro OMeTAD | TiO2 | 1.1 | 22.21 | 70.85 | 17.31 | [87] |
| (MAI)0.964(FeCl2)0.036 | Spiro OMeTAD | TiO2 | 1.08 | 21.34 | 69.02 | 15.91 | [87] |
| (MAI)0.928(FeCl2)0.072 | Spiro OMeTAD | TiO2 | 1.08 | 18.94 | 65.14 | 13.32 | [87] |
| Bi0.8La0.2FeO3 | QSPE | TiO2 | 0.604 | 0.346 | 63.6 | 0.133 | [88] |
| BiFeO | Graphite | ZnO | 0.642 | 12.47 | 50.4 | 3.98 | [89] |
| Doped-BiFeO3 | NiO | TiO2 | 1.83 | 9.45 | 86.74 | 15 | [90] |
| La2Ni0.8Fe0.2MnO6 | Spiro OMeTAD | TiO2 | 0.495 | 1.6 | 47 | 0.37 | [19] |
| La2Ni0.8Fe0.2MnO6 | Spiro OMeTAD | ZrO2 | 0.74 | 8.5 | 58 | 3.7 | [19] |
| CaV0.5Fe0.5O3 | Spiro OMeTAD | TiO2 | 1.38 | 19.8 | 85.2 | 23.28 | This Study |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moiz, S.A.; Masud, M.I. Enhancing CaV0.5Fe0.5O3-Based Lead-Free Perovskite Solar Cell Efficiency by over 23% via Transport Layer Engineering. Nanomaterials 2025, 15, 1646. https://doi.org/10.3390/nano15211646
Moiz SA, Masud MI. Enhancing CaV0.5Fe0.5O3-Based Lead-Free Perovskite Solar Cell Efficiency by over 23% via Transport Layer Engineering. Nanomaterials. 2025; 15(21):1646. https://doi.org/10.3390/nano15211646
Chicago/Turabian StyleMoiz, Syed Abdul, and Muhammad I. Masud. 2025. "Enhancing CaV0.5Fe0.5O3-Based Lead-Free Perovskite Solar Cell Efficiency by over 23% via Transport Layer Engineering" Nanomaterials 15, no. 21: 1646. https://doi.org/10.3390/nano15211646
APA StyleMoiz, S. A., & Masud, M. I. (2025). Enhancing CaV0.5Fe0.5O3-Based Lead-Free Perovskite Solar Cell Efficiency by over 23% via Transport Layer Engineering. Nanomaterials, 15(21), 1646. https://doi.org/10.3390/nano15211646







