Optical Waveguide-Pair Design for CMOS-Compatible Hybrid III-V-on-Silicon Quantum Dot Lasers
Abstract
1. Introduction
2. Materials and Methods
3. Results
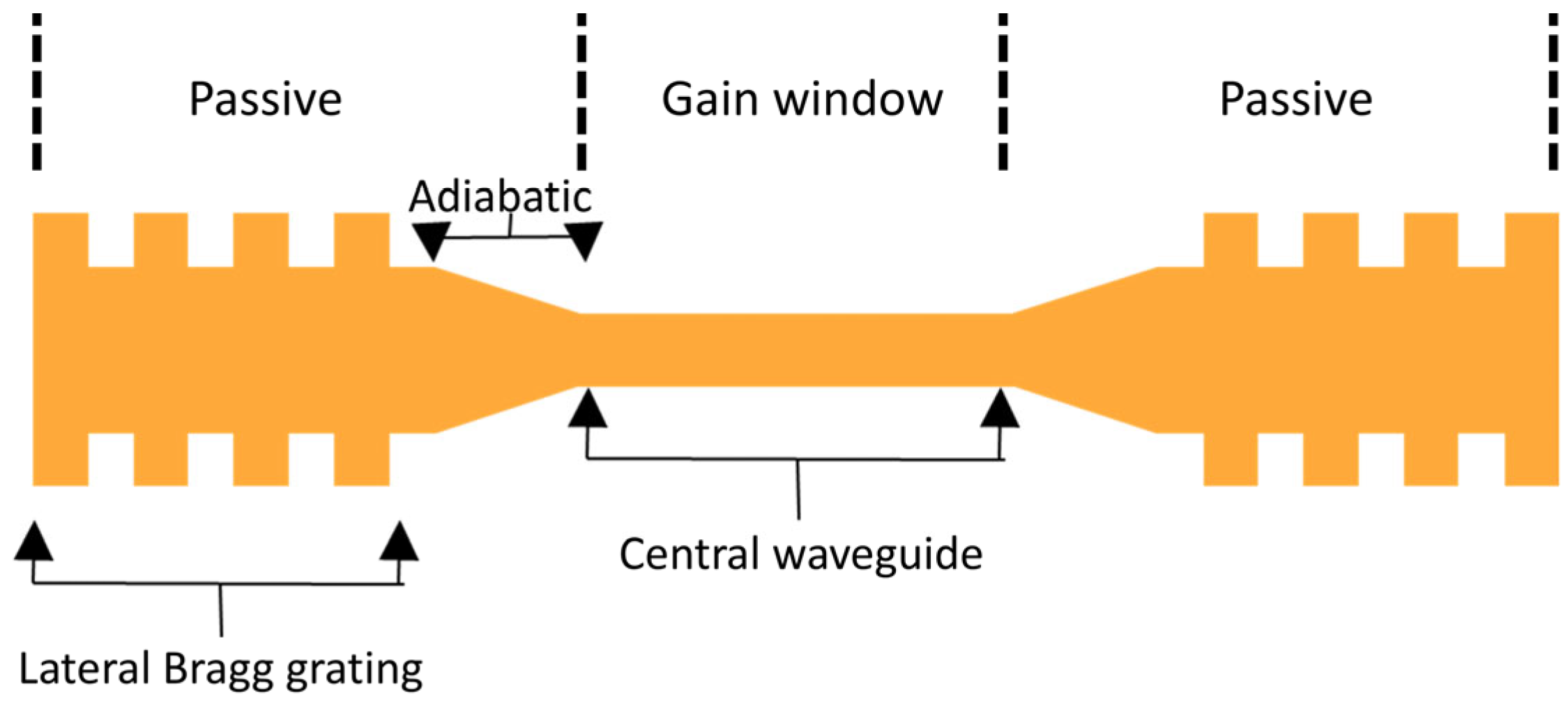
3.1. Implementation of Supermode Theory in Hybrid Laser Design
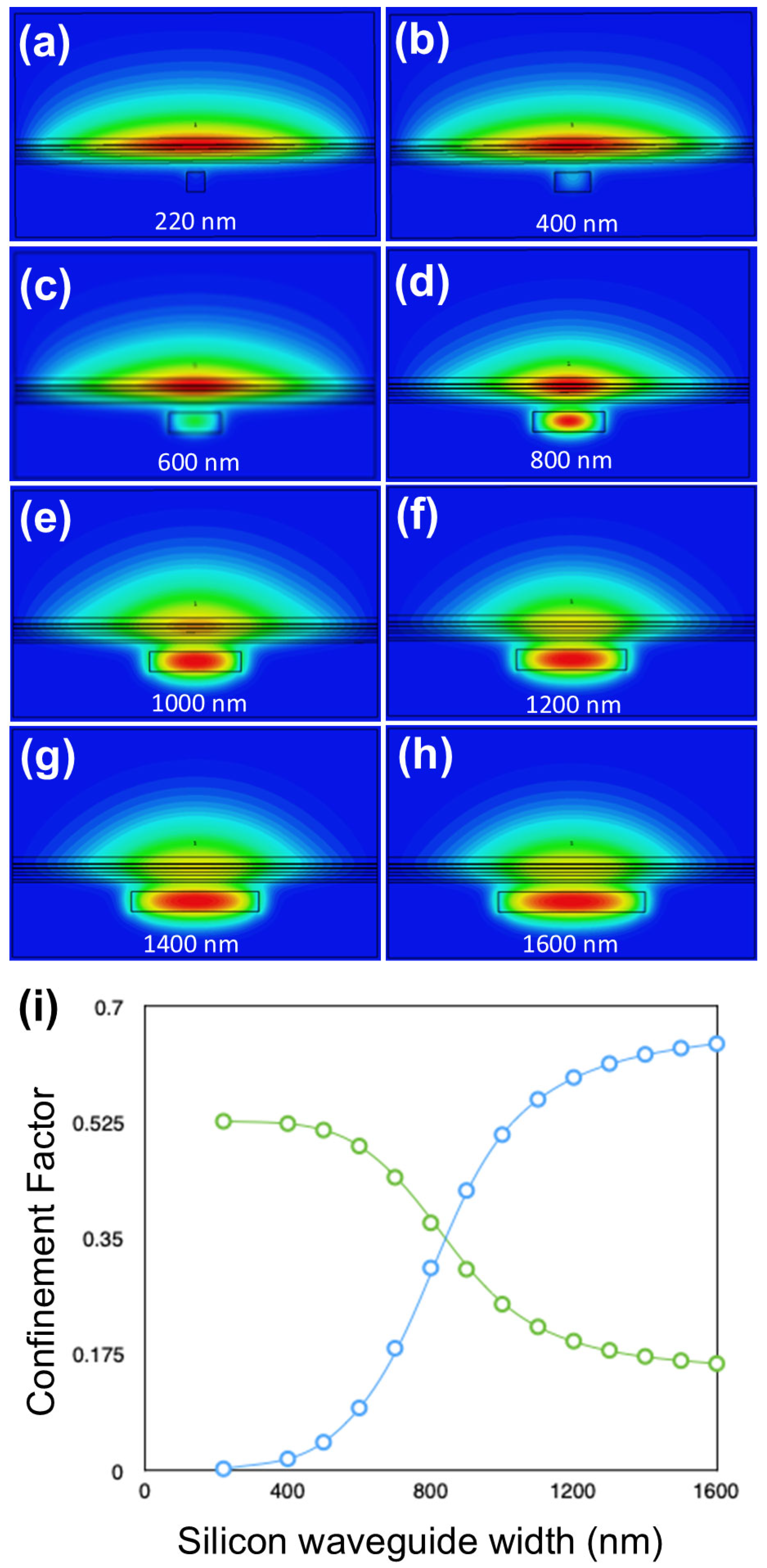
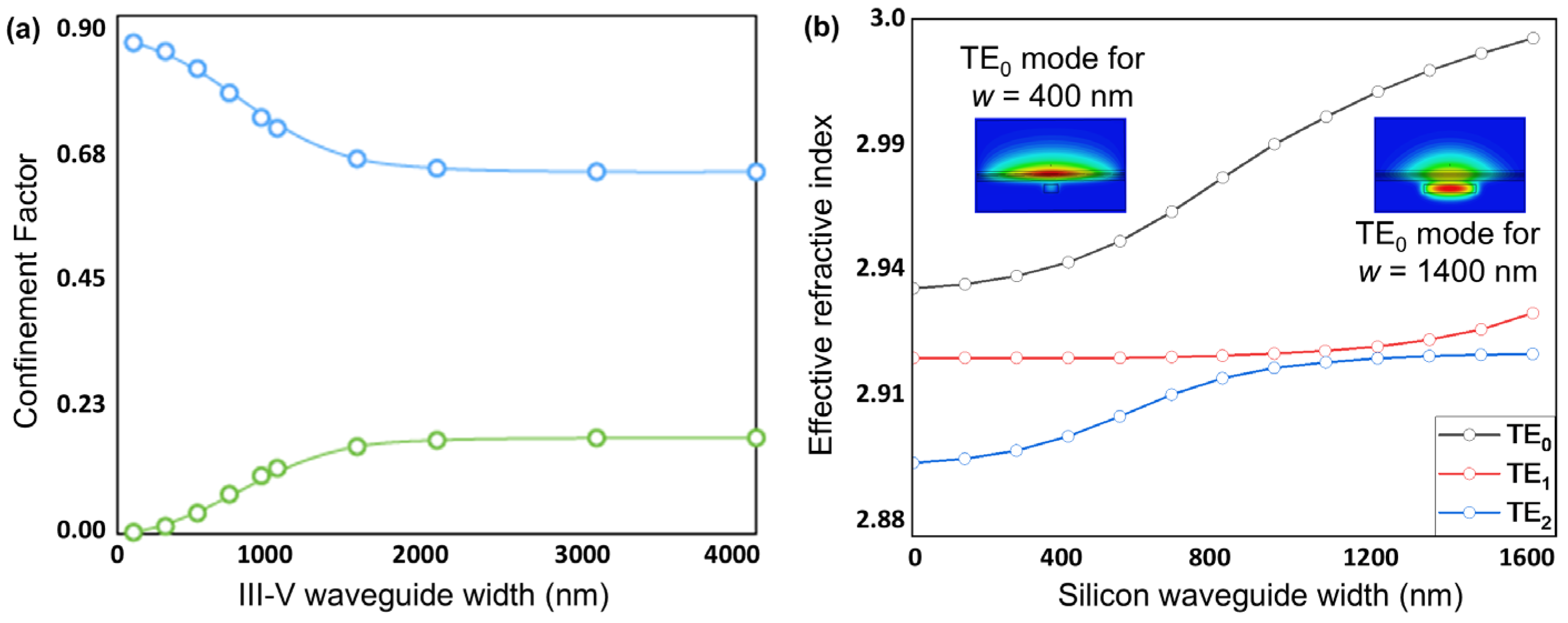
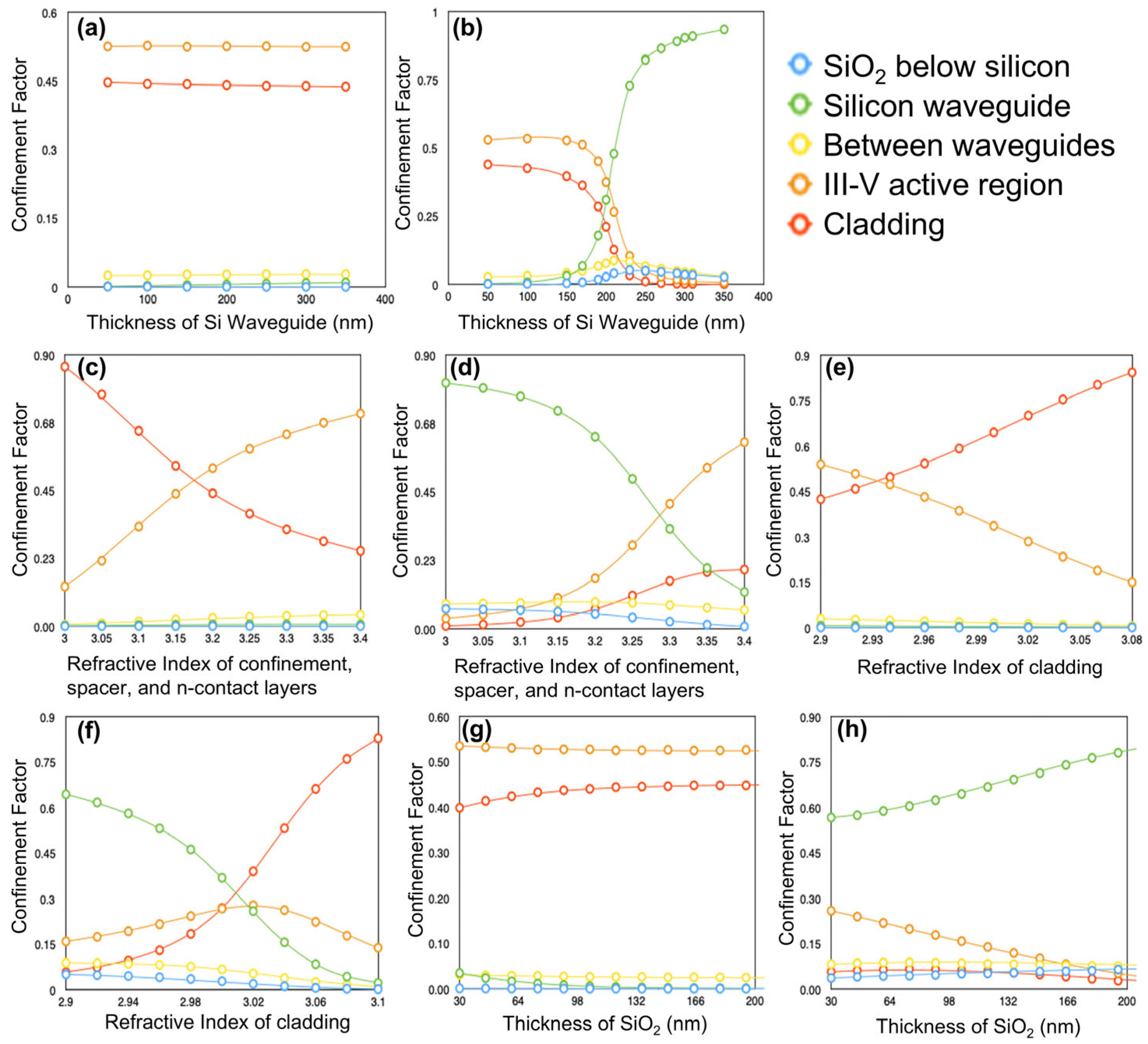
3.2. Silicon Waveguide Design
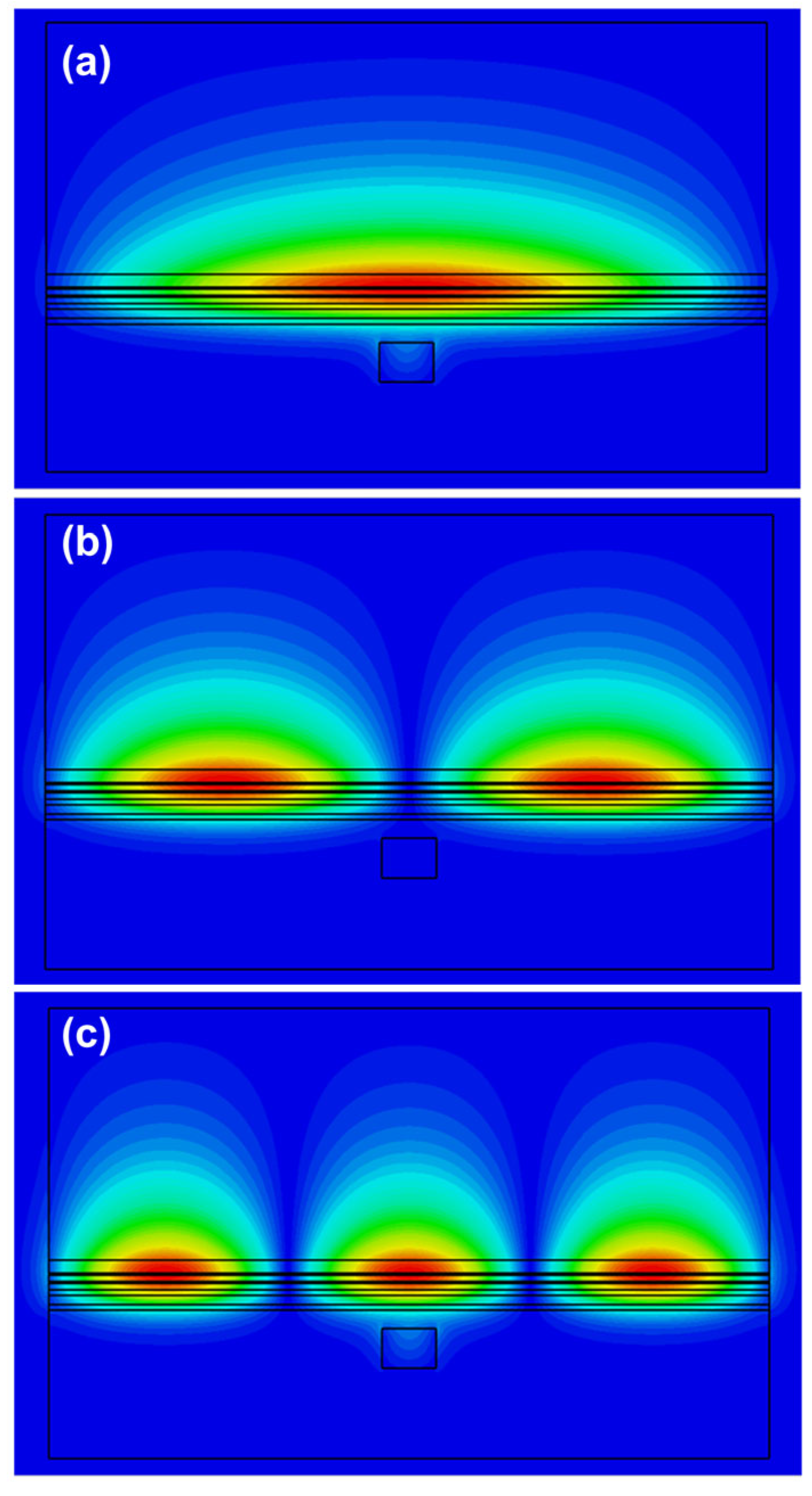
3.3. Tolerances to Growth and Fabrication Inaccuracies
3.4. Environmental Sensitivity and Open-System Considerations
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Greenberg, A.; Hamilton, J.R.; Jain, N.; Kandula, S.; Kim, C.; Lahiri, P.; Maltz, D.A.; Patel, P.; Sengupta, S. VL2: A scalable and flexible data center network. SIGCOMM Comput. Commun. Rev. 2009, 39, 51–62. [Google Scholar] [CrossRef]
- Papatryfonos, K.; Selviah, D.R.; Maman, A.; Hasharoni, K.; Brimont, A.; Zanzi, A.; Kraft, J.; Sidorov, V.; Seifried, M.; Baumgartner, Y.; et al. Co-Package Technology Platform for Low-Power and Low-Cost Data Centers. Appl. Sci. 2021, 11, 6098. [Google Scholar] [CrossRef]
- Xiao, Z.; Liu, W.; Xu, S.; Zhou, J.; Ren, Z. Lee Recent Progress in Silicon-Based Photonic Integrated Circuits and Emerging Applications. Adv. Opt. Mater. 2023, 11, 2301028. [Google Scholar] [CrossRef]
- Cheng, Q.; Bahadori, M.; Glick, M.; Rumley, S. Bergman Recent advances in optical technologies for data centers: A review. Optica 2018, 5, 1354–1370. [Google Scholar] [CrossRef]
- Shang, C.; Wan, Y.; Selvidge, J.; Hughes, E.; Herrick, R.; Mukherjee, K.; Duan, J.; Grillot, F.; Chow, W.W.; Bowers, J.E. Perspectives on advances in quantum dot lasers and integration with Si photonic integrated circuits. ACS Photonics 2021, 8, 2555–2566. [Google Scholar] [CrossRef]
- Papatryfonos, K.; Girard, J.C.; Tang, M.; Deng, H.; Seeds, A.J.; David, C.; Rodary, G.; Liu, H.; Selviah, D.R. Low-Defect Quantum Dot Lasers Directly Grown on Silicon Exhibiting Low Threshold Current and High Output Power at Elevated Temperatures. Adv. Photonics Res. 2024, 24, 00082. [Google Scholar] [CrossRef]
- Murphy, T.; Broderick, C.A.; Peters, E.F.H. O’Reilly Lateral Quantum-Confined Stark Effect for Integrated Quantum Dot Electroabsorption Modulators. IEEE J. Sel. Top. Quantum Electron. 2025, 31, 1–10. [Google Scholar] [CrossRef]
- Seifried, M.; Villares, G.; Baumgartner, Y.; Hahn, H.; Halter, M.; Horst, F.; Caimi, D.; Caer, C.; Sousa, M.; Dangel, R.F.; et al. Monolithically Integrated CMOS-Compatible III–V on Silicon Lasers. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 1–9. [Google Scholar] [CrossRef]
- Wan, Y.; Shang, C.; Norman, J.; Shi, B.; Li, Q.; Collins, N.; Dumont, M.; Lau, K.M.; Gossard, A.C.; Bowers, J.E. Low Threshold Quantum Dot Lasers Directly Grown on Unpatterned Quasi-Nominal (001) Si. IEEE J. Sel. Top. Quantum Electron. 2020, 26, 1900409. [Google Scholar] [CrossRef]
- Koscica, R.; Skipper, A.; Shi, B.; Feng, K.; Leake, G.; Zylstra, M.; Herman, J.; Netherton, A.; Prabakaran, A.; Shang, C.; et al. Quantum Dot DBR Lasers Monolithically Integrated on Silicon Photonics by In-Pocket Heteroepitaxy. J. Light. Technol. 2025, 43, 5773–5781. [Google Scholar] [CrossRef]
- Xiang, C.; Jin, W.; Huang, D.; Tran, M.A.; Guo, J.; Wan, Y.; Xie, W.; Kurczveil, G.; Netherton, A.M.; Liang, D.; et al. High-Performance Silicon Photonics Using Heterogeneous Integration. IEEE J. Sel. Top. Quantum Electron. 2022, 28, 1. [Google Scholar] [CrossRef]
- Liang, D.; Bowers, J.E. Recent Progress in Heterogeneous III-V-on-Silicon Photonic Integration. Adv. Manuf. 2021, 2, 59. [Google Scholar] [CrossRef]
- Li, Q.; Lau, K.M. Epitaxial growth of highly mismatched III-V materials on (001) silicon for electronics and optoelectronics. Prog. Cryst. Growth Charact. Mater. 2017, 63, 105–120. [Google Scholar] [CrossRef]
- Liang, D.; Fiorentino, M.; Okumura, T.; Chang, H.-H.; Spencer, D.T.; Kuo, Y.-H.; Fang, A.W.; Dai, D.; Beausoleil, R.G.; Bowers, J.E. Electrically-pumped compact hybrid silicon microring lasers for optical interconnects. Opt. Express 2009, 17, 20355–20364. [Google Scholar] [CrossRef]
- Fang, A.W.; Lively, E.; Kuo, Y.-H.; Liang, D.; Bowers, J.E. A distributed feedback silicon evanescent laser. Opt. Express 2008, 16, 4413–4419. [Google Scholar] [CrossRef]
- Fang, A.W.; Kocha, B.R.; Jones, R.; Lively, E.; Liang, D.; Kuo, Y.-H.; Bowers, J.E. A distributed Bragg reflector silicon evanescent laser. IEEE Photonics Technol. Lett. 2008, 20, 1667–1669. [Google Scholar] [CrossRef]
- Park, H.; Fang, A.W.; Kodama, S.; Bowers, J.E. Hybrid silicon evanescent laser fabricated with a silicon waveguide and III-V offset quantum wells. Opt. Express 2005, 13, 9460–9464. [Google Scholar] [CrossRef]
- Zia, N.; Tuorila, H.; Viheriälä, J.; Ojanen, S.-P.; Koivusalo, E.; Hilska, J.; Guina, M. Hybrid silicon photonics DBR laser based on flip-chip integration of GaSb amplifiers and µm-scale SOI waveguides. Opt. Express 2022, 30, 24995–25005. [Google Scholar] [CrossRef]
- Fang, A.; Park, H.; Jones, R.; Cohen, O.; Paniccia, M.; Bowers, J. A continuous-wave hybrid AlGaInAs-silicon evanescent laser. IEEE Photon. Technol. Lett. 2006, 18, 1143–1145. [Google Scholar] [CrossRef]
- Fang, A.W.; Park, H.; Kuo, Y.-H.; Jones, R.; Cohen, O.; Liang, D.; Raday, O.; Sysak, M.N.; Paniccia, M.J.; Bowers, J.E. Hybrid silicon evanescent devices. Mater. Today 2007, 10, 28–35. [Google Scholar] [CrossRef]
- Fang, A.W.; Jones, R.; Park, H.; Cohen, O.; Raday, O.; Paniccia, M.J.; Bowers, J.E. Integrated AlGaInAs-silicon evanescent racetrack laser and photodetector. Opt. Express 2007, 15, 2315–2322. [Google Scholar] [CrossRef] [PubMed]
- Monroy, B.M.; Crégut, O.; Gallart, M.; Hönerlage, B.; Gilliot, P. Optical gain observation on silicon nanocrystals embedded in silicon nitride under femtosecond pumping. Appl. Phys. Lett. 2011, 98, 261108. [Google Scholar] [CrossRef]
- Heck, M.J.R.; Chen, H.-W.; Fang, A.W.; Koch, B.R.; Liang, D.; Park, H.; Sysak, M.N.; Bowers, J.E. Hybrid silicon photonics for optical interconnects. IEEE J. Sel. Top. Quantum Electron. 2010, 17, 333–346. [Google Scholar] [CrossRef]
- Lamponi, M.; Keyvaninia, S.; Jany, C.; Poingt, F.; Lelarge, F.; de Valicourt, G.; Roelkens, G.; Van Thourhout, D.; Messaoudene, S.; Fedeli, J.-M.; et al. Low-threshold heterogeneously integrated InP/SOI lasers with a double adiabatic taper coupler. IEEE Photon-Technol. Lett. 2012, 24, 76–78. [Google Scholar] [CrossRef]
- Xu, D.-X.; Schmid, J.H.; Reed, G.T.; Mashanovich, G.Z.; Thomson, D.J.; Nedeljkovic, M.; Chen, X.; Van Thourhout, D.; Keyvaninia, S.; Selvaraja, S.K. Silicon Photonic Integration Platform—Have We Found the Sweet Spot? IEEE J. Sel. Top. Quantum Electron. 2014, 20, 189–205. [Google Scholar] [CrossRef]
- Dhoore, S.; Li, L.; Abbasi, A.; Roelkens, G.; Morthier, G. Demonstration of a Discretely Tunable III-V-on-Silicon Sampled Grating DFB Laser. IEEE Photon-Technol. Lett. 2016, 28, 2343–2346. [Google Scholar] [CrossRef]
- Jang, B.; Tanabe, K.; Kako, S.; Iwamoto, S.; Tsuchizawa, T.; Nishi, H.; Hatori, N.; Noguchi, M.; Nakamura, T.; Takemasa, K.; et al. A hybrid silicon evanescent quantum dot laser. Appl. Phys. Express 2016, 9, 092102. [Google Scholar] [CrossRef]
- Morais, N.; Fujikata, J.; Kwoen, J.; Nakamura, T.; Ota, Y.; Arakawa, Y. Hybrid distributed Bragg reflector laser on Si with a transfer printed InAs/GaAs quantum dot amplifier. Opt. Express 2024, 32, 4295–4304. [Google Scholar] [CrossRef]
- Chen, S.; Li, W.; Wu, J.; Jiang, Q.; Tang, M.; Shutts, S.; Elliott, S.N.; Sobiesierski, A.; Seeds, A.J.; Ross, I.; et al. Electrically pumped continuous-wave III–V quantum dot lasers on silicon. Nat. Photon. 2016, 10, 307–311. [Google Scholar] [CrossRef]
- Wang, J.; Bai, Y.; Liu, H.; Cheng, Z.; Tang, M.; Chen, S.; Wu, J.; Papatryfonos, K.; Liu, Z.; Huang, Y.; et al. Optimization of 1.3 μm InAs/GaAs quantum dot lasers epitaxially grown on silicon: Taking the optical loss of metamorphic epilayers into account. Laser Phys. 2018, 28, 126206. [Google Scholar] [CrossRef]
- Wang, P.; Wang, Z.; Yu, Y.; Liu, X.; Lu, H.; Meng, B.; Wang, L.; Wang, Y.; Tong, C. Room temperature CW operation of 1.3 μm quantum dot triple-lattice photonic crystal surface-emitting lasers with buried structure. Opt. Express 2025, 33, 27429–27437. [Google Scholar] [CrossRef]
- Papatryfonos, K.; Rodary, G.; David, C.; Lelarge, F.; Ramdane, A.; Girard, J.C. One-Dimensional Nature of InAs/InP Quantum Dashes Revealed by Scanning Tunneling Spectroscopy. Nano Lett. 2015, 15, 4488–4497. [Google Scholar] [CrossRef]
- Papatryfonos, K.; Saladukha, D.; Merghem, K.; Joshi, S.; Lelarge, F.; Bouchoule, S.; Kazazis, D.; Guilet, S.; Le Gratiet, L.; Ochalski, T.J.; et al. Laterally coupled distributed feedback lasers emitting at 2 μm with quantum dash active region and high-duty-cycle etched semiconductor gratings. J. Appl. Phys. 2017, 121, 053101. [Google Scholar] [CrossRef]
- Papatryfonos, K.; Joshi, S.; Merghem, K.; Bouchoule, S.; Guilet, S.; Le Gratiet, L.; Martinez, A.; Ramdane, A. Quantum dash based lasers for gas sensing. In Proceedings of the 26th International Conference on Indium Phosphide and Related Materials (IPRM) (2014), Montpellier, France, 11–15 May 2014; pp. 1–2. [Google Scholar] [CrossRef]
- Chu, R.J.; Laryn, T.; Ahn, D.H.; Han, J.H.; Kim, H.; Choi, W.J.; Jung, D. Jung Low-threshold 2 µm InAs/InP quantum dash lasers enabled by punctuated growth. Opt. Express 2024, 32, 1334–1341. [Google Scholar] [CrossRef] [PubMed]
- Chu, R.J.; Laryn, T.; Choi, W.J.; Jung, D. InAs quantum dash lasers for 2-μm photonics Proc. SPIE 12905. In Novel In-Plane Semiconductor Lasers XXIII; SPIE: Bellingham, WA, USA, 2024; Volume 129050Q. [Google Scholar] [CrossRef]
- Banyoudeh, S.; Abdollahinia, A.; Eyal, O.; Schnabel, F.; Sichkovskyi, V.; Eisenstein, G.; Reithmaier, J.P. Temperature-Insensitive High-Speed Directly Modulated 1.55-μm Quantum Dot Lasers. IEEE Photon Technol. Lett. 2016, 28, 2451–2454. [Google Scholar] [CrossRef]
- Sugawara, M.; Usami, M. Quantum dot devices: Handling the heat. Nat. Photonics 2009, 3, 1. [Google Scholar] [CrossRef]
- Arakawa, Y.; Sakaki, H. Multidimensional quantum well laser and temperature dependence of its threshold current. Appl. Phys. Lett. 1982, 40, 939–941. [Google Scholar] [CrossRef]
- Bimberg, D.; Kirstaedter, N.; Ledentsov, N.N.; Alferov, Z.I.; Kop’Ev, P.S.; Ustinov, V.M. InGaAs-GaAs quantum-dot lasers. IEEE J. Sel. Top. Quantum Electron. 1997, 3, 196–205. [Google Scholar] [CrossRef]
- Yariv, A.; Sun, X. Supermode Si/III-V hybrid lasers, optical amplifiers and modulators: A proposal and analysis. Opt. Express 2007, 15, 9147–9151. [Google Scholar] [CrossRef]
- Sun, X. Supermode Silicon/III–V Lasers and Circular Bragg Lasers. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 2010. [Google Scholar]
- Sun, X.; Yariv, A. Engineering supermode silicon/III-V hybrid waveguides for laser oscillation. J. Opt. Soc. Am. B 2008, 25, 923–926. [Google Scholar] [CrossRef]
- Yariv, A. Optical Electronics in Modern Communications, 5th ed.; Oxford U. Press: Oxford, UK, 1997; pp. 526–531. [Google Scholar]
- Yang, Y.; Ma, Y.; Guan, H.; Liu, Y.; Danziger, S.; Ocheltree, S.; Bergman, K.; Baehr-Jones, T.; Hochberg, M. Phase coherence length in silicon photonic platform. Opt. Express 2015, 23, 16890–16902. [Google Scholar] [CrossRef] [PubMed]
- Ben Bakir, B.; Descos, A.; Olivier, N.; Bordel, D.; Grosse, P.; Augendre, E.; Fulbert, L.; Fedeli, J.M. Electrically driven hybrid Si/III-V Fabry-Pérot lasers based on adiabatic mode transformers. Opt. Express 2011, 19, 10317–10325. [Google Scholar] [CrossRef] [PubMed]
- Westerveld, W.J.; Leinders, S.M.; van Dongen, K.W.A.; Urbach, H.P.; Yousefi, M. Extension of Marcatili’s Analytical Approach for Rectangular Silicon Optical Waveguides. J. Light. Technol. 2012, 30, 2388–2401. [Google Scholar] [CrossRef]
- Gehrsitz, S.; Reinhart, F.K.; Gourgon, C.; Herres, N.; Vonlanthen, A.; Sigg, H. The refractive index of AlxGa1−xAs below the band gap: Accurate determination and empirical modeling. J. Appl. Phys. 2000, 87, 7825–7837. [Google Scholar] [CrossRef]
- Somaschi, N.; Giesz, V.; De Santis, L.; Loredo, J.C.; Almeida, M.P.; Hornecker, G.; Portalupi, S.L.; Grange, T.; Antón, C.; Demory, J.; et al. Near-optimal single-photon sources in the solid state. Nat. Photon. 2016, 10, 340–345. [Google Scholar] [CrossRef]
- Tomm, N.; Javadi, A.; Antoniadis, N.O.; Najer, D.; Löbl, M.C.; Korsch, A.R.; Schott, R.; Valentin, S.R.; Wieck, A.D.; Ludwig, A.; et al. A bright and fast source of coherent single photons. Nat. Nanotechnol. 2021, 16, 399–403. [Google Scholar] [CrossRef]
- Xiang, C.; de Oliveira, E.R.C.; Sandeep, S.; Papatryfonos, K.; Morassi, M.; Le Gratiet, L.; Harouri, A.; Sagnes, I.; Lemaitre, A.; Ortiz, O.; et al. Interference of ultrahigh frequency acoustic phonons from distant quasi-continuous sources. arXiv 2024, arXiv:2407.06821. [Google Scholar] [CrossRef]
- Papatryfonos, K.; Rodriguez, A.; de Oliveira, E.R.C.; Lanzillotti-Kimura, N.D. High-order topological states using alignment of different bandgaps in 1D superlattices. In Nanophotonics X; Proc. SPIE: Bellingham, WA, USA, 2024; Volume 12991, pp. 24–29. [Google Scholar] [CrossRef]
- Rodriguez, A.; Papatryfonos, K.; de Oliveira, E.R.C.; Lanzillotti-Kimura, N.D. Topological nanophononic interface states using high-order bandgaps in the one-dimensional Su-Schrieffer-Heeger model. Phys. Rev. B 2023, 108, 205301. [Google Scholar] [CrossRef]
- Papatryfonos, K.; de Oliveira, E.R.C.; Lanzillotti-Kimura, N.D. Effects of surface roughness and top layer thickness on the performance of Fabry-Perot cavities and responsive open resonators based on distributed Bragg reflectors. arXiv 2023, arXiv:2309.13649. [Google Scholar] [CrossRef]
- Papatryfonos, K.; Angelova, T.; Brimont, A.; Reid, B.; Guldin, S.; Smith, P.R.; Tang, M.; Li, K.; Seeds, A.J.; Liu, H.; et al. Refractive indices of MBE-grown AlxGa(1−x)As ternary alloys in the transparent wavelength region. AIP Adv. 2021, 11, 025327. [Google Scholar] [CrossRef]
- Papatryfonos, K.; de Oliveira, E.R.C.; Lanzillotti-Kimura, N.D. Effects of top layer inhomogeneities on the performance of Fabry-Perot cavities and open resonators based on distributed Bragg reflectors. In Optical Sensing and Detection VIII; Proc. SPIE: Bellingham, WA, USA, 2024; Volume 12999, pp. 149–155. [Google Scholar] [CrossRef]
- Papatryfonos, K.; Vervoort, L. Proposed Experiments for Detecting Contextual Hidden Variables. Found. Phys. 2025, 55, 1–18. [Google Scholar] [CrossRef]
- Papatryfonos, K.; Ruelle, M.; Bourdiol, C.; Nachbin, A.; Bush, J.W.M.; Labousse, M. Hydrodynamic superradiance in wave-mediated cooperative tunneling. Commun. Phys. 2022, 5, 142. [Google Scholar] [CrossRef]
- Papatryfonos, K.; Vervoort, L.; Nachbin, A.; Labousse, M.; Bush, J.W.M. Static Bell test in pilot-wave hydrodynamics. Phys. Rev. Fluids 2024, 9, 084001. [Google Scholar] [CrossRef]
- Bush, J.W.M.; Papatryfonos, K.; Frumkin, V. The state of play in Hydrodynamic Quantum Analogs. In Advances in Pilot Wave Theory; Castro, P., Bush, J.W.M., Croca, J., Eds.; Springer International Publishing: Cham, Switzerland, 2024; Volume 344, pp. 7–34, Boston Studies in the Philosophy and History of Science. [Google Scholar]
- Papakonstantinou, I.; James, R.; Selviah, D.R. Radiation- and Bound-Mode Propagation in Rectangular, Multimode Dielectric, Channel Waveguides With Sidewall Roughness. J. Light. Technol. 2009, 27, 4151–4163. [Google Scholar] [CrossRef]
- CST-Computer Simulation Technology (2017). Available online: https://www.cst.com/applications (accessed on 1 July 2025).
- Erdogan, T. Fiber grating spectra. J. Light. Technol. 1997, 15, 1277–1294. [Google Scholar] [CrossRef]
- Snyder, A.W.; Love, J.D. Optical Waveguide Theory; Chapman & Hall: London, UK, 1983. [Google Scholar]
- Li, Z.Y.; Shen, H.Z. Non-Markovian dynamics with a giant atom coupled to a semi-infinite photonic waveguide. Phys. Rev. A 2024, 109, 023712. [Google Scholar] [CrossRef]
- Shen, H.Z.; Yang, J.F.; Yi, X.X. Unconventional photon blockade with non-Markovian effects in driven dissipative coupled cavities. Phys. Rev. A 2024, 109, 043714. [Google Scholar] [CrossRef]
- Zhou, Y.-H.; Liu, T.; Su, Q.-P.; Zhang, X.-Y.; Wu, Q.-C.; Chen, D.-X.; Shi, Z.-C.; Shen, H.Z.; Yang, C.-P. Universal Photon Blockade. Phys. Rev. Lett. 2025, 134, 183601. [Google Scholar] [CrossRef]
- Abbas, A.; Luo, Y.; Ahmad, W.; Mustaqeem, M.; Kong, L.; Chen, J.; Zhou, G.; Tabish, T.A.; Zhang, Q.; Liang, Q. Recent progress, challenges, and opportunities in 2D materials for flexible displays. Nano Today 2024, 56, 102256. [Google Scholar] [CrossRef]


| Material | Thickness | n | Repeats | |
|---|---|---|---|---|
| p-type | GaAs p-contact 1 × 1018 | 50 nm | 3.412 | |
| Cladding | Al0.4Ga0.6As | 1400 nm | 3.212 | 1 |
| GaAs waveguide | 70 nm | 3.412 | ||
| Active Region | In0.18Ga0.82As capping | 2 nm | 3.434 | 5 |
| InAs | 2.7 ML | 3.532 | ||
| In0.18Ga0.82As capping | 6 nm | 3.434 | ||
| GaAs barrier | 37.5 nm | 3.412 | ||
| GaAs waveguide | 32.5 nm | 3.412 | ||
| n-type | GaAs n-contact 5 × 1018 | 50 nm | 3.412 | |
| Bonding Layer | Al2O3 | 30 nm | 1.75 | |
| SiO2 | 100 nm | 1.45 | 1 | |
| SOI | Si Waveguide | 220 nm | 3.5 | |
| SiO2 | 500 nm | 1.45 | ||
| Si Substrate | 300 μm | 3.5 | ||
| Material | Thickness | n | Repeats | |
|---|---|---|---|---|
| p-type | Al0.375Ga0.625As p+ 1 × 1018 | 50 nm | 3.2 | |
| Cladding | AlAs | 1400 nm | 2.91 | 1 |
| Al0.375Ga0.625As waveguide | 70 nm | 3.2 | ||
| Active Region | In0.18Ga0.82As capping | 2 nm | 3.434 | 2 |
| InAs | 2.7 ML | 3.532 | ||
| In0.18Ga0.82As capping | 6 nm | 3.434 | ||
| Al0.375Ga0.625As barrier | 37.5 nm | 3.2 | ||
| Al0.375Ga0.625As waveguide | 32.5 nm | 3.2 | ||
| n-type | Al0.375Ga0.625As n+ 5 × 1018 | 50 nm | 3.2 | |
| Bonding Layer | Al2O3 | 30 nm | 1.75 | |
| SiO2 | 100 nm | 1.45 | 1 | |
| SOI | Si Waveguide | 220 nm | 3.5 | |
| SiO2 | 500 nm | 1.45 | ||
| Si Substrate | 300 μm | 3.5 | ||
| Section | Si Width | Lateral Modes at 1.3 μm | Mode Mostly in | Notes |
|---|---|---|---|---|
| Central gain window | wc = 300 nm | Multi-mode in x and y | III-V | Current injection |
| Adiabatic taper (each) | wc = 300 nm → 1500 nm (smooth) | Multi-mode in x: Only TE0 and TE2 supported 1 | Shifts from III-V to Si | TE0 → TE0 > 98.5%; passive |
| DBR mirror section | we = 1500 nm | Multi-mode in x: Only TE0 and TE2 guided | Predominantly (82%) in Si | Passive—no gain |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smith, P.R.; Papatryfonos, K.; Selviah, D.R. Optical Waveguide-Pair Design for CMOS-Compatible Hybrid III-V-on-Silicon Quantum Dot Lasers. Nanomaterials 2025, 15, 1645. https://doi.org/10.3390/nano15211645
Smith PR, Papatryfonos K, Selviah DR. Optical Waveguide-Pair Design for CMOS-Compatible Hybrid III-V-on-Silicon Quantum Dot Lasers. Nanomaterials. 2025; 15(21):1645. https://doi.org/10.3390/nano15211645
Chicago/Turabian StyleSmith, Peter Raymond, Konstantinos Papatryfonos, and David R. Selviah. 2025. "Optical Waveguide-Pair Design for CMOS-Compatible Hybrid III-V-on-Silicon Quantum Dot Lasers" Nanomaterials 15, no. 21: 1645. https://doi.org/10.3390/nano15211645
APA StyleSmith, P. R., Papatryfonos, K., & Selviah, D. R. (2025). Optical Waveguide-Pair Design for CMOS-Compatible Hybrid III-V-on-Silicon Quantum Dot Lasers. Nanomaterials, 15(21), 1645. https://doi.org/10.3390/nano15211645






