A Wavelet-Based Bilateral Segmentation Study for Nanowires
Abstract
1. Introduction
- (1)
- We propose WaveBiSeNet, a wavelet-based bilateral segmentation network, that improves upon BiSeNetV1 [15] for the accurate segmentation of one-dimensional nanowires with complex backgrounds and blurred edges.
- (2)
- We introduce the Dual Wavelet Convolution Module (DWCM), which enhances feature extraction, and the Flexible Upsampling Module (FUM), which refines fine edge details.
- (3)
- Experiments on the peptide nanowire dataset demonstrate that WaveBiSeNet outperforms ten existing semantic segmentation models.
2. Related Work
3. Materials and Methods
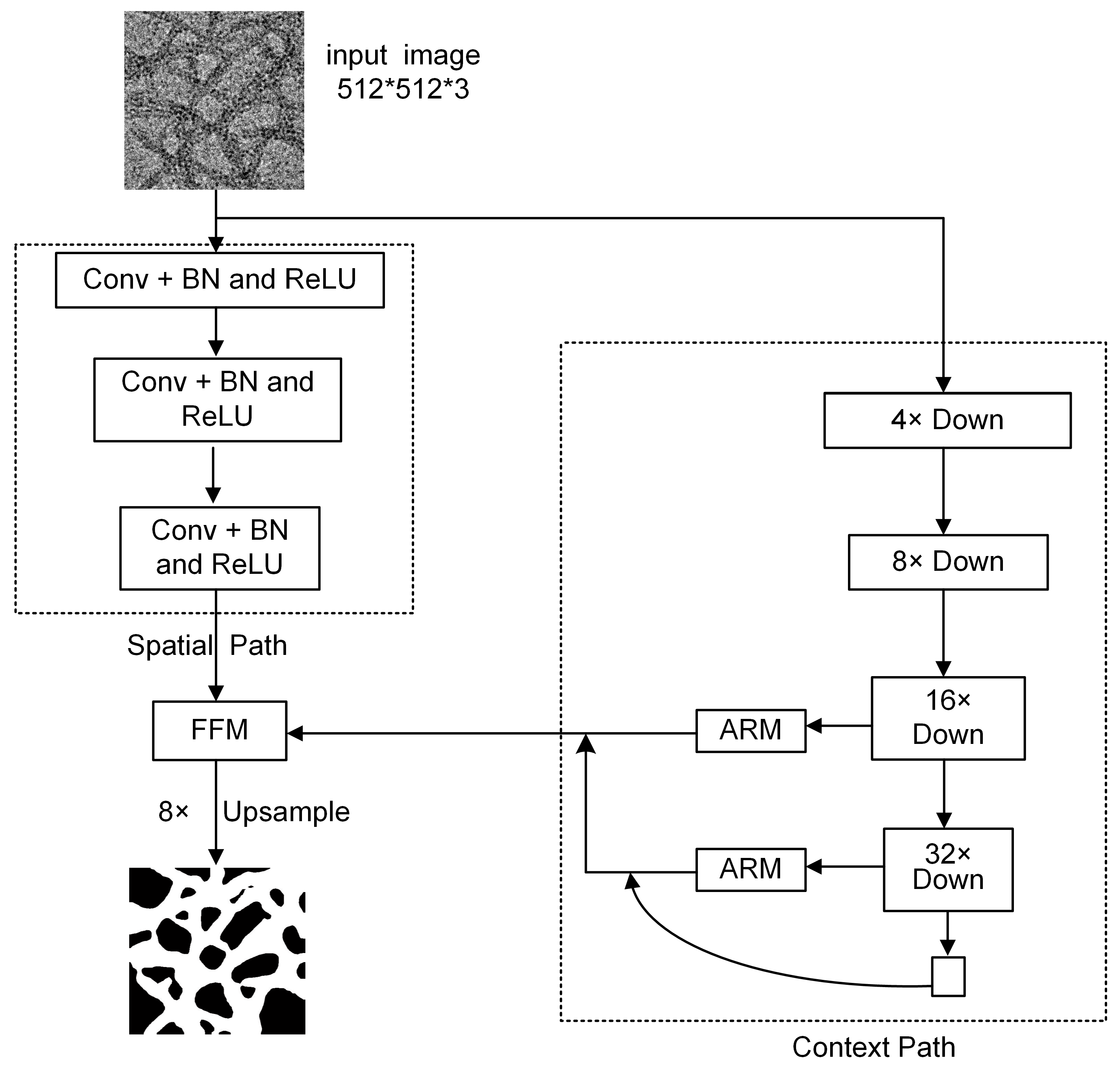
3.1. BiSeNetV1 Model Architecture
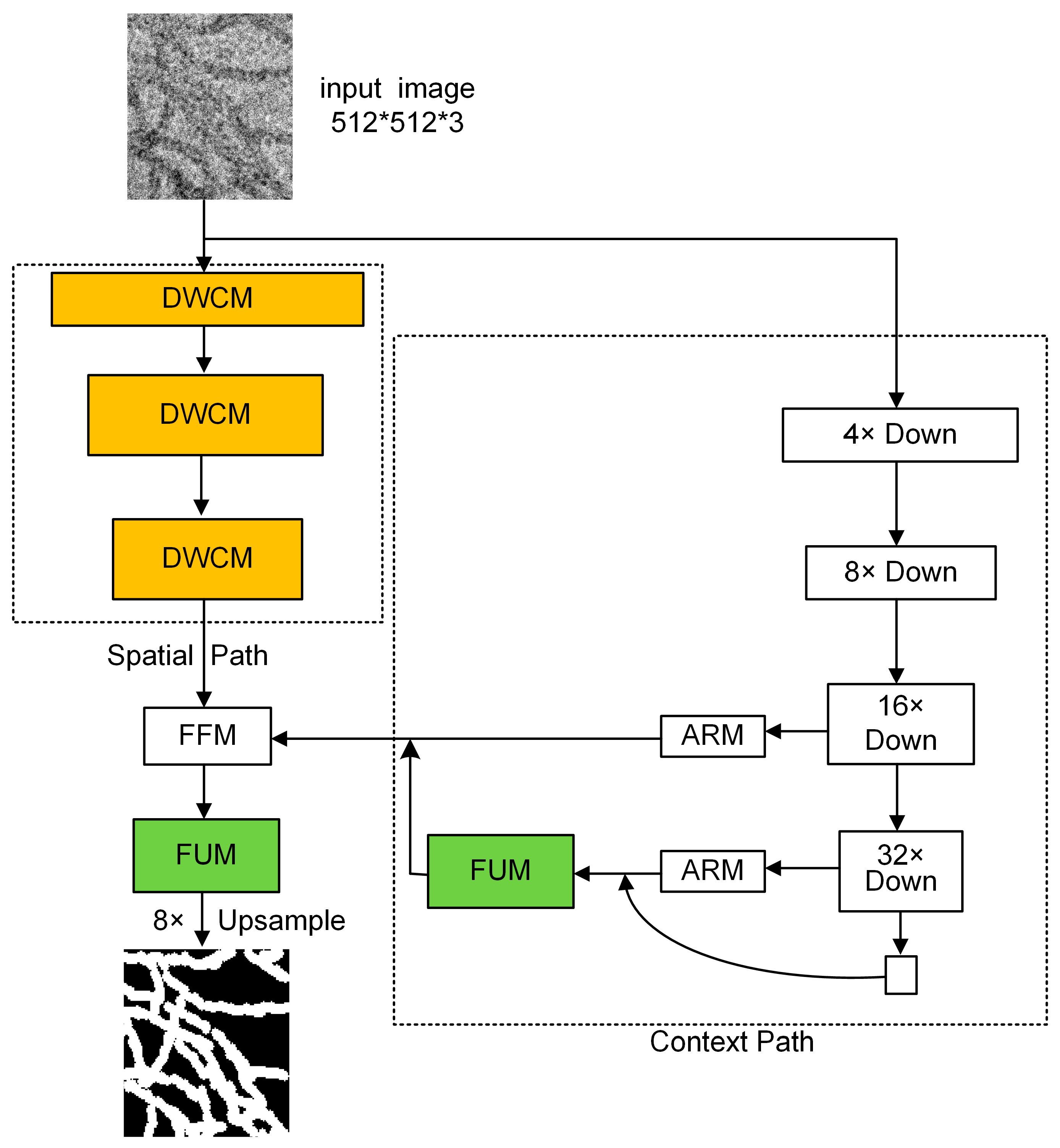
3.2. The Structure of the Proposed WaveBiSeNet Model
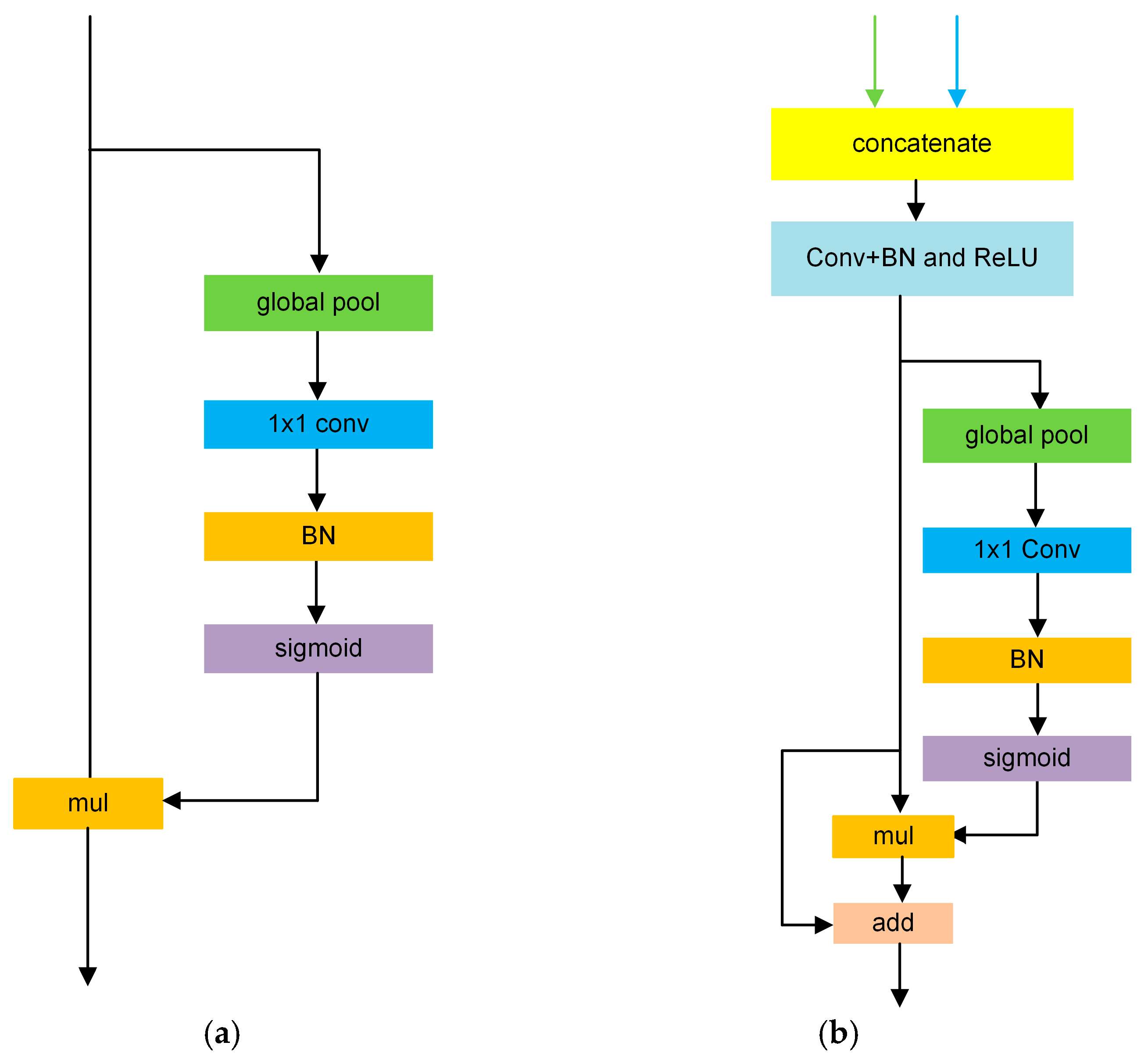
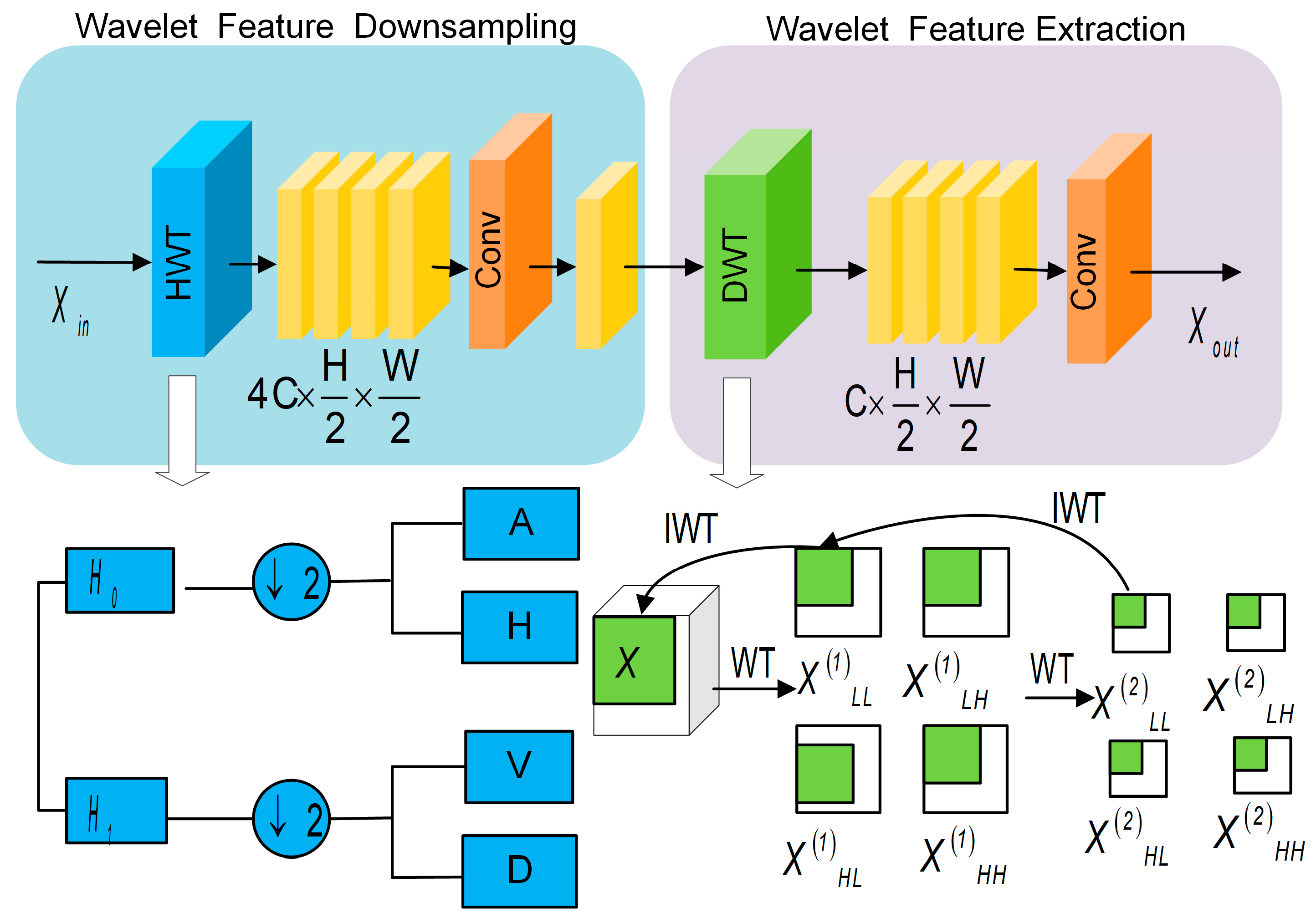
3.2.1. Dual Wavelet Convolution Module
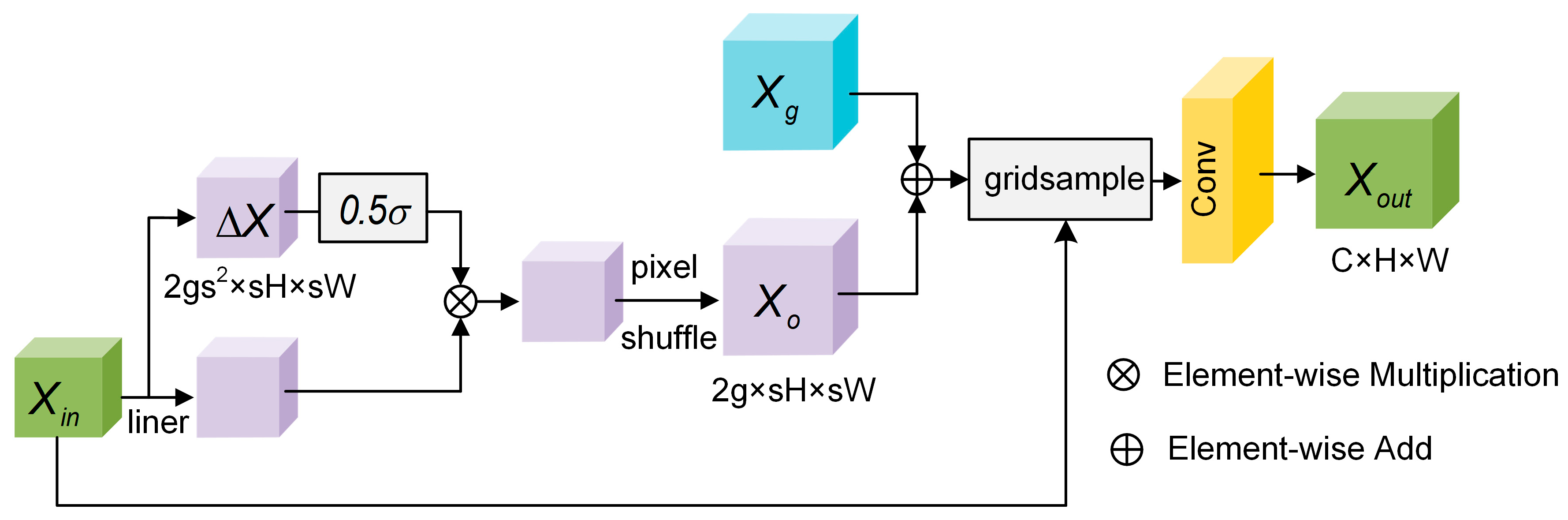
3.2.2. Flexible Upsampling Module
4. Results and Discussion
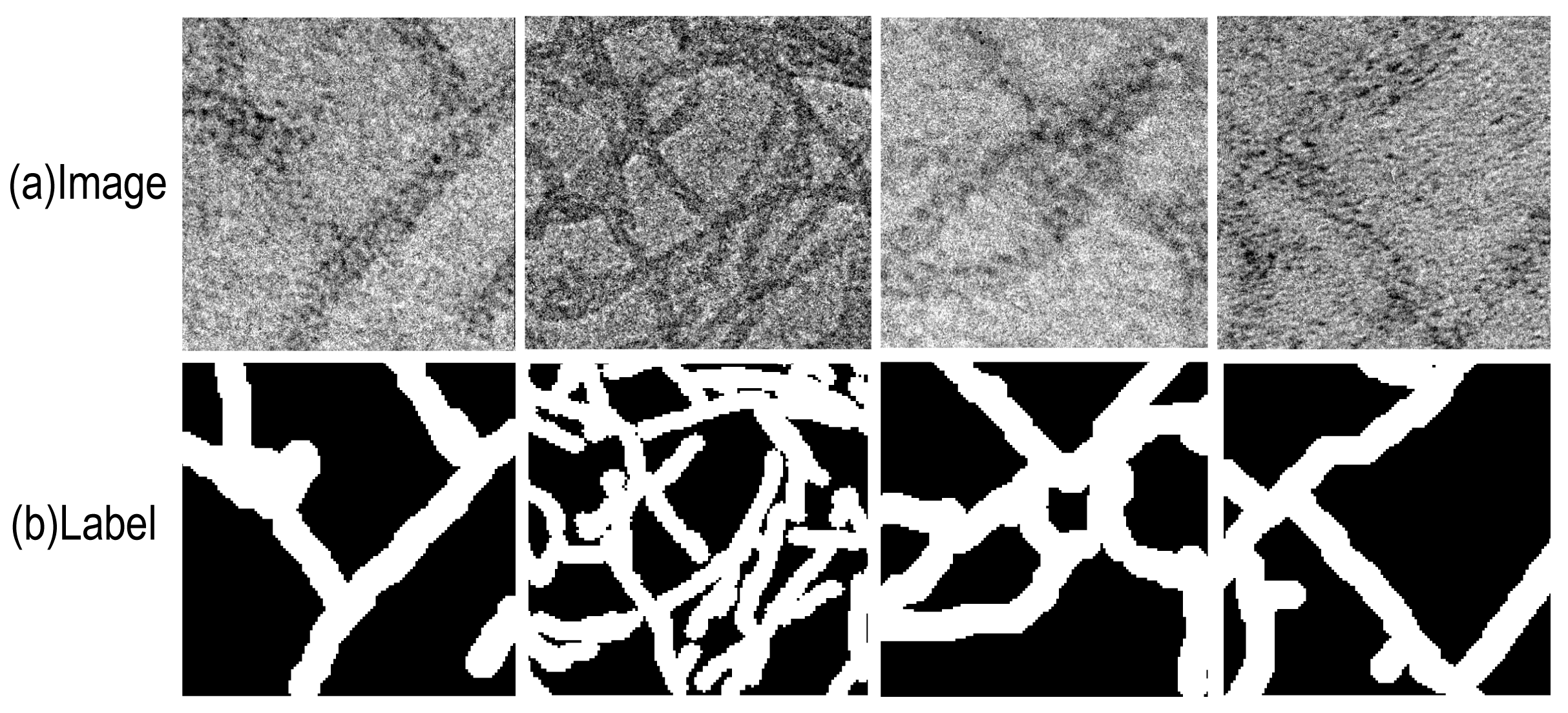
4.1. Dataset
4.2. Experimental Setup
4.3. Evaluation Metric
| Prediction | ||
| Reference | TP: 19,502,345 | FN: 1,636,842 |
| FP: 5,798,124 | TN: 51,705,679 | |
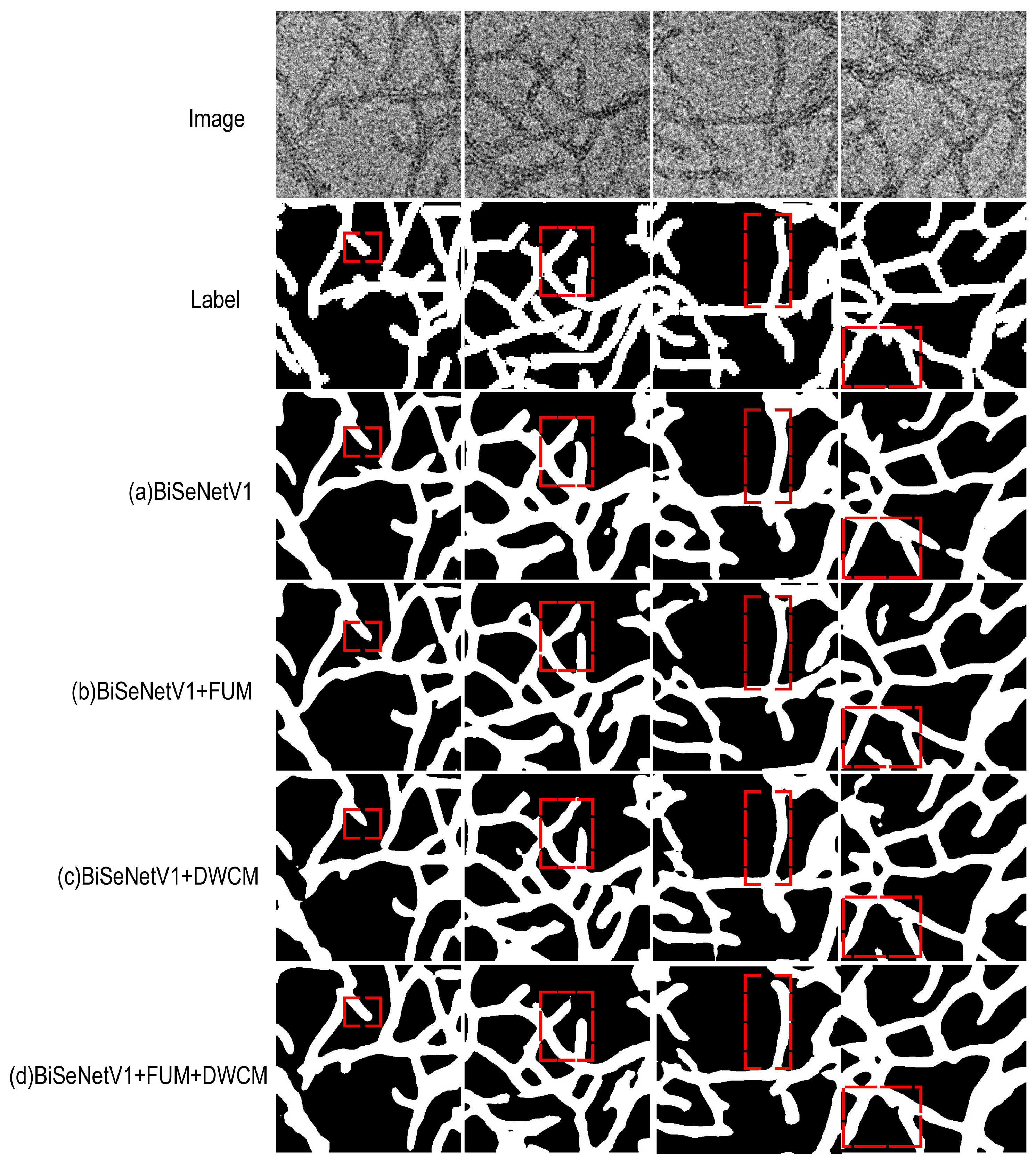
4.4. Ablation Experiments
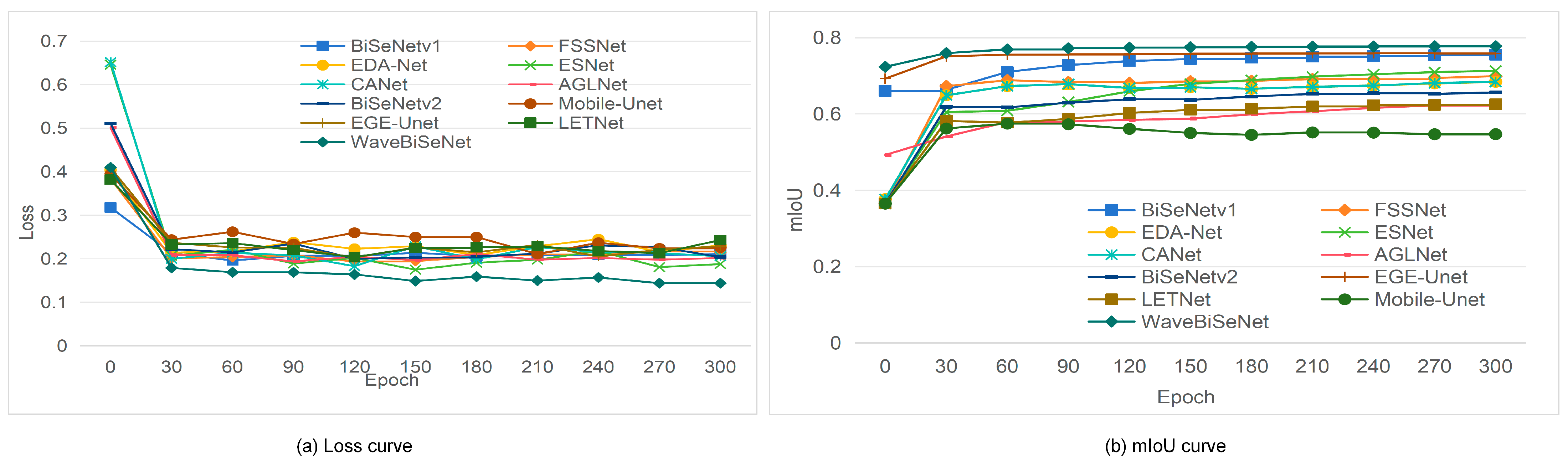
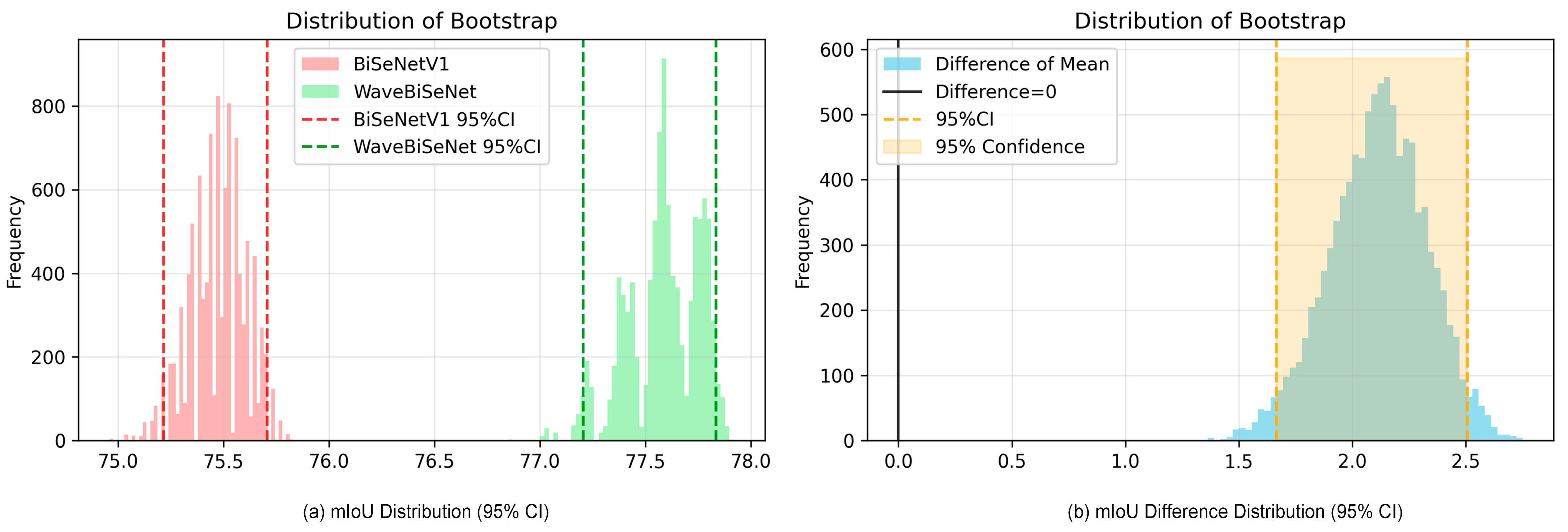
4.5. Model Comparison and Analysis
4.6. Visual Comparison of Segmentation Performance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Garnett, E.; Mai, L.; Yang, P. Introduction: 1D Nanomaterials/Nanowires. Chem. Rev. 2019, 119, 8955–8957. [Google Scholar] [CrossRef]
- Dasgupta, N.P.; Sun, J.; Liu, C.; Brittman, S.; Andrews, S.C.; Lim, J.; Gao, H.; Yan, R.; Yang, P. ChemInform Abstract: 25th Anniversary Article: Semiconductor Nanowires—Synthesis, Characterization, and Applications. ChemInform 2014, 45. [Google Scholar] [CrossRef]
- Jiu, J.; Suganuma, K. Metallic Nanowires and Their Application. IEEE Trans. Compon. Packag. Manuf. Technol. 2016, 6, 1733–1751. [Google Scholar] [CrossRef]
- Comini, E.; Sberveglieri, G. Metal oxide nanowires as chemical sensors. Mater. Today 2010, 13, 36–44. [Google Scholar] [CrossRef]
- Shi, C.; Owusu, K.A.; Xu, X.; Zhu, T.; Zhang, G.; Yang, W.; Mai, L. 1D Carbon-Based Nanocomposites for Electrochemical Energy Storage. Small 2019, 15, e1902348. [Google Scholar] [CrossRef]
- Liu, X.; Gao, H.; Ward, J.E.; Liu, X.; Yin, B.; Fu, T.; Chen, J.; Lovley, D.R.; Yao, J. Power generation from ambient humidity using protein nanowires. Nature 2020, 578, 550–554. [Google Scholar] [CrossRef]
- Creasey, R.C.G.; Mostert, A.B.; Solemanifar, A.; Nguyen, T.A.H.; Virdis, B.; Freguia, S.; Laycock, B. Biomimetic Peptide Nanowires Designed for Conductivity. ACS Omega 2019, 4, 1748–1756. [Google Scholar] [CrossRef]
- Azam, Z.; Singh, A. Various applications of nanowires. In Innovative Applications of Nanowires for Circuit Design; IGI Global Scientific Publishing: Hershey, PA, USA, 2021; pp. 17–53. [Google Scholar]
- Tang, C.Y.; Yang, Z. Transmission electron microscopy (TEM). In Membrane Characterization; Hilal, N., Ismail, A.F., Matsuura, T., Oatley-Radcliffe, D., Eds.; Elsevier: Pokfulam, Hong Kong, 2017; pp. 145–159. [Google Scholar]
- Yao, L.; Chen, Q. Machine learning in nanomaterial electron microscopy data analysis. In Intelligent Nanotechnology; Zheng, Y., Wu, Z., Eds.; Elsevier: Urbana, IL, USA, 2023; pp. 279–305. [Google Scholar]
- Russell, B.C.; Torralba, A.; Murphy, K.P.; Freeman, W.T. LabelMe: A Database and Web-Based Tool for Image Annotation. Int. J. Comput. Vis. 2007, 77, 157–173. [Google Scholar] [CrossRef]
- Shahab, W.; Al-Otum, H.; Al-Ghoul, F. A modified 2D chain code algorithm for object segmentation and contour tracing. Int. Arab J. Inf. Technol. 2009, 6, 250–257. [Google Scholar]
- Bai, H.; Wu, S. Deep-learning-based nanowire detection in AFM images for automated nanomanipulation. Nanotechnol. Precis. Eng. 2021, 4, 013002. [Google Scholar] [CrossRef]
- Lin, B.; Emami, N.; Santos, D.A.; Luo, Y.; Banerjee, S.; Xu, B.-X. A deep learned nanowire segmentation model using synthetic data augmentation. Npj Comput. Mater. 2022, 8, 1–12. [Google Scholar] [CrossRef]
- Yu, C.; Wang, J.; Peng, C.; Gao, C.; Yu, G.; Sang, N. Bisenet: Bilateral segmentation network for real-time semantic seg-mentation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 325–341. [Google Scholar]
- Liu, W.; Wu, Y.; Hong, Y.; Zhang, Z.; Yue, Y.; Zhang, J. Applications of machine learning in computational nanotechnology. Nanotechnology 2022, 33, 162501. [Google Scholar] [CrossRef]
- Masson, J.-F.; Biggins, J.S.; Ringe, E. Machine learning for nanoplasmonics. Nat. Nanotechnol. 2023, 18, 111–123. [Google Scholar] [CrossRef]
- Dahy, G.; Soliman, M.M.; Alshater, H.; Slowik, A.; Hassanien, A.E. Optimized deep networks for the classification of nanoparticles in scanning electron microscopy imaging. Comput. Mater. Sci. 2023, 223. [Google Scholar] [CrossRef]
- Singh, A.V.; Maharjan, R.-S.; Kanase, A.; Siewert, K.; Rosenkranz, D.; Singh, R.; Laux, P.; Luch, A. Machine-Learning-Based Approach to Decode the Influence of Nanomaterial Properties on Their Interaction with Cells. ACS Appl. Mater. Interfaces 2020, 13, 1943–1955. [Google Scholar] [CrossRef]
- Lee, B.; Yoon, S.; Lee, J.W.; Kim, Y.; Chang, J.; Yun, J.; Ro, J.C.; Lee, J.-S.; Lee, J.H. Statistical Characterization of the Morphologies of Nanoparticles through Machine Learning Based Electron Microscopy Image Analysis. ACS Nano 2020, 14, 17125–17133. [Google Scholar] [CrossRef]
- Banerjee, A.; Kar, S.; Pore, S.; Roy, K. Efficient predictions of cytotoxicity of TiO2-based multi-component nanoparticles using a machine learning-based q-RASAR approach. Nanotoxicology 2023, 17, 78–93. [Google Scholar] [CrossRef] [PubMed]
- Bannigidad, P.; Potraj, N.; Gurubasavaraj, P. Metal and Metal Oxide Nanoparticle Image Analysis Using Machine Learning Algorithm. In Proceedings of the International Conference on Big Data Innovation for Sustainable Cognitive Computing, Coimbatore, India, 16–17 December 2022; pp. 27–38. [Google Scholar]
- Jia, Y.; Hou, X.; Wang, Z.; Hu, X. Machine Learning Boosts the Design and Discovery of Nanomaterials. ACS Sustain. Chem. Eng. 2021, 9, 6130–6147. [Google Scholar] [CrossRef]
- Taylor, J.R.; Das Sarma, S. Vision transformer based deep learning of topological indicators in Majorana nanowires. Phys. Rev. B 2025, 111. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S. An image is worth 16×16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar] [CrossRef]
- Lee, J.; Oh, J.; Chi, H.; Lee, M.; Hwang, J.; Jeong, S.; Kang, S.; Jee, H.; Bae, H.; Hyun, J.; et al. Deep Learning-Assisted Design of Bilayer Nanowire Gratings for High-Performance MWIR Polarizers. Adv. Mater. Technol. 2024, 9, 2302176. [Google Scholar] [CrossRef]
- Guo, G.; Wang, H.; Bell, D.; Bi, Y.; Greer, K. KNN model-based approach in classification. In OTM Confederated International Conferences” On The Move to Meaningful Internet Systems; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2888, pp. 986–996. [Google Scholar]
- Bai, H.; Wu, S. Nanowire Detection in AFM Images Using Deep Learning. Microsc. Microanal. 2020, 27, 54–64. [Google Scholar] [CrossRef]
- Li, L. Zno SEM Image Segmentation Based on Deep Learning. In Proceedings of the IOP Conference Series Materials Science and Engineering, Qingdao, China, 28–29 December 2019. [Google Scholar] [CrossRef]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask r-cnn. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar] [CrossRef]
- Kendall, J.D.; Pantone, R.D.; Nino, J.C. Deep learning in memristive nanowire networks. arXiv 2020, arXiv:2003.02642. [Google Scholar] [CrossRef]
- Hu, X.; Jia, X.; Zhang, K.; Lo, T.W.; Fan, Y.; Liu, D.; Wen, J.; Yong, H.; Rahmani, M.; Zhang, L.; et al. Deep-learning-augmented microscopy for super-resolution imaging of nanoparticles. Opt. Express 2023, 32, 879–890. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar] [CrossRef]
- Xu, G.; Liao, W.; Zhang, X.; Li, C.; He, X.; Wu, X. Haar wavelet downsampling: A simple but effective downsampling module for semantic segmentation. Pattern Recognit. 2023, 143, 109819. [Google Scholar] [CrossRef]
- Finder, S.E.; Amoyal, R.; Treister, E.; Freifeld, O. Wavelet convolutions for large receptive fields. In Proceedings of the European Conference on Computer Vision, Milan, Italy, 29 September–4 October 2024; pp. 363–380. [Google Scholar]
- AMS NOTICES. Bull. Am. Meteorol. Soc. 1997, 78, 2696–2697. [CrossRef][Green Version]
- Liu, W.; Lu, H.; Fu, H.; Cao, Z. Learning to upsample by learning to sample. In Proceedings of the 2023 IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 1–6 October 2023; pp. 6027–6037. [Google Scholar][Green Version]
- Lu, S.; Montz, B.; Emrick, T.; Jayaraman, A. Semi-supervised machine learning workflow for analysis of nanowire morphologies from transmission electron microscopy images. Digit. Discov. 2022, 1, 816–833. [Google Scholar] [CrossRef]
- Lu, S.; Montz, B.; Emrick, T.; Jayaraman, A. Transmission Electron Microscopy (TEM) Image Datasets of Peptide/Protein Nanowire Morphologies. Digit. Discov. 2022, 1, 816–833. [Google Scholar] [CrossRef]
- Kirillov, A.; Mintun, E.; Ravi, N.; Mao, H.; Rolland, C.; Gustafson, L.; Xiao, T.; Whitehead, S.; Berg, A.C.; Lo, W.-Y. Segment anything. In Proceedings of the 2023 IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 1–6 October 2023; pp. 4015–4026. [Google Scholar]
- Mao, A.; Mohri, M.; Zhong, Y. Cross-entropy loss functions: Theoretical analysis and applications. In Proceedings of the International conference on Machine learning, Vienna, Austria, 21–27 July 2024. [Google Scholar]
- Sudre, C.H.; Li, W.; Vercauteren, T.; Ourselin, S.; Cardoso, M.J. Generalised Dice overlap as a deep learning loss function for highly unbalanced segmentations. arXiv 2017, arXiv:1707.03237. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014. [Google Scholar] [CrossRef]
- Lateef, F.; Ruichek, Y. Survey on semantic segmentation using deep learning techniques. Neurocomputing 2019, 338, 321–348. [Google Scholar] [CrossRef]
- Minaee, S.; Boykov, Y.Y.; Porikli, F.; Plaza, A.J.; Kehtarnavaz, N.; Terzopoulos, D. Image Segmentation Using Deep Learning: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 3523–3542. [Google Scholar] [CrossRef] [PubMed]
- Takos, G. A survey on deep learning methods for semantic image segmentation in real-time. arXiv 2009, arXiv:2009.12942. [Google Scholar] [CrossRef]
- Arefin, S.; Chowdhury; Parvez, R.; Ahmed, T.; Abrar, A.S.; Sumaiya, F. Understanding APT detection using Machine learning algorithms: Is superior accuracy a thing? In Proceedings of the 2024 IEEE International Conference on Electro Information Technology (eIT), Eau Claire, WI, USA, 30 May–1 June 2024; pp. 532–537. [Google Scholar]
- Lee, C.-Y.; Hung, C.-H.; Le, T.-A. Intelligent Fault Diagnosis for BLDC with Incorporating Accuracy and False Negative Rate in Feature Selection Optimization. IEEE Access 2022, 10, 69939–69949. [Google Scholar] [CrossRef]
- Tan, S.C.; Zhu, S. Binary search of the optimal cut-point value in ROC analysis using the F1 score. In Proceedings of the 5th International Conference on Computer Science and Application Engineering (CSAE 2022), Sanya, China, 25–27 October 2022; p. 012002. [Google Scholar]
- Lam, K.F.Y.; Gopal, V.; Qian, J. Confidence Intervals for the F1 Score: A Comparison of Four Methods. arXiv 2023, arXiv:2309.14621. [Google Scholar] [CrossRef]
- McHugh, M.L. Interrater reliability: The kappa statistic. Biochem. Med. 2012, 22, 276–282. [Google Scholar] [CrossRef]
- Shang, H.; Langlois, J.-M.; Tsioutsiouliklis, K.; Kang, C. Precision/recall on imbalanced test data. In Proceedings of the 26th International Conference on Artificial Intelligence and Statistics (AISTATS 2023), Valencia, Spain, 25–27 April 2023; pp. 9879–9891. [Google Scholar]
- Miao, J.; Zhu, W. Precision–recall curve (PRC) classification trees. Evol. Intell. 2021, 15, 1545–1569. [Google Scholar] [CrossRef]
- Wang, J.; Zhuang, Y.; Liu, Y. FSS-Net: A Fast Search Structure for 3D Point Clouds in Deep Learning. Int. J. Netw. Dyn. Intell. 2023, 2, 100005. [Google Scholar] [CrossRef]
- Yang, C.; Gao, F. EDA-Net: Dense aggregation of deep and shallow information achieves quantitative photoacoustic blood oxygenation imaging deep in human breast. In Proceedings of the Medical Image Computing and Computer Assisted In-tervention–MICCAI 2019: 22nd International Conference, Shenzhen, China, 13–17 October 2019; pp. 246–254. [Google Scholar]
- Wang, Y.; Zhou, Q.; Xiong, J.; Wu, X.; Jin, X. ESNet: An efficient symmetric network for real-time semantic segmentation. In Proceedings of the Pattern Recognition and Computer Vision: Second Chinese Conference, PRCV 2019, Xi’an, China, 8–11 November 2019; pp. 41–52. [Google Scholar]
- Zhang, C.; Lin, G.; Liu, F.; Yao, R.; Shen, C. CANet: Class-Agnostic Segmentation Networks with Iterative Refinement and Attentive Few-Shot Learning. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 5212–5221. [Google Scholar]
- Zhou, Q.; Wang, Y.; Fan, Y.; Wu, X.; Zhang, S.; Kang, B.; Latecki, L.J. AGLNet: Towards real-time semantic segmentation of self-driving images via attention-guided lightweight network. Appl. Soft Comput. 2020, 96, 106682. [Google Scholar] [CrossRef]
- Yu, C.; Gao, C.; Wang, J.; Yu, G.; Shen, C.; Sang, N. BiSeNet V2: Bilateral Network with Guided Aggregation for Real-Time Semantic Segmentation. Int. J. Comput. Vis. 2021, 129, 3051–3068. [Google Scholar] [CrossRef]
- Jing, J.; Wang, Z.; Rätsch, M.; Zhang, H. Mobile-Unet: An efficient convolutional neural network for fabric defect detection. Text. Res. J. 2020, 92, 30–42. [Google Scholar] [CrossRef]
- Ta, N.; Chen, H.; Liu, X.; Jin, N. LET-Net: Locally enhanced transformer network for medical image segmentation. Multimed. Syst. 2023, 29, 3847–3861. [Google Scholar] [CrossRef]


| Method | mIoU (%) | Accuracy (%) | F1 (%) | Kappa (%) |
|---|---|---|---|---|
| BiSeNetV1 | 75.47% ± 0.31 | 88.69% ± 0.26 | 85.66% ± 0.40 | 71.51% ± 0.62 |
| BiSeNetV1 + FUM | 76.32% ± 0.35 | 89.34% ± 0.24 | 86.44% ± 0.34 | 72.40% ± 0.46 |
| BiSeNetV1 + DWCM | 77.29% ± 0.38 | 89.75% ± 0.25 | 86.73% ± 0.35 | 76.62% ± 0.49 |
| BiSeNetV1 + FUM + DWCM | 77.59% ± 0.42 | 89.95% ± 0.23 | 87.22% ± 0.30 | 74.13% ± 0.33 |
| Models | Backbone | MIoU (%) | Accuracy (%) | F1 (%) | Kappa (%) |
|---|---|---|---|---|---|
| WaveBiSeNet | ResNet18 | 77.59% ± 0.42 | 89.95% ± 0.23 | 87.22% ± 0.30 | 74.13% ± 0.33 |
| BiSeNetV1 | ResNet18 | 75.47% ± 0.31 | 88.69% ± 0.26 | 85.66% ± 0.40 | 71.51% ± 0.62 |
| FSSNet | - | 69.53% ± 0.69 | 85.22% ± 0.55 | 81.47% ± 0.60 | 63.43% ± 0.53 |
| EDA-Net | - | 68.18% ± 0.66 | 84.51% ± 0.45 | 80.45% ± 0.69 | 61.14% ± 0.64 |
| ESNet | - | 71.21% ± 0.31 | 86.13% ± 0.53 | 82.48% ± 0.55 | 65.34% ± 0.63 |
| CANet | MobilenetV2 | 71.28% ± 0.62 | 86.57% ± 0.67 | 82.81% ± 0.60 | 65.63% ± 0.51 |
| AGLNet | - | 62.50% ± 0.45 | 79.95% ± 0.56 | 75.76% ± 0.58 | 52.13% ± 0.43 |
| BiSeNetV2 | - | 65.50% ± 0.35 | 82.46% ± 0.34 | 78.31% ± 0.40 | 57.21% ± 0.35 |
| Mobile-Unet | MobileNet | 54.37% ± 0.46 | 75.22% ± 0.58 | 69.51% ± 0.30 | 38.64% ± 0.57 |
| EGE-Unet | - | 75.84% ± 0.40 | 88.91% ± 0.62 | 85.84% ± 0.46 | 71.75% ± 0.38 |
| LETNet | - | 62.55% ± 0.35 | 80.44% ± 0.35 | 76.01% ± 0.35 | 52.20% ± 0.45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, Y.; Zhang, Y.; Liang, F.; Liu, G. A Wavelet-Based Bilateral Segmentation Study for Nanowires. Nanomaterials 2025, 15, 1612. https://doi.org/10.3390/nano15211612
Hou Y, Zhang Y, Liang F, Liu G. A Wavelet-Based Bilateral Segmentation Study for Nanowires. Nanomaterials. 2025; 15(21):1612. https://doi.org/10.3390/nano15211612
Chicago/Turabian StyleHou, Yuting, Yu Zhang, Fengfeng Liang, and Guangjie Liu. 2025. "A Wavelet-Based Bilateral Segmentation Study for Nanowires" Nanomaterials 15, no. 21: 1612. https://doi.org/10.3390/nano15211612
APA StyleHou, Y., Zhang, Y., Liang, F., & Liu, G. (2025). A Wavelet-Based Bilateral Segmentation Study for Nanowires. Nanomaterials, 15(21), 1612. https://doi.org/10.3390/nano15211612






