Gas–Water Two-Phase Flow Mechanisms in Deep Tight Gas Reservoirs: Insights from Nanofluidics
Abstract
1. Introduction
2. Materials and Method
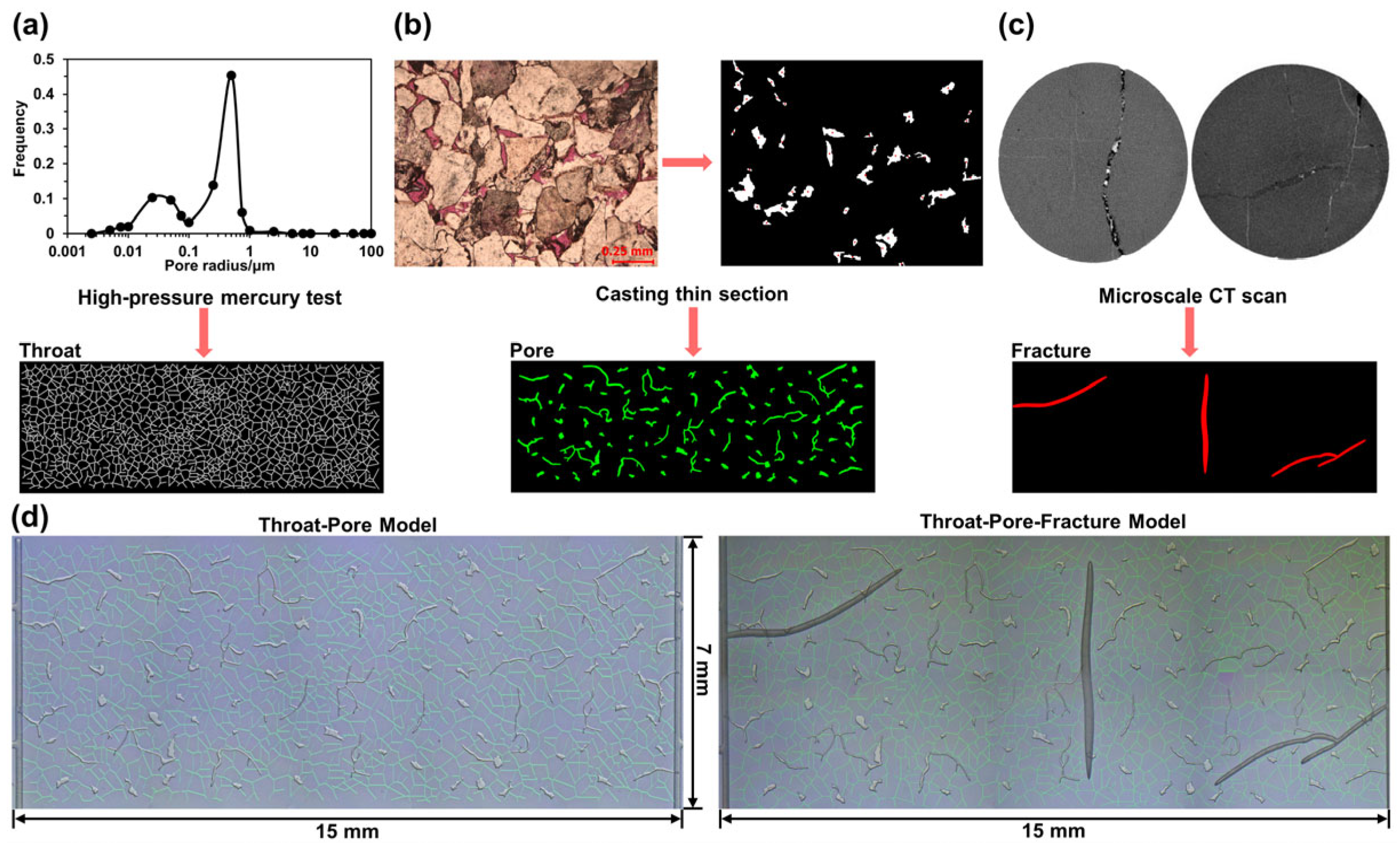
2.1. Nanofluidic Chip Design and Fabrication
2.2. Experimental Apparatus and Procedure
2.3. Image Processing and Analysis
3. Results and Discussion
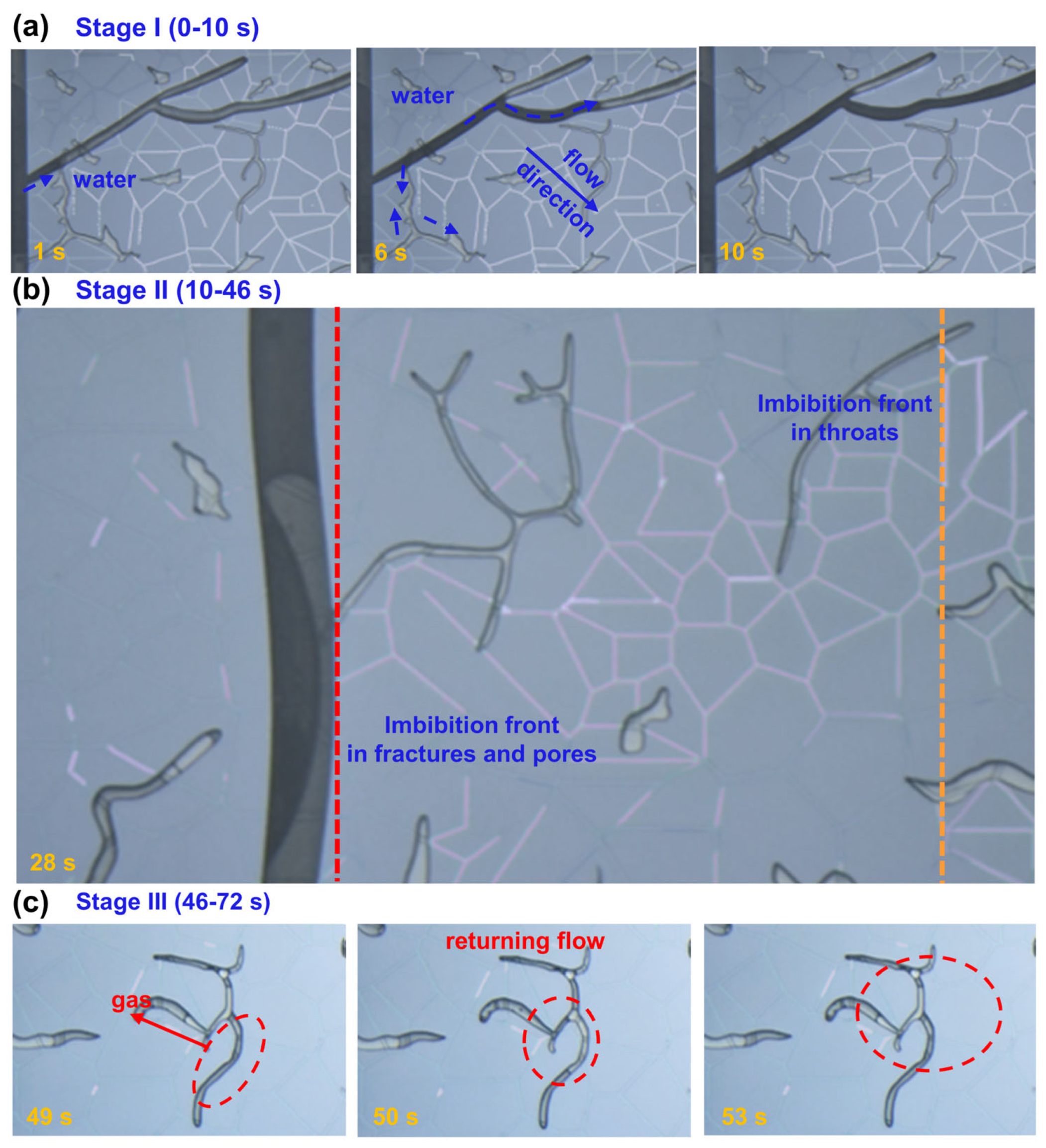
3.1. Water Imbibition Dynamics in Throat-Pore Structures
3.2. Water Imbibition Dynamics in Throat-Pore-Fracture Structure
3.3. Threshold Pressure Gradient in Multiscale Porous Media
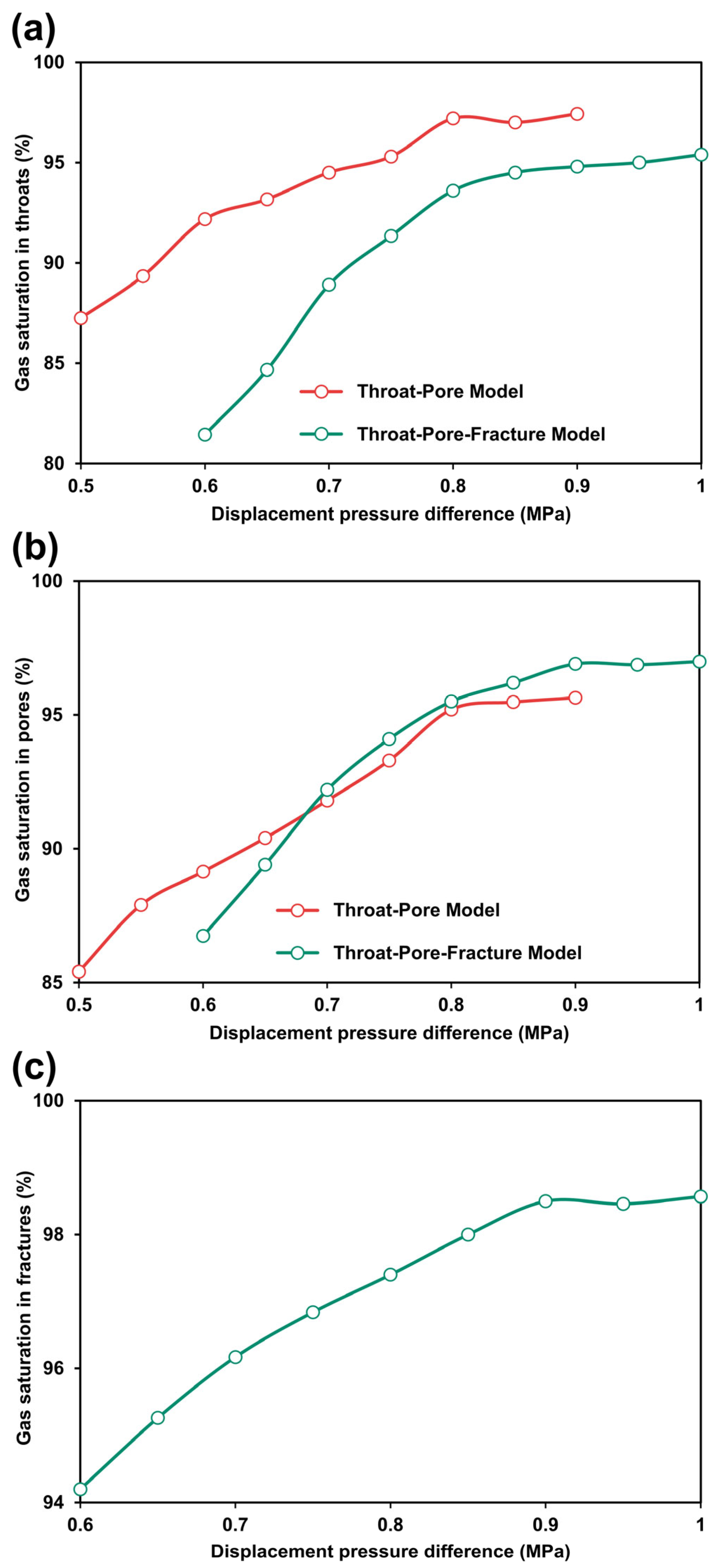
3.4. Gas Displacement of Water in Multiscale Porous Media
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Guo, X.; Wang, R.; Shen, B.; Wang, G.; Wan, C.; Wang, Q. Geological characteristics, resource potential, and development direction of shale gas in China. Pet. Explor. Develop. 2025, 52, 17–32. [Google Scholar] [CrossRef]
- Deng, P.; Chen, Z.; Peng, X.; Zhu, S.; Liu, B.; Lei, X.; Di, C. Converting underground natural gas storage for hydrogen: A review of advantages, challenges and economics. Renew. Sustain. Energy Rev. 2025, 213, 115438. [Google Scholar] [CrossRef]
- Cai, L.; Wu, J.; Zhang, M.; Wang, K.; Li, B.; Yu, X.; Hou, Y.; Zhao, Y. Investigating the Potential of CO2 Nanobubble Systems for Enhanced Oil Recovery in Extra-Low-Permeability Reservoirs. Nanomaterials 2024, 14, 1280. [Google Scholar] [CrossRef]
- Abdulhadi, D.; Ali, J.A.; Hama, S.M. Advanced Techniques for Improving the Production of Natural Resources from Unconventional Reservoirs: A State-of-the-Art Review. Energy Fuels 2025, 39, 10853–10876. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, T.; Peng, C.; Yao, J.; Sun, H.; Yang, Y.; Zhang, L.; Zhong, J. Effects of pore geometry and wall property on nanoscale fluid miscible behavior. Chem. Eng. J. 2025, 519, 164976. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, T.; Liu, S.; Jia, C.; Yao, J.; Sun, H.; Yang, Y.; Zhang, L.; Delshad, M.; Sepehrnoori, K.; et al. Adsorption effects on CO2-oil minimum miscibility pressure in tight reservoirs. Energy 2024, 288, 129815. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, J.; Yong, Z.; Qu, X. The Differential Enrichment Law of Tight Sandstone Gas in the Eighth Member of Shihezi Formation in the North and South of Ordos Basin. Energies 2024, 17, 5978. [Google Scholar] [CrossRef]
- Omari, A.; Wang, C.; Li, Y.; Xu, X. The progress of enhanced gas recovery (EGR) in shale gas reservoirs: A review of theory, experiments, and simulations. J. Pet. Sci. Eng. 2022, 213, 110461. [Google Scholar] [CrossRef]
- Shen, W.; Ma, T.; Zuo, L.; Yang, X.; Cai, J. Advances and Prospects of Supercritical CO2 for Shale Gas Extraction and Geological Sequestration in Gas Shale Reservoirs. Energy Fuels 2024, 38, 789–805. [Google Scholar] [CrossRef]
- Mudoi, M.P.; Sharma, P.; Khichi, A.S. A review of gas adsorption on shale and the influencing factors of CH4 and CO2 adsorption. J. Pet. Sci. Eng. 2022, 217, 110897. [Google Scholar] [CrossRef]
- Zhong, J.; Abedini, A.; Xu, L.; Xu, Y.; Qi, Z.; Mostowfi, F.; Sinton, D. Nanomodel visualization of fluid injections in tight formations. Nanoscale 2018, 10, 21994–22002. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Chen, D.; Gao, Z.; Wu, Y.; Zhang, Y.; Fan, K.; Chang, B.; Zhou, P.; Huang, W.; Hu, C. 3D geological modeling of deep fractured low porosity sandstone gas reservoir in the Kuqa Depression, Tarim Basin. Front. Earth Sci. 2023, 11, 1171050. [Google Scholar] [CrossRef]
- Wang, Q.; Guo, Z.; Tang, H.; Cheng, G.; Liu, Z.; Zhou, K. Natural Fractures in Tight Sandstone Gas Condensate Reservoirs and Their Influence on Production in the Dina 2 Gas Field in the Kuqa Depression, Tarim Basin, China. Energies 2024, 17, 4488. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Y.; Zou, R.; Yuan, Y.; Zou, R.; Huang, L.; Liu, Y.; Ding, J.; Meng, Z. Applications of molecular dynamics simulation in studying shale oil reservoirs at the nanoscale: Advances, challenges and perspectives. Pet. Sci. 2025, 22, 234–254. [Google Scholar] [CrossRef]
- Yang, X.; Meng, Y.; Shi, X.; Li, G. Influence of porosity and permeability heterogeneity on liquid invasion in tight gas reservoirs. J. Nat. Gas Sci. Eng. 2017, 37, 169–177. [Google Scholar] [CrossRef]
- Chen, Y.; Jing, J.; Karimov, R.; Sun, J.; Wang, K.; Yang, F.; Guo, Y. Experimental investigation on flow patterns and pressure gradients of shale oil-water flow in a horizontal pipe. Int. J. Multiph. Flow 2024, 176, 104839. [Google Scholar] [CrossRef]
- Huang, X.; Guo, X.; Zhou, X.; Shen, C.; Lu, X.; Qi, Z.; Xiao, Q.; Yan, W. Effects of water invasion law on gas wells in high temperature and high pressure gas reservoir with a large accumulation of water-soluble gas. J. Nat. Gas Sci. Eng. 2019, 62, 68–78. [Google Scholar] [CrossRef]
- Gong, T.; Tang, J.; Cheng, Q.; Lu, Y.; Liu, C.; Zhou, J.; Zhao, G. Effect of CO2/Brine/Shale Interaction on Shale Water Wettability and Spontaneous Imbibition. Energy Fuels 2024, 38, 21018–21027. [Google Scholar]
- Lin, L.; Lu, H.; Huang, L.; Luo, P. A molecular dynamics study of methane/water diffusion and water-blocking effects in coalbed methane. Fuel 2025, 386, 134234. [Google Scholar] [CrossRef]
- Huang, Y.; Li, X.; Liu, X.; Zhai, Y.; Fang, F.; Guo, W.; Qian, C.; Han, L.; Cui, Y.; Jia, Y. Review of the productivity evaluation methods for shale gas wells. J. Pet. Explor. Prod. Technol. 2024, 14, 25–39. [Google Scholar] [CrossRef]
- Chen, F.; Wang, Z.; Fu, S.; Li, A.; Zhong, J. Research on Transformation of Connate Water to Movable Water in Water-Bearing Tight Gas Reservoirs. Energies 2023, 16, 6961. [Google Scholar] [CrossRef]
- Tian, W.; Li, A.; Ren, X.; Josephine, Y. The threshold pressure gradient effect in the tight sandstone gas reservoirs with high water saturation. Fuel 2018, 226, 221–229. [Google Scholar] [CrossRef]
- Liu, J.; Yan, X.; Yi, S.; Jiang, L.; You, X. Modeling bimodal capillary bundle two-phase flow in the shale matrix for predicting water saturation distribution. Geoenergy Sci. Eng. 2023, 228, 211966. [Google Scholar] [CrossRef]
- Wang, Z.; Ding, K.; Liu, T.; Yao, J.; Sun, H.; Yang, Y.; Zhang, L.; Song, W.; Zhang, K.; Zhong, J. Minireview of Microscopic CO2 Interactions with Fluids and Minerals in Shale: Advances and Outlook. Energy Fuels 2023, 37, 9895–9913. [Google Scholar] [CrossRef]
- Zhong, J.; Alibakhshi, M.A.; Xie, Q.; Riordon, J.; Xu, Y.; Duan, C.; Sinton, D. Exploring Anomalous Fluid Behavior at the Nanoscale: Direct Visualization and Quantification via Nanofluidic Devices. Acc. Chem. Res. 2020, 53, 347–357. [Google Scholar] [CrossRef]
- Zhong, J.; Zandavi, S.H.; Li, H.; Bao, B.; Persad, A.H.; Mostowfi, F.; Sinton, D. Condensation in One-Dimensional Dead-End Nanochannels. ACS Nano 2017, 11, 304–313. [Google Scholar] [CrossRef]
- Zhong, J.; Riordon, J.; Zandavi, S.H.; Xu, Y.; Persad, A.H.; Mostowfi, F.; Sinton, D. Capillary Condensation in 8 nm Deep Channels. J. Phys. Chem. Lett. 2018, 9, 497–503. [Google Scholar] [CrossRef]
- Zhong, J.; Zhao, Y.; Lu, C.; Xu, Y.; Jin, Z.; Mostowfi, F.; Sinton, D. Nanoscale Phase Measurement for the Shale Challenge: Multicomponent Fluids in Multiscale Volumes. Langmuir 2018, 34, 9927–9935. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, T.; Liu, S.; Ding, K.; Liu, T.; Yao, J.; Sun, H.; Yang, Y.; Zhang, L.; Wang, W.; et al. Unveiling nanoscale fluid miscible behaviors with nanofluidic slim-tube. Energy Environ. Sci. 2024, 17, 9635–9651. [Google Scholar] [CrossRef]
- Chen, S.; Li, X.; Zhu, G.; Lu, Z.; Wang, R.; Huang, Y.; Lan, W.; Jia, F.; Zhu, Y. Classification, controlling factors, and multi-scale characterization techniques in shale reservoir pores: A comprehensive review. Gas Sci. Eng. 2025, 140, 205662. [Google Scholar] [CrossRef]
- Zhong, J.; Talebi, S.; Xu, Y.; Pang, Y.; Mostowfi, F.; Sinton, D. Fluorescence in sub-10 nm channels with an optical enhancement layer. Lab Chip 2018, 18, 568–573. [Google Scholar] [CrossRef] [PubMed]
- Ren, W.; Ma, C.; Huang, X.; Gu, W.; Chen, Y.; Liu, X. Dynamic and static imbibition characteristics of tight sandstone based on NMR. Geoenergy Sci. Eng. 2023, 229, 212052. [Google Scholar] [CrossRef]
- Zong, P.; Xu, H.; Tang, D.; Huo, F. Threshold pressure gradient in fractured reservoirs: Experimental simulation and mathematical modeling. Phys. Fluids 2024, 36, 063104. [Google Scholar] [CrossRef]
- Zeng, Y.; Bian, X.; Wang, L.; Zhang, L. Coupling model of gas-water two-phase productivity calculation for fractured horizontal wells in tight gas reservoirs. Geoenergy Sci. Eng. 2024, 234, 212666. [Google Scholar] [CrossRef]
- Ding, J.; Yang, S.; Nie, X.; Wang, Z. Dynamic threshold pressure gradient in tight gas reservoir. J. Nat. Gas Sci. Eng. 2024, 20, 155–160. [Google Scholar] [CrossRef]
- Zafar, A.; Su, Y.; Li, L.; Fu, J.; Mehmood, A.; Ouyang, W.; Zhang, M. Tight gas production model considering TPG as a function of pore pressure, permeability and water saturation. Pet. Sci. 2020, 17, 1356–1369. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pei, X.; Dai, L.; Wang, C.; Zhong, J.; Ren, X.; Wang, Z.; Peng, C.; Zhang, Q.; Zhang, N. Gas–Water Two-Phase Flow Mechanisms in Deep Tight Gas Reservoirs: Insights from Nanofluidics. Nanomaterials 2025, 15, 1601. https://doi.org/10.3390/nano15201601
Pei X, Dai L, Wang C, Zhong J, Ren X, Wang Z, Peng C, Zhang Q, Zhang N. Gas–Water Two-Phase Flow Mechanisms in Deep Tight Gas Reservoirs: Insights from Nanofluidics. Nanomaterials. 2025; 15(20):1601. https://doi.org/10.3390/nano15201601
Chicago/Turabian StylePei, Xuehao, Li Dai, Cuili Wang, Junjie Zhong, Xingnan Ren, Zengding Wang, Chaofu Peng, Qihui Zhang, and Ningtao Zhang. 2025. "Gas–Water Two-Phase Flow Mechanisms in Deep Tight Gas Reservoirs: Insights from Nanofluidics" Nanomaterials 15, no. 20: 1601. https://doi.org/10.3390/nano15201601
APA StylePei, X., Dai, L., Wang, C., Zhong, J., Ren, X., Wang, Z., Peng, C., Zhang, Q., & Zhang, N. (2025). Gas–Water Two-Phase Flow Mechanisms in Deep Tight Gas Reservoirs: Insights from Nanofluidics. Nanomaterials, 15(20), 1601. https://doi.org/10.3390/nano15201601






