Tunable Electrokinetic Motion of Charged Nanoparticles in an Aqueous Solution Using Interdigitated Microelectrodes
Abstract
1. Introduction
2. Materials and Methods
2.1. Microchip Fabrication and Sample Preparation
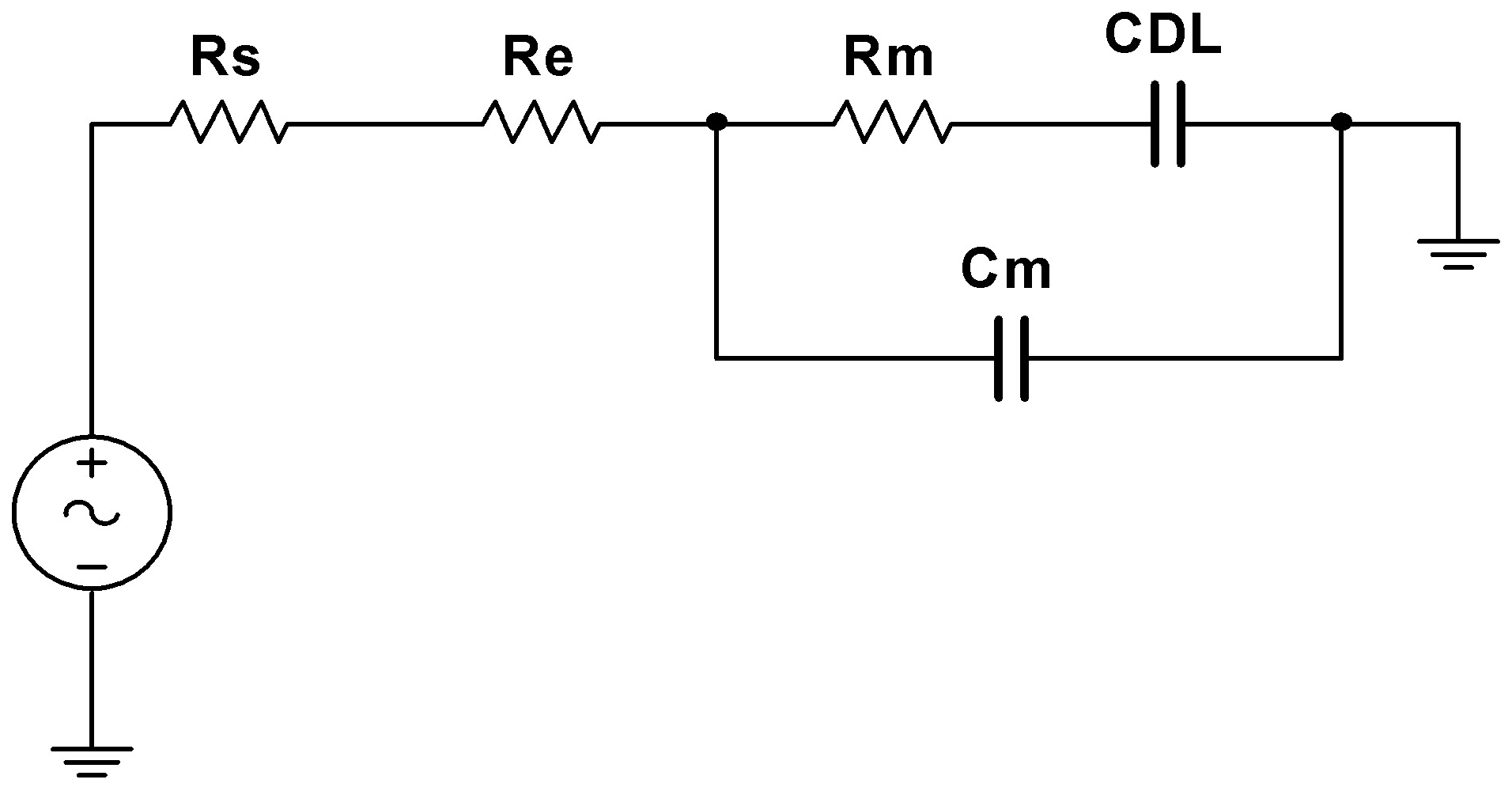
2.2. Electric Circuit Model
2.3. Electric Field Calculations
2.4. Experimental Procedure
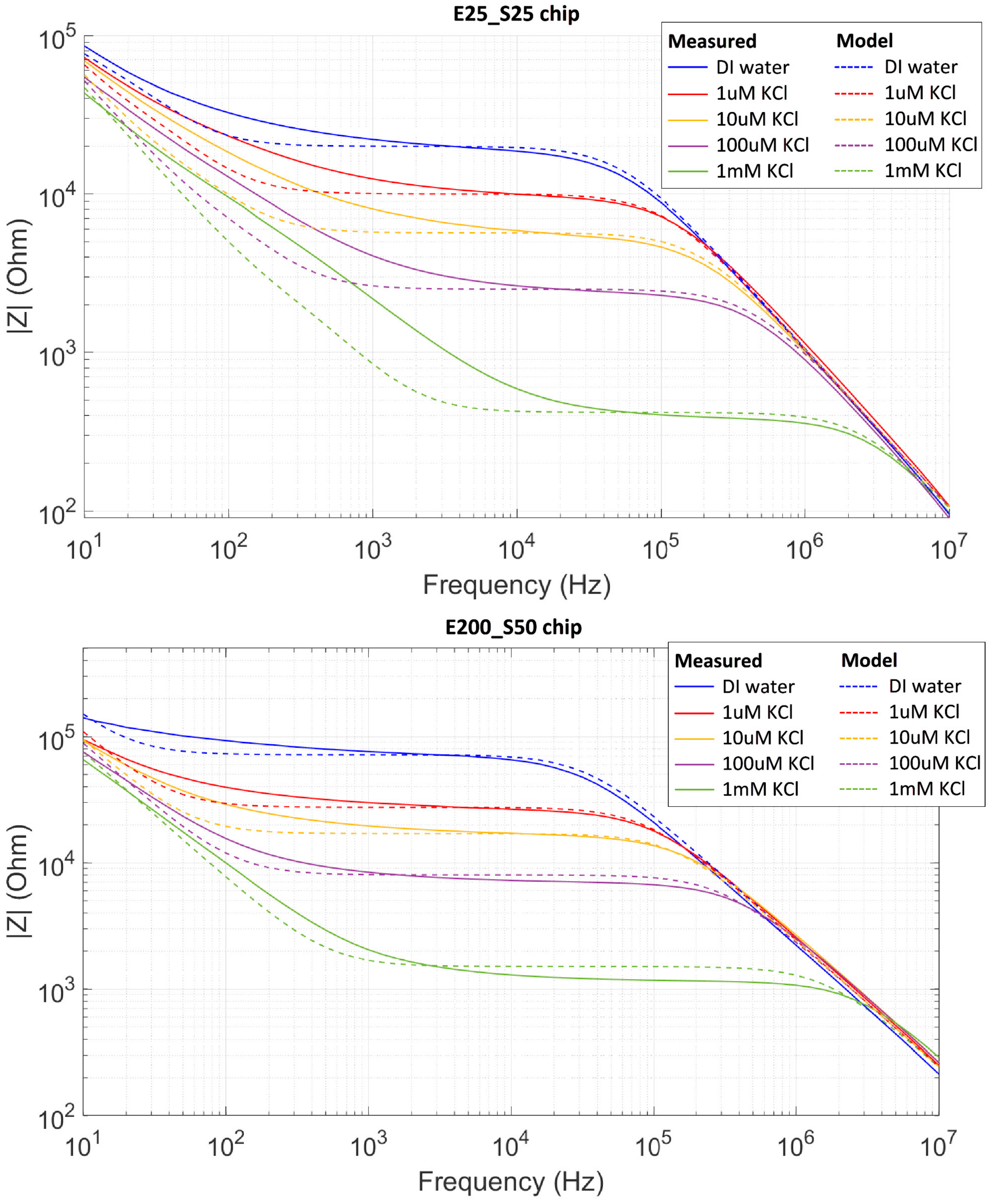
2.5. Electrical Impedance Measurement
3. Results and Discussion
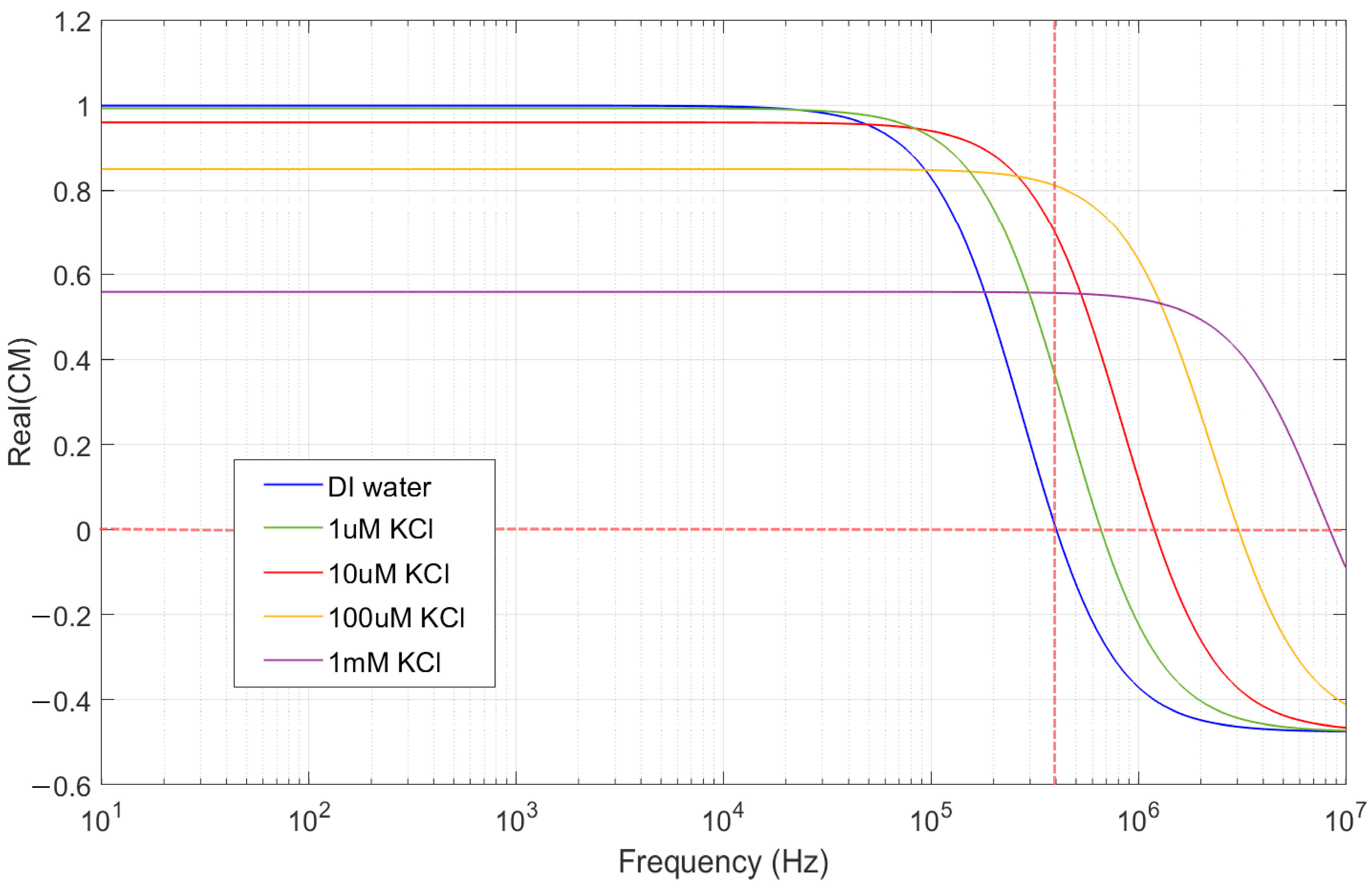
3.1. Electrokinetic Forces Acting on Particles
- Re [CM(ω)] > 0: Positive DEP (pDEP)—particles move toward high-field regions.
- Re [CM(ω)] < 0: Negative DEP (nDEP)—particles move toward low-field regions.
3.2. Electrokinetic Motion of the Particles in DI Water
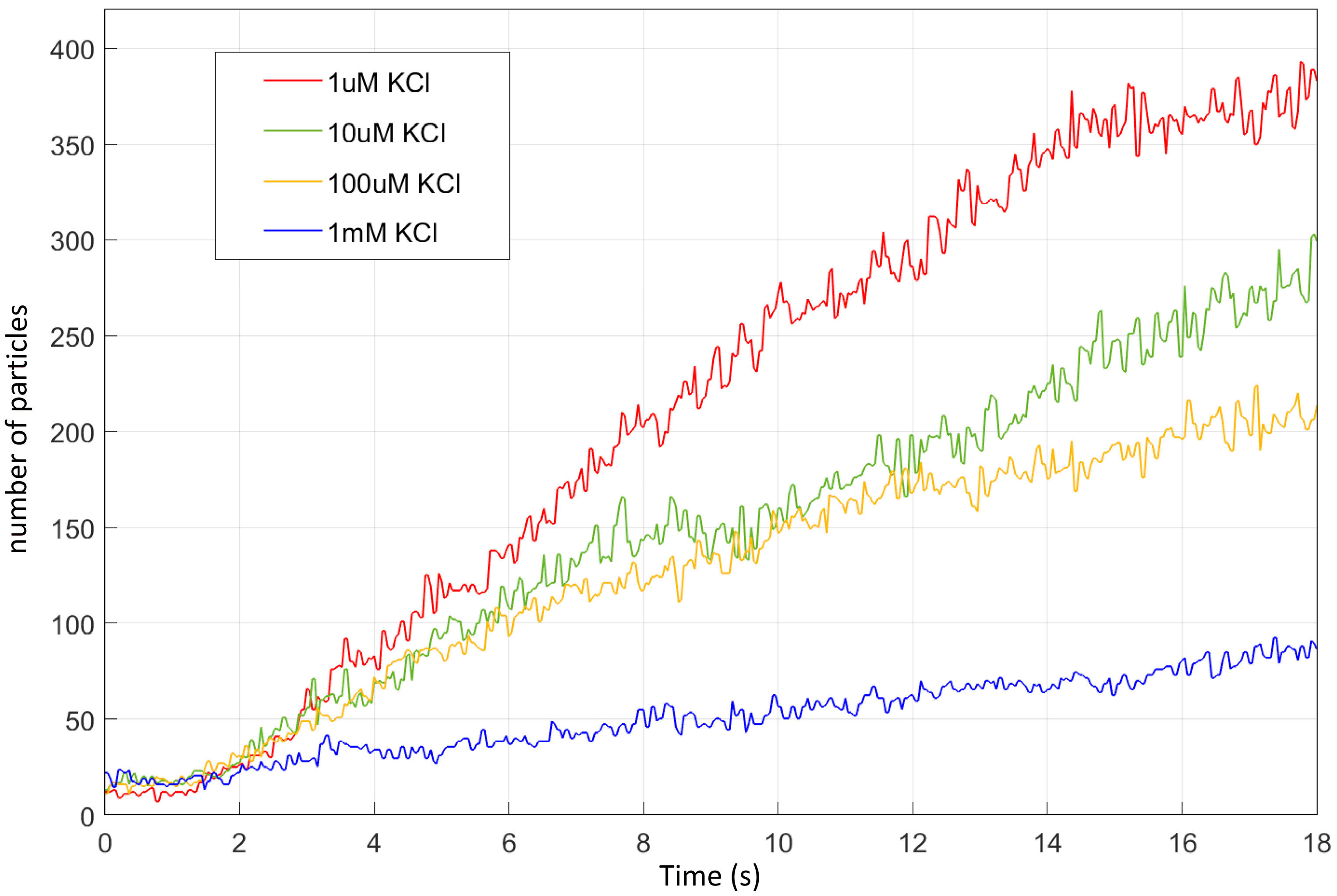
3.3. Electrokinetic Particle Motion for Different Salt Concentrations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ITO | Indium tin oxide | |
| IDE | Interdigitated electrodes | |
| AC | Alternating current | |
| DC | Direct current | |
| DI | Deionized | |
| DEP | Dielectrophoresis | |
| EP | Electrophoresis | |
| EO | Electroosmosis | |
| TC | Thermal convection | |
| List of Symbols | ||
| Symbol | Explanation | Amount |
| Rm | Resistance of the liquid on the electrodes inside the channel | - |
| Cm | Capacitance of the liquid on the electrodes inside the channel | - |
| umax | The ratio of distance between middle of two adjacent electrodes to the distance between them | - |
| ρm | Resistivity of the medium | - |
| ε0 | Vacuum permittivity | 8.854 × 10−12 (F/m) |
| εm | Relative permittivity of the medium | - |
| l | Electrode length | - |
| n | Number of electrodes | - |
| w | Electrode width | - |
| A | Area of electrodes (w × l) | - |
| ni | Number of ions i in the compound in the medium (e.g., salts) | - |
| nb | Concentration of compound (e.g., salts) | - |
| λi | Molar ionic conductivity for ion i | - |
| σi | Total ionic conductivity of the medium | - |
| CDL | Double layer capacitance | - |
| CPB | Poisson–Boltzmann model capacitance of double layer | - |
| CH | Helmholtz layer capacitance | - |
| λd | Debye–Hückel screening length | - |
| kB | Boltzmann constant | 1.38 × 10−23 (m2 kg2/s2 K) |
| e | Electron charge | 1.602 × 10−19 C |
| ψs | Constant surface potential | - |
| dH | Helmholtz layer thickness | - |
| r, rp | Particle radius | - |
| CM | Clausius–Mossotti factor | - |
| T | Absolute temperature in Kelvin | 298 K |
| Complex permittivity of medium | - | |
| Complex permittivity of particle | - | |
| εm | Relative permittivity of medium (water) | 80 |
| εp | Relative permittivity of particle (polystyrene) | 2.9 |
| σm | Conductivity of medium | - |
| σp | Conductivity of particle | ~1 × 10−19 S |
| ω | Angular frequency (2πf) | - |
| Ks | Surface conductivity of the particle | - |
| FF | Faraday constant | 96,485.3 (s.A/mol) |
| Rg | Gas constant | 8.314 (J/mol.K) |
| z | Ion valency | - |
| D | Particle diffusion coefficient | - |
| κ | Inverse Debye–Hückel length | - |
| η | Dynamic viscosity of the liquid | - |
| ζ | Electrokinetic potential | 30 mV |
| ζdl | Double layer zeta potential | - |
| vp | Particle velocity | - |
| E | Electric field | - |
| FEP | Electrophoretic force | - |
| FDEP | Dielectrophoretic force | - |
| FTC | Thermal convection force | - |
| FEO | Electroosmotic force | - |
| Fdrag | Drag force | - |
| vEO | Electroosmotic velocity | - |
| vET | Electrothermal velocity | - |
References
- Veiga, N.; Diesendruck, Y.; Peer, D. Targeted nanomedicine: Lessons learned and future directions. J. Control. Release 2023, 355, 446–457. [Google Scholar] [CrossRef]
- Swami, A.; Shi, J.; Gadde, S.; Votruba, A.R.; Kolishetti, N.; Farokhzad, O.C. Nanoparticles for Targeted and Temporally Controlled Drug Delivery. In Multifunctional Nanoparticles for Drug Delivery Applications; Springer: Boston, MA, USA, 2012; pp. 9–29. [Google Scholar] [CrossRef]
- Probstein, R.F.; Hicks, R.E. Removal of Contaminants from Soils by Electric Fields. Science 1993, 260, 498–503. [Google Scholar] [CrossRef]
- Sprocati, R.; Rolle, M. Charge interactions, reaction kinetics and dimensionality effects on electrokinetic remediation: A model-based analysis. J. Contam. Hydrol. 2020, 229, 103567. [Google Scholar] [CrossRef]
- van Blaaderen, A. Colloids under External Control. MRS Bull. 2004, 29, 85–90. [Google Scholar] [CrossRef]
- Liu, P.; Yang, S.; Fang, M.; Luo, X.; Cai, W. Complex nanostructures synthesized from nanoparticle colloids under an external electric field. Nanoscale 2011, 3, 3933. [Google Scholar] [CrossRef]
- Islam, M.N.; Gagnon, Z. Dielectrophoretic Trapping in Paper: Paper-based Electric Field Gradients for High-Throughput Particle Trapping. engrXiv 2022. [Google Scholar] [CrossRef]
- Chiou, P.Y.; Ohta, A.T.; Wu, M.C. Massively parallel manipulation of single cells and microparticles using optical images. Nature 2005, 436, 370–372. [Google Scholar] [CrossRef] [PubMed]
- Pethig, R. Review Article—Dielectrophoresis: Status of the theory, technology, and applications. Biomicrofluidics 2010, 4, 022811. [Google Scholar] [CrossRef]
- Castellanos, A.; Ramos, A.; González, A.; Green, N.G.; Morgan, H. Electrohydrodynamics and dielectrophoresis in microsystems: Scaling laws. J. Phys. D Appl. Phys. 2003, 36, 2584–2597. [Google Scholar] [CrossRef]
- Sadek, S.H.; Pimenta, F.; Pinho, F.T.; Alves, M.A. Measurement of electroosmotic and electrophoretic velocities using pulsed and sinusoidal electric fields. Electrophoresis 2017, 38, 1022–1037. [Google Scholar] [CrossRef]
- Cid, Í.A.; Ussembayev, Y.Y.; Neyts, K.; Strubbe, F. Measurement of the amplitude and phase of the electrophoretic and electroosmotic mobility based on fast single-particle tracking. Electrophoresis 2021, 42, 1623–1635. [Google Scholar] [CrossRef]
- Oorlynck, L.; Ussembayev, Y.Y.; Cid, I.A.; Fraire, J.; Hinnekens, C.; Braeckmans, K.; Strubbe, F. Laser-Scanning Microscopy for Electrophoretic Mobility Characterization of Single Nanoparticles. Part. Part. Syst. Charact. 2023, 40, 2200152. [Google Scholar] [CrossRef]
- Wang, Q.; Moerner, W.E. Single-molecule motions enable direct visualization of biomolecular interactions in solution. Nat. Methods 2014, 11, 555–558. [Google Scholar] [CrossRef] [PubMed]
- Fields, A.P.; Cohen, A.E. Electrokinetic trapping at the one nanometer limit. Proc. Natl. Acad. Sci. USA 2011, 108, 8937–8942. [Google Scholar] [CrossRef]
- Ussembayev, Y.; Rezakhanloo, F.; Neyts, K.; Strubbe, F. Axial electrokinetic trapping of label-free nanoparticles using evanescent field scattering. Nanoscale 2025, 17, 8496–8504. [Google Scholar] [CrossRef]
- Yu, Y.; Cilliers, J.; Hadler, K.; Starr, S.; Wang, Y. A review of particle transport and separation by electrostatic traveling wave methods. J. Electrost. 2022, 119, 103735. [Google Scholar] [CrossRef]
- Velev, O.D.; Gangwal, S.; Petsev, D.N. Particle-localized AC and DC manipulation and electrokinetics. Annu. Rep. Sect. C Phys. Chem. 2009, 105, 213. [Google Scholar] [CrossRef]
- Tian, Z.; Wang, X.; Chen, J. On-chip dielectrophoretic single-cell manipulation. Microsyst. Nanoeng. 2024, 10, 117. [Google Scholar] [CrossRef]
- Pesch, G.R.; Lorenz, M.; Sachdev, S.; Salameh, S.; Du, F.; Baune, M.; Boukany, P.E.; Thöming, J. Bridging the scales in high-throughput dielectrophoretic (bio-)particle separation in porous media. Sci. Rep. 2018, 8, 10480. [Google Scholar] [CrossRef]
- Kang, Y.; Cetin, B.; Wu, Z.; Li, D. Continuous particle separation with localized AC-dielectrophoresis using embedded electrodes and an insulating hurdle. Electrochim. Acta 2009, 54, 1715–1720. [Google Scholar] [CrossRef]
- Ussembayev, Y.; Beunis, F.; Oorlynck, L.; Bahrami, M.; Strubbe, F.; Neyts, K. Single Elementary Charge Fluctuations on Nanoparticles in Aqueous Solution. ACS Nano 2023, 17, 22952–22959. [Google Scholar] [CrossRef]
- McCleskey, R.B.; Nordstrom, D.K.; Ryan, J.N. Comparison of electrical conductivity calculation methods for natural waters. Limnol. Oceanogr. Methods 2012, 10, 952–967. [Google Scholar] [CrossRef]
- Marion, G.M.; Babcock, K.L. Predicting Specific Conductance and Salt Concentration in Dilute Aqueous Solutions. Soil Sci. 1976, 122, 181–187. [Google Scholar] [CrossRef]
- Nakayama, Y.; Andelman, D. Differential capacitance of the electric double layer: The interplay between ion finite size and dielectric decrement. J. Chem. Phys. 2015, 142, 044706. [Google Scholar] [CrossRef]
- Velikonja, A.; Kralj-Iglič, V.; Iglič, A. On Asymmetric Shape of Electric Double Layer Capacitance Curve. Int. J. Electrochem. Sci. 2015, 10, 1–7. [Google Scholar] [CrossRef]
- Wang, H.; Pilon, L. Accurate Simulations of Electric Double Layer Capacitance of Ultramicroelectrodes. J. Phys. Chem. C 2011, 115, 16711–16719. [Google Scholar] [CrossRef]
- Rodà, C.; Salzmann, B.B.V.; Wagner, I.; Ussembayev, Y.; Chen, K.; Hodgkiss, J.M.; Neyts, K.; Moreels, I.; Vanmaekelbergh, D.; Geiregat, P. Stimulated Emission through an Electron–Hole Plasma in Colloidal CdSe Quantum Rings. Nano Lett. 2021, 21, 10062–10069. [Google Scholar] [CrossRef]
- Ussembayev, Y.Y.; Zawacka, N.K.; Strubbe, F.; Hens, Z.; Neyts, K. Waveguiding of Photoluminescence in a Layer of Semiconductor Nanoparticles. Nanomaterials 2021, 11, 683. [Google Scholar] [CrossRef]
- Harrington, D.A.; van den Driessche, P. Mechanism and equivalent circuits in electrochemical impedance spectroscopy. Electrochim. Acta 2011, 56, 8005–8013. [Google Scholar] [CrossRef]
- Wu, J.; Ben, Y.; Battigelli, D.; Chang, H.-C. Long-Range AC Electroosmotic Trapping and Detection of Bioparticles. Ind. Eng. Chem. Res. 2005, 44, 2815–2822. [Google Scholar] [CrossRef]
- Zhou, Q.; Dong, P.; Liu, L.; Cheng, B. Study on the sedimentation self-assembly of colloidal SiO2 particles under gravitational field. Colloids Surf. A Physicochem. Eng. Asp. 2005, 253, 169–174. [Google Scholar] [CrossRef]
- Strubbe, F.; Beunis, F.; Neyts, K. Detection of Elementary Charges on Colloidal Particles. Phys. Rev. Lett. 2008, 100, 218301. [Google Scholar] [CrossRef]
- Deivasigamani, R.; Maidin, N.N.M.; Wee, M.F.M.R.; Mohamed, M.A.; Buyong, M.R. Dielectrophoresis Prototypic Polystyrene Particle Synchronization toward Alive Keratinocyte Cells for Rapid Chronic Wound Healing. Sensors 2021, 21, 3007. [Google Scholar] [CrossRef]
- Pethig, R. Review—Where Is Dielectrophoresis (DEP) Going? J. Electrochem. Soc. 2017, 164, B3049–B3055. [Google Scholar] [CrossRef]
- MyDEP|MyDEP Is a Computational Tool Dedicated to the Study of Dielectric Particle Response to AC Electric Fields. Available online: https://mydepsoftware.github.io/ (accessed on 23 May 2025).
- Lyklema, J. Electrokinetics and Related Phenomena. Fundam. Interface Colloid Sci. 1995, 2, 4-1–4-135. [Google Scholar] [CrossRef]
- Nguyen, H.-T.; Bouchaudy, A.; Salmon, J.-B. Microfluidic free interface diffusion: Measurement of diffusion coefficients and evidence of interfacial-driven transport phenomena. Phys. Fluids 2022, 34, 052008. [Google Scholar] [CrossRef]
- Manshadi, M.K.D.; Beskok, A. Competing effects of buoyancy-driven and electrothermal flows for Joule heating-induced transport in microchannels. Flow 2023, 3, E23. [Google Scholar] [CrossRef]
- García-Sánchez, P.; Ramos, A.; Mugele, F. Electrothermally driven flows in ac electrowetting. Phys. Rev. E 2010, 81, 015303. [Google Scholar] [CrossRef] [PubMed]
- Tathireddy, P.; Choi, Y.-H.; Skliar, M. Particle AC electrokinetics in planar interdigitated microelectrode geometry. J. Electrost. 2008, 66, 609–619. [Google Scholar] [CrossRef]
- Voß, J.; Wittkowski, R. Hydrodynamic resistance matrices of colloidal particles with various shapes. arXiv 2018, arXiv:1811.01269. [Google Scholar]
- Brady, J.F.; Bossis, G. Stokesian Dynamics. Annu. Rev. Fluid Mech. 1988, 20, 111–157. [Google Scholar] [CrossRef]
- Green, N.G.; Ramos, A.; González, A.; Morgan, H.; Castellanos, A. Fluid flow induced by nonuniform ac electric fields in electrolytes on microelectrodes. III. Observation of streamlines and numerical simulation. Phys. Rev. E 2002, 66, 026305. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; White, L.R.; Tilton, R.D. Lateral separation of colloids or cells by dielectrophoresis augmented by AC electroosmosis. J. Colloid Interface Sci. 2005, 285, 179–191. [Google Scholar] [CrossRef]
- de Xammer Oro, J.R.; Ruderman, G.; Grigera, J.R.; Vericat, F. Threshold frequency for the ionic screening of electric fields in electrolyte solutions. J. Chem. Soc. Faraday Trans. 1992, 88, 699. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rezakhanloo, F.; Ussembayev, Y.; Bahrami, M.; Beunis, F.; Braeckmans, K.; Goemaere, I.; Punj, D.; Ahmad, A.; Van der Meeren, L.; Neyts, K. Tunable Electrokinetic Motion of Charged Nanoparticles in an Aqueous Solution Using Interdigitated Microelectrodes. Nanomaterials 2025, 15, 1568. https://doi.org/10.3390/nano15201568
Rezakhanloo F, Ussembayev Y, Bahrami M, Beunis F, Braeckmans K, Goemaere I, Punj D, Ahmad A, Van der Meeren L, Neyts K. Tunable Electrokinetic Motion of Charged Nanoparticles in an Aqueous Solution Using Interdigitated Microelectrodes. Nanomaterials. 2025; 15(20):1568. https://doi.org/10.3390/nano15201568
Chicago/Turabian StyleRezakhanloo, Farshad, Yera Ussembayev, Mohammadreza Bahrami, Filip Beunis, Kevin Braeckmans, Ilia Goemaere, Deep Punj, Amin Ahmad, Louis Van der Meeren, and Kristiaan Neyts. 2025. "Tunable Electrokinetic Motion of Charged Nanoparticles in an Aqueous Solution Using Interdigitated Microelectrodes" Nanomaterials 15, no. 20: 1568. https://doi.org/10.3390/nano15201568
APA StyleRezakhanloo, F., Ussembayev, Y., Bahrami, M., Beunis, F., Braeckmans, K., Goemaere, I., Punj, D., Ahmad, A., Van der Meeren, L., & Neyts, K. (2025). Tunable Electrokinetic Motion of Charged Nanoparticles in an Aqueous Solution Using Interdigitated Microelectrodes. Nanomaterials, 15(20), 1568. https://doi.org/10.3390/nano15201568









