Review of the Current State of Optical Characterization and Design of Electronic States in Plasmonic Materials—From Noble Metals to Silverene and Goldene
Abstract
1. Introduction
2. Electronic Structure, Hot Electrons, and Nanoantenna Effect
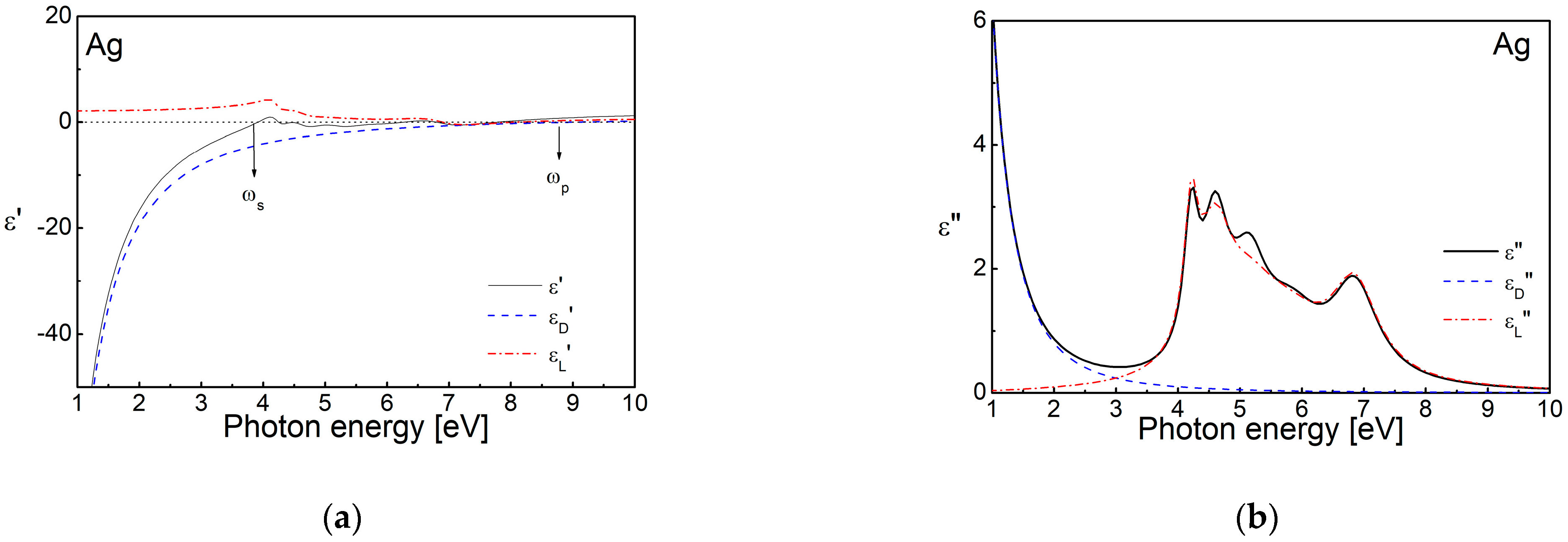
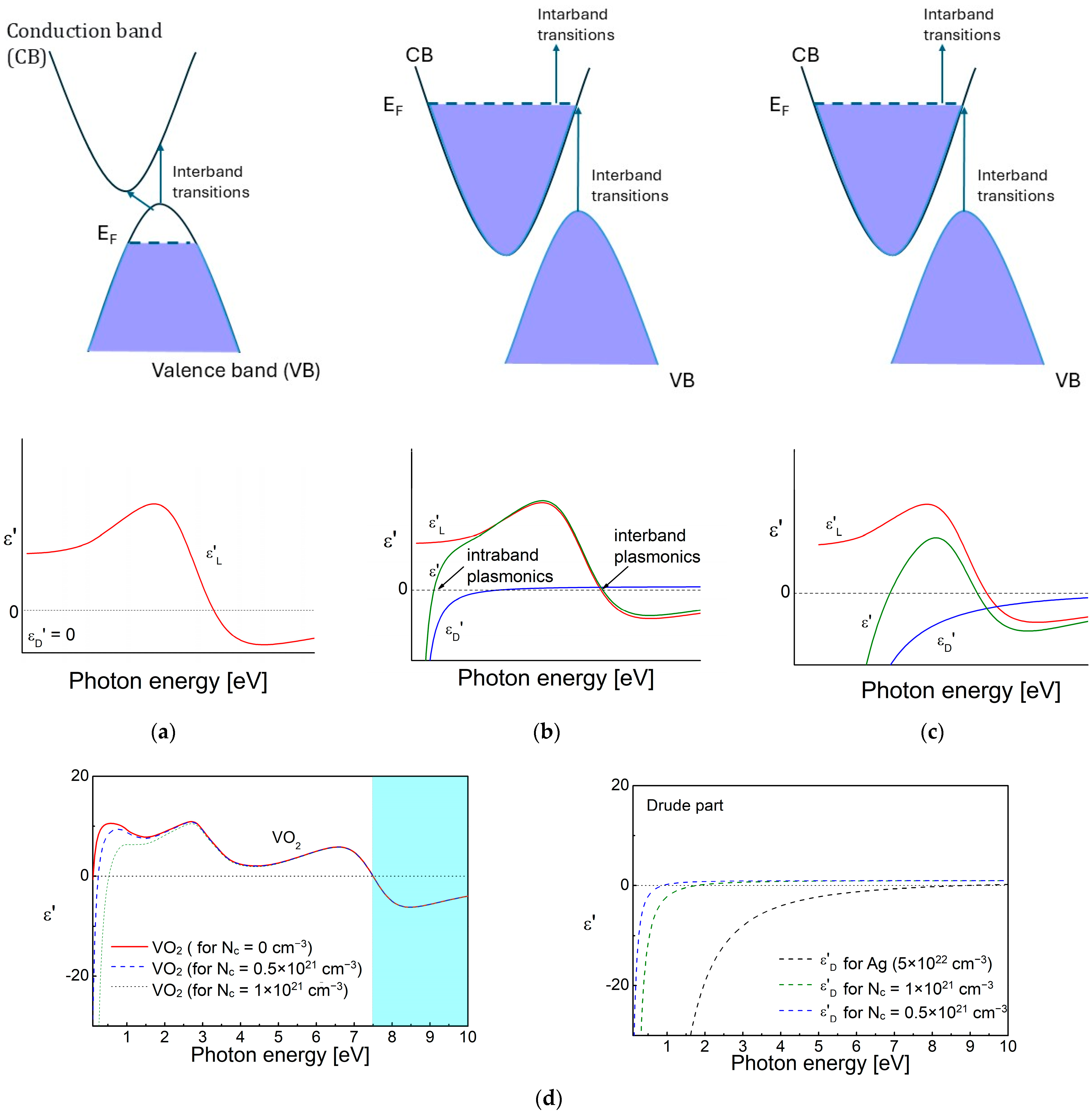
2.1. Band Structure and Complex Permittivity
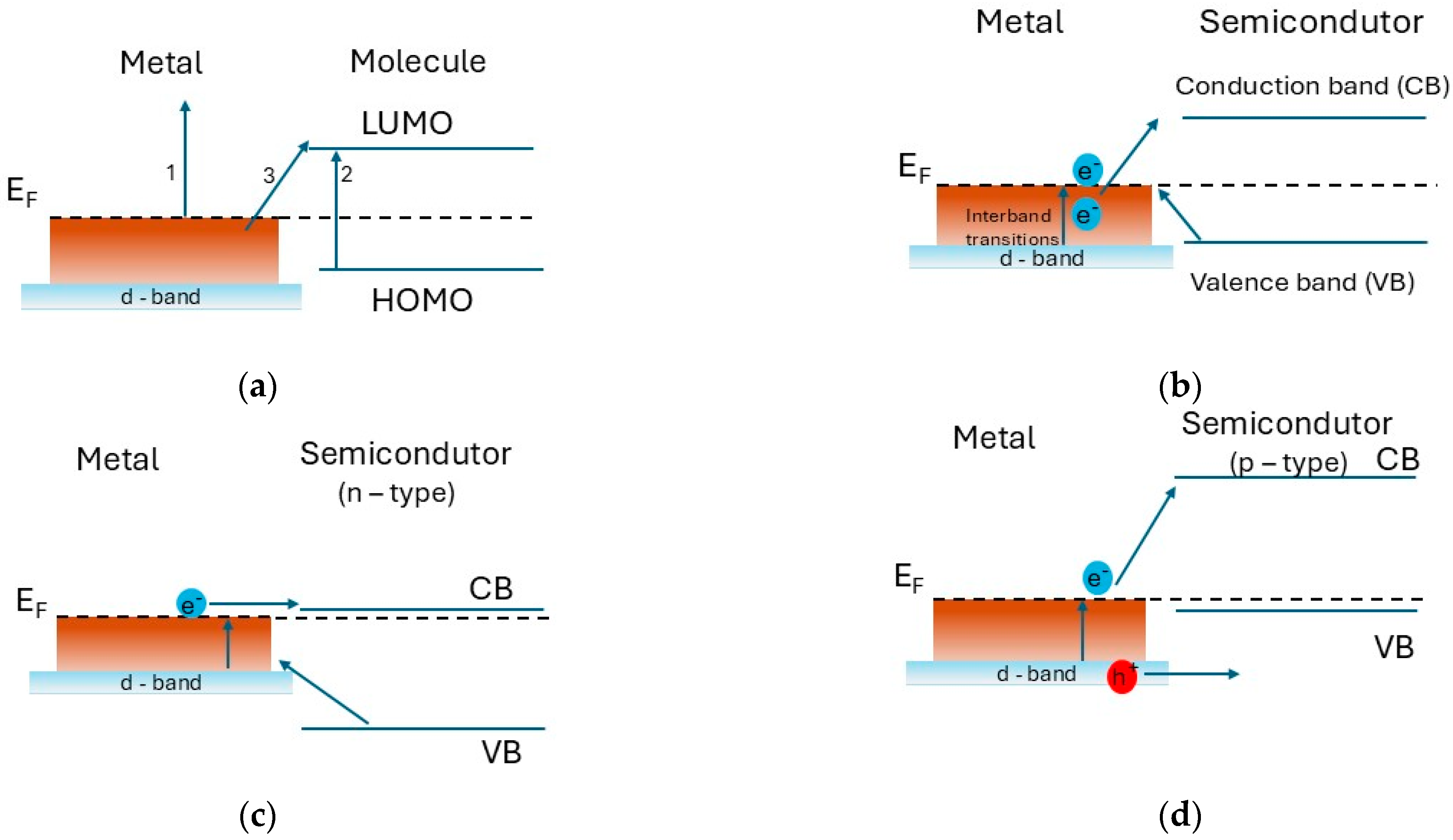
2.2. Hot Electrons and Charge Transfer
2.3. Nanoantenna Effect
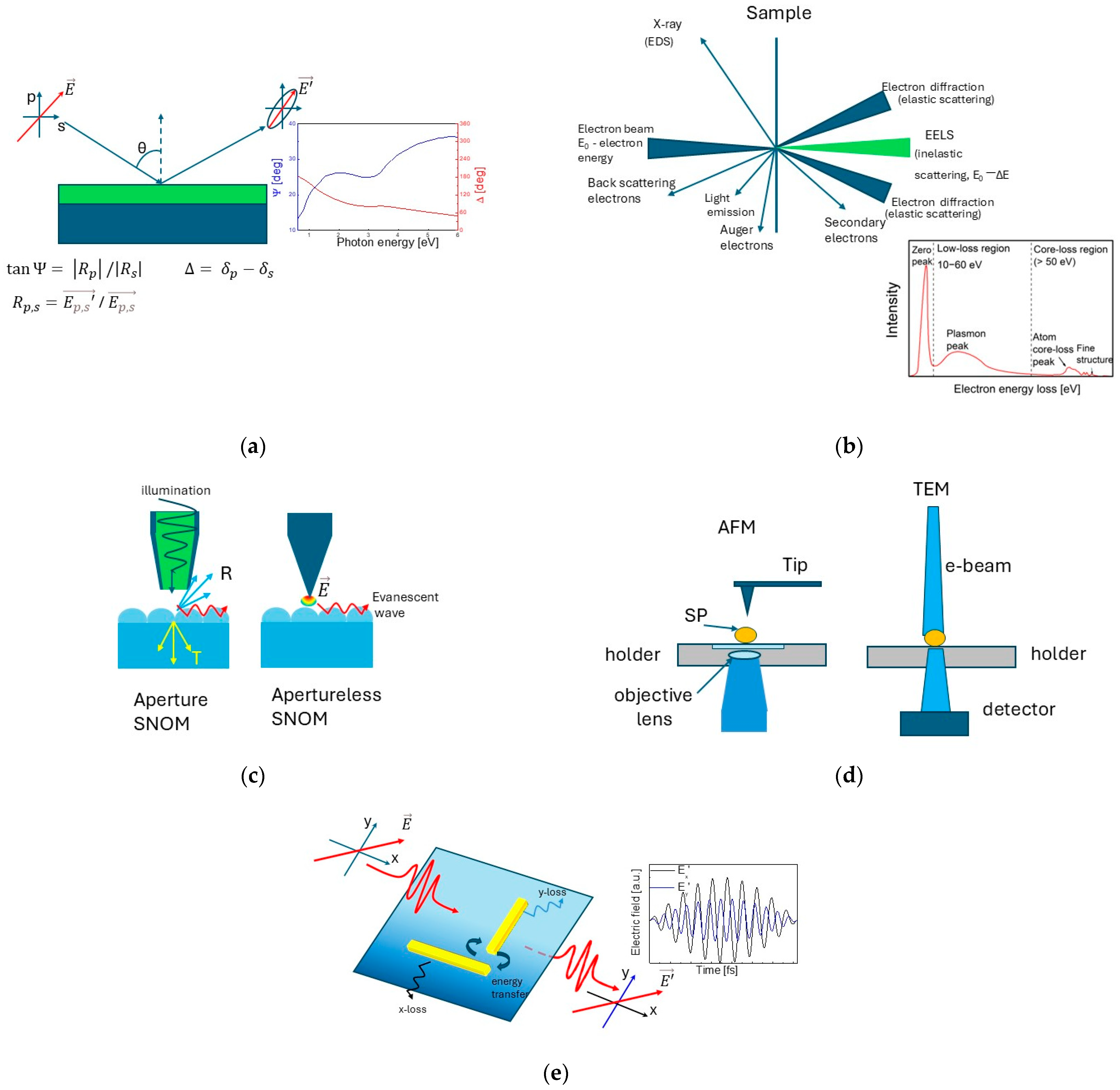
3. Techniques for Characterization of Plasmonic Materials and Nanostructures
3.1. Spectroscopic Ellipsometry
3.2. Electron Energy Loss Spectroscopy (EELS)
3.3. UV-Vis Spectroscopy and Dynamic Light Scattering
3.4. Near-Field Imaging
3.5. Single Particle Spectroscopy
3.6. Interferometric and Polarimetric Microscopy
3.7. Deep Learning-Based Characterization
4. Plasmonic Materials and Approaches for Design of Their Electronic States
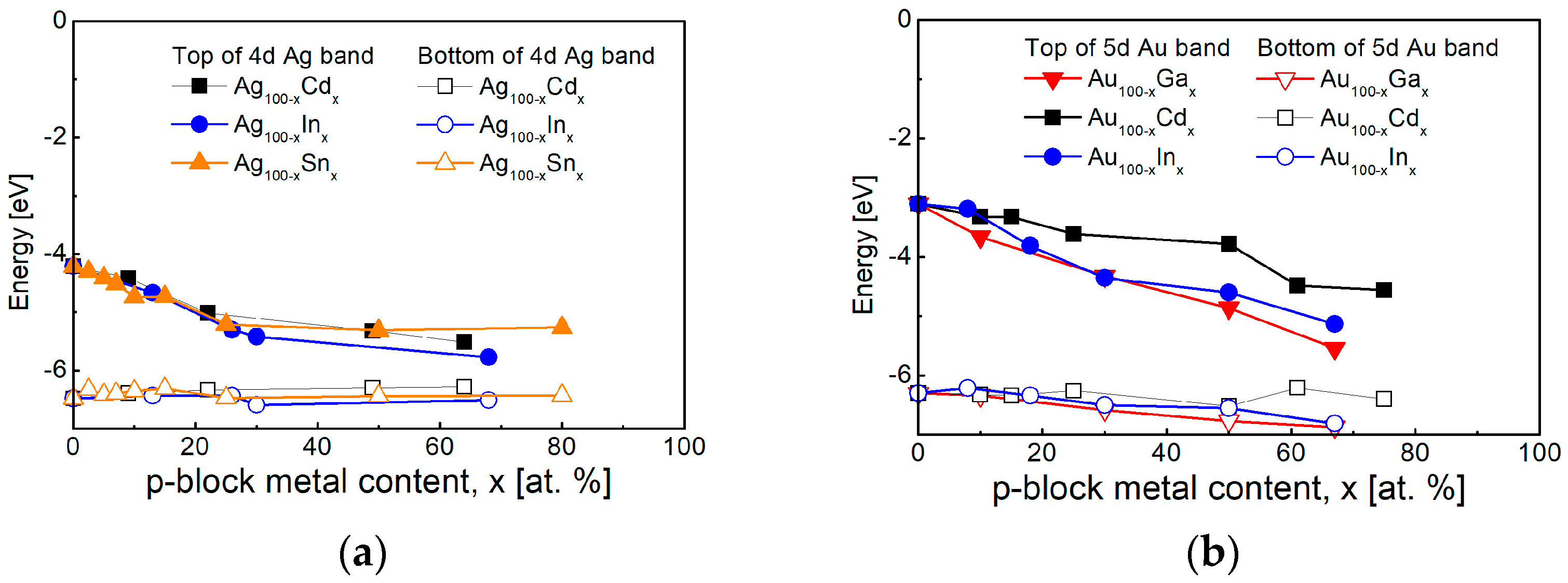
4.1. Noble Metals and Their Alloys
4.2. Two-Dimensional Plasmonics
4.2.1. Graphene and Graphene Oxide
4.2.2. Plasmons in Semiconductors—Transition Metal Chalcogenides
4.2.3. MXene
4.3. Future Challenges–2D Noble Metals and Their Intermetallic Compounds
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
List of Abbreviations
| General | |
| 2D | Two-Dimensional |
| 3D | Three-Dimensional |
| CRISPR | Clustered Regularly Interspaced Short Palindromic Repeats |
| ENZ | Epsilon-Near-Zero |
| FCC lattice | Face Centred Cubic lattice |
| HOMO level | energy level of the Highest Occupied Molecular Orbital |
| IR | Infrared spectrum (NIR—near IR) |
| LSPR | Localized Surface Plasmon Resonance |
| LUMO level | energy level of the Lowest Unoccupied Molecular Orbital |
| MS | MetaSurface |
| NP | NanoParticle |
| Q | Quality factor |
| SP | Single Particle |
| SPR | Surface Plasmon Resonance |
| TF | Thin Film |
| UV | Ultraviolet spectrum |
| Vis | Visible spectrum |
| Δ | Ellipsometric angle; difference between the phases of the reflection amplitude coefficient for p- and s-polarizations |
| Ψ | Ellipsometric angle; ratio of the reflection amplitude coefficient for p- and s-polarizations |
| Methods | |
| AFM | Atomic Force Microscopy |
| ANN | Artificial Neural Network |
| DETECTR | DNA Endonuclease-Targeted CRISPR Trans Reporter |
| DFT | Density Functional Theory |
| DL | Deep Learning |
| DLS | Dynamic Light Scattering |
| EELS | Electron Energy Loss Spectroscopy |
| EMA | Effective Media Approximation theory |
| FDTD | Finite-Difference Time-Domain method |
| GPN | Geometry-Predicting-Network |
| IM | Interferometric Microscopy |
| PM | Polarimetric Microscopy |
| SE | Spectroscopic Ellipsometry |
| SEF | Surface-Enhanced Fluorescence |
| SEHRS | Surface-Enhanced Hyper Raman Scattering |
| SEIRA | Surface-Enhanced InfraRed Absorption |
| SEROA | Surface-Enhanced Raman Optical Activity |
| SERS | Surface-Enhanced Raman Spectroscopy |
| SHERLOCK | Specific High-Sensitivity Enzymatic Reporter UnLOCKing |
| SNOM | Scattering Near-field Optical Microscopy (NSOM—Near-field Scanning Optical Microscopy) |
| SPN | Spectrum-Predicting-Network |
| SPS | Single Particle Spectroscopy |
| SPRM | Surface Plasmon Resonance Microscopy |
| STEM | Scanning Transmission Electron Microscopy |
| STM | Scanning Tunnelling Microscopy |
| TEM | Transmission Electron Microscopy |
| TERS | Tip-Enhanced Raman Spectroscopy |
| UV-Vis-NIR | UV-Vis-NIR spectrophotometry |
| XPS | X-ray Photo-electron Spectroscopy |
| Materials | |
| AZO | Al:ZnO |
| CuPc | Copper PhtaloCyanine |
| EG | Epitaxially grown Graphene |
| Goldene | 2D gold (single-atom-layer) |
| GZO | Ga:ZnO |
| ITO | Indium Tin Oxide |
| MXene | metal (M) carbide/nitride (X) in the form of alternating layers |
| MAX phase | MXene with an intermediate layer of a post-transition element |
| R6G | Rhodamine6G |
| Silverene | 2D silver (few-atom-layer) |
References
- Dai, H.; Liu, J.; Wang, S.; Wang, B.; Kai, T.; Wu, P.; Ding, P. Recent advance in optical sensors for microcystin-LR: From recognition elements to signal transduction. Analyst 2025, 150, 1470–1489. [Google Scholar] [CrossRef]
- Mcoyi, M.P.; Mpofu, K.T.; Sekhwama, M.; Mthunzi-Kufa, P. Developments in localized surface plasmon resonance. Plasmonics 2025, 20, 5481–5520. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, L. Lab-on-fiber: Plasmonic nano-arrays for sensing. Nanoscale 2020, 12, 7485–7499. [Google Scholar] [CrossRef]
- Lu, R.; Ni, J.; Yin, S.; Ji, Y. Responsive plasmonic nanomaterials for advanced cancer diagnostics. Front. Chem. 2021, 9, 652287. [Google Scholar] [CrossRef]
- Fu, R.; Warnakula, T.; Shi, Q.; Yap, L.W.; Dong, D.; Liu, Y.; Premaratne, M.; Cheng, W. Plasmene nanosheets as optical skin strain sensors. Nanoscale Horiz. 2020, 5, 1515–1523. [Google Scholar] [CrossRef]
- Wang, Q.; Ren, Z.H.; Zhao, W.M.; Wang, L.; Yan, X.; Zhu, A.S.; Qiu, F.M.; Zhang, K.K. Research advances on surface plasmon resonance biosensors. Nanoscale 2022, 14, 564–591. [Google Scholar] [CrossRef]
- Chai, M.; Wang, Y.; Chen, C.; Zhao, Z.; Jin, M.; He, T. Metamaterials-Based Photoelectric Conversion: From Microwave to Optical Range. Laser Photonics Rev. 2022, 16, 2100458. [Google Scholar] [CrossRef]
- Fu, X.; Bu, T.; Li, C.; Liu, G.; Zhang, C. Overview of micro/nano-wind energy harvesters and sensors. Nanoscale 2020, 12, 23929–23944. [Google Scholar] [CrossRef]
- Liu, D.; Xue, C. Plasmonic coupling architectures for enhanced photocatalysis. Adv. Mater. 2021, 33, 2005738. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Bowen, C.R.; Valev, V.K. Plasmonic-pyroelectric materials and structures. Adv. Funct. Mater. 2024, 34, 2312245. [Google Scholar] [CrossRef]
- Dorodnyy, A.; Smajic, J.; Leuthold, J. Mie scattering for photonic devices. Laser Photonics Rev. 2023, 17, 2300055. [Google Scholar] [CrossRef]
- Kim, S.; Jeong, T.I.; Park, J.; Ciappina, M.F.; Kim, S. Recent advances in ultrafast plasmonics: From strong field physics to ultraprecision spectroscopy. Nanophotonics 2022, 11, 2393–2431. [Google Scholar] [CrossRef] [PubMed]
- Cai, W.; Shalaev, V. Optical Metamaterials; Springer: New York, NY, USA, 2010; pp. 1–37. [Google Scholar] [CrossRef]
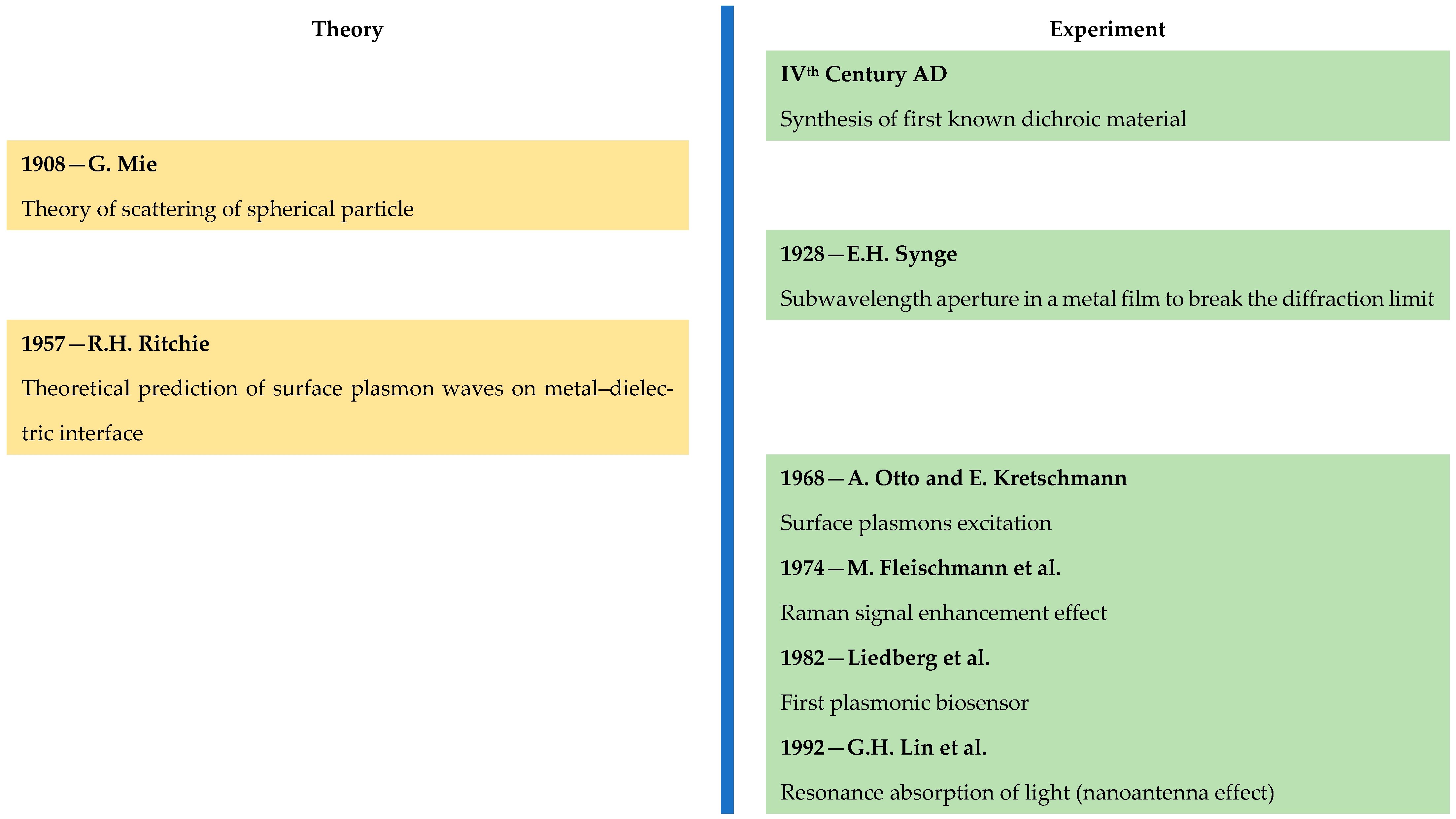
- Mie, G. Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen. Ann. Phys. 1908, 25, 377–445. [Google Scholar] [CrossRef]
- Synge, E.H. A suggested method for extending microscopic resolution into the ultra-microscopic region. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1928, 6, 356–362. [Google Scholar] [CrossRef]
- Ritchie, R.H. Plasma losses by fast electrons in thin films. Phys. Rev. 1957, 106, 874–881. [Google Scholar] [CrossRef]
- Otto, A. Excitation of nonradiative surface plasma waves in silver by the method of frustrated total reflection. Z. Phys. A Hadron. Nucl. 1968, 216, 398–410. [Google Scholar] [CrossRef]
- Kretschmann, E.; Raether, H. Radiative decay of nonradiative surface plasmons excited by light. Z. Nat. A 1968, 23, 2135–2136. [Google Scholar] [CrossRef]
- Fleischmann, M.; Hendra, P.J.; McQuillan, A.J. Raman spectra of pyridine adsorbed at a silver electrode. Chem. Phys. Lett. 1974, 26, 163–166. [Google Scholar] [CrossRef]
- Nylander, C.; Liedberg, B.; Lind, T. Gas detection by means of surface plasmon resonance. Sens. Actuators 1982, 3, 79–88. [Google Scholar] [CrossRef]
- Liedberg, B.; Nylander, C.; Lundstrom, I. Surface plasmon resonance for gas detection and biosensing. Sens. Actuators 1983, 4, 299–304. [Google Scholar] [CrossRef]
- Lin, G.H.; Abdu, R.; Bockris, J.O.M. Investigation of resonance light absorption and rectification by subnanostructures. J. Appl. Phys. 1996, 80, 565–568. [Google Scholar] [CrossRef]
- Queffélec, C.; Knight, D.A. Plasmonic Nanomaterials: Characterization and Applications in Organic Synthesis and Catalysis, 1st ed.; Jenny Stanford Publishing: New York, NY, USA, 2024; pp. 1–47. [Google Scholar] [CrossRef]
- Stockman, M. Nanoplasmonics: From Present into Future. In Plasmonics: Theory and Applications; Shahbazyan, T.V., Stockman, M.I., Eds.; Springer: Dordrecht, Netherlands, 2013; Volume 15, pp. 1–101. [Google Scholar] [CrossRef]
- Haes, A.J.; Stuart, D.A.; Nie, S.; Van Duyne, R.P. Using Solution-Phase Nanoparticles, Surface-Confined Nanoparticle Arrays and Single Nanoparticles as Biological Sensing Platforms. J. Fluoresc. 2004, 14, 355–367. [Google Scholar] [CrossRef]
- Kreibig, U.; Zacharias, P. Surface plasma resonances in small spherical silver and gold particles. Z. Phys. A Hadron. Nucl. 1970, 231, 128–143. [Google Scholar] [CrossRef]
- Doremus, R.H. Optical properties of thin metallic films in island form. J. Appl. Phys. 1966, 37, 2775–2781. [Google Scholar] [CrossRef]
- Yoshida, S.; Yamaguchi, T.; Kinbara, A. Changes of the optical properties of aggregated silver films after deposition. J. Opt. Soc. Am. 1971, 61, 463–469. [Google Scholar] [CrossRef]
- Truong, V.V.; Scott, G.D. Light scattering from aggregated noble-metal films. J. Opt. Soc. Am. 1978, 68, 189–193. [Google Scholar] [CrossRef]
- Marton, J.P.; Lemon, J.R. Optical properties of aggregated metal systems: Real metals. J. Appl. Phys. 1973, 44, 3953–3959. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Yoshida, S.; Kinbara, A. Effects of Optical Anisotropy of Aggregated Silver Films on Ellipsometric Determination of n, k, and d. J. Opt. Soc. Am. 1972, 62, 634–638. [Google Scholar] [CrossRef]
- Liz-Marzán, L.M. Tailoring surface plasmons through the morphology and assembly of metal nanoparticles. Langmuir 2005, 22, 32–41. [Google Scholar] [CrossRef] [PubMed]
- Petryayeva, E.; Krull, U.J. Localized surface plasmon resonance: Nanostructures, bioassays and biosensing—A review. Anal. Chim. Acta 2011, 706, 8–24. [Google Scholar] [CrossRef]
- Kabashin, A.V.; Patskovsky, S.; Grigorenko, A.N. Phase and amplitude sensitivities in surface plasmon resonance bio and chemical sensing. Opt. Express 2009, 17, 21191–21204. [Google Scholar] [CrossRef]
- Piliarik, M.; Vaisocherová, H.; Homola, J. A new surface plasmon resonance sensor for high-throughput screening applications. Biosens. Bioelectron. 2005, 20, 2104–2110. [Google Scholar] [CrossRef]
- Sharma, A.K.; Jha, R.; Gupta, B.D. Fiber-optic sensors based on surface plasmon resonance: A comprehensive review. IEEE Sens. J. 2007, 7, 1118–1129. [Google Scholar] [CrossRef]
- Qu, J.H.; Dillen, A.; Saeys, W.; Lammertyn, J.; Spasic, D. Advancements in SPR biosensing technology: An overview of recent trends in smart layers design, multiplexing concepts, continuous monitoring and in vivo sensing. Anal. Chim. Acta 2020, 1104, 10–27. [Google Scholar] [CrossRef] [PubMed]
- Butt, M.A. Surface plasmon resonance-based biodetection systems: Principles, progress and applications—A comprehensive review. Biosensors 2025, 15, 35. [Google Scholar] [CrossRef]
- Ashrafi, T.M.S.; Mohanty, G. Surface plasmon resonance sensors: A critical review of recent advances, market analysis, and future directions. Plasmonics 2025, 20, 6825–6845. [Google Scholar] [CrossRef]
- Kuzyk, A.; Schreiber, R.; Fan, Z.; Pardatscher, G.; Roller, E.-M.; Högele, A.; Simmel, F.C.; Govorov, O.A.; Liedl, T. DNA-based self-assembly of chiral plasmonic nanostructures with tailored optical response. Nature 2012, 483, 311–314. [Google Scholar] [CrossRef] [PubMed]
- Kurt, H.; Pishva, P.; Pehlivan, Z.S.; Arsoy, E.G.; Saleem, Q.; Bayazıt, M.K.; Yüce, M. Nanoplasmonic biosensors: Theory, structure, design, and review of recent applications. Anal. Chim. Acta 2021, 1185, 338842. [Google Scholar] [CrossRef]
- Heritage, J.P.; Bergman, J.G.; Pinczuk, A.; Worlock, J.M. Surface picosecond Raman gain spectroscopy of a cyanide monolayer on silver. Chem. Phys. Lett. 1979, 67, 229–232. [Google Scholar] [CrossRef]
- Moskovits, M. Surface-enhanced spectroscopy. Rev. Mod. Phys. 1985, 57, 783–826. [Google Scholar] [CrossRef]
- Sen, T.; Haldar, K.K.; Patra, A. Au nanoparticle-based surface energy transfer probe for conformational changes of BSA protein. J. Phys. Chem. C 2008, 112, 17945–17951. [Google Scholar] [CrossRef]
- Moula, G.; Rodriguez-Oliveros, R.; Albella, P.; Sanchez-Gil, J.A.; Aroca, R.F. Plasmonics and single-molecule detection in evaporated silver-island films. Ann. Phys. 2012, 524, 697–704. [Google Scholar] [CrossRef]
- Choi, N.; Schlücker, S. Convergence of surface-enhanced Raman scattering with molecular diagnostics: A perspective on future directions. ACS Nano 2024, 18, 5998–6007. [Google Scholar] [CrossRef]
- Tran, V.A.; Tran, T.T.V.; Doan, V.D.; Vo, G.N.; Tran, V.H.; Jeong, H.; Vo, T.T.T. Advanced nano engineering of surface-enhanced Raman scattering technologies for sensing applications. Appl. Mater. Today 2024, 38, 102217. [Google Scholar] [CrossRef]
- Michałowska, A.; Weyher, J.L.; Kudelski, A. Immobilization of DNA on nanostructured gold and silver substrates via alkanethiolate linkers: The influence of linker length. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2025, 340, 126344. [Google Scholar] [CrossRef] [PubMed]
- Liz-Marzán, L.M.; Willets, K.A.; Chen, X. Fifty years of surface-enhanced spectroscopy. ACS Nano 2024, 18, 5995–5997. [Google Scholar] [CrossRef]
- Święch, D.; Palumbo, G.; Piergies, N.; Kollbek, K.; Marzec, M.; Szkudlarek, A.; Paluszkiewicz, C. Surface modification of Cu nanoparticles coated commercial titanium in the presence of tryptophan: Comprehensive electrochemical and spectroscopic investigations. Appl. Surf. Sci. 2023, 608, 155138. [Google Scholar] [CrossRef]
- Pięta, E.; Paluszkiewicz, C.; Kwiatek, W.M. Multianalytical approach for surface-and tip-enhanced infrared spectroscopy study of a molecule–metal conjugate: Deducing its adsorption geometry. Phys. Chem. Chem. Phys. 2018, 20, 27992–28000. [Google Scholar] [CrossRef]
- McDonagh, C.; Stranik, O.; Nooney, R.; MacCraith, B.D. Nanoparticle strategies for enhancing the sensitivity of fluorescence-based biochips. Nanomedicine 2009, 4, 645–656. [Google Scholar] [CrossRef] [PubMed]
- Bohren, C.F. How can a particle absorb more than the light incident on it? Am. J. Phys. 1983, 51, 323–327. [Google Scholar] [CrossRef]
- Boardman, A.D.; Paranjape, B.V. The optical surface modes of metal spheres. J. Phys. F Met. Phys. 1977, 7, 1935–1945. [Google Scholar] [CrossRef]
- Chaumet, P.C.; Dufour, J.P. Electric potential and field between two different spheres. J. Electrost. 1998, 43, 145–159. [Google Scholar] [CrossRef]
- Lekner, J. Near approach of two conducting spheres: Enhancement of external electric field. J. Electrost. 2011, 69, 559–563. [Google Scholar] [CrossRef]
- Smythe, E.J.; Dickey, M.D.; Bao, J.; Whitesides, G.M.; Capasso, F. Optical antenna arrays on a fiber facet for in situ surface-enhanced Raman scattering detection. Nano Lett. 2009, 9, 1132–1138. [Google Scholar] [CrossRef]
- Sánchez, E.J.; Novotny, L.; Xie, X.S. Near-Field Fluorescence Microscopy Based on Two-Photon Excitation with Metal Tips. Phys. Rev. Lett. 1999, 82, 4014–4017. [Google Scholar] [CrossRef]
- Biagioni, P.; Huang, J.S.; Hecht, B. Nanoantennas for visible and infrared radiation. Rep. Prog. Phys. 2012, 75, 024402. [Google Scholar] [CrossRef]
- Novotny, L. From near-field optics to optical antennas. Phys. Today 2011, 64, 47–52. [Google Scholar] [CrossRef]
- Haes, A.J.; Haynes, C.L.; McFarland, A.D.; Schatz, G.C.; Van Duyne, R.P.; Zou, S. Plasmonic materials for surface-enhanced sensing and spectroscopy. MRS Bull. 2005, 30, 368–375. [Google Scholar] [CrossRef]
- Yao, J.D.; Zheng, Z.Q.; Yang, G.W. Production of large-area 2D materials for high-performance photodetectors by pulsed-laser deposition. Prog. Mater. Sci. 2019, 106, 100573. [Google Scholar] [CrossRef]
- Elbanna, A.; Jiang, H.; Fu, Q.; Zhu, J.F.; Liu, Y.; Zhao, M.; Liu, D.; Lai, S.; Chua, X.W.; Pan, J.; et al. 2D material infrared photonics and plasmonics. ACS Nano 2023, 17, 4134–4179. [Google Scholar] [CrossRef]
- Kumar, R.A.; Rohit, J.V. Surface functionalized MXene as emerging 2D optical sensors for the monitoring of chemical and biological contaminants. FlatChem 2025, 53, 100922. [Google Scholar] [CrossRef]
- Solovan, M.N.; Brus, V.V.; Maistruk, E.V.; Maryanchuk, P.D. Electrical and optical properties of TiN thin films. Inorg. Mater. 2014, 50, 40–45. [Google Scholar] [CrossRef]
- Kinsey, N.; DeVault, C.; Boltasseva, A.; Shalaev, V.M. Near-zero-index materials for photonics. Nat. Rev. Mater. 2019, 4, 742–760. [Google Scholar] [CrossRef]
- Munkhbat, B.; Wróbel, P.; Antosiewicz, T.J.; Shegai, T.O. Optical constants of several multilayer transition metal dichalcogenides measured by spectroscopic ellipsometry in the 300–1700 nm range: High index, anisotropy, and hyperbolicity. ACS Photonics 2022, 9, 2398–2407. [Google Scholar] [CrossRef] [PubMed]
- Darabian, H.R.; Toudert, J.; Bliokh, K.Y.; Pawlak, D.A. Compendium of Natural Epsilon-Near-Zero Materials. ACS Photonics 2025, 12, 3042–3052. [Google Scholar] [CrossRef]
- McMahon, J.M.; Schatz, G.C.; Gray, S.K. Plasmonics in the ultraviolet with the poor metals Al, Ga, In, Sn, Tl, Pb, and Bi. Phys. Chem. Chem. Phys. 2013, 15, 5415–5423. [Google Scholar] [CrossRef]
- Gutiérrez, Y.; Alcaraz de la Osa, R.; Ortiz, D.; Saiz, J.M.; González, F.; Moreno, F. Plasmonics in the ultraviolet with aluminum, gallium, magnesium and rhodium. Appl. Sci. 2018, 8, 64. [Google Scholar] [CrossRef]
- Blaber, M.G.; Arnold, M.D.; Ford, M.J. A review of the optical properties of alloys and intermetallics for plasmonics. J. Phys. Condens. Matter 2010, 22, 143201. [Google Scholar] [CrossRef]
- Ross, M.B.; Schatz, G.C. Aluminum and indium plasmonic nanoantennas in the ultraviolet. J. Phys. Chem. C 2014, 118, 12506–12514. [Google Scholar] [CrossRef]
- Guzman, M.V.F.; King, M.E.; Mason, N.L.; Sullivan, C.S.; Jeong, S.; Ross, M.B. Plasmon manipulation by post-transition metal alloying. Matter 2023, 6, 838–854. [Google Scholar] [CrossRef]
- Todorov, R.; Hristova-Vasileva, T.; Katrova, V.; Atanasova, A. Silver and gold containing compounds of p-block elements as perspective materials for UV plasmonics. ACS Omega 2023, 8, 14321–14341. [Google Scholar] [CrossRef]
- Lei, D.; Su, D.; Maier, S.A. New insights into plasmonic hot-electron dynamics. Light Sci. Appl. 2024, 13, 243. [Google Scholar] [CrossRef]
- Sun, M.; Wang, A.; Zhang, M.; Zou, S.; Wang, H. Interband and intraband hot carrier-driven photocatalysis on plasmonic bimetallic nanoparticles: A case study of Au–Cu alloy nanoparticles. ACS Nanosci. Au 2024, 4, 360–373. [Google Scholar] [CrossRef]
- Lin, W.; Cao, E.; Zhang, L.; Xu, X.; Song, Y.; Liang, W.; Sun, M. Electrically enhanced hot hole driven oxidation catalysis at the interface of a plasmon–exciton hybrid. Nanoscale 2018, 10, 5482–5488. [Google Scholar] [CrossRef]
- Cong, S.; Liu, X.; Jiang, Y.; Zhang, W.; Zhao, Z. Surface enhanced Raman scattering revealed by interfacial charge-transfer transitions. Innovation 2020, 1, 100051. [Google Scholar] [CrossRef]
- Todorov, R.; Hristova-Vasileva, T. Simplified Biochemical Analysis Using p-Block Metals and Their Compounds with Silver- Surface Enhancement from the Point of View of Electronic Structure. ACS Omega 2025, 10, 19243–19255. [Google Scholar] [CrossRef] [PubMed]
- Zayats, A.V.; Smolyaninov, I.I.; Maradudin, A.A. Nano-optics of surface plasmon polaritons. Phys. Rep. 2005, 408, 131–314. [Google Scholar] [CrossRef]
- Simmons, J.H.; Potter, K.S. Optical Materials; Academic Press: Cambridge, MA, USA, 2000; pp. 57–80. [Google Scholar] [CrossRef]
- Pena-Rodríguez, O. Modelling the dielectric function of Au-Ag alloys. J. Alloys Compd. 2017, 694, 857–863. [Google Scholar] [CrossRef]
- Chaib, A.B.; Zouini, M.; Tahiri, A. Drude-Lorentz oscillators’ effect on the optical response of a vanadium dioxide semiconductor. Opt. Mater. 2022, 133, 112895. [Google Scholar] [CrossRef]
- Driouach, A.; Samad, B.A.; Ashrit, P.V. Electron transport properties and free electron density evolution during the phase change in VO2 thin films. Mater. Res. Bull. 2023, 165, 112325. [Google Scholar] [CrossRef]
- Toudert, J.; Serna, R. Ultraviolet-visible interband plasmonics with p-block elements. Opt. Mater. Express 2016, 6, 2434–2447. [Google Scholar] [CrossRef]
- Jaffray, W.; Saha, S.; Shalaev, V.M.; Boltasseva, A.; Ferrera, M. Transparent conducting oxides: From all-dielectric plasmonics to a new paradigm in integrated photonics. Adv. Opt. Photonics 2022, 14, 148–208. [Google Scholar] [CrossRef]
- Bohórquez, C.; Bakkali, H.; Delgado, J.J.; Blanco, E.; Herrera, M.; Domínguez, M. Spectroscopic ellipsometry study on tuning the electrical and optical properties of Zr-doped ZnO thin films grown by atomic layer deposition. ACS Appl. Electron. Mater. 2022, 4, 925–935. [Google Scholar] [CrossRef] [PubMed]
- Ushanov, V.I.; Eremeev, S.V.; Silkin, V.M.; Chaldyshev, V.V. Plasmon Resonance in a System of Bi Nanoparticles Embedded into (Al, Ga) As Matrix. Nanomaterials 2024, 14, 109. [Google Scholar] [CrossRef]
- Bhardwaj, A.; Verma, S.S. Theoretical study on plasmonic applications of Gallium alloy (GaX, X= Ag, Al, Hg and In) nanospheres and nanoshells. J. Quant. Spectrosc. Radiat. Transf. 2022, 281, 108109. [Google Scholar] [CrossRef]
- Bhatia, P.; Verma, S.S. Enhancement of LSPR properties of temperature-dependent gold nanoparticles. Mater. Today Proc. 2023, 78, 871–876. [Google Scholar] [CrossRef]
- Sørensen, L.K.; Khrennikov, D.E.; Gerasimov, V.S.; Ershov, A.E.; Vysotin, M.A.; Monti, S.; Zakomirnyi, V.I.; Polyutov, S.P.; Ågren, H.; Karpov, S.V. Thermal degradation of optical resonances in plasmonic nanoparticles. Nanoscale 2022, 14, 433–447. [Google Scholar] [CrossRef]
- Manchon, D.; Lermé, J.; Zhang, T.; Mosset, A.; Jamois, C.; Bonnet, C.; Rye, J.M.; Belarouci, A.; Broyer, M.; Pellarin, M.; et al. Plasmonic coupling with most of the transition metals: A new family of broad interband and near infrared nanoantennas. Nanoscale 2015, 7, 1181–1192. [Google Scholar] [CrossRef]
- Marquez-Ibarra, C.A.; Engel, N.; Montes-Bojorquez, J.R.; Hernandez-Robles, A.; Mayer, K.M. Thick-Shelled Magnetite-Gold Core–Shell Nanoparticles: Oleic Acid-Mediated Overcoating for Extended Optical Tunability. J. Phys. Chem. C 2025, 129, 5980–5989. [Google Scholar] [CrossRef]
- Romero-Quitl, D.O.; Krishnan, S.K.; Palomino-Ovando, M.A.; Hernández-Cristobal, O.; Torres-Guzmán, J.C.; Lugo, J.E.; Toledo-Solano, M. Optical Response Tailoring via Morphosynthesis of Ag@Au Nanoparticles. Nanomaterials 2025, 15, 1125. [Google Scholar] [CrossRef]
- Eghbali, A.; Pak, N.V.; Arsenin, A.V.; Volkov, V.; Vyshnevyy, A.A. Photothermal Performance of 2D Material-Based Nanoparticles for Biomedical Applications. Nanomaterials 2025, 15, 942. [Google Scholar] [CrossRef]
- Skriver, H.L. The LMTO Method: Muffin-Tin Orbitals and Electronic Structure; Springer Science & Business Media: New York, NY, USA, 1984. [Google Scholar] [CrossRef]
- Takeuchi, N.; Chan, C.T.; Ho, K.M. First-principles calculations of equilibrium ground-state properties of Au and Ag. Phys. Rev. B 1989, 40, 1565–1570. [Google Scholar] [CrossRef][Green Version]
- Maksimov, E.G.; Mazin, I.I.; Rashkeev, S.N.; Uspenski, Y.A. First-principles calculations of the optical properties of metals. J. Phys. F Met. Phys. 1988, 18, 833. [Google Scholar] [CrossRef]
- Holmberg, N.; Laasonen, K.; Peljo, P. Charge distribution and Fermi level in bimetallic nanoparticles. Phys. Chem. Chem. Phys. 2016, 18, 2924–2931. [Google Scholar] [CrossRef]
- Prandini, G.; Rignanese, G.M.; Marzari, N. Photorealistic modelling of metals from first principles. npj Comput. Mater. 2019, 5, 129. [Google Scholar] [CrossRef]
- Evecen, M.; Ciftci, Y.O. Theoretical investigation of the electronic structure, elastic, dynamic properties of intermetallic compound NiBe under pressure. Eur. Phys. J. B 2021, 94, 19. [Google Scholar] [CrossRef]
- Tesch, R.; Kowalski, P.M. Hubbard U parameters for transition metals from first principles. Phys. Rev. B 2022, 105, 195153. [Google Scholar] [CrossRef]
- Chaudhary, M.; Weissker, H.C. Optical spectra of silver clusters and nanoparticles from 4 to 923 atoms from the TDDFT+ U method. Nat. Commun. 2024, 15, 9225. [Google Scholar] [CrossRef]
- Bajaj, A.; Kulik, H.J. Molecular DFT+ U: A transferable, low-cost approach to eliminate delocalization error. J. Phys. Chem. Lett. 2021, 12, 3633–3640. [Google Scholar] [CrossRef]
- Coviello, V.; Badocco, D.; Pastore, P.; Fracchia, M.; Ghigna, P.; Martucci, A.; Amendola, V.; Forrer, D. Accurate prediction of the optical properties of nanoalloys with both plasmonic and magnetic elements. Nat. Commun. 2024, 15, 834. [Google Scholar]
- Yi, Z.; Li, X.; Xu, X.; Chen, X.; Ye, X.; Yi, Y.; Duan, T.; Tang, Y.; Liu, J.; Yi, Y. Nanostrip-induced high tunability multipolar fano resonances in a Au ring-strip nanosystem. Nanomaterials 2018, 8, 568. [Google Scholar] [CrossRef]
- Amendola, V.; Bakr, O.M.; Stellacci, F. A study of the surface plasmon resonance of silver nanoparticles by the discrete dipole approximation method: Effect of shape, size, structure, and assembly. Plasmonics 2010, 5, 85–97. [Google Scholar] [CrossRef]
- Zhao, N.; Shi, P.; Wang, Z.; Sun, Z.; Sun, K.; Ye, C.; Fu, L.; Lin, C.T. Advances in surface-enhanced raman spectroscopy for urinary metabolite analysis: Exploiting noble metal nanohybrids. Biosensors 2024, 14, 564. [Google Scholar] [CrossRef] [PubMed]
- Wan, M.J.; Wu, Y.T.; Wang, Y.H.; Wu, X.H.; You, E.M.; Wang, A.; Liu, S.H.; Chen, J.C.; Zhang, Y.J.; Jin, S.; et al. Engineered Plasmonic multi-hot spots on magnetic Nanospheres for quantitative detection of pesticide residues on food surfaces via SERS tagging analysis. Food Chem. 2025, 492, 145529. [Google Scholar] [CrossRef] [PubMed]
- Negrín-Montecelo, Y.; Elsaidy, A.; Giráldez-Martínez, J.; Carbó-Argibay, E.; Wang, Z.; Govorov, A.O.; Alvarez-Puebla, R.A.; Correa-Duarte, M.A.; Besteiro, L.V. Unveiling multimodal hot carrier excitation in plasmonic bimetallic Au@ Ag nanostars for photochemistry and SERS sensing. Nano Res. 2024, 17, 10355–10362. [Google Scholar] [CrossRef]
- Guan, J.; Wu, S.; Li, L.; Wang, X.; Ji, W.; Ozaki, Y. New insights of charge transfer at metal/semiconductor interfaces for hot-electron generation studied by surface-enhanced Raman spectroscopy. J. Phys. Chem. Lett. 2022, 13, 3571–3578. [Google Scholar] [CrossRef]
- AbdElFatah, T.; Jalali, M.; Yedire, S.G.; Hosseini, I.I.; del Real Mata, C.; Khan, H.; Hamidi, S.V.; Jeanne, O.; Siavash Moakhar, R.; McLean, M.; et al. Nanoplasmonic amplification in microfluidics enables accelerated colorimetric quantification of nucleic acid biomarkers from pathogens. Nat. Nanotechnol. 2023, 18, 922–932. [Google Scholar] [CrossRef]
- Bailey, R.L. Electromagnetic Wave Energy Converter. U.S. Patent No. 3,760,257, 18 September 1973. Available online: https://patents.google.com/patent/US3760257A/en (accessed on 7 September 2025).
- Marks, A.M. Device for Conversion of Light Power to Electrical Power. U.S. Patent 4,445,050A, 24 April 1984. Available online: https://patents.google.com/patent/US4445050A/en (accessed on 7 September 2025).
- Lin, G.H.; He, M.Z.; Kapur, M.; Bockris, J.O.M. Electric Power Research Institute Inc, Amorphous silicon-based photovoltaic semiconductor materials free from Staebler-Wronski effects. U.S. Patent 5,242,505A, 7 September 1993. Available online: https://patents.google.com/patent/US5242505A/en (accessed on 7 September 2025).
- Huber, A.J.; Deutsch, B.; Novotny, L.; Hillenbrand, R. Focusing of surface phonon polaritons. Appl. Phys. Lett. 2008, 92, 203104. [Google Scholar] [CrossRef]
- Höppener, C.; Lapin, Z.J.; Bharadwaj, P.; Novotny, L. Self-similar gold-nanoparticle antennas for a cascaded enhancement of the optical field. Phys. Rev. Lett. 2012, 109, 017402. [Google Scholar] [CrossRef]
- Braun, K.; Laible, F.; Hauler, O.; Wang, X.; Pan, A.; Fleischer, M.; Meixner, A.J. Active optical antennas driven by inelastic electron tunneling. Nanophotonics 2018, 7, 1503–1516. [Google Scholar] [CrossRef]
- Höppener, C.; Novotny, L. Antenna-based optical imaging of single Ca2+ transmembrane proteins in liquids. Nano Lett. 2008, 8, 642–646. [Google Scholar] [CrossRef]
- Höppener, C.; Novotny, L. Imaging of membrane proteins using antenna-based optical microscopy. Nanotechnology 2008, 19, 384012. [Google Scholar] [CrossRef]
- Hecht, B.; Pohl, D.W.; Heinzelmann, H.; Novotny, L. “Tunnel” near-field optical microscopy: TNOM-2. Ultramicroscopy 1995, 61, 99–104. [Google Scholar] [CrossRef]
- Harutyunyan, H.; Volpe, G.; Quidant, R.; Novotny, L. Enhancing the nonlinear optical response using multifrequency gold-nanowire antennas. Phys. Rev. Lett. 2012, 108, 217403. [Google Scholar] [CrossRef] [PubMed]
- Qarony, W.; Hossain, M.I.; Tamang, A.; Jovanov, V.; Shahiduzzaman, M.; Ahamed, M.S.; Pala, R.A.; Salleo, A.; Tsang, Y.H.; Knipp, D. On the potential of optical nanoantennas for visibly transparent solar cells. ACS Photonics 2023, 10, 4205–4214. [Google Scholar] [CrossRef]
- Fukai, R.; Sakai, Y.; Fujita, T.; Kiyama, H.; Ludwig, A.; Wieck, A.D.; Oiwa, A. Detection of photogenerated single electrons in a lateral quantum dot with a surface plasmon antenna. Appl. Phys. Express 2021, 14, 125001. [Google Scholar] [CrossRef]
- Barreda, A.; Hell, S.; Weissflog, M.A.; Minovich, A.; Pertsch, T.; Staude, I. Metal, dielectric and hybrid nanoantennas for enhancing the emission of single quantum dots: A comparative study. J. Quant. Spectrosc. Radiat. Transf. 2021, 276, 107900. [Google Scholar] [CrossRef]
- Polimeno, P.; Magazzu, A.; Iati, M.A.; Patti, F.; Saija, R.; Boschi, C.D.E.; Donato, M.G.; Gucciardi, P.G.; Jones, P.H.; Volpe, G.; et al. Optical tweezers and their applications. J. Quant. Spectrosc. Radiat. Transf. 2018, 218, 131–150. [Google Scholar] [CrossRef]
- Novotny, L.; Bian, R.X.; Xie, X.S. Theory of nanometric optical tweezers. Phys. Rev. Lett. 1997, 79, 645. [Google Scholar] [CrossRef]
- Vedam, K. Spectroscopic ellipsometry: A historical overview. Thin Solid Film. 1998, 313, 1–9. [Google Scholar] [CrossRef]
- Drude, P. Beobachtungen über die Reflexion des Lichtes am Antimonglanz. Ann. Phys. 1888, 270, 489–531. [Google Scholar] [CrossRef]
- Aspnes, D.E. Spectroscopic ellipsometry of solids. In Optical Properties of Solids: New Developments; Elsevier: New York, NY, USA, 1976; pp. 815–831. ISBN 9780720403633. [Google Scholar]
- Chang, K.Y.; Huang, L.C.; Asaga, K.; Tsai, M.S.; Rego, L.; Huang, P.C.; Mashiko, H.; Oguri, K.; Hernandez-Garcia, C.; Chen, M.C. High-order nonlinear dipole response characterized by extreme ultraviolet ellipsometry. Optica 2021, 8, 484–492. [Google Scholar] [CrossRef]
- Stanislavchuk, T.N.; Kang, T.D.; Rogers, P.D.; Standard, E.C.; Basistyy, R.; Kotelyanskii, A.M.; Nita, G.; Zhou, T.; Carr, G.L.; Kotelyanskii, M.; et al. Synchrotron radiation-based far-infrared spectroscopic ellipsometer with full Mueller-matrix capability. Rev. Sci. Instrum. 2013, 84, 023901. [Google Scholar] [CrossRef]
- Kim, S.; Kim, Y.; Kang, M.A.; Sohn, J.M.; No, K. Optical properties of a-Si films for 157-nm lithography. In Photomask and Next-Generation Lithography Mask Technology X, Proceedings of SPIE, Yokohama, Japan, 16–18 April 2003; Society of Photo-Optical Instrumentation Engineers (SPIE): Bellingham, WA, USA, 2003; Volume 5130, pp. 127–135. [Google Scholar] [CrossRef]
- Fabijanić, I.; Janicki, V.; Ferré-Borrull, J.; Bubaš, M.; Blažek Bregović, V.; Marsal, L.F.; Sancho-Parramon, J. Plasmonic nanoparticles and island films for solar energy harvesting: A comparative study of Cu, Al, Ag and Au performance. Coatings 2019, 9, 382. [Google Scholar] [CrossRef]
- Mendoza-Luna, L.G.; Guarin, C.A.; de la Vega, E.C.; Sánchez, F.N.N.; Haro-Poniatowski, E.; Hernández-Pozos, J.L. Experimental and computational investigation on the surface plasmon resonance of copper thin-films produced via pulsed laser deposition. Results Opt. 2025, 19, 100803. [Google Scholar] [CrossRef]
- Lyu, P.; Matusalem, F.; Deniz, E.; Rocha, A.R.; Leite, M.S. In Situ Solid-State Dewetting of Ag–Au–Pd Alloy: From Macro-to Nanoscale. ACS Appl. Mater. Interfaces 2024, 16, 62860–62870. [Google Scholar] [CrossRef] [PubMed]
- Todorov, R.; Hristova-Vasileva, T.; Atanasova, A.; Katrova, V. Thin Ag/Bi coatings as epsilon-near-zero material with low optical losses. Opt. Mater. 2022, 124, 112040. [Google Scholar] [CrossRef]
- Yakubovsky, D.I.; Arsenin, A.V.; Stebunov, Y.V.; Fedyanin, D.Y.; Volkov, V.S. Optical constants and structural properties of thin gold films. Opt. Express 2017, 25, 25574–25587. [Google Scholar] [CrossRef] [PubMed]
- Guo, W.P.; Mishra, R.; Cheng, C.W.; Wu, B.H.; Chen, L.J.; Lin, M.T.; Gwo, S. Titanium nitride epitaxial films as a plasmonic material platform: Alternative to gold. ACS Photonics 2019, 6, 1848–1854. [Google Scholar] [CrossRef]
- Buzavaite-Verteliene, E.; Valavicius, A.; Grineviciute, L.; Tolenis, T.; Lukose, R.; Niaura, G.; Balevicius, Z. Influence of the graphene layer on the strong coupling in the hybrid Tamm-plasmon polariton mode. Opt. Express 2020, 28, 10308–10319. [Google Scholar] [CrossRef]
- Halim, J.; Persson, I.; Moon, E.J.; Kühne, P.; Darakchieva, V.; Persson, P.O.Å.; Eklund, P.; Rosen, J.; Barsoum, M.W. Electronic and optical characterization of 2D Ti2C and Nb2C (MXene) thin films. J. Phys. Condens. Matter 2019, 31, 165301. [Google Scholar] [CrossRef] [PubMed]
- Simon, J.; Choi, K.R.; Ippolito, S.; Prokopeva, L.; Fruhling, C.; Shalaev, V.M.; Kildishev, A.V.; Gogotsi, Y.; Boltasseva, A. Tailoring optical response of MXene thin films. Nanophotonics 2025, in press. [Google Scholar] [CrossRef]
- Mukherjee, D.; Burger, S.; Siefke, T.; Gour, J.; Bodermann, B.; Petrik, P. Spectroscopic Ellipsometry of Plasmonic Gratings─ Ideal Parameters for Sensing and Subpicometer Measurement Uncertainty. ACS Omega 2025, 10, 14466–14473. [Google Scholar] [CrossRef]
- Verre, R.; Modreanu, M.; Ualibek, O.; Fox, D.; Fleischer, K.; Smith, C.; Zhang, H.; Pemble, M.; McGilp, J.F.; Shvets, I.V. General approach to the analysis of plasmonic structures using spectroscopic ellipsometry. Phys. Rev. B 2013, 87, 235428. [Google Scholar] [CrossRef]
- Todorov, R.; Lozanova, V.; Knotek, P.; Černošková, E.; Vlček, M. Microstructure and ellipsometric modelling of the optical properties of very thin silver films for application in plasmonics. Thin Solid Films 2017, 628, 22–30. [Google Scholar] [CrossRef]
- Todorov, R.; Atanasova, A.; Katrova, V.; Hristova-Vasileva, T. Surface plasmon-like properties of one-dimensional photonic crystal and its application in surface-enhanced fluorescence. J. Phys. Conf. Ser. 2023, 2436, 012021. [Google Scholar] [CrossRef]
- Garahan, A.; Pilon, L.; Yin, J.; Saxena, I. Effective optical properties of absorbing nanoporous and nanocomposite thin films. J. Appl. Phys. 2007, 101, 014320. [Google Scholar] [CrossRef]
- Drachev, V.P.; Chettiar, U.K.; Kildishev, A.V.; Yuan, H.K.; Cai, W.; Shalaev, V.M. The Ag dielectric function in plasmonic metamaterials. Opt. Express 2008, 16, 1186–1195. [Google Scholar] [CrossRef]
- Mendoza Herrera, L.J.; Arboleda, D.M.; Schinca, D.C.; Scaffardi, L.B. Determination of plasma frequency, damping constant, and size distribution from the complex dielectric function of noble metal nanoparticles. J. Appl. Phys. 2014, 116, 233105. [Google Scholar] [CrossRef]
- Lozanova, V.; Tasseva, J.; Todorov, R. Grain size effect on the optical properties of thin silver films. Bulg. Chem. Commun. 2013, 45, 43–46. [Google Scholar]
- Bortchagovsky, E.; Dai, F.; Tang, J.; Kenaz, R.; Milekhin, I.; Demydenko, Y.; Bogoslovska, A.; Adam, P.M.; Rapaport, R.; Fleischer, M.; et al. Ordered arrays of metal nanostructures on insulator/metal film: Dependence of plasmonic properties on lattice orientation. Nano Express 2025, 6, 025011. [Google Scholar] [CrossRef]
- Poursharif, A.; Sahebsara, P.; Monirvaghefi, S.M.; Hamidi, S.M.; Kharaziha, M.; Bagheri, M. Magneto-plasmonic response of nickel nano-rings prepared by electroless method. Sens. Actuators A Phys. 2025, 383, 116261. [Google Scholar] [CrossRef]
- Kapetanovic, V.; Bicket, I.C.; Lazar, S.; Lagos, M.J.; Botton, G.A. Tunable Infrared Plasmon Response of Lithographic Sn-doped Indium Oxide Nanostructures. Adv. Opt. Mater. 2020, 8, 2001024. [Google Scholar] [CrossRef]
- Gkogkou, D.; Schreiber, B.; Shaykhutdinov, T.; Ly, H.K.; Kuhlmann, U.; Gernert, U.; Facsko, S.; Hildebrandt, P.; Esser, N.; Hinrichs, K.; et al. Polarization-and wavelength-dependent surface-enhanced Raman spectroscopy using optically anisotropic rippled substrates for sensing. ACS Sens. 2016, 1, 318–323. [Google Scholar] [CrossRef]
- Mukherjee, D.; Petrik, P. Real-time ellipsometry at high and low temperatures. ACS Omega 2023, 8, 3684–3697. [Google Scholar] [CrossRef]
- Chen, X.; Gu, H.; Liu, J.; Chen, C.; Liu, S. Advanced Mueller matrix ellipsometry: Instrumentation and emerging applications. Sci. China Technol. Sci. 2022, 65, 2007–2030. [Google Scholar] [CrossRef]
- Kwon, S.; Ma, P.J.; Lum, C.; Hajarian, A.; Seo, J.; Nam, S. Nano-optical metrologies for characterizing the carrier dynamics in two-dimensional materials. Mater. Res. Bull. 2025, 187, 113382. [Google Scholar] [CrossRef]
- Sehmi, H.S.; Langbein, W.; Muljarov, E.A. Optimizing the Drude-Lorentz model for material permittivity: Method, program, and examples for gold, silver, and copper. Phys. Rev. B 2017, 95, 115444. [Google Scholar] [CrossRef]
- Todorov, R.; Hristova-Vasileva, T.; Katrova, V.; Atanasova, A.; Milushev, G. Electronic structure and plasmonic activity in co-evaporated Ag-In bimetallic alloys. J. Alloys Compd. 2022, 897, 163253. [Google Scholar] [CrossRef]
- Cuenca, J.M.; Triviño-Sánchez, S.; Barcina, J.O.; Peña-Rodríguez, O.; Guerrero-Martínez, A.; González-Rubio, G.; Pal, U. Resilience of Fano Resonances in Gold–Silver Nanostructures under Laser-Induced Morphological Transformations. J. Phys. Chem. C 2025, 129, 4530–4537. [Google Scholar] [CrossRef]
- Rioux, D.; Vallières, S.; Besner, S.; Muñoz, P.; Mazur, E.; Meunier, M. An analytic model for the dielectric function of Au, Ag, and their alloys. Adv. Opt. Mater. 2014, 2, 176–182. [Google Scholar] [CrossRef]
- Kim, K.J.; Chen, L.Y.; Lynch, D.W. Ellipsometric study of optical transitions in Ag1−xInx alloys. Phys. Rev. B 1988, 38, 13107–13112. [Google Scholar] [CrossRef]
- Kalas, B.; Sáfrán, G.; Serényi, M.; Fried, M.; Petrik, P. Scanning-resonance optical sensing based on a laterally graded plasmonic layer—Optical properties of AgxAl1−x in the range of x = 0 to 1. Appl. Surf. Sci. 2022, 606, 154770. [Google Scholar] [CrossRef]
- Powell, C.J.; Swan, J.B. Origin of the characteristic electron energy losses in aluminum. Phys. Rev. 1959, 115, 869. [Google Scholar] [CrossRef]
- Powell, C.J. The Origin of the Characteristic Electron Energy Losses in Ten Elements. Proc. Phys. Soc. 1960, 76, 593–610. [Google Scholar] [CrossRef]
- Leng, D.; Wang, T.; Li, Y.; Huang, Z.; Wang, H.; Wan, Y.; Pei, X.; Wang, J. Plasmonic bismuth nanoparticles: Thiolate pyrolysis synthesis, size-dependent LSPR property, and their oxidation behavior. Inorg. Chem. 2021, 60, 17258–17267. [Google Scholar] [CrossRef]
- Tanaka, H.; Shinotsuka, H.; Yoshikawa, H.; Tanuma, S. Determination of Energy Loss Functions for GaN, GaP, and GaSb by Angle-resolved Electron Energy Loss Spectroscopy with Factor Analysis: Applications to Electron Transport Parameter Calculations. e-J. Surf. Sci. Nanotechnol. 2025, 23, 143–159. [Google Scholar] [CrossRef]
- Shin, S.Y.; Kim, N.D.; Kim, J.G.; Kim, K.S.; Noh, D.Y.; Kim, K.S.; Chung, J.W. Control of the π plasmon in a single layer graphene by charge doping. Appl. Phys. Lett. 2011, 99, 082110. [Google Scholar] [CrossRef]
- Schaffer, B.; Hohenester, U.; Trügler, A.; Hofer, F. High-resolution surface plasmon imaging of gold nanoparticles by energy-filtered transmission electron microscopy. Phys. Rev. B 2009, 79, 041401. [Google Scholar] [CrossRef]
- Cherqui, C.; Thakkar, N.; Li, G.; Camden, J.P.; Masiello, D.J. Characterizing localized surface plasmons using electron energy-loss spectroscopy. Annu. Rev. Phys. Chem. 2016, 67, 331–357. [Google Scholar] [CrossRef]
- Koh, A.L.; McComb, D.W.; Maier, S.A.; Low, H.Y.; Yang, J.K. Sub-10 nm patterning of gold nanostructures on silicon-nitride membranes for plasmon mapping with electron energy-loss spectroscopy. J. Vac. Sci. Technol. B 2010, 28, C6O45–C6O49. [Google Scholar] [CrossRef]
- Minnai, C.; Vanzan, A.; Reidy, L.C.; LaGrow, A.P.; Di Vece, M. Visible Light Silver Nanoantenna on UV Responding Tin Nanoparticles. Adv. Opt. Mater. 2025, 13, 2403432. [Google Scholar] [CrossRef]
- Babicheva, V.E. Optical processes behind plasmonic applications. Nanomaterials 2023, 13, 1270. [Google Scholar] [CrossRef]
- Mkhitaryan, V.; March, K.; Tseng, E.N.; Li, X.; Scarabelli, L.; Liz-Marzán, L.M.; Chen, S.Y.; Tizei, L.H.; Stéphan, O.; Song, J.M.; et al. Can copper nanostructures sustain high-quality plasmons? Nano Lett. 2021, 21, 2444–2452. [Google Scholar] [CrossRef]
- Zanfrognini, M.; Rotunno, E.; Frabboni, S.; Sit, A.; Karimi, E.; Hohenester, U.; Grillo, V. Orbital angular momentum and energy loss characterization of plasmonic excitations in metallic nanostructures in TEM. ACS Photonics 2019, 6, 620–627. [Google Scholar] [CrossRef]
- Chu, M.W.; Sharma, P.; Chang, C.P.; Liou, S.C.; Tsai, K.T.; Wang, J.K.; Wang, Y.L.; Chen, C.H. Probing surface plasmons in individual Ag nanoparticles in the ultra-violet spectral regime. Nanotechnology 2009, 20, 235705. [Google Scholar] [CrossRef][Green Version]
- Scholl, J.A.; García-Etxarri, A.; Koh, A.L.; Dionne, J.A. Observation of quantum tunneling between two plasmonic nanoparticles. Nano Lett. 2013, 13, 564–569. [Google Scholar] [CrossRef] [PubMed]
- Kadkhodazadeh, S.; Nugroho, F.A.A.; Langhammer, C.; Beleggia, M.; Wagner, J.B. Optical property–composition correlation in noble metal alloy nanoparticles studied with EELS. ACS Photonics 2019, 6, 779–786. [Google Scholar] [CrossRef]
- Rodríguez Echarri, A.; Skjølstrup, E.J.H.; Pedersen, T.G.; García de Abajo, F.J. Theory of electron energy-loss spectroscopy in atomically thin metallic films. Phys. Rev. Res. 2020, 2, 023096. [Google Scholar] [CrossRef]
- Nicoletti, O.; de La Peña, F.; Leary, R.K.; Holland, D.J.; Ducati, C.; Midgley, P.A. Three-dimensional imaging of localized surface plasmon resonances of metal nanoparticles. Nature 2013, 502, 80–84. [Google Scholar] [CrossRef]
- Rosei, R.; Colavita, E.; Modesti, S.; Nisticò, N. Electronic structure of dilute α-phase Ag-Cd alloys from thermoreflectance and XPS measurements. Phys. Status Solidi B 1978, 85, 445–452. [Google Scholar] [CrossRef]
- Norrman, S.; Andersson, T.; Granqvist, C.G.; Hunderi, O. Optical properties of discontinuous gold films. Phys. Rev. B 1978, 18, 674–695. [Google Scholar] [CrossRef]
- Hruška, P.; Jakubik, M.; More-Chevalier, J.; Volfová, L.; Novotný, M. In situ optical monitoring and effect of initial film temperature on pulsed laser-induced dewetting of ultrathin Ag films. J. Appl. Phys. 2025, 138, 055305. [Google Scholar] [CrossRef]
- Todorov, R.; Tasseva, J.; Babeva, T.; Petkov, K. Multilayer As2Se3/GeS2 quarter wave structures for photonic applications. J. Phys. D Appl. Phys. 2010, 43, 505103. [Google Scholar] [CrossRef]
- Heinzelmann, H.; Huser, T.R.; Lacoste, T.D.; Guentherodt, H.J.; Pohl, D.W.; Hecht, B.; Novotny, L.; Martin, O.J.; Hafner, C.; Baggenstos, H.; et al. Scanning near-field optical microscopy in Basel, Ruschlikon, and Zurich. Opt. Eng. 1995, 34, 2441–2454. [Google Scholar] [CrossRef][Green Version]
- Novotny, L. Chapter 5 The history of near-field optics. In Progress in Optics; Wolf, E., Ed.; Elsevier: Amsterdam, The Netherlands, 2007; Volume 50, pp. 137–184. [Google Scholar] [CrossRef]
- Hecht, B.; Bielefeldt, H.; Novotny, L.; Inouye, Y.; Pohl, D.W. Local excitation, scattering, and interference of surface plasmons. Phys. Rev. Lett. 1996, 77, 1889–1892. [Google Scholar] [CrossRef]
- Minn, K.; Birmingham, B.; Zhang, Z. New development of nanoscale spectroscopy using scanning probe microscope. J. Vac. Sci. Technol. A 2020, 38, 030801. [Google Scholar] [CrossRef]
- Song, M.; Fumagalli, P.; Schmid, M. Scanning near-field optical microscopy measurements and simulations of regularly arranged silver nanoparticles. Nanotechnology 2023, 35, 065702. [Google Scholar] [CrossRef]
- An, X.; Lang, P.; Shi, X.; Ji, B.; Lin, F.; Lin, Y.; Xu, Y.; Song, X.; Lin, J. Modulation of the type and excitation region of plasmonic topological quasiparticles in a metasurface by tailoring the excitation light. Nanophotonics 2025, in press. [Google Scholar] [CrossRef]
- Fischer, H.; Nesci, A.; Leveque, G.; Martin, O.J.F. Characterization of the polarization sensitivity anisotropy of a near-field probe using phase measurements. J. Microsc. 2008, 230, 27–31. [Google Scholar] [CrossRef] [PubMed]
- Martin, O.J.F.; Paulus, M. Influence of metal roughness on the near-field generated by an aperture/apertureless probe. J. Microsc. 2002, 205, 147–152. [Google Scholar] [CrossRef][Green Version]
- Shiotari, A.; Nishida, J.; Hammud, A.; Schulz, F.; Wolf, M.; Kumagai, T.; Müller, M. Scattering near-field optical microscopy at 1-nm resolution using ultralow tip oscillation amplitudes. Sci. Adv. 2025, 11, eadu1415. [Google Scholar] [CrossRef] [PubMed]
- Pechou, R.; Alves, E.; Coratger, R.; Mlayah, A. Light emission from a hybrid plasmonic-excitonic STM tunneling junction. Opt. Express 2025, 33, 32429–32442. [Google Scholar] [CrossRef] [PubMed]
- Péchou, R.; Jia, S.; Rigor, J.; Guillermet, O.; Seine, G.; Lou, J.; Large, N.; Mlayah, A.; Coratger, R. Plasmonic-induced luminescence of MoSe2 monolayers in a scanning tunneling microscope. ACS Photonics 2020, 7, 3061–3070. [Google Scholar] [CrossRef]
- Xi, M.; Reinhard, B.M. Evolution of near-and far-field optical properties of Au bipyramids upon epitaxial deposition of Ag. Nanoscale 2020, 12, 5402–5411. [Google Scholar] [CrossRef]
- Dallapiccola, R.; Gopinath, A.; Stellacci, F.; Dal Negro, L. Quasi-periodic distribution of plasmon modes in two-dimensional Fibonacci arrays of metal nanoparticles. Opt. Express 2008, 16, 5544–5555. [Google Scholar] [CrossRef] [PubMed]
- Camus, É.; Pellarin, M.; Blanchard, N.; Boisron, O.; Hillenkamp, M.; Roiban, L.; Andreazza, P.; Cottancin, E. Structural and optical characterization of nanoalloys mixing gold or silver with aluminium or indium: Evolution under various reactive environments. Faraday Discuss. 2023, 242, 478–498. [Google Scholar] [CrossRef]
- Jo, J.; Ryu, J.; Huh, J.H.; Kim, H.; Seo, D.H.; Lee, J.; Kwon, M.; Lee, S.; Nam, K.T.; Kim, M. Direct three-dimensional observation of the plasmonic near-fields of a nanoparticle with circular dichroism. ACS Nano 2024, 18, 32769–32780. [Google Scholar] [CrossRef]
- Guo, X.; He, X.; Degnan, Z.; Chiu, C.C.; Donose, B.C.; Bertling, K.; Fedorov, A.; Rakić, A.D.; Jacobson, P. Terahertz nanospectroscopy of plasmon polaritons for the evaluation of doping in quantum devices. Nanophotonics 2023, 12, 1865–1875. [Google Scholar] [CrossRef]
- Kociak, M.; Stephan, O.; Taverna, D.; Nelayah, J.; Colliex, C. Probing surface plasmons on individual nano-objects by near-field electron energy loss spectroscopy. In Plasmonics: Metallic Nanostructures and Their Optical Properties III, Proceedings of SPIE, San Diego, CA, USA, 26 August 2005; Society of Photo-Optical Instrumentation Engineers (SPIE): Bellingham, WA, USA, 2005; Volume 5927, pp. 217–232. [Google Scholar] [CrossRef]
- Al-Zubeidi, A.; McCarthy, L.A.; Rafiei-Miandashti, A.; Heiderscheit, T.S.; Link, S. Single-particle scattering spectroscopy: Fundamentals and applications. Nanophotonics 2021, 10, 1621–1655. [Google Scholar] [CrossRef]
- Cade, N.I.; Culfaz, F.; Eligal, L.; Ritman-Meer, T.; Huang, F.M.; Festy, F.; Richards, D. Plasmonic enhancement of fluorescence and Raman scattering by metal nanotips. NanoBiotechnology 2007, 3, 203–211. [Google Scholar] [CrossRef]
- Lv, M.; Zhang, X.; Li, B.; Huang, B.; Zheng, Z. Single-particle fluorescence spectroscopy for elucidating charge transfer and catalytic mechanisms on nanophotocatalysts. ACS Nano 2024, 18, 30247–30268. [Google Scholar] [CrossRef]
- Forcherio, G.T.; Ostovar, B.; Boltersdorf, J.; Cai, Y.-Y.; Leff, A.C.; Grew, K.N.; Lundgren, C.A.; Link, S.; Baker, D.R. Single-Particle Insights into Plasmonic Hot Carrier Separation Augmenting Photoelectrochemical Ethanol Oxidation with Photocatalytically Synthesized Pd-Au Bimetallic Nanorods. ACS Nano 2022, 16, 12377–12389. [Google Scholar] [CrossRef] [PubMed]
- Lohmuller, T.; Iversen, L.; Schmidt, M.; Rhodes, C.; Tu, H.L.; Lin, W.C.; Groves, J.T. Single molecule tracking on supported membranes with arrays of optical nanoantennas. Nano Lett. 2012, 12, 1717–1721. [Google Scholar] [CrossRef]
- Ignatovich, F.V.; Topham, D.; Novotny, L. Optical detection of single nanoparticles and viruses. IEEE J. Sel. Top. Quantum Electron. 2006, 12, 1292–1300. [Google Scholar] [CrossRef]
- Chang, W.S.; Lassiter, J.B.; Swanglap, P.; Sobhani, H.; Khatua, S.; Nordlander, P.; Halas, N.J.; Link, S. A plasmonic Fano switch. Nano Lett. 2012, 12, 4977–4982. [Google Scholar] [CrossRef]
- Lazar, S.; Tiemeijer, P.; Schnohr, C.S.; Meledina, M.; Patzig, C.; Höche, T.; Longo, P.; Freitag, B. Enabling electron-energy-loss spectroscopy at very high energy losses: An opportunity to obtain x-ray absorption spectroscopy–like information using an electron microscope. Phys. Rev. Appl. 2025, 23, 054095. [Google Scholar] [CrossRef]
- Nelayah, J.; Kociak, M.; Stéphan, O.; García de Abajo, F.J.; Tencé, M.; Henrard, L.; Taverna, D.; Pastoriza-Santos, I.; Liz-Marzán, L.M.; Colliex, C. Mapping surface plasmons on a single metallic nanoparticle. Nat. Phys. 2007, 3, 348–353. [Google Scholar] [CrossRef]
- Röhrich, R.; Hoekmeijer, C.; Osorio, C.I.; Koenderink, A.F. Quantifying single plasmonic nanostructure far-fields with interferometric and polarimetric k-space microscopy. Light Sci. Appl. 2018, 7, 65. [Google Scholar] [CrossRef]
- Ghaffari, A.; Kashani, S.; Li, J.; Gkoupidenis, P.; Riehn, R.; Gu, Q. Plasmonic Double-Hole Bull’s Eye Nanoantenna for Far-Field Polarization Control. ACS Nanosci. Au 2025, 5, 306–313. [Google Scholar] [CrossRef]
- Rubin, N.A.; Chevalier, P.; Juhl, M.; Tamagnone, M.; Chipman, R.; Capasso, F. Imaging polarimetry through metasurface polarization gratings. Opt. Express 2022, 30, 9389–9412. [Google Scholar] [CrossRef]
- Sahu, R.R.; Ramasamy, A.S.; Bhonsle, S.; Vailshery, M.; Archana, S.; Kumar, H.; Das Gupta, T. Single-step fabrication of liquid gallium nanoparticles via capillary interaction for dynamic structural colours. Nat. Nanotechnol. 2024, 19, 766–774. [Google Scholar] [CrossRef]
- Drezet, A.; Genet, C.; Ebbesen, T.W. Miniature plasmonic wave plates. Phys. Rev. Lett. 2008, 101, 043902. [Google Scholar] [CrossRef]
- El Samad, S.; Jneid, M.; Yassine, H.E.B.; Marhaba, S. Light polarization effect on the extinction spectrum of silver nanostructures. Phys. Lett. A 2025, 546, 130509. [Google Scholar] [CrossRef]
- Zhao, Y.; Alù, A. Manipulating light polarization with ultrathin plasmonic metasurfaces. Phys. Rev. B 2011, 84, 205428. [Google Scholar] [CrossRef]
- Majorel, C.; Girard, C.; Arbouet, A.; Muskens, O.L.; Wiecha, P.R. Deep learning enabled strategies for modeling of complex aperiodic plasmonic metasurfaces of arbitrary size. ACS Photonics 2022, 9, 575–585. [Google Scholar] [CrossRef]
- Ni, H.; Ping, A.; Cai, T.; Ni, B.; Chang, J.; Krasavin, A.V. Tunable polarization control with self-assembled arrays of anisotropic plasmonic coaxial nanocavities. Opt. Express 2024, 32, 16901–16912. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Chiang, H.; Wen, T.; Ye, L.; Lin, H.; Xu, H.; Gong, Q.; Lu, G. Correction to Exotic Coupling Between Plasmonic Nanoparticles Through Geometric Configurations. J. Light. Technol. 2021, 39, 6646–6652, Erratum in J. Light. Technol. 2022, 40, 918–918. [Google Scholar] [CrossRef]
- Laible, F.; Horneber, A.; Fleischer, M. Mechanically tunable nanogap antennas: Single-structure effects and multi-structure applications. Adv. Opt. Mater. 2021, 9, 2100326. [Google Scholar] [CrossRef]
- Patoux, A.; Majorel, C.; Wiecha, P.R.; Cuche, A.; Muskens, O.L.; Girard, C.; Arbouet, A. Polarizabilities of complex individual dielectric or plasmonic nanostructures. Phys. Rev. B 2022, 101, 235418. [Google Scholar] [CrossRef]
- Black, L.J.; Wang, Y.; De Groot, C.H.; Arbouet, A.; Muskens, O.L. Optimal polarization conversion in coupled dimer plasmonic nanoantennas for metasurfaces. ACS Nano 2014, 8, 6390–6399. [Google Scholar] [CrossRef]
- Chauhan, B.V.; Verma, S.; Rahman, B.A.; Wyche, K.P. Deep Learning in Airborne Particulate Matter Sensing and Surface Plasmon Resonance for Environmental Monitoring. Atmosphere 2025, 16, 359. [Google Scholar] [CrossRef]
- Waseer, W.I.; Baqir, M.A.; Saqlain, M.; Mughal, M.J.; Khan, S. Predictive modeling of MXene-based solar absorbers using a deep neural network. J. Opt. Soc. Am. B 2025, 42, 763–772. [Google Scholar] [CrossRef]
- Tao, W.; Shen, L.; Wu, Y.; Zheng, S.; Hu, Q.; Yin, L.; Bassir, D.; Maurer, T.; Fleischer, M. Deep learning-driven spectral exploration for metal-insulator-metal plasmonic metasurfaces. Opt. Express 2025, 33, 31410–31428. [Google Scholar] [CrossRef]
- Jiang, H.; Zhang, Y.; Zhang, L.; Liu, L.; Wang, H.; Wang, Y.; Chen, M. Comprehensive Serum Analysis via an AI-Assisted Magnetically Driven SERS Platform for the Diagnosis and Etiological Differentiation of Childhood Epilepsy. ACS Appl. Mater. Interfaces 2025, 17, 11731–11741. [Google Scholar] [CrossRef] [PubMed]
- Davison, G.; Jones, T.; Liu, J.; Kim, J.; Yin, Y.; Kim, D.; Chio, W.I.K.; Parkin, I.P.; Jeong, H.H.; Lee, T.C. Computer-Aided Design and Analysis of Spectrally Aligned Hybrid Plasmonic Nanojunctions for SERS Detection of Nucleobases. Adv. Mater. Technol. 2023, 8, 2201400. [Google Scholar] [CrossRef]
- Jones, T.; Zhou, D.; Liu, J.; Parkin, I.P.; Lee, T.C. Quantitative multiplexing of uric acid and creatinine using polydisperse plasmonic nanoparticles enabled by electrochemical-SERS and machine learning. J. Mater. Chem. B 2024, 12, 10563–10572. [Google Scholar] [CrossRef] [PubMed]
- Moreira, M.; Hillenkamp, M.; Rodrigues, V.; Ugarte, D. Ag Surface Segregation in Sub-10-nm Bimetallic AuAg Nanoparticles Quantified by STEM-EDS and Machine Learning: Implications for Fine-Tuning Physicochemical Properties for Plasmonics and Catalysis Applications. ACS Appl. Nano Mater. 2024, 7, 1369–1378. [Google Scholar] [CrossRef]
- Ibrar, M.; Huang, S.Y.; McCurtain, Z.; Naha, S.; Crandall, D.J.; Jacobson, S.C.; Skrabalak, S.E. Modular Anti-Counterfeit Tags Formed by Template-Assisted Self-Assembly of Plasmonic Nanocrystals and Authenticated by Machine Learning. Adv. Funct. Mater. 2024, 34, 2400842. [Google Scholar] [CrossRef]
- Jo, K.; Linh, V.T.N.; Yang, J.Y.; Heo, B.; Kim, J.Y.; Mun, N.E.; Im, J.H.; Kim, K.S.; Park, S.G.; Lee, M.Y.; et al. Machine learning-assisted label-free colorectal cancer diagnosis using plasmonic needle-endoscopy system. Biosens. Bioelectron. 2024, 264, 116633. [Google Scholar] [CrossRef]
- Wang, W.; Chen, Z.; Wang, Z.; Yu, Y.; Dong, T.; Lai, J.; Li, B.; Li, H.; Zheng, G.; Wang, L. Dynamic Confinement and Interfacial Engineering in Mesoporous Ag@ SiO2 Core–Shell Architecture for Acidic Electrocatalytic CO2-to-Methane Conversion. Adv. Funct. Mater. 2025, 35, 2503126. [Google Scholar] [CrossRef]
- Gogoi, D.; Namdeo, A.; Golder, A.K.; Peela, N.R. Ag-doped TiO2 photocatalysts with effective charge transfer for highly efficient hydrogen production through water splitting. Int. J. Hydrogen Energy 2020, 45, 2729–2744. [Google Scholar] [CrossRef]
- Lapresta-Fernández, A.; Athanasopoulou, E.N.; Silva, P.J.; Güven, Z.P.; Stellacci, F. Site-selective surface enhanced Raman scattering study of ligand exchange reactions on aggregated Ag nanocubes. J. Colloid. Interface Sci. 2022, 616, 110–120. [Google Scholar] [CrossRef]
- Li, J.; She, Q.; Wang, W.; Liu, R.; You, R.; Wu, Y.; Weng, J.; Liu, Y.; Lu, Y. Label-free SERS analysis of serum using Ag NPs/cellulose nanocrystal/graphene oxide nanocomposite film substrate in screening colon cancer. Nanomaterials 2023, 13, 334. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Zhang, Y.; Zhang, W.; Hu, P.; Zhang, M.; Meng, X.; Zhang, X.; Shang, M.; Duan, X.; Wang, C. Portable SERS-based POCT kit for ultrafast and sensitive determining paraquat in human gastric juice and urine. ACS Omega 2024, 9, 18576–18583. [Google Scholar] [CrossRef] [PubMed]
- Peng, J.; Song, Y.; Lin, Y.; Huang, Z. Introduction and development of surface-enhanced Raman scattering (SERS) substrates: A review. Nanomaterials 2024, 14, 1648. [Google Scholar] [CrossRef] [PubMed]
- Pięta, Ł.; Kisielewska, A.; Warzybok, A.; Piwoński, I.; Malek, K. Long-lived photoexcitation probed by photo-induced enhanced Raman spectroscopy: Unveiling charge dynamics in Ag–TiO2 nano-heterojunctions. Sci. Rep. 2025, 15, 5587. [Google Scholar] [CrossRef]
- Zheng, W.J.; Liao, P.; Niku, G.; Fan, X. Self-cleaning Au-TiO2/ePTFE membrane via plasma grafting and ion implantation with anti-agglomeration. Appl. Surf. Sci. 2025, 712, 164167. [Google Scholar] [CrossRef]
- Cho, H.S.; Koh, J.; Yim, G.; Jang, H.; Kim, Y.K. Laser Desorption/Ionization on Au@TiO2 Core@ Shell Nanostars for Mass Spectrometric Analysis of Small Molecules. Nanomaterials 2024, 14, 1946. [Google Scholar] [CrossRef]
- Aoudjit, L.; Queirós, J.M.; Castro, A.S.; Zioui, D.; González-Ballesteros, N.; Lanceros-Mendez, S.; Martins, P.M. Sunlight-Induced Photocatalytic Removal of Paracetamol Using Au-TiO2 Nanoparticles. Nanomaterials 2025, 15, 358. [Google Scholar] [CrossRef]
- Gong, L.; Jin, Y.; Zhao, S.; Wang, K.; Martínez-Alanis, P.R.; Cabot, A. Electrocatalytic Oxidation of Benzaldehyde on Gold Nanoparticles Supported on Titanium Dioxide. Nanomaterials 2024, 14, 1005. [Google Scholar] [CrossRef]
- He, Z.; Xue, W.; Cui, W.; Li, C.; Li, Z.; Pu, L.; Feng, J.; Xiao, X.; Wang, X.; Li, G. Tunable Fano resonance and enhanced sensing in a simple Au/TiO2 hybrid metasurface. Nanomaterials 2020, 10, 687. [Google Scholar] [CrossRef]
- Trang, T.N.Q.; Doanh, T.T.; Vinh, L.Q.; Thu, V.T.H. A hybrid Ag/TiO2 nanoarray-based in situ charge transfer toward multi-functional active-platform. Ceram. Int. 2021, 47, 27524–27534. [Google Scholar] [CrossRef]
- You, D.; Wang, R.; Xie, J.; Liu, L.; Li, K.; Han, X.; Guo, T.; Xu, C. Synergistic SERS enhancement and in situ monitoring of photocatalytic reactions in a plasmonic metal/ferroelectric hybrid system by the light-induced pyroelectric effect. J. Mater. Chem. A 2022, 10, 14078–14089. [Google Scholar] [CrossRef]
- Liz-Marzan, L.M.; Philipse, A.P. Stable hydrosols of metallic and bimetallic nanoparticles immobilized on imogolite fibers. J. Phys. Chem. 1995, 99, 15120–15128. [Google Scholar] [CrossRef]
- Kim, M.J.; Na, H.J.; Lee, K.C.; Yoo, E.A.; Lee, M. Preparation and characterization of Au–Ag and Au–Cu alloy nanoparticles in chloroform. J. Mater. Chem. 2003, 13, 1789–1792. [Google Scholar] [CrossRef]
- Philip, R.; Kumar, G.R.; Sandhyarani, N.; Pradeep, T. Picosecond optical nonlinearity in monolayer-protected gold, silver, and gold-silver alloy nanoclusters. Phys. Rev. B 2000, 62, 13160–13166. [Google Scholar] [CrossRef]
- Nishijima, Y.; Hashimoto, Y.; Seniutinas, G.; Rosa, L.; Juodkazis, S. Engineering gold alloys for plasmonics. Appl. Phys. A 2014, 117, 641–645. [Google Scholar] [CrossRef]
- Wilcoxon, J.P.; Martino, A.; Baughmann, R.L.; Klavetter, E.; Sylwester, A.P. Synthesis of transition metal clusters and their catalytic and optical properties. Mater. Res. Soc. Symp. Proc. 1992, 286, 131–136. [Google Scholar] [CrossRef]
- dos Santos, L.H.; Kiss, F.D.; Ferraz, A.C.; Miotto, R. Ag@Au and Au@Ag Core–Shell Nanoparticles: Insights on the Growth Process and Interactions with Small Molecules. J. Phys. Chem. C 2024, 128, 10751–10760. [Google Scholar] [CrossRef]
- Bi, C.; Song, Y.; Zhao, H.; Liu, G. Shape controlled synthesis of concave octahedral Au@AuAg nanoparticles to improve their surface-enhanced Raman scattering performance. RSC Adv. 2022, 12, 19571–19578. [Google Scholar] [CrossRef] [PubMed]
- Pramanick, B. Hot Electron-Mediated photocatalytic reduction of para nitrophenol and organic dye sensing using Cu-Ag heterostructure. Inorg. Chem. Commun. 2024, 161, 112040. [Google Scholar] [CrossRef]
- Green, E.L.; Muldawer, L. Optical properties of the alpha-phase alloys Ag-Zn and Ag-Cd. Phys. Rev. B 1970, 2, 330–340. [Google Scholar] [CrossRef]
- Riley, J.D.; Leckey, R.C.G.; Jenkin, J.G.; Liesegang, J.; Poole, R.T. Ultraviolet photoelectron spectra of the outer d bands of Ag-In and Ag-Cd alloys. J. Phys. F Met. Phys. 1976, 6, 293. [Google Scholar] [CrossRef]
- Nicholson, J.A.; Riley, J.D.; Leckey, R.C.G.; Liesegang, J.; Jenkin, J.G. Ultraviolet photoelectron spectroscopy of the valence bands of some Ag alloys. J. Phys. F Met. Phys. 1978, 7, 351–356. [Google Scholar] [CrossRef]
- Nicholson, J.A.; Riley, J.D.; Leckey, R.C.G.; Jenkin, J.G.; Liesegang, J.; Azoulay, J. Ultraviolet photoelectron spectroscopy of the valence bands of some Au alloys. Phys. Rev. B 1978, 18, 2561–2567. [Google Scholar] [CrossRef]
- Keast, V.J.; Birt, K.; Koch, C.T.; Supansomboon, S.; Cortie, M.B. The role of plasmons and interband transitions in the color of AuAl2, AuIn2, and AuGa2. Appl. Phys. Lett. 2011, 99, 111908. [Google Scholar] [CrossRef]
- Todorov, R.; Hristova-Vasileva, T.; Atanasova, A.; Katrova, V.; Milushev, G. February. Preparation and optical characterization of Au–In films for plasmonic applications. J. Phys. Conf. Ser. 2021, 1762, 012022. [Google Scholar] [CrossRef]
- Todorov, R.; Hristova-Vasileva, T.; Milushev, G.; Milanov, E. February. Spectroscopic ellipsometry modelling of thin AuSn films and nanostructures as plasmonics materials. J. Phys. Conf. Ser. 2024, 2710, 012007. [Google Scholar] [CrossRef]
- Todorov, R.; Katrova, V.; Hristova-Vasileva, T.; Milushev, G. Structural and optical characterization of thin films from bimetallic Au-Sb system as tuneable plasmonic material for UV spectral range. J. Phys. Conf. Ser. 2023, 2436, 012023. [Google Scholar] [CrossRef]
- Todorov, R.; Hristova-Vasileva, T.; Katrova, V.; Strijkova, V.; Atanasova, A.; Milushev, G. Formation, structure, and optical performance of AgCd/Ag5Cd8 phases in thin film form. J. Mater. Sci. Mater. Electron. 2023, 34, 1093. [Google Scholar] [CrossRef]
- Luong, H.M.; Pham, M.T.; Nguyen, T.D.; Zhao, Y. Magneto-plasmonic properties of Ag–Co composite nano-triangle arrays. Nanotechnology 2019, 30, 425203. [Google Scholar] [CrossRef]
- Itina, T.E. Understanding mono-and bi-metallic Au and Ni nanoparticle responses to fast heating. Nanoscale Adv. 2024, 6, 5451–5463. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Loh, K.P.; Huang, H.; Chen, W.; Wee, A.T.S. Plasmon dispersion on epitaxial graphene studied using high-resolution electron energy-loss spectroscopy. Phys. Rev. B 2009, 80, 113410. [Google Scholar] [CrossRef]
- Garcia de Abajo, F.J. Graphene plasmonics: Challenges and opportunities. ACS Photonics 2014, 1, 135–152. [Google Scholar] [CrossRef]
- Han, Q.; Lu, Z.; Gao, W.; Wu, M.; Wang, Y.; Wang, Z.; Qi, J.; Dong, J. Three-dimensional AuAg alloy NPs/graphene/AuAg alloy NP sandwiched hybrid nanostructure for surface enhanced Raman scattering properties. J. Mater. Chem. C 2020, 8, 12599–12606. [Google Scholar] [CrossRef]
- Dobrik, G.; Nemes-Incze, P.; Majerus, B.; Süle, P.; Vancsó, P.; Piszter, G.; Menyhárd, M.; Kalas, B.; Petrik, P.; Henrard, L.; et al. Large-area nanoengineering of graphene corrugations for visible-frequency graphene plasmons. Nat. Nanotechnol. 2022, 17, 61–66. [Google Scholar] [CrossRef]
- Tomarchio, L.; Macis, S.; D’Arco, A.; Mou, S.; Grilli, A.; Romani, M.; Guidi, M.C.; Hu, K.; Kukunuri, S.; Jeong, S.; et al. Disordered photonics behavior from terahertz to ultraviolet of a three-dimensional graphene network. NPG Asia Mater. 2021, 13, 73. [Google Scholar] [CrossRef]
- Fan, W.; Lee, Y.H.; Pedireddy, S.; Zhang, Q.; Liu, T.; Ling, X.Y. Graphene oxide and shape-controlled silver nanoparticle hybrids for ultrasensitive single-particle surface-enhanced Raman scattering (SERS) sensing. Nanoscale 2014, 6, 4843–4851. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, Y. Interplay of graphene–DNA interactions: Unveiling sensing potential of graphene materials. App. Phys. Rev. 2024, 11, 011306. [Google Scholar] [CrossRef]
- Xu, A.H.; Zaidan, L.; Takaloo, S.; Belyakov, I.; Irannejad, M.; Medvedeva, X.; Labas, S.; Bastug Azer, B.; Gulsaran, A.; Ozyigit, D.; et al. Reduced graphene oxide/gold composite synthesis via laser irradiation for surface enhanced Raman spectroscopy biosensors. J. Mater. Sci. Mater. Electron. 2025, 36, 269. [Google Scholar] [CrossRef]
- Shao, M.; Ji, C.; Tan, J.; Du, B.; Zhao, X.; Yu, J.; Man, B.; Xu, K.; Zhang, C.; Li, Z. Ferroelectrically modulate the Fermi level of graphene oxide to enhance SERS response. Opto-Electron. Adv. 2023, 6, 230094. [Google Scholar] [CrossRef]
- Wu, Y.; Sun, T.; Shao, M.; Ji, C.; Li, C.; Zhang, C.; Li, Z. Pyroelectrically Driven Charge Transfer and its Advantages on SERS and Self-Cleaning Property. Laser Photonics Rev. 2025, 19, 2401152. [Google Scholar] [CrossRef]
- Vasanelli, A.; Todorov, Y.; Dailly, B.; Cosme, S.; Gacemi, D.; Haky, A.; Sagnes, I.; Sirtori, C. Semiconductor quantum plasmons for high frequency thermal emission. Nanophotonics 2020, 10, 607–615. [Google Scholar] [CrossRef]
- Gjerding, M.N.; Petersen, R.; Pedersen, T.G.; Mortensen, N.A.; Thygesen, K.S. Layered van der Waals crystals with hyperbolic light dispersion. Nat. Commun. 2017, 8, 320. [Google Scholar] [CrossRef]
- Gjerding, M.N.; Pandey, M.; Thygesen, K.S. Band structure engineered layered metals for low-loss plasmonics. Nat. Commun. 2017, 8, 15133. [Google Scholar] [CrossRef]
- Rossi, A.W.; Bourgeois, M.R.; Walton, C.; Masiello, D.J. Probing the polarization of low-energy excitations in 2D materials from atomic crystals to nanophotonic arrays using momentum-resolved electron energy loss spectroscopy. Nano Lett. 2024, 24, 7748–7756. [Google Scholar] [CrossRef]
- Rano, B.R.; Syed, I.M.; Naqib, S.H. Elastic, electronic, bonding, and optical properties of WTe2 Weyl semimetal: A comparative investigation with MoTe2 from first principles. Results Phys. 2020, 19, 103639. [Google Scholar] [CrossRef]
- Tang, H.; Yin, L.; Csonka, G.I.; Ruzsinszky, A. Exploring the exciton insulator state in 1 T-TiSe2 monolayer with advanced electronic structure methods. Phys. Rev. B 2025, 111, L201401. [Google Scholar] [CrossRef]
- Bonnet, N.; Baaboura, J.; Castioni, F.; Woo, S.Y.; Ho, C.H.; Watanabe, K.; Taniguchi, T.; Tizei, L.H.; Coenen, T. Cathodoluminescence emission and electron energy loss absorption from a 2D transition metal dichalcogenide in van der Waals heterostructures. Nanotechnology 2024, 35, 405702. [Google Scholar] [CrossRef] [PubMed]
- Buchkov, K.; Todorov, R.; Terziyska, P.; Gospodinov, M.; Strijkova, V.; Dimitrov, D.; Marinova, V. Anisotropic optical response of WTe2 single crystals studied by ellipsometric analysis. Nanomaterials 2021, 11, 2262. [Google Scholar] [CrossRef]
- Nam, K.; Im, J.; Han, G.H.; Park, J.Y.; Kim, H.; Park, S.; Yoo, S.; Haddadnezhad, M.; Ahn, J.S.; Park, K.D.; et al. Photoluminescence of MoS2 on Plasmonic Gold Nanoparticles Depending on the Aggregate Size. ACS Omega 2024, 9, 21587–21594. [Google Scholar] [CrossRef]
- Mueller, N.S.; Arul, R.; Kang, G.; Saunders, A.P.; Johnson, A.C.; Sánchez-Iglesias, A.; Hu, S.; Jakob, L.A.; Bar-David, J.; de Nijs, B.; et al. Photoluminescence upconversion in monolayer WSe2 activated by plasmonic cavities through resonant excitation of dark excitons. Nat. Commun. 2023, 14, 5726. [Google Scholar] [CrossRef]
- Pincelli, T.; Vasileiadis, T.; Dong, S.; Beaulieu, S.; Dendzik, M.; Zahn, D.; Lee, S.E.; Seiler, H.; Qi, Y.; Xian, R.P.; et al. Observation of Multi-Directional Energy Transfer in a Hybrid Plasmonic–Excitonic Nanostructure. Adv. Mater. 2023, 35, 2209100. [Google Scholar] [CrossRef]
- Naguib, M.; Kurtoglu, M.; Presser, V.; Lu, J.; Niu, J.; Heon, M.; Hultman, L.; Gogotsi, Y.; Barsoum, M.W. Two-dimensional nanocrystals produced by exfoliation of Ti3AlC2. Adv. Mater. 2011, 23, 4248–4253. [Google Scholar] [CrossRef]
- Naguib, M.; Mochalin, V.N.; Barsoum, M.W.; Gogotsi, Y. 25th anniversary article: MXenes: A new family of two-dimensional materials. Adv. Mater. 2014, 26, 992–1005. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.B.; Guo, S.D.; Lv, B. Strain manipulates the electric, elastic, thermal, and optical properties of MXene Lu2CT2 (T = F, OH). Eur. Phys. J. Plus 2024, 139, 526. [Google Scholar] [CrossRef]
- Semiromi, E.H.; Baghini, Z.K.; Mostafaei, A. Electronic and optical properties of Y2CCl2 Mxene: Tuning the band gap by biaxial strain. Solid State Commun. 2024, 381, 115451. [Google Scholar] [CrossRef]
- Debow, S.; Zhang, T.; Liu, X.; Song, F.; Qian, Y.; Han, J.; Maleski, K.; Zander, Z.B.; Creasy, W.R.; Kuhn, D.L.; et al. Charge dynamics in TiO2/MXene composites. J. Phys. Chem. C 2021, 125, 10473–10482. [Google Scholar] [CrossRef]
- Li, M.Y.; Li, Z.; Li, H.; Liu, S.; Lu, H.; Wen, X.; Yang, Y. ZnO quantum dot/MXene nanoflake hybrids for ultraviolet photodetectors. ACS Appl. Nano Mater. 2021, 4, 13674–13682. [Google Scholar] [CrossRef]
- Yang, J.; Wang, R.; Sun, X.; Li, Y.; Liu, J.; Kuang, X. Au/Ti3C2/g-C3N4 ternary composites boost H2 evolution efficiently with remarkable long-term stability by synergistic strategies. ACS Appl. Mater. Interfaces 2024, 16, 12385–12397. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, M.; Wang, Z.; Zhang, N.; Ge, C. Engineering the band gap of Hf2CO2 MXene semiconductor by C/O doping. J. Mater. Res. 2021, 36, 1678–1685. [Google Scholar] [CrossRef]
- Furchner, A.; Parker, T.; Mauchamp, V.; Hurand, S.; Plaickner, J.; Rappich, J.; Emerenciano, A.A.; Hinrichs, K.; Gogotsi, Y.; Petit, T. Ti3C2Tx MXene Thin Films and Intercalated Species Characterized by IR-to-UV Broadband Ellipsometry. J. Phys. Chem. C 2025, 129, 500–507. [Google Scholar] [CrossRef] [PubMed]
- Bai, Y.; Zhou, K.; Srikanth, N.; Pang, J.H.L.; He, X.; Wang, R. Dependence of elastic and optical properties on surface terminated groups in two-dimensional MXene monolayers: A first-principles study. RSC Adv. 2016, 6, 35731–35739. [Google Scholar] [CrossRef]
- Reddy, H.; Guler, U.; Kudyshev, Z.; Kildishev, A.V.; Shalaev, V.M.; Boltasseva, A. Temperature-dependent optical properties of plasmonic titanium nitride thin films. ACS Photonics 2017, 4, 1413–1420. [Google Scholar] [CrossRef]
- Mendoza-Galvan, A.; Rybka, M.; Järrendahl, K.; Arwin, H.; Magnuson, M.; Hultman, L.; Barsoum, M.W. Spectroscopic ellipsometry study on the dielectric function of bulk Ti2AlN, Ti2AlC, Nb2AlC, (Ti0.5,Nb0.5)2AlC, and Ti3GeC2 MAX-phases. J. Appl. Phys. 2011, 109, 013530. [Google Scholar] [CrossRef]
- Chen, Y.; Fan, Z.; Zhang, Z.; Niu, W.; Li, C.; Yang, N.; Chen, B.; Zhang, H. Two-dimensional metal nanomaterials: Synthesis, properties, and applications. Chem. Rev. 2018, 118, 6409–6455. [Google Scholar] [CrossRef] [PubMed]
- Jang, S.W.; Dutta, S.; Kumar, A.; Hong, Y.R.; Kang, H.; Lee, S.; Ryu, S.; Choi, W.; Lee, I.S. Holey Pt nanosheets on NiFe-hydroxide laminates: Synergistically enhanced electrocatalytic 2D interface toward hydrogen evolution reaction. ACS Nano 2020, 14, 10578–10588. [Google Scholar] [CrossRef]
- Zhu, J.Y.; Chen, S.Q.; Xue, Q.; Li, F.M.; Yao, H.C.; Xu, L.; Chen, Y. Hierarchical porous Rh nanosheets for methanol oxidation reaction. Appl. Catal. B Environ. 2020, 264, 118520. [Google Scholar] [CrossRef]
- Feng, F.; Han, S.; Lu, Q.; Yun, Q. Two-dimensional noble metal-based intermetallics for electrocatalysis. Energy Mater. Devices 2023, 1, 9370008. [Google Scholar] [CrossRef]
- Campbell, C.T. Ultrathin metal films and particles on oxide surfaces: Structural, electronic and chemisorptive properties. Surf. Sci. Rep. 1997, 27, 1–111. [Google Scholar] [CrossRef]
- Zhao, J.; Li, L.; Li, P.; Dai, L.; Dong, J.; Zhou, L.; Wang, Y.; Zhang, P.; Ji, K.; Zhang, Y.; et al. Realization of 2D metals at the ångström thickness limit. Nature 2025, 639, 354–359. [Google Scholar] [CrossRef]
- Jang, H.S.; Seong, B.; Zang, X.; Lee, H.; Bae, J.W.; Cho, D.H.; Kao, E.; Yang, C.; Kang, G.; Liu, Y.; et al. 2D Silver Nanosheets: Ultrafast growth of large 2D silver nanosheets by highly ordered biological template at air/gel interface. Adv. Mater. Interfaces 2018, 5, 1870050. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, X.; Ding, J.; Ban, C.; Feng, Y.; Xu, C.; Zhou, X. Realizing ampere-level CO2 electrolysis at low voltage over a woven network of few-atom-layer ultralong silverene nanobelts with ultrahigh aspect ratio by pairing with formaldehyde oxidation. Nanoscale 2024, 16, 7076–7084. [Google Scholar] [CrossRef] [PubMed]
- Kashiwaya, S.; Shi, Y.; Lu, J.; Sangiovanni, D.G.; Greczynski, G.; Magnuson, M.; Andersson, M.; Rosen, J.; Hultman, L. Synthesis of goldene comprising single-atom layer gold. Nat. Synth. 2024, 3, 744–751. [Google Scholar] [CrossRef]
- Pereira, M.L.; Dos Santos, E.J.; Ribeiro, L.A.; Galvão, D.S. How does goldene stack? Mater. Horiz. 2025, 12, 1144–1154. [Google Scholar] [CrossRef] [PubMed]


| Method | Measured Parameters | Calculated Parameters | Sample Type | Spot Limit | Combination with Other Methods | Additional Data | ||
|---|---|---|---|---|---|---|---|---|
| TF | MS | SP | ||||||
| SE | Ellipsometric angles (Ψ, Δ) | Optical constants Anisotropy | + * | + * | − | ≥10 μm | UV-Vis-NIR | Thickness Homogeneity Porosity |
| UV-Vis-NIR | Reflection Absorption Transmittance * | Optical constants | + * | + * | − | >1 mm | SE SPS | Thickness Homogeneity Porosity |
| DLS | Scattered light intensity | Particle size distribution | + | − | + | ≥1 mm | ||
| EELS | Number of electrons passed through the sample after inelastic scattering. | Optical losses Band structure Dielectric properties SPR and LSPR modes | + | + | + ** | sub-10 nm | TEM SEM SAED | Surface image Composition Crystalline structure |
| SNOM | Surface image Plasmon modes Fluorescence emission | + | + | + | sub-10 nm | AFM TEM STM EELS THz spectroscopy | Surface image Chemical state Registration of different phases | |
| SPS | SP absorption and emission. Geometry and surface of SP. Optical heterogeneity | Chemical composition | − | − | + | sub-10 nm | SNOM TEM SEM TERS | NP emission Hot carriers’ excitation in metallic NPs Charge transfer in catalytic reactions |
| IM | Amplitude and phase of electromagnetic waves | Polarization states Small changes in refractive index | + | + | + | λ/4 | ||
| PM | Amplitude, phase and polarization states of electromagnetic waves | Stokes parameters Anisotropy | + | + | + | λ/2 | ||
| DL | Data analysis | Materials design Signal prediction Data processing | + *** | + *** | + *** | All methods | ||
| Material | ωs [eV] | ωp [eV] | QLSPRMAX/ω(QLSPRMAX) [eV] | QSPR/ω(QSPR) [eV] | ε″ | Ref. |
|---|---|---|---|---|---|---|
| Ag | 3.9 | 9.02 | ~20 * (2.0 eV) | 32–2000 * (3.5–0.5 eV) | 0.87–8 * (3.5–0.5 eV) | [82] |
| Au | 2.5 | 8.76 | ~12 * (1.5 eV) | 10–1500 * (2.2–0.5 eV) | 2.50 (1.5 eV) 2.3–50 (2–0.5 eV) | [82] |
| Al | 14.3 | 9.3 (8.6 eV) | n.a. | [69] | ||
| Ga | 14.05 | 13.6 * (11 eV) | n.a. | [69] | ||
| In | 10.9 | 11.7 | 4.60 (5.10 eV) | 5.6 (3.5 eV) * | 5.2 (3.5 eV) 1.7 (5.10 eV) | [151] |
| Ag48Au52 | 3.7 | 8.89 | ~6.7 (1.7 eV) | 10–700 * (2.6–0.5 eV) | 1.84–90 (2.6–0.5 eV) | [82] |
| AuAl2 | 6.7 | 13.4 | 3 (1.3 eV) * | 10–80 (1.7–1 eV)* | 10–80 (1.7–1 eV) | [259] |
| AuGa2 | 7.8 | 13.1 | 1.8 (3.36 eV) * | 22–10 (3–4 eV) * 10–70 * (1.5–1 eV) | ~4.5–11 (3–4 eV) ~23–38 (1.5–1 eV) | [259] |
| Ag3In | 8.3 | 11.9 | 14.4 (2.2 eV) * | 10-2000 * (4–0.5 eV) | 1.7–6.7 (3.6–0.5 eV) | [151] |
| AgIn2 | 6.0 | 11.2 | 1.1 (5.5 eV) * | 10–50 * (0.8–0.5 eV) | 1.87 (5.5 eV) 18.0–41.3 (0.8–0.5 eV) | [151] |
| AuIn2 | 7.2 | 11.8 | 2 (3.4 eV) * | 10–25 * (4–2.9 eV) * 10–45 * (1.4–1 eV) | 3–12 (4–2.9 eV) 22–40 (1.4–1 eV) | [259] |
| Material | ωs [eV] | QLSPRMAX/ω(QLSPRMAX) [eV] | QSPRMAX/ω(QSPRMAX) [eV] | ε″ | Ref. |
|---|---|---|---|---|---|
| TaS2 | 1.11 | ~1.5 * (1.37) | ~17 * (1.37) | 2.97 (1.37) 7.2 (1.37) | [67] |
| TaSe2 | 1.01 | ~1.5 * (1.37) | ~14 * (1.37) | 3.5 (1.37) | [67] |
| NbSe2 | 0.89 | 0.8 * (0.89 eV) | ~8 * (0.89 eV) | [67] | |
| TiN | 2.66 | ~4 * (1.1 eV) | ~10–250 * (2–0.5 eV) | 3.2–42 (2–0.5 eV) | [298] |
| HfN | 3.1 | ~3 * (1.9 eV) | ~10–98 * (2.4–1 eV) | 2.5–25 (2.4–1 eV) | |
| Ti3C2Tx | 1.05 | ~1 * (0.5 eV) | ~10–25 * (0.7–0.5 eV) | [142] | |
| Ti2AlC | 0.5 ~2.65 | ~1.5 * (0.3 eV) | ~10–250 * (0.3–0.2 eV) | 90–100 (0.3–0.1 eV) | [298] |
| (Ti0.5Nb0.5)2AlC | 0.55 | ~ 0.5 * (0.2 eV) | ~ 10–40 * (0.1–0.2 eV) | 90–140 | [299] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Todorov, R.; Hristova-Vasileva, T. Review of the Current State of Optical Characterization and Design of Electronic States in Plasmonic Materials—From Noble Metals to Silverene and Goldene. Nanomaterials 2025, 15, 1548. https://doi.org/10.3390/nano15201548
Todorov R, Hristova-Vasileva T. Review of the Current State of Optical Characterization and Design of Electronic States in Plasmonic Materials—From Noble Metals to Silverene and Goldene. Nanomaterials. 2025; 15(20):1548. https://doi.org/10.3390/nano15201548
Chicago/Turabian StyleTodorov, Rosen, and Temenuga Hristova-Vasileva. 2025. "Review of the Current State of Optical Characterization and Design of Electronic States in Plasmonic Materials—From Noble Metals to Silverene and Goldene" Nanomaterials 15, no. 20: 1548. https://doi.org/10.3390/nano15201548
APA StyleTodorov, R., & Hristova-Vasileva, T. (2025). Review of the Current State of Optical Characterization and Design of Electronic States in Plasmonic Materials—From Noble Metals to Silverene and Goldene. Nanomaterials, 15(20), 1548. https://doi.org/10.3390/nano15201548







