Interface Rotation in Accumulative Rolling Bonding (ARB) Cu/Nb Nanolaminates Under Constrained and Unconstrained Loading Conditions as Revealed by In Situ Micromechanical Testing
Abstract
1. Introduction
2. Materials and Methods
2.1. Assembly of ARB Cu/Nb Nanolaminates
2.2. Fabrication of Cu/Nb ARB Rectangular Micropillar Samples
2.3. Fabrication of Cu/Nb ARB Microbeam Samples
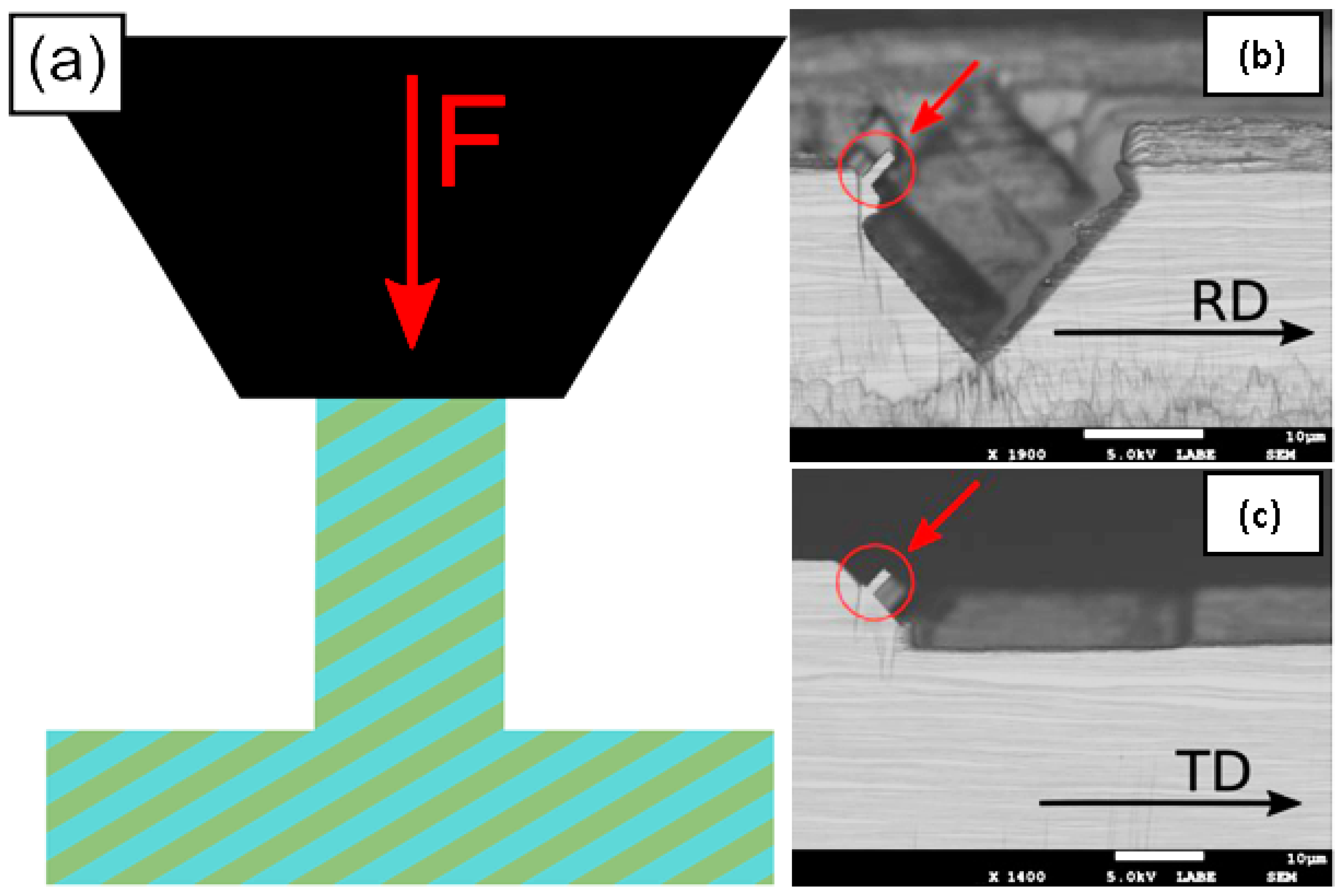
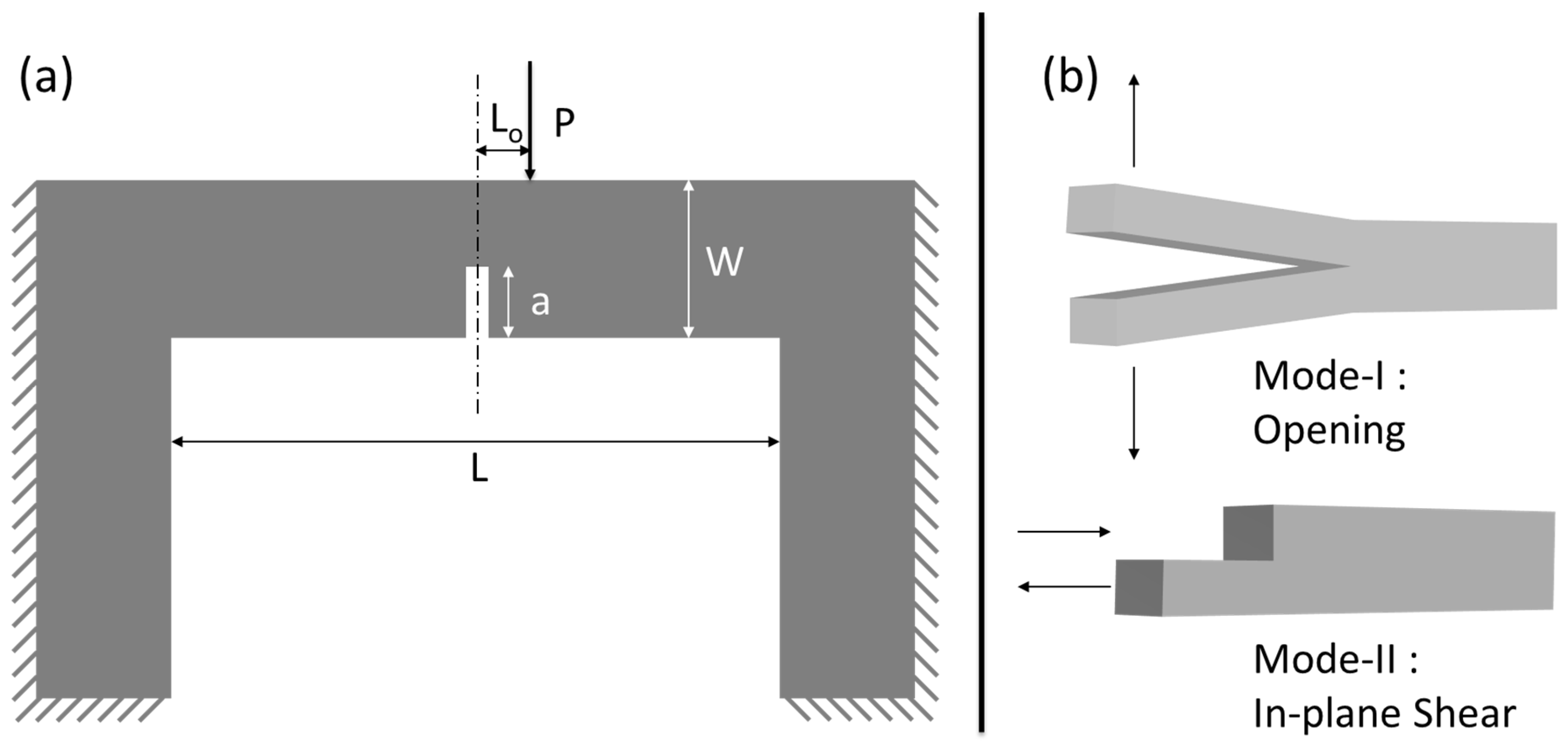
2.4. In Situ Microbeam Bending
3. Experimental Results
3.1. In Situ Rectangular Micropillar Compression
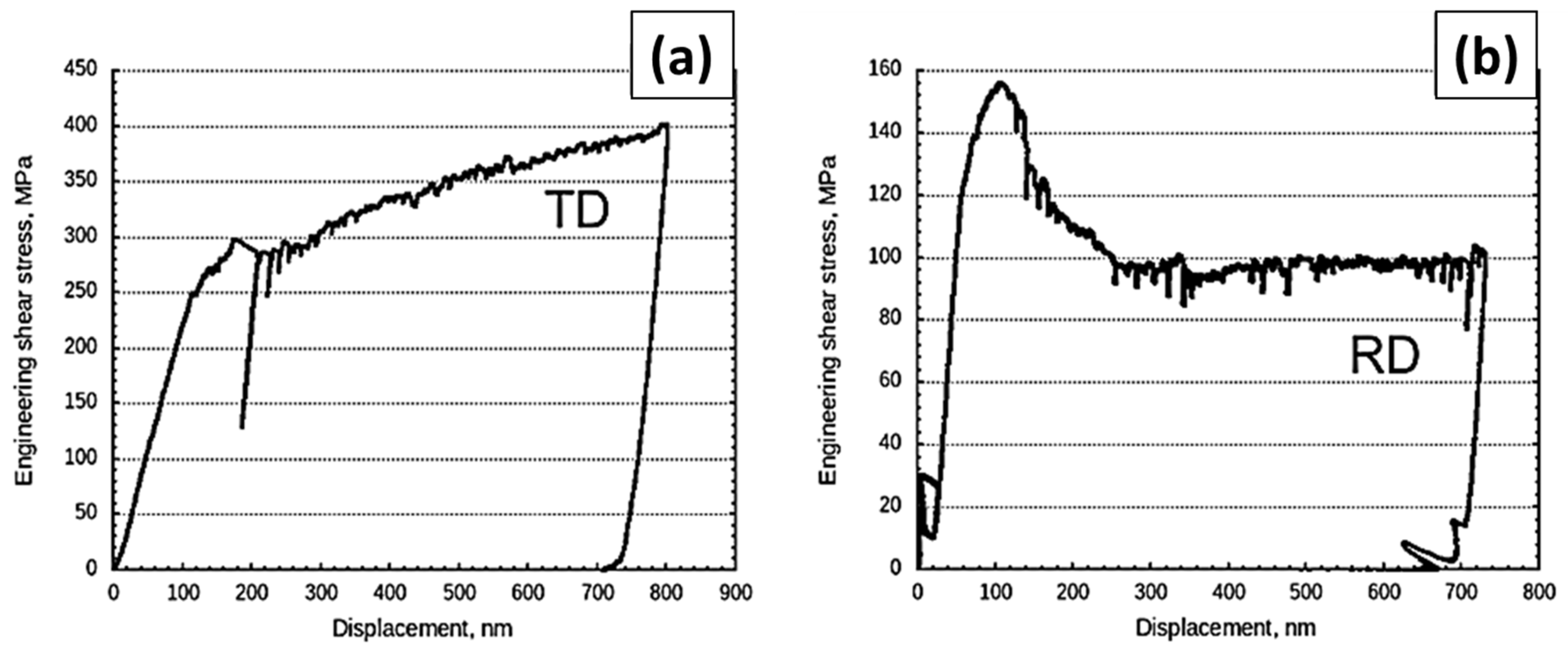
3.1.1. Interface Shear in the TD Rectangular Micropillar Compression
3.1.2. Interface Plasticity in the RD Rectangular Micropillar Compression
3.2. In Situ Cu/Nb ARB Microbeam Bending
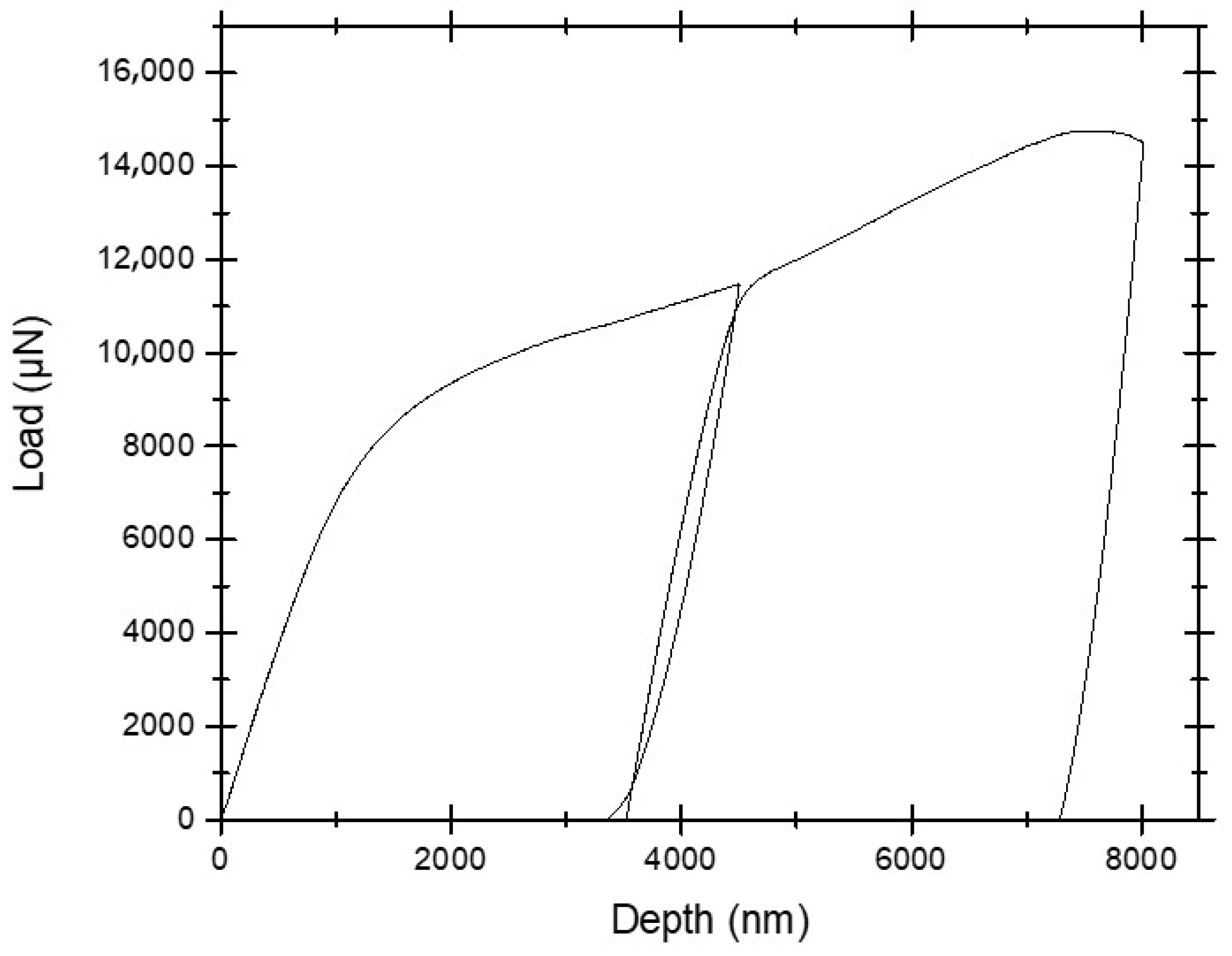
3.2.1. In Situ Microbeam Bending of Cu/Nb ARB Microbeam with No Offset Loading (Cu/Nb-NOL)
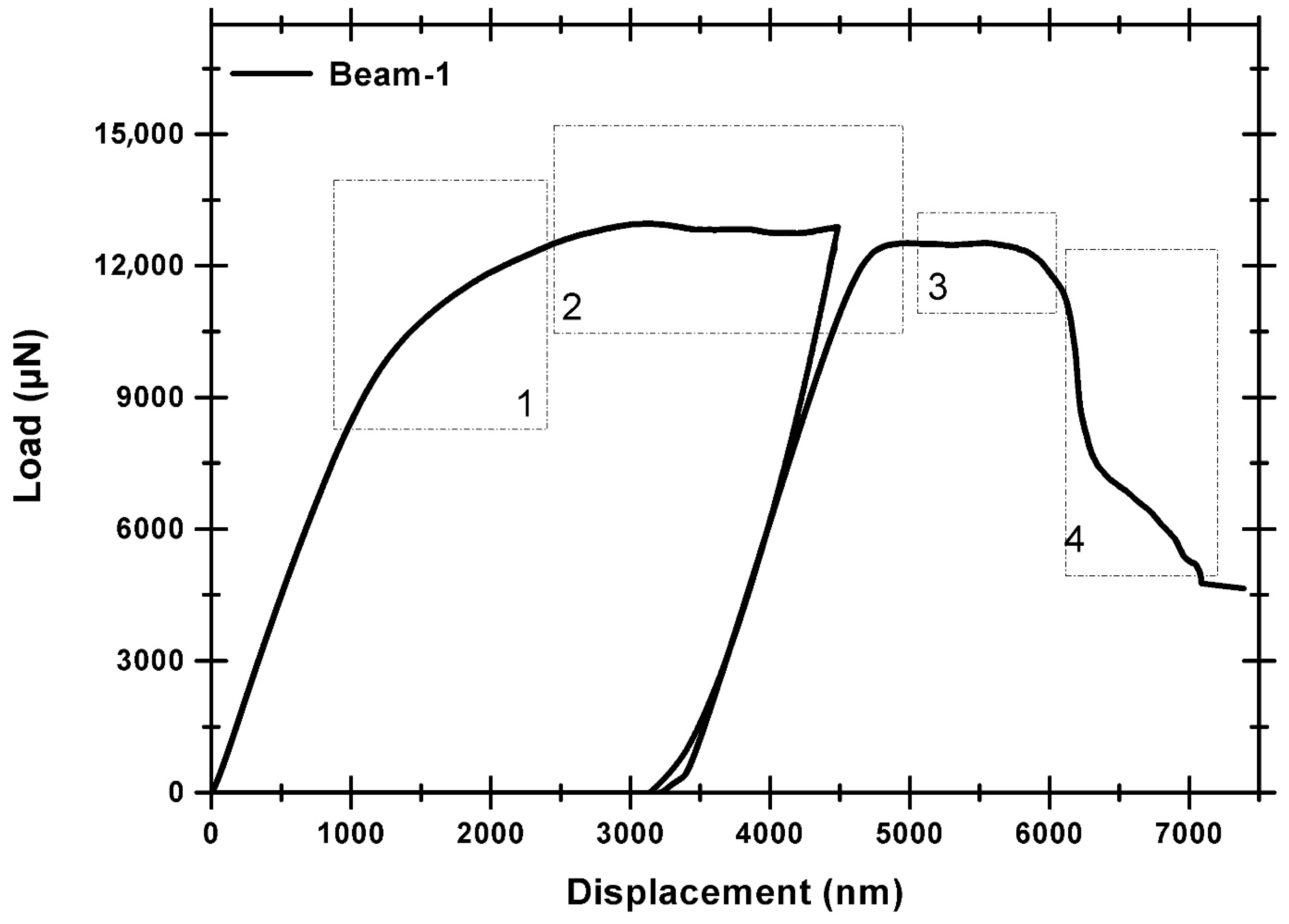
3.2.2. In Situ Microbeam Bending Experiments of Cu/Nb ARB Microbeam with Offset Loading (Cu/Nb-OL)
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Holleck, H.; Schier, V. Multilayer PVD coatings for wear protection. Surf. Coat. Technol. 1995, 76, 328–336. [Google Scholar] [CrossRef]
- Beyerlein, I.J.; Mara, N.A.; Carpenter, J.S.; Nizolek, T.; Mook, W.M.; Wynn, T.A.; McCabe, R.J.; Mayeur, J.R.; Kang, K.; Zheng, S.; et al. Interface-driven microstructure development and ultra high strength of bulk nanostructured Cu-Nb multilayers fabricated by severe plastic deformation. J. Mater. Res. 2013, 28, 1799–1812. [Google Scholar] [CrossRef]
- Hoagland, R.G.; Mitchell, T.E.; Hirth, J.P.; Kung, H. On the strengthening effects of interfaces in multilayer fee metallic composites. Philos. Mag. A 2002, 82, 643–664. [Google Scholar] [CrossRef]
- Han, W.; Cerreta, E.; Mara, N.; Beyerlein, I.; Carpenter, J.; Zheng, S.; Trujillo, C.; Dickerson, P.; Misra, A. Deformation and failure of shocked bulk Cu–Nb nanolaminates. Acta Mater. 2014, 63, 150–161. [Google Scholar] [CrossRef]
- Misra, A.; Demkowicz, M.J.; Zhang, X.; Hoagland, R.G. The radiation damage tolerance of ultra-high strength nanolayered composites. JOM 2007, 59, 62–65. [Google Scholar] [CrossRef]
- Demkowicz, M.; Wang, Y.; Hoagland, R.; Anderoglu, O. Mechanisms of He escape during implantation in CuNb multilayer composites. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2007, 261, 524–528. [Google Scholar] [CrossRef]
- Lim, S.; Rollett, A. Length scale effects on recrystallization and texture evolution in Cu layers of a roll-bonded Cu–Nb composite. Mater. Sci. Eng. A 2009, 520, 189–196. [Google Scholar] [CrossRef]
- Beyerlein, I.; Demkowicz, M.; Misra, A.; Uberuaga, B. Defect-interface interactions. Prog. Mater. Sci. 2015, 74, 125–210. [Google Scholar] [CrossRef]
- Wang, J.; Misra, A. An overview of interface-dominated deformation mechanisms in metallic multilayers. Curr. Opin. Solid State Mater. Sci. 2011, 15, 20–28. [Google Scholar] [CrossRef]
- Shao, S.; Medyanik, S.N. Dislocation–interface interaction in nanoscale fcc metallic bilayers. Mech. Res. Commun. 2010, 37, 315–319. [Google Scholar] [CrossRef]
- Zhang, R.; Germann, T.; Wang, J.; Liu, X.-Y.; Beyerlein, I. Role of interface structure on the plastic response of Cu/Nb nanolaminates under shock compression: Non-equilibrium molecular dynamics simulations. Scr. Mater. 2013, 68, 114–117. [Google Scholar] [CrossRef]
- Radchenko, I.; Zhu, W.; Qing, L.; Navarro, E.; Sahay, R.; Lee, P.S.; Chen, K. Interface Rotation in Cu/Nb Accumulative Roll Bonded (ARB) Nanolaminates. SSRN Electron. J. 2022. [Google Scholar] [CrossRef]
- Sahay, R.; Budiman, A.S.; Aziz, I.; Navarro, E.; Escoubas, S.; Cornelius, T.W.; Gunawan, F.E.; Harito, C.; Lee, P.S.; Thomas, O.; et al. Crystallographic Anisotropy Dependence of Interfacial Sliding Phenomenon in a Cu(16)/Nb(16) ARB (Accumulated Rolling Bonding) Nanolaminate. Nanomaterials 2022, 12, 308. [Google Scholar] [CrossRef]
- Demkowicz, M.; Thilly, L. Structure, shear resistance and interaction with point defects of interfaces in Cu–Nb nanocomposites synthesized by severe plastic deformation. Acta Mater. 2011, 59, 7744–7756. [Google Scholar] [CrossRef]
- Ali, H.P.A.; Budiman, A. Advances in In situ microfracture experimentation techniques: A case of nanoscale metal–metal multilayered materials. J. Mater. Res. 2019, 34, 1449–1468. [Google Scholar] [CrossRef]
- Radchenko, I.; Anwarali, H.P.; Tippabhotla, S.K.; Budiman, A.S. Effects of interface shear strength during failure of sem-icoherent metal–metal nanolaminates: An example of accumulative roll-bonded Cu/Nb. Acta Mater. 2018, 156, 125–135. [Google Scholar] [CrossRef]
- Ali, H.P.A.; Radchenko, I.; Li, N.; Budiman, A. The roles of interfaces and other microstructural features in Cu/Nb nanolayers as revealed by in situ beam bending experiments inside an scanning electron microscope (SEM). Mater. Sci. Eng. A 2018, 738, 253–263. [Google Scholar] [CrossRef]
- Ali, H.P.A.; Radchenko, I.; Li, N.; Budiman, A. Effect of multilayer interface through in situ fracture of Cu/Nb and Al/Nb metallic multilayers. J. Mater. Res. 2019, 34, 1564–1573. [Google Scholar] [CrossRef]
- Zheng, S.; Wang, J.; Carpenter, J.; Mook, W.; Dickerson, P.; Mara, N.; Beyerlein, I. Plastic instability mechanisms in bimetallic nanolayered composites. Acta Mater. 2014, 79, 282–291. [Google Scholar] [CrossRef]
- Saito, Y.; Utsunomiya, H.; Tsuji, N.; Sakai, T. Novel ultra-high straining process for bulk materials—Development of the accumulative roll-bonding (ARB) process. Acta Mater. 1999, 47, 579–583. [Google Scholar] [CrossRef]
- Wang, J.; Hoagland, R.; Liu, X.; Misra, A. The influence of interface shear strength on the glide dislocation–interface interactions. Acta Mater. 2011, 59, 3164–3173. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, Q.; Shao, S.; Misra, A. Strength and plasticity of nanolaminated materials. Mater. Res. Lett. 2017, 5, 1–19. [Google Scholar] [CrossRef]
- Wang, J.; Misra, A.; Hoagland, R.; Hirth, J. Slip transmission across fcc/bcc interfaces with varying interface shear strengths. Acta Mater. 2012, 60, 1503–1513. [Google Scholar] [CrossRef]
- Misra, A.; Hirth, J.P.; Kung, H. Single-dislocation-based strengthening mechanisms in nanoscale metallic multilayers. Philos. Mag. A 2002, 82, 2935–2951. [Google Scholar] [CrossRef]
- Zheng, S.; Beyerlein, I.J.; Carpenter, J.S.; Kang, K.; Wang, J.; Han, W.; Mara, N.A. High-strength and thermally stable bulk nanolayered composites due to twin-induced interfaces. Nat. Commun. 2013, 4, 1696. [Google Scholar] [CrossRef] [PubMed]
- Nix, W.D.; Gao, H. Indentation size effects in crystalline materials: A law for strain gradient plasticity. J. Mech. Phys. Solids 1998, 46, 411–425. [Google Scholar] [CrossRef]
- Wu, K.; Zhang, J.; Zhang, P.; Wang, Y.; Liu, G.; Zhang, G.; Sun, J. Fracture behavior and adhesion energy of nanostructured Cu/Mo multilayer films. Mater. Sci. Eng. A 2014, 613, 130–135. [Google Scholar] [CrossRef]
- Greer, J.R.; Oliver, W.C.; Nix, W.D. Size dependence of mechanical properties of gold at the micron scale in the absence of strain gradients. Acta Mater. 2005, 53, 1821–1830. [Google Scholar] [CrossRef]
- Greer, J.R.; De Hosson, J.T.M. Plasticity in small-sized metallic systems: Intrinsic versus extrinsic size effect. Prog. Mater. Sci. 2011, 56, 654–724. [Google Scholar] [CrossRef]
- Mara, N.A.; Bhattacharyya, D.; Dickerson, P.; Hoagland, R.G.; Misra, A. Deformability of ultrahigh strength 5 nm Cu/Nb nanolayered composites. Appl. Phys. Lett. 2008, 92, 231901. [Google Scholar] [CrossRef]
- Zhang, H.; Schuster, B.; Wei, Q.; Ramesh, K. The design of accurate micro-compression experiments. Scr. Mater. 2006, 54, 181–186. [Google Scholar] [CrossRef]
- Li, N.; Mara, N.; Wang, J.; Dickerson, P.; Huang, J.; Misra, A. Ex situ and in situ measurements of the shear strength of interfaces in metallic multilayers. Scr. Mater. 2012, 67, 479–482. [Google Scholar] [CrossRef]
- Jaya, B.N.; Kirchlechner, C.; Dehm, G. Can microscale fracture tests provide reliable fracture toughness values? A case study in silicon. J. Mater. Res. 2015, 30, 686–698. [Google Scholar] [CrossRef]
- Mayer, C.; Yang, L.; Singh, S.; Llorca, J.; Materialia, J.L.-A.; Shen, Y.L.; Chawla, N. Anisotropy, size, and aspect ratio effects on micropillar compression of AlSiC nanolaminate composites. Acta Mater. 2016, 114, 25–32. [Google Scholar] [CrossRef]
- Zeng, Z.; Xiao, Y.; Wheeler, J.M.; Tan, J.-C. In situ micropillar compression of an anisotropic metal-organic framework single crystal. Commun. Chem. 2023, 6, 63. [Google Scholar] [CrossRef] [PubMed]
- Maeder, X.; Mook, W.; Niederberger, C.; Michler, J. Quantitative stress/strain mapping during micropillar compression. Philos. Mag. 2011, 91, 1097–1107. [Google Scholar] [CrossRef]
- Dimiduk, D.M.; Woodward, C.; LeSar, R.; Uchic, M.D. Scale-free intermittent flow in crystal plasticity. Science 2006, 312, 1188–1190. [Google Scholar] [CrossRef] [PubMed]
- Weygand, D.; Poignant, M.; Gumbsch, P.; Kraft, O. Three-dimensional dislocation dynamics simulation of the influence of sample size on the stress–strain behavior of fcc single-crystalline pillars. Mater. Sci. Eng. A 2008, 483–484, 188–190. [Google Scholar] [CrossRef]
- Zhou, J.; Averback, R.; Bellon, P. Stability and amorphization of Cu–Nb interfaces during severe plastic deformation: Molecular dynamics simulations of simple shear. Acta Mater. 2014, 73, 116–127. [Google Scholar] [CrossRef]
- Zheng, S.; Beyerlein, I.; Wang, J.; Carpenter, J.; Han, W.; Mara, N. Deformation twinning mechanisms from bimetal interfaces as revealed by in situ straining in the TEM. Acta Mater. 2012, 60, 5858–5866. [Google Scholar] [CrossRef]
- Wang, J.; Kang, K.; Zhang, R.F.; Zheng, S.J.; Beyerlein, I.J.; Mara, N.A. Structure and property of interfaces in ARB Cu/Nb laminated composites. JOM 2012, 64, 1208–1217. [Google Scholar] [CrossRef]
- Anderson, P.M.; Bingert, J.F.; Misra, A.; Hirth, J.P. Rolling textures in nanoscale Cu/Nb multilayers. Acta Mater. 2003, 51, 6059–6075. [Google Scholar] [CrossRef]
- Anderson, P.; Foecke, T.; Hazzledine, P. Dislocation-based deformation mechanisms in metallic nanolaminates. MRS Bull. 1999, 24, 27–33. [Google Scholar] [CrossRef]
- Nizolek, T.; Beyerlein, I.J.; Mara, N.A.; Avallone, J.T.; Pollock, T.M. Tensile behavior and flow stress anisotropy of accumulative roll bonded Cu-Nb nanolaminates. Appl. Phys. Lett. 2016, 108, 051903. [Google Scholar] [CrossRef]
- Wang, J.; Hoagland, R.; Hirth, J.; Misra, A. Atomistic simulations of the shear strength and sliding mechanisms of copper–niobium interfaces. Acta Mater. 2008, 56, 3109–3119. [Google Scholar] [CrossRef]
- Wang, J.; Hoagland, R.G.; Hirth, J.P.; Misra, A. Atomistic modeling of the interaction of glide dislocations with “weak” interfaces. Acta Mater. 2008, 56, 5685–5693. [Google Scholar] [CrossRef]
- Budiman, A.S.; Sahay, R.; Ali, H.P.A.; Tippabhotla, S.K.; Radchenko, I.; Raghavan, N. Interface-mediated plasticity and fracture in nanoscale Cu/Nb multilayers as revealed by in situ clamped microbeam bending. Mater. Sci. Eng. A 2021, 803, 140705. [Google Scholar] [CrossRef]
- Pilkey, W.D.; Pilkey, D.F. Peterson’s Stress Concentration Factors; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Li, Y.; Zhou, Q.; Zhang, S.; Huang, P.; Xu, K.; Wang, F.; Lu, T. On the role of weak interface in crack blunting process in nanoscale layered composites. Appl. Surf. Sci. 2018, 433, 957–962. [Google Scholar] [CrossRef]
- Liu, Z.; Monclús, M.; Yang, L.; Castillo-Rodríguez, M.; Molina-Aldareguía, J.; Llorca, J. Tensile deformation and fracture mechanisms of Cu/Nb nanolaminates studied by in situ TEM mechanical tests. Extrem. Mech. Lett. 2018, 25, 60–65. [Google Scholar] [CrossRef]
- Carpenter, J.S.; McCabe, R.J.; Zheng, S.J.; Wynn, T.A.; Mara, N.A.; Beyerlein, I.J. Processing parameter influence on texture and microstructural evolution in Cu-Nb multilayer composites fabricated via accumulative roll bonding. Metall. Mater. Trans. A 2014, 45, 2192–2208. [Google Scholar] [CrossRef]
- Hattar, K.; Misra, A.; Dosanjh, M.R.F.; Dickerson, P.; Robertson, I.M.; Hoagland, R.G. Direct observation of crack propagation in copper–niobium multilayers. J. Eng. Mater. Technol. 2012, 134, 021014. [Google Scholar] [CrossRef]
- Beyerlein, I.; Mayeur, J.; McCabe, R.; Zheng, S.; Carpenter, J.; Mara, N. Influence of slip and twinning on the crystallographic stability of bimetal interfaces in nanocomposites under deformation. Acta Mater. 2014, 72, 137–147. [Google Scholar] [CrossRef]
- Demkowicz, M.J.; Beyerlein, I.J. The effects of nanoscale confinement on the behavior of metal laminates. Scr. Mater. 2020, 187, 130–136. [Google Scholar] [CrossRef]
- Chen, T.; Yuan, R.; Beyerlein, I.J.; Zhou, C. Predicting the size scaling in strength of nanolayered materials by a discrete slip crystal plasticity model. Int. J. Plast. 2020, 124, 247–260. [Google Scholar] [CrossRef]
- Dong, S.; Chen, T.; Huang, S.; Li, N.; Zhou, C. Thickness-dependent shear localization in Cu/Nb metallic nanolayered composites. Scr. Mater. 2020, 187, 323–328. [Google Scholar] [CrossRef]
- Budiman, A.S.; Han, S.-M.; Li, N.; Wei, Q.-M.; Dickerson, P.; Tamura, N.; Kunz, M.; Misra, A. Plasticity in the nanoscale Cu/Nb single-crystal multilayers as revealed by synchrotron Laue x-ray microdiffraction. J. Mater. Res. 2012, 27, 599–611. [Google Scholar] [CrossRef]
- Misra, A.; Demkowicz, M.J.; Wang, J.; Hoagland, R.G. The multiscale modeling of plastic deformation in metallic nanolayered composites. JOM 2008, 60, 39–42. [Google Scholar] [CrossRef]
- Mara, N.A.; Bhattacharyya, D.; Hirth, J.P.; Dickerson, P.; Misra, A. Mechanism for shear banding in nanolayered composites. Appl. Phys. Lett. 2010, 97, 021909. [Google Scholar] [CrossRef]
- Jonnalagadda, K.; Alankar, A.; Balila, N.J.; Bhandakkar, T. Advances in Structural Integrity: Structural Integrity over Multiple Length Scales; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sahay, R.; Radchenko, I.; Ananthasubramanian, P.; Harito, C.; Briffod, F.; Yasuda, K.; Shiraiwa, T.; Jhon, M.; Speaks, R.; Speaks, D.; et al. Interface Rotation in Accumulative Rolling Bonding (ARB) Cu/Nb Nanolaminates Under Constrained and Unconstrained Loading Conditions as Revealed by In Situ Micromechanical Testing. Nanomaterials 2025, 15, 1528. https://doi.org/10.3390/nano15191528
Sahay R, Radchenko I, Ananthasubramanian P, Harito C, Briffod F, Yasuda K, Shiraiwa T, Jhon M, Speaks R, Speaks D, et al. Interface Rotation in Accumulative Rolling Bonding (ARB) Cu/Nb Nanolaminates Under Constrained and Unconstrained Loading Conditions as Revealed by In Situ Micromechanical Testing. Nanomaterials. 2025; 15(19):1528. https://doi.org/10.3390/nano15191528
Chicago/Turabian StyleSahay, Rahul, Ihor Radchenko, Pavithra Ananthasubramanian, Christian Harito, Fabien Briffod, Koki Yasuda, Takayuki Shiraiwa, Mark Jhon, Rachel Speaks, Derrick Speaks, and et al. 2025. "Interface Rotation in Accumulative Rolling Bonding (ARB) Cu/Nb Nanolaminates Under Constrained and Unconstrained Loading Conditions as Revealed by In Situ Micromechanical Testing" Nanomaterials 15, no. 19: 1528. https://doi.org/10.3390/nano15191528
APA StyleSahay, R., Radchenko, I., Ananthasubramanian, P., Harito, C., Briffod, F., Yasuda, K., Shiraiwa, T., Jhon, M., Speaks, R., Speaks, D., Lee, K., Enoki, M., Raghavan, N., & Budiman, A. S. (2025). Interface Rotation in Accumulative Rolling Bonding (ARB) Cu/Nb Nanolaminates Under Constrained and Unconstrained Loading Conditions as Revealed by In Situ Micromechanical Testing. Nanomaterials, 15(19), 1528. https://doi.org/10.3390/nano15191528








