Frequency Dependence of FINEMET/Ni/G Composite Ribbons Coated with As-Grown Graphene Layer via Chemical Vapor Deposition
Abstract
1. Introduction
2. Experiments
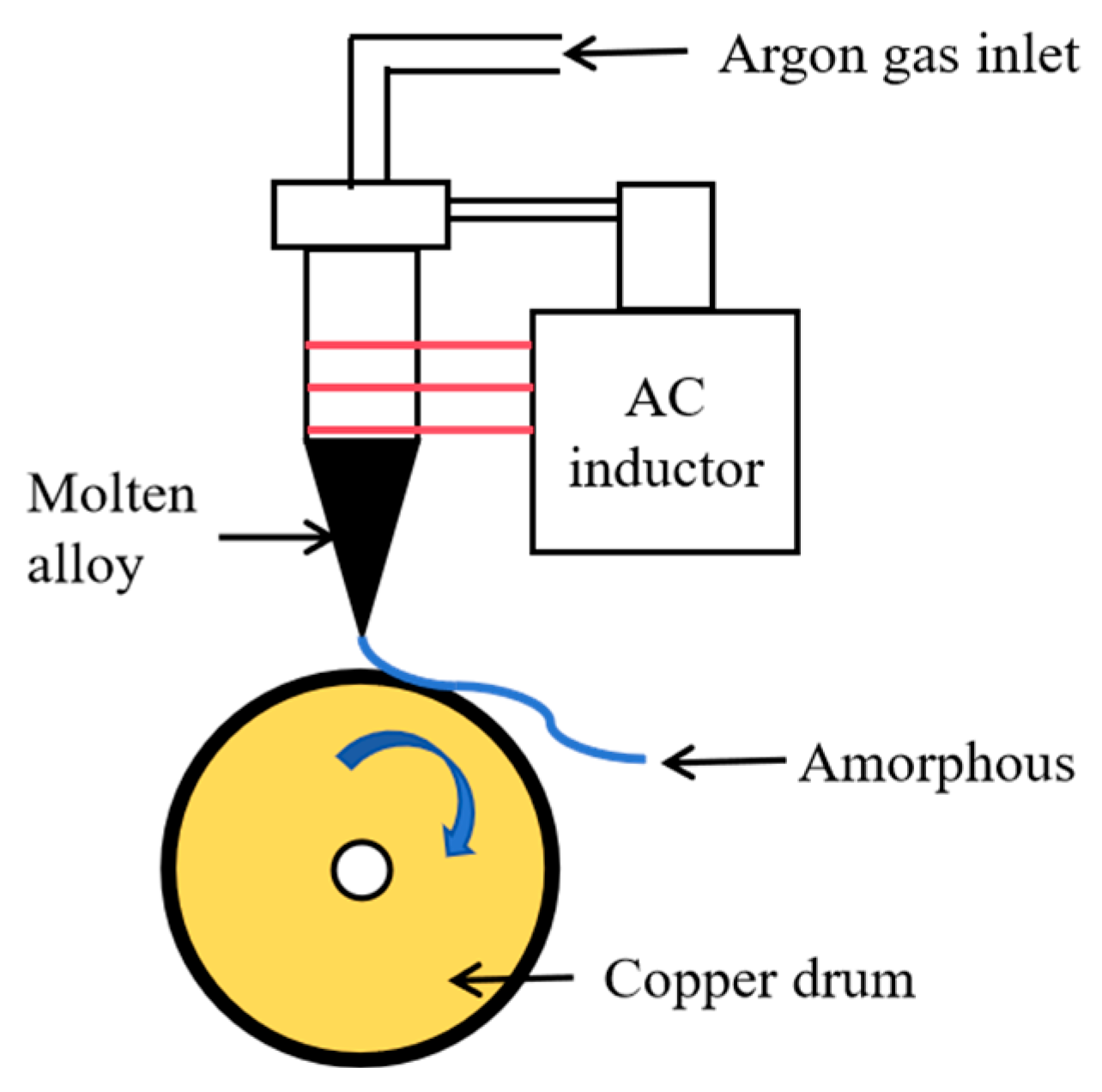
2.1. Preparation of FINEMET Ribbons
2.2. Preparation of FINEMET/G
2.3. Preparation of FINEMET/Ni/G
2.4. Characterization
3. Results and Discussion
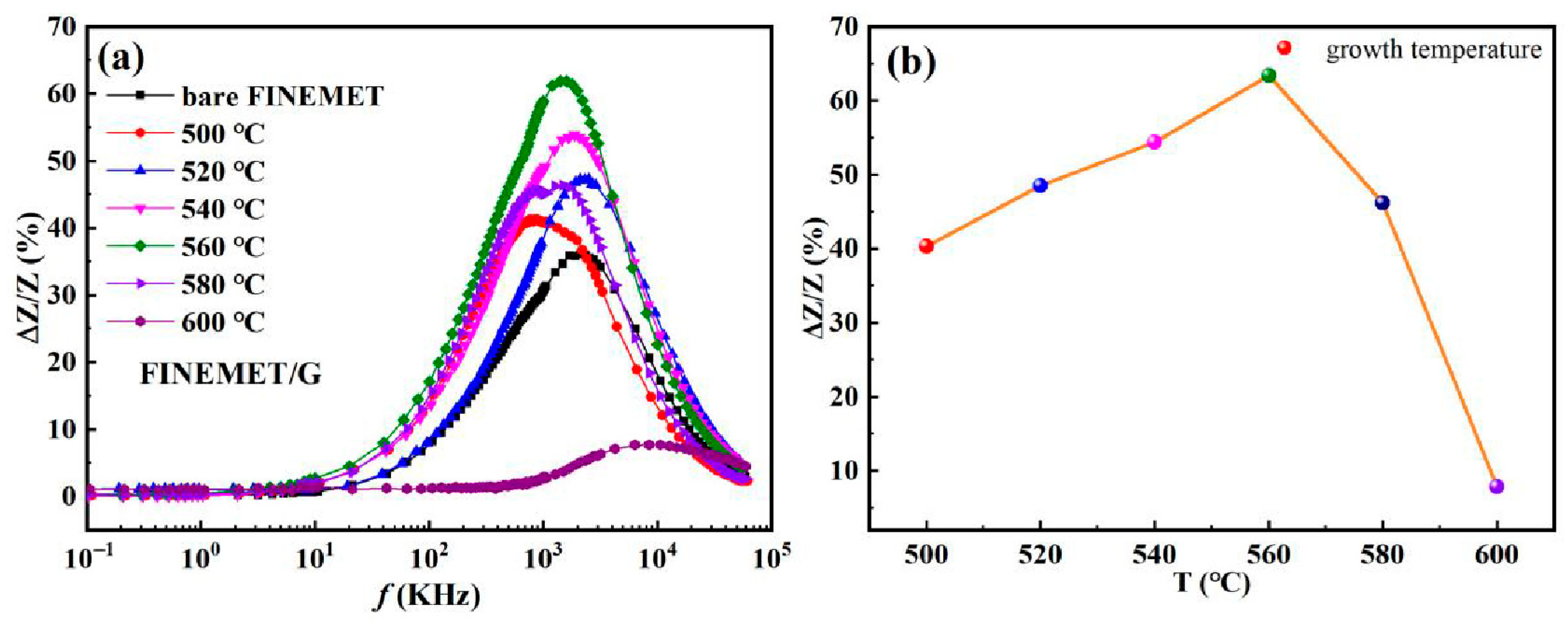
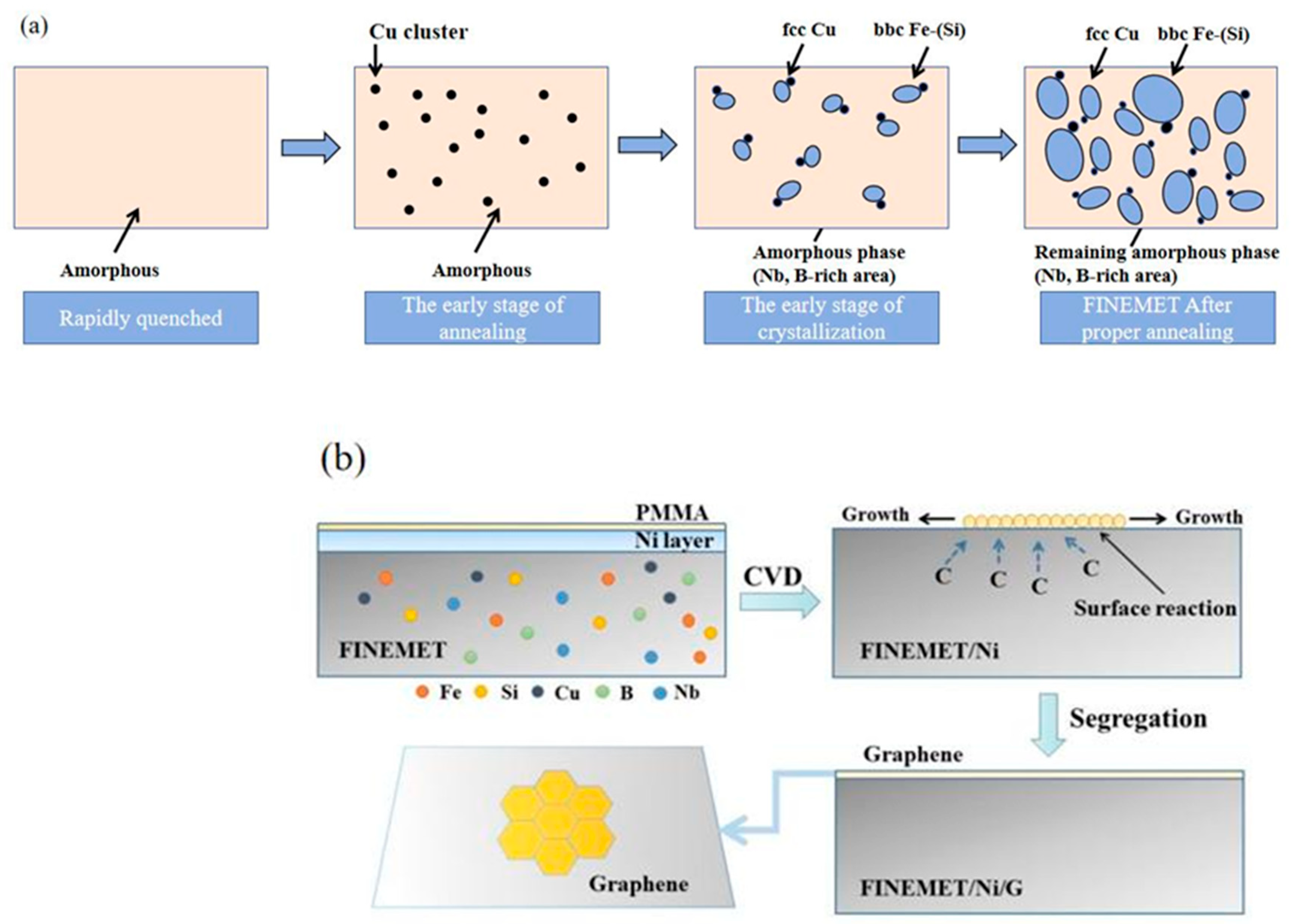
3.1. Micro-Structure, Morphologies, and GMI Measurement of FINEMET/G
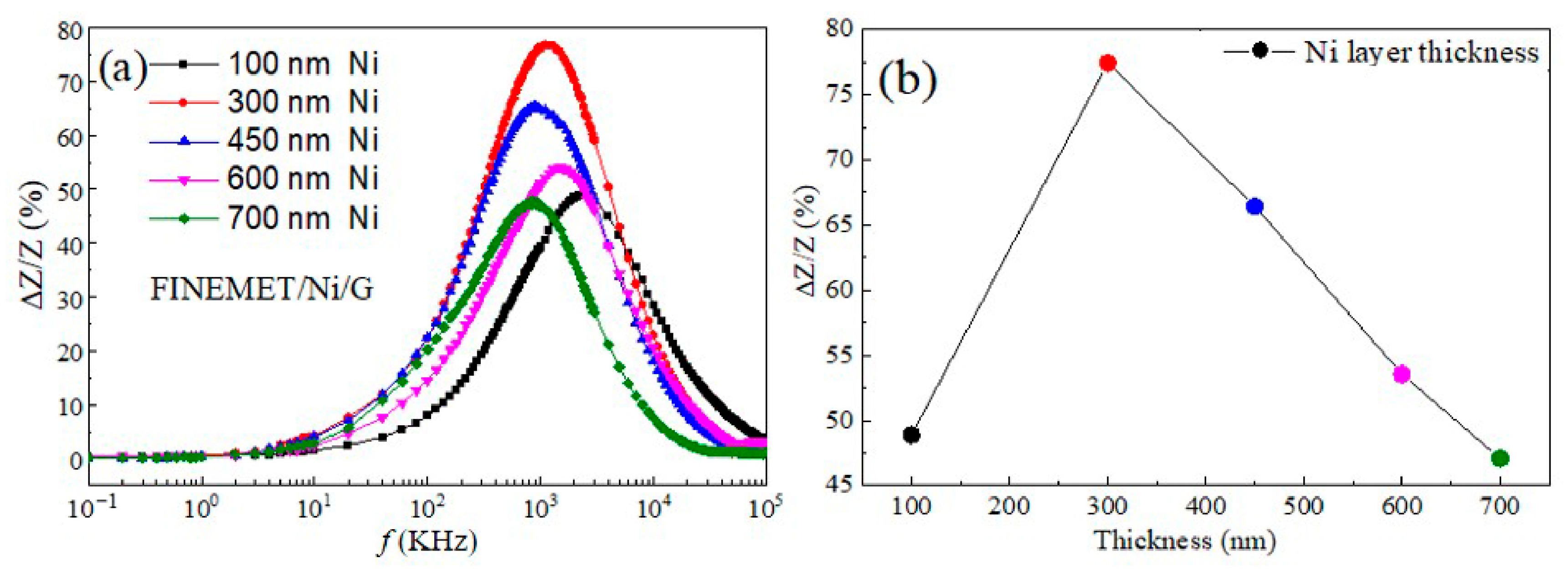
3.2. Microstructure, Morphologies, and GMI Measurement of FINEMET/Ni/G
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lv, H.; da Silva, A.; Figueroa, A.I.; Guillemard, C.; Aguirre, I.F.; Camosi, L.; Aballe, L.; Valvidares, M.; Valenzuela, S.O.; Schubert, J.; et al. Large-Area Synthesis of Ferromagnetic Fe5−xGeTe2/Graphene van der Waals Heterostructures with Curie Temperature above Room Temperature. Small 2023, 19, 2302387. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, Z.; Liu, M.; Sun, X. Non-Contact Current Sensing System Based on the Giant Magnetoimpedance Effect of CoFeNiSiB Amorphous Ribbon Meanders. Micromachines 2024, 15, 161. [Google Scholar] [CrossRef]
- Wang, Y.J.; Li, J.F.; Viehland, D. Magneto-electrics for magnetic sensor applications: Status, challenges and perspectives. Mater. Today 2014, 17, 269–275. [Google Scholar] [CrossRef]
- Reig, C.; Cubells-Beltran, M.D.; Muñoz, D.R. Magnetic field sensors based on giant magnetoresistance (GMR) technology: Applications in electrical current sensing. Sensors 2009, 10, 7919–7942. [Google Scholar] [CrossRef]
- Panina, L.V.; Mohri, K. Magneto-impedance effect in amorphous wires. Appl. Phys. Lett. 1994, 65, 1189–1191. [Google Scholar] [CrossRef]
- Phan, M.H.; Peng, H.X. Giant magnetoimpedance materials: Fundamentals and applications. Prog. Mater. Sci. 2008, 53, 323–420. [Google Scholar] [CrossRef]
- Nabias, J.; Asfour, A.; Yonnet, J.P. Temperature effect on GMI sensor: Comparison between diagonal and off-diagonal response. Sens. Actuators A Phys. 2019, 289, 50–56. [Google Scholar] [CrossRef]
- Dokukin, M.E.; Perov, N.S.; Kim, C.O.; Kim, C.G. The cryogenic treatment effect on the magneto-impedance properties of the Co- and Fe-based amorphous ribbons. Phys. Status Solidi A Appl. Mater. Sci. 2004, 201, 1988–1991. [Google Scholar] [CrossRef]
- Xiao, S.Q.; Liu, Y.H.; Dai, Y.Y.; Zhang, L.; Zhou, S.X.; Liu, G.D. Giant magneto-impedance effect in sandwiched films. J. Appl. Phys. 1999, 85, 4127–4130. [Google Scholar] [CrossRef]
- Morikawa, T.; Nishile, Y.; Yamadera, H.; Nonomura, Y.; Takeuchi, M.; Sakata, J.; Taga, Y. Enhancement of giant magneto-impedance in layered film by insulator separation. IEEE Trans. Magn. 1996, 32, 4965–4967. [Google Scholar] [CrossRef]
- García, C.; Florez, J.M.; Vargas, P.; Ross, C.A. Asymmetrical giant magnetoimpedance in exchange-biased NiFe. Appl. Phys. Lett. 2010, 96, 232501. [Google Scholar] [CrossRef]
- Barandiaran, J.M.; Kurlyandskaya, G.V.; Vazquez, M.; Gutierrez, J.; Garcia, D.; Munoz, J.L. A simple model of the magnetoresistance contribution to the magneto-impedance effect in thin films. Phys. Status Solidi A Appl. Mater. Sci. 1999, 171, R3–R4. [Google Scholar] [CrossRef]
- Ku, W.J.; Ge, F.D.; Zhu, J.N. Effects of magnetic permeability and resistivity on magneto-impedance in Fe-Cu-Nb-Si-B alloy ribbons. Phys. D Appl. Phys. 1997, 30, 1842–1845. [Google Scholar] [CrossRef]
- Luan, H.Y.; Li, X.; Wang, R.L.; Peng, H.L.; Chen, D.L.; Zhao, Z.J. Influence of pH value on the properties of the composite wires by chemical deposition. J. East China Norm. Univ. Nat. Sci. 2013, 127–132. [Google Scholar]
- Zhang, G.H.; Cheng, J.K.; Wang, Q.J.; Yuan, W.Z.; Zhao, Z.J. Effect of PH on the giant magneto-impedance properties of Cu/CoNiP composite wire prepared by chemical deposition. Chin. J. Appl. Chem. 2008, 25, 1277–1280. [Google Scholar]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef]
- Zhu, Y.W.; Murali, S.; Cai, W.W.; Li, X.S.; Suk, J.; Ruoff, R.S. Graphene and graphene oxide: Synthesis, properties, and applications. Adv. Mater. 2010, 22, 3906–3924. [Google Scholar] [CrossRef]
- Neto, A.H.C.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109–162. [Google Scholar] [CrossRef]
- Lee, C.; Wei, X.D.; Kysar, J.W.; Hone, J. Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef]
- Geim, A.K. Graphene: Status and Prospects. Science 2009, 324, 1530–1534. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Fal’ko, V.I.; Colombo, L.; Gellert, P.R.; Schwab, M.G.; Kim, K. A roadmap for graphene. Nature 2012, 490, 192–200. [Google Scholar] [CrossRef] [PubMed]
- Rao, C.N.R.; Sood, A.K.; Subrahmanyam, K.S.; Govindaraj, A. Graphene: The new two-dimensional nanomaterial. Angew. Chem. Int. Ed. 2009, 48, 7752–7777. [Google Scholar] [CrossRef]
- Zou, J.T.; Chen, Y.J.; Li, X.; Song, Y.N.; Zhao, Z.J. Observation of the transition state of domain wall displacement and GMI effect of FINEMET/graphene composite ribbons. RSC Adv. 2019, 9, 39133–39142. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.J.; Zou, J.T.; Shu, X.F.; Song, Y.N.; Zhao, Z.J. Enhanced giant magneto-impedance effects in sandwich FINEMET/rGO/FeCo composite ribbons. Appl. Surf. Sci. 2021, 545, 149021. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, C.; Duan, Z.; Liu, Q.; Wang, J.; Shi, W. Enhanced magneto-impedance effect of Fe75.5Cu1Nb3Si13.5B7 ribbon covered by in-situ growth vertical graphene sheets. Mater. Lett. 2018, 222, 131–134. [Google Scholar] [CrossRef]
- Yang, Z.; Chong, L.; Sun, X.C.; Zhou, Y.; Liu, Y. Enhanced GMI effect in tortuous-shaped Co-based amorphous ribbons coated with graphene. J. Mater. Sci. Mater. Electron. 2016, 27, 3493–3498. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin aarbon films. Science 2004, 306, 666–669. [Google Scholar]
- Yan, K.; Peng, H.; Zhou, Y.; Li, H.; Liu, Z. Formation of bilayer bernal graphene: Layer-by-layer epitaxy via chemical vapor deposition. Nano Lett. 2011, 11, 1106. [Google Scholar] [CrossRef]
- Alfonso, R.; Xiaoting, J.; John, H.; Nezich, D.; Dresselhaus, M.S.; Kong, J. Large area, few-layer graphene films on arbitrary substrates by chemical vapor deposition. Nano Lett. 2009, 9, 30–35. [Google Scholar]
- Li, X.S.; Cai, W.W.; An, J.H.; Yang, D.X. Large-Area Synthesis of High-Quality and Uniform Graphene Films on Copper Foils. Science 2009, 324, 1312–1314. [Google Scholar] [CrossRef]
- Tang, L.H.; Wang, Y.; Li, Y.M.; Feng, H.B.; Lu, J.; Li, J.H. Preparation; Structure, and Electrochemical Properties of Reduced Graphene Sheet Films. Adv. Funct. Mater. 2009, 19, 2782–2789. [Google Scholar] [CrossRef]
- Botas, C.; Alvarez, P.; Blanco, P.; Granda, M.; Blanco, C.; Santamaria, R.; Romasanta, L.J.; Verdejo, R.; Lopez-Manchado, M.A.; Menendez, R. Graphene materials with different structures prepared from the same graphite by the Hummers and Brodie methods. Carbon 2013, 65, 156–164. [Google Scholar] [CrossRef]
- Phan, M.H.; Peng, H.X.; Wisnom, M.R.; Yu, S.C.; Chau, N. Effect of annealing on the microstructure and magnetic properties of Fe-based nanocomposite materials. Compos. Part A Appl. Sci. Manuf. 2006, 37, 191–196. [Google Scholar] [CrossRef]
- Xie, L.; Li, X.; Zou, J.T.; Pan, H.L.; Xie, W.H.; Zhao, Z.J. Optimized giant magneto-impedance effect in electroless-deposited NiFeP/Cu composite wires. Surf. Coat. Technol. 2018, 334, 158–163. [Google Scholar] [CrossRef]
- Kraus, L. Theory of giant magneto-impedance in the planar conductor with uniaxial magnetic anisotropy. Magn. Magn. Mater. 1999, 195, 764–778. [Google Scholar] [CrossRef]
- Zhong, Z.Y.; Lan, Z.W.; Zhang, H.W.; Liu, Y.L.; Wang, H.C. Computation on giant magneto-impedance effects in ferromagnetic/non-ferromagnetic/ferromagnetic layered thin films. Acta Phys. Sin. 2001, 50, 1610–1615. [Google Scholar] [CrossRef]
- Stroscio, J.A.; Bare, S.R.; Ho, W. The chemisorption and decomposition of ethylene and acetylene on Ni(110). Surf. Sci. 1984, 148, 499–525. [Google Scholar] [CrossRef]
- Gao, J.; Yip, J.; Zhao, J. Graphene nucleation on transition metal surface: Structure transformation and role of the metal step edge. J. Am. Chem. Soc. 2011, 133, 5009–5015. [Google Scholar] [CrossRef]
- Ferrari, A.C.; Meyer, J.C.; Scardaci, V.; Casiraghi, C.; Lazzeri, M.; Mauri, F. Raman spectrum of graphene and graphene Layers. Phys. Rev. Lett. 2006, 97, 4. [Google Scholar] [CrossRef]
- Muzyka, R.; Drewniak, S.; Pustelny, T.; Sajdak, M.; Drewniak, L. Characterization of graphite oxide and reduced graphene oxide obtained from different graphite precursors and oxidized by different methods using Raman spectroscopy. Materials 2018, 11, 1050. [Google Scholar] [CrossRef]
- Stankovich, S.; Dikin, D.A.; Pinera, R.D.; Kohlhaas, K.A.; Kleinhammes, A.; Jia, Y.Y.; Wu, Y.; Ruffo, R.S. Synthesis of graphene-based nanosheets via chemical reduction of exfoliated graphite oxide. Carbon 2007, 45, 1558–1565. [Google Scholar] [CrossRef]
- Compton, O.C.; Nguyen, S.T. Graphene oxide, highly reduced graphene oxide, and graphene: Versatile building blocks for carbon-based materials. Small 2010, 6, 711–723. [Google Scholar] [CrossRef] [PubMed]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Chen, Y.; Zhao, Z.; Song, Y. Frequency Dependence of FINEMET/Ni/G Composite Ribbons Coated with As-Grown Graphene Layer via Chemical Vapor Deposition. Nanomaterials 2025, 15, 1310. https://doi.org/10.3390/nano15171310
Wu Y, Chen Y, Zhao Z, Song Y. Frequency Dependence of FINEMET/Ni/G Composite Ribbons Coated with As-Grown Graphene Layer via Chemical Vapor Deposition. Nanomaterials. 2025; 15(17):1310. https://doi.org/10.3390/nano15171310
Chicago/Turabian StyleWu, Yupo, Yijun Chen, Zhenjie Zhao, and Yenan Song. 2025. "Frequency Dependence of FINEMET/Ni/G Composite Ribbons Coated with As-Grown Graphene Layer via Chemical Vapor Deposition" Nanomaterials 15, no. 17: 1310. https://doi.org/10.3390/nano15171310
APA StyleWu, Y., Chen, Y., Zhao, Z., & Song, Y. (2025). Frequency Dependence of FINEMET/Ni/G Composite Ribbons Coated with As-Grown Graphene Layer via Chemical Vapor Deposition. Nanomaterials, 15(17), 1310. https://doi.org/10.3390/nano15171310






