Use of Factorial Design for Calculation of Second Hyperpolarizabilities
Abstract
1. Introduction
2. State of the Art and Challenges in Second Hyperpolarizability Calculations
3. Materials Studied
4. Computational Methods
- Computational methodology (one statistical level: coupled-perturbed Hartree–Fock or Kohn–Sham augmented with the finite field for the third dimension (CPHF+FF or CPKS+FF); another statistical level: response-equation formalism—RE);
- two-electron (exchange and correlation) Hamiltonian: up to 18 statistical levels in total—(a) wave-function-based methods: HF [107], CC2 [108], CCSD [109]; (b) global-hybrid (GH) density functionals: B3LYP [110,111] ( = 0.2), BH&HLYP [112] ( = 0.2); here is the contribution of HF-like exchange; (c) -meta-global-hybrid (MGH) density functionals: M06 [113] ( = 0.27), M06-2X [113] ( = 0.54) [114], MN15 [115] ( = 0.44); (d) eight range-separated-hybrid (RSH) density functionals, based on LC-BLYP [116] and CAM-B3LYP [117], scheme, with systematic variation in , , parameters (see the Supporting Information); (e) a -meta-range-separated-hybrid density functional M11 [118] ( = 0.25, = 0.43 and = 1.00);
- integration grid for DFT methods, tested separately for Gaussian and Dalton because of incomplete compatibility between software suites; the differences are explained in Section 2 “The details of the quantum chemical calculations performed”, paragraphs g and h, in Supplementary Information.
- static or dynamic calculation of the second hyperpolarizability (two statistical levels)—available only for Dalton calculations; this is explained in Section 2 “The details of the quantum chemical calculations performed”, paragraph i, in the Supplementary Information.
5. Design and Statistics: Comparison Between the Calculated and the Experimental Data
5.1. Choice of Quality Descriptors for Modeling
5.2. Factorial Design of the Study
5.3. Statistical Analysis of the Results
6. Results and Discussion
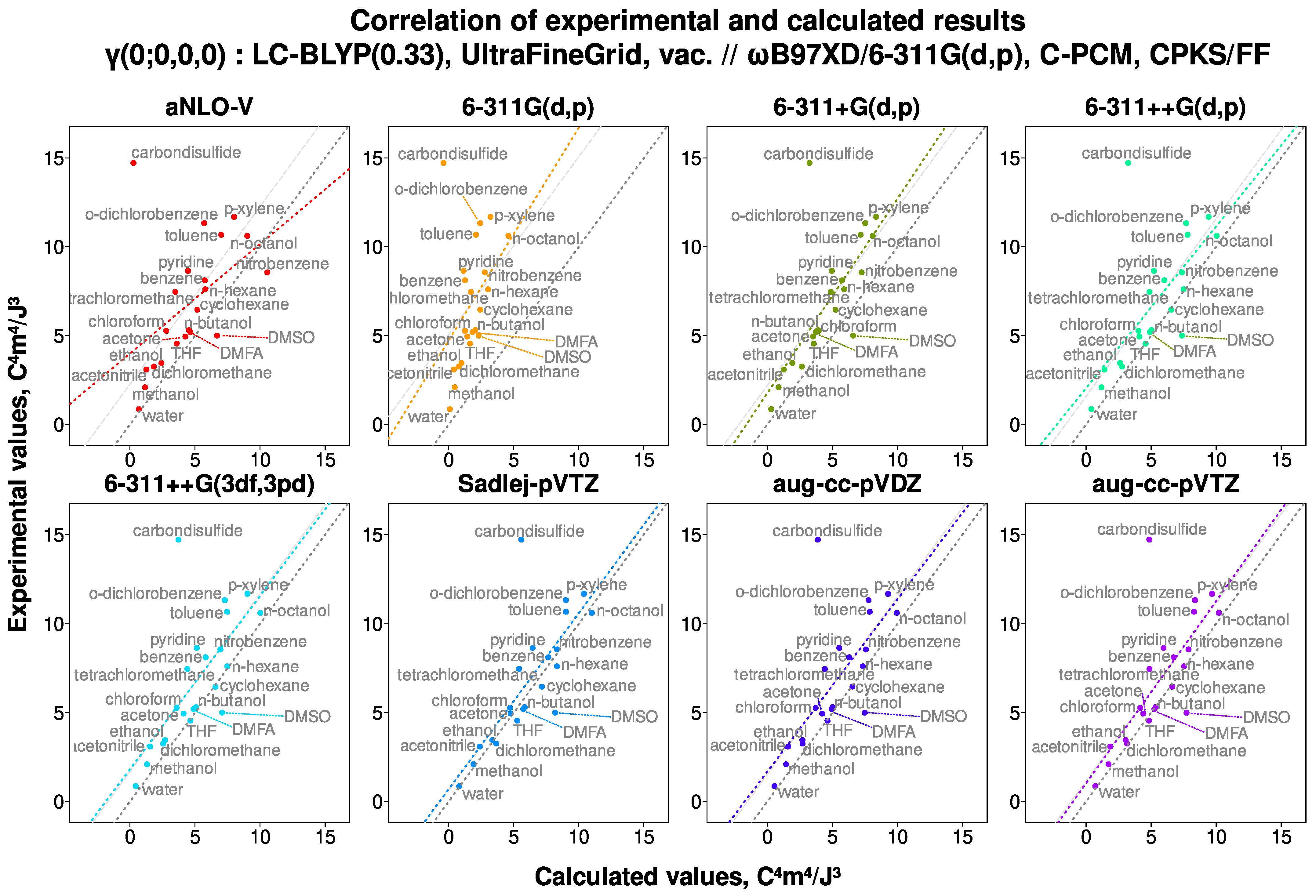
6.1. Examination of Scatter Plots
6.2. Analysis of Factor Influence
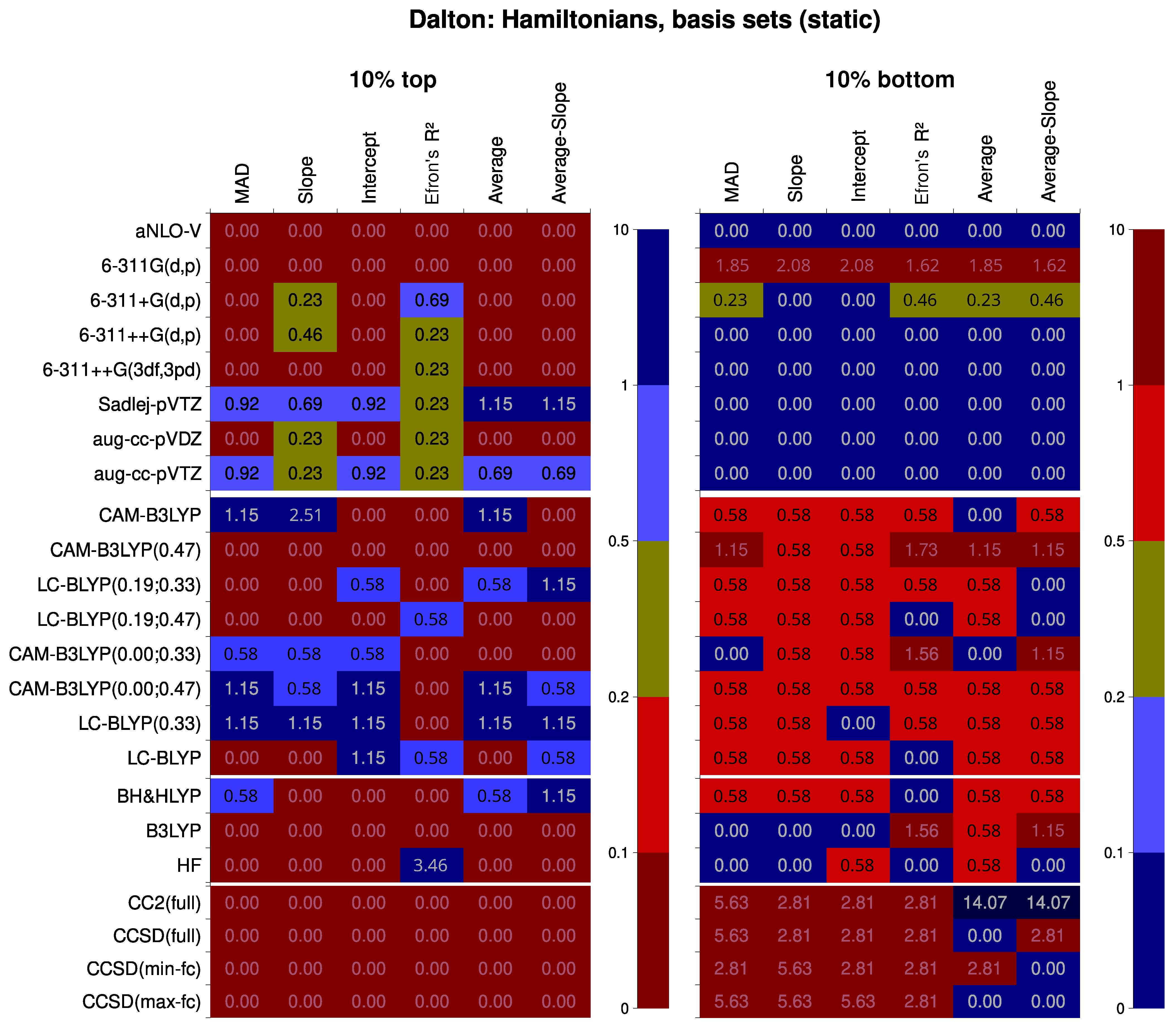
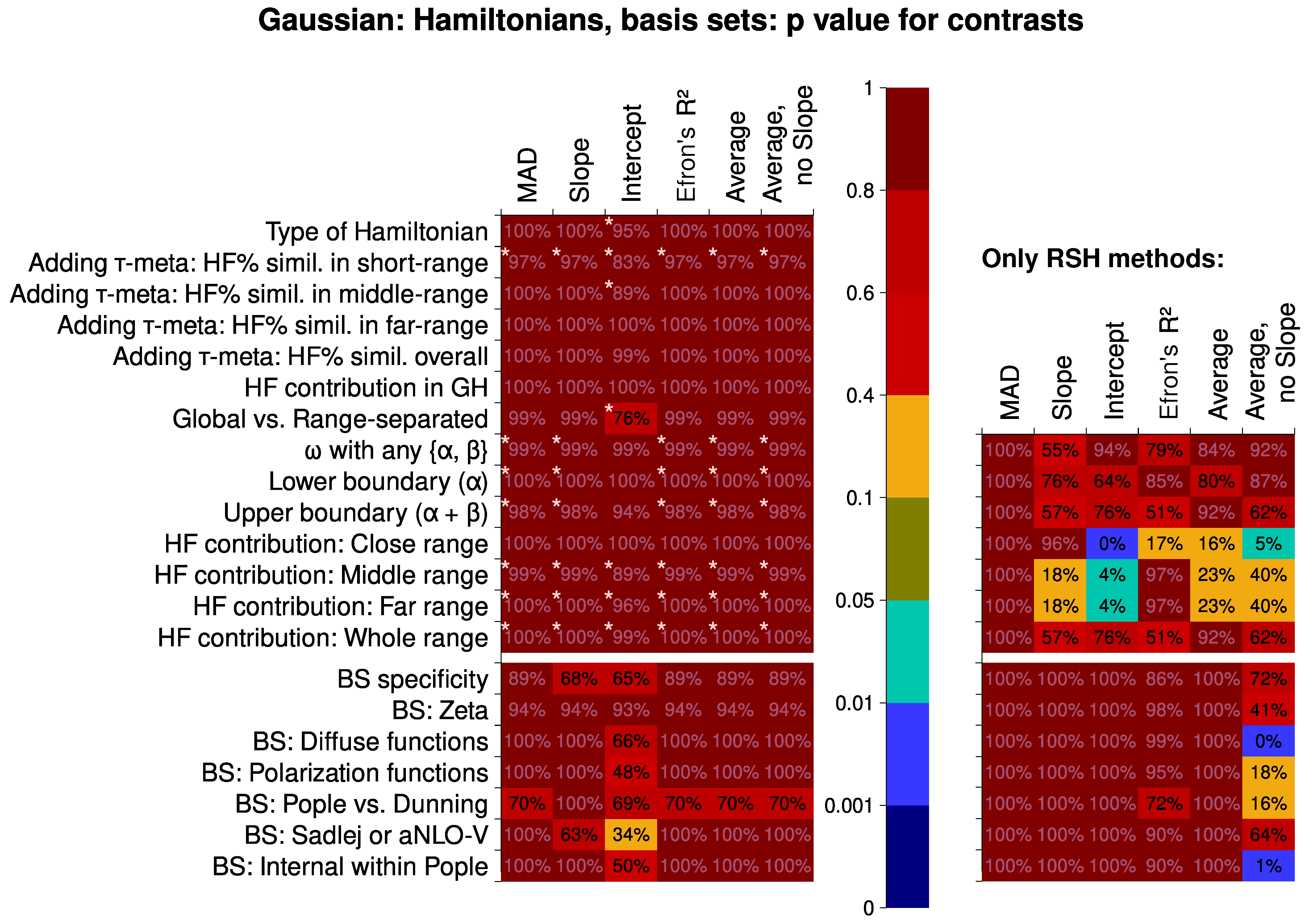
6.2.1. Hamiltonians and Basis Sets
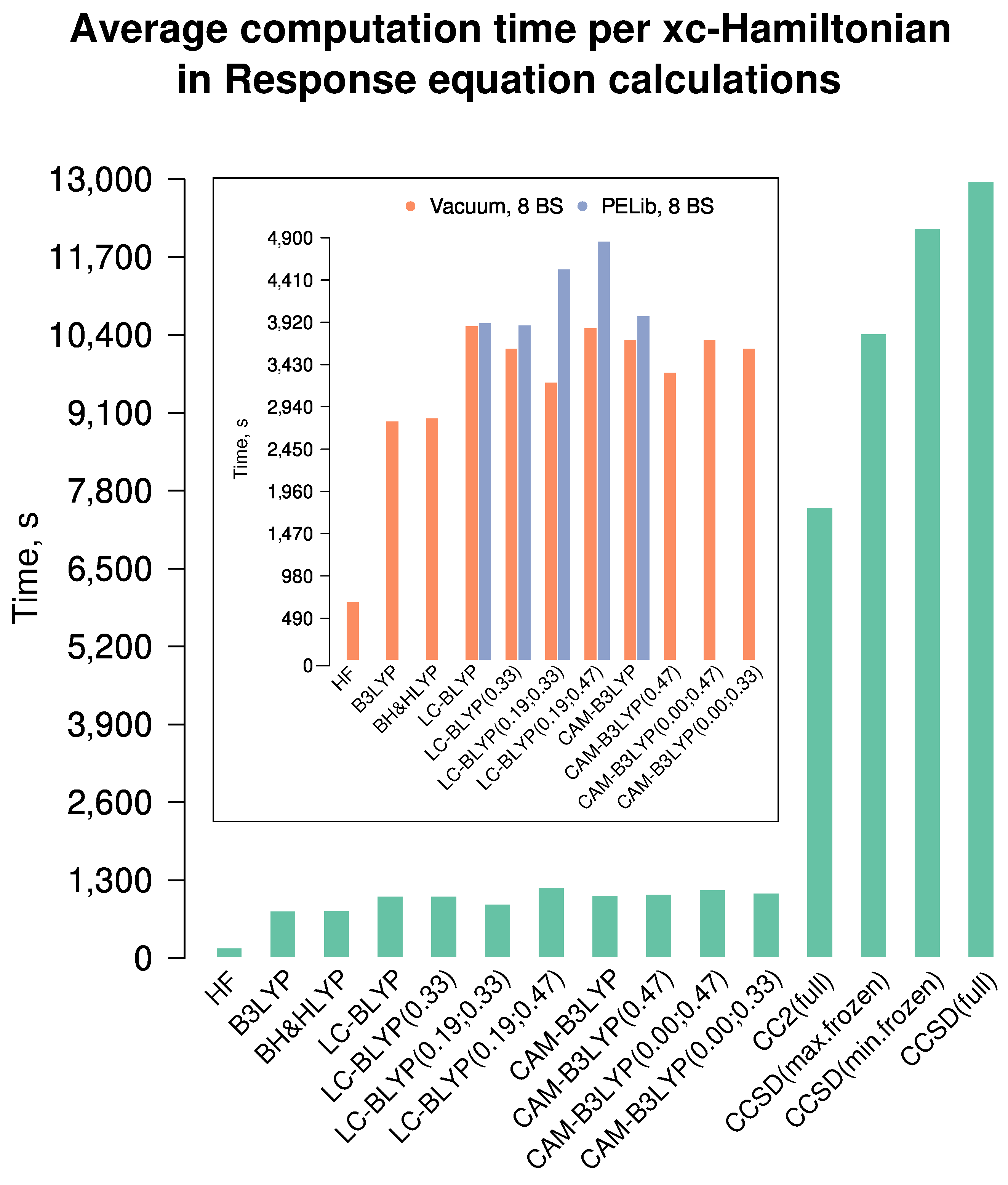
6.2.2. Computation Time
6.2.3. Effect of Hydrogen Bond Formation and Multiple Conformers Possible
7. Conclusions
- Presence of diffuse functions is mandatory in a basis set used for the calculations of the second hyperpolarizability. Adding large amounts of polarization functions, contrariwise, does not improve results but leads to great computational expenses. Sadlej et al.’s basis set (POL or Sadlej-pVTZ) [104,105] is computationally very robust and resource-efficient, and thus highly recommended for calculations. The basis set aug-cc-pVTZ is only slightly and only sometimes performing better, yet it is much more resource-demanding.
- LC-BLYP(0.33)/Sadlej-pVTZ is a very well-performing choice of model chemistry in terms of both predictive power and computational efficiency.
- HF/Sadlej-pVTZ is a very good model chemistry for fast and crude screening of compounds. To increase its predictive power, the slope and the intercept should be determined using some more advanced reference calculations.
- Coupled-cluster (CC) formalism as implemented for the response-equation formalism in Dalton 2020.0.1 is not well suited for the production calculations of the second hyperpolarizability, possibly because the formalism is not yet well implemented. In addition, coupled-cluster calculations are rather sensitive to the basis set used.
- Even the maximal available freezing of the core orbitals does not diminish the performance of the CC methods but significantly decreases the resource consumption.
- The meta-global-hybrid density functionals are not suited for the calculations of the second hyperpolarizability. Also, they are basis-set-dependent and basis-set-inefficient.
- In the construction of a range-separated hybrid density functional (RSH) for the calculations of the second hyperpolarizability, it is generally important to have comparatively low HF-like exchange percentage in the far- and middle-range inter-electronic distances and (to a lesser extent) even slightly lower percentage in the close range. It is not worthwhile to use the overall average percentage of the HF-like exchange as a parameter for optimizing the results. However, a specific combination of RSH parameters can produce better results than following these rules.
- The mean absolute deviation (MAD) descriptor provides less efficient discrimination between factors when comparing different quantum chemical methods. The correlation descriptors should be used instead. The most susceptible descriptor is the intercept of the linear correlation.
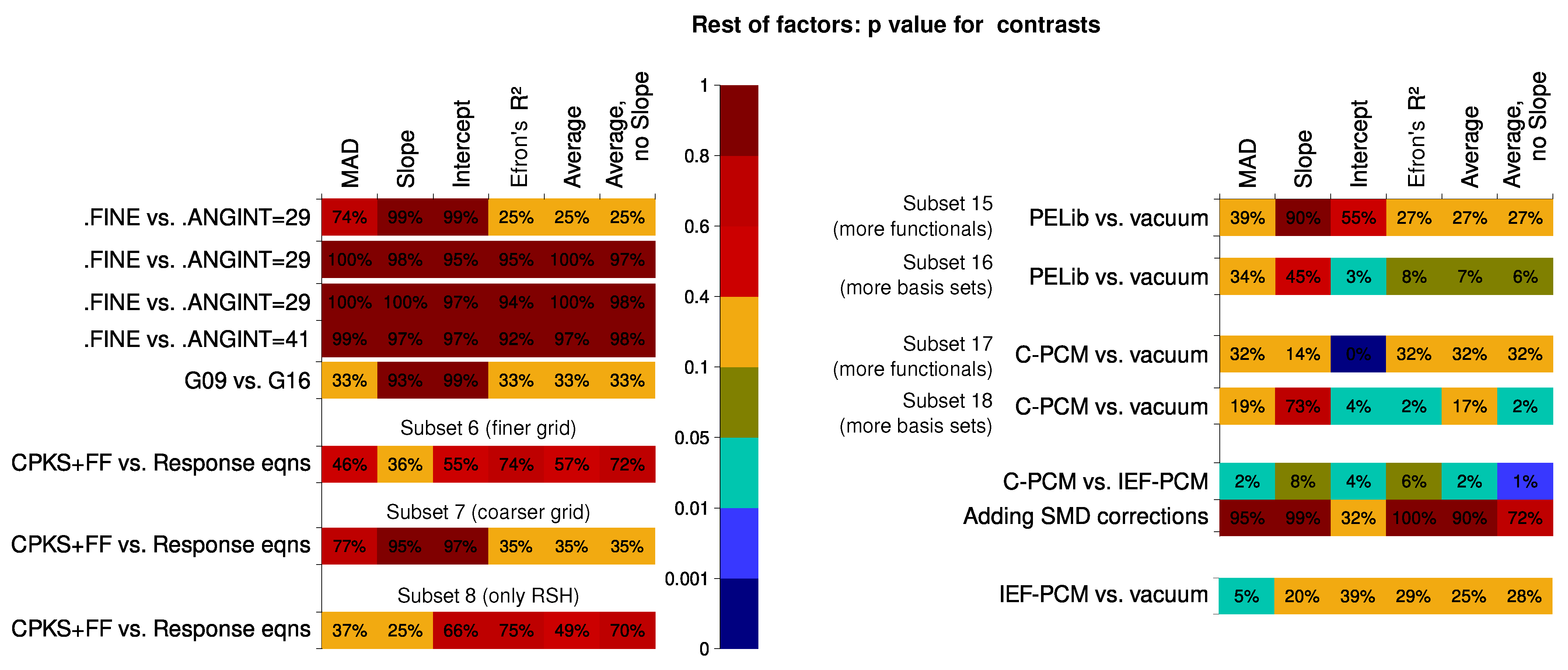
- There is little difference in whether the coupled-perturbed KS/HF plus finite field (CPKS+FF) or the response-equation formalism is used for the calculation of the second hyperpolarizability.
- Calculations in the vacuum are still more robust than calculations with contemporary solvent models included in the Hamiltonian. However, the PELib model is close in its performance to the vacuum calculations and never yields results that are particularly far from the experiment in terms of statistical descriptors. IEF-PCM and SMD do not outperform the simple C-PCM solvation model.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| a.u. | Atomic Units |
| C-PCM | Conductor-like Polarizable Continuum Model |
| CC2 | Coupled-Cluster Singles and Approximate Doubles |
| CCSD | Coupled-Cluster Singles and Doubles |
| CCn | Coupled Cluster (in general) |
| CPHF | Coupled-Perturbed Hartree–Fock |
| CPKS | Coupled-Perturbed Kohn–Sham |
| DFT | Density Functional Theory |
| DMSO | DiMethyl SulfOxide |
| DMFA | -DiMethylFormAmide |
| FF | Finite Field |
| FFD | Full-Factorial Design |
| GH | Global-Hybrid [density functionals] |
| HF | Hartree–Fock |
| IEF-PCM | Integral Equation Formalism PCM |
| MAD | Mean Absolute Deviation |
| MCSCF | Multi-Configurational Self-Consistent Field |
| MGH | -Meta-Global-Hybrid [density functionals] |
| MP2 | Møller–Plesset Perturbation Theory (second-order) |
| MPn | Møller–Plesset Perturbation Theory (in general) |
| OKE | Optical Kerr effect |
| PCM | Polarizable Continuum Model |
| RE | Response Equation |
| RSH | Range-Separated-Hybrid [density functionals] |
| SMD | Solvation Model based on Density |
| SOS | Sum-Over-States |
| TDDFT | Time-Dependent Density Functional Theory |
References
- Cui, Y.; Ren, H.; Yu, J.; Wang, Z.; Qian, G. An indanone-based alkoxysilane dye with second order nonlinear optical properties. Dye. Pigment. 2009, 81, 53–57. [Google Scholar] [CrossRef]
- Manjunatha, M.; Adhikari, A.; Hegde, P.; Sandeep, C.S.S.; Philip, R. A New Nonlinear Optically Active Donor–Acceptor-Type Conjugated Polymer: Synthesis and Electrochemical and Optical Characterization. J. Electron. Mater. 2010, 39, 2711–2719. [Google Scholar] [CrossRef]
- Qiu, Y.; Li, Z.H.; Ma, N.; Sun, S.; Zhang, M.; Liu, P.J. Third-order nonlinear optical properties of molecules containing aromatic diimides: Effects of the aromatic core size and a redox-switchable modification. J. Mol. Graph. Model. 2013, 41, 79–88. [Google Scholar] [CrossRef]
- Agarwal, P.; Choudhary, N.; Gupta, A.; Tandon, P. Density functional theory studies on the structure, spectra (FT-IR, FT-Raman, and UV) and first order molecular hyperpolarizability of 2-hydroxy-3-methoxy-N-(2-chloro-benzyl)-benzaldehyde-imine: Comparison to experimental data. Vibr. Spectrosc. 2013, 64, 134–147. [Google Scholar] [CrossRef]
- Hatua, K.; Nandi, P.K. Double coned inverse sandwich complexes M-(ηn4-C4H4)-M’ of Gr-IA and Gr-IIA metals: Theoretical study of electronic structure and second hyperpolarizability. J. Mol. Model. 2014, 20, 2440. [Google Scholar] [CrossRef]
- Altürk, S.; Avcı, D.; Tamer, Ö.; Atalay, Y. Comparison of different hybrid DFT methods on structural, spectroscopic, electronic and NLO parameters for a potential NLO material. Comput. Theor. Chem. 2017, 1100, 34–45. [Google Scholar] [CrossRef]
- May, J.; Lim, J.; Biaggio, I.; Moonen, N.; Michinobu, T.; Diederich, F. Highly efficient third-order optical nonlinearities in donor-substituted cyanoethynylethene molecules. Opt. Lett. 2005, 30, 3057–3059. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.; Bao, Y.; Lin, L.; Xu, H.; Liu, R.; Zhou, Z. Large third-order optical nonlinearity and ultrafast optical response in thin Au nanodisks. Opt. Mater. Express 2019, 9, 3021–3034. [Google Scholar] [CrossRef]
- Yoneda, K.; Nakano, M.; Fukuda, K.; Matsui, H.; Takamuku, S.; Hirosaki, Y.; Kubo, T.; Kamada, K.; Champagne, B. Third-order nonlinear optical properties of one-dimensional open-shell molecular aggregates composed of phenalenyl radicals. Chem. Eur. J. 2014, 20, 11129–11136. [Google Scholar] [CrossRef]
- Sain, B.; Meier, C.; Zentgraf, T. Nonlinear optics in all-dielectric nanoantennas and metasurfaces: A review. Adv. Photonics 2019, 1, 024002. [Google Scholar] [CrossRef]
- Sreedharan, R.; Ravi, S.; Raghi, K.R.; Kumar, T.K.M.; Naseema, K. Growth, linear- nonlinear optical studies and quantum chemistry formalism on an organic NLO crystal for opto-electronic applications: Experimental and theoretical approach. SN Appl. Sci. 2020, 2, 578. [Google Scholar] [CrossRef]
- Ecclestone, B.R.; Bell, K.; Sparkes, S.; Dinakaran, D.; Mackey, J.R.; Reza, P.H. Label-free complete absorption microscopy using second generation photoacoustic remote sensing. Sci. Rep. 2022, 12, 8464. [Google Scholar] [CrossRef] [PubMed]
- Huber, L.; Maehrlein, S.; Wang, F.; Liu, Y.; Zhu, X. The ultrafast Kerr effect in anisotropic and dispersive media. J. Chem. Phys. 2020, 154, 094202. [Google Scholar] [CrossRef]
- Tykwinski, R.; Gubler, U.; Martin, R.; Diederich, F.; Bosshard, C.; Günter, P. Structure–property relationships in third-order nonlinear optical chromophores. J. Phys. Chem. B 1998, 102, 4451–4465. [Google Scholar] [CrossRef]
- Armaković, S.; Armaković, S.; Šetrajčić, J.; Holodkov, V. Aromaticity, response, and nonlinear optical properties of sumanene modified with boron and nitrogen atoms. J. Mol. Model. 2014, 20, 2538. [Google Scholar] [CrossRef]
- Brandão, I.; Fonseca, T.L.; Franco, L.R.; Georg, H.C.; Castro, M.A. Applicability of DFT Functionals for Evaluating the First Hyperpolarizability of Phenol Blue in Solution. J. Chem. Phys. 2021, 154, 094501. [Google Scholar] [CrossRef]
- Suponitsky, K.Y.; Tafur, S.; Masunov, A.E. Applicability of Hybrid Density Functional Theory Methods to Calculation of Molecular Hyperpolarizability. J. Chem. Phys. 2008, 129, 044109. [Google Scholar] [CrossRef]
- Mishra, V.R.; Ghanavatkar, C.W.; Sharma, S.; Premarani, A.; Mathew, E.; Joe, I.H.; Sekar, N. Linear and NLO Properties of Functional Group and Position Isomers of Azo and Azomethine: Comparative Photophysical-Electrochemical Properties, Z-Scan and DFT Studies. Chem. Select 2020, 5, 10743–10753. [Google Scholar] [CrossRef]
- Nénon, S.; Champagne, B.; Spassova, M.I. Assessing Long-Range Corrected Functionals with Physically-Adjusted Range-Separated Parameters for Calculating the Polarizability and the Second Hyperpolarizability of Polydiacetylene and Polybutatriene Chains. Phys. Chem. Chem. Phys. 2014, 16, 7083–7088. [Google Scholar] [CrossRef]
- Mondal, A.; Hatua, K.; Roy, R.S.; Nandi, P.K. Successive Lithiation of Acetylene, Ethylene and Benzene: A Comprehensive Computational Study of Large Static Second Hyperpolarizability. Phys. Chem. Chem. Phys. 2017, 19, 4768–4777. [Google Scholar] [CrossRef]
- Wang, C.; Yuan, Y.; Tian, X.; Sun, J.; Yuan, J. The effects of exact exchange of density functionals on the evaluation of second hyperpolarizabilities of streptocyanines using sum-over-states method. Comput. Theor. Chem. 2016, 1085, 40–45. [Google Scholar] [CrossRef]
- Lu, S.I.; Chiu, C.C.; Wang, Y.F. Density functional theory calculations of dynamic first hyperpolarizabilities for organic molecules in organic solvent: Comparison to experiment. J. Chem. Phys. 2011, 135, 134104. [Google Scholar] [CrossRef] [PubMed]
- Bundulis, A.; Nitiss, E.; Mihailovs, I.; Busenbergs, J.; Rutkis, M. Study of structure–third-order susceptibility relation of indandione derivatives. J. Phys. Chem. C 2016, 120, 27515–27522. [Google Scholar] [CrossRef]
- Zaleśny, R.; Medved’, M.; Sitkiewicz, S.P.; Matito, E.; Luis, J.M. Can Density Functional Theory Be Trusted for High-Order Electric Properties? The Case of Hydrogen-Bonded Complexes. J. Chem. Theory Comput. 2019, 15, 3570–3579. [Google Scholar] [CrossRef]
- Zhang, C.C.; Xu, H.L.; Hu, Y.Y.; Sun, S.L.; Su, Z.M. Quantum Chemical Research on Structures, Linear and Nonlinear Optical Properties of the Li@n-Acenes Salt (n = 1, 2, 3, and 4). J. Phys. Chem. A 2011, 115, 2035–2040. [Google Scholar] [CrossRef]
- Hatua, K.; Nandi, P.K. Beryllium-Cyclobutadiene Multidecker Inverse Sandwiches: Electronic Structure and Second-Hyperpolarizability. J. Phys. Chem. A 2013, 117, 12581–12589. [Google Scholar] [CrossRef]
- Paschoal, D.; Dos Santos, H.F. Assessing the Quantum Mechanical Level of Theory for Prediction of Linear and Nonlinear Optical Properties of Push-Pull Organic Molecules. J. Mol. Model. 2013, 19, 2079–2090. [Google Scholar] [CrossRef] [PubMed]
- Li, H.P.; Shen, X.P.; Han, K.; Tang, G.; Zhang, Z.H. Quantum Chemistry Study on the Third-Order Nonlinear Optical Properties of Spirobifluorene Derivatives. Comput. Theor. Chem. 2013, 1023, 95–98. [Google Scholar] [CrossRef]
- Yang, J.; Song, Y.; Gu, J.; Zheng, H. Determinations of the transient thermal lensing effect in metal cluster polymer {WS4Cu4I2(bpe)3}n solution by the use of the Z-scan. Opt. Commun. 2009, 282, 122–125. [Google Scholar] [CrossRef]
- Sheik-Bahae, M.; Said, A.; Wei, T.H.; Hagan, D.; Stryland, E.V. Sensitive measurement of optical nonlinearities using a single beam. IEEE J. Quantum Electron. 1990, 26, 760–769. [Google Scholar] [CrossRef]
- Zhao, P.; Reichert, M.; Benis, S.; Hagan, D.; Stryland, E.V. Temporal and polarization dependence of the nonlinear optical response of solvents. Optica 2018, 5, 583–594. [Google Scholar] [CrossRef]
- Bundulis, A.; Mihailovs, I.; Rutkis, M. Origin of the Kerr effect: Investigation of solutions by polarization-dependent Z-scan. J. Opt. Soc. Am. B 2020, 37, 1806–1811. [Google Scholar] [CrossRef]
- Kirtman, B.; Maschio, L.; Rérat, M.; Springborg, M. Response Properties of Periodic Materials Subjected to External Electric and Magnetic Fields. In Frontiers of Quantum Chemistry; Wójcik, M.J., Nakatsuji, H., Kirtman, B., Ozaki, Y., Eds.; Springer: Singapore, 2018; pp. 87–115. [Google Scholar] [CrossRef]
- Gu, F.L.; Aoki, Y.; Springborg, M.; Kirtman, B. Applications of the Elongation Method to NLO Properties. In Calculations on Nonlinear Optical Properties for Large Systems: The Elongation Method; Springer International Publishing: Cham, Switzerland, 2015; pp. 67–83. [Google Scholar] [CrossRef]
- McWeeny, R. Some Recent Advances in Density Matrix Theory. Rev. Mod. Phys. 1960, 32, 335–369. [Google Scholar] [CrossRef]
- McWeeny, R. Perturbation Theory for the Fock–Dirac Density Matrix. Phys. Rev. 1962, 126, 1028–1034. [Google Scholar] [CrossRef]
- Gerratt, J.; Mills, I.M. Force Constants and Dipole-Moment Derivatives of Molecules from Perturbed Hartree–Fock Calculations. I. J. Chem. Phys. 1968, 49, 1719–1729. [Google Scholar] [CrossRef]
- Dodds, J.L.; McWeeny, R.; Raynes, W.T.; Riley, J.P. SCF Theory for Multiple Perturbations. Mol. Phys. 1977, 33, 611–617. [Google Scholar] [CrossRef]
- Dodds, J.L.; McWeeny, R.; Sadlej, A.J. Self-Consistent Perturbation Theory. Mol. Phys. 1977, 34, 1779–1791. [Google Scholar] [CrossRef]
- Dykstra, C.E.; Jasien, P.G. Derivative Hartree–Fock Theory to All Orders. Chem. Phys. Lett. 1984, 109, 388–393. [Google Scholar] [CrossRef]
- Pulay, P. Second and Third Derivatives of Variational Energy Expressions: Application to Multiconfigurational Self-Consistent Field Wave Functions. J. Chem. Phys. 1983, 78, 5043–5051. [Google Scholar] [CrossRef]
- Pedersen, T.B. Introduction to Response Theory. In Handbook of Computational Chemistry; Leszczynski, J., Kaczmarek-Kedziera, A., Puzyn, T., Papadopoulos, M.G., Reis, H., Shukla, M.K., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 269–294. [Google Scholar] [CrossRef]
- Ahmadzadeh, K.; Scott, M.; Brand, M.; Vahtras, O.; Li, X.; Rinkevicius, Z.; Norman, P. Efficient Implementation of Isotropic Cubic Response Functions for Two-Photon Absorption Cross Sections within the Self-Consistent Field Approximation. J. Chem. Phys. 2021, 154, 024111. [Google Scholar] [CrossRef] [PubMed]
- Parker, S.M.; Furche, F. Response Theory and Molecular Properties. In Frontiers of Quantum Chemistry; Wójcik, M.J., Nakatsuji, H., Kirtman, B., Ozaki, Y., Eds.; Springer: Singapore, 2018; pp. 69–86. [Google Scholar] [CrossRef]
- Antoine, R.; Bonačić-Koutecký, V. A Brief Survey of Nonlinear Optics: Second Harmonic Generation and Two-Photon Absorption. In Liganded Silver and Gold Quantum Clusters: Towards a New Class of Nonlinear Optical Nanomaterials; Springer International Publishing: Cham, Switzerland, 2018; pp. 21–27. [Google Scholar] [CrossRef]
- Olsen, J.; Jørgensen, P. Linear and Nonlinear Response Functions for an Exact State and for an MCSCF State. J. Chem. Phys. 1985, 82, 3235–3264. [Google Scholar] [CrossRef]
- Jørgensen, P.; Jensen, H.J.A.; Olsen, J. Linear Response Calculations for Large Scale Multiconfiguration Self-Consistent Field Wave Functions. J. Chem. Phys. 1988, 89, 3654–3661. [Google Scholar] [CrossRef]
- Rinkevicius, Z.; Tunell, I.; Sałek, P.; Vahtras, O.; Ågren, H. Restricted Density Functional Theory of Linear Time-Dependent Properties in Open-Shell Molecules. J. Chem. Phys. 2003, 119, 34–46. [Google Scholar] [CrossRef]
- Hettema, H.; Jensen, H.J.A.; Jørgensen, P.; Olsen, J. Quadratic Response Functions for a Multiconfigurational Self-Consistent Field Wave Function. J. Chem. Phys. 1992, 97, 1174–1190. [Google Scholar] [CrossRef]
- Norman, P.; Jonsson, D.; Vahtras, O.; Ågren, H. Cubic Response Functions in the Random Phase Approximation. Chem. Phys. Lett. 1995, 242, 7–16. [Google Scholar] [CrossRef]
- Jonsson, D.; Norman, P.; Ågren, H. Cubic Response Functions in the Multiconfiguration Self-Consistent Field Approximation. J. Chem. Phys. 1996, 105, 6401–6419. [Google Scholar] [CrossRef]
- Kruhlak, R.J.; Kuzyk, M.G. A General Theory of Inhomogeneous Broadening for Nonlinear Susceptibilities: The Polarizability and Hyperpolarizability. IEEE J. Sel. Top. Quantum Electron. 2008, 14, 1272–1280. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 09 Revision D.01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Baerends, E.J.; Ziegler, T.; Atkins, A.J.; Autschbach, J.; Baseggio, O.; Bashford, D.; Bérces, A.; Bickelhaupt, F.M.; Bo, C.; Boerrigter, P.M.; et al. ADF 2021, SCM: Theoretical Chemistry; Software for Chemistry and Materials; Vrije Universiteit: Amsterdam, The Netherlands, 2021. [Google Scholar]
- te Velde, G.; Bickelhaupt, F.M.; Baerends, E.J.; Fonseca Guerra, C.; van Gisbergen, S.J.A.; Snijders, J.G.; Ziegler, T. Chemistry with ADF. J. Comput. Chem. 2001, 22, 931–967. [Google Scholar] [CrossRef]
- Aidas, K.; Angeli, C.; Bak, K.L.; Bakken, V.; Bast, R.; Boman, L.; Christiansen, O.; Cimiraglia, R.; Coriani, S.; Dahle, P.; et al. The Dalton Quantum Chemistry Program System. WIREs Comput. Mol. Sci. 2014, 4, 269–284. [Google Scholar] [CrossRef]
- Dalton Project. Dalton, a Molecular Electronic Structure Program, Release v2020.0.1. 2020. Available online: http://daltonprogram.org (accessed on 5 January 2021).
- Barca, G.M.J.; Bertoni, C.; Carrington, L.; Datta, D.; De Silva, N.; Deustua, J.E.; Fedorov, D.G.; Gour, J.R.; Gunina, A.O.; Guidez, E.; et al. Recent Developments in the General Atomic and Molecular Electronic Structure System. J. Chem. Phys. 2020, 152, 154102. [Google Scholar] [CrossRef]
- Li, H.P.; Shen, X.P.; Han, K.; Tang, G. Solvent Effects on Polarizability and Hyperpolarizability of Spirobifluorene Derivative. J. Mol. Model. 2014, 20, 2126. [Google Scholar] [CrossRef] [PubMed]
- Hatua, K.; Mondal, A.; Nandi, P.K. Static Second Hyperpolarizability of Inverse Sandwich Compounds (M1–C5H5–M2) of Alkali (M1 = Li, Na, K) and Alkaline Earth Metals (M2 = Be, Mg, Ca). Phys. Chem. Chem. Phys. 2018, 20, 13331–13339. [Google Scholar] [CrossRef] [PubMed]
- Marder, S.R.; Gorman, C.B.; Tiemann, B.G.; Perry, J.W.; Bourhill, G.; Mansour, K. Relation Between Bond-Length Alternation and Second Electronic Hyperpolarizability of Conjugated Organic Molecules. Science 1993, 261, 186–189. [Google Scholar] [CrossRef]
- Zhu, W.; Wu, G.S.; Jiang, Y. Incorporation of Solvent Effects into Density Functional Predictions of Molecular Polarizabilities and Hyperpolarizabilities. Int. J. Quantum Chem. 2002, 86, 347–355. [Google Scholar] [CrossRef]
- Hrivnák, T.; Medveď, M.; Bartkowiak, W.; Zaleśny, R. Hyperpolarizabilities of Push–Pull Chromophores in Solution: Interplay between Electronic and Vibrational Contributions. Molecules 2022, 27, 8738. [Google Scholar] [CrossRef]
- Jacquemin, D.; Perpète, E.A.; André, J.M. NLO Response of Polymethineimine and Polymethineimine/Polyacetylene Conformers: Assessment of Electron Correlation Effects. Int. J. Quantum Chem. 2005, 105, 553–563. [Google Scholar] [CrossRef]
- Franco, L.R.; Brandão, I.; Fonseca, T.L.; Georg, H.C. Elucidating the Structure of Merocyanine Dyes with the ASEC-FEG Method. Phenol Blue in Solution. J. Chem. Phys. 2016, 145, 194301. [Google Scholar] [CrossRef]
- Janowska, I.; Zakrzewski, J.; Nakatani, K.; Palusiak, M.; Walak, M.; Scholl, H. Ferrocenyl D–π–A Conjugated Polyenes with 3-Dicyanomethylidene-1-indanone and 1,3-Bis(dicyanomethylidene)indane Acceptor Groups: Synthesis, Linear and Second-Order Nonlinear Optical Properties and Electrochemistry. J. Organomet. Chem. 2006, 691, 323–330. [Google Scholar] [CrossRef]
- Raptis, S.G.; Nasiou, S.M.; Demetropoulos, I.N.; Papadopoulos, M.G. Static and Frequency Dependent Polarizabilities and Hyperpolarizabilities of H2Sn. J. Comput. Chem. 1998, 19, 1698–1715. [Google Scholar] [CrossRef]
- Jacobsen, H.; Cavallo, L. Directions for Use of Density Functional Theory: A Short Instruction Manual for Chemists. In Handbook of Computational Chemistry; Springer International Publishing: Cham, Switzerland, 2017; pp. 225–267. [Google Scholar]
- Lewars, E.G. Computational Chemistry: Introduction to the Theory and Applications of Molecular and Quantum Mechanics, 3rd ed.; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar]
- Wu, K.; Snijders, J.G.; Lin, C. Reinvestigation of Hydrogen Bond Effects on the Polarizability and Hyperpolarizability of Urea Molecular Clusters. J. Phys. Chem. B 2002, 106, 8954–8958. [Google Scholar] [CrossRef]
- Datta, A.; Pati, S.K. Dipolar interactions and hydrogen bonding in supramolecular aggregates: Understanding cooperative phenomena for 1st hyperpolarizability. Chem. Soc. Rev. 2006, 35, 1305–1323. [Google Scholar] [CrossRef]
- Berland, K.; Jiao, Y.; Lee, J.H.; Rangel, T.; Neaton, J.B.; Hyldgaard, P. Assessment of two hybrid van der Waals density functionals for covalent and non-covalent binding of molecules. J. Chem. Phys. 2017, 146, 234106. [Google Scholar] [CrossRef] [PubMed]
- Brauer, B.; Kesharwani, M.K.; Kozuch, S.; Martin, J.M.L. The S66x8 benchmark for noncovalent interactions revisited: Explicitly correlated ab initio methods and density functional theory. Phys. Chem. Chem. Phys. 2016, 18, 20905–20925. [Google Scholar] [CrossRef]
- Jacquemin, D.; Perpète, E.A.; Ciofini, I.; Adamo, C. Assessment of recently developed density functional approaches for the evaluation of the bond length alternation in polyacetylene. Chem. Phys. Lett. 2005, 405, 376–381. [Google Scholar] [CrossRef]
- Lu, S.I. Computational Study of Static First Hyperpolarizability of Donor–Acceptor Substituted (E)-Benzaldehyde Phenylhydrazone. J. Comput. Chem. 2011, 32, 730–736. [Google Scholar] [CrossRef] [PubMed]
- Karamanis, P.; Maroulis, G. An ab initio study of CX3-substitution (X = H, F, Cl, Br, I) effects on the static electric polarizability and hyperpolarizability of diacetylene. J. Phys. Org. Chem. 2011, 24, 588–599. [Google Scholar] [CrossRef]
- Jacquemin, D.; Perpète, E.A.; Scuseria, G.E.; Ciofini, I.; Adamo, C. Extensive TD-DFT investigation of the first electronic transition in substituted azobenzenes. Chem. Phys. Lett. 2008, 465, 226–229. [Google Scholar] [CrossRef]
- Kaka, K.S.; Beaujean, P.; Castet, F.; Champagne, B. A quantum chemical investigation of the second hyperpolarizability of p-nitroaniline. J. Chem. Phys. 2023, 159, 114104. [Google Scholar] [CrossRef]
- Mondal, A.; Hatua, K.; Nandi, P.K. Static second hyperpolarizability of twisted ethylene: A comprehensive computational study. J. Theor. Comput. Chem. 2015, 14, 1550060. [Google Scholar] [CrossRef]
- Bulik, I.W.; Zaleśny, R.; Bartkowiak, W.; Luis, J.M.; Kirtman, B.; Scuseria, G.E.; Avramopoulos, A.; Reis, H.; Papadopoulos, M.G. Performance of density functional theory in computing nonresonant vibrational (hyper)polarizabilities. J. Comput. Chem. 2013, 34, 1775–1784. [Google Scholar] [CrossRef]
- Besalú-Sala, P.; Sitkiewicz, S.P.; Salvador, P.; Matito, E.; Luis, J.M. A new tuned range-separated density functional for the accurate calculation of second hyperpolarizabilities. Phys. Chem. Chem. Phys. 2020, 22, 11871–11880. [Google Scholar] [CrossRef]
- Cardenuto, M.H.; Champagne, B. The first hyperpolarizability of nitrobenzene in benzene solutions: Investigation of the effects of electron correlation within the sequential QM/MM approach. Phys. Chem. Chem. Phys. 2015, 17, 23634–23642. [Google Scholar] [CrossRef]
- Torrent-Sucarrat, M.; Anglada, J.M.; Luis, J.M. Evaluation of the Nonlinear Optical Properties for Annulenes with Hückel and Möbius Topologies. J. Chem. Theory Comput. 2011, 7, 3935–3943. [Google Scholar] [CrossRef] [PubMed]
- Marques, S.; Castro, M.A.; Leão, S.A.; Fonseca, T.L. Electronic and Vibrational Hyperpolarizabilities of Lithium Substituted (Aza)benzenes and (Aza)naphthalenes. J. Phys. Chem. A 2018, 122, 7402–7412. [Google Scholar] [CrossRef] [PubMed]
- Marques, S.; Castro, M.A.; Pontes, R.B.; Leão, S.A.; Fonseca, T.L. 155. Second hyperpolarizabilities of alkali- and alkaline-earth-doped boron nitride nanotubes. Chem. Phys. Lett. 2023, 821, 140473. [Google Scholar] [CrossRef]
- Castet, F.; Lerychard, T.; Pielak, K.; Szalóki, G.; Dalinot, C.; Leriche, P.; Sanguinet, L.; Champagne, B.; Rodriguez, V. How Dimerization Through a Spiro Junction Modifies the Nonlinear Optical Properties of a Push–Pull Organic Dye: Insights from Theory and Hyper-Rayleigh Scattering. ChemPhotoChem 2017, 1, 93–101. [Google Scholar] [CrossRef]
- Jensen, L.; van Duijnen, P.T.; Snijders, J.G.; Chong, D.P. Time-dependent density functional study of the static second hyperpolarizability of BB-, NN- and BN-substituted C60. Chem. Phys. Lett. 2002, 359, 524–529. [Google Scholar] [CrossRef]
- Govindarasu, K.; Kavitha, E. Vibrational spectra, molecular structure, NBO, NMR, UV first order hyperpolarizability, analysis of (S)-(-)-N-(5-Nitro-2-pyridyl) alaninol by Density functional theory. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2014, 127, 498–510. [Google Scholar] [CrossRef]
- Govindarasu, K.; Kavitha, E. Molecular structure, vibrational spectra, NBO, UV and first order hyperpolarizability, analysis of 4-Chloro-DL-phenylalanine by density functional theory. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2014, 133, 799–810. [Google Scholar] [CrossRef]
- Govindarasu, K.; Kavitha, E. Vibrational spectra, molecular structure, NBO, UV, NMR, first order hyperpolarizability, analysis of 4-Methoxy-4′-Nitrobiphenyl by density functional theory. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2014, 122, 130–141. [Google Scholar] [CrossRef]
- Govindarasu, K.; Kavitha, E.; Sundaraganesan, N. Synthesis, structural, spectral (FTIR, FT-Raman, UV, NMR), NBO and first order hyperpolarizability analysis of N-phenylbenzenesulfonamide by density functional theory. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2014, 133, 417–431. [Google Scholar] [CrossRef]
- Migalska-Zalas, A.; Korchi, K.E.; Chtouki, T. Enhanced nonlinear optical properties due to electronic delocalization in conjugated benzodifuran derivatives. Opt. Quantum Electron. 2018, 50, 389. [Google Scholar] [CrossRef]
- Vishnumurthy, K.A.; Girish, K.H.; Adhikari, A.V. Synthesis, physicochemical properties and computational study of donor–acceptor polymer for optical limiting application. SN Appl. Sci. 2020, 2, 1727. [Google Scholar] [CrossRef]
- Bonness, S.; Fukui, H.; Yoneda, K.; Kishi, R.; Champagne, B.; Botek, E.; Nakano, M. Theoretical investigation on the second hyperpolarizabilities of open-shell singlet systems by spin-unrestricted density functional theory with long-range correction: Range separating parameter dependence. Chem. Phys. Lett. 2010, 493, 195–199. [Google Scholar] [CrossRef]
- Nakano, M.; Yamada, S.; Kiribayashi, S.; Yamaguchi, K. Hyperpolarizabilities of one-dimensional Hn systems: Second hyperpolarizability density analyses for regular and charged solitonlike linear chains. Int. J. Quantum Chem. 1998, 70, 269–282. [Google Scholar] [CrossRef]
- Jørgensen, M.W.; Faber, R.; Ligabue, A.; Sauer, S.P. Benchmarking Correlated Methods for Frequency-Dependent Polarizabilities: Aromatic Molecules with the CC3, CCSD, CC2, SOPPA, SOPPA(CC2), and SOPPA(CCSD) Methods. J. Chem. Theory Comput. 2020, 16, 3006–3018. [Google Scholar] [CrossRef]
- Beaujean, P.; Champagne, B. Coupled cluster evaluation of the frequency dispersion of the first and second hyperpolarizabilities of water, methanol, and dimethyl ether. J. Chem. Phys. 2016, 145, 044311. [Google Scholar] [CrossRef]
- Labidi, S.N.; Kanoun, M.B.; De Wergifosse, M.; Champagne, B. Theoretical Assessment of New Molecules for Second-Order Nonlinear Optics. Int. J. Quantum Chem. 2011, 111, 1583–1595. [Google Scholar] [CrossRef]
- Banerjee, P.; Nandi, P.K. Hydrides, Alkalides, and Halides of Calcium Metal Chain: Electronic Structure and NLO Property. Struct. Chem. 2018, 29, 859–870. [Google Scholar] [CrossRef]
- Pecul, M. Density functional and coupled cluster calculations of dynamic hyperpolarizabilities and their geometry derivatives. Chem. Phys. Lett. 2005, 404, 217–226. [Google Scholar] [CrossRef]
- Champagne, B.; Botek, E.; Nakano, M.; Nitta, T.; Yamaguchi, K. Basis set and electron correlation effects on the polarizability and second hyperpolarizability of model open-shell conjugated systems. J. Chem. Phys. 2005, 122, 114315. [Google Scholar] [CrossRef]
- Banerjee, P.; Avramopoulos, A.; Nandi, P.K. Static second-hyperpolarizability of diffuse electron cyclic compounds M2A2 (M = Be, Mg, Ca; A = Li, Na, K): Effect of basis set and electron correlation. Chem. Phys. Lett. 2019, 729, 92–98. [Google Scholar] [CrossRef]
- Sadlej, A.J. Medium-size polarized basis sets for high-level correlated calculations of molecular electric properties. Collect. Czechoslov. Chem. Commun. 1988, 53, 1995–2016. [Google Scholar] [CrossRef]
- Sadlej, A.J. Medium-size polarized basis sets for high-level-correlated calculations of molecular electric properties. Theor. Chim. Acta 1991, 79, 123–140. [Google Scholar] [CrossRef]
- Mead, R.; Gilmour, S.G.; Mead, A. Statistical Principles for the Design of Experiments; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar] [CrossRef]
- Roothaan, C.C.J. New Developments in Molecular Orbital Theory. Rev. Mod. Phys. 1951, 23, 69–89. [Google Scholar] [CrossRef]
- Christiansen, O.; Koch, H.; Jørgensen, P. The second-order approximate coupled cluster singles and doubles model CC2. Chem. Phys. Lett. 1995, 243, 409–418. [Google Scholar] [CrossRef]
- Purvis, G.D.; Bartlett, R.J. A full coupled-cluster singles and doubles model: The inclusion of disconnected triples. J. Chem. Phys. 1982, 76, 1910–1918. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Becke, A.D. A new mixing of Hartree–Fock and local density-functional theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Accounts 2007, 120, 215–241. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. Comparative DFT Study of van der Waals Complexes: Rare-Gas Dimers, Alkaline-Earth Dimers, Zinc Dimer, and Zinc-Rare-Gas Dimers. J. Phys. Chem. A 2006, 110, 5121–5129. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.S.; He, X.; Li, S.L.; Truhlar, D.G. MN15: A Kohn–Sham global-hybrid exchange–correlation density functional with broad accuracy for multi-reference and single-reference systems and noncovalent interactions. Chem. Sci. 2016, 7, 5032–5051. [Google Scholar] [CrossRef]
- Tawada, Y.; Tsuneda, T.; Yanagisawa, S.; Yanai, T.; Hirao, K. A long-range-corrected time-dependent density functional theory. J. Chem. Phys. 2004, 120, 8425–8433. [Google Scholar] [CrossRef]
- Yanai, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- Peverati, R.; Truhlar, D.G. Improving the Accuracy of Hybrid Meta-GGA Density Functionals by Range Separation. J. Phys. Chem. Lett. 2011, 2, 2810–2817. [Google Scholar] [CrossRef]
- Barone, V.; Cossi, M. Quantum Calculation of Molecular Energies and Energy Gradients in Solution by a Conductor Solvent Model. J. Phys. Chem. A 1998, 102, 1995–2001. [Google Scholar] [CrossRef]
- Cossi, M.; Rega, N.; Scalmani, G.; Barone, V. Energies, structures, and electronic properties of molecules in solution with the C-PCM solvation model. J. Comput. Chem. 2003, 24, 669–681. [Google Scholar] [CrossRef]
- Olsen, J.M.H.; Kongsted, J. Molecular Properties through Polarizable Embedding. Adv. Quantum Chem. 2011, 61, 107–143. [Google Scholar] [CrossRef]
- Olsen, J.M.H. Development of Quantum Chemical Methods towards Rationalization and Optimal Design of Photoactive Proteins. Ph.D. Thesis, University of Southern Denmark, Odense, Denmark, 2012. [Google Scholar] [CrossRef]
- Cancès, E.; Mennucci, B.; Tomasi, J. A new integral equation formalism for the polarizable continuum model: Theoretical background and applications to isotropic and anisotropic dielectrics. J. Chem. Phys. 1997, 107, 3032–3041. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
- Woon, D.E.; Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon. J. Chem. Phys. 1993, 98, 1358–1371. [Google Scholar] [CrossRef]
- Davidson, E.R. Comment on “Comment on Dunning’s correlation-consistent basis sets”. Chem. Phys. Lett. 1996, 260, 514–518. [Google Scholar] [CrossRef]
- Hanwell, M.D.; Curtis, D.E.; Lonie, D.C.; Vandermeersch, T.; Zurek, E.; Hutchison, G.R. Avogadro: An advanced semantic chemical editor, visualization, and analysis platform. J. Cheminf. 2012, 4, 17. [Google Scholar] [CrossRef] [PubMed]
- Avogadro: An Open-Source Molecular Builder and Visualization Tool. Version 1.2.0. 2016. Available online: http://avogadro.cc (accessed on 17 May 2022).
- Avogadro: An Open-Source Molecular Builder and Visualization Tool. Version 1.93.0. 2023. Available online: https://www.openchemistry.org/projects/avogadro2 (accessed on 17 May 2022).
- Pettersen, E.F.; Goddard, T.D.; Huang, C.C.; Couch, G.S.; Greenblatt, D.M.; Meng, E.C.; Ferrin, T.E. UCSF Chimera—A visualization system for exploratory research and analysis. J. Comput. Chem. 2004, 25, 1605–1612. [Google Scholar] [CrossRef]
- UCSF Chimera, version 1.15 (build 42258); Resource for Biocomputing, Visualization, and Informatics at the University of California, San Francisco: San Francisco, CA, USA, 2020.
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2024. [Google Scholar]
- Fox, J.; Weisberg, S. An R Companion to Applied Regression; Sage: Thousand Oaks, CA, USA, 2019. [Google Scholar]
- Mangiafico, S.S. rcompanion: Functions to Support Extension Education Program Evaluation; Rutgers Cooperative Extension: New Brunswick, NJ, USA, 2024. [Google Scholar]
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S; Springer: New York, NY, USA, 2002. [Google Scholar]
- Barrett, T.; Dowle, M.; Srinivasan, A. data.table: Extension of data.frame, version 1.14.10; The Comprehensive R Archive Network: Wien, Austria, 2023.
- Fellows, I. Wordcloud: Word Clouds, version 2.6; The Comprehensive R Archive Network: Wien, Austria, 2018.
- Gu, B.; Ji, W.; Huang, X.Q. Analytical expression for femtosecond-pulsed z scans on instantaneous nonlinearity. Appl. Opt. 2008, 47, 1187–1192. [Google Scholar] [CrossRef] [PubMed]
- Bundulis, A.; Kim, V.V.; Grube, J.; Ganeev, R.A. Variation of Nonlinear Refraction and Three-Photon Absorption of Indium–Tin Oxide Quantum Dot Thin Films and Solutions in Near Infrared Range. Opt. Mater. 2021, 122, 111778. [Google Scholar] [CrossRef]
- Zhang, X.; Cui, Z.; Cheng, Z.; Li, Y.; Xiao, H. Quantitative detection of H2S and CS2 mixed gases based on UV absorption spectrometry. RSC Adv. 2017, 7, 50889–50898. [Google Scholar] [CrossRef]
- Grosch, H.; Fateev, A.; Clausen, S. UV absorption cross-sections of selected sulfur-containing compounds at temperatures up to 500 °C. J. Quant. Spectrosc. Radiat. Transf. 2015, 154, 28–34. [Google Scholar] [CrossRef]
- Grammaticakis, P. Contribution à l’étude de l’absorption dans l’ultraviolet moyen des anilines ortho-substituées. III. Orthonitro- et orthocarboxy- anilines N-substituées. Bull. Soc. Chim. Fr. 1950, 17, 158–166. [Google Scholar]
- Talrose, V.; Stern, E.B.; Goncharova, A.A.; Messineva, N.A.; Trusova, N.V.; Efimkina, M.V. Benzene, nitro-. In NIST Chemistry WebBook, NIST Standard Reference Database Number 69; Linstrom, P.J., Mallard, W.G., Eds.; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2021; Available online: https://webbook.nist.gov/cgi/cbook.cgi?Name=nitrobenzene&Units=SI (accessed on 4 May 2022).
- Kim, V.V.; Bundulis, A.; Grube, J.; Ganeev, R.A. Variation of the sign of nonlinear refraction of carbon disulfide in the short-wavelength region. Opt. Mater. Express 2022, 12, 2053–2062. [Google Scholar] [CrossRef]
- Kong, D.G.; Chang, Q.; Ye, H.A.; Gao, Y.C.; Wang, Y.X.; Zhang, X.R.; Yang, K.; Wu, W.Z.; Song, Y.L. The fifth-order nonlinearity of CS2. J. Phys. B At. Mol. Opt. Phys. 2009, 42, 065401. [Google Scholar] [CrossRef]
- Ganeev, R.A.; Ryasnyansky, A.I.; Ishizawa, N.; Baba, M.; Suzuki, M.; Turu, M.; Sakakibara, S.; Kuroda, H. Two- and three-photon absorption in CS2. Opt. Commun. 2004, 231, 431–436. [Google Scholar] [CrossRef]
- Peverati, R.; Truhlar, D.G. Quest for a universal density functional: The accuracy of density functionals across a broad spectrum of databases in chemistry and physics. Philos. Trans. R. Soc. A 2014, 372, 20120476. [Google Scholar] [CrossRef] [PubMed]
- Pernot, P.; Savin, A. Probabilistic performance estimators for computational chemistry methods: The empirical cumulative distribution function of absolute errors. J. Chem. Phys. 2018, 148, 241707. [Google Scholar] [CrossRef]
- Pernot, P.; Savin, A. Probabilistic performance estimators for computational chemistry methods: Systematic improvement probability and ranking probability matrix. I. Theory. J. Chem. Phys. 2020, 152, 164108. [Google Scholar] [CrossRef] [PubMed]
- Bootsma, A.N.; Wheeler, S.E. Popular Integration Grids Can Result in Large Errors in DFT-Computed Free Energies. ChemRxiv 2019. [Google Scholar] [CrossRef] [PubMed]





| Methodology | Static | Dynamic | Model Chemistries | Benefits | Challenges |
|---|---|---|---|---|---|
| FF | Yes | No | HF, DFT, MPn, CCn, MCSCF | Simple implementation; Efficient for large systems | Selecting field strength; Numerical differentiation challenges |
| CPKS+FF | Yes | Partially * | HF, DFT | Comparatively easy to implement | * Numerical differentiation challenges |
| RE+FF | Yes | Partially | HF, DFT, CCn, MCSCF | Comparatively easy to implement | Numerical differentiation challenges |
| Fully analytical RE | Yes | Yes | HF, DFT, CCn, MCSCF | Full frequency dependence (incl. OKE) | Undertaking to implement |
| Fully analytical CPHF | Yes | Yes | HF, DFT | Full frequency dependence (incl. OKE) | Undertaking to implement |
| SOS | Yes | Yes | HF, DFT, MPn, CCn, MCSCF | Easy to implement; Full frequency dependence (incl. OKE) | In practice, truncation is mandatory, which requires tuning for particular systems |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mihailovs, I.; Belobrovko, E.; Bundulis, A.; Bocharov, D.V.; Kotomin, E.A.; Rutkis, M. Use of Factorial Design for Calculation of Second Hyperpolarizabilities. Nanomaterials 2025, 15, 1302. https://doi.org/10.3390/nano15171302
Mihailovs I, Belobrovko E, Bundulis A, Bocharov DV, Kotomin EA, Rutkis M. Use of Factorial Design for Calculation of Second Hyperpolarizabilities. Nanomaterials. 2025; 15(17):1302. https://doi.org/10.3390/nano15171302
Chicago/Turabian StyleMihailovs, Igors, Ekaterina Belobrovko, Arturs Bundulis, Dmitry V. Bocharov, Eugene A. Kotomin, and Martins Rutkis. 2025. "Use of Factorial Design for Calculation of Second Hyperpolarizabilities" Nanomaterials 15, no. 17: 1302. https://doi.org/10.3390/nano15171302
APA StyleMihailovs, I., Belobrovko, E., Bundulis, A., Bocharov, D. V., Kotomin, E. A., & Rutkis, M. (2025). Use of Factorial Design for Calculation of Second Hyperpolarizabilities. Nanomaterials, 15(17), 1302. https://doi.org/10.3390/nano15171302







