Theoretical Studies of Non-Metal Endohedral Fullerenes
Abstract
1. Introduction
2. H2 Encapsulation in C60
3. N2 Encapsulation in C60
4. NH3 Encapsulation in C60
5. CO Encapsulation in C60
6. H2O2 Encapsulation in C60
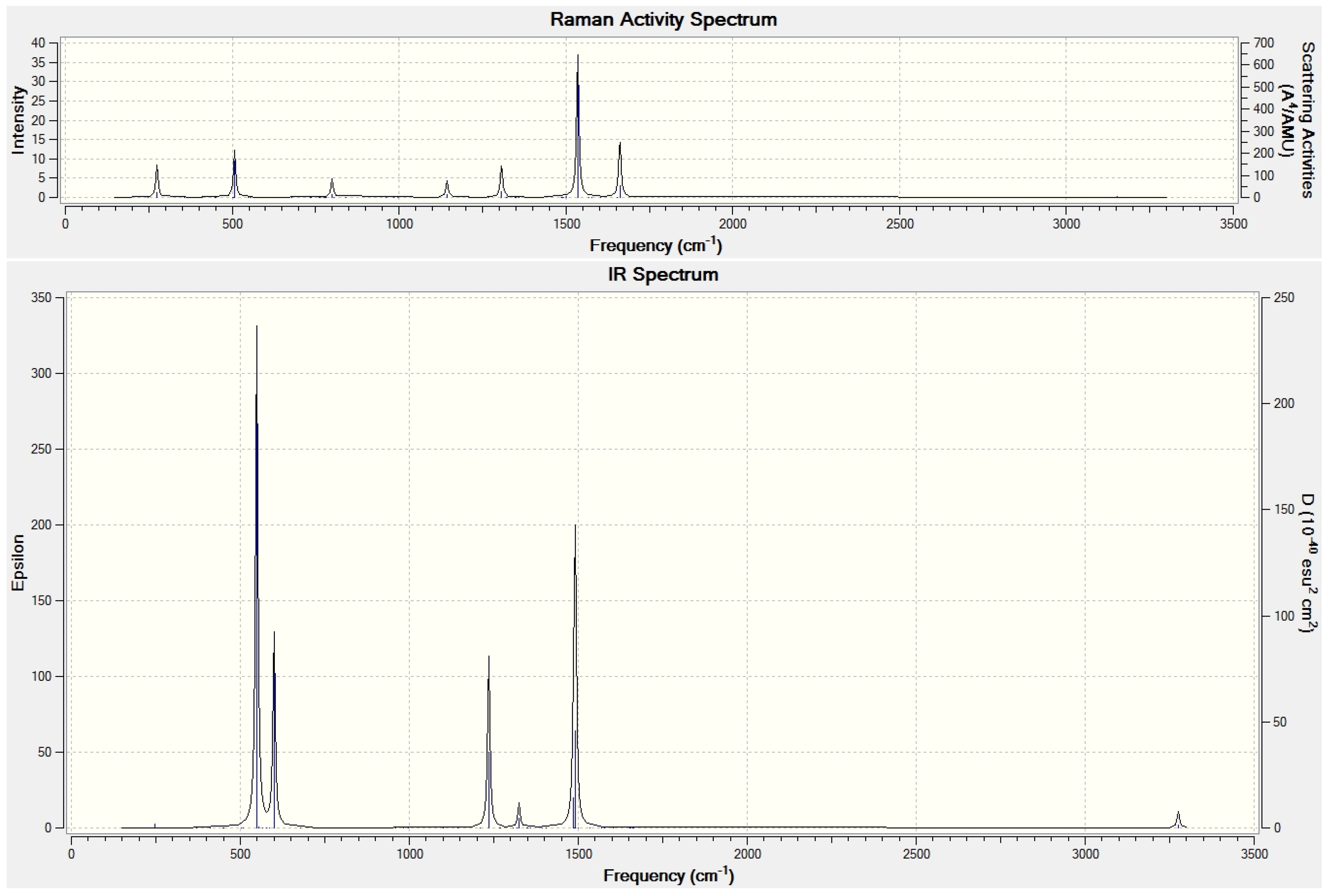
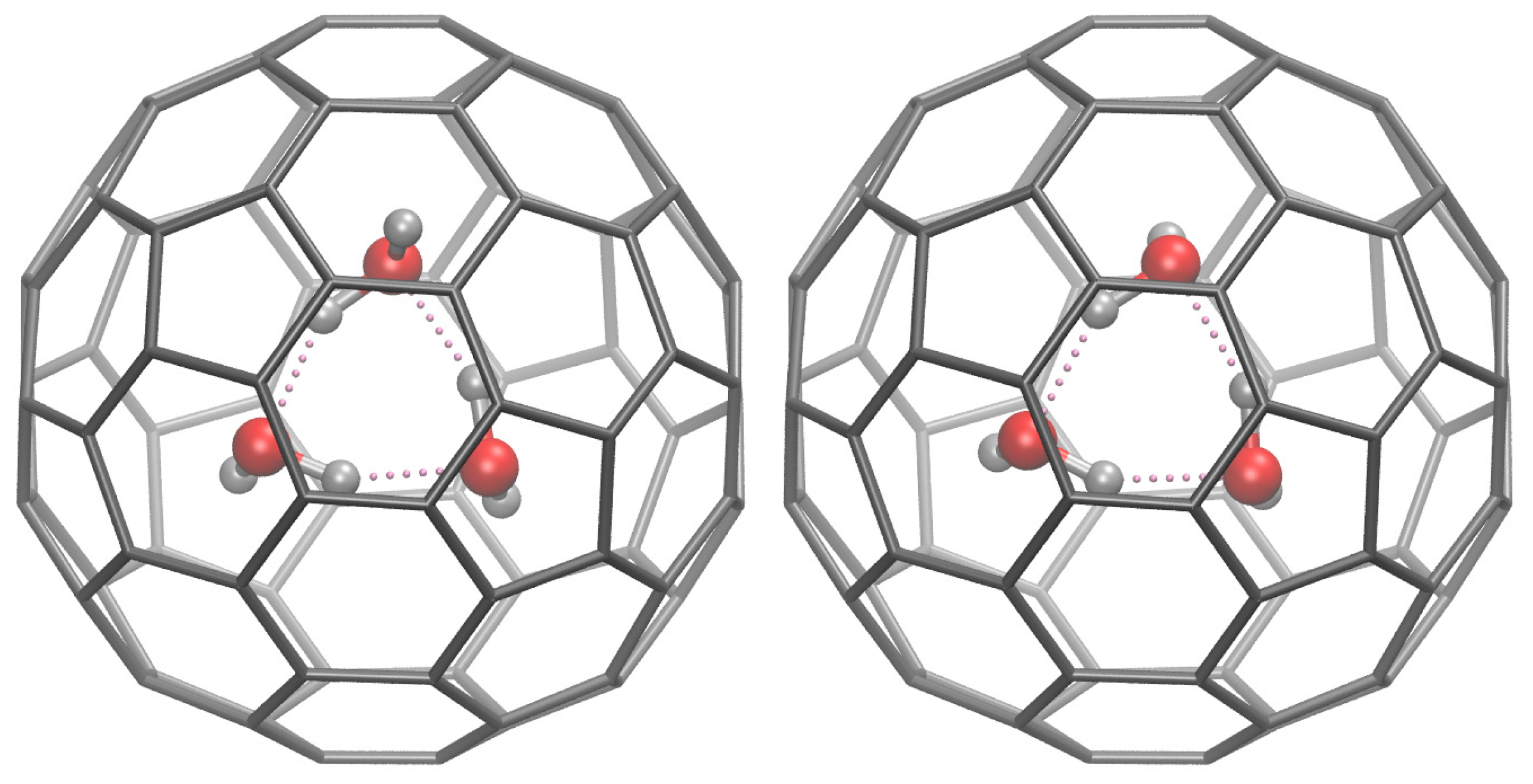
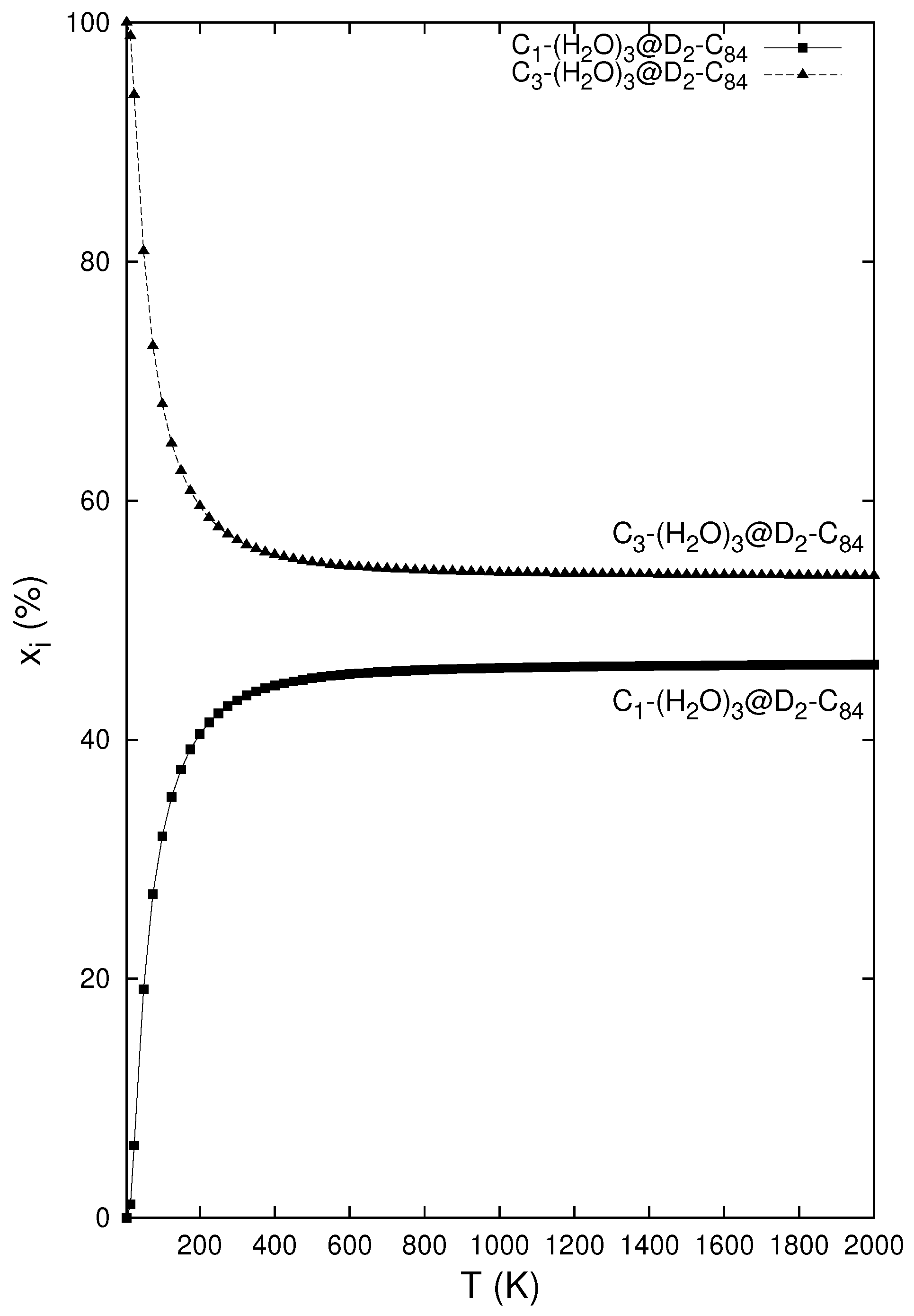
7. Encapsulation of H2O and Its Aggregates into Fullerenes
8. Encapsulation of H2O and HF in C70
9. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Dresselhaus, M.S.; Dresselhaus, G.; Eklund, P.C. Science of Fullerenes and Carbon Nanotubes: Their Properties and Applications; Academic Press: San Diego, CA, USA, 1996; p. 316. [Google Scholar]
- Peres, T.; Cao, B.P.; Cui, W.D.; Khong, A.; Cross, R.J.; Saunders, M.; Lifshitz, C. Some new diatomic molecule containing endohedral fullerenes. Int. J. Mass Spectr. 2001, 210/211, 241–247. [Google Scholar] [CrossRef]
- Suetsuna, T.; Dragoe, N.; Harneit, W.; Weidinger, A.; Shimotani, H.; Ito, S.; Takagi, H.; Kitazawa, K. Separation of N2@C60 and N@C60. Chem. Eur. J. 2002, 8, 5079–5083. [Google Scholar] [CrossRef]
- Murphy, T.A.; Pawlik, T.; Weidinger, A.; Höhne, M.; Alcala, R.; Spaeth, J.-M. Observation of atomlike nitrogen in nitrogen-implanted solid C60. Phys. Rev. Lett. 1996, 77, 1075–1078. [Google Scholar] [CrossRef]
- Knapp, C.; Dinse, K.-P.; Pietzak, B.; Waiblinger, M.; Weidinger, A. Fourier transform EPR study of N@C60 in solution. Chem. Phys. Lett. 1997, 272, 433–437. [Google Scholar] [CrossRef]
- Pietzak, B.; Waiblinger, M.; Murphy, T.A.; Weidinger, A.; Höhne, M.; Dietel, E.; Hirsch, A. Buckminsterfullerene C60: A chemical Faraday cage for atomic nitrogen. Chem. Phys. Lett. 1997, 279, 259–263. [Google Scholar] [CrossRef]
- Cao, B.P.; Peres, T.; Cross, R.J.; Saunders, M.; Lifshitz, C. Do nitrogen-atom-containing endohedral fullerenes undergo the shrink-wrap mechanism? J. Phys. Chem. A 2001, 105, 2142–2146. [Google Scholar] [CrossRef]
- Kobayashi, K.; Nagase, S.; Dinse, K.-P. A theoretical study of spin density distributions and isotropic hyperfine couplings of N and P atoms in N@C60, P@C60, N@C70, N@C60(CH2)6, and N@C60(SiH2)6. Chem. Phys. Lett. 2003, 377, 93–98. [Google Scholar] [CrossRef]
- Wakahara, T.; Matsunaga, Y.; Katayama, A.; Maeda, Y.; Kako, M.; Akasaka, T.; Okamura, M.; Kato, T.; Choe, Y.K.; Kobayashi, K.; et al. A comparison of the photochemical reactivity of N@C60 and C60: Photolysis with disilirane. Chem. Commun. 2003, 39, 2940–2941. [Google Scholar] [CrossRef]
- Saunders, M.; Jiménez-Vázquez, H.A.; Cross, R.J.; Poreda, R.J. Stable compounds of helium and neon: He@C60 and Ne@C60. Science 1993, 259, 1428–1430. [Google Scholar] [CrossRef]
- Saunders, M.; Jiménez-Vázquez, H.A.; Cross, R.J.; Mroczkowski, S.; Freedberg, D.I.; Anet, F.A.L. Probing the interior of fullerenes by 3He NMR spectroscopy of endohedral 3He@C60 and 3He@C70. Nature 1994, 367, 256–258. [Google Scholar] [CrossRef]
- Cross, R.J.; Saunders, M.; Prinzbach, H. Putting helium inside dodecahedrane. Org. Lett. 1999, 1, 1479–1481. [Google Scholar] [CrossRef]
- Cross, R.J.; Saunders, M. Catalyzed incorporation of noble gases in fullerenes. In Recent Advances in the Chemistry and Physics of Fullerenes and Related Materials, Volume 11—Fullerenes for the New Millennium; Kadish, K.M., Kamat, p.V., Guldi, D., Eds.; The Electrochemical Society: Pennington, NJ, USA, 2001; pp. 298–300. [Google Scholar]
- Rubin, Y.; Jarrosson, T.; Wang, G.-W.; Bartberger, M.D.; Houk, K.N.; Schick, G.; Saunders, M.; Cross, R.J. Insertion of helium and molecular hydrogen through the orifice of an open fullerene. Angew. Chem. Int. Ed. Engl. 2001, 40, 1543–1546. [Google Scholar] [CrossRef]
- Carravetta, M.; Murata, Y.; Murata, M.; Heinmaa, I.; Stern, R.; Tontcheva, A.; Samoson, A.; Rubin, Y.; Komatsu, K.; Levitt, M.H. Solid-state NMR spectroscopy of molecular hydrogen trapped inside an open-cage fullerene. J. Am. Chem. Soc. 2004, 126, 4092–4093. [Google Scholar] [CrossRef] [PubMed]
- Iwamatsu, S.-I.; Uozaki, T.; Kobayashi, K.; Re, S.; Nagase, S.; Murata, S. A bowl-shaped fullerene encapsulates a water into the cage. J. Am. Chem. Soc. 2004, 126, 2668–2669. [Google Scholar] [CrossRef]
- Komatsu, K.; Murata, M.; Murata, Y. Encapsulation of molecular hydrogen in fullerene C60 by organic synthesis. Science 2005, 307, 238–240. [Google Scholar] [CrossRef]
- Kurotobi, K.; Murata, Y. A single molecule of water encapsulated in fullerene C60. Science 2011, 333, 613–616. [Google Scholar] [CrossRef]
- Zhang, R.; Murata, M.; Aharen, T.; Wakamiya, A.; Shimoaka, T.; Hasegawa, T.; Murata, Y. Synthesis of a distinct water dimer inside fullerene C70. Nat. Chem. 2016, 8, 435–441. [Google Scholar] [CrossRef]
- Iwamatsu, S.; Stanisky, C.M.; Cross, R.J.; Saunders, M.; Mizorogi, N.; Nagase, S.; Murata, S. Carbon monoxide inside an open-cage fullerene. Angew. Chem. Int. Ed. 2006, 45, 5337–5340. [Google Scholar] [CrossRef]
- Shi, L.J.; Yang, D.Z.; Colombo, F.; Yu, Y.M.; Zhang, W.X.; Gan, L.B. Punching a carbon atom of C60 into its own cavity to form an endohedral complex CO@C59O6 under mild conditions. Chem. Eur. J. 2013, 19, 16545–16549. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Lou, N.; Xu, D.; Pan, C.; Lu, X.; Gan, L. Oxygen-delivery materials: Synthesis of an open-cage fullerene derivative suitable for encapsulation of H2O2 and O2. Angew. Chem. Int. Ed. 2018, 57, 14144–14148. [Google Scholar] [CrossRef] [PubMed]
- Gan, L. Molecular containers derived from 60.fullerene through peroxide chemistry. Acc. Chem. Res. 2019, 52, 1793–1801. [Google Scholar] [CrossRef]
- Cioslowski, J. Endohedral chemistry: Electronic structures of molecules trapped inside the C60 cage. J. Am. Chem. Soc. 1991, 113, 4139–4141. [Google Scholar] [CrossRef]
- Charkin, O.P.; Klimenko, N.M.; Charkin, D.O.; Mebel, A.M. Theoretical study of host-guest interaction in model endohedral fullerenes with tetrahedral molecules and ions of MH4 hydrides inside the C60H36, C60H24, C84, and C60 cages. Russ. J. Inorg. Chem. 2004, 49, 868–880. [Google Scholar]
- Slanina, Z.; Uhlík, F.; Adamowicz, L.; Nagase, S. Computing fullerene encapsulation of non-metallic molecules: N2@C60 and NH3@C60. Mol. Simul. 2005, 31, 801–806. [Google Scholar] [CrossRef]
- Ramachandran, C.N.; Sathyamurthy, N. Water clusters in a confined nonpolar environment. Chem. Phys. Let. 2005, 410, 348–351. [Google Scholar] [CrossRef]
- Slanina, Z.; Nagase, S. A computational characterization of N2@C60. Mol. Phys. 2006, 104, 3167–3171. [Google Scholar] [CrossRef]
- Shameema, O.; Ramachandran, C.N.; Sathyamurthy, N. Blue shift in X-H stretching frequency of molecules due to confinement. J. Phys. Chem. A 2006, 110, 2–4. [Google Scholar] [CrossRef] [PubMed]
- Slanina, Z.; Pulay, P.; Nagase, S. H2, Ne, and N2 energies of encapsulation into C60 evaluated with the MPWB1K functional. J. Chem. Theory Comput. 2006, 2, 782–785. [Google Scholar] [CrossRef]
- Mazurek, A.P.; Sadlej-Sosnowska, N. Is fullerene C60 large enough to host an aromatic molecule? Int. J. Quantum Chem. 2011, 111, 2398–2405. [Google Scholar] [CrossRef]
- Rodríguez-Fortea, A.; Balch, A.L.; Poblet, J.M. Endohedral metallofullerenes: A unique host-guest association. Chem. Soc. Rev. 2011, 40, 3551–3563. [Google Scholar] [CrossRef]
- Varadwaj, A.; Varadwaj, P.R. Can a single molecule of water be completely isolated within the subnano-space inside the fullerene C60 cage? A Quantum chemical prospective. Chem. Eur. J. 2012, 18, 15345–15360. [Google Scholar] [CrossRef]
- Farimani, A.B.; Wu, Y.B.; Aluru, N.R. Rotational motion of a single water molecule in a buckyball. Phys. Chem. Chem. Phys. 2013, 15, 17993–18000. [Google Scholar] [CrossRef]
- Popov, A.A.; Yang, S.; Dunsch, L. Endohedral fullerenes. Chem. Rev. 2013, 113, 5989–6113. [Google Scholar] [CrossRef]
- Uhlík, F.; Slanina, Z.; Lee, S.-L.; Wang, B.-C.; Adamowicz, L.; Nagase, S. Water-dimer stability and its fullerene encapsulations. J. Comput. Theor. Nanosci. 2015, 12, 959–964. [Google Scholar] [CrossRef]
- Slanina, Z.; Uhlík, F.; Lu, X.; Akasaka, T.; Lemke, K.H.; Seward, T.M.; Nagase, S.; Adamowicz, L. Calculations of the water-dimer encapsulations into C84. Fullerenes Nanotub. Carbon Nanostruct. 2016, 24, 1–7. [Google Scholar] [CrossRef]
- Slanina, Z.; Uhlík, F.; Nagase, S.; Lu, X.; Akasaka, T.; Adamowicz, L. Computed relative populations of D2(22)-C84 endohedrals with encapsulated monomeric and dimeric water. ChemPhysChem 2016, 17, 1109–1111. [Google Scholar] [CrossRef]
- Slanina, Z.; Uhlík, F.; Nagase, S.; Akasaka, T.; Adamowicz, L.; Lu, X. Computational comparison of the water-dimer encapsulations into D2(22)-C84 and D2d(23)-C84. ECS J. Solid State Sci. Technol. 2017, 6, M3113–M3115. [Google Scholar] [CrossRef]
- Slanina, Z.; Uhlík, F.; Nagase, S.; Akasaka, T.; Adamowicz, L.; Lu, X. A computational characterization of CO@C60. Fullerenes Nanotubes Carbon Nanostruct. 2017, 25, 624–629. [Google Scholar] [CrossRef]
- Zhang, R.; Murata, M.; Wakamiya, A.; Shimoaka, T.; Hasegawa, T.; Murata, Y. Isolation of the simplest hydrated acid. Sci. Adv. 2017, 3, e1602833. [Google Scholar] [CrossRef]
- Slanina, Z.; Uhlík, F.; Nagase, S.; Akasaka, T.; Lu, X.; Adamowicz, L. Cyclic water-trimer encapsulation into D2(22)-C84 fullerene. Chem. Phys. Lett. 2018, 695, 245–248. [Google Scholar] [CrossRef]
- Slanina, Z.; Uhlík, F.; Adamowicz, L.; Pan, C.; Lu, X. A computational characterization of H2O2@C60. Fullerenes Nanotubes Carbon Nanostruct. 2022, 30, 258–262. [Google Scholar] [CrossRef]
- Slanina, Z.; Uhlík, F.; Adamowicz, L. Theoretical predictions of fullerene stabilities. In Handbook of Fullerene Science and Technology; Lu, X., Akasaka, T., Slanina, Z., Eds.; Springer: Singapore, 2022; pp. 111–179. [Google Scholar]
- Slanina, Z.; Uhlík, F.; Lu, X.; Akasaka, T.; Adamowicz, L. H2O.HF@C70: Encapsulation energetics and thermodynamics. Inorganics 2023, 11, 123. [Google Scholar] [CrossRef]
- Slanina, Z.; Uhlík, F.; Akasaka, T.; Lu, X.; Adamowicz, L. A Computational characterization of CH4@C60. Inorganics 2024, 12, 64. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. Hybrid meta density functional theory methods for thermochemistry, thermochemical kinetics, and noncovalent interactions: The MPW1B95 and MPWB1K models and comparative assessments for hydrogen bonding and van der Waals interactions. J. Phys. Chem. A 2004, 108, 6908–6918. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Rev. D.01; Gaussian Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
- Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the difference of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Schwenke, D.W.; Truhlar, D.G. Systematic study of basis set superposition errors in the calculated interaction energy of two HF molecules. J. Chem. Phys. 1985, 82, 2418–2426. [Google Scholar] [CrossRef]
- van Duijneveldt, F.B.; van Duijneveldt—Van de Rijdt, J.G.C.M.; van Lenthe, J.H. State-of-the-Art in counterpoise theory. Chem. Rev. 1994, 94, 1873–1885. [Google Scholar] [CrossRef]
- Simon, S.; Bertran, J.; Sodupe, M. Effect of counterpoise correction on the geometries and vibrational frequencies of hydrogen bonded systems. J. Phys. Chem. A 2001, 105, 4359–4364. [Google Scholar] [CrossRef]
- Slanina, Z.; Lee, S.-L.; Adamowicz, L.; Uhlík, F.; Nagase, S. Computed atructure and energetics of La@C60. Int. J. Quantum Chem. 2005, 104, 272–277. [Google Scholar] [CrossRef]
- Slanina, Z.; Uhlík, F.; Lee, S.-L.; Adamowicz, L.; Akasaka, T.; Nagase, S. Computed stabilities in metallofullerene series: Al@C82, Sc@C82, Y@C82, and La@C82. Int. J. Quantum Chem. 2011, 111, 2712–2718. [Google Scholar] [CrossRef]
- Basiuk, V.A.; Tahuilan-Anguiano, D.E. Complexation of free-base and 3d transition metal(II) phthalocyanines with endohedral fullerene Sc3N@C80. Chem. Phys. Lett. 2019, 722, 146–152. [Google Scholar] [CrossRef]
- Tahuilan-Anguiano, D.E.; Basiuk, V.A. Complexation of free-base and 3d transition metal(II) phthalocyanines with endohedral fullerenes H@C60, H2@C60 and He@C60: The effect of encapsulated species. Diam. Rel. Mat. 2021, 118, 108510. [Google Scholar] [CrossRef]
- Moller, C.; Plesset, M.S. Note on an approximation treatment for many-electron systems. Phys. Rev. 1934, 46, 618–622. [Google Scholar] [CrossRef]
- Schwabe, T.; Grimme, S. Double-hybrid density functionals with long-range dispersion corrections: Higher accuracy and extended applicability. Phys. Chem. Chem. Phys. 2007, 9, 3397–3406. [Google Scholar] [CrossRef]
- Grimme, S. Improved second-order Møller-Plesset perturbation theory by separate scaling of parallel- and antiparallel-spin pair correlation energies. J. Chem. Phys. 2003, 118, 9095–9102. [Google Scholar] [CrossRef]
- Cross, R.J. Does H2 rotate freely inside fullerenes? J. Phys. Chem. 2001, 105, 6943–6944. [Google Scholar] [CrossRef]
- Akasaka, T.; Nagase, S.; Kobayashi, K.; Walchli, M.; Yamamoto, K.; Funasaka, H.; Kako, M.; Hoshino, T.; Erata, T. 13C and 139La NMR studies of La2@C80: First evidence for circular motion of metal atoms in endohedral dimetallofullerenes. Angew. Chem. Int. Ed. 1997, 36, 1643–1645. [Google Scholar] [CrossRef]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef]
- Tsuzuki, S.; Lüthi, H.P. Interaction energies of van der Waals and hydrogen bonded systems calculated using density functional theory: Assessing the PW91 model. J. Chem. Phys. 2001, 114, 3949–3957. [Google Scholar] [CrossRef]
- Lebedkin, S.; Renker, B.; Heid, R.; Schober, H.; Rietschel, H. A spectroscopic study of M@C82 metallofullerenes: Raman, far-infrared, and neutron scattering results. Appl. Phys. A 1998, 66, 273–280. [Google Scholar] [CrossRef]
- Slanina, Z.; Rudziński, J.M.; Togasi, M.; Ōsawa, E. Quantum-chemically supported vibrational analysis of giant molecules: The C60 and C70 clusters. J. Mol. Struct. (Theochem) 1989, 202, 169–176. [Google Scholar] [CrossRef]
- Frum, C.I.; Engleman Jr., R.; Hedderich, H.G.; Bernath, P.F.; Lamb, L.D.; Huffman, D.R. The infrared emission spectrum of gas-phase C60 (buckmisterfullerene). Chem. Phys. Lett. 1991, 176, 504–508. [Google Scholar] [CrossRef]
- Slanina, Z. Some aspects of mathematical chemistry of equilibrium and rate processes: Steps towards a completely non-empirical computer design of syntheses. J. Mol. Struct. (Theochem) 1989, 185, 217–228. [Google Scholar] [CrossRef]
- Slanina, Z. A program for determination of composition and thermodynamics of the ideal gas-phase equilibrium isomeric mixtures. Comput. Chem. 1989, 13, 305–311. [Google Scholar] [CrossRef]
- Slanina, Z.; Uhlík, F.; François, J.-P.; Ōsawa, E. Thermodynamic data bases and optical isomerism. Croat. Chem. Acta 2000, 73, 1047–1055. [Google Scholar]
- Slanina, Z.; Lee, S.-L.; Uhlík, F.; Adamowicz, L.; Nagase, S. Computing relative stabilities of metallofullerenes by Gibbs energy treatments. Theor. Chem. Acc. 2007, 117, 315–322. [Google Scholar] [CrossRef]
- Slanina, Z.; Uhlík, F.; Lee, S.-L.; Adamowicz, L.; Akasaka, T.; Nagase, S. Calculations of metallofullerene yields. J. Comput. Theor. Nanosci. 2011, 8, 2233–2239. [Google Scholar] [CrossRef]
- Slanina, Z. A comparative study of the water-dimer gas-phase thermodynamics in the BJH- and MCYL-type flexible potentials. Chem. Phys. 1991, 150, 321–329. [Google Scholar] [CrossRef]
- Ganji, M.D.; Mohseni, M.; Goli, O. Modeling complexes of NH3 molecules confined in C60 fullerene. J. Mol. Struct. (Theochem) 2009, 913, 54–57. [Google Scholar] [CrossRef]
- Medrek, M.; Pluciński, F.; Mazurek, A.P. Endohedral complexes of fullerene C60 with small convalent molecules (H2O, NH3, H2, 2H2, 3H2, 4H2, O2, O3) in the context of potential drug transporter system. Acta Pol. Pharm. 2013, 70, 659–665. [Google Scholar]
- Park, J.M.; Tarakeshwar, P.; Kim, K.S.; Clark, T. Nature of the interaction of paramagnetic atoms (A=4N,4P,3O,3S) with π systems and C60: A theoretical investigation of A… C6H6 and endohedral fullerenes A@C60. J. Chem. Phys. 2002, 116, 10684–10691. [Google Scholar] [CrossRef]
- Slanina, Z. Entropy-controlled reactions: An interesting textbook error. J. Chem. Educ. 1991, 68, 474–475. [Google Scholar] [CrossRef]
- Walsh, T.R.; Wales, D.J. Relaxation dynamics of C60. J. Chem. Phys. 1998, 109, 6691–6700. [Google Scholar] [CrossRef]
- Kobayashi, K.; Nagase, S. Structures and electronic properties of endohedral metallofullerenes: Theory and experiment. In Endofullerenes—A New Family of Carbon Clusters; Akasaka, T., Nagase, S., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2002; pp. 99–119. [Google Scholar]
- Eggen, B.R.; Heggie, M.I.; Jungnickel, G.; Latham, C.D.; Jones, R.; Briddon, P.R. Autocatalysis during fullerene growth. Science 1996, 272, 87–89. [Google Scholar] [CrossRef]
- Patchkovskii, S.; Thiel, W. How does helium get into buckminsterfullerene. J. Am. Chem. Soc. 1996, 118, 7164–7172. [Google Scholar] [CrossRef]
- Patchkovskii, S.; Thiel, W. Radical impurity mechanisms for helium incorporation into buckminsterfullerene. Helv. Chim. Acta 1997, 80, 495–509. [Google Scholar] [CrossRef]
- Shimshi, R.; Khong, A.; Jiménez-Vázquez, H.A.; Cross, R.J.; Saunders, M. Release of noble gas atoms from inside fullerenes. Tetrahedron 1996, 52, 5143–5148. [Google Scholar] [CrossRef]
- Eggen, B.R.; Heggie, M.I.; Jungnickel, G.; Latham, C.D.; Jones, R.; Briddon, P.R. Carbon atoms catalyse fullerene growth. Fullerene Sci. Technol. 1997, 5, 727–745. [Google Scholar] [CrossRef]
- Slanina, Z.; Zhao, X.; Uhlík, F.; Ozawa, M.; Ōsawa, E. Computational modelling of the metal and other elemental catalysis in the Stone-Wales fullerene rearrangements. J. Organomet. Chem. 2000, 599, 57–61. [Google Scholar] [CrossRef]
- Slanina, Z.; Zhao, X.; Ozawa, M.; Adamowicz, L.; Ōsawa, E. Computational evaluations of the elemental-catalytical effects on the kinetics of the Stone-Wales isomerizations. In Recent Advances in the Chemistry and Physics of Fullerenes and Related Materials: Vol. 10—Chemistry and Physics of Fullerenes and Carbon Nanomaterials; Kamat, p.V., Guldi, D.M., Kadish, K.M., Eds.; The Electrochemical Society: Pennington, NJ, USA, 2000; pp. 129–141. [Google Scholar]
- Haynes, W.M.; Lide, D.R.; Bruno, T.J. (Eds.) CRC Handbook of Chemistry and Physics, 95th ed.; CRC Press: Boca Raton, FL, USA, 2014; pp. 6–83. [Google Scholar]
- Slanina, Z.; Uhlík, F.; Stobinski, L.; Lin, H.-M.; Adamowicz, L. Computing narrow nanotubes and their derivatives. Int. J. Nanosci. 2002, 1, 303–312. [Google Scholar] [CrossRef]
- Slanina, Z.; Stobinski, L.; Tomasik, P.; Lin, H.-M.; Adamowicz, L. Quantum-chemical evaluations of thermodynamics and kinetics of oxygen additions to narrow nanotubes. J. Nanosci. Nanotech. 2003, 3, 193–198. [Google Scholar] [CrossRef]
- Slanina, Z.; Uhlík, F.; Juha, L.; Tanabe, K.; Adamowicz, L.; Ōsawa, E. Computations on C84O: Thermodynamic, kinetic and photochemical stability. J. Mol. Struct. (Theochem) 2004, 684, 129–133. [Google Scholar] [CrossRef]
- Sure, R.; Tonner, R.; Schwerdtfeger, P. Systematic study of rare gas atoms encapsulated in small fullerenes using dispersion corrected density functional theory. J. Comput. Chem. 2015, 36, 88–96. [Google Scholar] [CrossRef] [PubMed]
- Wang, E.; Gao, Y. H2 + H2O → H4O: Synthesizing hyperhydrogenated water in small-sized fullerenes? J. Phys. Chem. A 2023, 127, 1190–1195. [Google Scholar] [CrossRef]
- Díaz-Tendero, S.; Alcamí, M.; Martín, F. Fullerene C50: Sphericity takes over, not strain. Chem. Phys. Lett. 2005, 407, 153–158. [Google Scholar] [CrossRef]
- Vukicevic, D.; Cataldo, F.; Ori, O.; Graovac, A. Topological efficiency of C66 fullerene. Chem. Phys. Lett. 2011, 501, 442–445. [Google Scholar] [CrossRef]
- Slanina, Z.; Chao, M.-C.; Lee, S.-L.; and Gutman, I. On applicability of the Wiener index to estimate relative stabilities of the higher-fullerene IPR isomers. J. Serb. Chem. Soc. 1997, 62, 211–217. [Google Scholar]
- Slanina, Z.; Uhlík, F.; Lee, S.-L.; Ōsawa, E. Geometrical and thermodynamic approaches to the relative stabilities of fullerene isomers. MATCH Commun. Math. Comput. Chem. 2001, 44, 335–348. [Google Scholar]
- Mina-Camilde, N.; Manzanares, I.C.; Caballero, J.F. Molecular constants of carbon monoxide at v = 0, 1, 2, and 3: A vibrational spectroscopy experiment in physical chemistry. J. Chem. Educ. 1996, 73, 804–807. [Google Scholar] [CrossRef]
- Muenter, J.S. Electric dipole moment of carbon monoxide. J. Mol. Spectrosc. 1975, 55, 490–491. [Google Scholar] [CrossRef]
- Billingsley II, F.P.; Krauss, M. Multiconfiguration self-consistent-field calculation of the dipole moment function of CO(X1Σ+). J. Chem. Phys. 1974, 60, 4130–4144. [Google Scholar] [CrossRef]
- Scuseria, G.E.; Miller, M.D.; Jensen, F.; Geertsen, J. The dipole moment of carbon monoxide. J. Chem. Phys. 1991, 94, 6660–6663. [Google Scholar] [CrossRef]
- Barnes, L.A.; Liu, B.; Lindh, R. Bond length, dipole moment, and harmonic frequency of CO. J. Chem. Phys. 1993, 98, 3972–3977. [Google Scholar] [CrossRef]
- Politzer, P.; Kammeyer, C.W.; Bauer, S.J.; Hedges, W.L. Polar properties of carbon monoxide. J. Phys. Chem. 1981, 85, 4057–4060. [Google Scholar] [CrossRef]
- Harrison, J.F. Relationship between the charge distribution and dipole moment functions of CO and the Related Molecules CS, SiO, and SiS. J. Phys. Chem. A 2006, 110, 10848–10857. [Google Scholar] [CrossRef] [PubMed]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Reduced and quenched polarizabilities of interior atoms in molecules. Chem. Sci. 2013, 4, 2349–2356. [Google Scholar] [CrossRef]
- Sabirov, D.S. Polarizability as a landmark property for fullerene chemistry and materials science. RSC Adv. 2014, 4, 44996–45028. [Google Scholar] [CrossRef]
- Ghosh, D.C. A quest for the origin of barrier to the internal rotation of hydrogen peroxide (H2O2) and fluorine peroxide (F2O2). Int. J. Mol. Sci. 2006, 7, 289–319. [Google Scholar] [CrossRef]
- Bergman, P.; Parise, B.; Liseau, R.; Larsson, B.; Olofsson, H.; Menten, K.M.; Güsten, R. Detection of interstellar hydrogen peroxide. Astronom. Astrophys. 2011, 531, L8. [Google Scholar] [CrossRef]
- Slanina, Z.; François, J.-P.; Kolb, M.; Bakowies, D.; Thiel, W. Calculated relative stabilities of C84. Fullerene Sci. Technol. 1993, 1, 221–230. [Google Scholar] [CrossRef]
- Slanina, Z.; Lee, S.-L. Chirality effects upon populations of C84 species. J. Mol. Struct. (Theochem) 1995, 333, 153–158. [Google Scholar] [CrossRef]
- Ōsawa, E.; Ueno, H.; Yoshida, M.; Slanina, Z.; Zhao, X.; Nishiyama, M.; Saito, H. Combined topological and energy analysis of the annealing process in fullerene formation. Stone-Wales interconversion pathways among IPR isomers of higher fullerenes. J. Chem. Soc. Perkin Trans. 1998, 2, 943–950. [Google Scholar] [CrossRef]
- Diederich, F.; Ettl, R.; Rubin, Y.; Whetten, R.L.; Beck, R.; Alvarez, M.; Anz, S.; Sensharma, D.; Wudl, F.; Khemani, K.C.; et al. The higher fullerenes: Isolation and characterization of C76, C84, C90, C94, and C70O, an oxide of D5h-C70. Science 1991, 252, 548–551. [Google Scholar] [CrossRef]
- Beck, R.D.; John, P.S.; Alvarez, M.M.; Diederich, F.; Whetten, R.L. Resilience of all-carbon molecules C60, C70, and C84: A surface-scattering time-of-flight investigation. J. Phys. Chem. 1991, 95, 8402–8409. [Google Scholar] [CrossRef]
- Kikuchi, K.; Nakahara, N.; Honda, M.; Suzuki, S.; Saito, K.; Shiromaru, H.; Yamauchi, K.; Ikemoto, I.; Kuramochi, T.; Hino, S.; et al. Separation, detection and UV/Visible absorption spectra of fullerenes, C76, C78 and C84. Chem. Lett. 1991, 1607–1610. [Google Scholar] [CrossRef]
- Raghavachari, K.; Rohlfing, C.M. Structures and vibrational frequencies of carbon molecules (C60, C70, and C84). J. Phys. Chem. 1991, 95, 5768–5773. [Google Scholar] [CrossRef]
- Manolopoulos, D.E.; Fowler, P.W. Molecular graphs, point groups, and fullerenes. J. Chem. Phys. 1992, 96, 7603–7614. [Google Scholar] [CrossRef]
- Bakowies, D.; Kolb, M.; Thiel, W.; Richard, S.; Ahlrichs, R.; Kappes, M.M. Quantum-chemical study of C84 fullerene isomers. Chem. Phys. Lett. 1992, 200, 411–417. [Google Scholar] [CrossRef]
- Dennis, T.J.S.; Kai, T.; Tomiyama, T.; Shinohara, H. Isolation and characterisation of the two major isomers of [84]fullerene (C84). Chem. Commun. 1998, 619–620. [Google Scholar] [CrossRef]
- Dennis, T.J.S.; Kai, T.; Asato, K.; Tomiyama, T.; Shinohara, H.; Yoshida, T.; Kobayashi, Y.; Ishiwatari, H.; Miyake, Y.; Kikuchi, K.; et al. Isolation and characterization by 13C NMR spectroscopy of [84]fullerene minor isomers. J. Phys. Chem. A 1999, 103, 8747–8752. [Google Scholar] [CrossRef]
- Slanina, Z. Does the global energy minimum always mean also the thermodynamically most stable structure? J. Mol. Struct. (Theochem) 1990, 65, 143–152. [Google Scholar] [CrossRef]
- Wakahara, T.; Nikawa, H.; Kikuchi, T.; Nakahodo, T.; Rahman, G.M.A.; Tsuchiya, T.; Maeda, Y.; Akasaka, T.; Yoza, K.; Horn, E.; et al. La@C72 Having a non-IPR carbon cage. J. Am. Chem. Soc. 2006, 128, 14228–14229. [Google Scholar] [CrossRef] [PubMed]
- Mercado, B.Q.; Stuart, M.A.; Mackey, M.A.; Pickens, J.E.; Confait, B.S.; Stevenson, S.; Easterling, M.L.; Valencia, R.; Rodríguez-Fortea, A.; Poblet, J.M.; et al. Sc2(μ2-O) trapped in a fullerene cage: The isolation and structural characterization of Sc2(μ2-O)@Cs(6)-C82 and the relevance of the thermal and entropic effects in fullerene isomer selection. J. Am. Chem. Soc. 2010, 132, 12098–12105. [Google Scholar] [CrossRef] [PubMed]
- Mercado, B.Q.; Chen, N.; Rodríguez-Fortea, A.; Mackey, M.A.; Stevenson, S.; Echegoyen, L.; Poblet, J.M.; Olmstead, M.M.; Balch, A.L. The shape of the Sc2(μ2-S) unit trapped in C82: Crystallographic, computational, and electrochemical studies of the isomers, Sc2(μ2-S)@Cs(6)-C82 and Sc2(μ2-S)@3v(8)-C82. J. Am. Chem. Soc. 2011, 133, 6752–6760. [Google Scholar] [CrossRef]
- Slanina, Z.; Uhlík, F.; Lee, S.-L.; Adamowicz, L.; Akasaka, T.; Nagase, S. Stability computations for isomers of La@Cn (n = 72, 74, 76). Molecules 2012, 17, 13146–13156. [Google Scholar] [CrossRef]
- Mulet-Gas, M.; Rodríguez-Fortea, A.; Echegoyen, L.; Poblet, J.M. Relevance of thermal effects in the formation of endohedral metallofullerenes: The case of Gd3N@Cs(39663)-C82 and other related systems. Inorg. Chem. 2013, 52, 1954–1959. [Google Scholar] [CrossRef]
- Rocher-Casterline, B.E.; Ch’ng, L.C.; Mollner, A.K.; Reisler, H. Communication: Determination of the bond dissociation energy (D0) of the water dimer, (H2O)2, by velocity map imaging. J. Chem. Phys. 2011, 134, 211101. [Google Scholar] [CrossRef]
- Ch’ng, L.C.; Samanta, A.K.; Wang, Y.; Bowman, J.M.; Reisler, H. Experimental and theoretical investigations of the dissociation energy (D0) and dynamics of the water trimer, (H2O)3. J. Phys. Chem. A 2013, 117, 7207–7216. [Google Scholar] [CrossRef]
- Slanina, Z.; Uhlík, F.; Lee, S.-L.; Nagase, S. Computational modelling for the clustering degree in the saturated steam and the water-containing complexes in the atmosphere. J. Quant. Spectr. Radiat. Transf. 2006, 97, 415–423. [Google Scholar] [CrossRef]
- Mukhopadhyay, A.; Cole, W.T.S.; Saykally, R.J. The water dimer I: Experimental characterization. Chem. Phys. Lett. 2015, 633, 13–26. [Google Scholar] [CrossRef]
- Mukhopadhyay, A.; Xantheas, S.S.; Saykally, R.J. The water dimer II: Theoretical investigations. Chem. Phys. Lett. 2018, 700, 163–175. [Google Scholar] [CrossRef]
- Slanina, Z. Contemporary Theory of Chemical Isomerism; D. Reidel Publishing Company: Prague, Czech Republic; Dordrecht, The Netherlands, 1986. [Google Scholar]
- Slanina, Z. Equilibrium isomeric mixtures: Potential energy hypersurfaces as originators of the description of the overall thermodynamics and kinetics. Int. Rev. Phys. Chem. 1987, 6, 251–267. [Google Scholar] [CrossRef]
- Legon, A.C.; Millen, D.J.; North, H.M. Experimental determination of the dissociation energies D0 0 and De of H2O...HF. Chem. Phys. Let. 1987, 135, 303–306. [Google Scholar] [CrossRef]
- Murata, M.; Murata, Y.; Komatsu, K. Surgery of fullerenes. Chem. Commun. 2008, 6083–6094. [Google Scholar] [CrossRef]
- Morinaka, Y.; Sato, S.; Wakamiya, A.; Nikawa, H.; Mizorogi, N.; Tanabe, F.; Murata, M.; Komatsu, K.; Furukawa, K.; Kato, T.; et al. X-ray observation of a helium atom and placing a nitrogen atom inside He@C60 and He@C70. Nat. Commun. 2013, 4, 1554. [Google Scholar] [CrossRef]
- Dodziuk, H.; Ruud, K.; Korona, T.; Demissie, T.B. Chiral recognition by fullerenes: CHFClBr enantiomers in the C82 cage. Phys. Chem. Chem. Phys. 2016, 18, 26057–26068. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, A.K.; Pandey, S.K.; Misra, N. Prediction of superalkali@C60 endofullerenes, their enhanced stability and interesting properties. Chem. Phys. Lett. 2016, 655–656, 71–75. [Google Scholar] [CrossRef]
- Hashikawa, Y.; Murata, M.; Wakamiya, A.; Murata, Y. Synthesis and properties of endohedral aza[60]fullerenes: H2O@C59N and H2@C59N as their dimers and monomers. J. Am. Chem. Soc. 2016, 138, 4096–4104. [Google Scholar] [CrossRef]
- Basiuk, V.A.; Basiuk, E.V. Noncovalent complexes of Ih-C80 fullerene with phthalocyanines. Fuller. Nanotub. Carbon Nanostruct. 2018, 26, 69–75. [Google Scholar] [CrossRef]
- Bloodworth, S.; Sitinova, G.; Alom, S.; Vidal, S.; Bacanu, G.R.; Elliott, S.J.; Light, M.E.; Herniman, J.M.; Langley, G.J.; Levitt, M.H.; et al. First synthesis and characterization of CH4@C60. Angew. Chem. Int. Ed. 2019, 58, 5038–5043. [Google Scholar] [CrossRef]
- Hashikawa, Y.; Kizaki, K.; Hirose, T.; Murata, Y. An orifice design: Water insertion into C60. RSC Adv. 2020, 10, 40406–40410. [Google Scholar] [CrossRef]
- Carrillo-Bohórquez, O.; Valdés, Á.; Prosmiti, R. Encapsulation of a water molecule inside C60 fullerene: The impact of confinement on quantum features. J. Chem. Theory Comput. 2021, 17, 5839–5848. [Google Scholar] [CrossRef]
- Pizzagalli, L. First principles molecular dynamics calculations of the mechanical properties of endofullerenes containing noble gas atoms or small molecules. Phys. Chem. Chem. Phys. 2022, 24, 9449–9458. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Zhao, R.; Dang, J.; Zhao, X. Theoretical study on the stabilities, electronic structures, and reaction and formation mechanisms of fullerenes and endohedral metallofullerenes. Coor. Chem. Rev. 2022, 471, 214762. [Google Scholar] [CrossRef]
- Menon, A.; Kaur, R.; Guldi, D.M. Merging carbon nanostructures with porphyrins. In Handbook of Fullerene Science and Technology; Lu, X., Akasaka, T., Slanina, Z., Eds.; Springe: Singapore, 2022; pp. 219–264. [Google Scholar]
- Huang, G.; Hasegawa, S.; Hashikawa, Y.; Ide, Y.; Hirose, T.; Murata, Y. An H2O2 molecule stabilized inside open-cage C60 derivatives by a hydroxy stopper. Chem. Eur. J. 2022, 28, e202103836. [Google Scholar] [CrossRef]
- Hashikawa, Y.; Fujikawa, N.; Murata, Y. NH3 encapsulation in π-extended fullerenes. J. Am. Chem. Soc. 2022, 144, 23292–23296. [Google Scholar] [CrossRef]
- Jia, A.; Huang, H.; Zuo, Z.-F.; Peng, Y.-J. Electronic structure and interaction in CH4@C60: A first-principle investigation. J. Mol. Model. 2022, 28, 179. [Google Scholar] [CrossRef] [PubMed]
- Hashikawa, Y.; Murata, Y. Water in fullerenes. Bull. Chem. Soc. Jpn. 2023, 96, 943–967. [Google Scholar] [CrossRef]
- Li, Y.B.; Biswas, R.; Kopcha, W.P.; Dubroca, T.; Abella, L.; Sun, Y.; Crichton, R.A.; Rathnam, C.; Yang, L.T.; Yeh, Y.W.; et al. Structurally defined water-soluble metallofullerene derivatives towards biomedical applications. Angew. Chem. Int. Ed. Engl. 2023, 62, e202211704. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Slanina, Z.; Uhlík, F.; Akasaka, T.; Lu, X.; Adamowicz, L. Theoretical Studies of Non-Metal Endohedral Fullerenes. Nanomaterials 2025, 15, 1287. https://doi.org/10.3390/nano15161287
Slanina Z, Uhlík F, Akasaka T, Lu X, Adamowicz L. Theoretical Studies of Non-Metal Endohedral Fullerenes. Nanomaterials. 2025; 15(16):1287. https://doi.org/10.3390/nano15161287
Chicago/Turabian StyleSlanina, Zdeněk, Filip Uhlík, Takeshi Akasaka, Xing Lu, and Ludwik Adamowicz. 2025. "Theoretical Studies of Non-Metal Endohedral Fullerenes" Nanomaterials 15, no. 16: 1287. https://doi.org/10.3390/nano15161287
APA StyleSlanina, Z., Uhlík, F., Akasaka, T., Lu, X., & Adamowicz, L. (2025). Theoretical Studies of Non-Metal Endohedral Fullerenes. Nanomaterials, 15(16), 1287. https://doi.org/10.3390/nano15161287









