Optimizing Inorganic Cs4CuSb2Cl12/Cs2TiI6 Dual-Absorber Solar Cells: SCAPS-1D Simulations and Machine Learning
Abstract
1. Introduction
2. Methods
2.1. SCAPS-1D Simulation
2.2. Machine Learning
3. Findings and Analysis
3.1. Choice of ETL and HTL
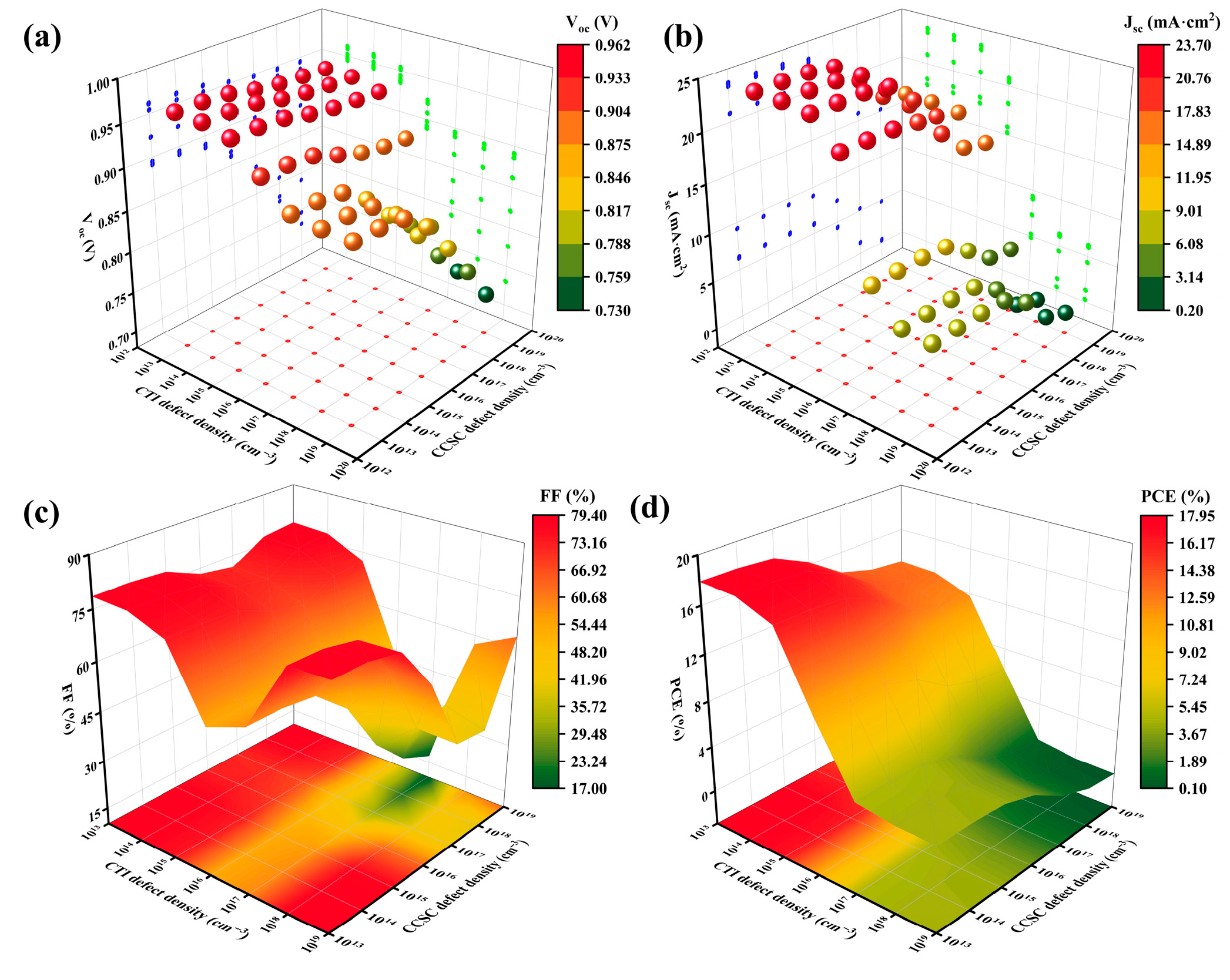
3.2. Impact of Defect Density of Absorber Layer on Properties
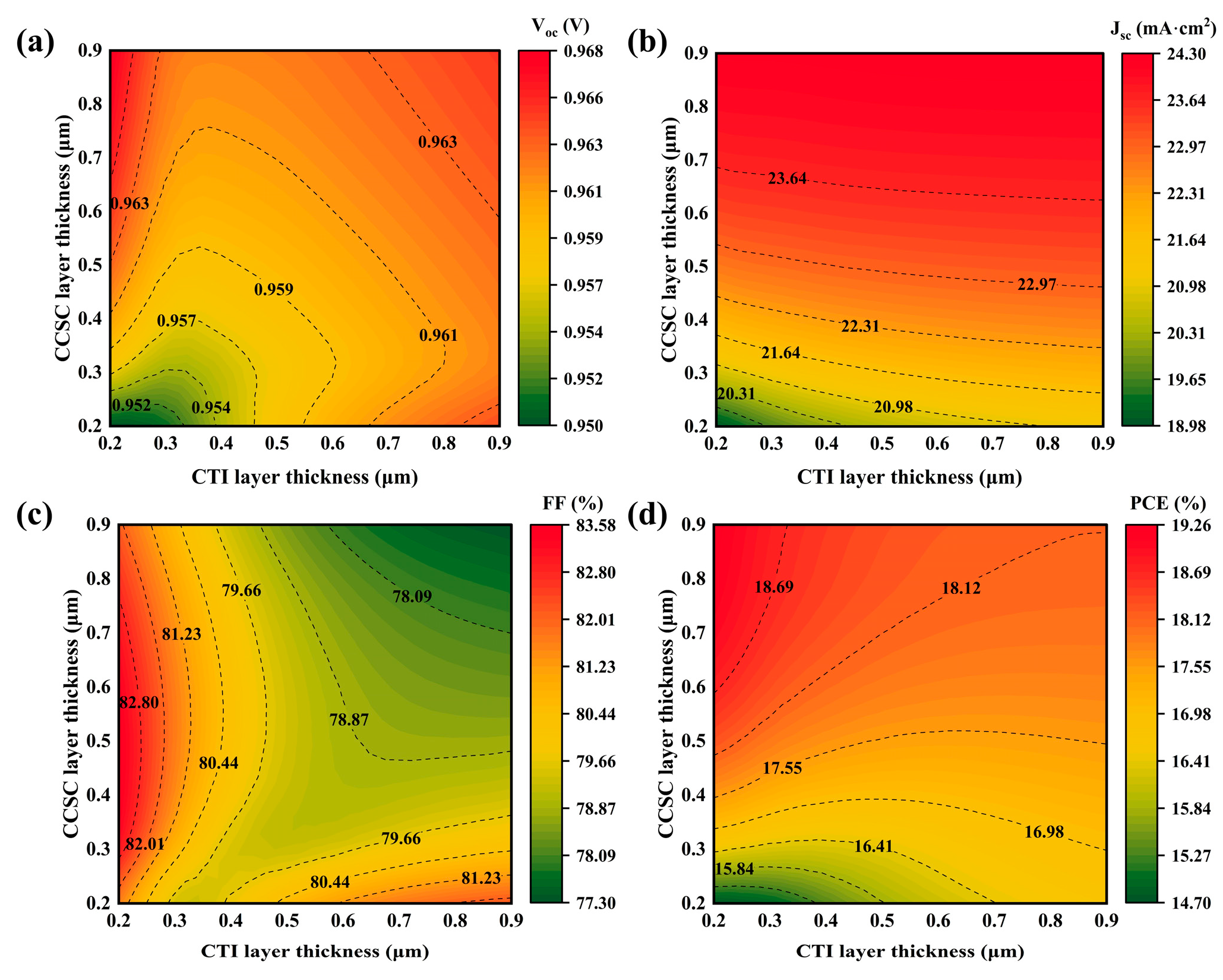
3.3. Impact of Absorber Layer Thickness on Properties
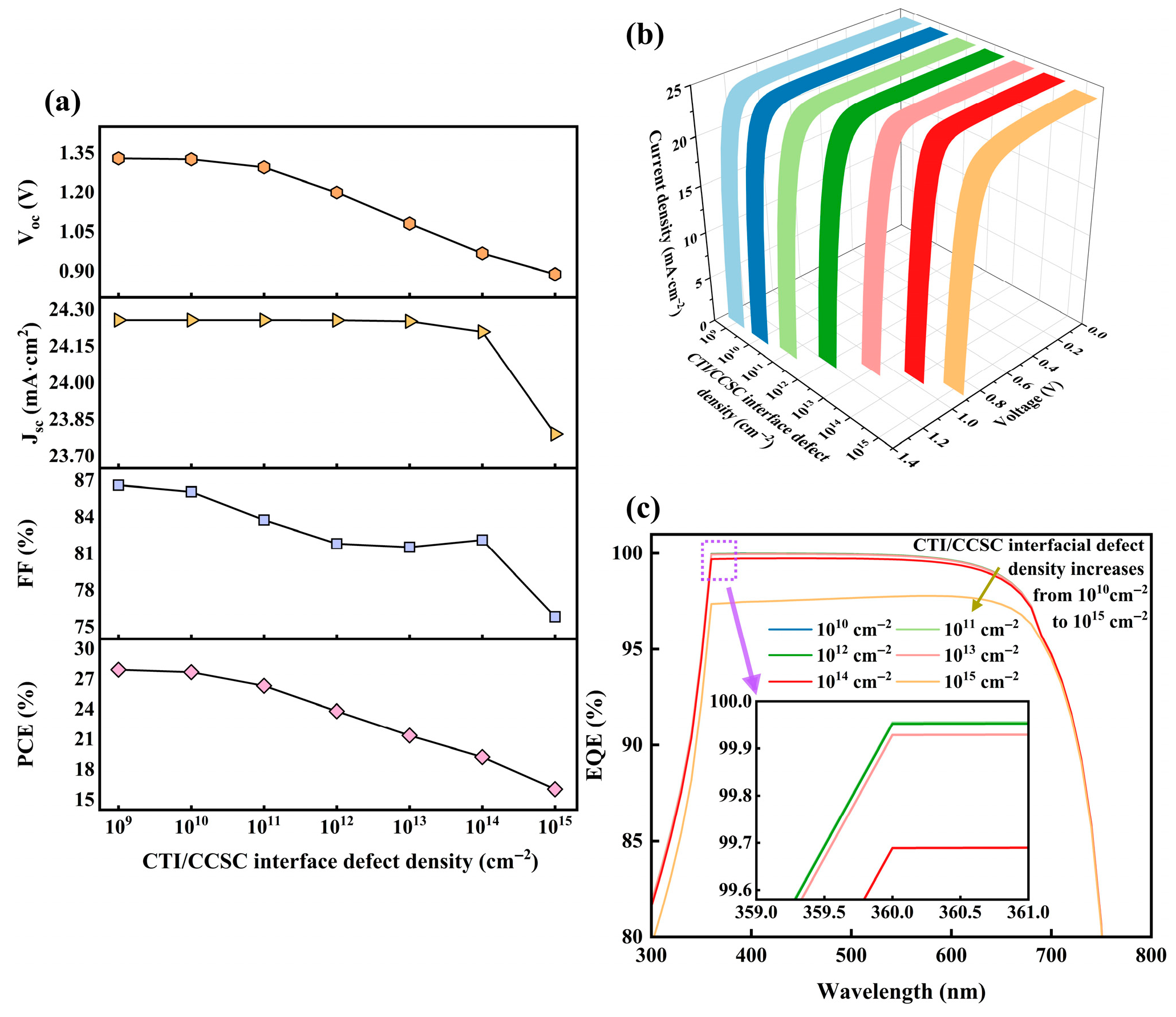
3.4. Impact of Interface Defect Density of Absorber Layer on Properties
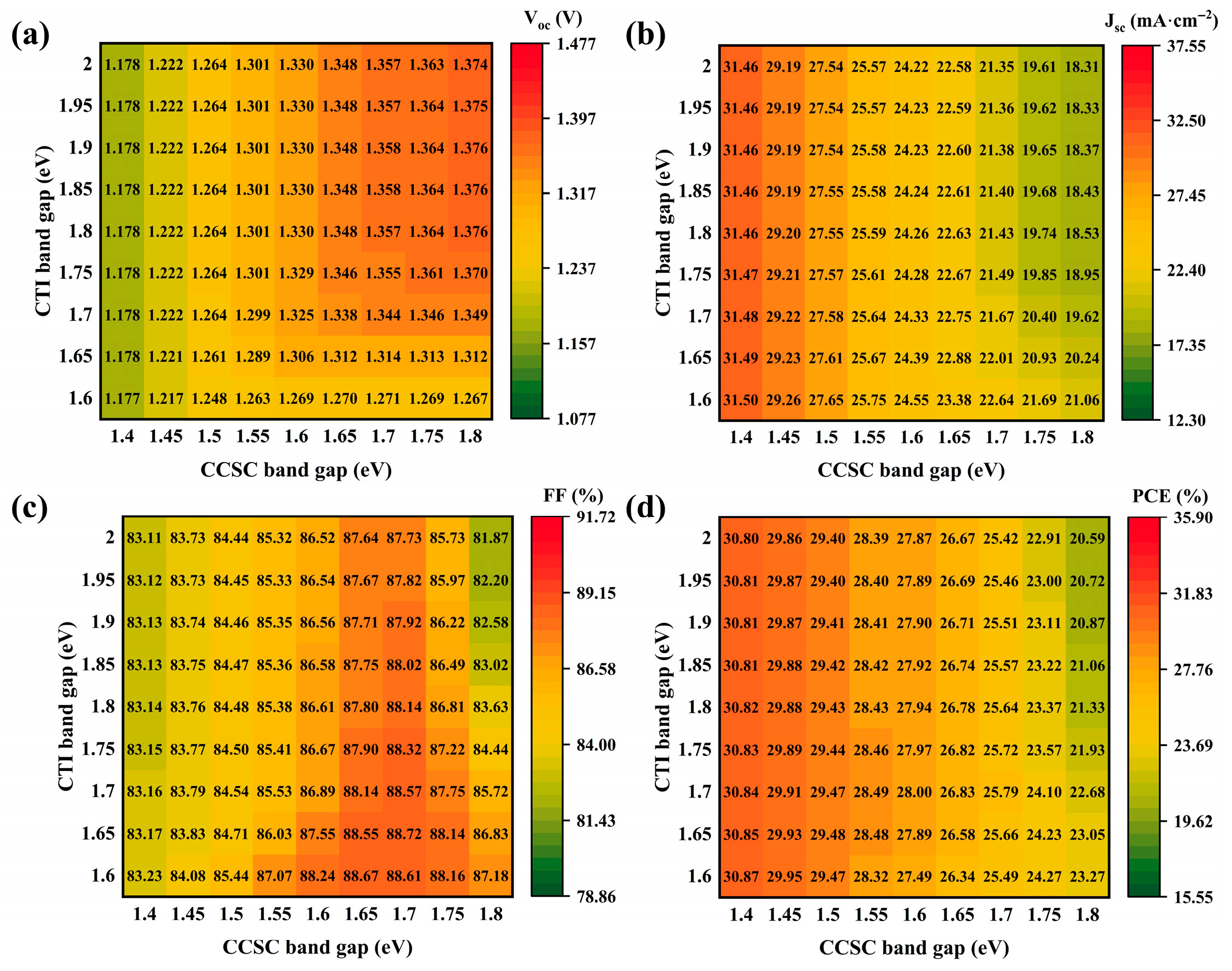
3.5. Impact of Band Gap of Absorber Layer on Properties
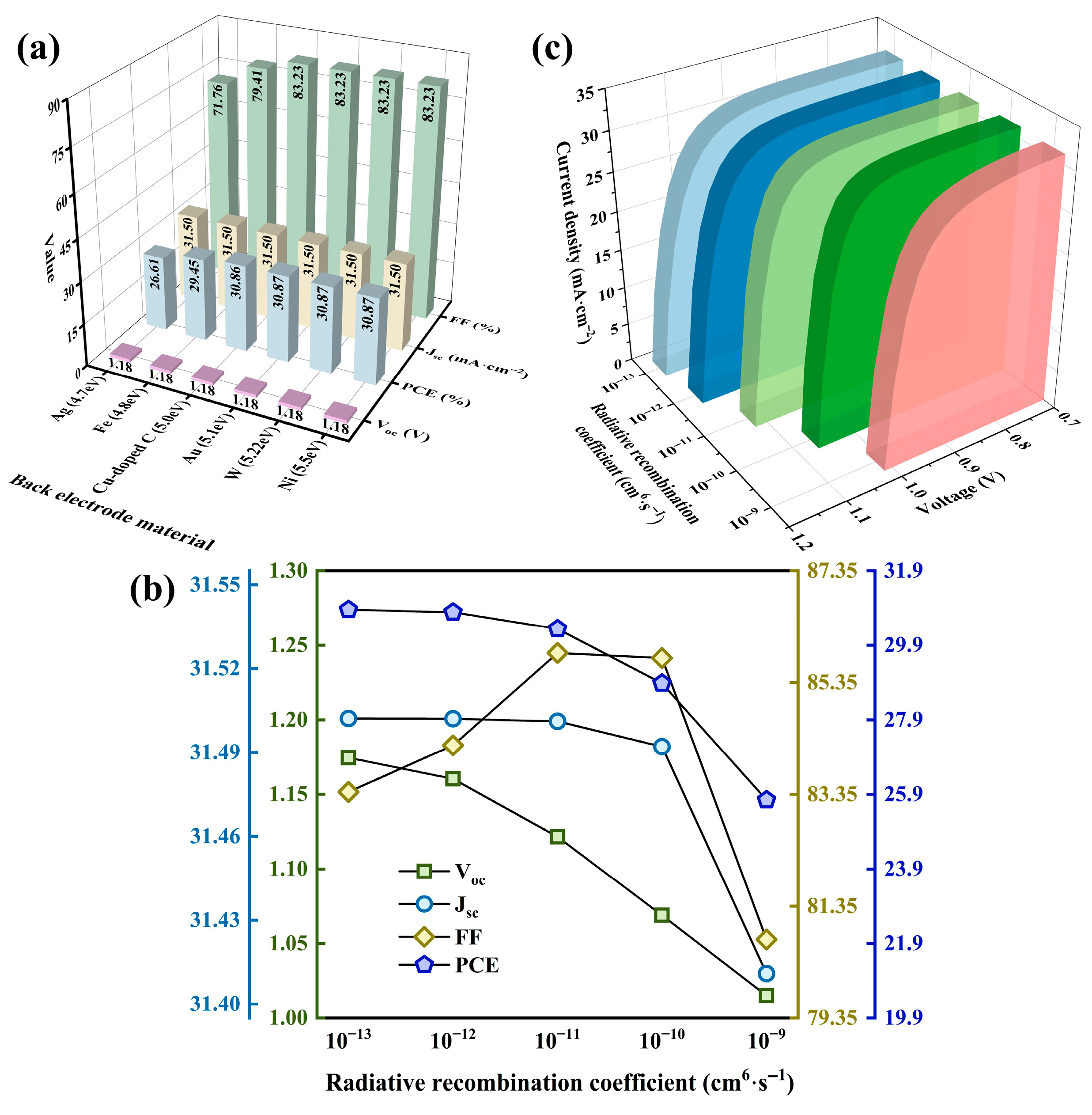
3.6. Impact of Back Electrode on Properties
3.7. Impact of Radiative Recombination on Properties
3.8. Impact of Resistance on Properties
3.9. Impact of Light Intensity on Properties
3.10. Impact of Temperature on Properties
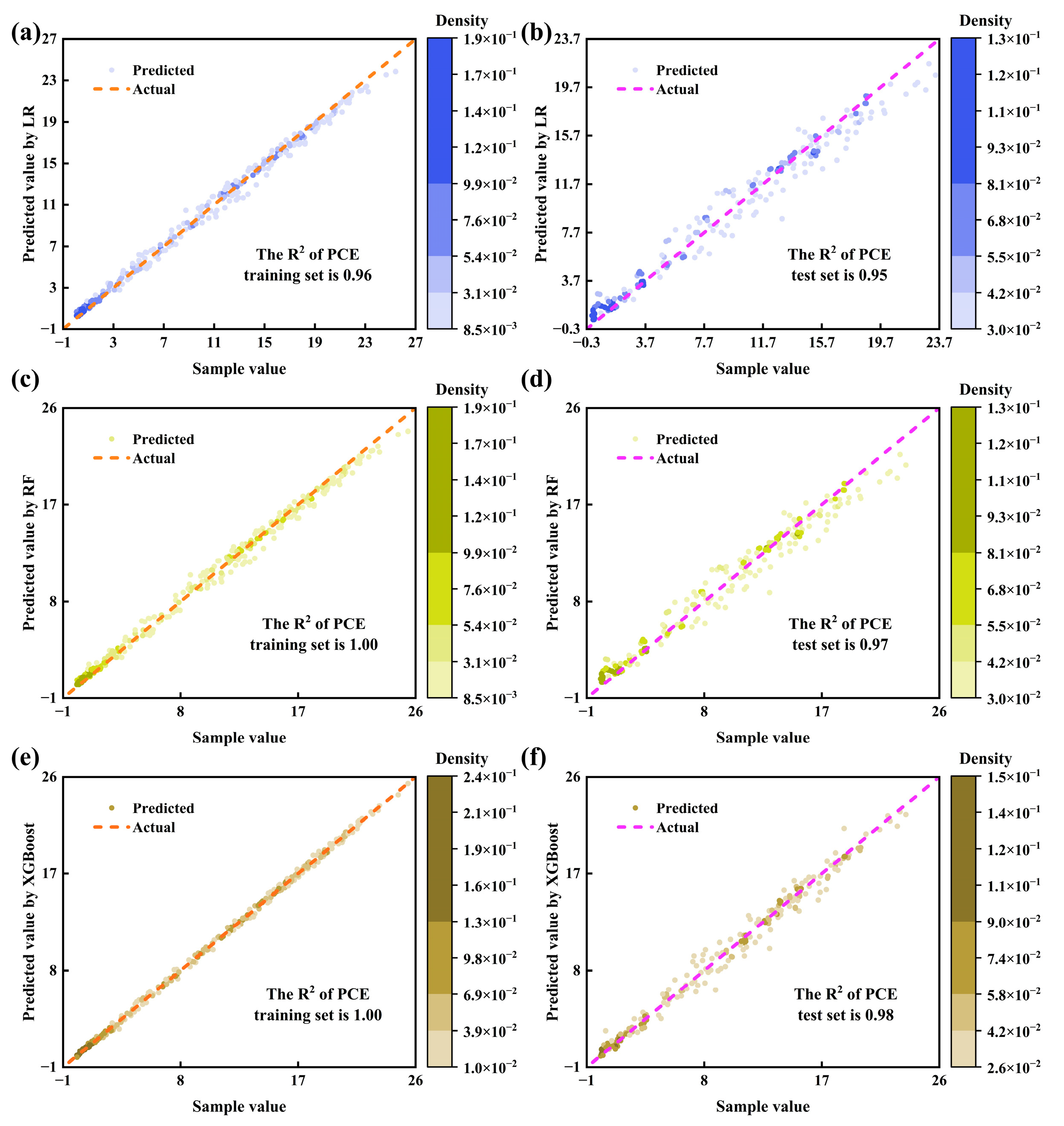
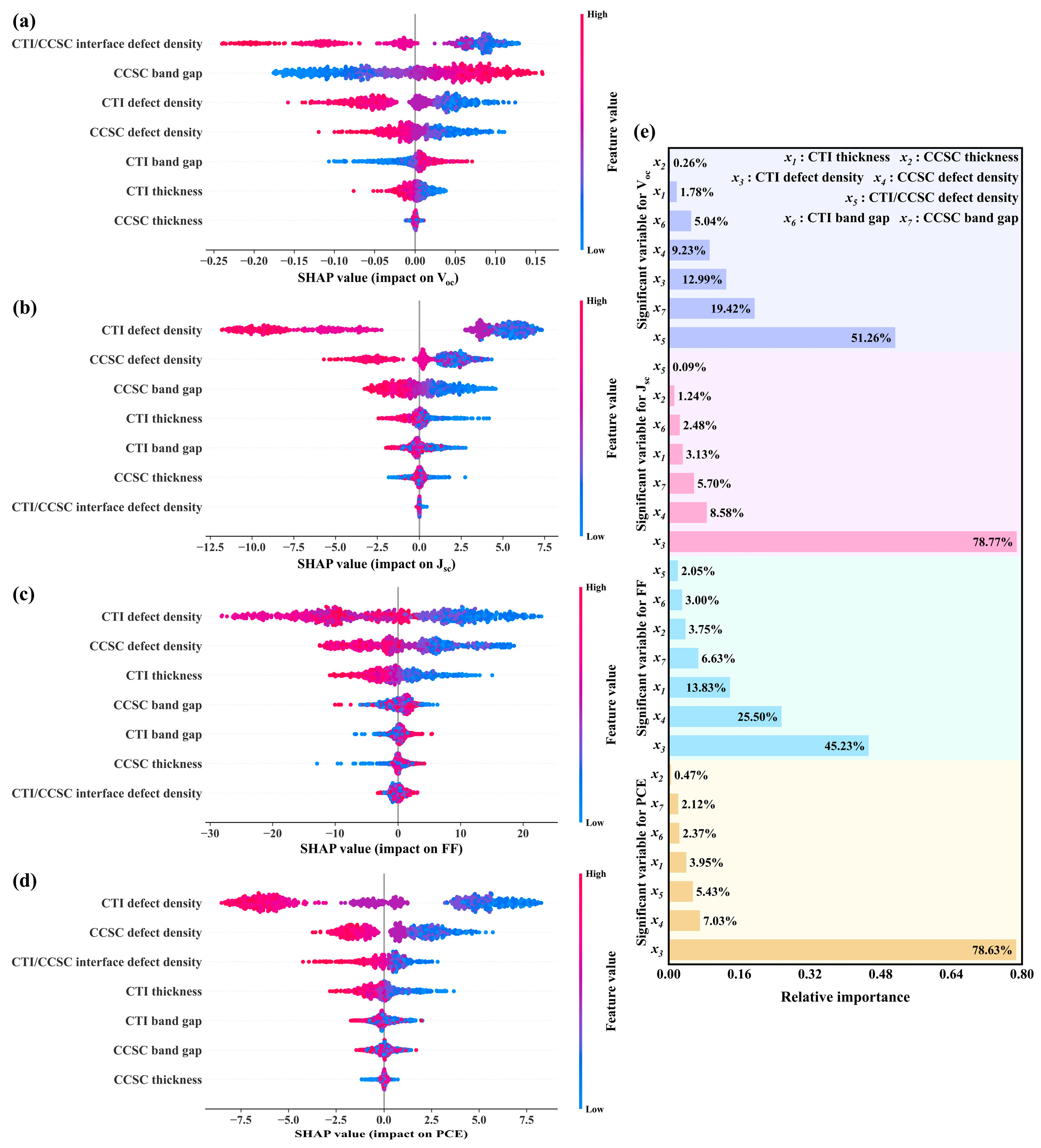
3.11. Multiple Algorithm-Driven PSC Property Research
3.12. Brief Discussion of Actual Factors
3.13. Optimized Device Properties
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Patel, P.K. Device simulation of highly efficient eco-friendly CH3NH3SnI3 perovskite solar cell. Sci. Rep. 2021, 11, 11. [Google Scholar] [CrossRef]
- Yadav, S.C.; Manjunath, V.; Srivastava, A.; Devan, R.S.; Shirage, P.M. Stable lead-free Cs4CuSb2Cl12 layered double perovskite solar cells yielding theoretical efficiency close to 30%. Opt. Mater. 2022, 132, 112676. [Google Scholar] [CrossRef]
- Mottakin, M.; Sobayel, K.; Sarkar, D.; Alkhammash, H.; Alharthi, S.; Techato, K.; Shahiduzzaman, M.; Amin, N.; Sopian, K.; Akhtaruzzaman, M. Design and Modelling of Eco-Friendly CH3NH3SnI3-Based Perovskite Solar Cells with Suitable Transport Layers. Energies 2021, 14, 7200. [Google Scholar] [CrossRef]
- Imani, S.; Seyed-Talebi, S.M.; Beheshtian, J.; Diau, E.W.G. Simulation and characterization of CH3NH3SnI3-based perovskite solar cells with different Cu-based hole transporting layers. Appl. Phys. A Mater. Sci. Process. 2023, 129, 13. [Google Scholar] [CrossRef]
- Bhattarai, S.; Mhamdi, A.; Hossain, I.; Raoui, Y.; Pandey, R.; Madan, J.; Bouazizi, A.; Maiti, M.; Gogoi, D.; Sharma, A. A detailed review of perovskite solar cells: Introduction, working principle, modelling, fabrication techniques, future challenges. Micro Nanostruct. 2022, 172, 207450. [Google Scholar] [CrossRef]
- Yusoff, A.B.; Nazeeruddin, M.K. Organohalide Lead Perovskites for Photovoltaic Applications. J. Phys. Chem. Lett. 2016, 7, 851–866. [Google Scholar] [CrossRef]
- Mercy, E.N.V.; Srinivasan, D.; Marasamy, L. Emerging BaZrS3 and Ba(Zr,Ti)S3 Chalcogenide Perovskite Solar Cells: A Numerical Approach Toward Device Engineering and Unlocking Efficiency. ACS Omega 2024, 9, 4359–4376. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Allam, L.; Bharadwaj, S.; Barman, B. Enhancing SrZrS3 perovskite solar cells: A comprehensive SCAPS-1D analysis of inorganic transport layers. J. Phys. Chem. Solids 2025, 196, 112378. [Google Scholar] [CrossRef]
- Kojima, A.; Teshima, K.; Shirai, Y.; Miyasaka, T. Organometal Halide Perovskites as Visible-Light Sensitizers for Photovoltaic Cells. J. Am. Chem. Soc. 2009, 131, 6050–6051. [Google Scholar] [CrossRef] [PubMed]
- Tockhorn, P.; Sutter, J.; Cruz, A.; Wagner, P.; Jäger, K.; Yoo, D.; Lang, F.; Grischek, M.; Li, B.R.; Li, J.Z.; et al. Nano-optical designs for high-efficiency monolithic perovskite-silicon tandem solar cells. Nat. Nanotechnol. 2022, 17, 1214–1221. [Google Scholar] [CrossRef]
- Jin, H.D.; Debroye, E.; Keshavarz, M.; Scheblykin, I.G.; Roeffaers, M.B.J.; Hofkens, J.; Steele, J.A. It’s a trap! On the nature of localised states and charge trapping in lead halide perovskites. Mater. Horizons 2020, 7, 397–410. [Google Scholar] [CrossRef]
- Ohara, K.; Yamada, T.; Tahara, H.; Aharen, T.; Hirori, H.; Suzuura, H.; Kanemitsu, Y. Excitonic enhancement of optical nonlinearities in perovskite CH3NH3PbCl3 single crystals. Phys. Rev. Mater. 2019, 3, 111601. [Google Scholar] [CrossRef]
- Xu, J.; Liu, J.B.; Wang, J.F.; Liu, B.X.; Huang, B. Prediction of Novel p-Type Transparent Conductors in Layered Double Perovskites: A First-Principles Study. Adv. Funct. Mater. 2018, 28, 1800332. [Google Scholar] [CrossRef]
- Tahir, S.; Mushtaq, S.; Saeed, R.; Iqbal, J.; Alshahrani, M.D.; Almufarij, R.S.; Ragab, I.; Ashfaq, A. Numerical simulation of Cs2AgInBr6/Cs4CuSb2Cl12 heterojunction perovskite solar cell: A path to achieve optimized performance. Phys. B Condens. Matter 2025, 703, 417011. [Google Scholar] [CrossRef]
- Tang, G.; Xiao, Z.W.; Hosono, H.; Kamiya, T.; Fang, D.N.; Hong, J.W. Layered Halide Double Perovskites Cs3+nM(II)nSb2X9+3n (M = Sn, Ge) for Photovoltaic Applications. J. Phys. Chem. Lett. 2018, 9, 43–48. [Google Scholar] [CrossRef]
- Wang, X.D.; Miao, N.H.; Liao, J.F.; Li, W.Q.; Xie, Y.; Chen, J.; Sun, Z.M.; Chen, H.Y.; Kuang, D.B. The top-down synthesis of single-layered Cs4CuSb2Cl12 halide perovskite nanocrystals for photoelectrochemical application. Nanoscale 2019, 11, 5180–5187. [Google Scholar] [CrossRef]
- He, Y.Z.; Xu, L.Y.; Yang, C.; Guo, X.W.; Li, S.R. Design and Numerical Investigation of a Lead-Free Inorganic Layered Double Perovskite Cs4CuSb2Cl12 Nanocrystal Solar Cell by SCAPS-1D. Nanomaterials 2021, 11, 2321. [Google Scholar] [CrossRef] [PubMed]
- Khan, A.H.H.; Khan, A.A.; Farid, A. Enhancing the efficiency of non toxic perovskite solar cell through Cs4CuSb2Cl12 as interface layer using SCAPS-1D. Phys. Scr. 2024, 99, 7. [Google Scholar] [CrossRef]
- Liu, D.W.; Sa, R.J. Theoretical study of Zr doping on the stability, mechanical, electronic and optical properties of Cs2TiI6. Opt. Mater. 2020, 110, 110497. [Google Scholar] [CrossRef]
- Urmi, S.S.; Khan, M.A.K.; Ferdous, T.T.; Adinehloo, D.; Perebeinos, V.; Alim, M.A. Cs2TiI6 (Cs2TiIxBr6-x) Halide Perovskite Solar Cell and Its Point Defect Analysis. Nanomaterials 2023, 13, 2100. [Google Scholar] [CrossRef]
- Kaewmeechai, C.; Laosiritaworn, Y.; Jaroenjittichai, A.P. DFT calculation on electronic properties of vacancy-ordered double perovskites Cs2(Ti, Zr, Hf)X6 and their alloys: Potential as light absorbers in solar cells. Results Phys. 2021, 30, 104785. [Google Scholar] [CrossRef]
- Chen, M.; Ju, M.G.; Carl, A.D.; Zong, Y.X.; Grimm, R.L.; Gu, J.J.; Zeng, X.C.; Zhou, Y.Y.; Padture, N.P. Cesium Titanium(IV) Bromide Thin Films Based Stable Lead-free Perovskite Solar Cells. Joule 2018, 2, 558–570. [Google Scholar] [CrossRef]
- Ahmad, O.; Rashid, A.; Ahmed, M.W.; Nasir, M.F.; Qasim, I. Performance evaluation of Au/p-CdTe/Cs2TiI6/n-TiO2/ITO solar cell using SCAPS-1D. Opt. Mater. 2021, 117, 111105. [Google Scholar] [CrossRef]
- Moiz, S.A.; Albadwani, S.A.; Alshaikh, M.S. Towards Highly Efficient Cesium Titanium Halide Based Lead-Free Double Perovskites Solar Cell by Optimizing the Interface Layers. Nanomaterials 2022, 12, 3435. [Google Scholar] [CrossRef] [PubMed]
- Kenfack, A.D.K.; Msimanga, M. Machine Learning Approaches to Optimize the Performance of the Novel Stable Lead-free Heterojunction CsGeI3/CsSn(I1-xBrx)3-based Perovskite Solar Cell. J. Electron. Mater. 2025, 54, 1278–1292. [Google Scholar] [CrossRef]
- Kaur, N.; Pandey, R.; Madan, J. Machine Learning-Driven Exploration of Cesium-Based All-Inorganic Mixed-Halide Perovskite Solar Cells with a Double Absorber Layer Architecture. J. Electron. Mater. 2024, 53, 5361–5373. [Google Scholar] [CrossRef]
- Hunde, B.R.; Woldeyohannes, A.D. Performance analysis and optimization of perovskite solar cell using SCAPS-1D and genetic algorithm. Mater. Today Commun. 2023, 34, 105420. [Google Scholar] [CrossRef]
- Uddin, M.S.; Rahman, S.M.A.; Rahman, M.A.; Mia, S.; Rahman, M.M.; Refat, M.S. Achieving over 28% efficiency in inorganic halide perovskite Ca3AsI3: Optimization of electron transport layers via DFT, SCAPS-1D, and machine learning. J. Phys. Chem. Solids 2025, 200, 112622. [Google Scholar] [CrossRef]
- Ghosh, A.; Hasan, M.R.; Moumita, M.; Apu, K.U.; Begum, S.; Rahman, A.; Bappy, M.A.; Ahmed, S.; Kumar, Y.A.; Hassan, A.A.; et al. Discovering the relationship between sulfide and selenide-based HTLs and cubic Ba3SbI3 solar cells with SCAPS-1D and machine learning modelling. Inorg. Chem. Commun. 2025, 173, 113782. [Google Scholar] [CrossRef]
- Maoucha, A.; Berghout, T.; Djeffal, F.; Ferhati, H. Machine learning-assisted analysis of lead-free FACsSnI3 solar cell degradation: Deep learning classification and design parameter importance assessment. Inorg. Chem. Commun. 2025, 174, 114114. [Google Scholar] [CrossRef]
- Polman, A.; Knight, M.; Garnett, E.C.; Ehrler, B.; Sinke, W.C. Photovoltaic materials: Present efficiencies and future challenges. Science 2016, 352, aad4424. [Google Scholar] [CrossRef]
- Dev, T.B.; Srivani, A.; Rajpoot, S.; Dhar, S. Novel lead-free dual absorber based perovskite solar cells: Efficient numerical harnessing towards high efficiency through SCAPS-1D. J. Phys. Chem. Solids 2025, 205, 112776. [Google Scholar] [CrossRef]
- Gholami-Milani, A.; Ahmadi-Kandjani, S.; Olyaeefar, B.; Kermani, M.H. Performance analyses of highly efficient inverted all-perovskite bilayer solar cell. Sci. Rep. 2023, 13, 8274. [Google Scholar] [CrossRef]
- Burgelman, M.; Nollet, P.; Degrave, S. Modelling polycrystalline semiconductor solar cells. Thin Solid Film. 2000, 361, 527–532. [Google Scholar] [CrossRef]
- Liu, M.Z.; Johnston, M.B.; Snaith, H.J. Efficient planar heterojunction perovskite solar cells by vapour deposition. Nature 2013, 501, 395–398. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Ibn Malek, I.; Imtiaz, H.; Subrina, S. Machine learning driven performance enhancement of perovskite solar cells with CNT as both hole transport layer and back contact. Sol. Energy 2024, 278, 112737. [Google Scholar] [CrossRef]
- Takahashi, K.; Takahashi, L.; Miyazato, I.; Tanaka, Y. Searching for Hidden Perovskite Materials for Photovoltaic Systems by Combining Data Science and First Principle Calculations. ACS Photonics 2018, 5, 771–775. [Google Scholar] [CrossRef]
- Guo, Z.M.; Lin, B. Machine learning stability and band gap of lead-free halide double perovskite materials for perovskite solar cells. Sol. Energy 2021, 228, 689–699. [Google Scholar] [CrossRef]
- Raj, A.; Kumar, M.; Bherwani, H.; Gupta, A.; Anshul, A. Evidence of improved power conversion efficiency in lead-free CsGeI3 based perovskite solar cell heterostructure via scaps simulation. J. Vac. Sci. Technol. B 2021, 39, 012401. [Google Scholar] [CrossRef]
- Xiao, Y.P.; Wang, H.P.; Kuang, H. Numerical simulation and performance optimization of Sb2S3 solar cell with a hole transport layer. Opt. Mater. 2020, 108, 110414. [Google Scholar] [CrossRef]
- Parveen, S.; Manamel, L.T.; Mukherjee, A.; Sagar, S.; Das, B.C. Analog Memristor of Lead-Free Cs4CuSb2Cl12 Layered Double Perovskite Nanocrystals as Solid-State Electronic Synapse for Neuromorphic Computing. Adv. Mater. Interfaces 2022, 9, 2200562. [Google Scholar] [CrossRef]
- Rahman, M.A. Enhancing the photovoltaic performance of Cd-free Cu2ZnSnS4 heterojunction solar cells using SnS HTL and TiO2 ETL. Sol. Energy 2021, 215, 64–76. [Google Scholar] [CrossRef]
- Al Ahmed, S.R. Investigation on the Performance Enhancement of Heterojunction SnS Thin-Film Solar Cell with a Zn3P2 Hole Transport Layer and a TiO2 Electron Transport Layer. Energy Fuels 2023, 38, 1462–1476. [Google Scholar] [CrossRef]
- Alam, I.; Ashraf, M.A. Effect of different device parameters on tin-based perovskite solar cell coupled with In2S3 electron transport layer and CuSCN and Spiro-OMeTAD alternative hole transport layers for high-efficiency performance. Energy Sources Part A-Recovery Util. Environ. Eff. 2024, 46, 17080–17096. [Google Scholar] [CrossRef]
- Tian, J.J.; Xue, Q.F.; Yao, Q.; Li, N.; Brabec, C.J.; Yip, H.L. Inorganic Halide Perovskite Solar Cells: Progress and Challenges. Adv. Energy Mater. 2020, 10, 2000183. [Google Scholar] [CrossRef]
- Chakraborty, K.; Medikondu, N.R.; Duraisamy, K.; Soliman, N.F.; El-Shafai, W.; Lavadiya, S.; Paul, S.; Das, S. Studies of Performance of Cs2TiI6-xBrx (Where x=0 to 6)-Based Mixed Halide Perovskite Solar Cell with CdS Electron Transport Layer. Micromachines 2023, 14, 447. [Google Scholar] [CrossRef]
- Shyma, A.P.; Sellappan, R. Computational Probing of Tin-Based Lead-Free Perovskite Solar Cells: Effects of Absorber Parameters and Various Electron Transport Layer Materials on Device Performance. Materials 2022, 15, 7859. [Google Scholar] [CrossRef]
- Cao, Y.; Zhu, X.Y.; Chen, H.B.; Zhang, X.T.; Zhou, J.; Hu, Z.Y.; Pang, J.B. Towards high efficiency inverted Sb2Se3 thin film solar cells. Sol. Energy Mater. Sol. Cells 2019, 200, 109945. [Google Scholar] [CrossRef]
- Wang, Y.; Xia, Z.G.; Liang, J.; Wang, X.W.; Liu, Y.M.; Liu, C.; Zhang, S.D.; Zhou, H. Towards printed perovskite solar cells with cuprous oxide hole transporting layers: A theoretical design. Semicond. Sci. Technol. 2015, 30, 054004. [Google Scholar] [CrossRef]
- Ni, Z.Y.; Bao, C.X.; Liu, Y.; Jiang, Q.; Wu, W.Q.; Chen, S.S.; Dai, X.Z.; Chen, B.; Hartweg, B.; Yu, Z.S.; et al. Resolving spatial and energetic distributions of trap states in metal halide perovskite solar cells. Science 2020, 367, 1352–1358. [Google Scholar] [CrossRef] [PubMed]
- Ouslimane, T.; Et-taya, L.; Elmaimouni, L.; Benami, A. Impact of absorber layer thickness, defect density, and operating temperature on the performance of MAPbI3 solar cells based on ZnO electron transporting material. Heliyon 2021, 7, e06379. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Zhang, Y.Z.; Wei, J.W.; Zeng, H.; Zhao, M.; Yang, C.A.; Feng, W.L.; Ma, Z.W. First Principles Calculation on Photoelectric Properties of Cs2TiBr6 by Substitution Doping with Cl and Pd. Chin. J. Inorg. Chem. 2022, 38, 884–890. [Google Scholar] [CrossRef]
- Wang, Y.T.; Ji, Y.X.; Yang, Y.L.; Chen, Z.Y.; Sun, H.; Wang, X.J.; Zou, Z.G.; Huang, H.L. Narrow-Bandgap Halide Perovskite Cs4CuSb2Cl12 with Full-Spectrum Photothermal Conversion. ACS Energy Lett. 2024, 9, 336–345. [Google Scholar] [CrossRef]
- Mishra, S.; Sapru, S.; Upadhyay, S.N.; Singh, A.; Pakhira, S.; De, A.K. Elucidating the Structure–Property Relationship and Ultrafast Exciton/Charge Carrier Dynamics of Layered Cs4CuSb2Cl12 Double-Perovskite Microcrystals. J. Phys. Chem. C 2023, 127, 1881–1890. [Google Scholar] [CrossRef]
- Das, A.; Peu, S.D.; Akanda, M.A.M.; Salah, M.M.; Hossain, M.S.; Das, B.K. Numerical Simulation and Optimization of Inorganic Lead-Free Cs3Bi2I9-Based Perovskite Photovoltaic Cell: Impact of Various Design Parameters. Energies 2023, 16, 2328. [Google Scholar] [CrossRef]
- Aslam, S.; Bakhsh, S.; Yusof, Y.; Rahman, M.Y.A.; Ibrahim, A.R.; Samsuri, S.A.M. Structural and optical properties of vacancy-ordered double halide perovskites, Cs2TiI6 films. Mater. Sci. Eng. B Adv. Funct. Solid-State Mater. 2023, 296, 116645. [Google Scholar] [CrossRef]
- Verma, D. Synthesis of 2D Layered Perovskite Cs4CuSb2Cl12 Nanocrystal and Their Sunlight Driven Photocatalysis Reaction; IISERM: Mumbai, Indian, 2021. [Google Scholar]
- Behrouznejad, F.; Shahbazi, S.; Taghavinia, N.; Wu, H.P.; Diau, E.W.G. A study on utilizing different metals as the back contact of CH3NH3PbI3 perovskite solar cells. J. Mater. Chem. A 2016, 4, 13488–13498. [Google Scholar] [CrossRef]
- Jayan, K.D.; Sebastian, V. Comprehensive device modelling and performance analysis of MASnI3 based perovskite solar cells with diverse ETM, HTM and back metal contacts. Sol. Energy 2021, 217, 40–48. [Google Scholar] [CrossRef]
- Toki, G.F.I.; Hossain, M.K.; Pandey, R.; Bhattarai, S.; Tawfeek, A.M.; Mohammad, S.; Habib, A.M.J.; Mahmud, N.; Rahman, M.F.; Sasikumar, P.; et al. Optimizing lead-free Cs3Bi2I9 perovskite solar cells: Exploring absorber and charge transport layers parameters for improved efficiency. J. Opt. 2024, 53, 4554–4570. [Google Scholar] [CrossRef]
- He, Y.Z.; Chen, H.Z.; Wang, S.Q.; Wang, Q.; Zhang, C.; Hao, Q.X.; Li, R.Y.; Li, S.R.; Liu, X.D.; Guo, X.W. Unveiling recombination in top cells: SCAPS-1D simulations for high-efficiency bifacial planar perovskite/silicon tandem solar cells. Sol. Energy 2024, 282, 112921. [Google Scholar] [CrossRef]
- Karthick, S.; Velumani, S.; Bouclé, J. Experimental and SCAPS simulated formamidinium perovskite solar cells: A comparison of device performance. Sol. Energy 2020, 205, 349–357. [Google Scholar] [CrossRef]
- Li, Y.; Ding, B.; Chu, Q.Q.; Yang, G.J.; Wang, M.K.; Li, C.X.; Li, C.J. Ultra-high open-circuit voltage of perovskite solar cells induced by nucleation thermodynamics on rough substrates. Sci. Rep. 2017, 7, 46141. [Google Scholar] [CrossRef] [PubMed]
- Karthick, S.; Velumani, S.; Bouclé, J. Chalcogenide BaZrS3 perovskite solar cells: A numerical simulation and analysis using SCAPS-1D. Opt. Mater. 2022, 126, 112250. [Google Scholar] [CrossRef]
- Saidarsan, A.; Guruprasad, S.; Malik, A.; Basumatary, P.; Ghosh, D.S. A critical review of unrealistic results in SCAPS-1D simulations: Causes, practical solutions and roadmap ahead. Sol. Energy Mater. Sol. Cells 2025, 279, 113230. [Google Scholar] [CrossRef]
- Li, H.; Huang, Y.T.; Zhu, M.Y.; Yan, P.Y.; Sheng, C.X. Analyzing Efficiency of Perovskite Solar Cells Under High Illumination Intensities by SCAPS Device Simulation. Nanomaterials 2025, 15, 286. [Google Scholar] [CrossRef]
- Wang, D.L.; Cui, H.J.; Hou, G.J.; Zhu, Z.G.; Yan, Q.B.; Su, G. Highly efficient light management for perovskite solar cells. Sci. Rep. 2016, 6, 18922. [Google Scholar] [CrossRef]
- Bouich, A.; Hartiti, B.; Ullah, S.; Ullah, H.; Touhami, M.E.; Santos, D.M.F.; Mari, B. Experimental, theoretical, and numerical simulation of the performance of CuInxGa(1−x) S2-based solar cells. Optik 2019, 183, 137–147. [Google Scholar] [CrossRef]
- Chakraborty, K.; Choudhury, M.G.; Paul, S. Numerical study of Cs2TiX6 (X = Br−, I−, F− and Cl−) based perovskite solar cell using SCAPS-1D device simulation. Sol. Energy 2019, 194, 886–892. [Google Scholar] [CrossRef]
- Singh, P.; Ravindra, N.M. Temperature dependence of solar cell performance-an analysis. Sol. Energy Mater. Sol. Cells 2012, 101, 36–45. [Google Scholar] [CrossRef]
- Arif, F.; Aamir, M.; Shuja, A.; Shahiduzzaman, M.; Akhtar, J. Simulation and numerical modeling of high performance CH3NH3SnI3 solar cell with cadmium sulfide as electron transport layer by SCAPS-1D. Results Opt. 2024, 14, 100595. [Google Scholar] [CrossRef]
- Choi, Y.O.; Kim, N.H.; Park, J.S.; Lee, W.S. Influences of thickness-uniformity and surface morphology on the electrical and optical properties of sputtered CdTe thin films for large-area II-VI semiconductor heterostructured solar cells. Mater. Sci. Eng. B Adv. Funct. Solid-State Mater. 2010, 171, 73–78. [Google Scholar] [CrossRef]
- Zuñiga, I.; Conde, J.; Tinoco, J.C.; Meza-Avendaño, C.; Ashok, A.; Ramírez-Gonzalez, F.; Vilchis, H. Analysis of optical and electrical properties in CZTSSe thin film solar cells through the 2d theoretical modeling. Mater. Today Commun. 2024, 39, 109124. [Google Scholar] [CrossRef]
- Khalaph, K.A.; Shanan, Z.J.; Jafar, A.M.; Al-Attar, F.M. Double Nanoperovskite Heterojunctions Based on SI-Porous. Int. J. Nanosci. 2023, 22, 2350016. [Google Scholar] [CrossRef]
- Mandal, A.; Mondal, A.; Bhattacharyya, R.; Bhattacharyya, S. Cs4CuSb2Cl12-xIx(x=0-10) nanocrystals for visible light photodetection. Nanotechnology 2022, 33, 415403. [Google Scholar] [CrossRef]
- Talebi, M.; Mokhtari, A. Comparative study of the physical properties for the A2TiX6(A= Cs or NH4 and X= Cl or Br) vacancy-ordered double perovskites. arXiv 2023. [Google Scholar] [CrossRef]
- Zhao, K.; Munir, R.; Yan, B.; Yang, Y.; Kim, T.; Amassian, A. Solution-processed inorganic copper(I) thiocyanate (CuSCN) hole transporting layers for efficient p-i-n perovskite solar cells. J. Mater. Chem. A 2015, 3, 20554–20559. [Google Scholar] [CrossRef]
- Bera, A.; Wu, K.W.; Sheikh, A.; Alarousu, E.; Mohammed, O.F.; Wu, T. Perovskite Oxide SrTiO3 as an Efficient Electron Transporter for Hybrid Perovskite Solar Cells. J. Phys. Chem. C 2014, 118, 28494–28501. [Google Scholar] [CrossRef]
- Chakraborty, K.; Medikondu, N.R.; Kanakavalli, P.B.; Kamesh, V.V.; Das, S.; Choudhury, M.G.; Paul, S. Comparative study of structural, opto-electronic properties of Cs2TiX6-based single halide double perovskite solar cells: Computational and experimental approach. Phys. Scr. 2024, 99, 105554. [Google Scholar] [CrossRef]
- Li, F.C.; Zhou, S.J.; Yuan, J.Y.; Qin, C.C.; Yang, Y.G.; Shi, J.W.; Ling, X.F.; Li, Y.Y.; Ma, W.L. Perovskite Quantum Dot Solar Cells with 15.6% Efficiency and Improved Stability Enabled by an α-CsPbI3/FAPbI3 Bilayer Structure. ACS Energy Lett. 2019, 4, 2571–2578. [Google Scholar] [CrossRef]
- Clark, C.P.; Mann, J.E.; Bangsund, J.S.; Hsu, W.J.; Aydil, E.S.; Holmes, R.J. Formation of Stable Metal Halide Perovskite/Perovskite Heterojunctions. ACS Energy Lett. 2020, 5, 3443–3451. [Google Scholar] [CrossRef]
- Zhao, Q.; Hazarika, A.; Chen, X.H.; Harvey, S.P.; Larson, B.W.; Teeter, G.R.; Liu, J.; Song, T.; Xiao, C.X.; Shaw, L.; et al. High efficiency perovskite quantum dot solar cells with charge separating heterostructure. Nat. Commun. 2019, 10, 2842. [Google Scholar] [CrossRef]
- Zhang, Y.N.; Li, B.; Fu, L.; Zou, Y.; Li, Q.; Yin, L.W. Enhanced optical absorption and efficient cascade electron extraction based on energy band alignment double absorbers perovskite solar cells. Sol. Energy Mater. Sol. Cells 2019, 194, 168–176. [Google Scholar] [CrossRef]
- Kanoun, A.A.; Kanoun, M.B.; Merad, A.E.; Goumri-Said, S. Toward development of high-performance perovskite solar cells based on CH3NH3GeI3 using computational approach. Sol. Energy 2019, 182, 237–244. [Google Scholar] [CrossRef]
- Homes, C.C.; Vogt, T.; Shapiro, S.M.; Wakimoto, S.; Ramirez, A.P. Optical response of high-dielectric-constant perovskite-related oxide. Science 2001, 293, 673–676. [Google Scholar] [CrossRef] [PubMed]
- Wehrenfennig, C.; Eperon, G.E.; Johnston, M.B.; Snaith, H.J.; Herz, L.M. High Charge Carrier Mobilities and Lifetimes in Organolead Trihalide Perovskites. Adv. Mater. 2014, 26, 1584–1589. [Google Scholar] [CrossRef]
- Giorgi, G.; Fujisawa, J.I.; Segawa, H.; Yamashita, K. Small Photocarrier Effective Masses Featuring Ambipolar Transport in Methylammonium Lead Iodide Perovskite: A Density Functional Analysis. J. Phys. Chem. Lett. 2013, 4, 4213–4216. [Google Scholar] [CrossRef]
- Shasti, M.; Mortezaali, A. Numerical Study of Cu2O, SrCu2O2, and CuAlO2 as Hole-Transport Materials for Application in Perovskite Solar Cells. Phys. Status Solidi A-Appl. Mat. 2019, 216, 1900337. [Google Scholar] [CrossRef]
- Ali, S.; Kumar, P.; Ahmad, K.; Khan, R.A. Simulation of Lead-Free Perovskite Solar Cells with Improved Performance. Crystals 2025, 15, 171. [Google Scholar] [CrossRef]
- Islam, M.A.; Haque, M.M.; Selvanathan, V.; Mottakin, M.; Sarkar, D.K.; Joya, K.; Alanazi, A.M.; Suemasu, T.; Syed, I.M.; Akhtaruzzaman, M. Theoretical Analysis on Interfacial Dynamics Between Charge Transport Layer and Different Absorbers in Pb-free All Inorganic Perovskites Solar Cells. J. Electron. Mater. 2024, 53, 6823–6837. [Google Scholar] [CrossRef]
- Bimli, S.; Manjunath, V.; Mulani, S.R.; Miglani, A.; Game, O.S.; Devan, R.S. Theoretical investigations of all inorganic Cs2SnI6 double perovskite solar cells for efficiency ~30%. Sol. Energy 2023, 256, 76–87. [Google Scholar] [CrossRef]
- Tara, A.; Bharti, V.; Dixit, H.; Sharma, S.; Gupta, R. Performance evaluation of all-inorganic cesium-based perovskite solar cell with BaSnO3 as ETL. J. Nanopart. Res. 2023, 25, 184. [Google Scholar] [CrossRef]
- Azri, F.; Meftah, A.; Sengouga, N.; Meftah, A. Electron and hole transport layers optimization by numerical simulation of a perovskite solar cell. Sol. Energy 2019, 181, 372–378. [Google Scholar] [CrossRef]
- Hossain, M.K.; Alsalman, O.; Rana, S.; Uddin, M.S.; Toki, G.F.I.; Shahatha, S.H.; Mohammad, M.R.; Darwish, M.A.; Sasikumar, P.; Haq, S.; et al. Enhancing efficiency and performance of Cs2TiI6-based perovskite solar cells through extensive optimization: A numerical approach. Inorg. Chem. Commun. 2024, 168, 112964. [Google Scholar] [CrossRef]
- AlZoubi, T.; Mourched, B.; Al Gharram, M.; Makhadmeh, G.; Noqta, O.A. Improving Photovoltaic Performance of Hybrid Organic-Inorganic MAGeI3 Perovskite Solar Cells via Numerical Optimization of Carrier Transport Materials (HTLs/ETLs). Nanomaterials 2023, 13, 2221. [Google Scholar] [CrossRef]
- Mandadapu, U.; Vedanayakam, V.; Thyagarajan, K. Simulation and Analysis of Lead based Perovskite Solar Cell using SCAPS-1D. Ind. J. Sci. Technol. 2017, 10, 1–8. [Google Scholar] [CrossRef]
- Rahmoune, A.; Babahani, O. Numerical analysis of Al/Gr/ETL/MoS2/Sb2S3/Ni solar cell using non-toxic In2S3/SnS2/ZnSe electron transport layer. Optik 2023, 283, 170875. [Google Scholar] [CrossRef]
- Bishnoi, S.; Pandey, S.K. Device performance analysis for lead-free perovskite solar cell optimization. IET Optoelectron. 2018, 12, 185–190. [Google Scholar] [CrossRef]
- Mukaddar, S. Optimization of efficiency of CsPbI2Br by using different electron transport and hole transport layers: A DFT and SCAPS-1D simulation. Micro Nanostruct. 2025, 197, 208024. [Google Scholar] [CrossRef]
- Matin, M.A.; Aliyu, M.M.; Quadery, A.H.; Amin, N. Prospects of novel front and back contacts for high efficiency cadmium telluride thin film solar cells from numerical analysis. Sol. Energy Mater. Sol. Cells 2010, 94, 1496–1500. [Google Scholar] [CrossRef]
- Jamal, S.; Khan, A.D.; Khan, A.D. High performance perovskite solar cell based on efficient materials for electron and hole transport layers. Optik 2020, 218, 164787. [Google Scholar] [CrossRef]
- Laidouci, A.; Aissat, A.; Vilcot, J.P. Numerical study of solar cells based on ZnSnN2 structure. Sol. Energy 2020, 211, 237–243. [Google Scholar] [CrossRef]
- Khattak, Y.H.; Baig, F.; Toura, H.; Beg, S.; Soucase, B.M. CZTSe Kesterite as an Alternative Hole Transport Layer for MASnI3 Perovskite Solar Cells. J. Electron. Mater. 2019, 48, 5723–5733. [Google Scholar] [CrossRef]
- Al Ahmed, S.R.; Rahaman, M.; Sunny, A.; Rahman, S.; Islam, M.S.; Taha, T.A.; Alrowaili, Z.A.; Mian, M.S. Enhancing the efficiency of Cu2Te thin-film solar cell with WS2 buffer layer: A simulation study. Opt. Laser Technol. 2023, 159, 108942. [Google Scholar] [CrossRef]
- Patel, A.K.; Rao, P.K.; Mishra, R.; Soni, S.K. Numerical study of a high-performance thin film CIGS solar cell with a-Si and MoTe2 hole transport layer. Optik 2021, 243, 167498. [Google Scholar] [CrossRef]
- Kareem, M.Q.; Hassan, S.A.; Alimardan, S.S.; Shareef, S.M.; Ameen, M.M. CHTS/Zn2P3-based solar cells with enhanced efficiency through ETL engineering: A numerical study. J. Phys. Chem. Solids 2024, 188, 111931. [Google Scholar] [CrossRef]
- Kumari, K.; Jana, A.; Dey, A.; Chakrabarti, T.; Sarkar, S.K. Lead free CH3NH3SnI3 based perovskite solar cell using ZnTe nano flowers as hole transport layer. Opt. Mater. 2021, 111, 110574. [Google Scholar] [CrossRef]
- Raoui, Y.; Ez-Zahraouy, H.; Tahiri, N.; El Bounagui, O.; Ahmad, S.; Kazim, S. Performance analysis of MAPbI3 based perovskite solar cells employing diverse charge selective contacts: Simulation study. Sol. Energy 2019, 193, 948–955. [Google Scholar] [CrossRef]
- Minbashi, M.; Ghobadi, A.; Ehsani, M.H.; Dizaji, H.R.; Memarian, N. Simulation of high efficiency SnS-based solar cells with SCAPS. Sol. Energy 2018, 176, 520–525. [Google Scholar] [CrossRef]
- Jayan, K.D. Bandgap Tuning and Input Parameter Optimization for Lead-Free All-Inorganic Single, Double, and Ternary Perovskite-Based Solar Cells. Sol. RRL 2022, 6, 2100971. [Google Scholar] [CrossRef]
- Karmaker, H.; Siddique, A.; Das, B.K.; Islam, M.N. Modeling and performance investigation of novel inorganic Cs4CuSb2Cl12 nanocrystal perovskite solar cell using SCAPS-1D. Results Eng. 2024, 22, 102106. [Google Scholar] [CrossRef]
- Fatema, K. Optimizing inorganic double halide (Cs2TiI6) perovskite solar cell for different hole transport layers using solar cell capacitance software (SCAPS-ID). Mater. Today Commun. 2023, 35, 105860. [Google Scholar] [CrossRef]
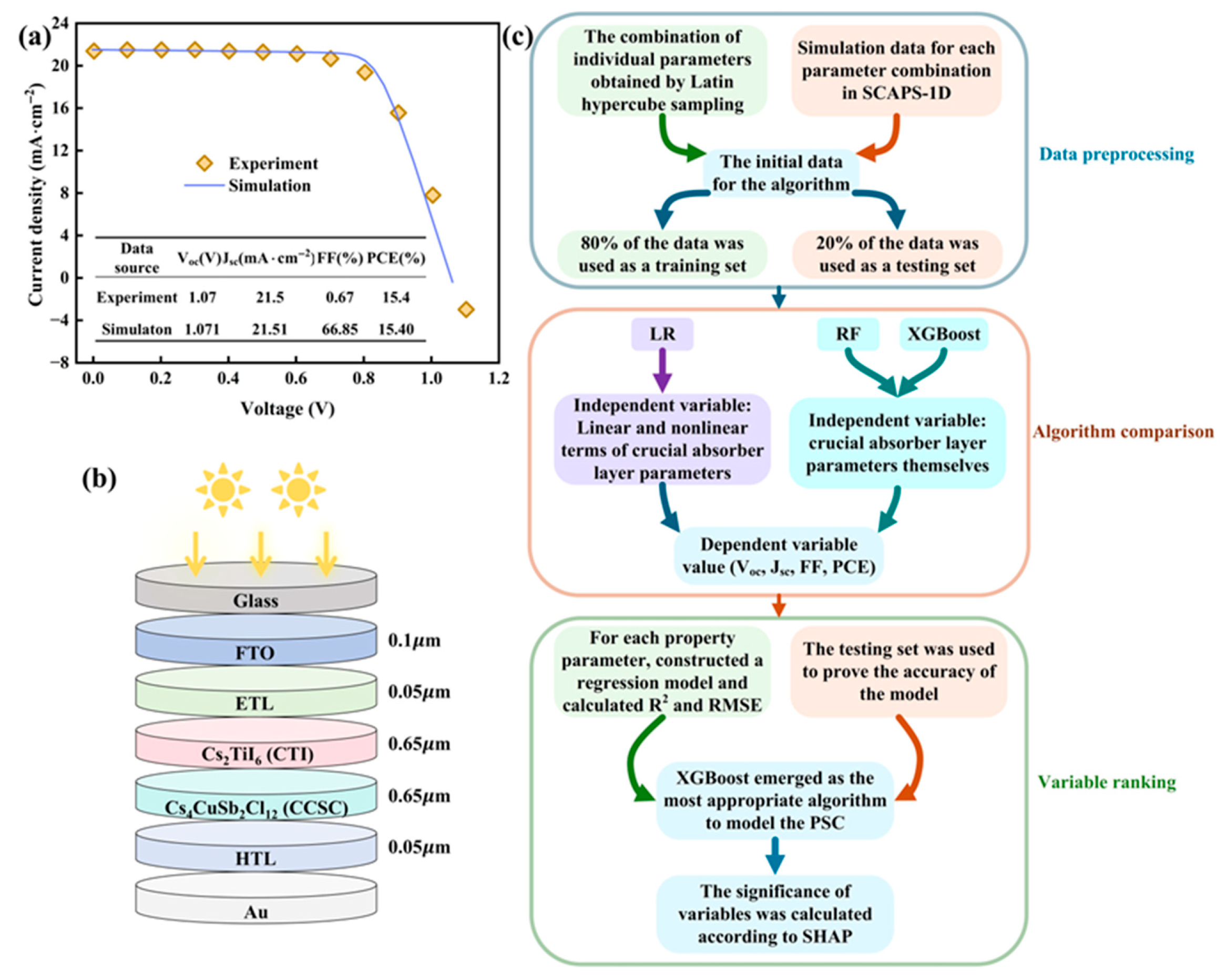
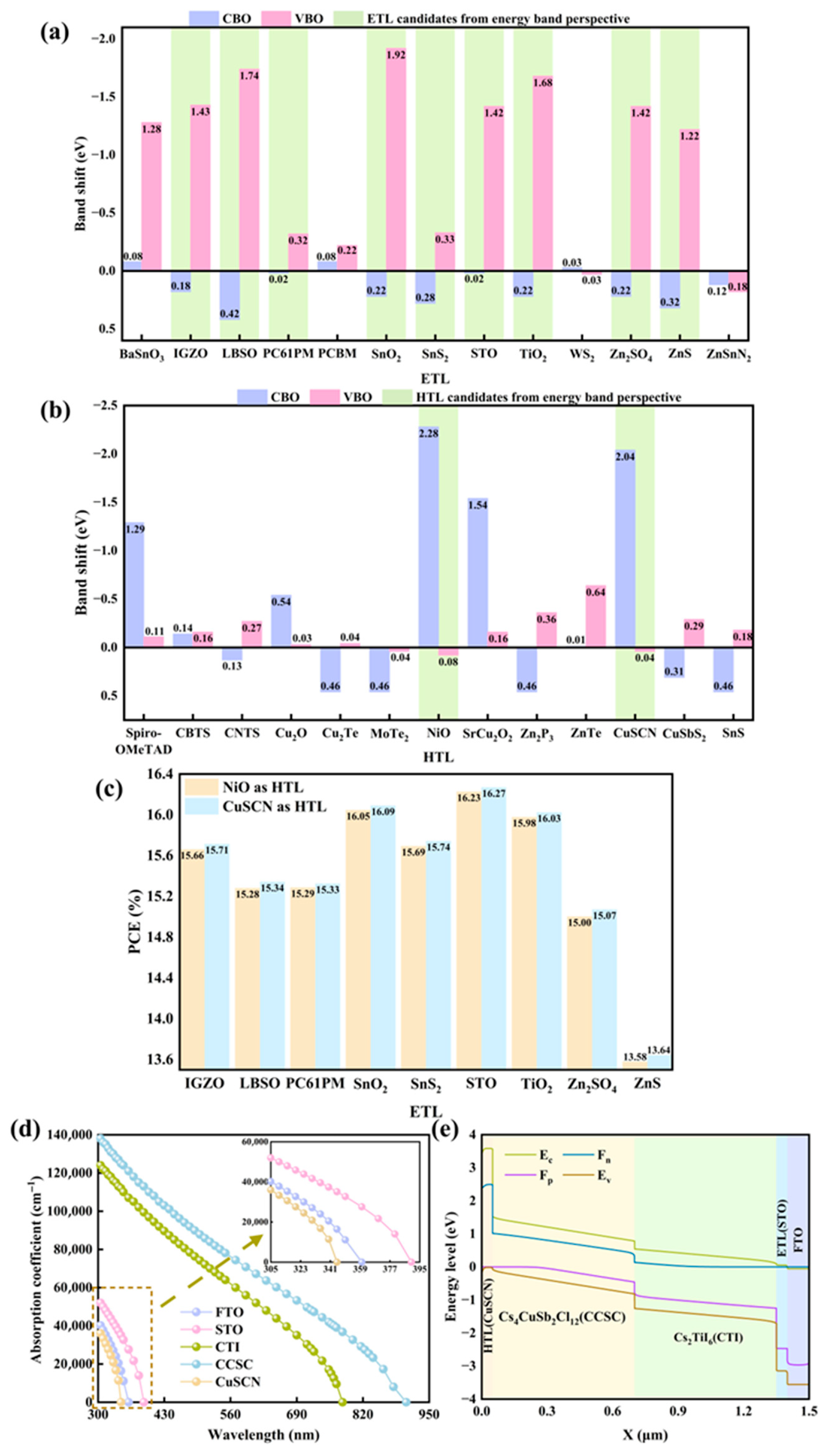




| Material | ) | ) | ) | δ (%) |
|---|---|---|---|---|
| CCSC | 13.083 | 7.3507 | 13.070 | – |
| NiO | 4.174 | 4.174 | 4.174 | 27.56 |
| CuSCN | 3.85 | – | 10.938 | 8.88 |
| Type | Parameters | Data Number | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | … | 1000 | ||
| Independent variable | CTI thickness (μm) | 0.2 | 0.7 | 0.4 | … | 0.8 |
| CCSC thickness (μm) | 0.3 | 0.5 | 0.2 | … | 0.4 | |
| CTI defect density (cm−3) | 1 1016 | 1 1014 | 1 1018 | … | 1 1018 | |
| CCSC defect density (cm−3) | 1 1017 | 1 1017 | 1 1013 | … | 1 1018 | |
| CTI/CCSC interface defect density (cm−3) | 1 1012 | 1 1013 | 1 1014 | … | 1 1011 | |
| CTI band gap (eV) | 1.6 | 1.84 | 1.89 | … | 1.67 | |
| CCSC band gap (eV) | 1.44 | 1.67 | 1.62 | … | 1.54 | |
| Dependent variable | Voc (V) | 0.9716 | 1.1282 | 0.9061 | … | 0.9044 |
| Jsc (mA·cm−2) | 23.0985 | 18.8206 | 5.9881 | … | 0.8438 | |
| FF (%) | 56.7202 | 69.6902 | 69.7301 | … | 31.6132 | |
| PCE (%) | 12.7296 | 14.7969 | 3.7833 | … | 0.2413 | |
| Regression Type | Data Type | Evaluation Type | Property Parameter | |||
|---|---|---|---|---|---|---|
| Voc (V) | cm−2) | FF (%) | PCE (%) | |||
| LR (Excluding nonlinear terms) | Training set | R2 | 0.8097 | 0.7771 | 0.4220 | 0.8148 |
| RMSE | 0.0696 | 3.6341 | 13.2479 | 2.7795 | ||
| Test set | R2 | 0.7727 | 0.8334 | 0.3483 | 0.8210 | |
| RMSE | 0.0770 | 3.2136 | 13.9988 | 2.6867 | ||
| LR (including nonlinear terms) | Training set | R2 | 0.9625 | 0.9353 | 0.7233 | 0.9575 |
| RMSE | 0.0309 | 1.9575 | 9.1671 | 1.3312 | ||
| Test set | R2 | 0.9422 | 0.9447 | 0.6961 | 0.9460 | |
| RMSE | 0.0388 | 1.8519 | 9.5591 | 1.4755 | ||
| RF | Training set | R2 | 0.9912 | 0.9958 | 0.9831 | 0.9954 |
| RMSE | 0.0149 | 0.5011 | 2.2629 | 0.4367 | ||
| Test set | R2 | 0.9308 | 0.9812 | 0.8886 | 0.9671 | |
| RMSE | 0.0425 | 1.0784 | 5.7889 | 1.1521 | ||
| XGBoost | Training set | R2 | 0.9980 | 0.9991 | 0.9921 | 0.9993 |
| RMSE | 0.0071 | 0.2299 | 1.5440 | 0.1742 | ||
| Test set | R2 | 0.9771 | 0.9904 | 0.9188 | 0.9845 | |
| RMSE | 0.0244 | 0.7725 | 4.9410 | 0.7908 | ||
| Regression Type | Parameter | Value | Function |
|---|---|---|---|
| RF | Decision tree number | 300 | Determine the accuracy and robustness of the model |
| The minimum sample size of leaf nodes | 1 | Control the complexity of a single tree | |
| XGBoost | Decision tree number | 300 | Determine the complexity of the model and the time consumed for training |
| Learning rate | 0.05 | The contribution weight of each tree to the prediction result | |
| Maximum depth of the decision tree | 5 | Limit the number of branch levels of the tree to control the complexity of feature interaction | |
| Random number seed | 42 | Fix all random processes, including feature and data sampling |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Fang, Y.; Zhao, J. Optimizing Inorganic Cs4CuSb2Cl12/Cs2TiI6 Dual-Absorber Solar Cells: SCAPS-1D Simulations and Machine Learning. Nanomaterials 2025, 15, 1245. https://doi.org/10.3390/nano15161245
Li X, Fang Y, Zhao J. Optimizing Inorganic Cs4CuSb2Cl12/Cs2TiI6 Dual-Absorber Solar Cells: SCAPS-1D Simulations and Machine Learning. Nanomaterials. 2025; 15(16):1245. https://doi.org/10.3390/nano15161245
Chicago/Turabian StyleLi, Xiangde, Yuming Fang, and Jiang Zhao. 2025. "Optimizing Inorganic Cs4CuSb2Cl12/Cs2TiI6 Dual-Absorber Solar Cells: SCAPS-1D Simulations and Machine Learning" Nanomaterials 15, no. 16: 1245. https://doi.org/10.3390/nano15161245
APA StyleLi, X., Fang, Y., & Zhao, J. (2025). Optimizing Inorganic Cs4CuSb2Cl12/Cs2TiI6 Dual-Absorber Solar Cells: SCAPS-1D Simulations and Machine Learning. Nanomaterials, 15(16), 1245. https://doi.org/10.3390/nano15161245









