Microwave Dielectric Permittivity of Nanostructured RMn2O5 Manganate, R2Ti2O7 Titanate, and LiCoPO4 and LiNi0.5Co0.5PO4 Orthophosphate Composites
Abstract
1. Introduction
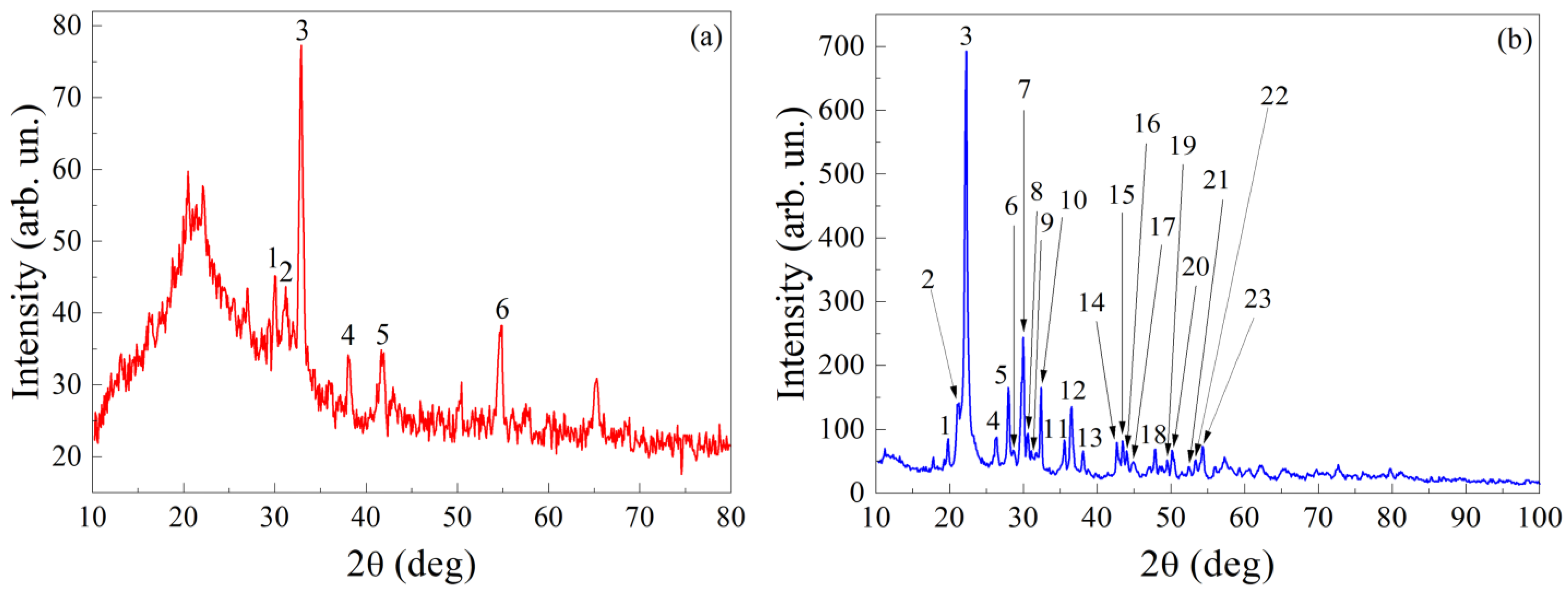
2. Preparation and Characterization of Nanocomposite Samples
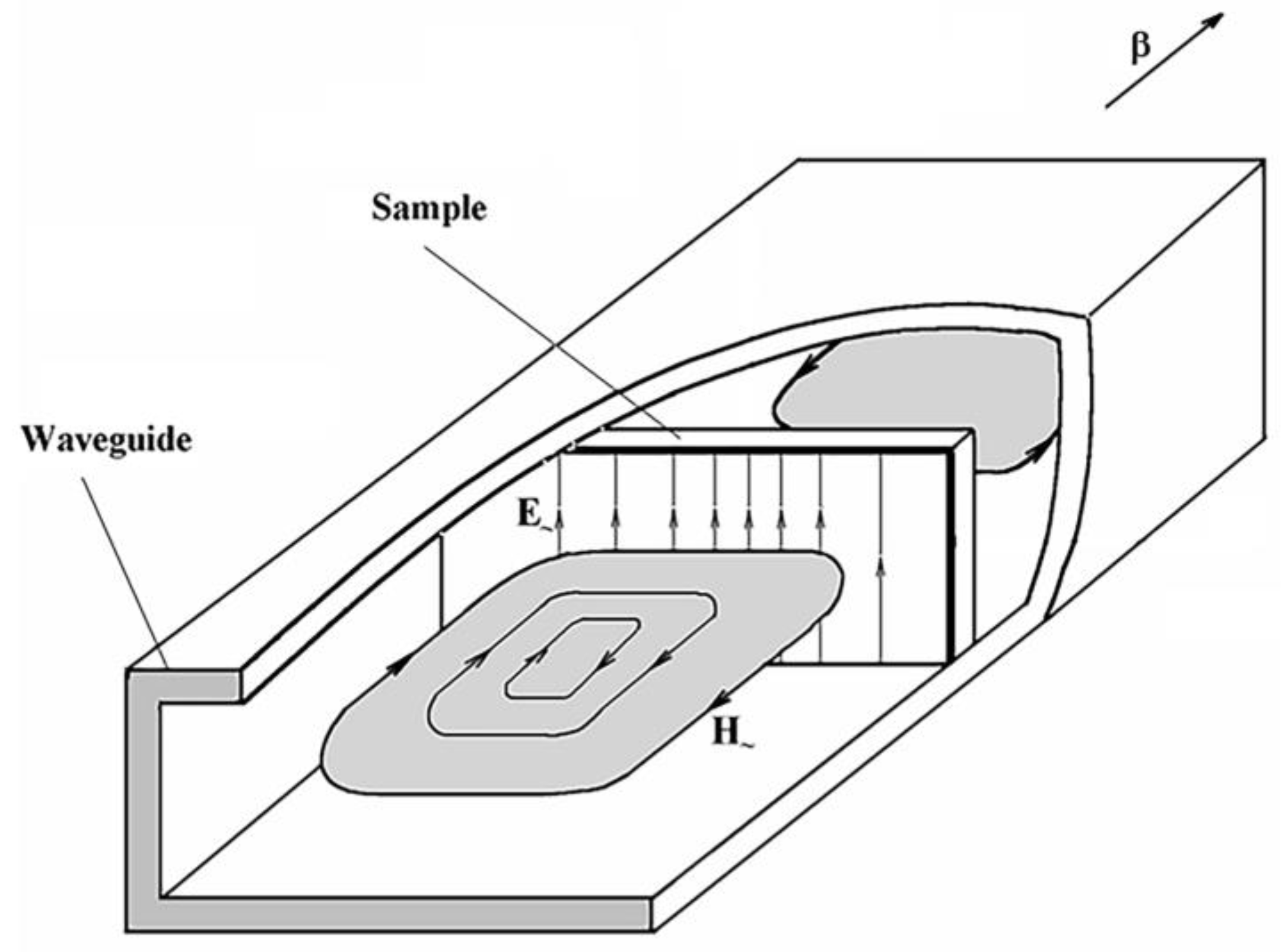
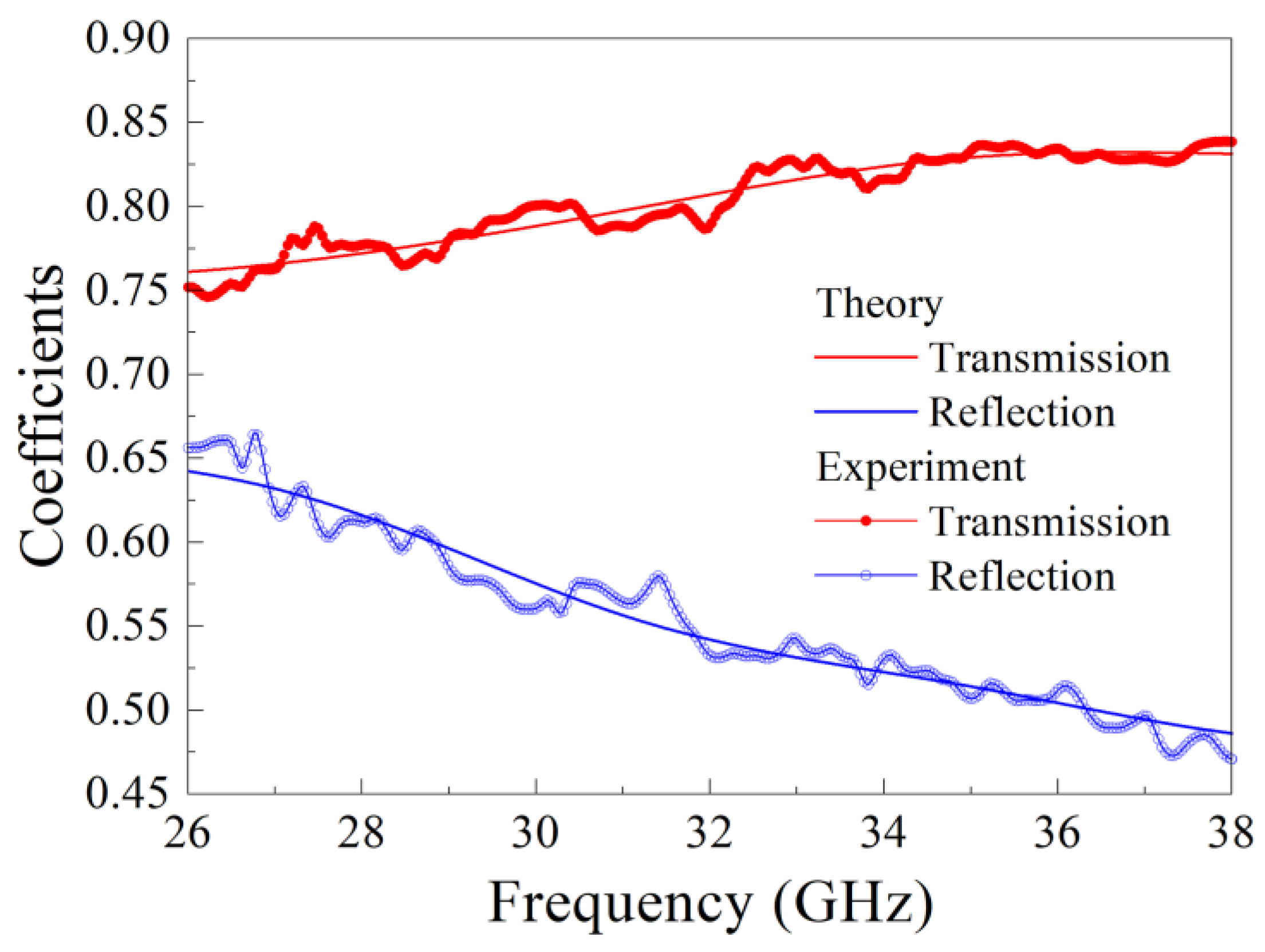
3. Measurement of Microwave Dielectric Permittivity
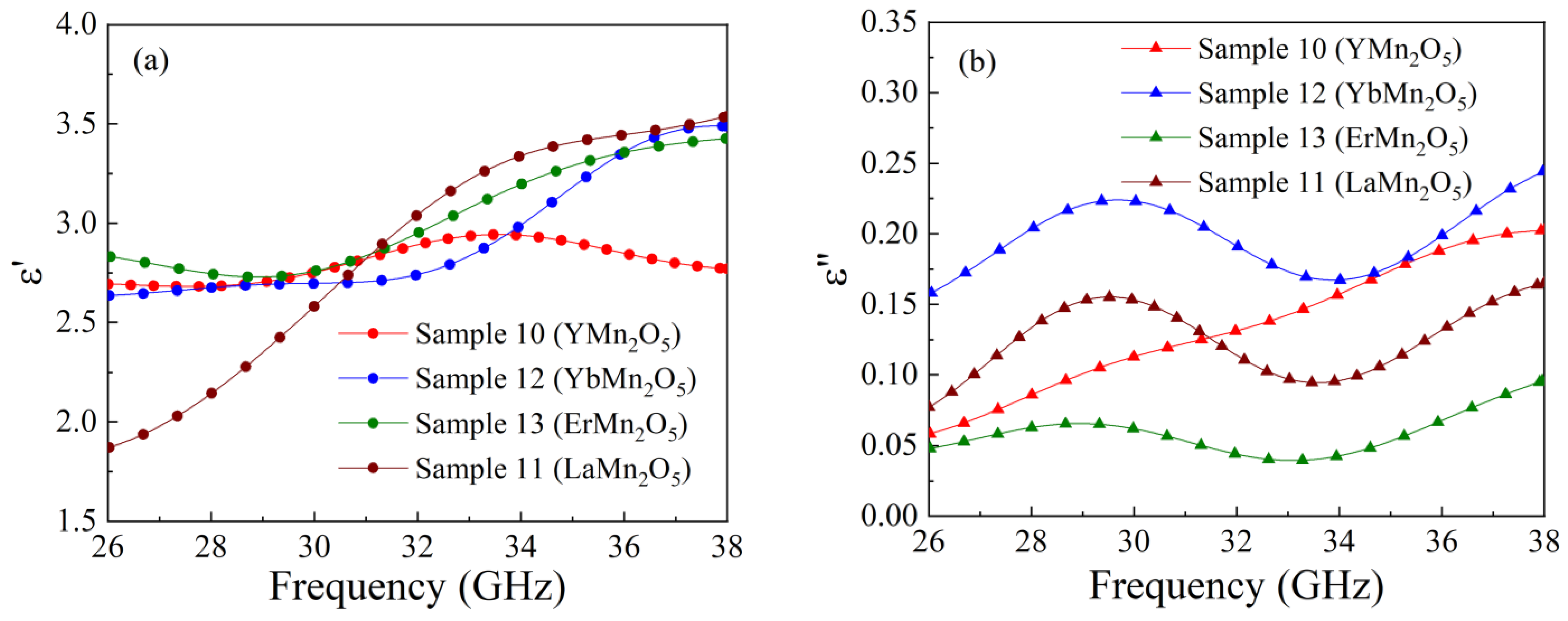
4. Dielectric Permittivity of Manganate Composites
5. Dielectric Permittivity of Rare Earth Titanate Composites
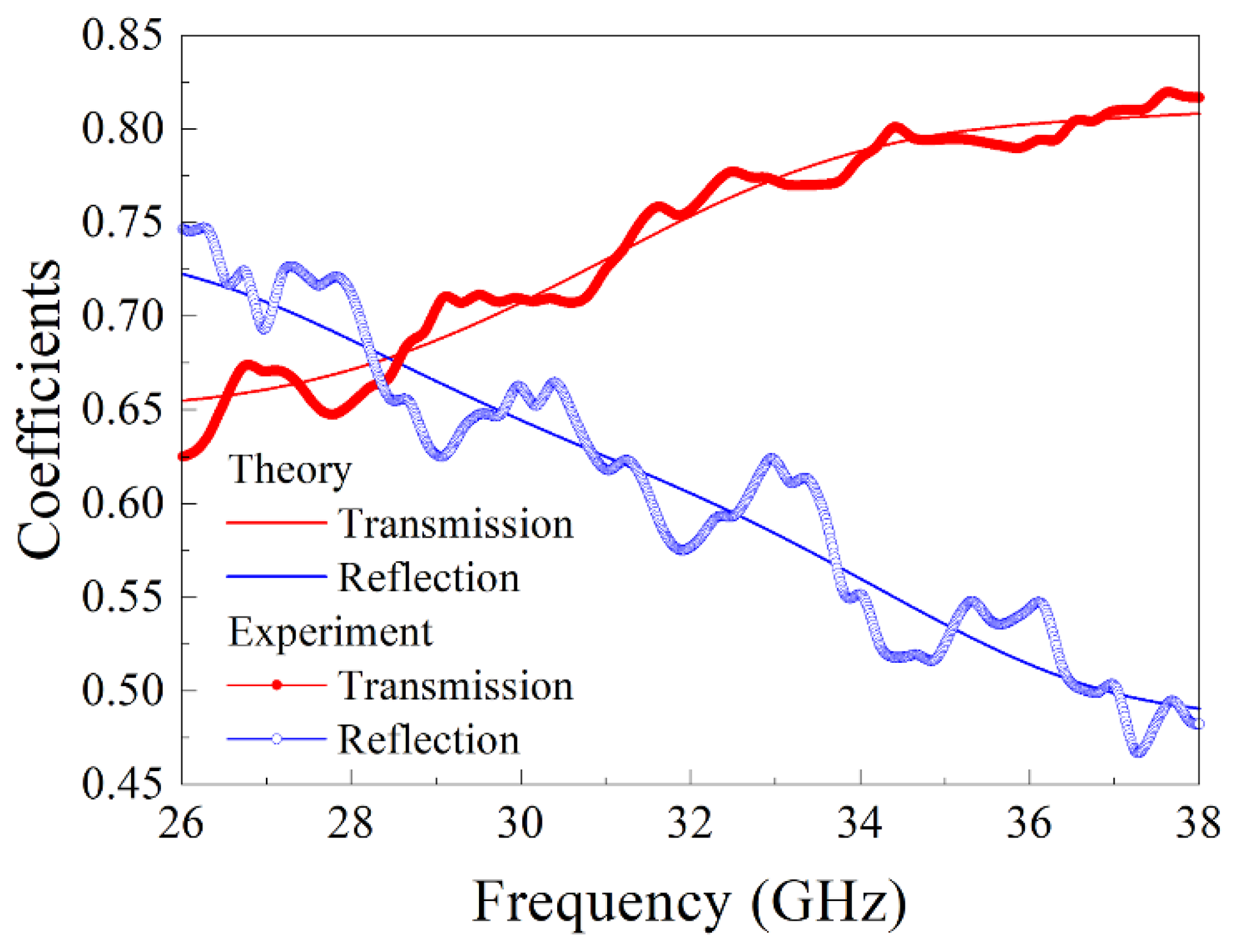
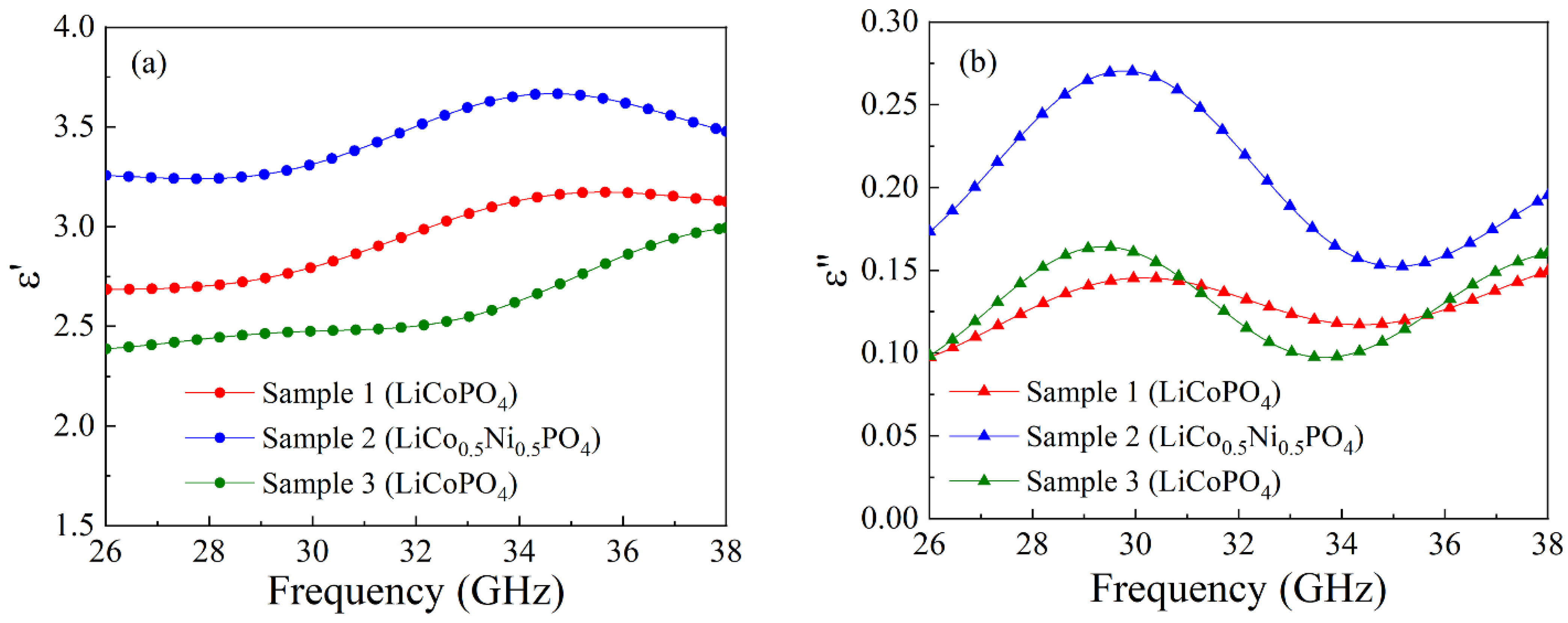
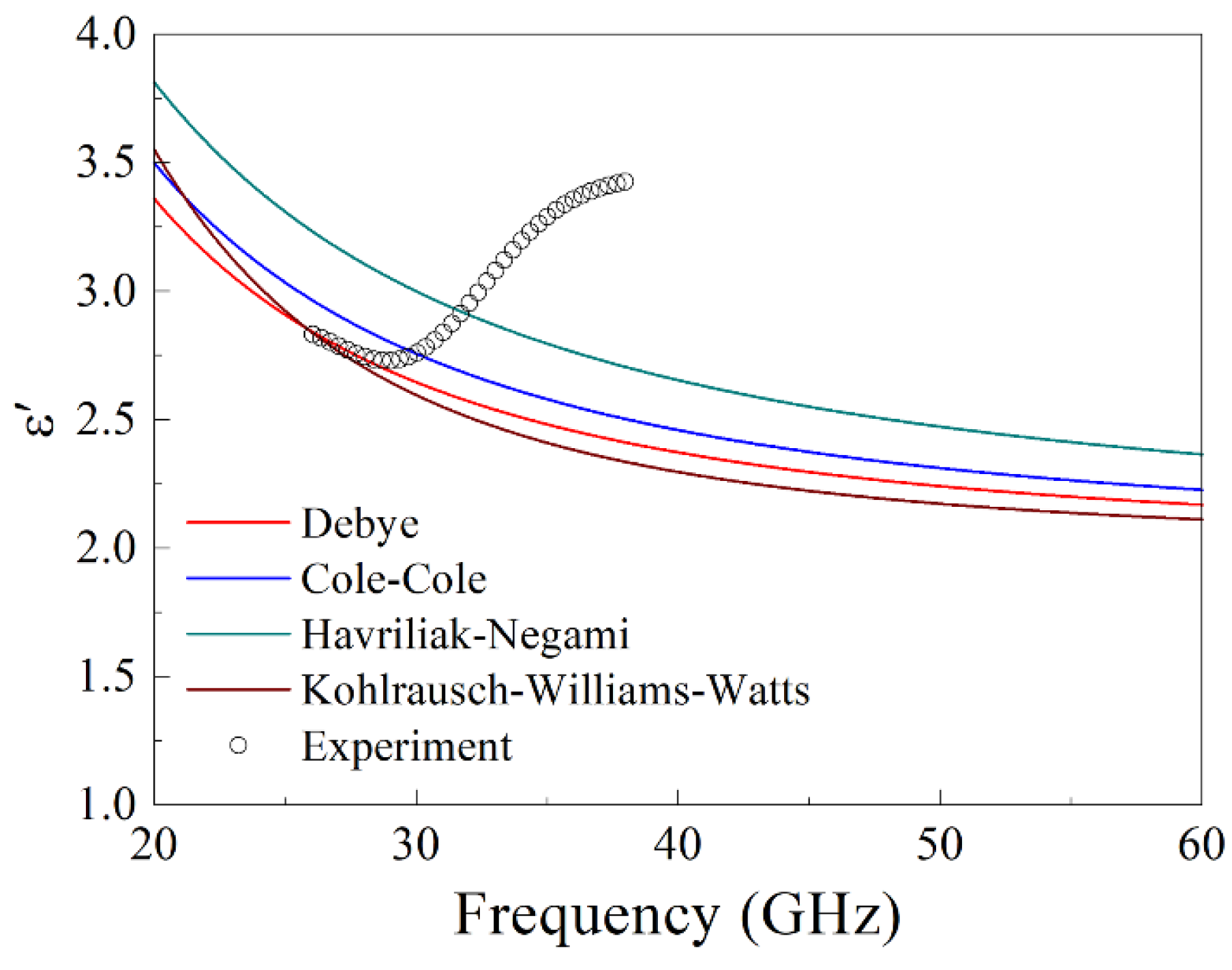
6. Dielectric Permittivity of Orthophosphate Composites
7. Discussion
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stroscio, M.A.; Dutta, M. Phonons in Nanostructures; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Kosevich, Y.A. Multichannel propagation and scattering of phonons and photons in low-dimensional nanostructures. Phys. Usp. 2008, 51, 848–859. [Google Scholar] [CrossRef]
- Liu, J.-M.; Dong, S. Ferrielectricity in DyMn2O5: A golden touchstone for multiferroicity of RMn2O5 family. J. Adv. Dielect. 2015, 5, 1530003. [Google Scholar] [CrossRef]
- Sushkov, A.B.; Kant, C.; Schiebl, M.; Shuvaev, A.M.; Pimenov, A.; Pimenov, A.; Lorenz, B.; Park, S.; Cheong, S.-W.; Mostovoy, M.; et al. Spectral origin of the colossal magnetodielectric effect in multiferroic DyMn2O5. Phys. Rev. B 2014, 90, 054417. [Google Scholar] [CrossRef]
- Bukhari, S.H.; Ahmad, J. Magnetoelectric effect in multiferroic NdMn2O5. Chin. Phys. B 2017, 26, 018103. [Google Scholar] [CrossRef]
- Fogh, E.; Kihara, T.; Toft-Petersen, R.; Bartkowiak, M.; Narumi, Y.; Prokhnenko, O.; Miyake, A.; Tokunaga, M.; Oikawa, K.; Sørensen, M.K.; et al. Magnetic structures and quadratic magnetoelectric effect in LiNiPO4 beyond 30 T. Phys. Rev. B 2020, 101, 024403. [Google Scholar] [CrossRef]
- Blake, G.R.; Chapon, L.C.; Radaelli, P.G.; Park, S.; Hur, N.; Cheong, S.-W.; Rodríguez-Carvajal, J. Spin structure and magnetic frustration in multiferroic RMn2O5 (R = Tb, Ho, Dy). Phys. Rev. B 2005, 71, 214402. [Google Scholar] [CrossRef]
- Noda, Y.; Kimura, H.; Fukunaga, M.; Kobayashi, S.; Kagomiya, I.; Kohn, K. Magnetic and ferroelectric properties of multiferroic RMn2O5. J. Phys. Condens. Matter. 2008, 20, 434206. [Google Scholar] [CrossRef]
- Khannanov, B.K.; Golovenchits, E.I.; Sanina, V.A. Effect of rare-earth ions on an electric polarization induced by the phase separation domains in RMn2O5 (R = Er, Tb). Phys. Solid State 2020, 62, 308–317. [Google Scholar] [CrossRef]
- Manley, M.E.; Lynn, J.W.; Abernathy, D.L.; Specht, E.D.; Delaire, O.; Bishop, A.R.; Sahul, R.; Budai, J.D. Phonon localization drives polar nanoregions in a relaxor ferroelectric. Nat. Commun. 2014, 5, 3683. [Google Scholar] [CrossRef]
- Han, T.C.; Lin, J.G.; Kuo, K.M.; Chern, G. Large dielectric permittivity in the paraelectric RMn2O5 with R = Tb, Dy, and Er. J. Appl. Phys. 2008, 103, 084106. [Google Scholar] [CrossRef]
- Ahmad, J.; Zaheer, H.; Khan, J.A.; Bukhari, S.H.; Nissar, U. Electrical and dielectric properties of multiferroic Gd1-xYxMn2O5. J. Nanoscope 2021, 2, 39–52. [Google Scholar] [CrossRef]
- Devaraju, M.K.; Truong, Q.D.; Hyodo, H.; Sasaki, Y.; Honma, I. Synthesis, characterization and observation of antisite defects in LiNiPO4 nanomaterials. Sci. Rep. 2015, 5, 11041. [Google Scholar] [CrossRef]
- Prabu, M.; Selvasekarapandian, S. Dielectric and modulus studies of LiNiPO4. Mater. Chem. Phys. 2012, 134, 366–370. [Google Scholar] [CrossRef]
- Ben Bechir, M.; Ben Rhaiem, A.; Guidara, K.A.c. conductivity and dielectric study of LiNiPO4 synthesized by solid-state method. Bull. Mater. Sci. 2014, 37, 473–480. [Google Scholar] [CrossRef]
- Xiao, E.; Cao, Z.; Li, J.; Li, X.-H.; Liu, M.; Yue, Z.; Chen, Y.; Chen, G.; Song, K.; Zhou, H.; et al. Crystal structure, dielectric properties, and lattice vibrational characteristics of LiNiPO4 ceramics sintered at different temperatures. J. Am. Ceram. Soc. 2020, 103, 2528–2539. [Google Scholar] [CrossRef]
- Vijaya Babu, K.; Seeta Devi, L.; Veeraiah, V.; Anand, K. Structural and dielectric studies of LiNiPO4 and LiNi0.5Co0.5PO4 cathode materials for lithium-ion batteries. J. Asian Ceram. Soc. 2016, 4, 269–276. [Google Scholar] [CrossRef]
- Karthickprabhu, S.; Hirankumar, G.; Maheswaran, A.; Daries Bella, R.S.; Sanjeeviraja, C. Structural and electrical studies on Zn2+ doped LiCoPO4. J. Electrostat. 2014, 72, 181–186. [Google Scholar] [CrossRef]
- Bokov, A.; Ye, Z.-G. Dielectric relaxation in relaxor ferroelectrics. J. Adv. Dielect. 2012, 2, 124101. [Google Scholar] [CrossRef]
- Fier, I.; Walmsley, L.; Souza, J.A. Relaxor behavior in multiferroic BiMn2O5 ceramics. J. Appl. Phys. 2011, 110, 084101. [Google Scholar] [CrossRef]
- Chouaibi, H.; Khirouni, K.; Dhahri, E. Enhanced dielectric performance of Dy—Substituted YMn2O5 for high-frequency applications. Prog. Nat. Sci. Mater. Int. 2021, 31, 762–777. [Google Scholar] [CrossRef]
- Jurlewicz, A.; Weron, K. Relaxation of dynamically correlated clusters. J. Non-Cryst. Solids 2002, 305, 112–121. [Google Scholar] [CrossRef]
- Feldman, Y.; Puzenko, A.; Ryabov, Y. Non-Debye dielectric relaxation in complex materials. Chem. Phys. 2002, 284, 139–168. [Google Scholar] [CrossRef]
- Petzelt, J.; Nuzhnyy, D.; Savinov, M.; Bovtun, V.; Kempa, M.; Ostapchuk, T.; Hlinka, J.; Canu, G.; Buscaglia, V. Broadband dielectric spectroscopy of Ba(Zr,Ti)O3: Dynamics of relaxors and diffuse ferroelectrics. Ferroelectrics 2014, 469, 14–25. [Google Scholar] [CrossRef]
- Kamba, S.; Veljko, S.; Kempa, M.; Savinov, M.; Bovtun, V.; Vanek, P.; Petzelt, J.; Stennett, M.C.; Reaney, I.M.; West, A.R. Dielectric spectra of a new relaxor ferroelectric system Ba2LnTi2Nb3O15 (Ln = La, Nd). J. Eur. Ceram. Soc. 2005, 25, 3069–3073. [Google Scholar] [CrossRef]
- Rinkevich, A.B.; Pakhomov, Y.A.; Perov, D.V. Millimeter waveband dielectric properties of nanocomposite 3d and rare-earth titanates. Mater. Today: Proc. 2019, 14, 144–147. [Google Scholar] [CrossRef]
- Zhang, P.; Wu, S.; Xiao, M. The microwave dielectric properties and crystal structure of low temperature sintering LiNiPO4 ceramics. J. Eur. Ceram. Soc. 2018, 38, 4433–4439. [Google Scholar] [CrossRef]
- Liu, P.; Ng, V.M.H.; Yao, Z.; Zhou, J.; Lei, Y.; Yang, Z.; Lv, H.; Kong, L.B. Facile synthesis and hierarchical assembly of flowerlike NiO structures with enhanced dielectric and microwave absorption properties. ACS Appl. Mater. Interfaces 2017, 9, 16404–16416. [Google Scholar] [CrossRef]
- Zou, D.; Yi, Y.; Song, Y.; Guan, D.; Xu, M.; Ran, R.; Wang, W.; Zhou, W.; Shao, Z. The BaCe0.16Y0.04Fe0.8O3−δ nanocomposite: A new high-performance cobalt-free triple-conducting cathode for protonic ceramic fuel cells operating at reduced temperatures. J. Mater. Chem. A 2022, 10, 5381–5390. [Google Scholar] [CrossRef]
- Rinkevich, A.B.; Burkhanov, A.M.; Samoilovich, M.I.; Belyanin, A.F.; Kleshcheva, S.M.; Kuznetsov, E.A. Three-dimensional nanocomposite metal dielectric materials on the basis of opal matrices. Russ. J. Gen. Chem. 2013, 83, 2148–2158. [Google Scholar] [CrossRef]
- Guan, D.; Xu, H.; Huang, Y.-C.; Jing, C.; Tsujimoto, Y.; Xu, X.; Lin, Z.; Tang, J.; Wang, Z.; Sun, X.; et al. Operando studies redirect spatiotemporal restructuration of model coordinated oxides in electrochemical oxidation. Adv. Mater. 2025, 37, 2413073. [Google Scholar] [CrossRef]
- Toft-Petersen, R.; Reehuis, M.; Jensen, T.B.S.; Andersen, N.H.; Li, J.; Le, M.D.; Laver, M.; Niedermayer, C.; Klemke, B.; Lefmann, K.; et al. Anomalous magnetic structure and spin dynamics in magnetoelectric LiFePO4. Phys. Rev. B 2015, 92, 024404. [Google Scholar] [CrossRef]
- Samoilovich, M.I.; Rinkevich, A.B.; Bovtun, V.; Belyanin, A.F.; Kempa, M.; Nuzhnyy, D.; Tsvetkov, M.Y.; Kleshcheva, S.M. Optical, magnetic, and dielectric properties of opal matrices with intersphere nanocavities filled with crystalline multiferroic, piezoelectric, and segnetoelectric materials. Russ. J. Gen. Chem. 2013, 83, 2132–2147. [Google Scholar] [CrossRef]
- Rinkevich, A.B.; Perov, D.V. Cole-Cole formula for dependence of dynamic magnetic susceptibility of rare-earth titanates on magnetic field. J. Magn. Magn. Mater. 2021, 530, 167917. [Google Scholar] [CrossRef]
- Ustinov, V.V.; Rinkevich, A.B.; Perov, D.V.; Burkhanov, A.M.; Samoilovich, M.I.; Kleshcheva, S.M.; Kuznetsov, E.A. Giant antiresonance in electromagnetic wave reflection from a 3D structure with ferrite spinel nanoparticles. Tech. Phys. 2013, 58, 568–577. [Google Scholar] [CrossRef]
- Brekhovskikh, L.M. Waves in Layered Media; Academic Press: Salt Lake City, UT, USA, 1960. [Google Scholar]
- Perov, D.V.; Rinkevich, A.B. Ferromagnetic resonance and antiresonance in composite medium with flakes of Finemet-like alloy. Nanomaterials 2021, 11, 1748. [Google Scholar] [CrossRef]
- Khan, A.R.; Goel, R.; Gupta, A.; Tripathi, H.; Kumar, N.; Bhardwaj, S.; Kumar, S.; Kuma, G.; Sharma, P. Improved multiferroic and magnetodielectric properties in Ni and Fe co-doped barium strontium titanate ceramics. J. Mater. Sci. Mater. Electron. 2024, 35, 1383. [Google Scholar] [CrossRef]
- Debye, P. Zur Theorie der anomalen Dispersion im Gebiete der langwelligen elektrischen Strahlung. Verh. Dtsch. Phys. Ges. 1913, 15, 777–793. [Google Scholar]
- Cole, K.S.; Cole, R.H. Dispersion and absorption in dielectrics I. Alternating current characteristics. J. Chem. Phys. 1941, 9, 341–351. [Google Scholar] [CrossRef]
- Davidson, D.W.; Cole, R.H. Dielectric relaxation in glycerol, propylene glycol, and n-propanol. J. Chem. Phys. 1951, 19, 1484–1490. [Google Scholar] [CrossRef]
- Havriliak, S.; Negami, S. A complex plane analysis of α-dispersions in some polymer systems. J. Polym. Sci. Part C 1966, 14, 99–117. [Google Scholar] [CrossRef]
- Volkov, A.S.; Koposov, G.D.; Perfil’ev, R.O.; Tyagunin, A.V. Analysis of experimental results by the Havriliak–Negami model in dielectric spectroscopy. Opt. Spectrosc. 2018, 124, 202–205. [Google Scholar] [CrossRef]
- Fröhlich, H. Theory of Dielectrics: Dielectric Constant and Dielectric Loss; Clarendon Press: Oxford, UK, 1949. [Google Scholar]
- Jonscher, A.K. Universal Relaxation Law; Chelsea Dielectrics Press: London, UK, 1996. [Google Scholar]
- Sihvola, A. Homogenization principles and effect of mixing on dielectric behavior. Photonics Nanostruct. Fundam. Appl. 2013, 11, 364–373. [Google Scholar] [CrossRef]
- Strashnikova, M.I.; Mozdor, E.V. Limits of applicability of the Kramers-Kronig relations in the presence of an additional light wave. J. Exp. Theor. Phys. 1998, 87, 756–763. [Google Scholar] [CrossRef]
- Agranovich, V.M.; Ginzburg, V.L. Crystal Optics with Spatial Dispersion, and Excitons; Springer: Berlin/Heidelberg, Germany, 1984. [Google Scholar]
- Mayoral, R.; Requena, J.; Lypez, C.; Moya, S.J.; Mhguez, H.; Vozquez, L.; Meseguer, F.; Holgado, M.; Cintas, A.; Blanco, A. 3D long-range ordering in an SiO2 submicrometer-sphere sintered superstructures. Adv. Mater. 1997, 9, 257–260. [Google Scholar] [CrossRef]



| Element | Type of Line | Wt.% | At.% |
|---|---|---|---|
| O | K | 51.46 | 66.97 |
| Si | K | 42.76 | 31.70 |
| Mn | L | 2.31 | 0.88 |
| Tb | M | 3.47 | 0.45 |
| Peak’s Number | Experimental Data | Data from ICDD PDF-2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Intensity, arb. un. | Intensity, % | Bragg Angle 2θ, deg. | Peak Semiwidth, deg. | Interplane Space, Å | Mn2O3—Cubic Syngony, Space Group Ia-3 (89-4836) | TbMn2O5—Orthorhombic Syngony, Space Group Pbam (50-0294) | |||||
| d, Å | hkl | I, % | d, Å | hkl | I, % | ||||||
| 1 | 17.93 | 23 | 29.820 | 0.396 | 2.9934 | 3.0400 | 121 | 65 | |||
| 2 | 17.30 | 22 | 30.967 | 0.396 | 2.8851 | 2.8580 | 211 | 100 | |||
| 3 | 77.25 | 100 | 32.688 | 0.396 | 2.7370 | 2.7152 | 222 | 100 | 2.7430 | 220 | 11 |
| 4 | 6.28 | 8 | 37.827 | 0.253 | 2.3761 | 2.3515 | 400 | 13.7 | 2.3740 | 131 | 9 |
| 5 | 10.48 | 14 | 41.745 | 0.417 | 2.1617 | 2.1540 | 311 | 30 | |||
| 6 | 15.51 | 20 | 54.716 | 0.341 | 1.6760 | 1.6627 | 440 | 39.9 | 1.6740 | 420 | 23 |
| 7 | 12.00 | 16 | 65.155 | 0.289 | 1.4304 | 1.4180 | 622 | 17.6 | 1.4140 | 060 | 18 |
| Element | Type of Line | Wt.% | At.% |
|---|---|---|---|
| O | K | 56.33 | 69.83 |
| Si | K | 41.28 | 29.15 |
| P | K | 0.69 | 0.45 |
| Co | K | 1.70 | 0.57 |
| Peak’s Number | Experimental Data | Data from ICDD PDF-2 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Intensity, arb. un. | Intensity, % | Bragg Angle 2θ, deg. | Peak Semiwidth, deg. | Interplane Space, Å | SiO2 (Cristobalite)— Tetragonal Syngony, Space Group P41212 (89-3434) | LiCoPO4— Orthorhombic Syngony, Space Group Pnma (85-0002) | SiO2 (Quartz)— Hexagonal Syngony, Space Group P3221 (86-1565) | |||||||
| d, Å | hkl | I, % | d, Å | hkl | I, % | d, Å | hkl | I, % | ||||||
| 1 | 34.99 | 5 | 19.523 | 0.328 | 4.5427 | |||||||||
| 2 | 105.34 | 15 | 20.908 | 0.328 | 4.2448 | 4.2610 | 101 | 67.5 | ||||||
| 3 | 692.02 | 100 | 21.984 | 0.328 | 4.0394 | 4.0281 | 101 | 100 | 4.0722 | 100 | 22.1 | |||
| 4 | 35.17 | 5 | 26.172 | 0.271 | 3.4017 | 3.4583 | 111 | 81.1 | ||||||
| 5 | 81.98 | 12 | 27.823 | 0.220 | 3.2035 | 3.2191 | 011 | 100 | ||||||
| 6 | 14.53 | 2 | 28.528 | 0.220 | 3.1259 | |||||||||
| 7 | 105.78 | 15 | 29.732 | 0.157 | 3.0020 | 2.9821 | 211 | 10.3 | ||||||
| 8 | 25.48 | 4 | 30.343 | 0.157 | 2.9430 | 2.9599 | 020 | 64.0 | ||||||
| 9 | 10.94 | 2 | 30.847 | 0.157 | 2.8960 | |||||||||
| 10 | 60.06 | 9 | 32.143 | 0.157 | 2.7821 | 2.8340 | 102 | 11.4 | 2.7527 | 301 | 24.5 | |||
| 11 | 35.20 | 5 | 35.237 | 0.316 | 2.5446 | 2.5600 | 220 | 2.4 | ||||||
| 12 | 97.48 | 14 | 36.186 | 0.316 | 2.4800 | 2.4793 | 200 | 13.5 | 2.4960 | 311 | 100 | |||
| 13 | 27.59 | 4 | 37.776 | 0.316 | 2.3792 | 2.3419 | 002 | 17.5 | 2.3511 | 110 | 12.0 | |||
| 14 | 40.96 | 6 | 42.391 | 0.225 | 2.1303 | 2.1114 | 211 | 2.6 | 2.1461 | 111 | 5.3 | |||
| 15 | 39.12 | 6 | 43.172 | 0.225 | 2.0935 | 2.1305 | 112 | 16.7 | ||||||
| 16 | 22.70 | 3 | 43.733 | 0.225 | 2.0680 | |||||||||
| 17 | 20.00 | 3 | 44.618 | 0.225 | 2.0290 | 2.0140 | 202 | 1.9 | 2.0157 | 321 | 4.4 | 2.0361 | 200 | 7.8 |
| 18 | 35.55 | 5 | 47.539 | 0.374 | 1.9109 | 1.9246 | 113 | 4.8 | 1.9319 | 420 | 2.2 | 1.8986 | 021 | 1.5 |
| 19 | 18.82 | 3 | 49.189 | 0.374 | 1.8506 | 1.8660 | 212 | 4.8 | ||||||
| 20 | 38.70 | 6 | 49.957 | 0.374 | 1.8239 | 1.8380 | 230 | 12.1 | ||||||
| 21 | 12.33 | 2 | 52.210 | 0.243 | 1.7504 | 1.7522 | 112 | 8.6 | ||||||
| 22 | 22.29 | 3 | 53.130 | 0.243 | 1.7222 | 1.7291 | ||||||||
| 23 | 50.37 | 7 | 54.088 | 0.243 | 1.6940 | 1.6871 | 203 | 2.3 | ||||||
| No. of Sample | Chemical Composition of Samples | Number of Impregnations | <ε′> | <ε″> |
|---|---|---|---|---|
| 1 | LiCoPO4 | 6 | 2.94 | 0.13 |
| 2 | LiCo0.5Ni0.5PO4 | 5 | 3.45 | 0.21 |
| 3 | LiCoPO4 | 5 | 2.59 | 0.13 |
| 4 | Gd2Ti2O7 | 5 | 3.17 | 0.16 |
| 5 | Tb2Ti2O7 | 5 | 2.73 | 0.07 |
| 6 | Yb2Ti2O7 + TiO2 | 5 | 2.52 | 0.07 |
| 7 | Er2Ti2O7 | 5 | 2.39 | 0.12 |
| 8 | Sm2Ti2O7 | 5 | 2.52 | 0.16 |
| 9 | Er2TiO5 | 5 | 2.74 | 0.023 |
| 10 | YMn2O5 | 10 | 2.36 | 0.13 |
| 11 | LaMn2O5 | 5 | 2.81 | 0.12 |
| 12 | YbMn2O5 | 6 | 2.85 | 0.2 |
| 13 | ErMn2O5 | 6 | 2.72 | 0.06 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rinkevich, A.B.; Perov, D.V.; Kuznetsov, E.A.; Stenina, M.S. Microwave Dielectric Permittivity of Nanostructured RMn2O5 Manganate, R2Ti2O7 Titanate, and LiCoPO4 and LiNi0.5Co0.5PO4 Orthophosphate Composites. Nanomaterials 2025, 15, 995. https://doi.org/10.3390/nano15130995
Rinkevich AB, Perov DV, Kuznetsov EA, Stenina MS. Microwave Dielectric Permittivity of Nanostructured RMn2O5 Manganate, R2Ti2O7 Titanate, and LiCoPO4 and LiNi0.5Co0.5PO4 Orthophosphate Composites. Nanomaterials. 2025; 15(13):995. https://doi.org/10.3390/nano15130995
Chicago/Turabian StyleRinkevich, Anatoly B., Dmitry V. Perov, Evgeny A. Kuznetsov, and Maria S. Stenina. 2025. "Microwave Dielectric Permittivity of Nanostructured RMn2O5 Manganate, R2Ti2O7 Titanate, and LiCoPO4 and LiNi0.5Co0.5PO4 Orthophosphate Composites" Nanomaterials 15, no. 13: 995. https://doi.org/10.3390/nano15130995
APA StyleRinkevich, A. B., Perov, D. V., Kuznetsov, E. A., & Stenina, M. S. (2025). Microwave Dielectric Permittivity of Nanostructured RMn2O5 Manganate, R2Ti2O7 Titanate, and LiCoPO4 and LiNi0.5Co0.5PO4 Orthophosphate Composites. Nanomaterials, 15(13), 995. https://doi.org/10.3390/nano15130995










