Electronic Transport Properties in a One-Dimensional Sequence of Laser-Dressed Modified Pöschl-Teller Potentials
Abstract
1. Introduction
2. Theoretical Framework
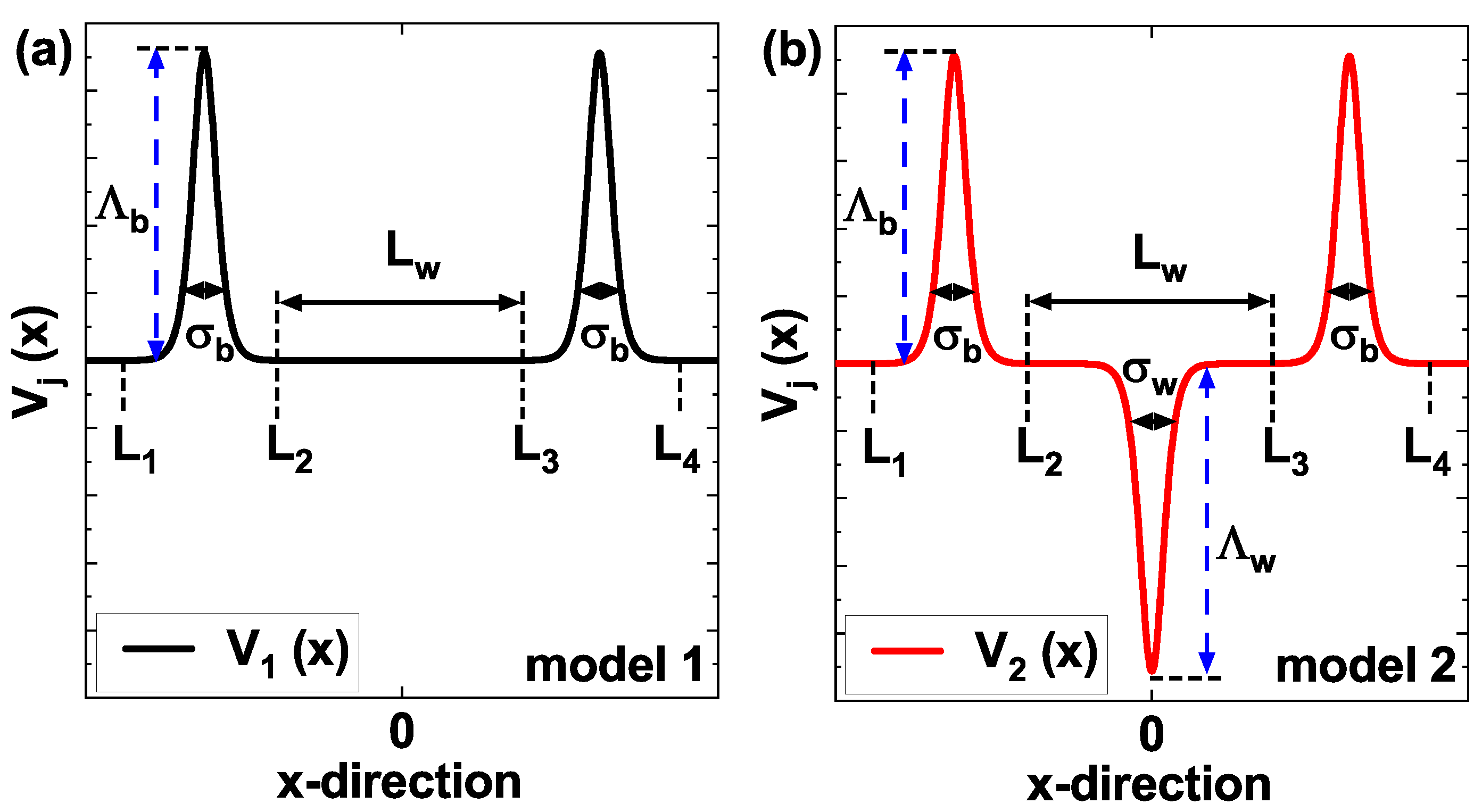
2.1. The Modified Pöschl-Teller Potential
2.2. The Laser-Dressed Modified Pöschl-Teller Potential
2.3. The Electronic Tunneling Current Density
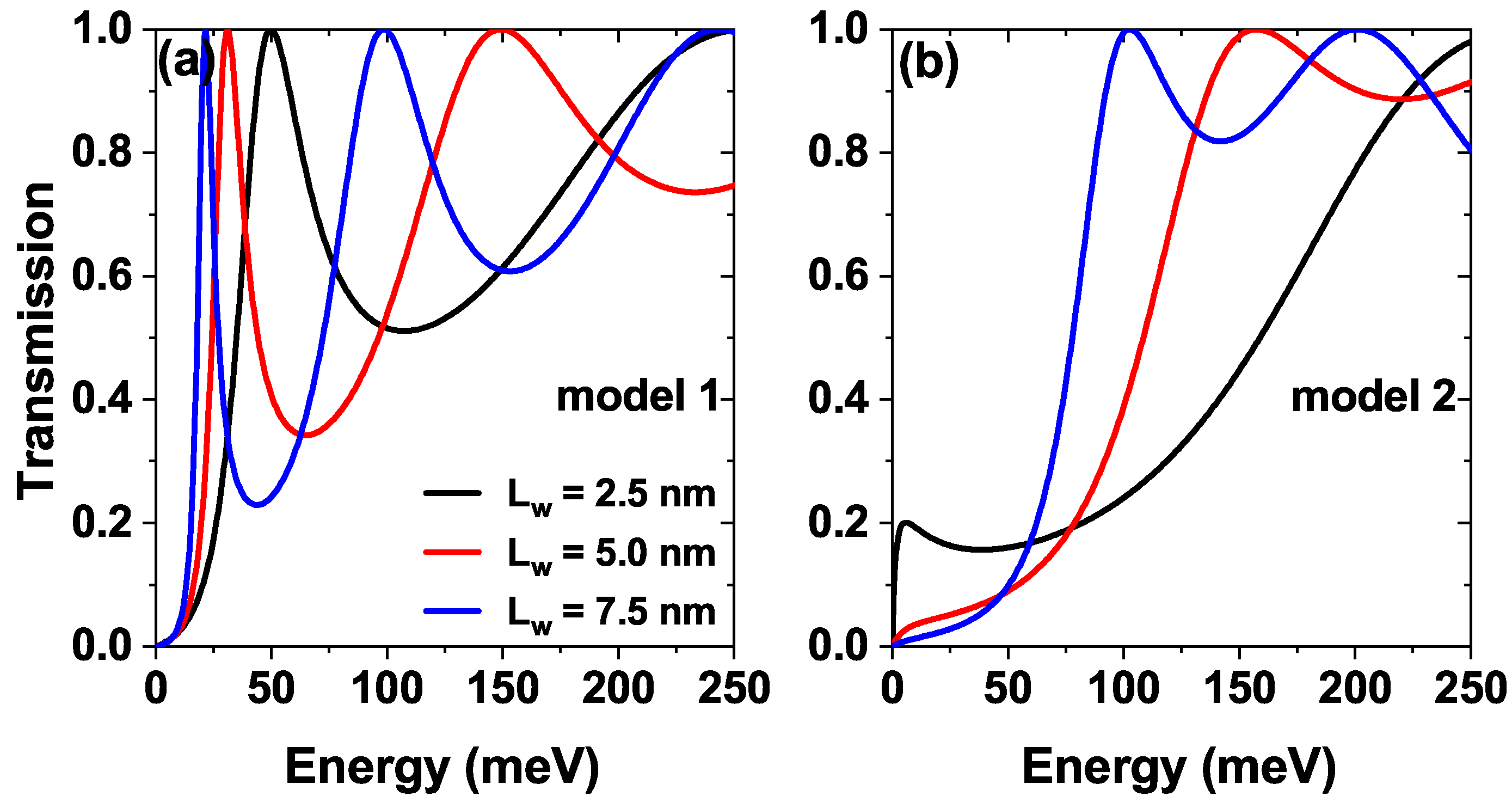
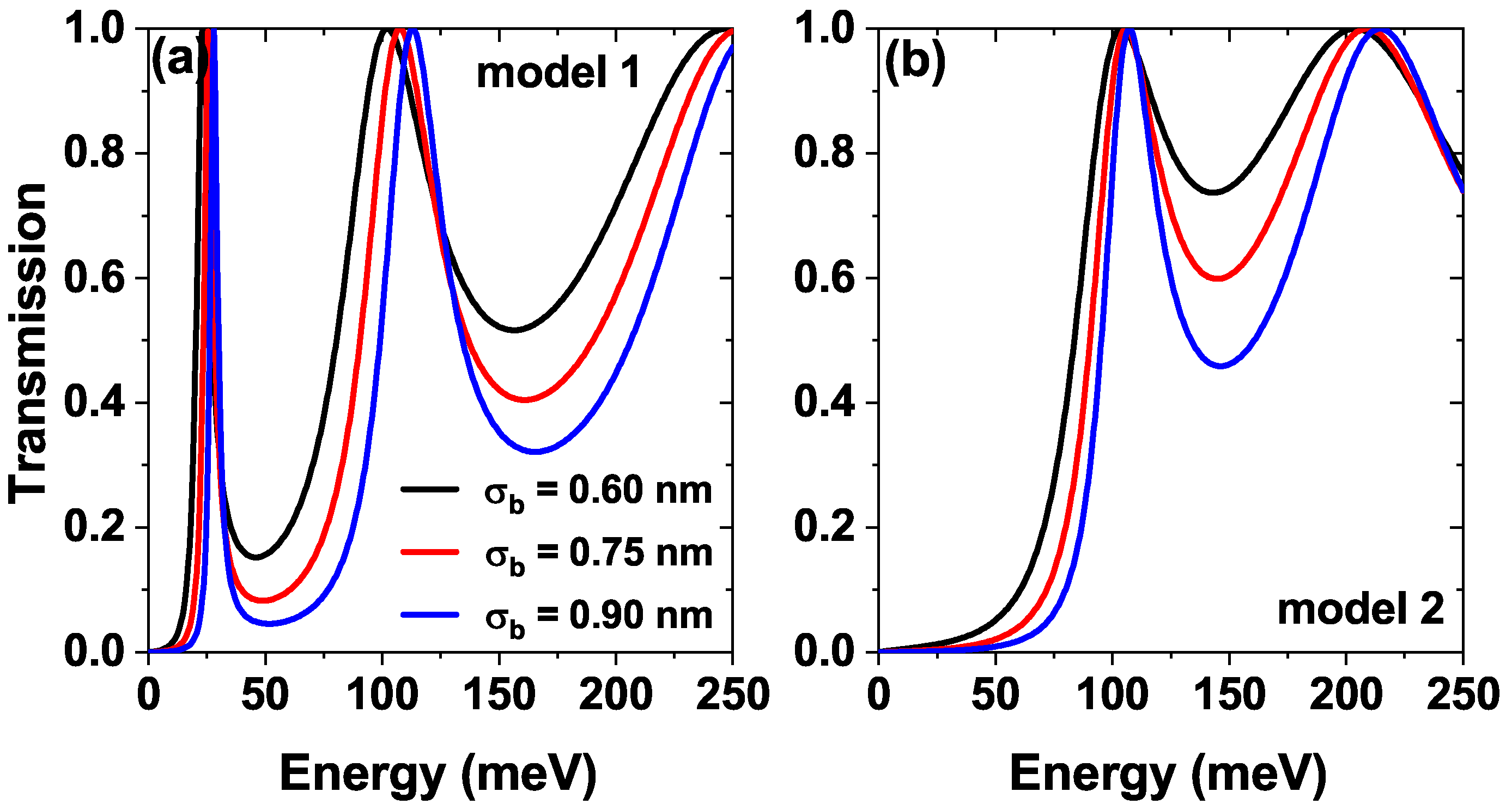
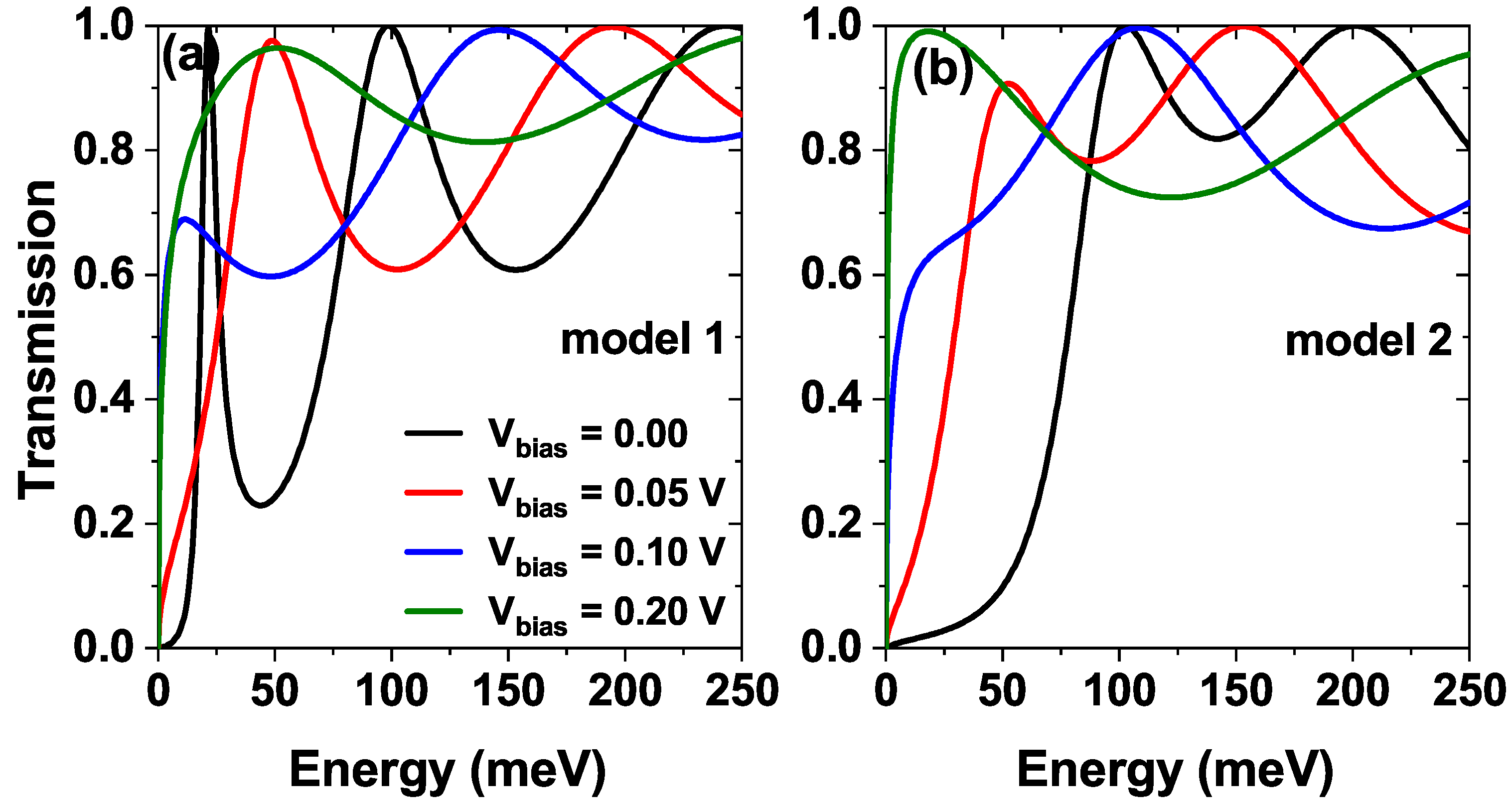
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guo, S.; Qu, H.; Zhou, W.; Yang, S.A.; Ang, Y.S.; Lu, J.; Zeng, H.; Zhang, S. High-performance and low-power transistors based on anisotropic monolayer β-TeO2. Phys. Rev. Appl. 2022, 17, 064010. [Google Scholar] [CrossRef]
- Kim, M.; Kim, K.; Hwang, J.; Moon, E.G.; Ahn, J. Rydberg quantum wires for maximum independent set problems. Phys. B 2022, 18, 755–759. [Google Scholar] [CrossRef]
- Koç, O.K.; Üzer, A.; Apak, R. High quantum yield nitrogen-doped carbon quantum dot-based fluorescent probes for selective sensing of 2, 4, 6-trinitrotoluene. ACS Appl. Nano Mater. 2022, 5, 5868–5881. [Google Scholar] [CrossRef]
- Lanka, A.; Brun, T. Improving a quantum-dot-based single-photon source with continuous measurements. Phys. Rev. A At. Mol. Opt. Phys. 2023, 108, 053711. [Google Scholar] [CrossRef]
- Hu, L.; Mandelis, A. Advanced characterization methods of carrier transport in quantum dot photovoltaic solar cells. J. Appl. Phys. 2021, 129, 091101. [Google Scholar] [CrossRef]
- Kambhampati, P. Nanoparticles, nanocrystals, and quantum dots: What are the implications of size in colloidal nanoscale materials? J. Phys. Chem. Lett. 2021, 12, 4769–4779. [Google Scholar] [CrossRef]
- Gil-Corrales, J.A.; Dagua-Conda, C.A.; Mora-Ramos, M.E.; Morales, A.L.; Duque, C.A. Shape and size effects on electronic thermodynamics in nanoscopic quantum dots. Phys. E 2025, 170, 116228. [Google Scholar] [CrossRef]
- Turkoglu, A.; Dakhlaoui, H.; Mora-Ramos, M.E.; Ungan, F. Optical properties of a quantum well with Razavy confinement potential: Role of applied external fields. Phys. E 2021, 134, 114919. [Google Scholar] [CrossRef]
- Dagua-Conda, C.A.; Gil-Corrales, J.A.; Hahn, R.V.H.; Mora-Ramos, M.E.; Morales, A.L.; Duque, C.A. Electro-Optical Modulation of the Nonlinear Optical Response in a GaAs/AlGaAs Symmetric Multiple Quantum Well System. Physics 2025, 7, 22. [Google Scholar] [CrossRef]
- Zangwill, G.; Granot, E.E. Dynamic resonant tunneling via a quasibound superstate. Phys. Rev. A At. Mol. Opt. Phys. 2022, 106, 032201. [Google Scholar] [CrossRef]
- Chang, L.; Esaki, L.; Tsu, R. Resonant tunneling in semiconductor double barriers. Appl. Phys. Lett. 1974, 24, 593–595. [Google Scholar] [CrossRef]
- Esaki, L.; Chang, L.L. New transport phenomenon in a semiconductor “superlattice”. Phys. Rev. Lett. 1974, 33, 495. [Google Scholar] [CrossRef]
- Cardozo de Oliveira, E.R.; Pfenning, A.; Guarin Castro, E.D.; Teodoro, M.D.; dos Santos, E.C.; Lopez-Richard, V.; Marques, G.E.; Worschech, L.; Hartmann, F. Electroluminescence on-off ratio control of n-i-n GaAs/AlGaAs-based resonant tunneling structures. Phys. Rev. B Condens. Matter. 2018, 98, 075302. [Google Scholar] [CrossRef]
- Samanta, S. GaAs-based resonant tunneling diode: Device aspects from design, manufacturing, characterization and applications. IEEE Trans. Electron Devices 2023, 44, 103101. [Google Scholar] [CrossRef]
- Ipsita, S.; Mahapatra, P.K.; Panchadhyayee, P. Optimum device parameters to attain the highest peak to valley current ratio (PVCR) in resonant tunneling diodes (RTD). Phys. B 2021, 611, 412788. [Google Scholar] [CrossRef]
- Wolak, E.; Özbay, E.; Park, B.G.; Diamond, S.K.; Bloom, D.M.; Harris, J.S., Jr. The design of GaAs/AlAs resonant tunneling diodes with peak current densities over 2×105 A cm-2. J. Appl. Phys. 1991, 69, 3345–3350. [Google Scholar] [CrossRef]
- Krüger, S.; Pfenning, A.; Jabeen, F.; Hartmann, F.; Höfling, S. Opto-electronic transport properties of resonant tunneling diodes with type-I and II postwells. Appl. Phys. Lett. 2023, 123, 133501. [Google Scholar] [CrossRef]
- Muttlak, S.G.; Abdulwahid, O.S.; Sexton, J.; Kelly, M.J.; Missous, M. InGaAs/AlAs resonant tunneling diodes for THz applications: An experimental investigation. IEEE J. Electron Devices Soc. 2018, 6, 254–262. [Google Scholar] [CrossRef]
- Romeira, B.; Pessoa, L.M.; Salgado, H.M.; Ironside, C.N.; Figueiredo, J.M. Photo-detectors integrated with resonant tunneling diodes. Sensors 2013, 13, 9464–9482. [Google Scholar] [CrossRef]
- Rothmayr, F.; Guarin Castro, E.D.; Hartmann, F.; Knebl, G.; Schade, A.; Höfling, S.; Koeth, J.; Pfenning, A.; Worschech, L.; Lopez-Richard, V. Resonant tunneling diodes: Mid-infrared sensing at room temperature. Nanomaterials 2022, 12, 1024. [Google Scholar] [CrossRef]
- Cimbri, D.; Yavas-Aydin, B.; Hartmann, F.; Jabeen, F.; Worschech, L.; Höfling, S.; Wasige, E. Accurate Quantum Transport Modeling of High-Speed In0.53Ga0.47As/AlAs Double-Barrier Resonant Tunneling Diodes. IEEE Trans. Electron Devices 2022, 69, 4638–4645. [Google Scholar] [CrossRef]
- Pöschl, G.; Teller, E. Bemerkungen zur Quantenmechanik des anharmonischen Oszillators. Z. Phys. 1933, 83, 143–151. [Google Scholar] [CrossRef]
- Duque, C.A.; Mora-Ramos, M.E.; Barseghyan, M.G. Electronic states in a Pöschl–Teller-like quantum well: Combined effects of electric field, hydrostatic pressure, and temperature. Superlattices Microstruct. 2011, 50, 480–490. [Google Scholar] [CrossRef]
- Oliveira, L.R.; da Luz, M.G. Basic Cells Special Features and Their Influence on Global Transport Properties of Long Periodic Structures. Entropy 2024, 26, 942. [Google Scholar] [CrossRef]
- Batı, M. Resonant tunneling properties of laser dressed hyperbolic Pöschl-Teller double barrier potential. Phys. E 2025, 165, 116126. [Google Scholar] [CrossRef]
- Rodríguez, A.; Cerveró, J.M. One-dimensional disordered wires with Pöschl-Teller potentials. Phys. Rev. B Condens. Matter. 2006, 74, 104201. [Google Scholar] [CrossRef]
- Brown, E.; Hernández de la Peña, L. A Simplified Pöschl–Teller Potential: An Instructive Exercise for Introductory Quantum Mechanics. J. Chem. Educ. 2018, 95, 1989–1995. [Google Scholar] [CrossRef]
- Henneberger, W.C. Perturbation method for atoms in intense light beams. Phys. Rev. Lett. 1968, 21, 838. [Google Scholar] [CrossRef]
- Sari, H.; Kasapoglu, E.; Sakiroglu, S.; Sökmen, I.; Duque, C.A. Impurity-related optical response in a 2D and 3D quantum dot with Gaussian confinement under intense laser field. Philos. Mag. 2019, 100, 619–641. [Google Scholar] [CrossRef]
- Gil-Corrales, J.A.; Morales, A.L.; Yücel, M.B.; Kasapoglu, E.; Duque, C.A. Electronic Transport Properties in GaAs/AlGaAs and InSe/InP Finite Superlattices under the Effect of a Non-Resonant Intense Laser Field and Considering Geometric Modifications. Int. J. Mol. Sci. 2022, 23, 5169. [Google Scholar] [CrossRef]
- Chu, S.I.; Telnov, D.A. Beyond the Floquet theorem: Generalized Floquet formalisms and quasienergy methods for atomic and molecular multiphoton processes in intense laser fields. Phys. Rep. 2004, 390, 1–131. [Google Scholar] [CrossRef]
- Gavrila, M. Atomic stabilization in superintense laser fields. J. Phys. B At. Mol. Opt. Phys. 2002, 35, R147. [Google Scholar] [CrossRef]
- Lima, F.M.S.; Amato, M.A.; Nunes, O.A.C.; Fonseca, A.L.A.; Enders, B.G.; Da Silva, E.F. Unexpected transition from single to double quantum well potential induced by intense laser fields in a semiconductor quantum well. J. Appl. Phys. 2009, 105, 123111. [Google Scholar] [CrossRef]
- COMSOL. Multiphysics v. 5.2a Semiconductor Module User’s Guide; COMSOL AB: Stockholm, Sweden, 2016. [Google Scholar]
- COMSOL. Multiphysics, version 6.1; COMSOL AB: Stockholm, Sweden, 2022. [Google Scholar]
- Büttiker, M.; Landauer, R. Traversal time for tunneling. Phys. Rev. Lett. 1982, 49, 1739. [Google Scholar] [CrossRef]
- Kriisa, A.; Samaraweera, R.L.; Heimbeck, M.S.; Everitt, H.O.; Reichl, C.; Wegscheider, W.; Mani, R.G. Cyclotron resonance in the high mobility GaAs/AlGaAs 2D electron system over the microwave, mm-wave, and terahertz- bands. Sci. Rep. 2019, 9, 2409. [Google Scholar] [CrossRef]
- Warburton, R.J.; Michels, J.G.; Nicholas, R.J. Optically detected cyclotron resonance of GaAs quantum wells: Effective-mass measurements and offset effects. Phys. Rev. B 1992, 46, 13394–13399. [Google Scholar] [CrossRef]
- Lassnig, R. k·p theory, effective-mass approach, and spin splitting for two-dimensional electrons in GaAs-GaA1As heterostructures. Phys. Rev. B 1985, 31, 8076–8086. [Google Scholar] [CrossRef]
- Pfeffer, P.; Zawadzki, W. Five-level k-p model for the conduction and valence bands of GaAs and InP. Phys. Rev. B 1996, 53, 12813–12828. [Google Scholar] [CrossRef]
- Adachi, S. Properties of Semiconductor Alloys: Group-IV, III-V and II-VI Semiconductors; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]



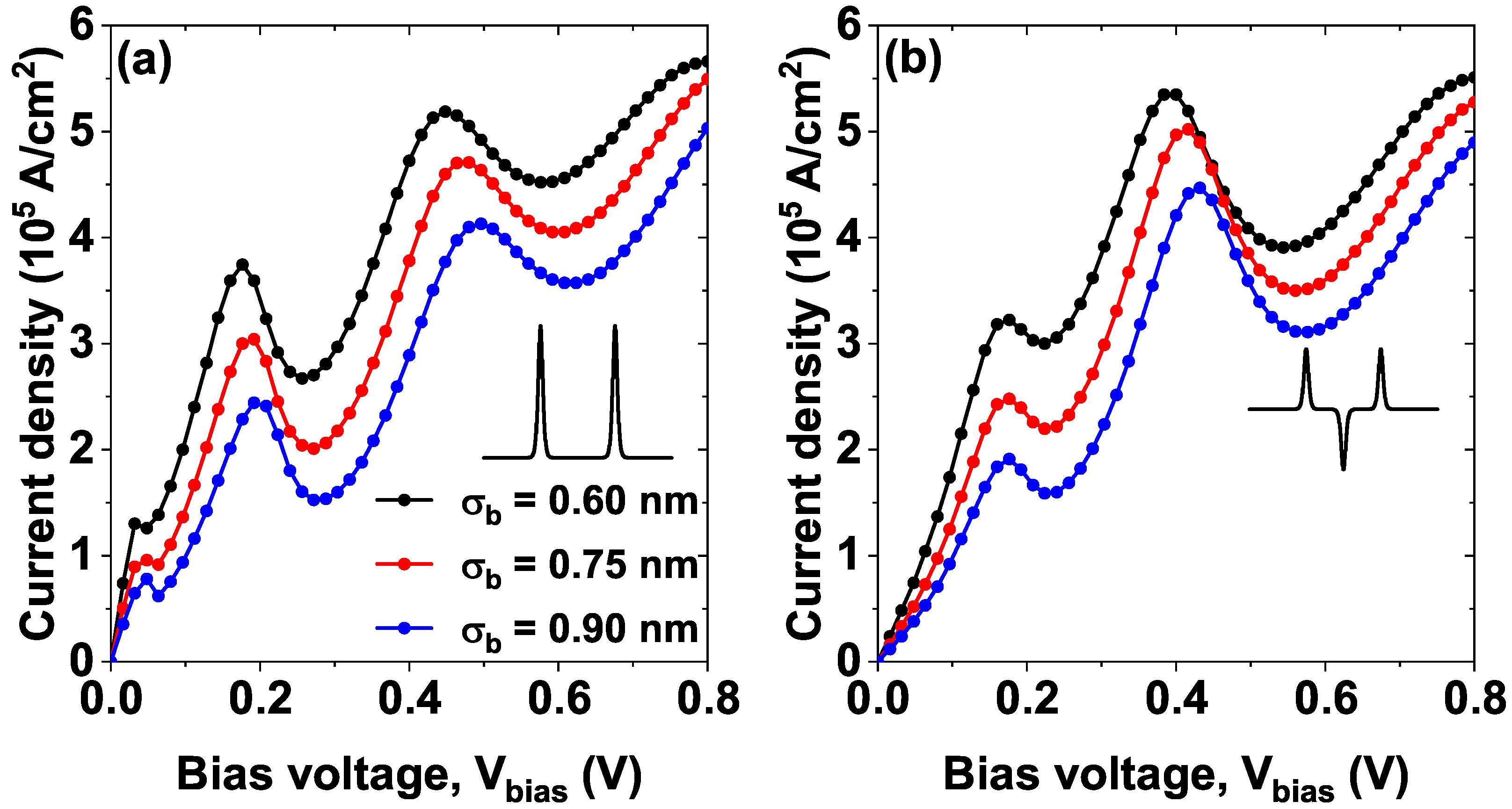
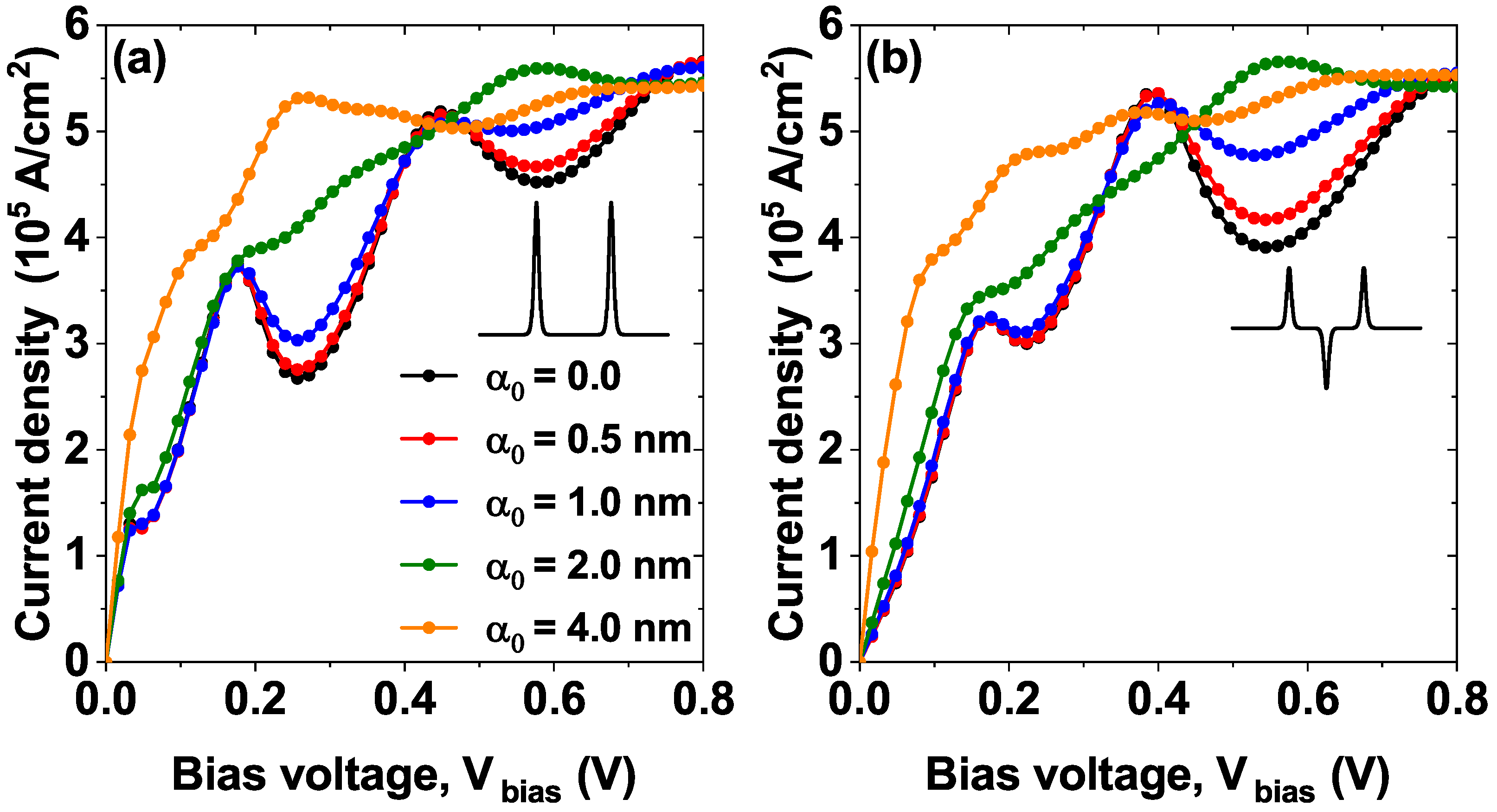
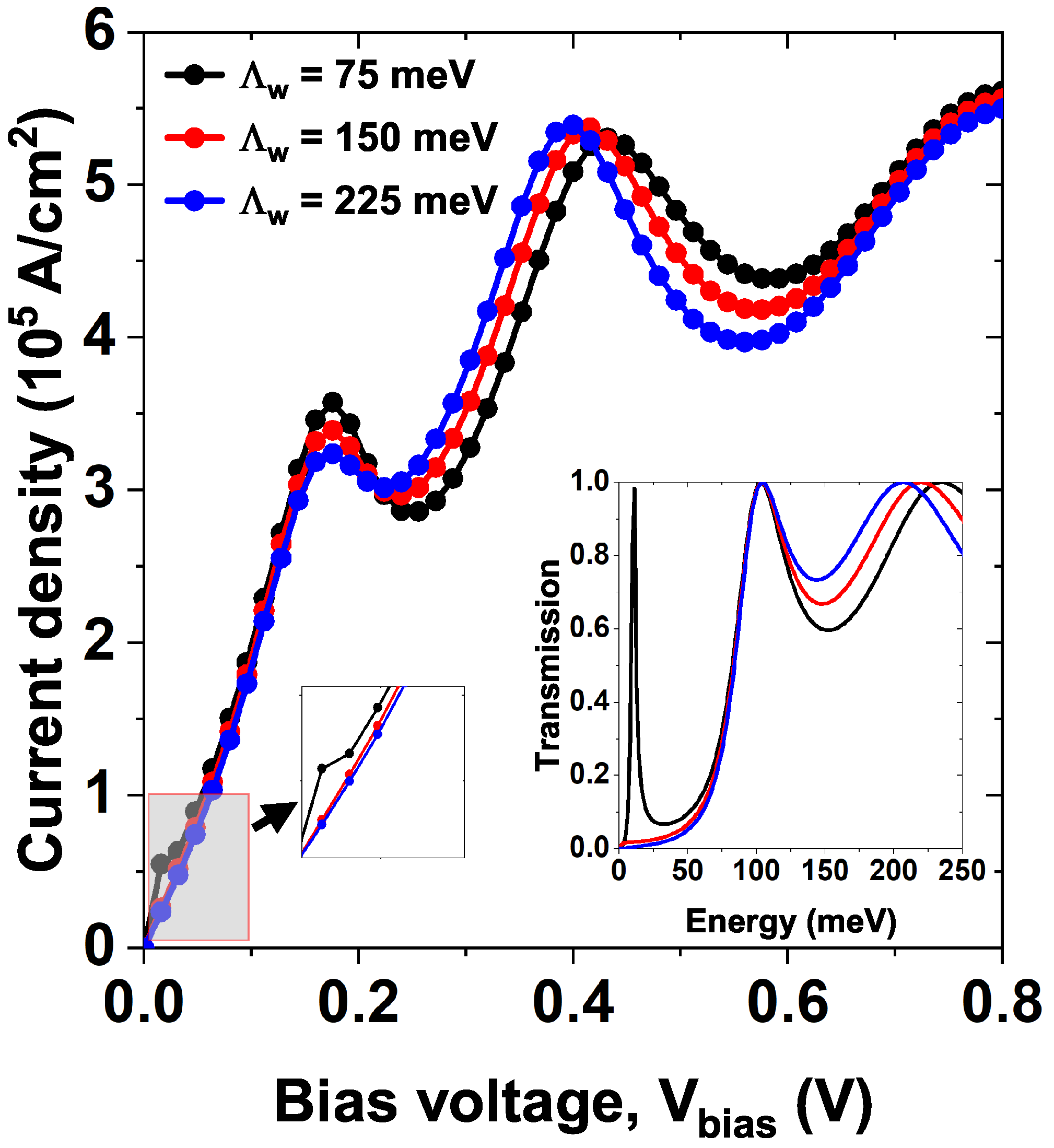
| Figure | Model | Parameter [L, , (nm)] [Λ (meV)] | PVCR | PVCR |
|---|---|---|---|---|
| Figure 7a | 1 | |||
| N/A | N/A | |||
| Figure 7b | 2 | |||
| Figure 8a | 1 | |||
| N/A | N/A | |||
| N/A | N/A | |||
| Figure 8b | 2 | |||
| N/A | N/A | |||
| N/A | N/A | |||
| Figure 9a | 1 | |||
| Figure 9b | 2 | |||
| Figure 10 | 2 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dagua-Conda, C.A.; Gil-Corrales, J.A.; Mora-Ramos, M.E.; Morales, A.L.; Duque, C.A. Electronic Transport Properties in a One-Dimensional Sequence of Laser-Dressed Modified Pöschl-Teller Potentials. Nanomaterials 2025, 15, 1009. https://doi.org/10.3390/nano15131009
Dagua-Conda CA, Gil-Corrales JA, Mora-Ramos ME, Morales AL, Duque CA. Electronic Transport Properties in a One-Dimensional Sequence of Laser-Dressed Modified Pöschl-Teller Potentials. Nanomaterials. 2025; 15(13):1009. https://doi.org/10.3390/nano15131009
Chicago/Turabian StyleDagua-Conda, Carlos A., John A. Gil-Corrales, Miguel E. Mora-Ramos, Alvaro L. Morales, and Carlos A. Duque. 2025. "Electronic Transport Properties in a One-Dimensional Sequence of Laser-Dressed Modified Pöschl-Teller Potentials" Nanomaterials 15, no. 13: 1009. https://doi.org/10.3390/nano15131009
APA StyleDagua-Conda, C. A., Gil-Corrales, J. A., Mora-Ramos, M. E., Morales, A. L., & Duque, C. A. (2025). Electronic Transport Properties in a One-Dimensional Sequence of Laser-Dressed Modified Pöschl-Teller Potentials. Nanomaterials, 15(13), 1009. https://doi.org/10.3390/nano15131009






