Causality Implications for Absorption by EM Metasurfaces
Abstract
1. Introductory Comment
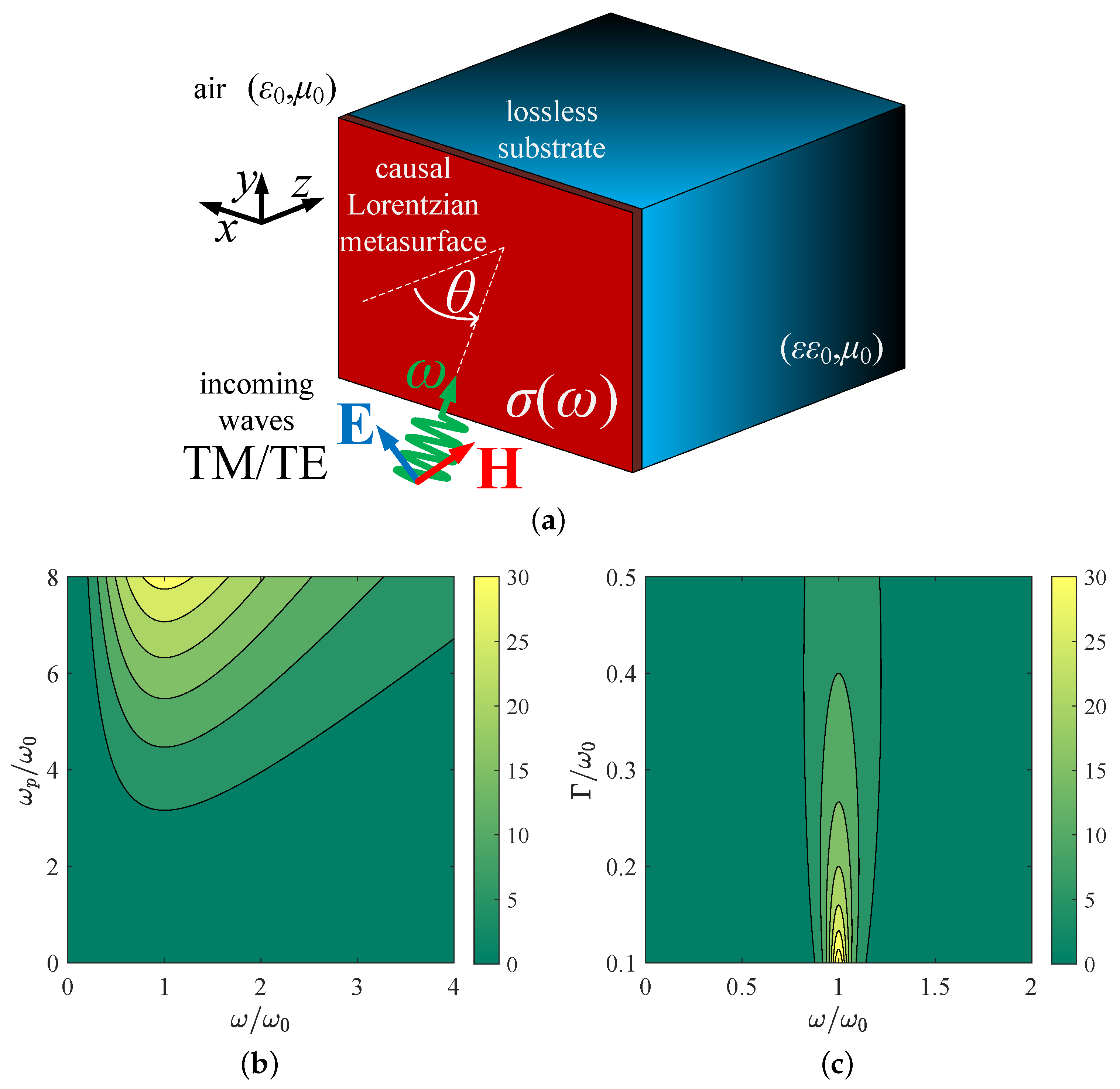
2. Mathematical Formulation
2.1. Causal Metasurface
2.2. Developed Waves
2.3. Absorption Global Sums
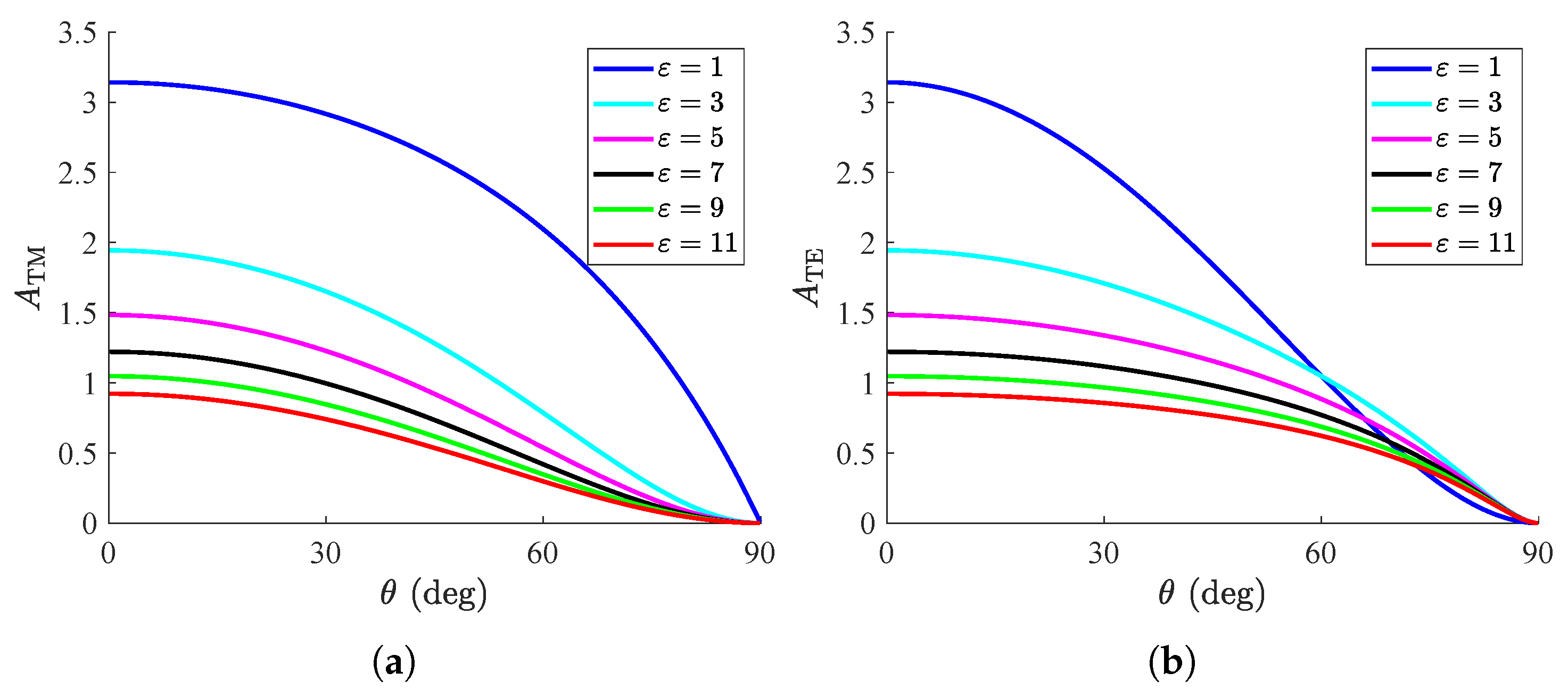
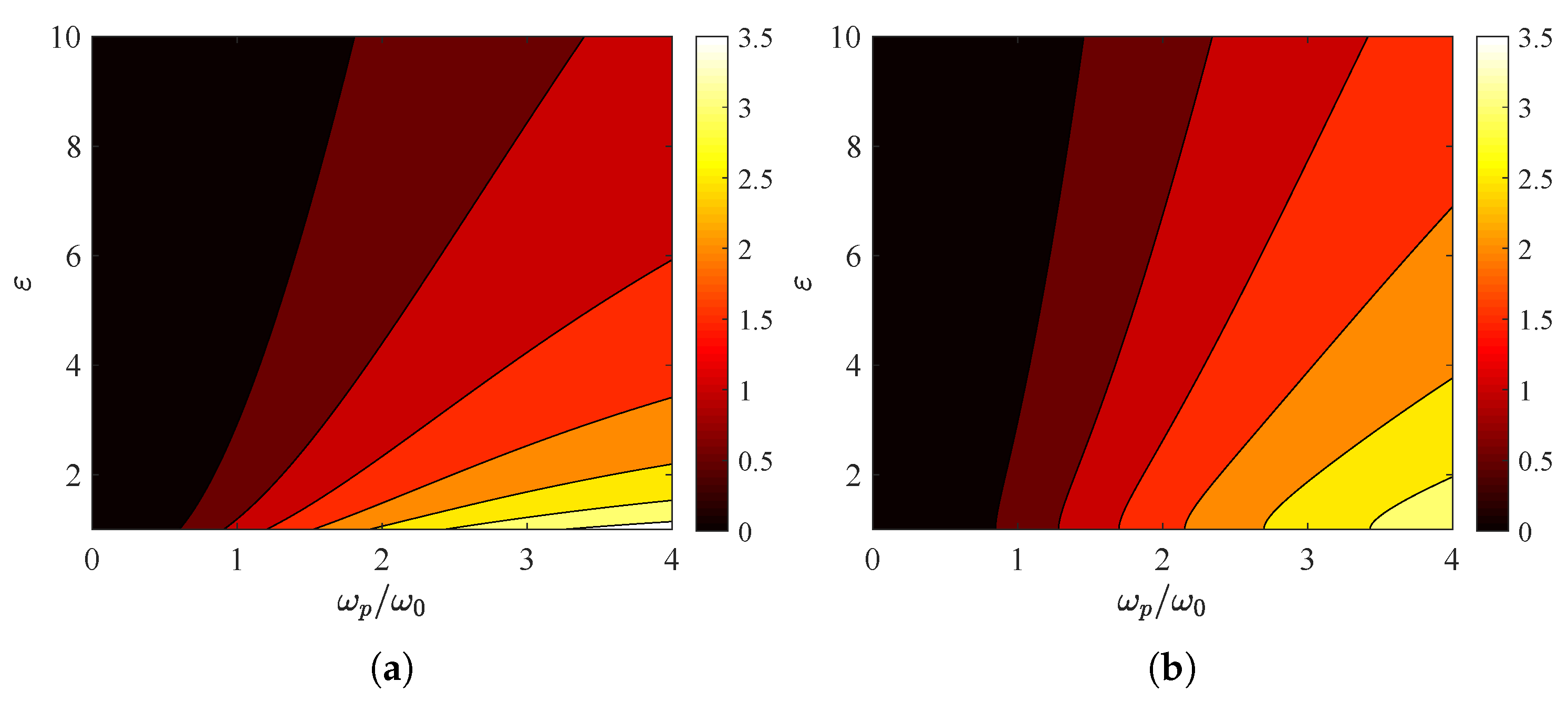
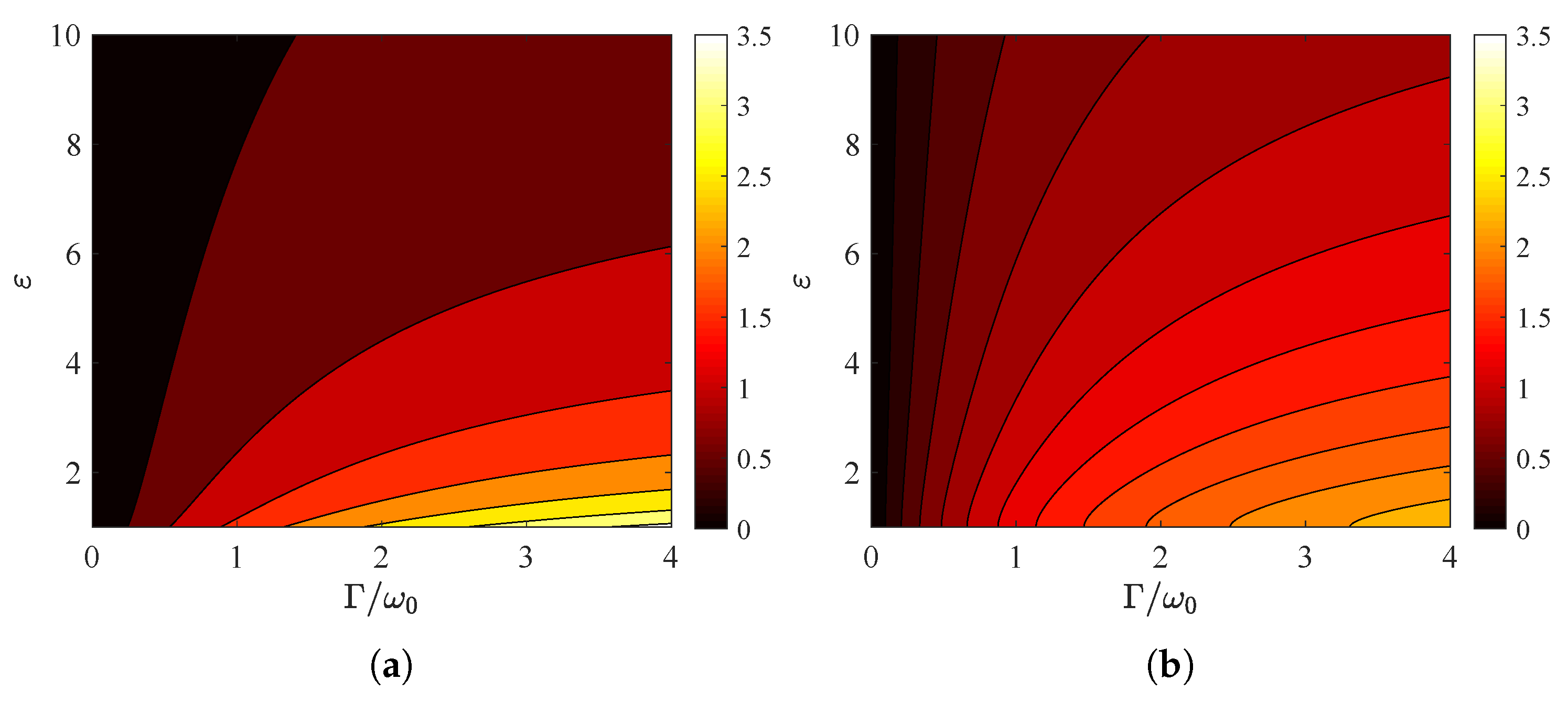
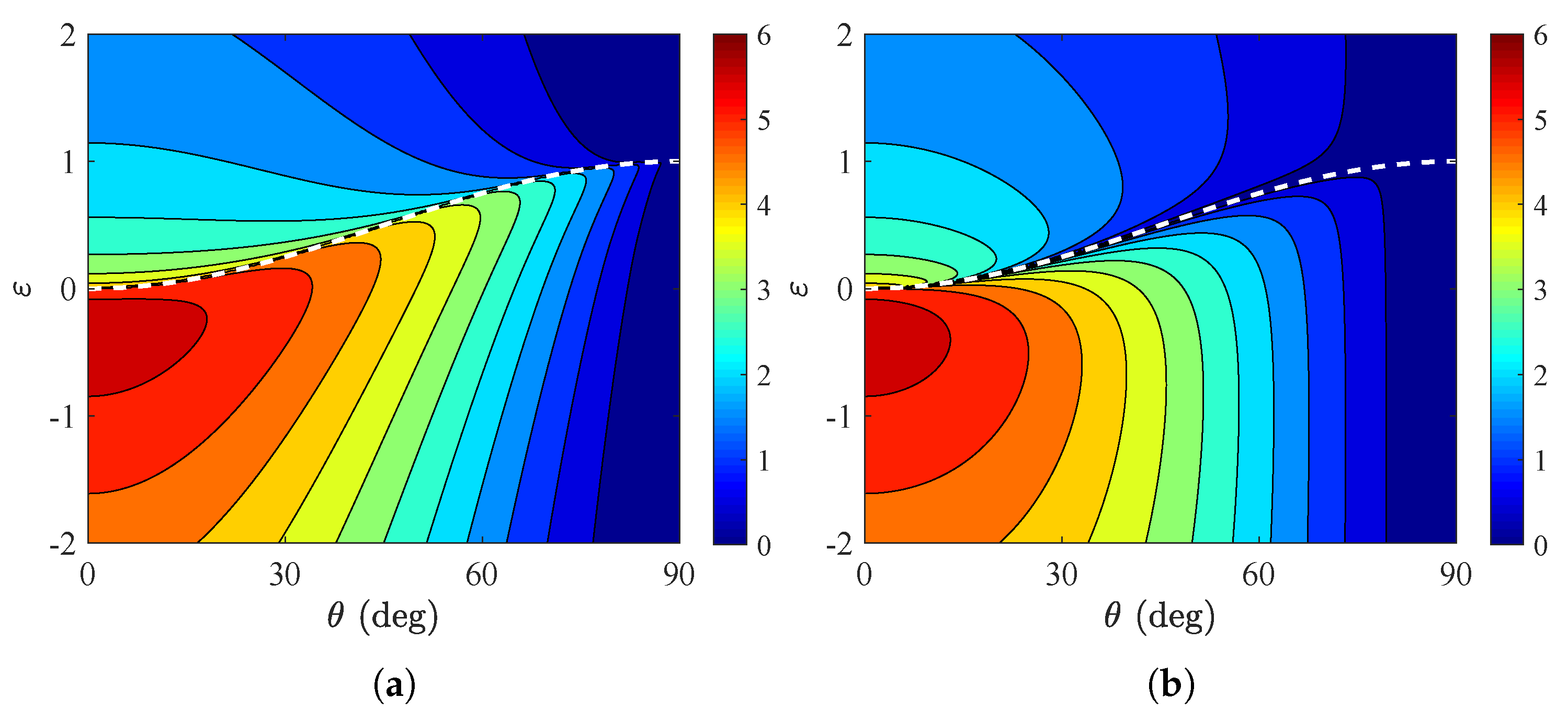
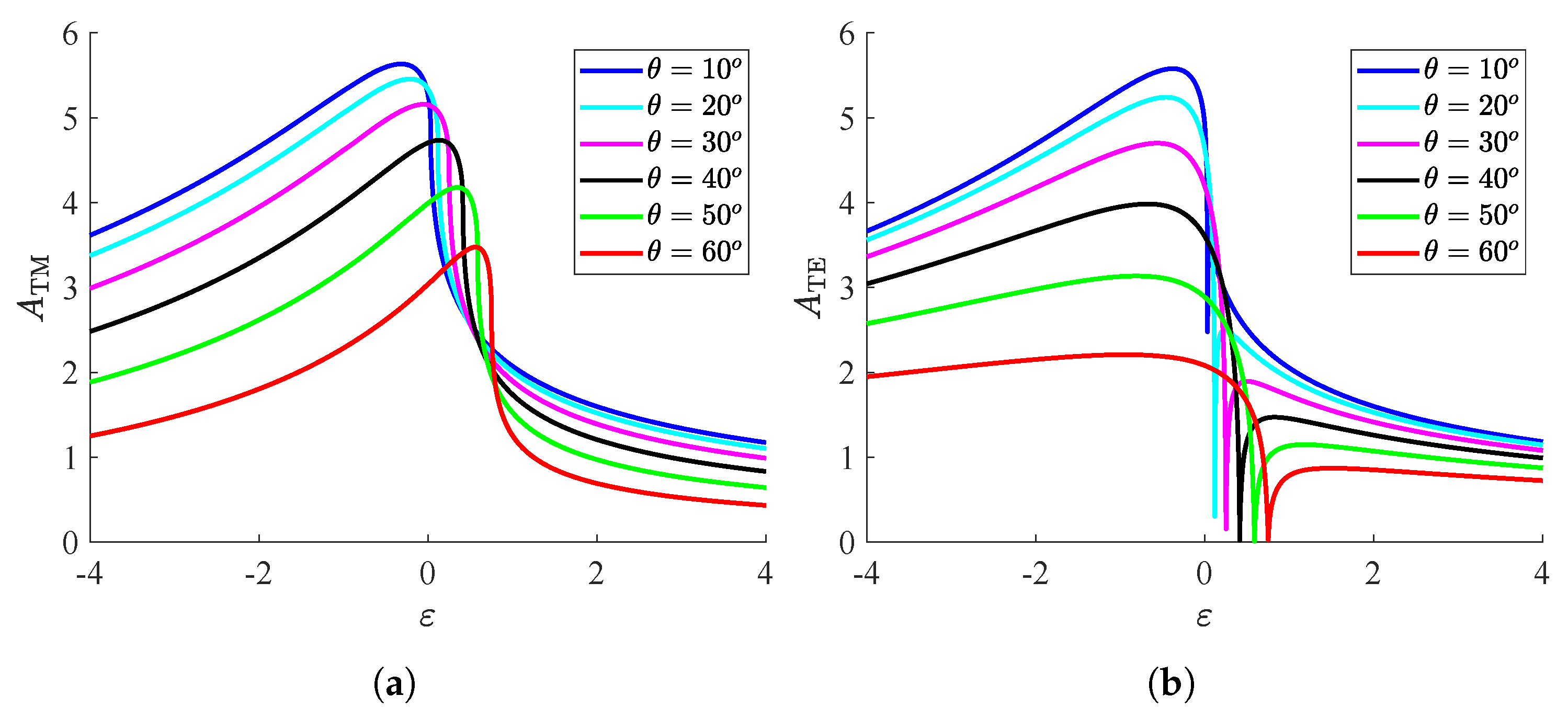
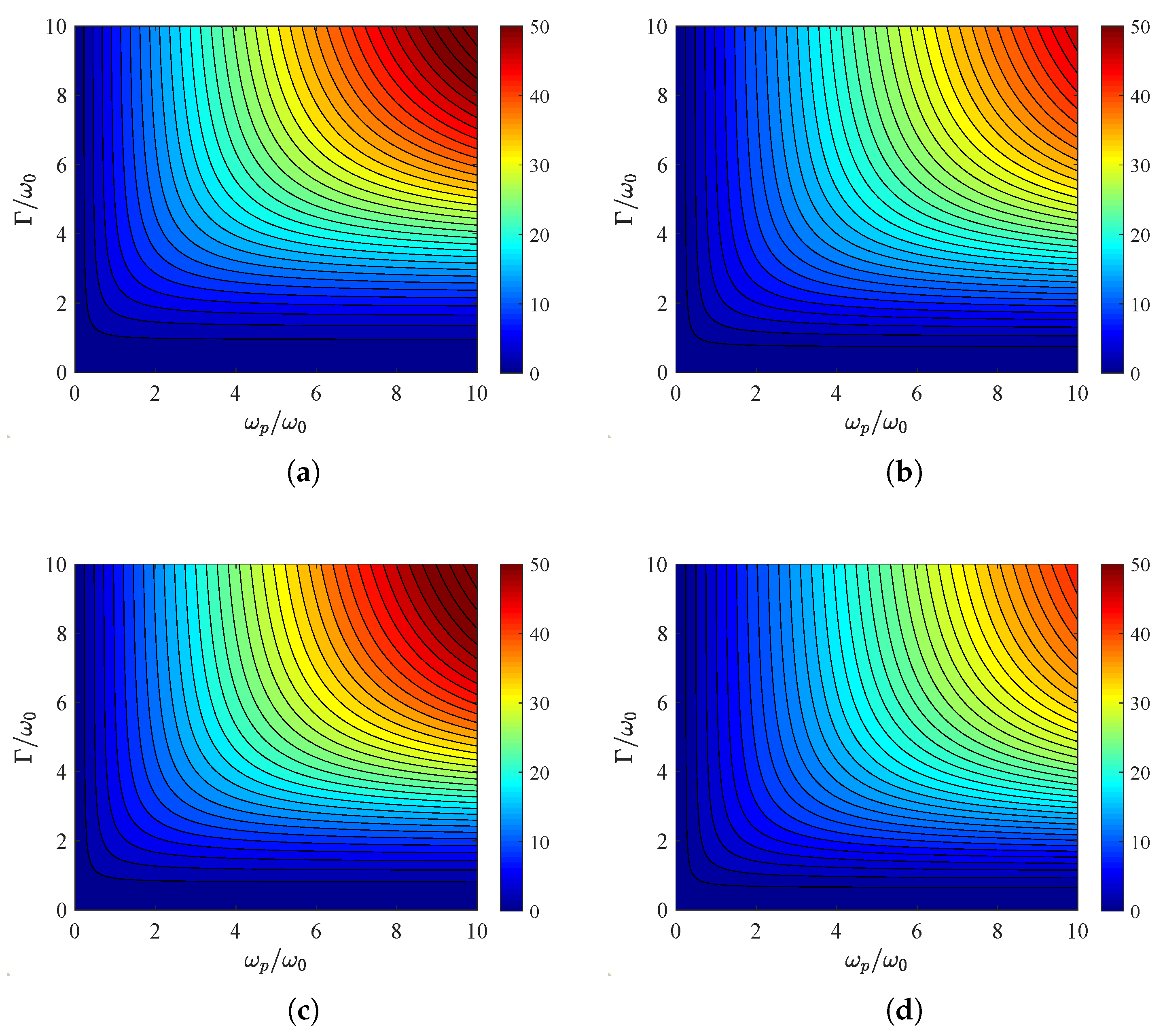
3. Numerical Results
3.1. Dielectric Substrates
3.2. Plasmonic Substrates
4. Concluding Remark
Funding
Data Availability Statement
Conflicts of Interest
References
- Martin, P.A. Sum rules in charged fluids. Rev. Mod. Phys. 1988, 60, 1075. [Google Scholar] [CrossRef]
- Bertlmann, R.A.; Launer, G.; Rafael, E.D. Gaussian sum rules in quantum chromodynamics and local duality. Nucl. Phys. 1985, 250, 61–108. [Google Scholar] [CrossRef]
- Rodini, S.; Metz, A.; Pasquini, B. Mass sum rules of the electron in quantum electrodynamics. J. High Energy Phys. 2020, 2020, 67. [Google Scholar] [CrossRef]
- Miller, D.; Weiner, J.; Chemla, D. Electric-field dependence of linear optical properties in quantum well structures: Waveguide electroabsorption and sum rules. IEEE J. Quantum Electron. 1986, 22, 1816–1830. [Google Scholar] [CrossRef]
- Kuzyk, M.G. Physical Limits on Electronic Nonlinear Molecular Susceptibilities. Phys. Rev. Lett. 2000, 85, 001218. [Google Scholar] [CrossRef]
- Xomalis, A.; Jung, Y.; Demirtzioglou, I.; Lacava, C.; Plum, E.; Richardson, D.J.; Petropoulos, P.; Zheludev, N.I. Nonlinear control of coherent absorption and its optical signal processing applications. APL Photonics 2024, 4, 106109. [Google Scholar] [CrossRef]
- Cardenas-Castillo, L.F.; Zhang, S.; Freire, F.L., Jr.; Kochan, D.; Chen, W. Detecting the spread of valence-band Wannier functions by optical sum rules. Phys. Rev. B 2024, 110, 075203. [Google Scholar] [CrossRef]
- Carlsson, A.E.; Ehrenreich, H.; Hass, K.C. Spectral limits for disordered semiconductors and their interfaces. Phys. Rev. B 1983, 28, 4468. [Google Scholar] [CrossRef]
- Sestu, N.; Cadelano, M.; Sarritzu, V.; Chen, F.; Marongiu, D.; Piras, R.; Mainas, M.; Quochi, F.; Saba, M.; Mura, A.; et al. Absorption F-Sum Rule for the Exciton Binding Energy in Methylammonium Lead Halide Perovskites. J. Phys. Chem. Lett. 2015, 6, 4566–4572. [Google Scholar] [CrossRef]
- Chu, L.J. Physical Limitations of Omni-Directional Antennas. J. Appl. Phys. 1948, 19, 1163–1175. [Google Scholar] [CrossRef]
- Fano, R.M. Theoretical limitations on the broadband matching of arbitrary impedances. J. Frankl. Inst. 1950, 249, 57–83. [Google Scholar] [CrossRef]
- Ziolkowski, R.W.; Kipple, A.D. Causality and double-negative metamaterials. Phys. Rev. E 2003, 68, 026615. [Google Scholar] [CrossRef] [PubMed]
- Valagiannopoulos, C.A.; Vehmas, J.; Simovski, C.R.; Tretyakov, S.A.; Maslovski, S.I. Electromagnetic energy sink. Phys. Rev. B 2015, 95, 245402. [Google Scholar] [CrossRef]
- Srivastava, A. Causality and passivity: From electromagnetism and network theory to metamaterials. Mech. Mater. 2021, 154, 103710. [Google Scholar] [CrossRef]
- Monticone, F.; Alu, A. Do Cloaked Objects Really Scatter Less? Phys. Rev. X 2013, 3, 041005. [Google Scholar] [CrossRef]
- Koutserimpas, T.T.; Monticone, F. Time-varying media, dispersion, and the principle of causality. Opt. Mater. Express 2024, 14, 1222–1236. [Google Scholar] [CrossRef]
- Baker-Jarvis, J.; Geyer, R.G.; Domich, P.D. A nonlinear least-squares solution with causality constraints applied to transmission line permittivity and permeability determination. IEEE Trans. Instrum. Meas. 1992, 41, 646–652. [Google Scholar] [CrossRef]
- Kuzuoglu, M.; Mittra, R. Frequency dependence of the constitutive parameters of causal perfectly matched anisotropic absorbers. IEEE Microw. Guid. Wave Lett. 1996, 6, 447–449. [Google Scholar] [CrossRef]
- Varadan, V.V.; Ro, R. Unique Retrieval of Complex Permittivity and Permeability of Dispersive Materials from Reflection and Transmitted Fields by Enforcing Causality. IEEE Trans. Microw. Theory Tech. 2007, 55, 2224–2230. [Google Scholar] [CrossRef]
- Yazdi, M.; Albooyeh, M.; Alaee, R.; Asadchy, V.; Komjani, N.; Rockstuhl, C.; Simovski, C.R.; Tretyakov, S. A Bianisotropic Metasurface with Resonant Asymmetric Absorption. IEEE Trans. Antennas Propag. 2015, 63, 3004–3015. [Google Scholar] [CrossRef]
- Alijabbari, M.; Karimzadeh, R.; Pakniyat, S.; Gomez-Diaz, J.S. Dual-band and spectrally selective infrared absorbers based on hybrid gold-graphene metasurfaces. Opt. Express 2024, 32, 16578–16590. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, S.K.; Das, S.; Bhattacharyya, S. Graphene-Based Metasurface for Tunable Absorption and Transmission Characteristics in the Near Mid-Infrared Region. IEEE Trans. Antennas Propag. 2022, 70, 4600–4612. [Google Scholar] [CrossRef]
- Su, J.; Li, W.; Qu, M.; Yu, H.; Li, Z.; Qi, K.; Yin, H. Ultrawideband RCS Reduction Metasurface Based on Hybrid Mechanism of Absorption and Phase Cancellation. IEEE Trans. Antennas Propag. 2022, 70, 9415–9424. [Google Scholar] [CrossRef]
- Papadimopoulos, A.N.; Kantartzis, N.V.; Tsitsas, N.L.; Valagiannopoulos, C.A. Wide-angle absorption of visible light from simple bilayers. Appl. Opt. 2017, 56, 9779–9786. [Google Scholar] [CrossRef]
- Valagiannopoulos, C.A. On smoothening the singular field developed in the vicinity of metallic edges. Int. J. Appl. Electromagn. Mech. 2009, 31, 67–77. [Google Scholar] [CrossRef]
- Alaee, R.; Albooyeh, M.; Rockstuhl, C. Theory of metasurface based perfect absorbers. J. Phys. Appl. Phys. 2017, 50, 503002. [Google Scholar] [CrossRef]
- Arup, E.M.; Liu, L.; Mekonnen, H.; Bosomtwi, D.; Babicheva, V.E. Metasurfaces with Multipolar Resonances and Enhanced Light–Matter Interaction. Nanomaterials 2025, 15, 477. [Google Scholar] [CrossRef]
- Monti, A.; Alù, A.; Toscano, A.; Bilotti, F. The Design of Optical Circuit-Analog Absorbers through Electrically Small Nanoparticles. Photonics 2019, 6, 26. [Google Scholar] [CrossRef]
- Lin, D.; Fan, P.; Hasman, E.; Brongersma, M.L. Dielectric gradient metasurface optical elements. Science 2014, 345, 298–302. [Google Scholar] [CrossRef]
- Devlin, R.C.; Khorasaninejad, M.; Chen, W.T.; Oh, J.; Capasso, F. Broadband high-efficiency dielectric metasurfaces for the visible spectrum. Proc. Natl. Acad. Sci. USA 2016, 113, 10473–10478. [Google Scholar] [CrossRef]
- Valagiannopoulos, C.A.; Tukiainen, A.; Aho, T.; Niemi, T.; Guina, M.; Tretyakov, S.A.; Simovski, C.R. Perfect magnetic mirror and simple perfect absorber in the visible spectrum. Phys. Rev. B 2015, 91, 115305. [Google Scholar] [CrossRef]
- Huang, Y.-W.; Lee, H.W.H.; Sokhoyan, R.; Pala, R.A.; Thyagarajan, K.; Han, S.; Tsai, D.P.; Atwater, H.A. Gate-Tunable Conducting Oxide Metasurfaces. Nano Lett. 2016, 16, 5319–5325. [Google Scholar] [CrossRef] [PubMed]
- Tittl, A.; Leitis, A.; Liu, M.; Yesilkoy, F.; Choi, D.-Y.; Neshev, D.N.; Kivshar, Y.S.; Altug, H. Imaging-based molecular barcoding with pixelated dielectric metasurfaces. Science 2018, 360, 1105–1109. [Google Scholar] [CrossRef] [PubMed]
- Umetaliev, T.; Valagiannopoulos, C. AI-based photonic inverse design: Hugely polarization-selective multilayered scatterers. J. Opt. Soc. Am. B 2025, 42, 621–630. [Google Scholar] [CrossRef]
- Terekhov, P.D.; Baryshnikova, K.V.; Greenberg, Y.; Fu, Y.H.; Evlyukhin, A.B.; Shalin, A.S.; Karabchevsky, A. Enhanced absorption in all-dielectric metasurfaces due to magnetic dipole excitation. Sci. Rep. 2019, 9, 3438. [Google Scholar] [CrossRef]
- Yang, C.-Y.; Yang, J.-H.; Yang, Z.-Y.; Zhou, Z.-X.; Sun, M.-G.; Babicheva, V.E.; Chen, K.-P. Nonradiating Silicon Nanoantenna Metasurfaces as Narrowband Absorbers. ACS Photonics 2018, 5, 2596–2601. [Google Scholar] [CrossRef]
- Tagay, Z.; Valagiannopoulos, C. Highly selective transmission and absorption from metasurfaces of periodically corrugated cylindrical particles. Phys. Rev. B 2018, 98, 115306. [Google Scholar] [CrossRef]
- Valagiannopoulos, C.A.; Tretyakov, S. Symmetric absorbers realized as gratings of PEC cylinders covered by ordinary dielectrics. IEEE Trans. Antennas Propag. 2014, 62, 5089–5098. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valagiannopoulos, C. Causality Implications for Absorption by EM Metasurfaces. Nanomaterials 2025, 15, 793. https://doi.org/10.3390/nano15110793
Valagiannopoulos C. Causality Implications for Absorption by EM Metasurfaces. Nanomaterials. 2025; 15(11):793. https://doi.org/10.3390/nano15110793
Chicago/Turabian StyleValagiannopoulos, Constantinos. 2025. "Causality Implications for Absorption by EM Metasurfaces" Nanomaterials 15, no. 11: 793. https://doi.org/10.3390/nano15110793
APA StyleValagiannopoulos, C. (2025). Causality Implications for Absorption by EM Metasurfaces. Nanomaterials, 15(11), 793. https://doi.org/10.3390/nano15110793





