Kondo-like Behavior in Lightly Gd-Doped Manganite CaMnO3
Abstract
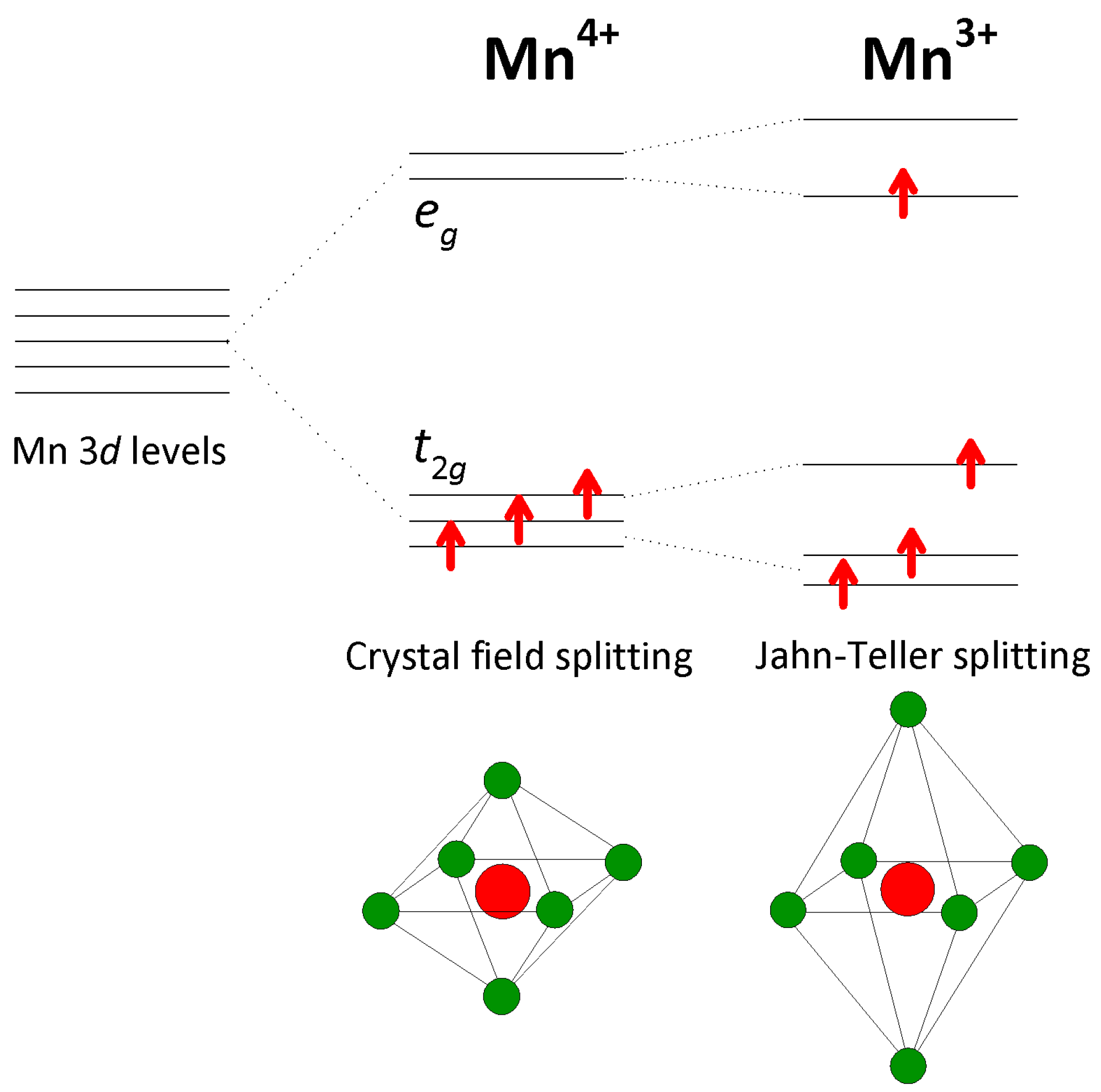
1. Introduction
2. Materials and Methods
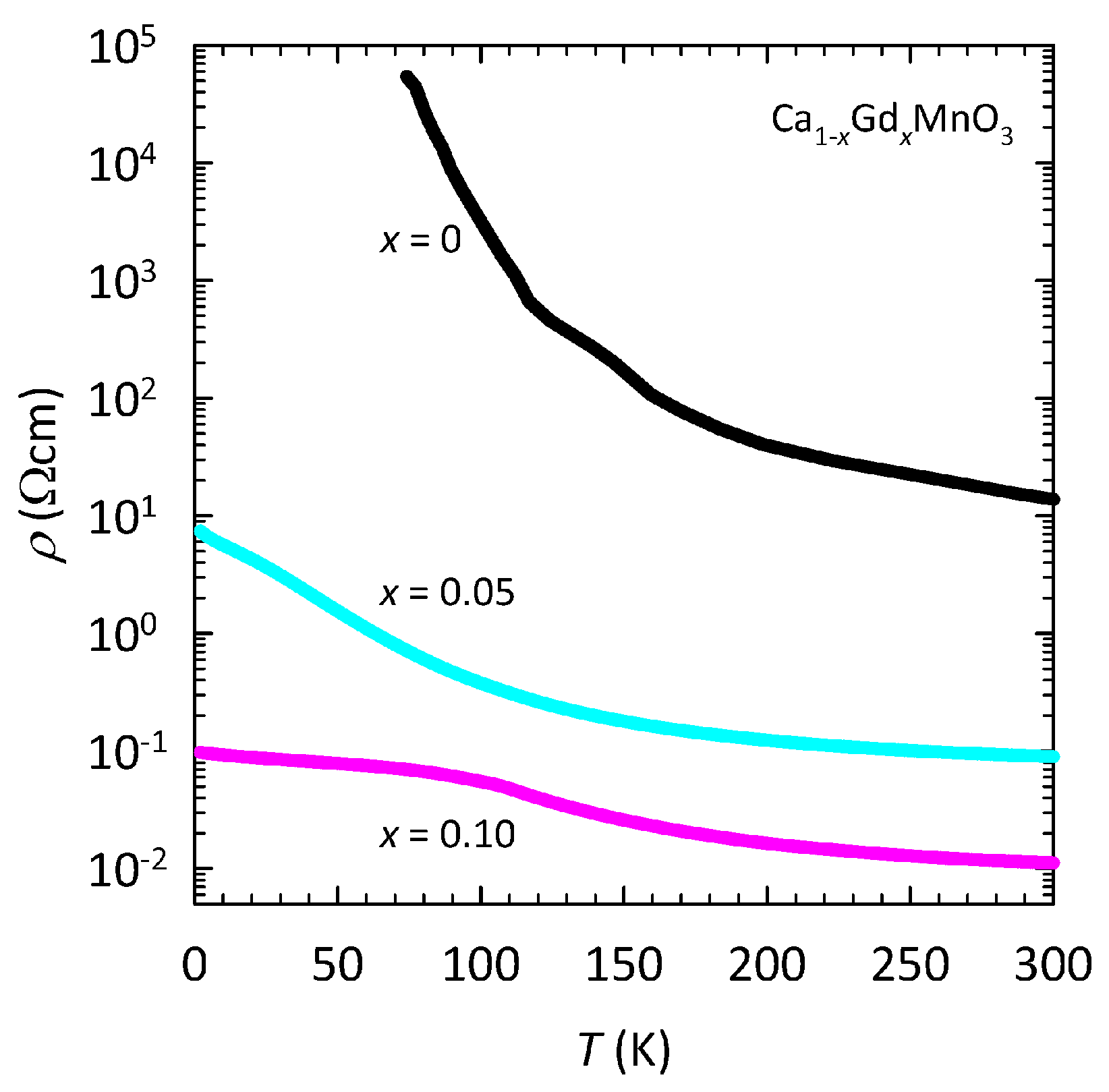
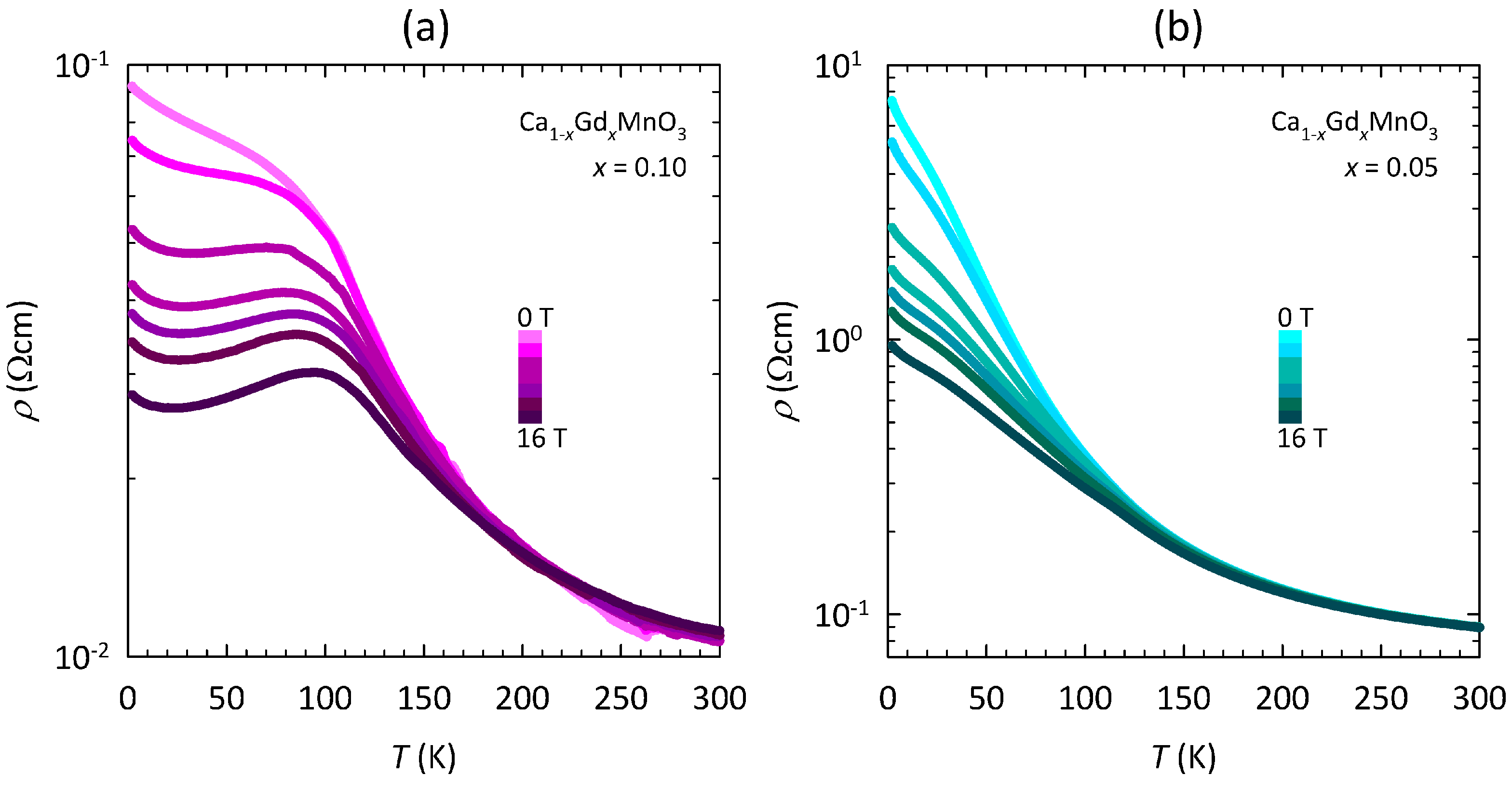
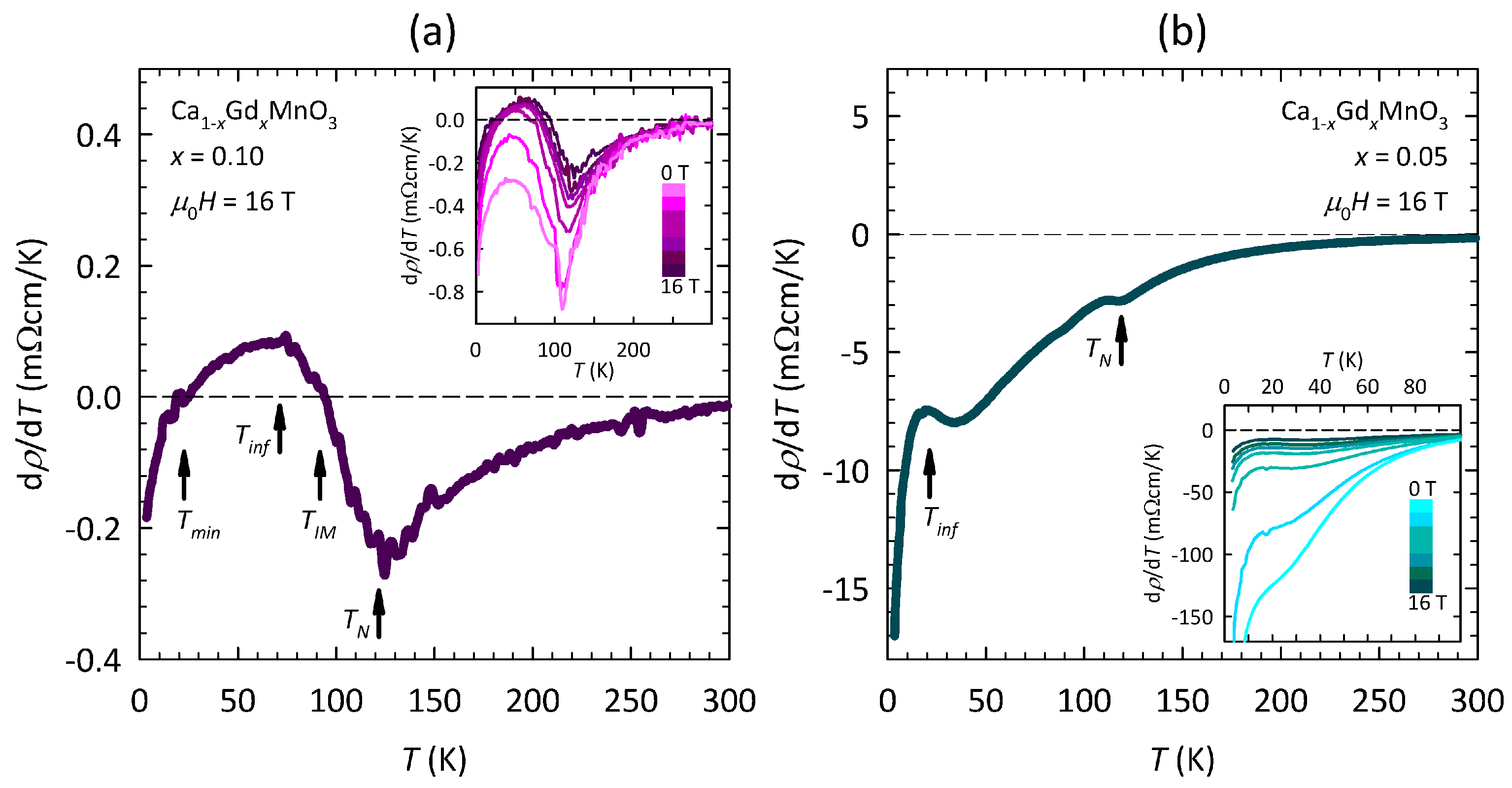
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jin, S.; Tiefel, T.H.; McCormack, M.; Fastnacht, R.A.; Ramesh, R.; Chen, L.H. Thousandfold Change in Resistivity in Magnetoresistive La-Ca-Mn-O Films. Science 1994, 264, 413–415. [Google Scholar] [CrossRef]
- Dagotto, E.; Hotta, T.; Moreo, A. Colossal magnetoresistant materials: The key role of phase separation. Phys. Rep. 2001, 344, 1–153. [Google Scholar] [CrossRef]
- Salamon, M.B.; Jaime, M. The physics of manganites: Structure and transport. Rev. Mod. Phys. 2001, 73, 583–628. [Google Scholar] [CrossRef]
- Nagaev, E. Colossal-magnetoresistance materials: Manganites and conventional ferromagnetic semiconductors. Phys. Rep. 2001, 346, 387–531. [Google Scholar] [CrossRef]
- Dagotto, E. Nanoscale Phase Separation and Colossal Magnetoresistance; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Zener, C. Interaction between the d -Shells in the Transition Metals. II. Ferromagnetic Compounds of Manganese with Perovskite Structure. Phys. Rev. 1951, 82, 403–405. [Google Scholar] [CrossRef]
- Anderson, P.W.; Hasegawa, H. Considerations on Double Exchange. Phys. Rev. 1955, 100, 675–681. [Google Scholar] [CrossRef]
- Kubo, K.; Ohata, N. A Quantum Theory of Double Exchange. I. J. Phys. Soc. Jpn. 1972, 33, 21–32. [Google Scholar] [CrossRef]
- Goodenough, J.B. Theory of the Role of Covalence in the Perovskite-Type Manganites [La, M(II)]MnO3. Phys. Rev. 1955, 100, 564–573. [Google Scholar] [CrossRef]
- Bîrsan, E. The superexchange interaction influence on the magnetic ordering in manganites. J. Magn. Magn. Mater. 2008, 320, 646–650. [Google Scholar] [CrossRef]
- Yi, H.; Yu, J.; Lee, S.I. Suppression of ferromagnetic ordering in doped manganites: Effects of the superexchange interaction. Phys. Rev. B 2000, 61, 428–431. [Google Scholar] [CrossRef]
- Bao, W.; Axe, J.; Chen, C.; Cheong, S.W.; Schiffer, P.; Roy, M. From double exchange to superexchange in charge-ordering perovskite manganites. Phys. B Condens. Matter 1997, 241–243, 418–420. [Google Scholar] [CrossRef]
- Ohtaki, M.; Koga, H.; Tokunaga, T.; Eguchi, K.; Arai, H. Electrical Transport Properties and High-Temperature Thermoelectric Performance of (Ca0.9M0.1)MnO3 (M = Y, La, Ce, Sm, In, Sn, Sb, Pb, Bi). J. Solid State Chem. 1995, 120, 105–111. [Google Scholar] [CrossRef]
- Jaime, M.; Salamon, M.B.; Pettit, K.; Rubinstein, M.; Treece, R.E.; Horwitz, J.S.; Chrisey, D.B. Magnetothermopower in La0.67Ca0.33MnO3 thin films. Appl. Phys. Lett. 1996, 68, 1576–1578. [Google Scholar] [CrossRef]
- Jaime, M.; Hardner, H.T.; Salamon, M.B.; Rubinstein, M.; Dorsey, P.; Emin, D. Hall-Effect Sign Anomaly and Small-Polaron Conduction in (La1-xGdx)0.67Ca0.33MnO3. Phys. Rev. Lett. 1997, 78, 951–954. [Google Scholar] [CrossRef]
- Palstra, T.T.M.; Ramirez, A.P.; Cheong, S.W.; Zegarski, B.R.; Schiffer, P.; Zaanen, J. Transport mechanisms in doped LaMnO3: Evidence for polaron formation. Phys. Rev. B 1997, 56, 5104–5107. [Google Scholar] [CrossRef]
- Chun, S.H.; Salamon, M.B.; Han, P.D. Hall effect of La2/3(Ca,Pb)1/3MnO3 single crystals. J. Appl. Phys. 1999, 85, 5573–5575. [Google Scholar] [CrossRef]
- Millis, A.J. Lattice effects in magnetoresistive manganese perovskites. Nature 1998, 392, 147–150. [Google Scholar] [CrossRef]
- Wollan, E.O.; Koehler, W.C. Neutron Diffraction Study of the Magnetic Properties of the Series of Perovskite-Type Compounds [(1-x)La,xCa]MnO3. Phys. Rev. 1955, 100, 545–563. [Google Scholar] [CrossRef]
- Ramirez, A.P.; Schiffer, P.; Cheong, S.W.; Chen, C.H.; Bao, W.; Palstra, T.T.M.; Gammel, P.L.; Bishop, D.J.; Zegarski, B. Thermodynamic and Electron Diffraction Signatures of Charge and Spin Ordering in La1-xCaxMnO3. Phys. Rev. Lett. 1996, 76, 3188–3191. [Google Scholar] [CrossRef]
- Chen, C.H.; Cheong, S.W. Commensurate to Incommensurate Charge Ordering and Its Real-Space Images in La0.5Ca0.5MnO3. Phys. Rev. Lett. 1996, 76, 4042–4045. [Google Scholar] [CrossRef]
- Mori, S.; Chen, C.H.; Cheong, S.W. Pairing of charge-ordered stripes in (La,Ca)MnO3. Nature 1998, 392, 473–476. [Google Scholar] [CrossRef]
- Zang, J.; Bishop, A.R.; Röder, H. Double degeneracy and Jahn-Teller effects in colossal-magnetoresistance perovskites. Phys. Rev. B 1996, 53, R8840–R8843. [Google Scholar] [CrossRef]
- Mishra, S.K.; Pandit, R.; Satpathy, S. Mean-field theory of charge ordering and phase transitions in the colossal-magnetoresistive manganites. J. Physics: Condens. Matter 1999, 11, 8561–8578. [Google Scholar] [CrossRef]
- Hotta, T.; Malvezzi, A.L.; Dagotto, E. Charge-orbital ordering and phase separation in the two-orbital model for manganites: Roles of Jahn-Teller phononic and Coulombic interactions. Phys. Rev. B 2000, 62, 9432–9452. [Google Scholar] [CrossRef]
- Dagotto, E. Complexity in Strongly Correlated Electronic Systems. Science 2005, 309, 257–262. [Google Scholar] [CrossRef]
- Nagaev, E.L. Lanthanum manganites and other giant-magnetoresistance magnetic conductors. Physics-Uspekhi 1996, 39, 781–805. [Google Scholar] [CrossRef]
- Kagan, M.; Kugel, K.; Rakhmanov, A. Electronic phase separation: Recent progress in the old problem. Phys. Rep. 2021, 916, 1–105. [Google Scholar] [CrossRef]
- Freitas, R.; Ghivelder, L.; Levy, P.; Parisi, F. Magnetization studies of phase separation in La0.5Ca0.5MnO3. Phys. Rev. B 2002, 65, 104403. [Google Scholar] [CrossRef]
- Giri, S.K.; Nath, T.K. Suppression of Charge and Antiferromagnetic Ordering in La0.5Ca0.5MnO3 Nanoparticles. J. Nanosci. Nanotechnol. 2011, 11, 4806–4814. [Google Scholar] [CrossRef]
- Dhieb, S.; Krichene, A.; Boudjada, N.C.; Boujelben, W. Suppression of Metamagnetic Transitions of Martensitic Type by Particle Size Reduction in Charge-Ordered La0.5Ca0.5MnO3. J. Phys. Chem. C 2020, 124, 17762–17771. [Google Scholar] [CrossRef]
- Levy, P.; Parisi, F.; Polla, G.; Vega, D.; Leyva, G.; Lanza, H.; Freitas, R.; Ghivelder, L. Controlled phase separation in La0.5Ca0.5MnO3. Phys. Rev. B 2000, 62, 6437–6441. [Google Scholar] [CrossRef]
- Quintero, M.; Passanante, S.; Irurzun, I.; Goijman, D.; Polla, G. Grain size modification in the magnetocaloric and non-magnetocaloric transitions in La0.5Ca0.5MnO3 probed by direct and indirect methods. Appl. Phys. Lett. 2014, 105, 152411. [Google Scholar] [CrossRef]
- Gamzatov, A.G.; Batdalov, A.B.; Aliev, A.M.; Amirzadeh, P.; Kameli, P.; Ahmadvand, H.; Salamati, H. Influence of the granule size on the magnetocaloric properties of manganite La0.5Ca0.5MnO3. Phys. Solid State 2013, 55, 502–507. [Google Scholar] [CrossRef]
- Sarkar, T.; Ghosh, B.; Raychaudhuri, A.K.; Chatterji, T. Crystal structure and physical properties of half-doped manganite nanocrystals of less than 100-nm size. Phys. Rev. B 2008, 77, 235112. [Google Scholar] [CrossRef]
- Novosel, N.; Rivas Góngora, D.; Jagličić, Z.; Tafra, E.; Basletić, M.; Hamzić, A.; Klaser, T.; Skoko, Ž.; Salamon, K.; Kavre Piltaver, I.; et al. Grain-Size-Induced Collapse of Variable Range Hopping and Promotion of Ferromagnetism in Manganite La0.5Ca0.5MnO3. Crystals 2022, 12, 724. [Google Scholar] [CrossRef]
- Aydogdu, G.; Habermeier, H. Half Ca-doped LaMnO3 films on (001) SLAO and STO substrate studied by magnetization and transport measurements. J. Magn. Magn. Mater. 2009, 321, 1731–1734. [Google Scholar] [CrossRef]
- Egilmez, M.; Ma, R.; Chow, K.H.; Jung, J. The anisotropic magnetoresistance in epitaxial thin films and polycrystalline samples of La0.65Ca0.35MnO3. J. Appl. Phys. 2009, 105, 07D706. [Google Scholar] [CrossRef]
- Zarifi, M.; Kameli, P.; Ehsani, M.; Ahmadvand, H.; Salamati, H. Effects of strain on the magnetic and transport properties of the epitaxial La0.5Ca0.5MnO3 thin films. J. Magn. Magn. Mater. 2016, 420, 33–38. [Google Scholar] [CrossRef]
- Gutiérrez, D.; Radaelli, G.; Sánchez, F.; Bertacco, R.; Fontcuberta, J. Bandwidth-limited control of orbital and magnetic orders in half-doped manganites by epitaxial strain. Phys. Rev. B 2014, 89, 075107. [Google Scholar] [CrossRef]
- Zhang, A.M.; Zhang, X.; Zhou, J.; Zhang, W.C.; Lin, J.G.; Wu, X.S. Strain Dependence of Magnetic and Transport Properties in Half-Doped La0.5Ca0.5MnO3 Films. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef]
- Xiong, Y.M.; Wang, G.Y.; Luo, X.G.; Wang, C.H.; Chen, X.H.; Chen, X.; Chen, C.L. Magnetotransport properties in La1-xCaxMnO3 (x=0.33,0.5) thin films deposited on different substrates. J. Appl. Phys. 2005, 97, 083909. [Google Scholar] [CrossRef]
- Tafra, E.; Novosel, N.; Skoko, Ž.; Ivek, T.; Basletić, M.; Mihaljević, B.; Jagličić, Z.; Góngora, D.R.; Tomić, S.; Hamzić, A.; et al. Colossal magnetoresistance effect and spin-dependent variable-range hopping in the charge ordered phase of overdoped (La, Ca)MnO3 manganites. Phys. Rev. B 2025, 111, 115107. [Google Scholar] [CrossRef]
- Dagotto, E. Open questions in CMR manganites, relevance of clustered states and analogies with other compounds including the cuprates. New J. Phys. 2005, 7, 67. [Google Scholar] [CrossRef]
- Rosić, M.; Kljaljević, L.; Jordanov, D.; Stoiljković, M.; Kusigerski, V.; Spasojević, V.; Matović, B. Effects of sintering on the structural, microstructural and magnetic properties of nanoparticle manganite Ca1-xGdxMnO3 (x=0.05,0.1,0.15,0.2). Ceram. Int. 2015, 41, 14964–14972. [Google Scholar] [CrossRef]
- Beiranvand, A.; Tikkanen, J.; Huhtinen, H.; Paturi, P. Electronic and magnetic phase diagram of polycrystalline Gd1-xCaxMnO3 manganites. J. Alloy. Compd. 2017, 720, 126–130. [Google Scholar] [CrossRef]
- Schulman, A.; Beiranvand, A.; Lähteenlahti, V.; Huhtinen, H.; Paturi, P. Appearance of glassy ferromagnetic behavior in Gd1-xCaxMnO3 (0≤x≤1) thin films: A revised phase diagram. J. Magn. Magn. Mater. 2020, 498, 166149. [Google Scholar] [CrossRef]
- Rosić, M.; Logar, M.; Devečerski, A.; Prekajski, M.; Radosavljević-Mihajlović, A.; Kusigerski, V.; Spasojević, V.; Matović, B. Synthesis, structural and magnetic properties of nanostructured Ca0.9Gd0.1MnO3 obtained by modified glycine nitrate procedure (MGNP). Ceram. Int. 2011, 37, 1313–1319. [Google Scholar] [CrossRef]
- Rosić, M.; Logar, M.; Zagorac, J.; Devečerski, A.; Egelja, A.; Kusigerski, V.; Spasojević, V.; Matović, B. Investigation of the structure and the magnetic behavior of nanostructure Ca1-xGdxMnO3 (x=0.05;0.1;0.15;0.2) obtained by modified glycine nitrate procedure. Ceram. Int. 2013, 39, 1853–1861. [Google Scholar] [CrossRef]
- Zeng, Z.; Greenblatt, M.; Croft, M. Large magnetoresistance in antiferromagnetic CaMnO3-δ. Phys. Rev. B 1999, 59, 8784–8788. [Google Scholar] [CrossRef]
- Costi, T.A.; Hewson, A.C.; Zlatic, V. Transport coefficients of the Anderson model via the numerical renormalization group. J. Phys. Condens. Matter 1994, 6, 2519–2558. [Google Scholar] [CrossRef]
- Goldhaber-Gordon, D.; Göres, J.; Kastner, M.A.; Shtrikman, H.; Mahalu, D.; Meirav, U. From the Kondo Regime to the Mixed-Valence Regime in a Single-Electron Transistor. Phys. Rev. Lett. 1998, 81, 5225–5228. [Google Scholar] [CrossRef]
- Lee, M.; Williams, J.R.; Zhang, S.; Frisbie, C.D.; Goldhaber-Gordon, D. Electrolyte Gate-Controlled Kondo Effect in SrTiO3. Phys. Rev. Lett. 2011, 107, 256601. [Google Scholar] [CrossRef] [PubMed]
- Cai, X.; Yue, J.; Xu, P.; Jalan, B.; Pribiag, V.S. From weak antilocalization to Kondo scattering in a magnetic complex oxide interface. Phys. Rev. B 2021, 103, 115434. [Google Scholar] [CrossRef]
- Kondo, J. Resistance Minimum in Dilute Magnetic Alloys. Prog. Theor. Phys. 1964, 32, 37–49. [Google Scholar] [CrossRef]
- Kouwenhoven, L.; Glazman, L. Revival of the Kondo effect. Phys. World 2001, 14, 33–38. [Google Scholar] [CrossRef]
- Arun, B.; Suneesh, M.; Vasundhara, M. Comparative Study of Magnetic Ordering and Electrical Transport in Bulk and Nano-Grained Nd0.67Sr0.33MnO3 Manganites. J. Magn. Magn. Mater. 2016, 418, 265–272. [Google Scholar] [CrossRef]
- Asmira, N.A.; Ibrahim, N.; Mohamed, Z. Effect of Bi substitution on the collapse of double metal–insulator peaks and induction of a Kondo-like effect in Pr0.67-xBixBa0.33MnO3 manganite. Appl. Phys. A 2023, 129, 741. [Google Scholar] [CrossRef]
- Hardy, V.; Wahl, A.; Martin, C. Percolation transitions tuned by temperature, magnetic field, and time in a phase-separated manganite. Phys. Rev. B 2001, 64, 064402. [Google Scholar] [CrossRef]
- Zhang, L.; Israel, C.; Biswas, A.; Greene, R.L.; De Lozanne, A. Direct Observation of Percolation in a Manganite Thin Film. Science 2002, 298, 805–807. [Google Scholar] [CrossRef]
- Zhou, Q.l.; Jin, K.j.; Zhao, K.; Guan, D.y.; Lu, H.b.; Chen, Z.h.; Yang, G.z. Transport study of percolation modes in the mixed-phase manganites. Phys. Rev. B 2005, 72, 224439. [Google Scholar] [CrossRef]
- Shang, C.; Xia, Z.; Zhai, X.; Liu, D.; Wang, Y. Percolation like transitions in phase separated manganites La0.5Ca0.5Mn1-xAlxO3-δ. Ceram. Int. 2019, 45, 18632–18639. [Google Scholar] [CrossRef]
- Ziese, M. Critical scaling and percolation in manganite films. J. Phys. Condens. Matter 2001, 13, 2919–2934. [Google Scholar] [CrossRef]
- Salazar-Muñoz, V.; Lobo Guerrero, A.; Palomares-Sánchez, S. Review of magnetocaloric properties in lanthanum manganites. J. Magn. Magn. Mater. 2022, 562, 169787. [Google Scholar] [CrossRef]
- Eto, T.; Oomi, G.; Honda, F.; Sundaresan, A. High-pressure studies of Kondo-like perovskite (La0.1Ce0.4Sr0.5)MnO3. J. Magn. Magn. Mater. 2001, 226–230, 879–881. [Google Scholar] [CrossRef]
- Syskakis, E.; Choudalakis, G.; Papastaikoudis, C. Crossover between Kondo and electron–electron interaction effects in La0.75Sr0.20MnO3 manganite doped with Co impurities? J. Phys. Condens. Matter 2003, 15, 7735–7749. [Google Scholar] [CrossRef]
- Guo, E.J.; Wang, L.; Wu, Z.P.; Wang, L.; Lu, H.B.; Jin, K.J.; Gao, J. Magnetic field mediated low-temperature resistivity upturn in electron-doped La1-xHfxMnO3 manganite oxides. J. Appl. Phys. 2012, 112, 123710. [Google Scholar] [CrossRef]
- Wilson, K.G. The renormalization group: Critical phenomena and the Kondo problem. Rev. Mod. Phys. 1975, 47, 773–840. [Google Scholar] [CrossRef]
- Maignan, A.; Martin, C.; Damay, F.; Raveau, B. Factors Governing the Magnetoresistance Properties of the Electron-Doped Manganites Ca1-xAxMnO3 (A = Ln, Th). Chem. Mater. 1998, 10, 950–954. [Google Scholar] [CrossRef]
- Kirkpatrick, S. Percolation and Conduction. Rev. Mod. Phys. 1973, 45, 574–588. [Google Scholar] [CrossRef]
- Rahaman, M.; Aldalbahi, A.; Govindasami, P.; Khanam, N.; Bhandari, S.; Feng, P.; Altalhi, T. A New Insight in Determining the Percolation Threshold of Electrical Conductivity for Extrinsically Conducting Polymer Composites through Different Sigmoidal Models. Polymers 2017, 9, 527. [Google Scholar] [CrossRef]
- Barrau, S.; Demont, P.; Peigney, A.; Laurent, C.; Lacabanne, C. DC and AC Conductivity of Carbon Nanotubes-Polyepoxy Composites. Macromolecules 2003, 36, 5187–5194. [Google Scholar] [CrossRef]
- Brigandi, P.J.; Cogen, J.M.; Pearson, R.A. Electrically conductive multiphase polymer blend carbon-based composites. Polym. Eng. Sci. 2014, 54, 1–16. [Google Scholar] [CrossRef]
- Potschke, P.; Arnaldo, M.H.; Radusch, H.J. Percolation behavior and mehanical properties of polycarbonate composites filled with carbon black/carbon nanotube systems. Polimery 2012, 57, 204–211. [Google Scholar] [CrossRef]
- Zhang, H.B.; Zheng, W.G.; Yan, Q.; Jiang, Z.G.; Yu, Z.Z. The effect of surface chemistry of graphene on rheological and electrical properties of polymethylmethacrylate composites. Carbon 2012, 50, 5117–5125. [Google Scholar] [CrossRef]
- Coelho, P.H.D.S.L.; Marchesin, M.S.; Morales, A.R.; Bartoli, J.R. Electrical percolation, morphological and dispersion properties of MWCNT/PMMA nanocomposites. Mater. Res. 2014, 17, 127–132. [Google Scholar] [CrossRef]
- Andrei, N.; Furuya, K.; Lowenstein, J.H. Solution of the Kondo problem. Rev. Mod. Phys. 1983, 55, 331–402. [Google Scholar] [CrossRef]
- Joshua, A.; Ruhman, J.; Pecker, S.; Altman, E.; Ilani, S. Gate-tunable polarized phase of two-dimensional electrons at the LaAlO3/SrTiO3 interface. Proc. Natl. Acad. Sci. USA 2013, 110, 9633–9638. [Google Scholar] [CrossRef] [PubMed]
- Hien-Hoang, V.; Chung, N.K.; Kim, H.J. Electrical transport properties and Kondo effect in La1-xPrxNiO3-δ thin films. Sci. Rep. 2021, 11, 5391. [Google Scholar] [CrossRef]
- Li, H.; Li, L.; Li, L.; Liang, H.; Cheng, L.; Zhai, X.; Zeng, C. Giant intrinsic tunnel magnetoresistance in manganite thin films etched with antidot arrays. Appl. Phys. Lett. 2014, 104, 082414. [Google Scholar] [CrossRef]
- Sboychakov, A.O.; Rakhmanov, A.L.; Kugel’, K.I.; Kagan, M.Y.; Brodsky, I.V. Tunneling magnetoresistance of phase-separated manganites. J. Exp. Theor. Phys. 2002, 95, 753–761. [Google Scholar] [CrossRef]

(T) | (cm) | q () | (cm) | (K) | (cm) | q () | (cm) | (K) |
| 0 | - | - | ||||||
| 1 | - | - | ||||||
| 5 | - | |||||||
| 8 | - | |||||||
| 10 | - | |||||||
| 12 | - | |||||||
| 16 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ivek, T.; Čulo, M.; Novosel, N.; Čebela, M.; Laban, B.; Čakar, U.; Rosić, M. Kondo-like Behavior in Lightly Gd-Doped Manganite CaMnO3. Nanomaterials 2025, 15, 784. https://doi.org/10.3390/nano15110784
Ivek T, Čulo M, Novosel N, Čebela M, Laban B, Čakar U, Rosić M. Kondo-like Behavior in Lightly Gd-Doped Manganite CaMnO3. Nanomaterials. 2025; 15(11):784. https://doi.org/10.3390/nano15110784
Chicago/Turabian StyleIvek, Tomislav, Matija Čulo, Nikolina Novosel, Maria Čebela, Bojana Laban, Uroš Čakar, and Milena Rosić. 2025. "Kondo-like Behavior in Lightly Gd-Doped Manganite CaMnO3" Nanomaterials 15, no. 11: 784. https://doi.org/10.3390/nano15110784
APA StyleIvek, T., Čulo, M., Novosel, N., Čebela, M., Laban, B., Čakar, U., & Rosić, M. (2025). Kondo-like Behavior in Lightly Gd-Doped Manganite CaMnO3. Nanomaterials, 15(11), 784. https://doi.org/10.3390/nano15110784










