First-Principles Calculations of Plasmon-Induced Hot Carrier Properties of μ-Ag3Al
Abstract
1. Introduction
2. Method
2.1. Computational Details
2.2. Optical Responses
2.3. Transport Properties
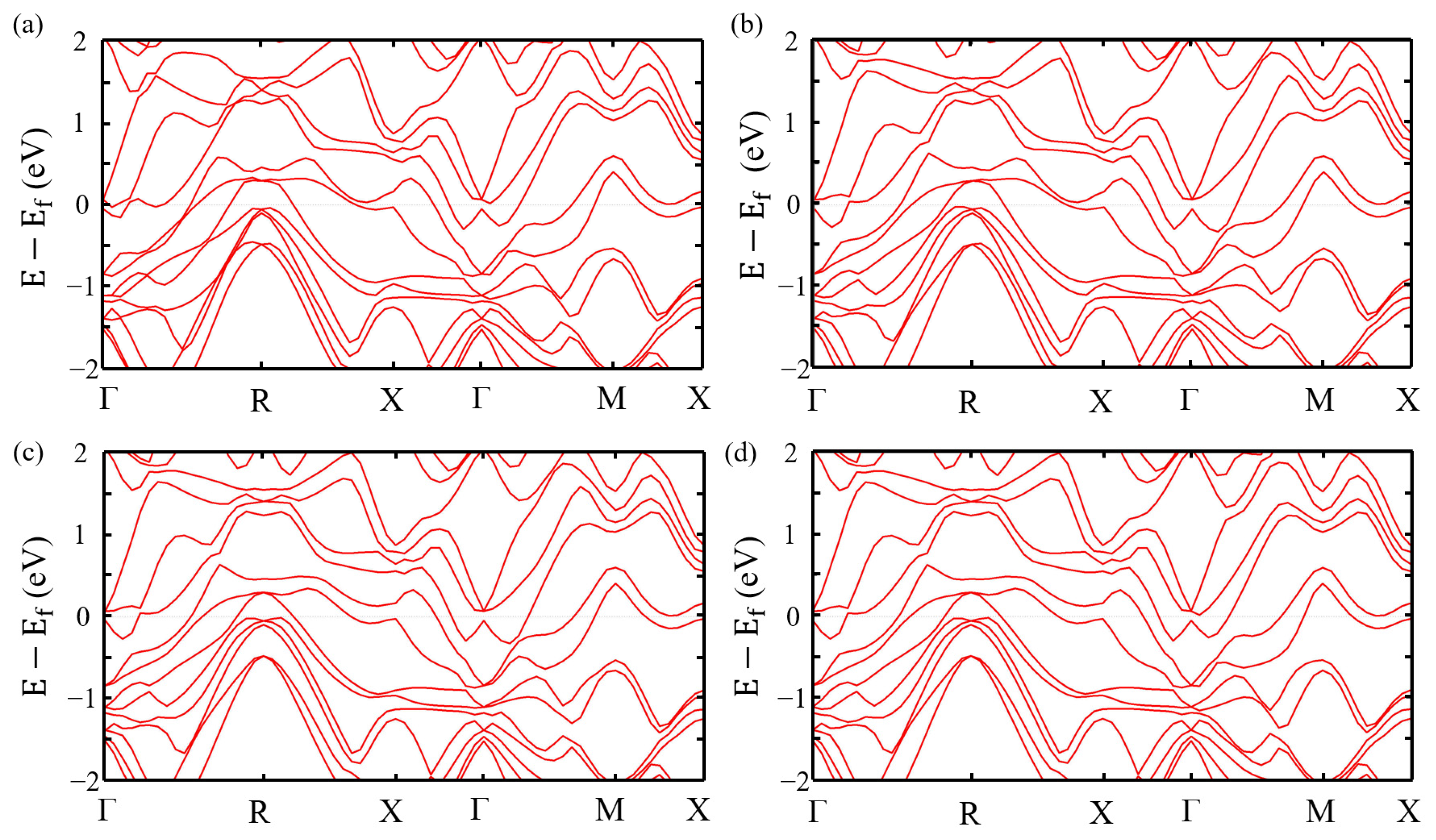
3. Result and Discussion
3.1. Structure and Stability
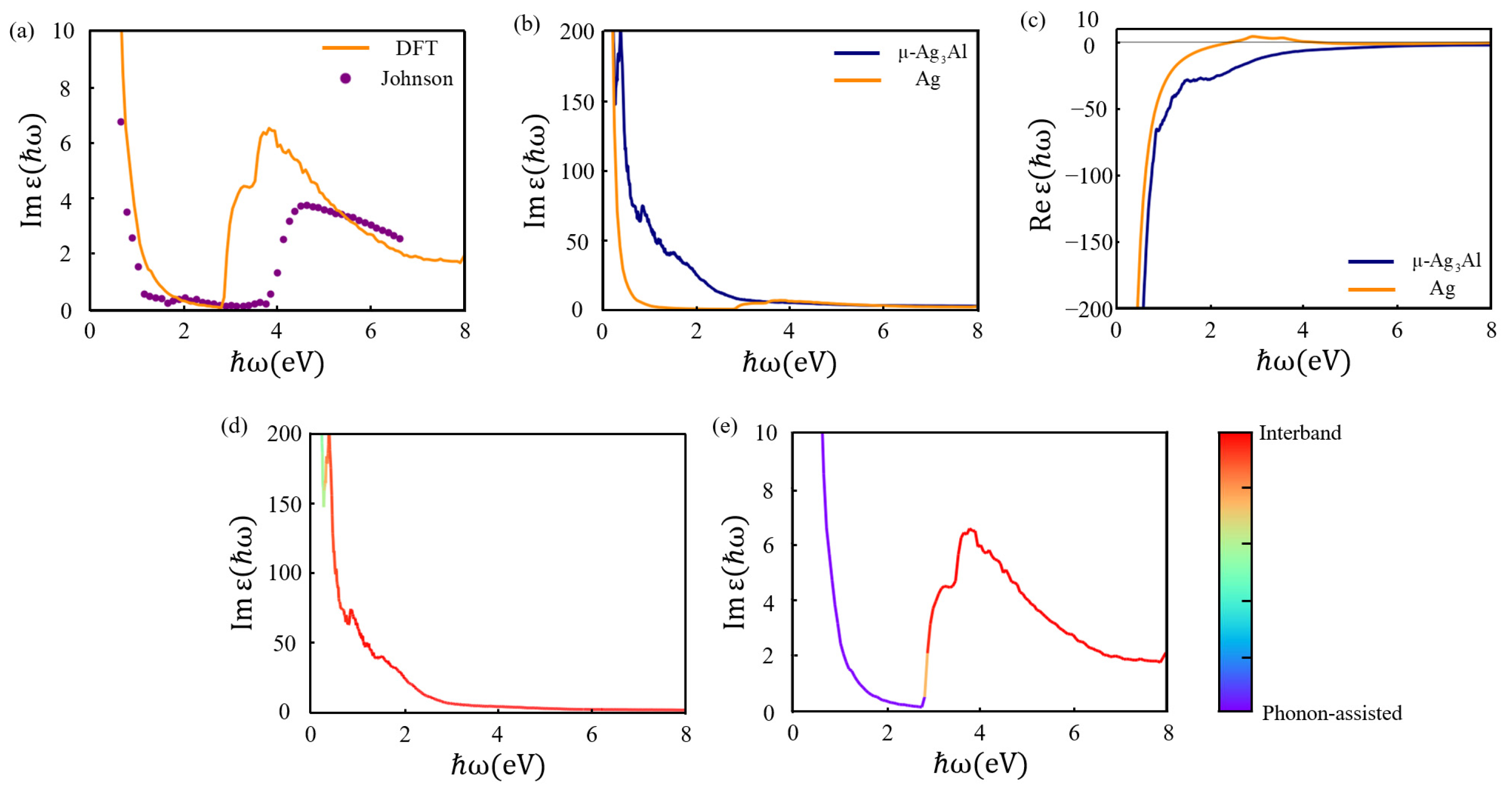
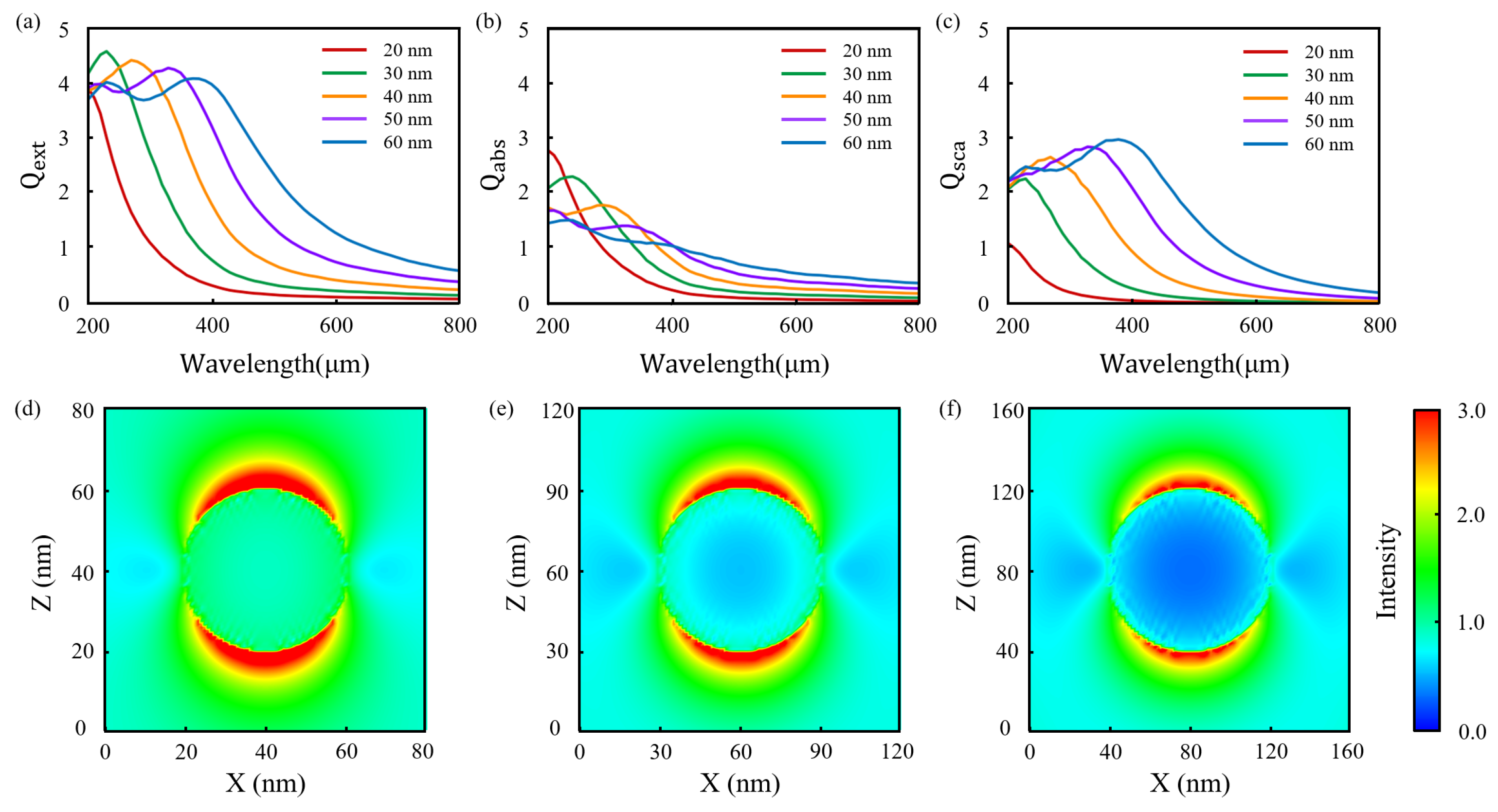
3.2. Optical Properties
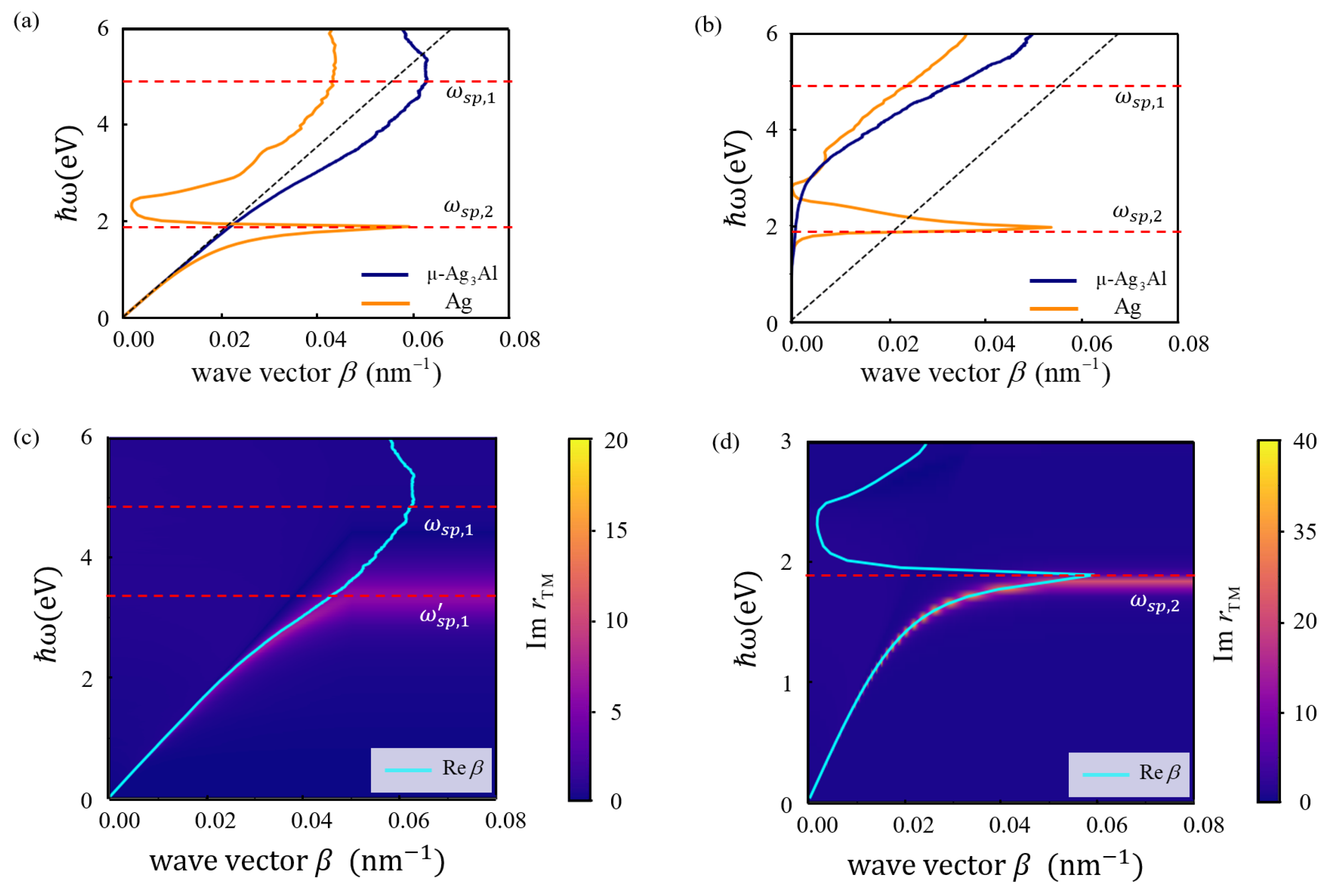
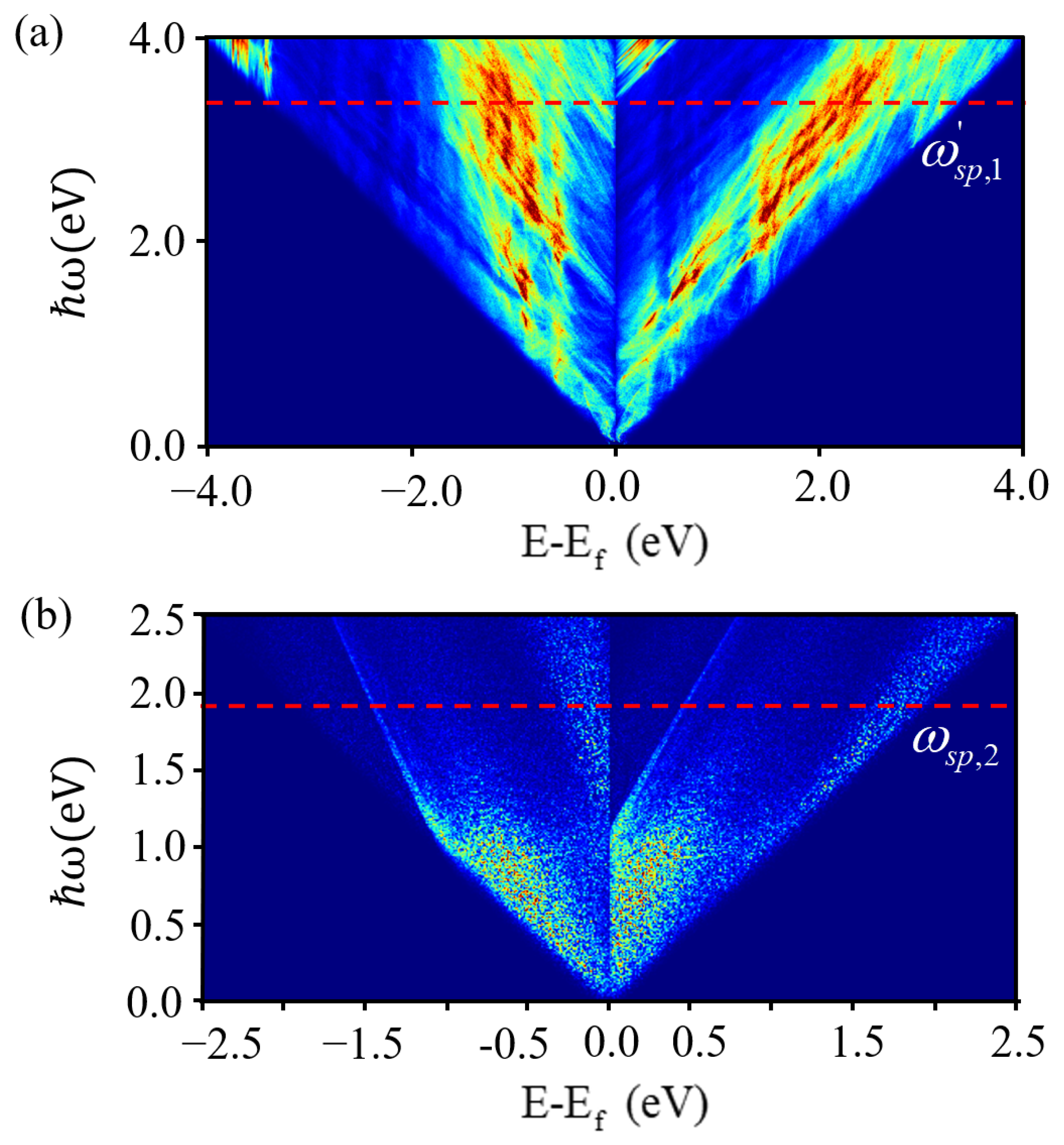
3.3. Plasmon Properties
3.4. Hot Carriers
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yu, H.; Peng, Y.; Yang, Y.; Li, Z. Plasmon-enhanced light–matter interactions and applications. npj Comput. Mater. 2019, 5, 45. [Google Scholar] [CrossRef]
- Guo, Y.; Xu, Z.; Curto, A.; Zeng, Y.; Van, D. Plasmonic semiconductors: Materials, tunability and applications. Prog. Mater. Sci. 2023, 138, 101158. [Google Scholar] [CrossRef]
- Zhou, L.; Huang, Q.; Xia, Y. Plasmon-Induced Hot Electrons in Nanostructured Materials: Generation, Collection, and Application to Photochemistry. Chem. Rev. 2024, 124, 8597. [Google Scholar] [CrossRef] [PubMed]
- Altug, H.; Oh, S.; Maier, S.; Homola, J. Advances and applications of nanophotonic biosensors. Nat. Nanotechnol. 2022, 17, 5. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Valentine, J. Harvesting the loss: Surface plasmon-based hot electron photodetection. Nanophotonics 2017, 6, 177. [Google Scholar] [CrossRef]
- Jang, Y.-H.; Jang, Y.J.; Kim, S.; Quan, L.; Chung, K.; Kim, D. Plasmonic solar cells: From rational design to mechanism overview. Chem. Rev. 2016, 116, 14982. [Google Scholar] [CrossRef]
- Clavero, C. Plasmon-induced hot-electron generation at nanoparticle/metal-oxide interfaces for photovoltaic and photocatalytic devices. Nat. Photon. 2014, 8, 95. [Google Scholar] [CrossRef]
- Akhil, S.; Akash, S.; Pasha, A.; Kulkarni, B.; Jalalah, M.; Alsaiari, M.; Harraz, F.; Balakrishna, R. The effect of hot electrons and surface plasmons on heterogeneous catalysis. Mater. Des. 2021, 211, 110138. [Google Scholar] [CrossRef]
- Kim, S.; Lee, S.; Moon, S.; Park, J. The effect of hot electrons and surface plasmons on heterogeneous catalysis. J. Phys. Condens. Matter. 2016, 28, 254002. [Google Scholar] [CrossRef]
- Zhang, Y.; He, S.; Guo, W.; Hu, Y.; Huang, J.; Mulcahy, J.; Wei, W. Surface-plasmon-driven hot electron photochemistry. Chem. Rev. 2017, 118, 2927. [Google Scholar] [CrossRef]
- Donohue, J.F. Excitation of The Radiative Surface Plasmon Mode in Metal-Oxide-Metal Tunnel Junctions. Ph.D. Dissertation, Arizona State University, Phoenix, AZ, USA, 1986. [Google Scholar]
- Maier, S. Plasmonics: Fundamentals and Applications; Springer: New York, NY, USA, 2007; p. 21. [Google Scholar]
- Zhang, Y.; Ding, X.; Sun, J.; Wang, T. Quantum steerability of two qubits mediated by one-dimensional plasmonic waveguides. Chin. Phys. B 2022, 31, 120305. [Google Scholar] [CrossRef]
- Sobhani, A.; Knight, M.W.; Wang, Y.; Zheng, B.; King, N.S.; Brown, L.V.; Fang, Z.; Nordlander, P.; Halas, N.J. Narrowband photodetection in the near-infrared with a plasmon-induced hot electron device. Nat. Commun. 2013, 4, 1643. [Google Scholar] [CrossRef] [PubMed]
- Zhou, F.; Wang, Q.; Liu, W. Au@ ZnO nanostructures on porous silicon for photocatalysis and gas-sensing: The effect of plasmonic hot-electrons driven by visible-light. Mater. Res. Express 2016, 3, 085006. [Google Scholar] [CrossRef]
- Yao, K.; Zhong, H.; Liu, Z.; Xiong, M.; Leng, S.; Zhang, J.; Xu, Y.-X.; Wang, W.; Zhou, L.; Huang, H. Plasmonic metal nanoparticles with core–bishell structure for high-performance organic and perovskite solar cells. ACS Nano 2019, 13, 5397. [Google Scholar] [CrossRef]
- Deepak, S.; Jyoti, S.; Diksha Pargam, V.; Shailesh, S.; Arman, A.; Sanjay, S. Enhanced Performance of Flexible Hybrid Solar Cells via Silver Nanoparticle Incorporation. ACS Appl. Nano Mater. 2024, 7, 23927. [Google Scholar]
- Zhang, C.; Ma, X.; Zhang, J. Theoretical study on surface plasmon and hot carrier transport properties of Au (111) films. Acta Phys. Sin. 2022, 71, 227801. (In Chinese) [Google Scholar] [CrossRef]
- Capelli, D.; Scognamiglio, V.; Montanari, R. Surface plasmon resonance technology: Recent advances, applications and experimental cases. TrAC Trends Anal. Chem. 2023, 163, 117079. [Google Scholar] [CrossRef]
- Song, Y.; Cao, Y.; Huang, S.; Li, K.; Du, R.; Yan, L.; Fu, Z.; Zhang, Z. Plasmon-induced nonlinear response on gold nanoclusters. Chin. Phys. B 2024, 33, 044204. [Google Scholar] [CrossRef]
- Gao, X.; Wang, Q.; Zhang, S.; Hong, R.; Zhang, D. Angle robust transmitted plasmonic colors with different surroundings utilizing localized surface plasmon resonance. Chin. Phys. B 2023, 32, 070204. [Google Scholar] [CrossRef]
- Jian, C.-C.; Zhang, J.; He, W.; Ma, X. Au-Al intermetallic compounds: A series of more efficient LSPR materials for hot carriers-based applications than noble metal Au. Nano Energy 2021, 82, 105763. [Google Scholar] [CrossRef]
- West, P.R.; Ishii, S.; Naik, G.V.; Emani, N.K.; Shalaev, V.M.; Boltasseva, A. Searching for better plasmonic materials. Laser Photonics Rev. 2010, 4, 795. [Google Scholar] [CrossRef]
- Bansal, A.; Verma, S. Searching for alternative plasmonic materials for specific applications. Indian J. Eng. Mater. Sci. 2014, 2014, 897125. [Google Scholar] [CrossRef]
- Gao, Z.; Wildenborg, A.; Kocoj, C.A.; Liu, E.; Sheofsky, C.; Rawashdeh, A.; Qu, H.; Guo, P.; Suh, J.Y.; Yang, A. Low-loss plasmonics with nanostructured potassium and sodium–potassium liquid alloys. Nano Lett. 2023, 23, 7150. [Google Scholar] [CrossRef]
- Gong, C.; Leite, M.S. Noble metal alloys for plasmonics. ACS Photonics 2016, 3, 507. [Google Scholar] [CrossRef]
- Sytwu, K.; Vadai, M.; Dionne, J.A. Bimetallic nanostructures: Combining plasmonic and catalytic metals for photocatalysis. Adv. Phys. X 2019, 4, 1619480. [Google Scholar] [CrossRef]
- Parashar, P.K.; Komarala, V.K. Engineered optical properties of silver-aluminum alloy nanoparticles embedded in SiON matrix for maximizing light confinement in plasmonic silicon solar cells. Sci. Rep. 2017, 7, 12520. [Google Scholar] [CrossRef]
- Wen, X.-M.; Bi, Y.-G.; Yi, F.-S.; Zhang, X.-L.; Liu, Y.-F.; Wang, W.-Q.; Feng, J.; Sun, H.-B. Tunable surface plasmon-polariton resonance in organic light-emitting devices based on corrugated alloy electrodes. Opto-Electron. Adv. 2021, 4, 200024. [Google Scholar] [CrossRef]
- Fu, S.-W.; Lee, C.C. A study on intermetallic compound formation in Ag–Al system and evaluation of its mechanical properties by micro-indentation. J. Mater. Sci. Mater. Electron. 2018, 29, 3985. [Google Scholar] [CrossRef]
- Wang, K.-K.; Gan, D. The orientation relationships of Ag3Al/Ag interfaces and formation sequence of Ag2Al and Ag3Al at the Ag/Al interface. Thin Solid Film 2025, 810, 140598. [Google Scholar] [CrossRef]
- Aboulfadl, H.; Gallino, I.; Busch, R.; Mucklich, F. Atomic scale analysis of phase formation and diffusion kinetics in Ag/Al multilayer thin films. J. Appl. Phys. 2016, 120, 195306. [Google Scholar] [CrossRef]
- Deng, Z.; Hu, Q.; Tian, Y.; Xue, R.; Zhang, L.; Liu, L. Experimental investigation and thermodynamic assessment of the Al–Ag–Sc system. J. Alloys Compd. 2023, 934, 167980. [Google Scholar] [CrossRef]
- Mcalister, A. The Ag–Al (silver-aluminum) system. Bull. Alloy Phase Diagr. 1987, 8, 526. [Google Scholar] [CrossRef]
- Kuiri, P.K. Tailoring localized surface plasmons in Ag-Al alloys nanoparticles. J. Alloys Compd. 2020, 826, 154250. [Google Scholar] [CrossRef]
- Ntemogiannis, D.; Diamantopoulos, N.C.; Papaggeli, M.; Grammatikopoilos, S.; Sigalas, M.; Poulopoulos, P. Localized surface plasmon resonances of AgAl alloy Nanoparticles self-organized by annealing of Ag/Al bilayer films. Photonics 2024, 11, 713. [Google Scholar] [CrossRef]
- Sundararaman, R.; Letchworth-Weaver, K.; Schwarz, K.A.; Gunceler, D.; Ozhabes, Y.; Arias, T.A. JDFTx: Software for joint density-functional theory. SoftwareX 2017, 6, 278. [Google Scholar] [CrossRef]
- Brown, A.M.; Sundararaman, R.; Narang, P.; Goddard, W.A., III; Atwater, H.A. Nonradiative plasmon decay and hot carrier dynamics: Effects of phonons, surfaces, and geometry. ACS Nano 2016, 10, 957. [Google Scholar] [CrossRef]
- Giustino, F.; Cohen, M.L.; Louie, S.G. Electron-phonon interaction using Wannier functions. Phys. Rev. B 2007, 76, 165108. [Google Scholar] [CrossRef]
- Jian, C.; Ma, X.; Zhang, J.; Jiang, J. The anisotropic broadband surface plasmon polariton and hot carrier properties of borophene monolayer. Nanophotonics 2022, 11, 531. [Google Scholar] [CrossRef]
- Szmulowicz, F.; Segall, B. Calculation of optical spectra of aluminum. Electron-phonon effects in the infrared properties of metals. Phys. Rev. B 1981, 24, 892. [Google Scholar] [CrossRef]
- Allen, P. Electron-phonon effects in the infrared properties of metals. Phys. Rev. B 1971, 3, 305. [Google Scholar] [CrossRef]
- Haberer, D.; Petaccia, L.; Fedorov, A.; Praveen, C.; Fabris, S.; Piccinin, S.; Vilkov, O.; Vyalikh, D.; Preobrajenski, A.; Verbitskiy, N. Anisotropic Eliashberg function and electron-phonon coupling in doped graphene. Phys. Rev. B 2013, 88, 081401. [Google Scholar] [CrossRef]
- Sundararaman, R.; Christensen, T.; Ping, Y.; Rivera, N.; Joannopoulos, J.D.; Soljacic, M.; Narang, P. Plasmonics in argentine. Phys. Rev. Mater. 2020, 4, 074011. [Google Scholar] [CrossRef]
- Lucarini, V.; Saarinen, J.J.; Peiponen, K.-E.; Vartiainen, E.M. Kramers-Kronig Relations in Optical Materials Research; Springer: New York, NY, USA, 2005; 15p. [Google Scholar]
- Kador, L. Kramers–Kronig relations in nonlinear optics. Appl. Phys. Lett. 1995, 66, 2938. [Google Scholar] [CrossRef]
- Ladstadter, F.; Hohenester, U.; Puschnig, P.; Ambrosch-Draxl, C. First-principles calculation of hot-electron scattering in metals. Phys. Rev. B 2004, 70, 235125. [Google Scholar] [CrossRef]
- Bernardi, M.; Vigil-Fowler, D.; Ong, C.S.; Neaton, J.B.; Louie, S.G. Ab initio study of hot electrons in GaAs. Proc. Natl. Acad. Sci. USA 2015, 112, 5291. [Google Scholar] [CrossRef]
- Jian, C.-C.; Ma, X.; Zhang, J.; Yong, X. Strained MoSi2N4 monolayers with excellent solar energy absorption and carrier transport properties. J. Phys. Chem. C 2021, 125, 15185. [Google Scholar] [CrossRef]
- Bermardo, M.; Mustafa, J.; Neatpm, J.B.; Louie, S.G. Theory and computation of hot carriers generated by surface plasmon polaritons in noble metals. Nat. Commun. 2015, 6, 7044. [Google Scholar] [CrossRef]
- Crystal, J. Kristallstrukturen einiger ternärer Phasen in TBB-Systemen. Int. J. Mater. Res. 1971, 62, 667. [Google Scholar]
- Matej, B.; Jordi, S.-P. Hot Carrier Distribution Engineering by Alloying: Picking Elements for the Desired Purposes. J. Phys. Chem. C 2024, 128, 3924. [Google Scholar]
- Johnson, P.B.; Christy, R.-W. Optical constants of the noble metals. Phys. Rev. B 1972, 6, 4370. [Google Scholar] [CrossRef]
- Gong, T.; Lyu, P.; Kevin, P.; Sarvenaz, M.; Jeremy, M.; Marina, L. Emergent Opportunities with Metallic Alloys: From Material Design to Optical Devices. Adv. Opt. Mater. 2020, 23, 21951071. [Google Scholar]
- Sturm, K. Electron energy loss in simple metals and semiconductors. Adv. Phys. 1982, 31, 1. [Google Scholar] [CrossRef]
- Jian, C.-C.; Zhang, J.; Ma, X. Cu–Ag alloy for engineering properties and applications based on the LSPR of metal nanoparticles. RSC Adv. 2020, 10, 13277. [Google Scholar] [CrossRef]
- Jablan, M.; Soljacic, M.; Buljan, H. Plasmons in graphene: Fundamental properties and potential applications. Proc. IEEE 2013, 101, 1689. [Google Scholar] [CrossRef]
- Kolwas, K.; Derkachova, A. Impact of the interband transitions in gold and silver on the dynamics of propagating and localized surface plasmons. Nanomaterials 2020, 10, 1411. [Google Scholar] [CrossRef]
- Zhang, Z.-Y.; Wang, H.-Y.; Du, J.-L.; Zhang, X.-L.; Hao, Y.-W.; Chen, Q.-D.; Sun, H.-B. Surface plasmon-modulated fluorescence on 2D metallic silver gratings. IEEE Photonics Technol. Lett. 2015, 27, 821. [Google Scholar] [CrossRef]
- Kitamura, R.; Pilon, L.; Jonasz, M. Optical constants of silica glass from extreme ultraviolet to far infrared at near room temperature. Appl. Opt. 2007, 46, 8118. [Google Scholar] [CrossRef]
- Siew, S.Y.; Li, B.; Gao, F.; Zheng, H.Y.; Zhang, W.; Guo, P.; Xie, S.W.; Song, A.; Dong, B.; Luo, L.W. Review of silicon photonics technology and platform development. J. Light. Technol. 2021, 39, 4374. [Google Scholar] [CrossRef]
- Soref, R. Mid-infrared photonics in silicon and germanium. Nat. Photonics 2010, 4, 495. [Google Scholar] [CrossRef]
- Biudov, Y.V.; Ferreira, A.; Peres, N.M.; Vasilevskiy, M.I. A primer on surface plasmon-polaritons in graphene. Int. J. Mod. Phys. B 2013, 27, 1341001. [Google Scholar]
- Novotny, L.; Hecht, B. Principles of Nano-Optics; Cambridge University Press: Cambridge, UK, 2012; pp. 378–381. [Google Scholar]
- Christopher, P.; Moskovits, M. Hot charge carrier transmission from plasmonic nanostructures. Annu. Rev. Phys. Chem. 2017, 68, 379. [Google Scholar] [CrossRef] [PubMed]
- Tang, H.; Chen, C.-J.; Huang, Z.; Bright, J.; Meng, G.; Liu, R.-S.; Wun, J. Plasmonic hot electrons for sensing, photodetection, and solar energy applications: A perspective. Chem. Phys. 2020, 152, 220901. [Google Scholar] [CrossRef]
- Echenique, P.; Pitarke, J.; Chulkov, E.; Rubio, A. Theory of inelastic lifetimes of low-energy electrons in metals. Chem. Phys. 2000, 251, 1. [Google Scholar] [CrossRef]
- Paragam, V.; Ajit, D.; Summeet, W.; Govind, G. Self-bias Mo-Sb-Ga multilayer photodector encompassing ultra-broad spectral response from UV-C to IR-B. Opt. Laser Technol. 2025, 181, 111705. [Google Scholar]
- Paragam, V.; Ritik, T.; Sudhanshu, G.; Lalit, G.; Sunil, S.; Govind, G. Wavelength-modulated polarity switch self-powered Bi2Se3/GaN heterostructure photodetector. Mater. Sci. Semicond. Process. 2024, 180, 108553. [Google Scholar]




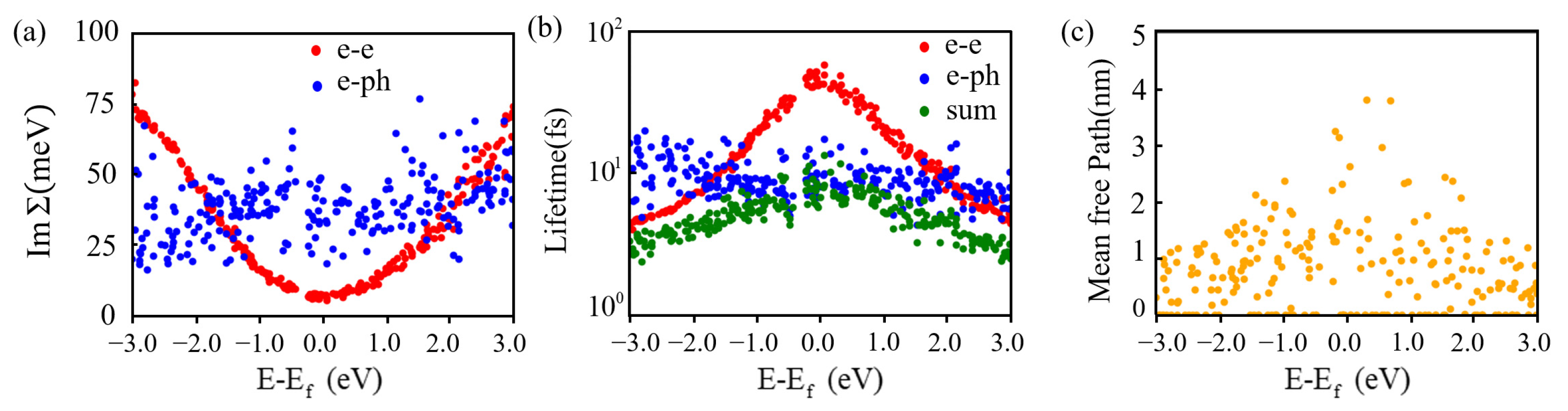
| Energy Level eV | Lifetime fs | Mean Free Path nm |
|---|---|---|
| −3.0 | 3.2 | 1.04 |
| −2.0 | 4.2 | 1.39 |
| −1.0 | 6.7 | 1.96 |
| 0.0 | 9.8 | 3.47 |
| 1.0 | 6.6 | 2.41 |
| 2.0 | 4.3 | 1.56 |
| 3.0 | 3.0 | 1.08 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Z.; Ren, H.; Wang, Y.; Ma, X.; Jiang, J.; Wei, L.; Liu, D. First-Principles Calculations of Plasmon-Induced Hot Carrier Properties of μ-Ag3Al. Nanomaterials 2025, 15, 761. https://doi.org/10.3390/nano15100761
Zhao Z, Ren H, Wang Y, Ma X, Jiang J, Wei L, Liu D. First-Principles Calculations of Plasmon-Induced Hot Carrier Properties of μ-Ag3Al. Nanomaterials. 2025; 15(10):761. https://doi.org/10.3390/nano15100761
Chicago/Turabian StyleZhao, Zihan, Hai Ren, Yucheng Wang, Xiangchao Ma, Jiali Jiang, Linfang Wei, and Delian Liu. 2025. "First-Principles Calculations of Plasmon-Induced Hot Carrier Properties of μ-Ag3Al" Nanomaterials 15, no. 10: 761. https://doi.org/10.3390/nano15100761
APA StyleZhao, Z., Ren, H., Wang, Y., Ma, X., Jiang, J., Wei, L., & Liu, D. (2025). First-Principles Calculations of Plasmon-Induced Hot Carrier Properties of μ-Ag3Al. Nanomaterials, 15(10), 761. https://doi.org/10.3390/nano15100761






