Electromagnetic Wavefront Engineering by Switchable and Multifunctional Kirigami Metasurfaces
Abstract
1. Introduction
2. Results and Discussions
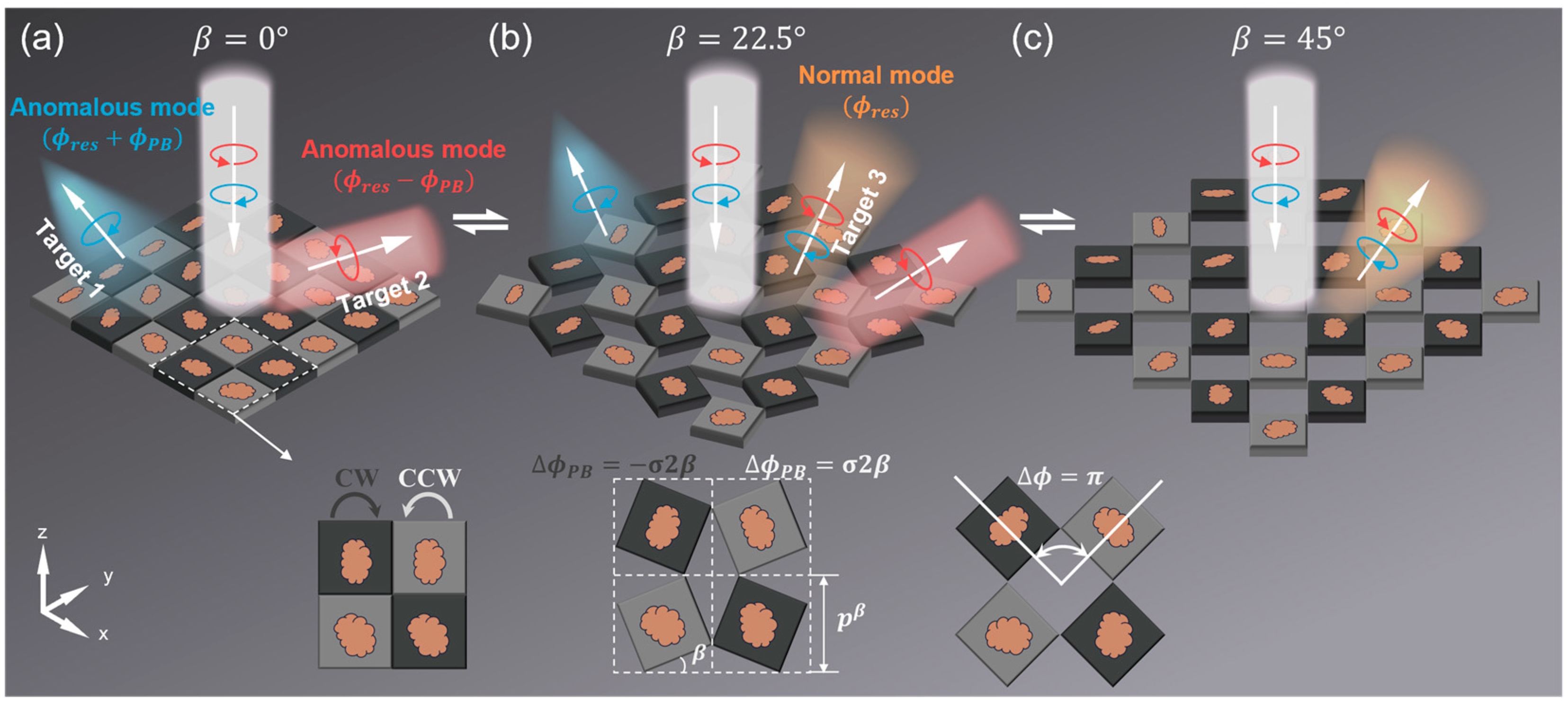
2.1. Basic Concept
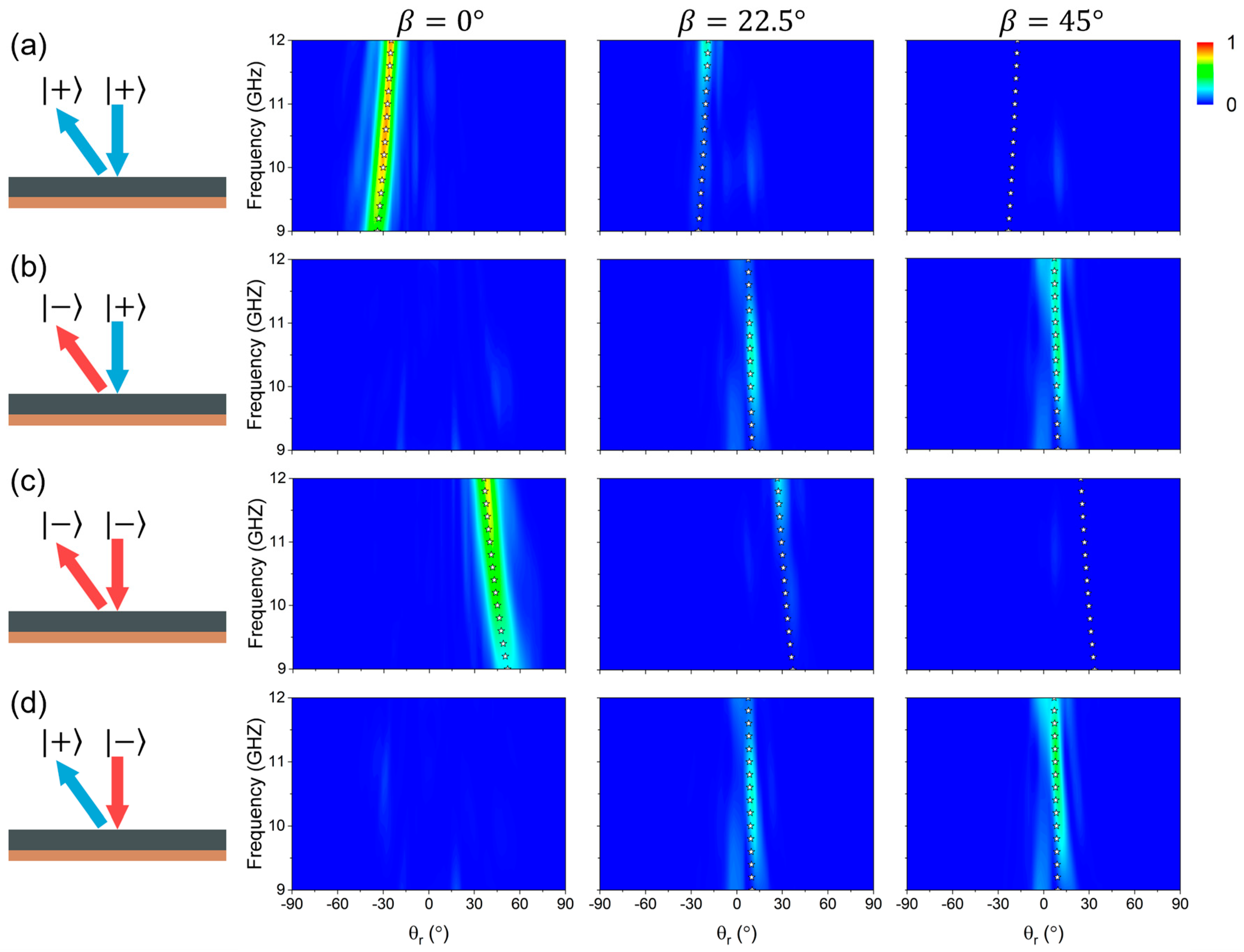
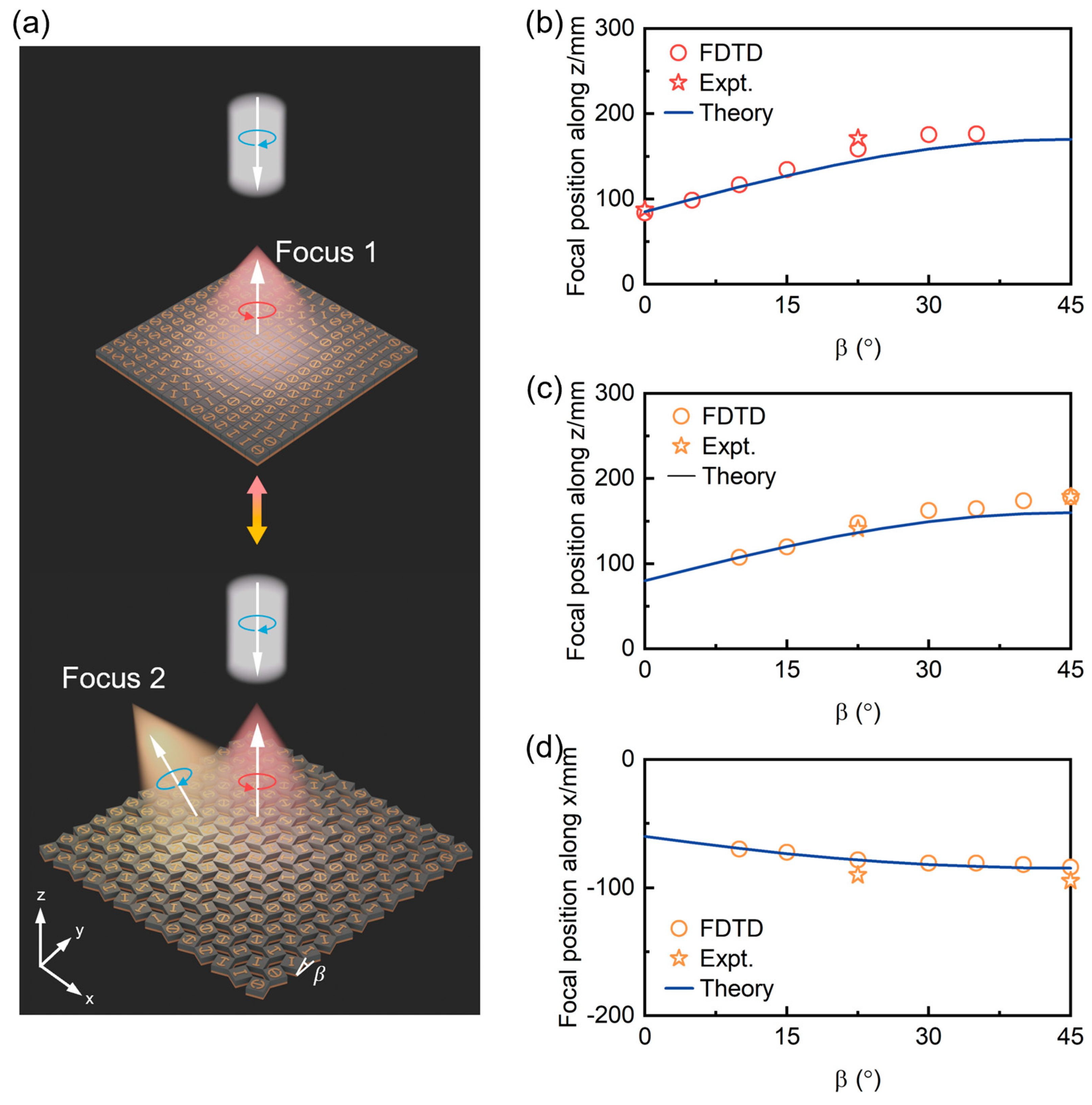
2.2. Switchable Multiple-Beam Meta-Reflector
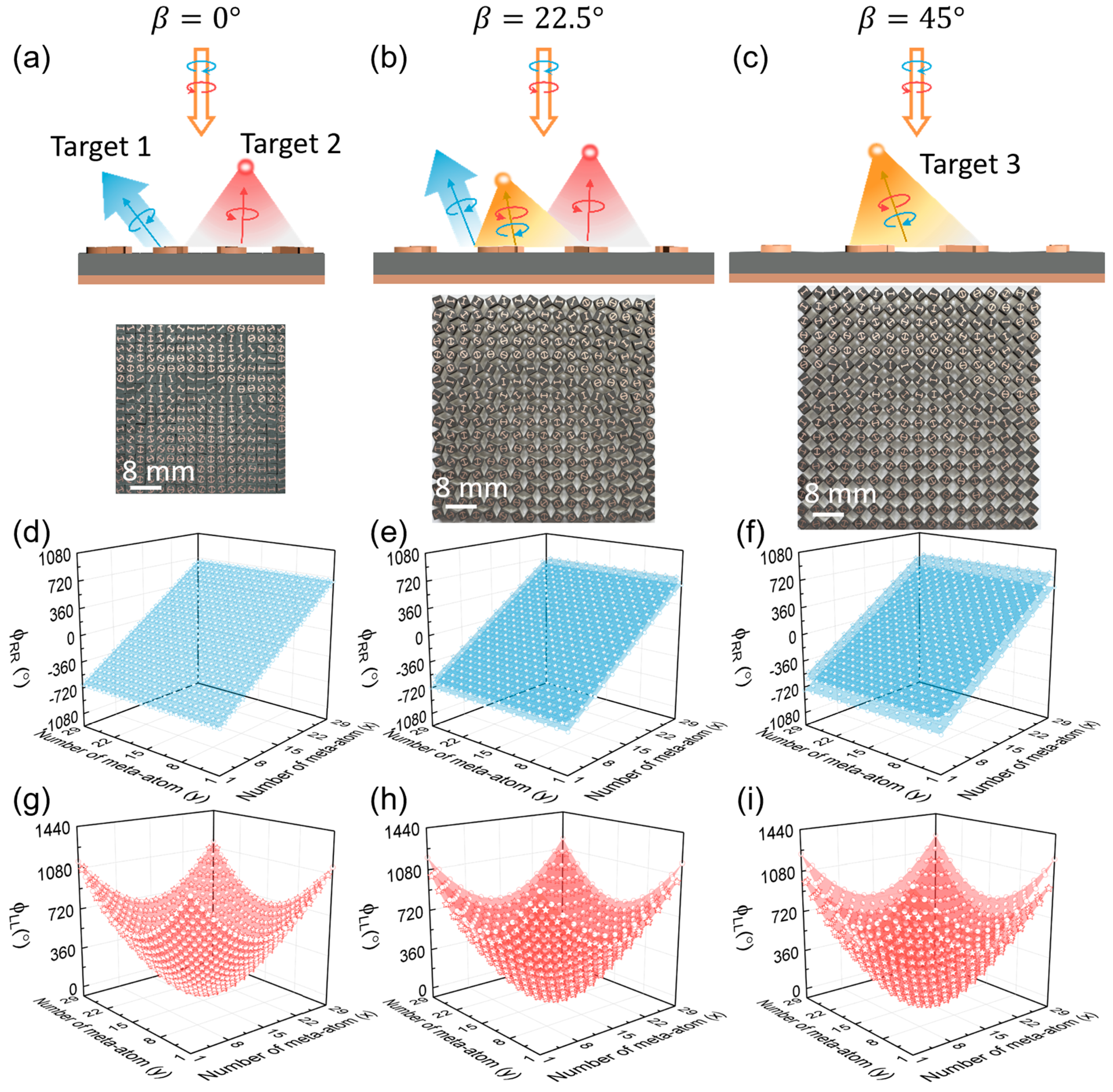
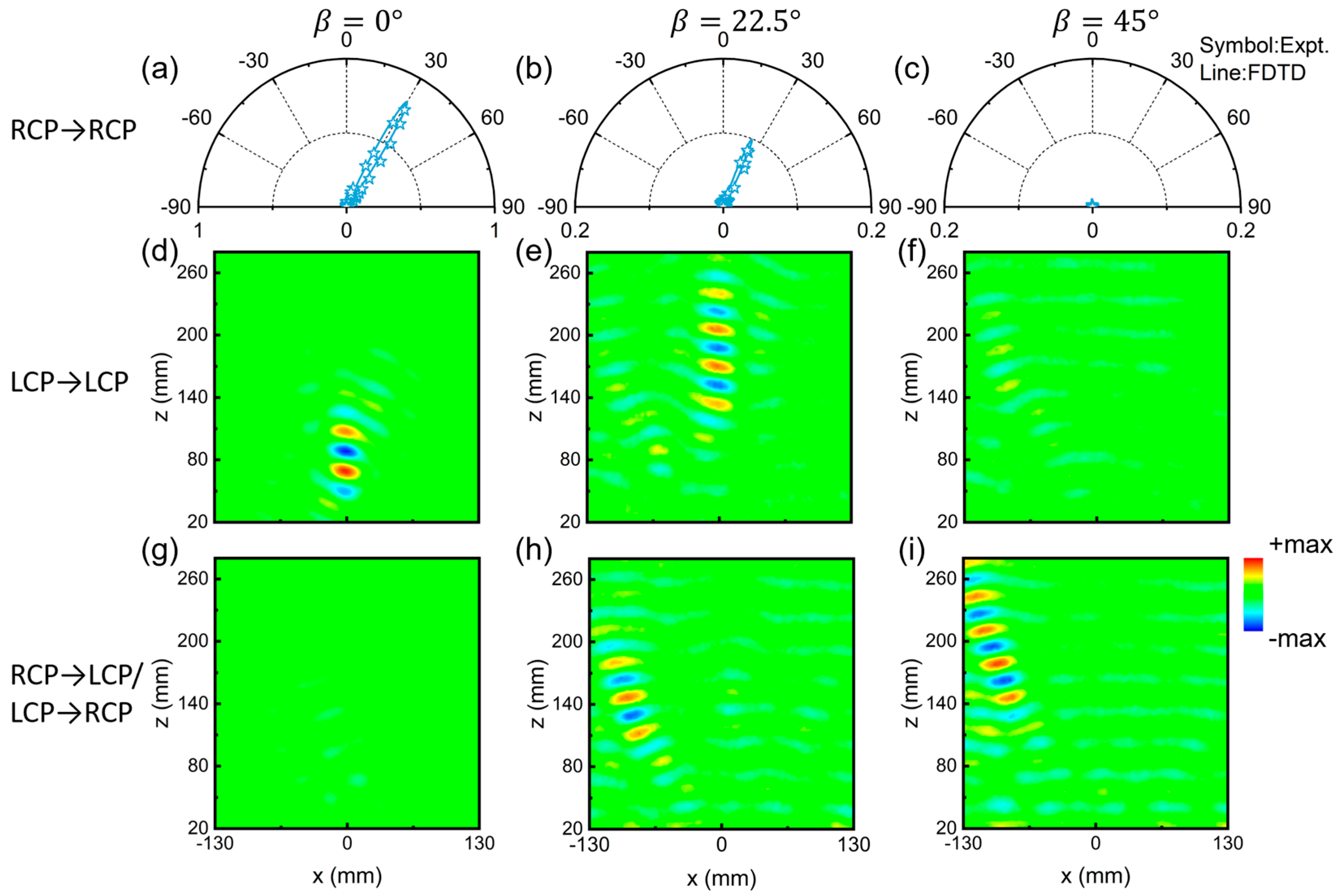
2.3. Kirigami Metadevice for Achieving Switchable Complex Wavefront Engineering
3. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sun, S.L.; Yang, K.Y.; Wang, C.M.; Juan, T.K.; Chen, W.T.; Liao, C.Y.; He, Q.; Xiao, S.Y.; Kung, W.T.; Guo, G.Y.; et al. High-Efficiency Broadband Anomalous Reflection by Gradient Meta-Surfaces. Nano Lett. 2012, 12, 6223–6229. [Google Scholar] [CrossRef] [PubMed]
- Yu, N.F.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.P.; Capasso, F.; Gaburro, Z. Light Propagation with Phase Discontinuities: Generalized Laws of Reflection and Refraction. Science 2011, 334, 333–337. [Google Scholar] [CrossRef]
- Sun, S.L.; He, Q.; Xiao, S.Y.; Xu, Q.; Li, X.; Zhou, L. Gradient-index meta-surfaces as a bridge linking propagating waves and surface waves. Nat. Mater. 2012, 11, 426–431. [Google Scholar] [CrossRef]
- Li, S.Q.; Wang, Z.; Dong, S.H.; Yi, S.X.; Guan, F.X.; Chen, Y.Z.; Guo, H.J.; He, Q.; Zhou, L.; Sun, S.L. Helicity-delinked manipulations on surface waves and propagating waves by metasurfaces. Nanophotonics 2020, 9, 3473–3481. [Google Scholar] [CrossRef]
- Huang, L.L.; Chen, X.Z.; Mühlenbernd, H.; Li, G.X.; Bai, B.F.; Tan, Q.F.; Jin, G.F.; Zentgraf, T.; Zhang, S. Dispersionless Phase Discontinuities for Controlling Light Propagation. Nano Lett. 2012, 12, 5750–5755. [Google Scholar] [CrossRef]
- Luo, W.J.; Xiao, S.Y.; He, Q.; Sun, S.L.; Zhou, L. Photonic Spin Hall Effect with Nearly 100% Efficiency. Adv. Opt. Mater. 2015, 3, 1102–1108. [Google Scholar] [CrossRef]
- Luo, W.J.; Sun, S.L.; Xu, H.X.; He, Q.; Zhou, L. Transmissive Ultrathin Pancharatnam-Berry Metasurfaces with nearly 100% Efficiency. Phys. Rev. Appl. 2017, 7, 1102–1108. [Google Scholar] [CrossRef]
- Li, X.; Xiao, S.Y.; Cai, B.G.; He, Q.; Cui, T.J.; Zhou, L. Flat metasurfaces to focus electromagnetic waves in reflection geometry. Opt. Lett. 2012, 37, 4940–4942. [Google Scholar] [CrossRef]
- Aieta, F.; Genevet, P.; Kats, M.A.; Yu, N.F.; Blanchard, R.; Gahurro, Z.; Capasso, F. Aberration-Free Ultrathin Flat Lenses and Axicons at Telecom Wavelengths Based on Plasmonic Metasurfaces. Nano Lett. 2012, 12, 4932–4936. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.T.; Yang, K.Y.; Wang, C.M.; Huang, Y.W.; Sun, G.; Chiang, I.D.; Liao, C.Y.; Hsu, W.L.; Lin, H.T.; Sun, S.; et al. High-Efficiency Broadband Meta-Hologram with Polarization-Controlled Dual Images. Nano Lett. 2014, 14, 225–230. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.L.; Chen, X.Z.; Mühlenbernd, H.; Zhang, H.; Chen, S.M.; Bai, B.F.; Tan, Q.F.; Jin, G.F.; Cheah, K.W.; Qiu, C.W.; et al. Three-dimensional optical holography using a plasmonic metasurface. Nat. Commun. 2013, 4, 2808. [Google Scholar] [CrossRef]
- Yang, Y.M.; Kelley, K.; Sachet, E.; Campione, S.; Luk, T.S.; Maria, J.P.; Sinclair, M.B.; Brener, I. Femtosecond optical polarization switching using a cadmium oxide-based perfect absorber. Nat. Photonics 2017, 11, 390–395. [Google Scholar] [CrossRef]
- Shu, F.Z.; Wang, J.N.; Peng, R.W.; Xiong, B.; Fan, R.H.; Gao, Y.J.; Liu, Y.M.; Qi, D.X.; Wang, M. Electrically Driven Tunable Broadband Polarization States via Active Metasurfaces Based on Joule-Heat-Induced Phase Transition of Vanadium Dioxide. Laser Photonics Rev. 2021, 15, 2100155. [Google Scholar] [CrossRef]
- Tittl, A.; Michel, A.K.U.; Schäferling, M.; Yin, X.H.; Gholipour, B.; Cui, L.; Wuttig, M.; Taubner, T.; Neubrech, F.; Giessen, H. A Switchable Mid-Infrared Plasmonic Perfect Absorber with Multispectral Thermal Imaging Capability. Adv. Mater. 2015, 27, 4597–4603. [Google Scholar] [CrossRef]
- Sautter, J.; Staude, I.; Decker, M.; Rusak, E.; Neshev, D.N.; Brener, I.; Kivshar, Y.S. Active Tuning of All-Dielectric Metasurfaces. ACS Nano 2015, 9, 4308–4315. [Google Scholar] [CrossRef] [PubMed]
- Zeng, B.B.; Huang, Z.Q.; Singh, A.; Yao, Y.; Azad, A.K.; Mohite, A.D.; Taylor, A.J.; Smith, D.R.; Chen, H.T. Hybrid graphene metasurfaces for high-speed mid-infrared light modulation and single-pixel imaging. Light Sci. Appl. 2018, 7, 51. [Google Scholar] [CrossRef] [PubMed]
- Biswas, S.; Grajower, M.Y.; Watanabe, K.; Taniguchi, T.; Atwater, H.A. Broadband electro-optic polarization conversion with atomically thin black phosphorus. Science 2021, 374, 448–453. [Google Scholar] [CrossRef]
- Fallahi, A.; Perruisseau-Carrier, J. Design of tunable biperiodic graphene metasurfaces. Phys. Rev. B 2012, 86, 195408. [Google Scholar] [CrossRef]
- Squires, A.D.; Gao, X.; Du, J.; Han, Z.J.; Seo, D.H.; Cooper, J.S.; Murdock, A.T.; Lam, S.K.H.; Zhang, T.; Van Der Laan, T. Electrically tuneable terahertz metasurface enabled by a graphene/gold bilayer structure. Commun. Mater. 2022, 3, 56. [Google Scholar] [CrossRef]
- Park, J.; Kang, J.H.; Liu, X.G.; Brongersma, M.L. Electrically Tunable Epsilon-Near-Zero (ENZ) Metafilm Absorbers. Sci. Rep. 2015, 5, 15754. [Google Scholar] [CrossRef]
- Liu, X.B.; Wang, Q.; Zhang, X.Q.; Li, H.; Xu, Q.; Xu, Y.H.; Chen, X.Y.; Li, S.X.; Liu, M.; Tian, Z.; et al. Thermally Dependent Dynamic Meta-Holography Using a Vanadium Dioxide Integrated Metasurface. Adv. Opt. Mater. 2019, 7, 1900175. [Google Scholar] [CrossRef]
- Shcherbakov, M.R.; Liu, S.; Zubyuk, V.V.; Vaskin, A.; Vabishchevich, P.P.; Keeler, G.; Pertsch, T.; Dolgova, T.V.; Staude, I.; Brener, I.; et al. Ultrafast all-optical tuning of direct-gap semiconductor metasurfaces. Nat. Commun. 2017, 8, 17. [Google Scholar] [CrossRef]
- Zhang, X.G.; Jiang, W.X.; Jiang, H.L.; Wang, Q.; Tian, H.W.; Bai, L.; Luo, Z.J.; Sun, S.; Luo, Y.; Qiu, C.W.; et al. An optically driven digital metasurface for programming electromagnetic functions. Nat. Electron. 2020, 3, 165–171. [Google Scholar] [CrossRef]
- Li, J.X.; Kamin, S.; Zheng, G.X.; Neubrech, F.; Zhang, S.; Liu, N. Addressable metasurfaces for dynamic holography and optical information encryption. Sci. Adv. 2018, 4, eaar6768. [Google Scholar] [CrossRef] [PubMed]
- Kim, I.; Kim, W.S.; Kim, K.; Ansari, M.A.; Mehmood, M.Q.; Badloe, T.; Kim, Y.; Gwak, J.; Lee, H.; Kim, Y.K.; et al. Holographic metasurface gas sensors for instantaneous visual alarms. Sci. Adv. 2021, 7, eabe9943. [Google Scholar] [CrossRef]
- Xu, H.X.; Sun, S.L.; Tang, S.W.; Ma, S.J.; He, Q.; Wang, G.M.; Cai, T.; Li, H.P.; Zhou, L. Dynamical control on helicity of electromagnetic waves by tunable metasurfaces. Sci. Rep. 2016, 6, 27503. [Google Scholar] [CrossRef] [PubMed]
- Tao, Z.; Wan, X.; Pan, B.C.; Cui, T.J. Reconfigurable conversions of reflection, transmission, and polarization states using active metasurface. Appl. Phys. Lett. 2017, 110, 121901. [Google Scholar] [CrossRef]
- Cui, T.J.; Qi, M.Q.; Wan, X.; Zhao, J.; Cheng, Q. Coding metamaterials, digital metamaterials and programmable metamaterials. Light Sci. Appl. 2014, 3, e218. [Google Scholar] [CrossRef]
- Huang, C.; Zhang, C.L.; Yang, J.N.; Sun, B.; Zhao, B.; Luo, X.G. Reconfigurable Metasurface for Multifunctional Control of Electromagnetic Waves. Adv. Opt. Mater. 2017, 5, 1700485. [Google Scholar] [CrossRef]
- Kossifos, K.M.; Georgiou, J.; Antoniades, M.A. ASIC-Enabled Programmable Metasurfaces-Part 2: Performance and Synthesis. IEEE Trans. Antennas Propag. 2024, 72, 2800–2810. [Google Scholar] [CrossRef]
- Kossifos, K.M.; Georgiou, J.; Antoniades, M.A. ASIC-Enabled Programmable Metasurfaces-Part 1: Design and Characterization. IEEE Trans. Antennas Propag. 2024, 72, 2790–2799. [Google Scholar] [CrossRef]
- Emara, M.K.; Kundu, D.; Macdonell, K.; Rufail, L.; Gupta, S. Reconfigurable Metasurface Reflectors Using Split-Ring Resonators With Co-Designed Biasing for Magnitude/Phase Control. IEEE Trans. Antennas Propag. 2024, 72, 7425–7430. [Google Scholar] [CrossRef]
- Selvanayagam, M.; Eleftheriades, G.V. Experimental Demonstration of Active Electromagnetic Cloaking. Phys. Rev. X 2013, 3, 041011. [Google Scholar] [CrossRef]
- Li, L.L.; Cui, T.J.; Ji, W.; Liu, S.; Ding, J.; Wan, X.; Li, Y.B.; Jiang, M.H.; Qiu, C.W.; Zhang, S. Electromagnetic reprogrammable coding-metasurface holograms. Nat. Commun. 2017, 8, 197. [Google Scholar] [CrossRef] [PubMed]
- Arbabi, E.; Arbabi, A.; Kamali, S.M.; Horie, Y.; Faraji-Dana, M.; Faraon, A. MEMS-tunable dielectric metasurface lens. Nat. Commun. 2018, 9, 812. [Google Scholar] [CrossRef] [PubMed]
- Colburn, S.; Zhan, A.; Majumdar, A. Varifocal zoom imaging with large area focal length adjustable metalenses. Optica 2018, 5, 825–831. [Google Scholar] [CrossRef]
- Liu, S.; Ma, S.J.; Shao, R.W.; Zhang, L.; Yan, T.; Ma, Q.; Zhang, S.; Cui, T.J. Moire metasurfaces for dynamic beamforming. Sci. Adv. 2022, 8, eabo1511. [Google Scholar] [CrossRef] [PubMed]
- Cai, X.D.; Tang, R.; Zhou, H.Y.; Li, Q.S.; Ma, S.J.; Wang, D.Y.; Liu, T.; Ling, X.H.; Tan, W.; He, Q.; et al. Dynamically controlling terahertz wavefronts with cascaded metasurfaces. Adv. Photonics 2021, 3, 036003. [Google Scholar] [CrossRef]
- Ee, H.S.; Agarwal, R. Tunable Metasurface and Flat Optical Zoom Lens on a Stretchable Substrate. Nano Lett. 2016, 16, 2818–2823. [Google Scholar] [CrossRef]
- Malek, S.C.; Ee, H.S.; Agarwal, R. Strain Multiplexed Metasurface Holograms on a Stretchable Substrate. Nano Lett. 2017, 17, 3641–3645. [Google Scholar] [CrossRef]
- Callewaert, F.; Velev, V.; Jiang, S.Z.; Sahakian, A.V.; Kumar, P.; Aydin, K. Inverse-designed stretchable metalens with tunable focal distance. Appl. Phys. Lett. 2018, 112, 091102. [Google Scholar] [CrossRef]
- Wang, Z.J.; Jing, L.Q.; Yao, K.; Yang, Y.H.; Zheng, B.; Soukoulis, C.M.; Chen, H.S.; Liu, Y.M. Origami-Based Reconfigurable Metamaterials for Tunable Chirality. Adv. Mater. 2017, 29, 1700412. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Shen, L.; Jing, L.Q.; Xu, S.; Zheng, B.; Lin, X.; Yang, Y.H.; Wang, Z.J.; Chen, H.S. Origami Metawall: Mechanically Controlled Absorption and Deflection of Light. Adv. Sci. 2019, 6, 1901434. [Google Scholar] [CrossRef]
- Zheng, Y.L.; Chen, K.; Yang, W.X.; Wu, L.X.; Qu, K.; Zhao, J.M.; Jiang, T.; Feng, Y.J. Kirigami Reconfigurable Gradient Metasurface. Adv. Funct. Mater. 2022, 32, 2107699. [Google Scholar] [CrossRef]
- Han, D.H.; Li, W.K.; Liu, M.; Sun, T.; Hou, Y.S.; Chen, X.M.; Shi, H.Y.; Fan, Z.J.; Wang, X.Q.; Meng, F.Q.; et al. Kirigami-Inspired Planar Deformable Metamaterials for Multiple Dynamic Electromagnetic Manipulations. Laser Photonics Rev. 2023, 17, 2300374. [Google Scholar] [CrossRef]
- Yang, Y.F.; Vallecchi, A.; Shamonina, E.; Stevens, C.J.; You, Z. A new class of transformable kirigami metamaterials for reconfigurable electromagnetic systems. Sci. Rep. 2023, 13, 1219. [Google Scholar] [CrossRef] [PubMed]
- Grima, J.N.; Evans, K.E. Auxetic behavior from rotating squares. J. Mater. Sci. Lett. 2000, 19, 1563–1565. [Google Scholar] [CrossRef]
- Shitrit, N.; Bretner, I.; Gorodetski, Y.; Kleiner, V.; Hasman, E. Optical Spin Hall Effects in Plasmonic Chains. Nano Lett. 2011, 11, 2038–2042. [Google Scholar] [CrossRef]
- Dong, S.H.; Li, S.Q.; Ling, X.H.; Hu, G.W.; Li, Y.; Zhu, H.Y.; Zhou, L.; Sun, S.L. Broadband spin-unlocked metasurfaces for bifunctional wavefront manipulations. Appl. Phys. Lett. 2022, 120, 181702. [Google Scholar] [CrossRef]
- Chen, Y.Z.; Zheng, X.Y.; Zhang, X.Y.; Pan, W.K.; Wang, Z.; Li, S.Q.; Dong, S.H.; He, Q.; Liu, F.F.; Zhou, L.; et al. Efficient Meta-couplers Squeezing Propagating Light into On-Chip Subwavelength Devices in a Controllable Way. Nano Lett. 2023, 23, 3326–3333. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Yao, Y.; Pan, W.K.; Zhou, H.Y.; Chen, Y.Z.; Lin, J.; Hao, J.M.; Xiao, S.Y.; He, Q.; Sun, S.L.; et al. Bifunctional Manipulation of Terahertz Waves with High-Efficiency Transmissive Dielectric Metasurfaces. Adv. Sci. 2023, 10, 2205499. [Google Scholar] [CrossRef] [PubMed]
- Kamali, S.M.; Arbabi, E.; Arbabi, A.; Horie, Y.; Faraon, A. Highly tunable elastic dielectric metasurface lenses. Laser Photonics Rev. 2016, 10, 1002–1008. [Google Scholar] [CrossRef]
- Cui, J.Z.; Huang, T.Y.; Luo, Z.C.; Testa, P.; Gu, H.R.; Chen, X.Z.; Nelson, B.J.; Heyderman, L.J. Nanomagnetic encoding of shape-morphing micromachines. Nature 2019, 575, 164–168. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.K.; Wang, W.; Sinhmar, H.; Griniasty, I.; Kim, J.Z.; Pelster, J.T.; Chaudhari, P.; Reynolds, M.F.; Cao, M.C.; Muller, D.A.; et al. Electronically configurable microscopic metasheet robots. Nat. Mater. 2025, 24, 109–115. [Google Scholar] [CrossRef] [PubMed]
- Smart, C.L.; Pearson, T.G.; Liang, Z.; Lim, M.X.; Abdelrahman, M.I.; Monticone, F.; Cohen, I.; McEuen, P.L. Magnetically programmed diffractive robotics. Science 2024, 386, 1031–1037. [Google Scholar] [CrossRef] [PubMed]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Shi, Y.; Li, L.; Zhu, Z.; Liu, M.; Jin, X.; Li, H.; Jiang, G.; Cui, J.; Ma, S.; et al. Electromagnetic Wavefront Engineering by Switchable and Multifunctional Kirigami Metasurfaces. Nanomaterials 2025, 15, 61. https://doi.org/10.3390/nano15010061
Wang Y, Shi Y, Li L, Zhu Z, Liu M, Jin X, Li H, Jiang G, Cui J, Ma S, et al. Electromagnetic Wavefront Engineering by Switchable and Multifunctional Kirigami Metasurfaces. Nanomaterials. 2025; 15(1):61. https://doi.org/10.3390/nano15010061
Chicago/Turabian StyleWang, Yingying, Yang Shi, Liangwei Li, Zhiyan Zhu, Muhan Liu, Xiangyu Jin, Haodong Li, Guobang Jiang, Jizhai Cui, Shaojie Ma, and et al. 2025. "Electromagnetic Wavefront Engineering by Switchable and Multifunctional Kirigami Metasurfaces" Nanomaterials 15, no. 1: 61. https://doi.org/10.3390/nano15010061
APA StyleWang, Y., Shi, Y., Li, L., Zhu, Z., Liu, M., Jin, X., Li, H., Jiang, G., Cui, J., Ma, S., He, Q., Zhou, L., & Sun, S. (2025). Electromagnetic Wavefront Engineering by Switchable and Multifunctional Kirigami Metasurfaces. Nanomaterials, 15(1), 61. https://doi.org/10.3390/nano15010061







