Author Contributions
Conceptualization, A.O.L.; Methodology, A.O.L.; Software, A.O.L. and N.M.; Validation, A.O.L. and N.M.; Formal analysis, A.O.L.; Investigation, A.O.L. and N.M.; Resources, A.O.L.; Data curation, A.O.L.; Writing—original draft, A.O.L.; Writing—review & editing, A.O.L.; Visualization, A.O.L. and N.M.; Supervision, A.O.L.; Project administration, A.O.L.; Funding acquisition, A.O.L. All authors have read and agreed to the published version of the manuscript.
Figure 1.
(
a) Schematics of isolated Néel Skyrmions in polar magnets with
symmetry (or in multilayers with the induced DMI). (
b,
c) Schematics of bimerons formed as ruptures of the cycloidal spiral according to (
3). The magnetization field wraps only the corresponding half of the S
2 sphere (
b). The upper anti-meron within the blue circle in (
c) and the lower meron within the red circle can mutually annihilate, leaving a bimeron pair with total charge
. (
d,
e) Schematics of bimerons formed as a result of wrapping the upper or lower hemisphere. There are two varieties, merons and anti-merons, with positive and negative vorticity
. (
f) Schematics of two bimerons with opposite polarity obtained from the axisymmetric Skyrmion (middle panel) by magnetization rotation around the
y axis with the angle
. The magnetization in the center of the isolated Skyrmion (the middle panel in (
f), point
O) now points horizontally along the dipole moment of the bimeron in the upper and lower panels of (
f). Two points
A and
B with
within the isolated Skyrmions (the middle panel in (
f)) now become the centers of circular and crescent-shaped merons (the upper and lower panels of (
f)).
Figure 1.
(
a) Schematics of isolated Néel Skyrmions in polar magnets with
symmetry (or in multilayers with the induced DMI). (
b,
c) Schematics of bimerons formed as ruptures of the cycloidal spiral according to (
3). The magnetization field wraps only the corresponding half of the S
2 sphere (
b). The upper anti-meron within the blue circle in (
c) and the lower meron within the red circle can mutually annihilate, leaving a bimeron pair with total charge
. (
d,
e) Schematics of bimerons formed as a result of wrapping the upper or lower hemisphere. There are two varieties, merons and anti-merons, with positive and negative vorticity
. (
f) Schematics of two bimerons with opposite polarity obtained from the axisymmetric Skyrmion (middle panel) by magnetization rotation around the
y axis with the angle
. The magnetization in the center of the isolated Skyrmion (the middle panel in (
f), point
O) now points horizontally along the dipole moment of the bimeron in the upper and lower panels of (
f). Two points
A and
B with
within the isolated Skyrmions (the middle panel in (
f)) now become the centers of circular and crescent-shaped merons (the upper and lower panels of (
f)).
![Nanomaterials 14 00504 g001]()
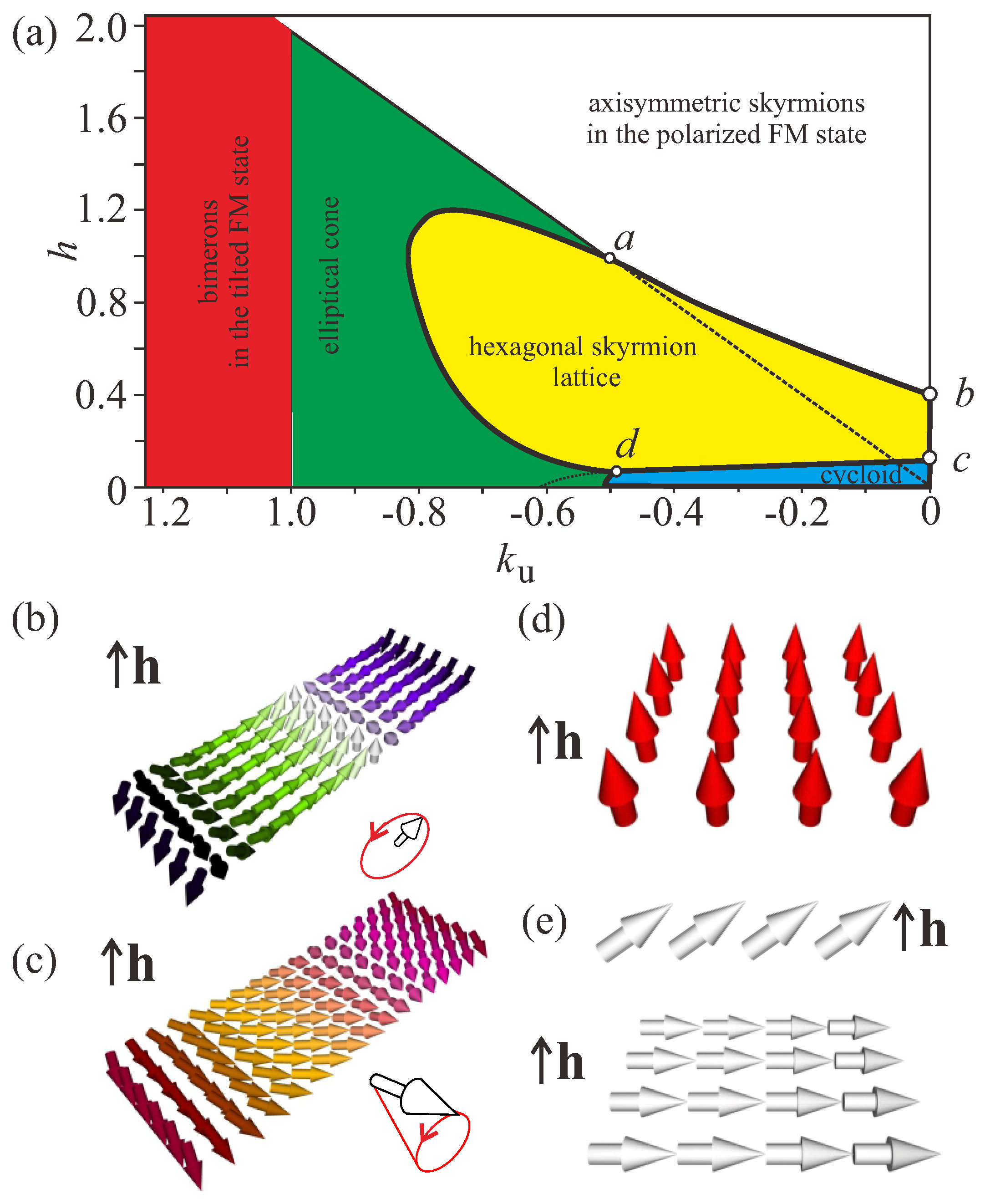
Figure 2.
(
a) Magnetic phase diagram of the solutions for model (
7) with easy-plane uniaxial anisotropy (EPA). The filled areas designate regions of thermodynamic stability of the corresponding phases: blue shading—cycloidal spiral (
b); green shading—elliptical cone (
c); white shading—polarized ferromagnetic state (
d); yellow shading—hexagonal Skyrmion lattice; red shading—tilted ferromagnetic state (
e). The thick black lines indicate the first-order phase transitions between corresponding phases, while the thin black lines indicate the second-order phase transitions. The field is measured in units of
, i.e.,
, and
is the non-dimensional anisotropy constant.
Figure 2.
(
a) Magnetic phase diagram of the solutions for model (
7) with easy-plane uniaxial anisotropy (EPA). The filled areas designate regions of thermodynamic stability of the corresponding phases: blue shading—cycloidal spiral (
b); green shading—elliptical cone (
c); white shading—polarized ferromagnetic state (
d); yellow shading—hexagonal Skyrmion lattice; red shading—tilted ferromagnetic state (
e). The thick black lines indicate the first-order phase transitions between corresponding phases, while the thin black lines indicate the second-order phase transitions. The field is measured in units of
, i.e.,
, and
is the non-dimensional anisotropy constant.
Figure 3.
Internal magnetic structure of an isolated bimeron characterized by the -color plots of the -component of the magnetization (a), the DMI and total energy densities (c,d), and the topological charge density (e); , . The cross-cut (b) along the meron center shows the part with the opposite rotational sense, the center of which is located at distance from the center of the circular meron, with p being the distance between the centers of the vortex and antivortex. The insets in (b) show corresponding zoomed 2D (i) and 1D (ii) magnetization distributions, i.e., in (i) the color indicates the magnetization value in the range . The corresponding color plots for the exchange energy density and the anisotropy energy densities are shown in (f,g). The Zeeman energy is 0, as , while the field is measured in the units of , i.e., . The magnetization vector is normalized to unity; is the nondimensional anisotropy constant; the spatial coordinates are measured in units of the characteristic length of modulated states ; and the value for zero magnetic field is the period of the cycloid.
Figure 3.
Internal magnetic structure of an isolated bimeron characterized by the -color plots of the -component of the magnetization (a), the DMI and total energy densities (c,d), and the topological charge density (e); , . The cross-cut (b) along the meron center shows the part with the opposite rotational sense, the center of which is located at distance from the center of the circular meron, with p being the distance between the centers of the vortex and antivortex. The insets in (b) show corresponding zoomed 2D (i) and 1D (ii) magnetization distributions, i.e., in (i) the color indicates the magnetization value in the range . The corresponding color plots for the exchange energy density and the anisotropy energy densities are shown in (f,g). The Zeeman energy is 0, as , while the field is measured in the units of , i.e., . The magnetization vector is normalized to unity; is the nondimensional anisotropy constant; the spatial coordinates are measured in units of the characteristic length of modulated states ; and the value for zero magnetic field is the period of the cycloid.
![Nanomaterials 14 00504 g003]()
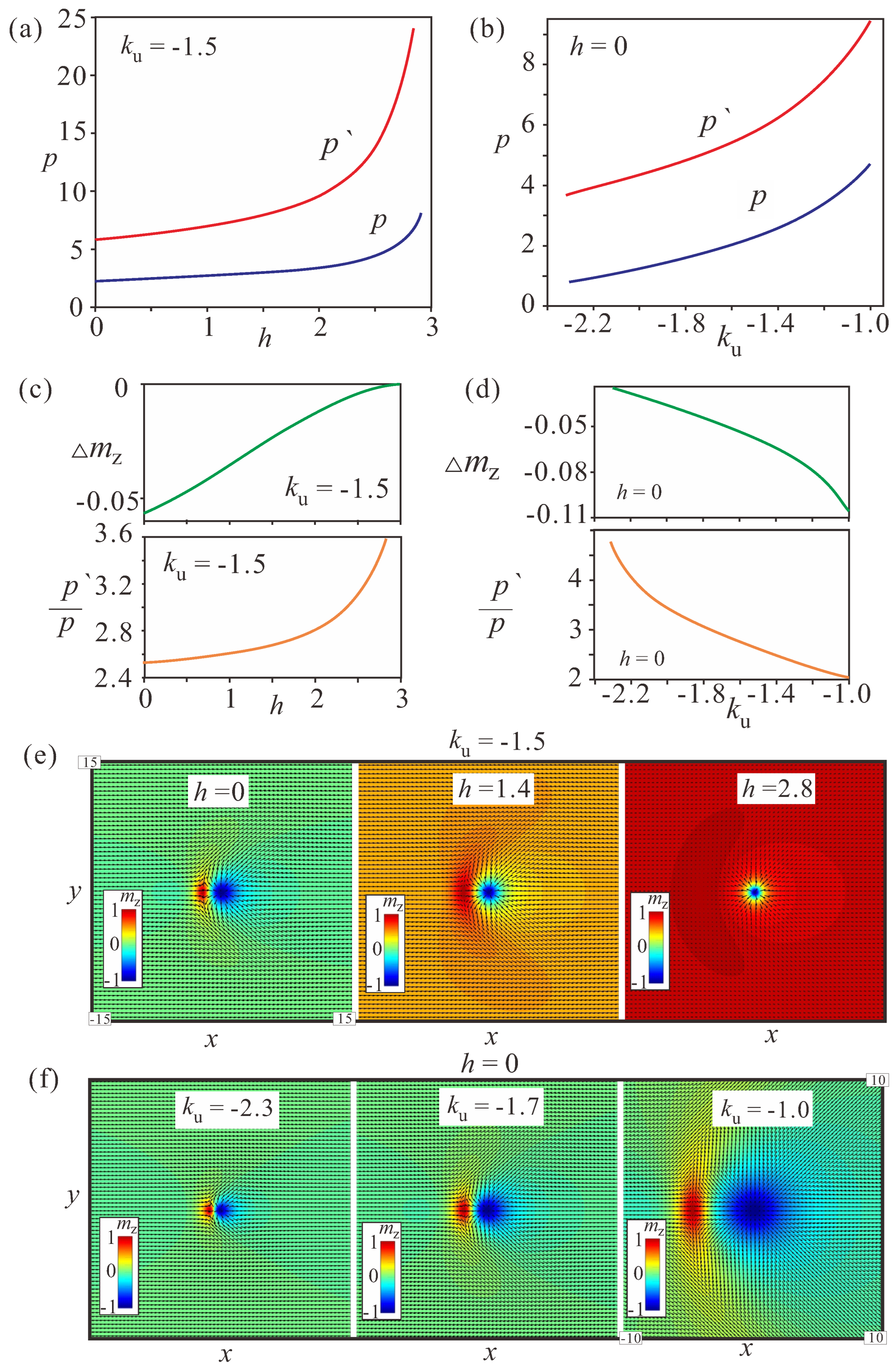
Figure 4.
(a,b) Field- and anisotropy-driven evolution of the parameters p and for a fixed value of the anisotropy (, (a)) and field (, (b)), correspondingly; p is the distance between the centers of the vortex and the antivortex, while is the distance from the center of the circular meron to the center of the circular area with the wrong rotational sense. For the field-driven transformation of bimerons, the parameters p and as well as their ratio (c) all increase. This means that the parameter increases faster than the parameter p, with both processes indicating the transformation into an isolated Skyrmion surrounded by a homogeneous state with . The depth of the region with the wrong twist tends to zero (c). Qualitatively, the same process occurs with growing anisotropy (b,d). At some critical anisotropy value, the bimerons become too small to be addressed using the chosen cell sizes of the numerical grids. The color plots of the magnetization in (e,f) reflect the above-mentioned field- and anisotropy-driven transformations. The black arrows in all color plots are the projections of the magnetization onto the plane.
Figure 4.
(a,b) Field- and anisotropy-driven evolution of the parameters p and for a fixed value of the anisotropy (, (a)) and field (, (b)), correspondingly; p is the distance between the centers of the vortex and the antivortex, while is the distance from the center of the circular meron to the center of the circular area with the wrong rotational sense. For the field-driven transformation of bimerons, the parameters p and as well as their ratio (c) all increase. This means that the parameter increases faster than the parameter p, with both processes indicating the transformation into an isolated Skyrmion surrounded by a homogeneous state with . The depth of the region with the wrong twist tends to zero (c). Qualitatively, the same process occurs with growing anisotropy (b,d). At some critical anisotropy value, the bimerons become too small to be addressed using the chosen cell sizes of the numerical grids. The color plots of the magnetization in (e,f) reflect the above-mentioned field- and anisotropy-driven transformations. The black arrows in all color plots are the projections of the magnetization onto the plane.
![Nanomaterials 14 00504 g004]()
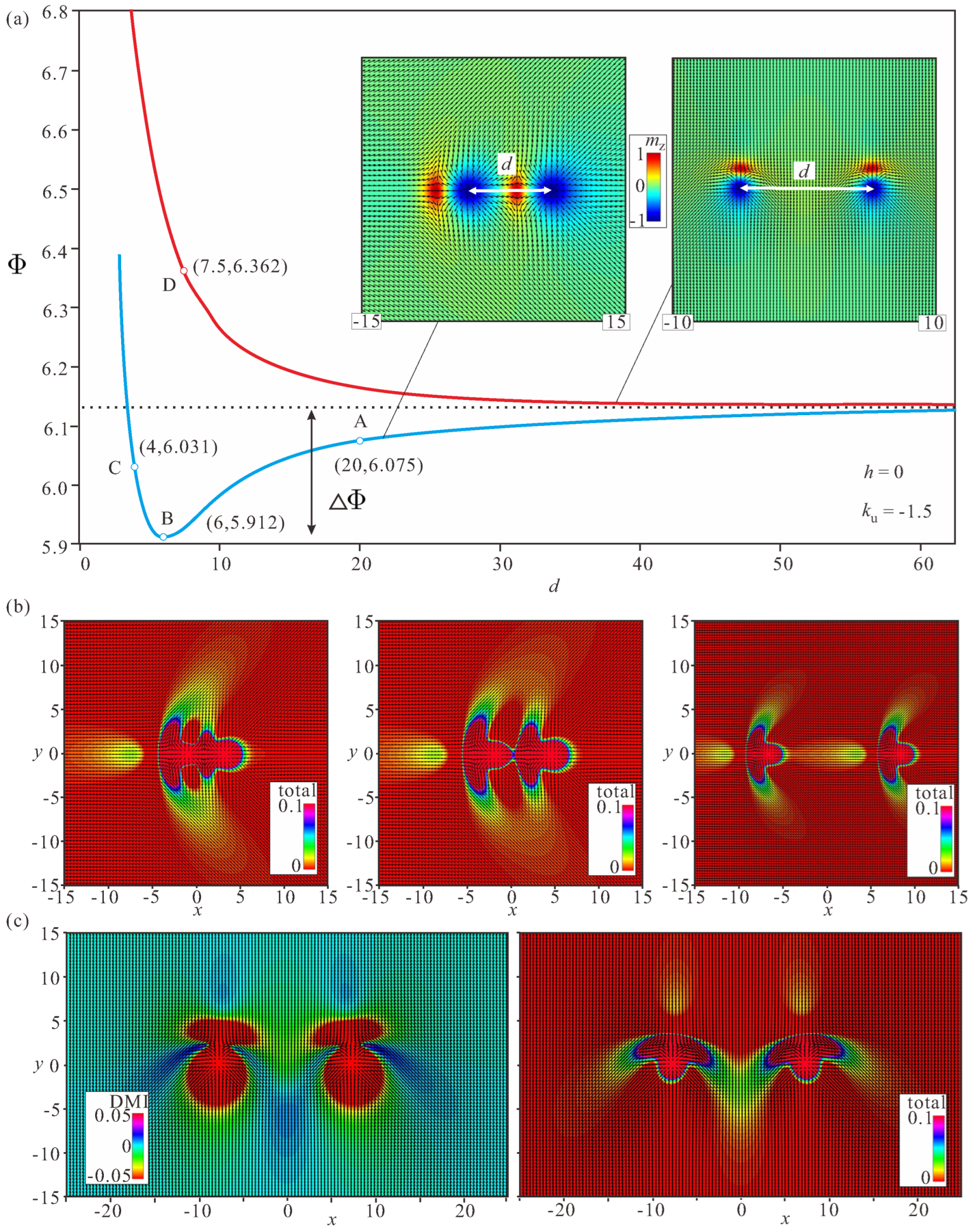
Figure 5.
(a) The inter-bimeron potential versus the distance d between the centers of circular anti-merons for two bimerons oriented head-to-tail (blue curve and left inset) and/or side-by-side (red curve and right inset). The color plots for the total energy density (b) are shown for bimerons located at larger distances (point A, right panel), in the minimum (point B, middle panel), and at shorter distances (point C, left panel). These color plots indicate the underlying reason for the attracting interaction and the minimum of ; at some optimal inter-meron distance, the first bimeron covers the circular region with the positive energy density of the subsequent bimeron. The color plots of the total energy and DMI energy density (c) do not demonstrate any energy benefit from coupling two bimerons. On the contrary, overlapping “wings” lead to an energy increase (red curve in (a)). Here, .
Figure 5.
(a) The inter-bimeron potential versus the distance d between the centers of circular anti-merons for two bimerons oriented head-to-tail (blue curve and left inset) and/or side-by-side (red curve and right inset). The color plots for the total energy density (b) are shown for bimerons located at larger distances (point A, right panel), in the minimum (point B, middle panel), and at shorter distances (point C, left panel). These color plots indicate the underlying reason for the attracting interaction and the minimum of ; at some optimal inter-meron distance, the first bimeron covers the circular region with the positive energy density of the subsequent bimeron. The color plots of the total energy and DMI energy density (c) do not demonstrate any energy benefit from coupling two bimerons. On the contrary, overlapping “wings” lead to an energy increase (red curve in (a)). Here, .
Figure 6.
(a) The interaction potential for two bimerons with the opposite polarities exhibits only the inter-particle repulsion. Here, we orient two bimerons with either their circular merons (the red curve and left panels in (b,c)) or with their crescents (the blue curve and right panels in (b,c)) facing the inter-meron area. The insets show color plots of the magnetization at the indicated points of the curves. To plot both curves, we pinned the magnetization in the centers of the circular anti-merons. Obviously, being unpinned, the two bimerons find a path to annihilate, as they have the opposite topological charges. The corresponding DMI and full energy density distributions are plotted in (c). , .
Figure 6.
(a) The interaction potential for two bimerons with the opposite polarities exhibits only the inter-particle repulsion. Here, we orient two bimerons with either their circular merons (the red curve and left panels in (b,c)) or with their crescents (the blue curve and right panels in (b,c)) facing the inter-meron area. The insets show color plots of the magnetization at the indicated points of the curves. To plot both curves, we pinned the magnetization in the centers of the circular anti-merons. Obviously, being unpinned, the two bimerons find a path to annihilate, as they have the opposite topological charges. The corresponding DMI and full energy density distributions are plotted in (c). , .
Figure 7.
Internal structure of a bimeron chain with six constituent bimerons. (a) Color plot for the -component of the magnetization. (b) Color plot for the DMI energy density. (c) Color plot for the total energy density. (d) Color plot for the energy density of the easy-plane anisotropy. (e) Color plot for the exchange energy density. , . The field is measured in units of , i.e., . The magnetization vector is normalized to unity. is the nondimensional anisotropy constant. Spatial coordinates are measured in units of the characteristic length of modulated states . The value for zero magnetic field is the period of the cycloid.
Figure 7.
Internal structure of a bimeron chain with six constituent bimerons. (a) Color plot for the -component of the magnetization. (b) Color plot for the DMI energy density. (c) Color plot for the total energy density. (d) Color plot for the energy density of the easy-plane anisotropy. (e) Color plot for the exchange energy density. , . The field is measured in units of , i.e., . The magnetization vector is normalized to unity. is the nondimensional anisotropy constant. Spatial coordinates are measured in units of the characteristic length of modulated states . The value for zero magnetic field is the period of the cycloid.
Figure 8.
Internal structure of a roundabout with counterclockwise circling of bimerons. (a) Color plot for the -component of the magnetization. (b) Color plot for the DMI energy density. (c) Color plot for the total energy density. (d) Color plot for the energy density of the easy-plane anisotropy. (e) Color plot for the exchange energy density. , . The field is measured in units of , i.e., . The magnetization vector is normalized to unity. is the nondimensional anisotropy constant. Spatial coordinates are measured in units of the characteristic length of modulated states . The value for zero magnetic field is the period of the cycloid.
Figure 8.
Internal structure of a roundabout with counterclockwise circling of bimerons. (a) Color plot for the -component of the magnetization. (b) Color plot for the DMI energy density. (c) Color plot for the total energy density. (d) Color plot for the energy density of the easy-plane anisotropy. (e) Color plot for the exchange energy density. , . The field is measured in units of , i.e., . The magnetization vector is normalized to unity. is the nondimensional anisotropy constant. Spatial coordinates are measured in units of the characteristic length of modulated states . The value for zero magnetic field is the period of the cycloid.
Figure 9.
Internal structure of a roundabout with clockwise circling of bimerons. (a) Color plot for the -component of the magnetization. (b) Color plot for the DMI energy density. (c) Color plot for the total energy density. (d) Color plot for the energy density of the easy-plane anisotropy. (e) Color plot for the exchange energy density. , . The field is measured in units of , i.e., . The magnetization vector is normalized to unity. is the nondimensional anisotropy constant. Spatial coordinates are measured in units of the characteristic length of modulated states . The value for zero magnetic field is the period of the cycloid.
Figure 9.
Internal structure of a roundabout with clockwise circling of bimerons. (a) Color plot for the -component of the magnetization. (b) Color plot for the DMI energy density. (c) Color plot for the total energy density. (d) Color plot for the energy density of the easy-plane anisotropy. (e) Color plot for the exchange energy density. , . The field is measured in units of , i.e., . The magnetization vector is normalized to unity. is the nondimensional anisotropy constant. Spatial coordinates are measured in units of the characteristic length of modulated states . The value for zero magnetic field is the period of the cycloid.
Figure 10.
Internal structure of a roundabout. (a) Color plot for the -component of the magnetization. (b) Color plot for the DMI energy density. (c) Color plot for the total energy density. (d) Color plot for the energy density of the easy-plane anisotropy. (e) Color plot for the exchange energy density. , . The field is measured in units of , i.e., . The magnetization vector is normalized to unity. is the nondimensional anisotropy constant. Spatial coordinates are measured in units of the characteristic length of modulated states . The value for zero magnetic field is the period of the cycloid.
Figure 10.
Internal structure of a roundabout. (a) Color plot for the -component of the magnetization. (b) Color plot for the DMI energy density. (c) Color plot for the total energy density. (d) Color plot for the energy density of the easy-plane anisotropy. (e) Color plot for the exchange energy density. , . The field is measured in units of , i.e., . The magnetization vector is normalized to unity. is the nondimensional anisotropy constant. Spatial coordinates are measured in units of the characteristic length of modulated states . The value for zero magnetic field is the period of the cycloid.
Figure 11.
Internal structure of a bimeron “crossing”. (a) Color plot for the -component of the magnetization. (b) Color plot for the DMI energy density. (c) Color plot for the total energy density. (d) Color plot for the energy density of the easy-plane anisotropy. (e) Color plot for the exchange energy density. , . The field is measured in units of , i.e., . The magnetization vector is normalized to unity. is the nondimensional anisotropy constant. Spatial coordinates are measured in units of the characteristic length of modulated states . The value for zero magnetic field is the period of the cycloid.
Figure 11.
Internal structure of a bimeron “crossing”. (a) Color plot for the -component of the magnetization. (b) Color plot for the DMI energy density. (c) Color plot for the total energy density. (d) Color plot for the energy density of the easy-plane anisotropy. (e) Color plot for the exchange energy density. , . The field is measured in units of , i.e., . The magnetization vector is normalized to unity. is the nondimensional anisotropy constant. Spatial coordinates are measured in units of the characteristic length of modulated states . The value for zero magnetic field is the period of the cycloid.
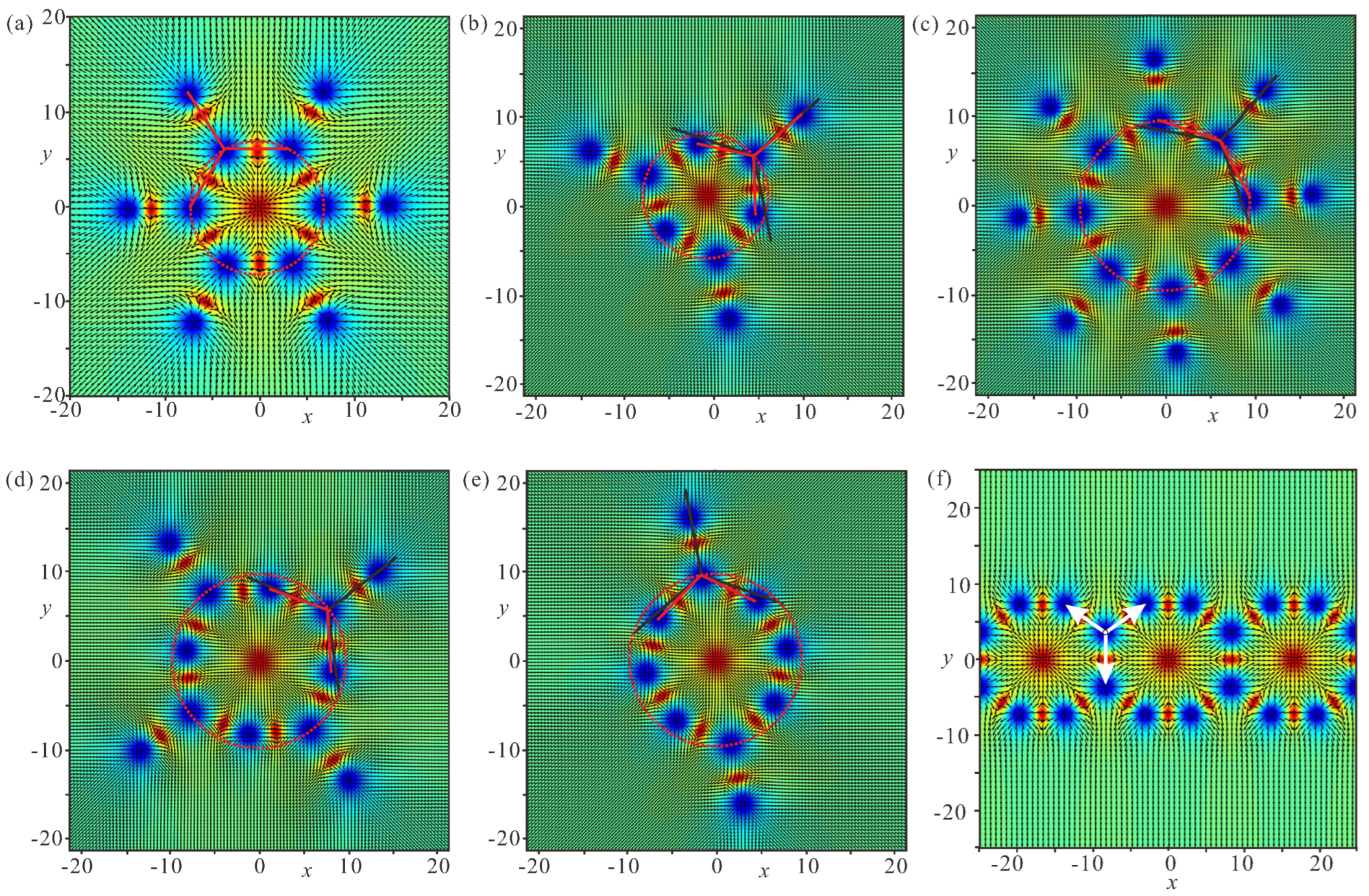
Figure 12.
(
a) Total energy of different bimeron macromolecules in dependence on the number
N of constituent bimerons. The energy of edge states formed at the specimen boundary is excluded. The inset shows the topological charge of the central meron formed in circular macromolecules, computed as
, where
Q is the total charge of the magnetization distribution excluding the edge states and
N is the number of exterior bimerons. The color coding is the same as used in the main graph: red for crossings, blue for
roundabouts, green for
roundabouts, and black for chains. For crossings and
roundabouts, the charges of the central merons are the same,
. Solid lines connecting points with a fixed number
N indicate macromolecules which are robust against transformation into chains. Other macromolecules, indicated by dotted lines, can be wrapped into chains by the displacement of the central meron, i.e., such macromolecules are stable for symmetrical scaling of inter-meron distances but loose their stability while being deformed. (
b) Total energy of bimeron macromolecules taking into account the energy of the edge states, which clearly favor
roundabouts. The edge states bear their own topological charges
, which uniformly shift the dependencies in the inset. (
c,
d) Transformation of a
roundabout with
into a buckled chain (see
Supplementary Video S1). (
e,
f) Transformation of a
roundabout with
into a looped chain (see
Supplementary Video S2). (
g,
h) Transformation of a crossing with
into a crossing with
and fragments of attached chains (see
Supplementary Video S3).
.
Figure 12.
(
a) Total energy of different bimeron macromolecules in dependence on the number
N of constituent bimerons. The energy of edge states formed at the specimen boundary is excluded. The inset shows the topological charge of the central meron formed in circular macromolecules, computed as
, where
Q is the total charge of the magnetization distribution excluding the edge states and
N is the number of exterior bimerons. The color coding is the same as used in the main graph: red for crossings, blue for
roundabouts, green for
roundabouts, and black for chains. For crossings and
roundabouts, the charges of the central merons are the same,
. Solid lines connecting points with a fixed number
N indicate macromolecules which are robust against transformation into chains. Other macromolecules, indicated by dotted lines, can be wrapped into chains by the displacement of the central meron, i.e., such macromolecules are stable for symmetrical scaling of inter-meron distances but loose their stability while being deformed. (
b) Total energy of bimeron macromolecules taking into account the energy of the edge states, which clearly favor
roundabouts. The edge states bear their own topological charges
, which uniformly shift the dependencies in the inset. (
c,
d) Transformation of a
roundabout with
into a buckled chain (see
Supplementary Video S1). (
e,
f) Transformation of a
roundabout with
into a looped chain (see
Supplementary Video S2). (
g,
h) Transformation of a crossing with
into a crossing with
and fragments of attached chains (see
Supplementary Video S3).
.
![Nanomaterials 14 00504 g012]()
Figure 13.
Stable bimeron macromolecules obtained by combinations of “crossings” and “roundabouts” for
(
a,
b) and
(
c–
e) in
roundabouts. In “benzene” (
a), all angles between bimerons are
, as dictated by both ring varieties. In its
counterpart (
c), however, the angle between the bimerons within the ring is
, as specified by the “roundabout”. Less symmetric macromolecules (
b,
d,
e) exhibit structural deformations and the inter-bimeron angles vary around the rings, which may lead to instability (see
Supplementary Video S4). In addition,
“roundabouts” with eight bimerons can alternatively be connected into a stripe—an analogue of the chain (
f).
.
Figure 13.
Stable bimeron macromolecules obtained by combinations of “crossings” and “roundabouts” for
(
a,
b) and
(
c–
e) in
roundabouts. In “benzene” (
a), all angles between bimerons are
, as dictated by both ring varieties. In its
counterpart (
c), however, the angle between the bimerons within the ring is
, as specified by the “roundabout”. Less symmetric macromolecules (
b,
d,
e) exhibit structural deformations and the inter-bimeron angles vary around the rings, which may lead to instability (see
Supplementary Video S4). In addition,
“roundabouts” with eight bimerons can alternatively be connected into a stripe—an analogue of the chain (
f).
.
Figure 14.
(a) The linking process of three chains with the same number of bimerons. The red cross highlights the crossing with the inter-bimeron angles , which facilitates the creation of a bimeron cluster with a square arrangement of bimerons (b). (c) Stable two-dimensional periodic tessellation with hexagonal ordering of bimerons. Such a state is possible only if the sides of the hexagonal cells contain several bimerons (two bimerons in the present case). .
Figure 14.
(a) The linking process of three chains with the same number of bimerons. The red cross highlights the crossing with the inter-bimeron angles , which facilitates the creation of a bimeron cluster with a square arrangement of bimerons (b). (c) Stable two-dimensional periodic tessellation with hexagonal ordering of bimerons. Such a state is possible only if the sides of the hexagonal cells contain several bimerons (two bimerons in the present case). .
Figure 15.
If the cell side of the periodic tessellations in
Figure 14c contains just one bimeron, such a hexagonal order transforms into a random bimeron distribution. As an initial state in the first panel, we use a hexagonal bimeron lattice with a periodic mixture of
roundabouts and
roundabouts. Therefore, periodic boundary conditions can be used at both sides of the numerical grid. The subsequent panels demonstrate the disintegration process toward a random bimeron polymer (see
Supplementary Video S5).
.
Figure 15.
If the cell side of the periodic tessellations in
Figure 14c contains just one bimeron, such a hexagonal order transforms into a random bimeron distribution. As an initial state in the first panel, we use a hexagonal bimeron lattice with a periodic mixture of
roundabouts and
roundabouts. Therefore, periodic boundary conditions can be used at both sides of the numerical grid. The subsequent panels demonstrate the disintegration process toward a random bimeron polymer (see
Supplementary Video S5).
.
Figure 16.
(
a–
d) The internal structure of the hexagonal SkL, shown as color plots of the topological charge density within the yellow-shaded region of the phase diagram in
Figure 2a. With increasing easy-plane anisotropy (from left to right in the first row), the nuclei of merons with the opposite topological charges emerge within the cell boundaries. Mutual transformation between the hexagonal SkL and a disordered bimeron polymer is achieved by changing the uniaxial anisotropy from
to
(second row) and back from
to
(third row). The ordered SkL (
e) is a local energy minimum for
. If the anisotropy is suddenly switched to
, then the SkL undergoes the following transformation: (
f) merons and anti-merons with positive polarity nucleate pairwise within the cell boundary (highlighted by black circles); (
g) the hexagonal cell becomes distorted, enabling merons and anti-merons to approach each other; (
h) merons and anti-merons merge and annihilate (highlighted by white circles); and (
i) only bimerons are left. The vortex originates from the Skyrmion in the center of the SkL, whereas the anti-vortex is a remainder of the boundary (see
Supplementary Video S6). A disordered bimeron polymer (
j) is a metastable cluster formed at
. If the anisotropy switches to
, then the SkL represents the global minimum of the energy functional (
7). This means that the circular merons with polarity against the field become energetically favorable. These anti-merons rearrange and fill the whole space, whereas the anti-vortices with polarity along the field squeeze into the boundary regions (
k,
l). In (
m), the Skyrmions form a disordered state but eventually manage to form an almost perfectly hexagonal arrangement (
n) (see
Supplementary Video S7).
Figure 16.
(
a–
d) The internal structure of the hexagonal SkL, shown as color plots of the topological charge density within the yellow-shaded region of the phase diagram in
Figure 2a. With increasing easy-plane anisotropy (from left to right in the first row), the nuclei of merons with the opposite topological charges emerge within the cell boundaries. Mutual transformation between the hexagonal SkL and a disordered bimeron polymer is achieved by changing the uniaxial anisotropy from
to
(second row) and back from
to
(third row). The ordered SkL (
e) is a local energy minimum for
. If the anisotropy is suddenly switched to
, then the SkL undergoes the following transformation: (
f) merons and anti-merons with positive polarity nucleate pairwise within the cell boundary (highlighted by black circles); (
g) the hexagonal cell becomes distorted, enabling merons and anti-merons to approach each other; (
h) merons and anti-merons merge and annihilate (highlighted by white circles); and (
i) only bimerons are left. The vortex originates from the Skyrmion in the center of the SkL, whereas the anti-vortex is a remainder of the boundary (see
Supplementary Video S6). A disordered bimeron polymer (
j) is a metastable cluster formed at
. If the anisotropy switches to
, then the SkL represents the global minimum of the energy functional (
7). This means that the circular merons with polarity against the field become energetically favorable. These anti-merons rearrange and fill the whole space, whereas the anti-vortices with polarity along the field squeeze into the boundary regions (
k,
l). In (
m), the Skyrmions form a disordered state but eventually manage to form an almost perfectly hexagonal arrangement (
n) (see
Supplementary Video S7).
![Nanomaterials 14 00504 g016]()