Graphene-Based Tunable Dual-Frequency Terahertz Sensor
Abstract
1. Introduction
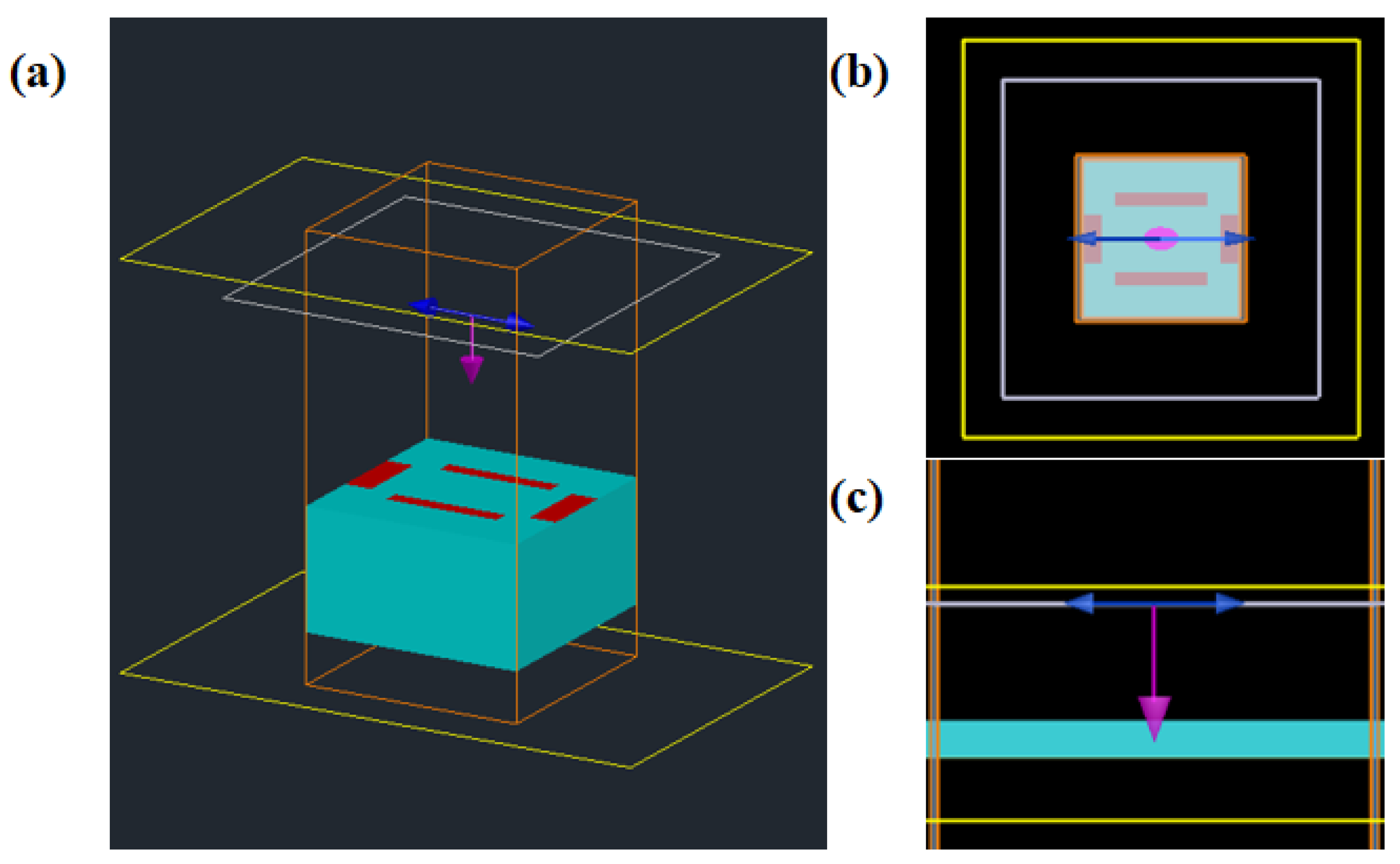
2. Design and Mechanism
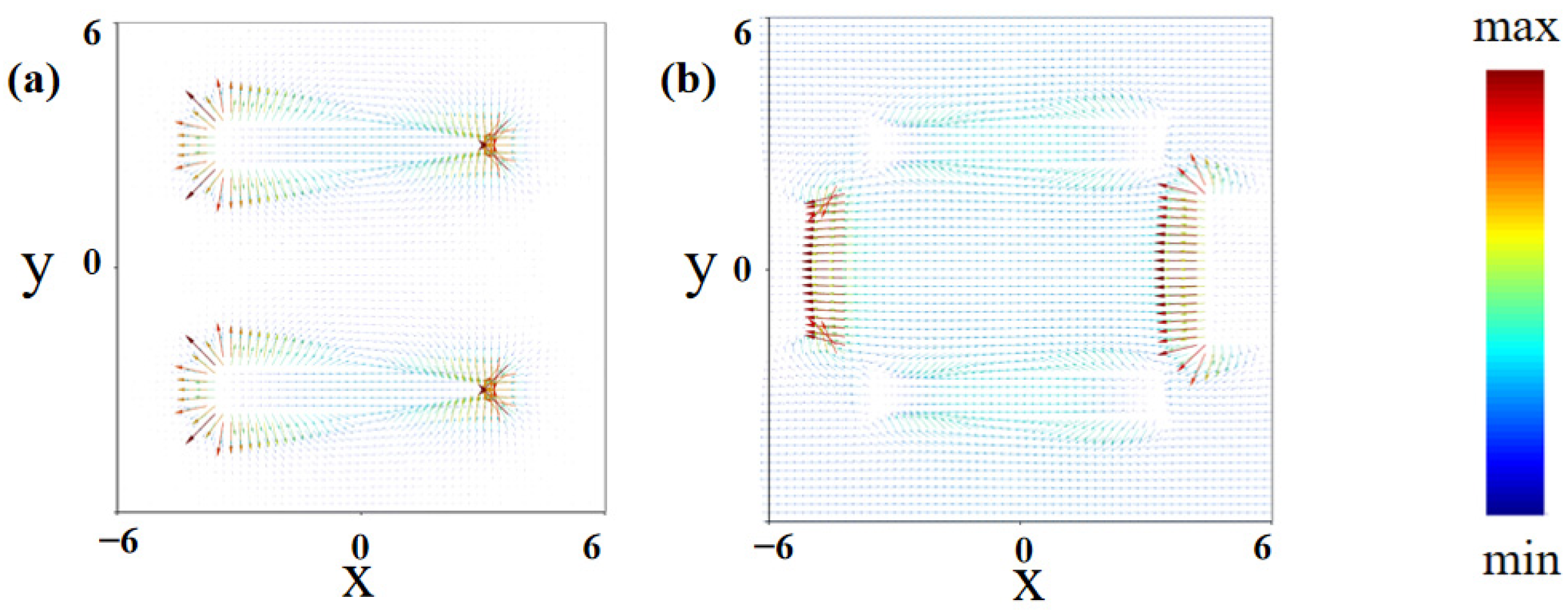
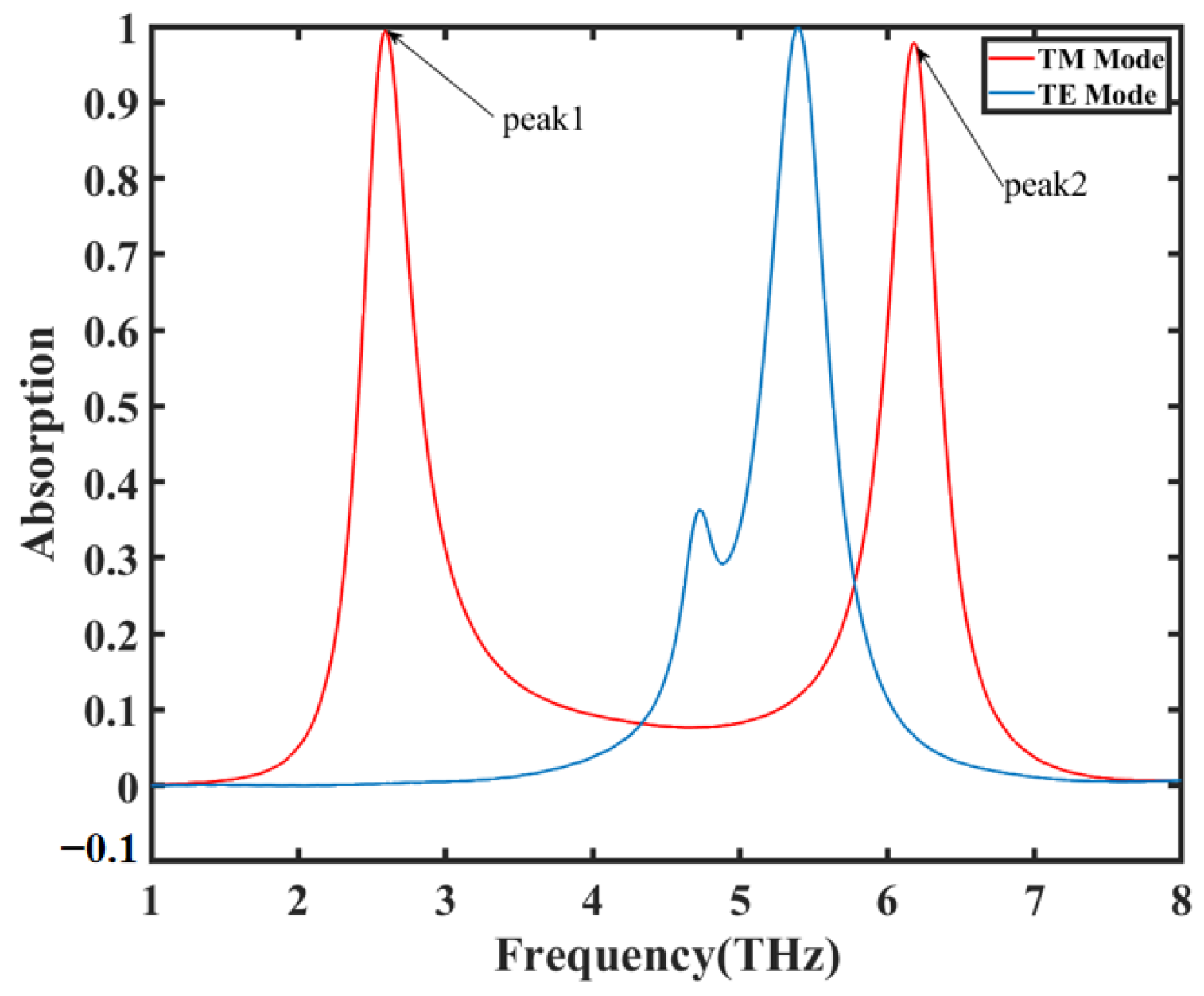
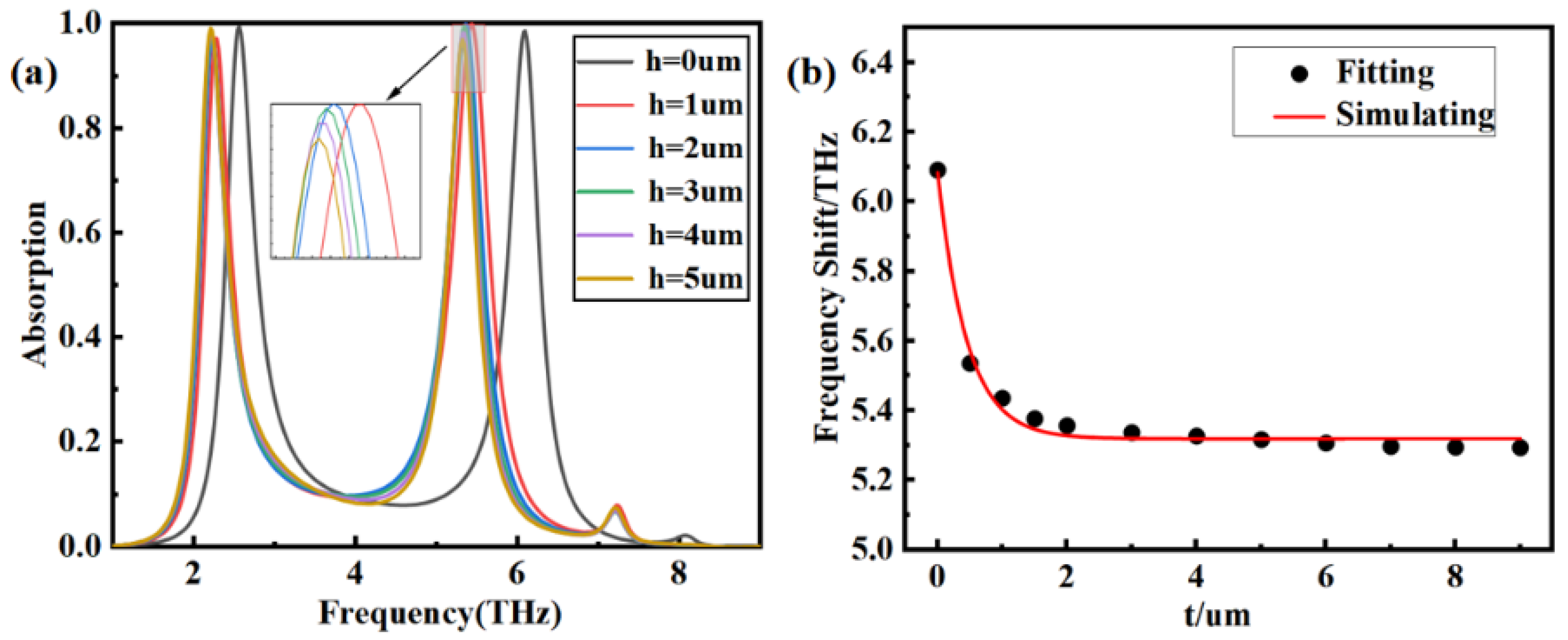
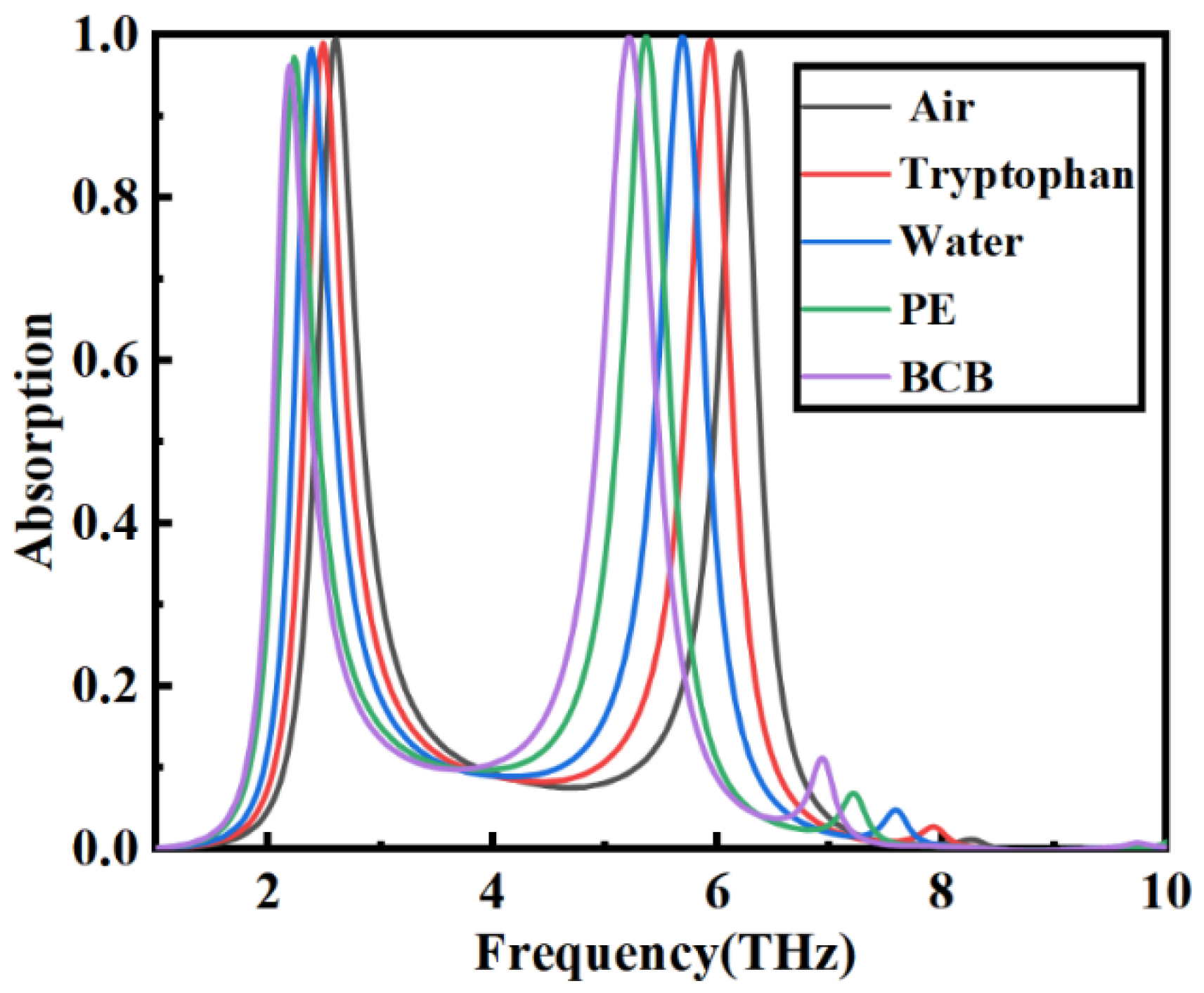
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nguyen, D.M.; Lee, D.; Rho, J. Control of light absorbance using plasmonic grating based perfect absorber at visible and near-infrared wavelengths. Sci. Rep. 2017, 7, 2611. [Google Scholar] [CrossRef]
- Ferguson, B.; Zhang, X.-C. Materials for terahertz science and technology. Nat. Mater. 2002, 1, 26–33. [Google Scholar] [CrossRef]
- Chen, Z.; Han, C.; Wu, Y.; Li, L.; Huang, C.; Zhang, Z.; Wang, G.; Tong, W. Terahertz wireless communications for 2030 and beyond: A cutting-edge frontier. IEEE Commun. Mag. 2021, 59, 66–72. [Google Scholar] [CrossRef]
- Song, H.J.; Nagatsuma, T. Present and future of terahertz communications. IEEE Trans. Terahertz Sci. Technol. 2011, 1, 256–263. [Google Scholar] [CrossRef]
- Zhang, M.; Pirandola, S.; Delfanazari, K. Millimetre-waves to terahertz SISO and MIMO continuous variable quantum key distribution. IEEE Trans. Quantum Eng. 2023, 4, 4100410. [Google Scholar] [CrossRef]
- Active terahertz modulator and slow light metamaterial devices with hybrid graphene–superconductor photonic integrated circuits. Nanomaterials 2021, 11, 2999. [CrossRef]
- Nagatsuma, T.; Horiguchi, S.; Minamikata, Y.; Yoshimizu, Y.; Hisatake, S.; Kuwano, S.; Yoshimoto, N.; Terada, J.; Takahashi, H. Terahertz wireless communications based on photonics technologies. Opt. Express 2013, 21, 23736–23747. [Google Scholar] [CrossRef]
- Wiersma, D.S. Disordered photonics. Nat. Photonics 2013, 7, 188–196. [Google Scholar] [CrossRef]
- Delfanazari, K.; Klemm, R.A.; Joyce, H.J.; Ritchie, D.A.; Kadowaki, K. Integrated, portable, tunable, and coherent terahertz sources and sensitive detectors based on layered superconductors. Proc. IEEE 2020, 108, 721–734. [Google Scholar] [CrossRef]
- Delfanazari, K.; Asai, H.; Tsujimoto, M.; Kashiwagi, T.; Kitamura, T.; Yamamoto, T.; Sawamura, M.; Ishida, K.; Watanabe, C.; Sekimoto, S.; et al. Tunable terahertz emission from the intrinsic Josephson junctions in acute isosceles triangular Bi2Sr2CaCu2O8+δ mesas. Opt. Express 2013, 21, 2171–2184. [Google Scholar] [CrossRef]
- Samizadeh Nikoo, M.; Jafari, A.; Perera, N.; Zhu, M.; Santoruvo, G.; Matioli, E. Nanoplasma-enabled picosecond switches for ultrafast electronics. Nature 2020, 579, 534–539. [Google Scholar] [CrossRef] [PubMed]
- Kalhor, S.; Savel’ev, S.; Delfanazari, K. Engineering ultrastrong coupling between Josephson plasmon polaritons and subwavelength microcavity arrays in silicon/van der Waals layered superconductor heterostructure for terahertz hybrid circuit cavity quantum electrodynamics. Phys. Rev. B 2022, 106, 245140. [Google Scholar] [CrossRef]
- Xiao, S.; Wang, T.; Liu, T.; Yan, X.; Li, Z.; Xu, C. Active modulation of electromagnetically induced transparency analogue in terahertz hybrid metal-graphene metamaterials. Carbon 2018, 126, 271–278. [Google Scholar] [CrossRef]
- Kordi, M.; Mirsalehi, M.M. Investigation of a metamaterial slab lens and an imaging system based on an ellipsoidal cavity. Appl. Opt. 2017, 56, 4772–4778. [Google Scholar] [CrossRef] [PubMed]
- Khavasi, A.; Chrostowski, L.; Lu, Z.; Bojko, R. Significant crosstalk reduction using all-dielectric CMOS-compatible metamaterials. IEEE Photonics Technol. Lett. 2016, 28, 2787–2790. [Google Scholar] [CrossRef]
- Legaria, S.; Teniente, J.; Kuznetsov, S.; Pacheco-Pena, V.; Beruete, M. Highly efficient focusing of terahertz waves with an ultrathin superoscillatory metalens: Experimental demonstration. Adv. Photonics Res. 2021, 2, 2000165. [Google Scholar] [CrossRef]
- Schurig, D.; Mock, J.J.; Justice, B.J.; Cummer, S.A.; Pendry, J.B.; Starr, A.F.; Smith, D.R. Metamaterial electromagnetic cloak at microwave frequencies. Science 2006, 314, 977–980. [Google Scholar] [CrossRef]
- Strikwerda, A.C.; Zalkovskij, M.; Lorenzen, D.L.; Krabbe, A.; Lavrinenko, A.V.; Jepsen, P.U. Metamaterial composite bandpass filter with an ultra-broadband rejection bandwidth of up to 240 terahertz. Appl. Phys. Lett. 2014, 104, 191103. [Google Scholar] [CrossRef]
- Fu, M.X.; Wang, J.Y.; Guo, S.S.; Wang, Z.Y.; Yang, P.X.; Niu, Y.Y. A polarization-insensitive broadband terahertz absorber using patterned graphene. Nanomaterials 2022, 12, 3763. [Google Scholar] [CrossRef]
- Bonaccorso, F.; Sun, Z.; Hasan, T.; Ferrari, A.C. Graphene photonics and optoelectronics. Nat. Photonics 2010, 4, 611–622. [Google Scholar] [CrossRef]
- Wen, Q.Y.; Tian, W.; Mao, Q.; Chen, Z.; Liu, W.W.; Yang, Q.H.; Sanderson, M.; Zhang, H.W. Graphene based all-optical spatial terahertz modulator. Sci. Rep. 2014, 4, 7409. [Google Scholar] [CrossRef]
- Hu, D.; Meng, T.H.; Wang, H.Y.; Fu, M.X. Actively tunable dual-broadband graphene-based terahertz metamaterial absorber. Chin. Phys. B 2021, 30, 126101. [Google Scholar] [CrossRef]
- He, Z.; Li, L.; Ma, H.; Pu, L.; Xu, H.; Yi, Z.; Cao, X.; Cui, W. Graphene-based metasurface sensing applications in terahertz band. Results Phys. 2021, 21, 103795. [Google Scholar] [CrossRef]
- Pianelli, A.; Kowerdziej, R.; Dudek, M.; Sielezin, K.; Olifierczuk, M.; Parka, J. Graphene-based hyperbolic metamaterial as a switchable reflection modulator. Opt. Express 2020, 28, 6708–6718. [Google Scholar] [CrossRef]
- Dudek, M.; Kowerdziej, R.; Pianelli, A.; Parka, J. Graphene-based tunable hyperbolic microcavity. Sci. Rep. 2021, 11, 74. [Google Scholar] [CrossRef]
- Wang, B.X.; Huang, W.Q.; Wang, L.L. Ultra-narrow terahertz perfect light absorber based on surface lattice resonance of a sandwich resonator for sensing application. RSC Adv. 2017, 7, 42956–42963. [Google Scholar] [CrossRef]
- Hu, D.; Meng, T.; Wang, H.; Ma, Y.; Zhu, Q. Ultra-narrow-band terahertz perfect metamaterial absorber for refractive index sensing application. Results Phys. 2020, 19, 103567. [Google Scholar] [CrossRef]
- Chen, T.; Jiang, W.; Yin, X. Dual-band ultrasensitive terahertz sensor based on tunable graphene metamaterial absorber. Superlattices Microstruct. 2021, 154, 106898. [Google Scholar] [CrossRef]
- Nickpay, M.R.; Danaie, M.; Shahzadi, A. Graphene-based metamaterial absorber for refractive index sensing applications in terahertz band. Diam. Relat. Mater. 2022, 130, 109539. [Google Scholar] [CrossRef]
- Li, L.; Ge, H.; Jiang, Y.; Li, G.; Wang, F.; Lv, M.; Ji, X.; Jia, Z.; Li, Z.; Zhang, Y. A four-band terahertz metamaterial sensor based on symmetric E-shaped structure. Coatings 2022, 12, 1694. [Google Scholar] [CrossRef]
- Thongrattanasiri, S.; Koppens, F.H.; De Abajo, F.J.G. Complete optical absorption in periodically patterned graphene. Phys. Rev. Lett. 2012, 108, 047401. [Google Scholar] [CrossRef]
- Zhan, Y.; Fan, C. Investigation on the tunable and polarization sensitive three-band terahertz graphene metamaterial absorber. Mater. Res. Express 2023, 10, 055802. [Google Scholar] [CrossRef]
- Gao, W.; Shi, G.; Jin, Z.; Shu, J.; Zhang, Q.; Vajtai, R.; Ajayan, P.M.; Kono, J.; Xu, Q. Excitation and active control of propagating surface plasmon polaritons in graphene. Nano Lett. 2013, 13, 3698–3702. [Google Scholar] [CrossRef]
- Saadeldin, A.S.; Hameed, M.F.O.; Elkaramany, E.M.; Obayya, S.S. Highly sensitive terahertz metamaterial sensor. IEEE Sens. J. 2019, 19, 7993–7999. [Google Scholar] [CrossRef]
- Nickpay, M.R.; Danaie, M.; Shahzadi, A. Highly sensitive THz refractive index sensor based on folded split-ring metamaterial graphene resonators. Plasmonics 2021, 17, 237–248. [Google Scholar] [CrossRef]
- Qi, Y.; Zhang, Y.; Liu, C.; Zhang, T.; Zhang, B.; Wang, L.; Deng, X.; Bai, Y.; Wang, X. A tunable terahertz metamaterial absorber composed of elliptical ring graphene arrays with refractive index sensing application. Results Phys. 2020, 16, 103012. [Google Scholar] [CrossRef]
- Lu, X.; Ge, H.; Jiang, Y.; Zhang, Y. Design and analysis of a dual-band THz metamaterial sensor with high refractive index sensitivity. Front. Phys. 2022, 10, 973033. [Google Scholar] [CrossRef]
- Ge, J.; You, C.; Feng, H.; Li, X.; Wang, M.; Dong, L.; Veronis, G.; Yun, M. Tunable dual plasmon-induced transparency based on a monolayer graphene metamaterial and its terahertz sensing performance. Opt. Express 2020, 28, 31781–31795. [Google Scholar] [CrossRef]






| Ref. | Pattern | Material | Number of Peaks | Operating Range (THz) | Sensitivity (GHz/RIU) | Quality Factor (Q) | FOM (RIU−1) |
|---|---|---|---|---|---|---|---|
| [34] | Split ring | Gold–dielectric–gold | 1 | 1.5–3 | 300 | 22.5 | 2.94 |
| [35] | Folded Split Ring | Graphene–SiO2–gold | 1 | 2–6 | 851 | 13.76 | 3.33 |
| [36] | Elliptical ring | Graphene–SiO2 | 1 | 3–10 | 1326 | / | 3.6 |
| [27] | cross-shaped patch | GaAs–Cu | 1 | 2–2.5 | 1942 | 637 | 506 |
| [26] | Square Au ring | Gold–dielectric–gold | 1 | 2.5–3.5 | 2584 | 442 | 385 |
| [37] | Split ring | Gold–PTFE | 2 | 0.2–3 | 730 | 10.17 | 2.52 |
| [38] | Two strips and ring | Graphene–SiO2 | 3 | 1–6 | 1083 | 16.2 | 3.78 |
| [29] | Split ring and ribbon | Graphene–TOPAS–gold | 3 | 2–10 | 1791 | 32.354 | 7.046 |
| Our work | Four strips | Graphene–TOPAS–gold | 2 | 1–10 | 1627 | 29.6 | 3.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, M.; Ye, Y.; Niu, Y.; Guo, S.; Wang, Z.; Liu, X. Graphene-Based Tunable Dual-Frequency Terahertz Sensor. Nanomaterials 2024, 14, 378. https://doi.org/10.3390/nano14040378
Fu M, Ye Y, Niu Y, Guo S, Wang Z, Liu X. Graphene-Based Tunable Dual-Frequency Terahertz Sensor. Nanomaterials. 2024; 14(4):378. https://doi.org/10.3390/nano14040378
Chicago/Turabian StyleFu, Maixia, Yuchao Ye, Yingying Niu, Shaoshuai Guo, Zhaoying Wang, and Xueying Liu. 2024. "Graphene-Based Tunable Dual-Frequency Terahertz Sensor" Nanomaterials 14, no. 4: 378. https://doi.org/10.3390/nano14040378
APA StyleFu, M., Ye, Y., Niu, Y., Guo, S., Wang, Z., & Liu, X. (2024). Graphene-Based Tunable Dual-Frequency Terahertz Sensor. Nanomaterials, 14(4), 378. https://doi.org/10.3390/nano14040378






