Micro-to-Nanoscale Characterization of Femtosecond Laser Photo-Inscribed Microvoids
Abstract
1. Introduction
2. Materials and Methods
3. Results
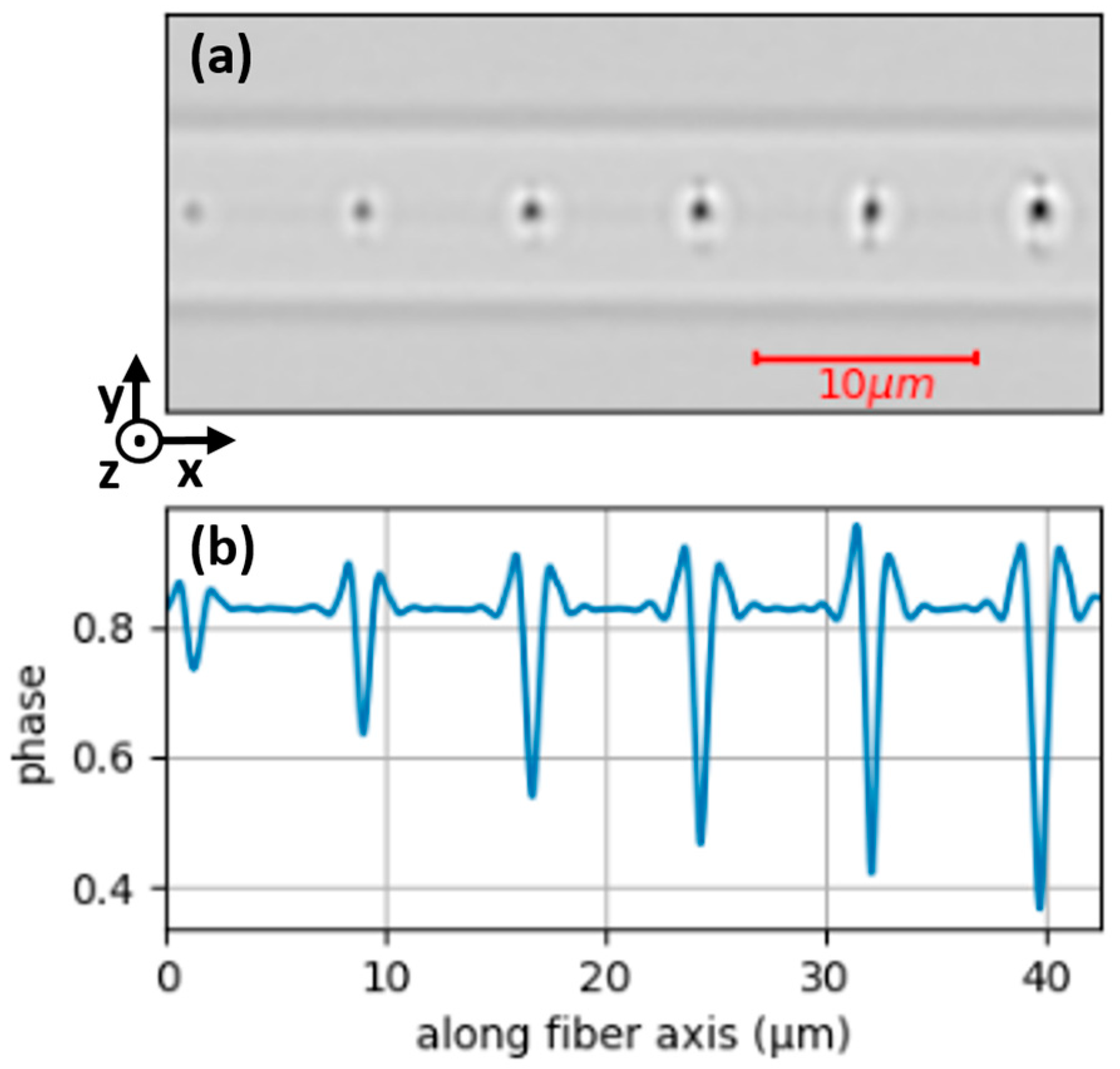
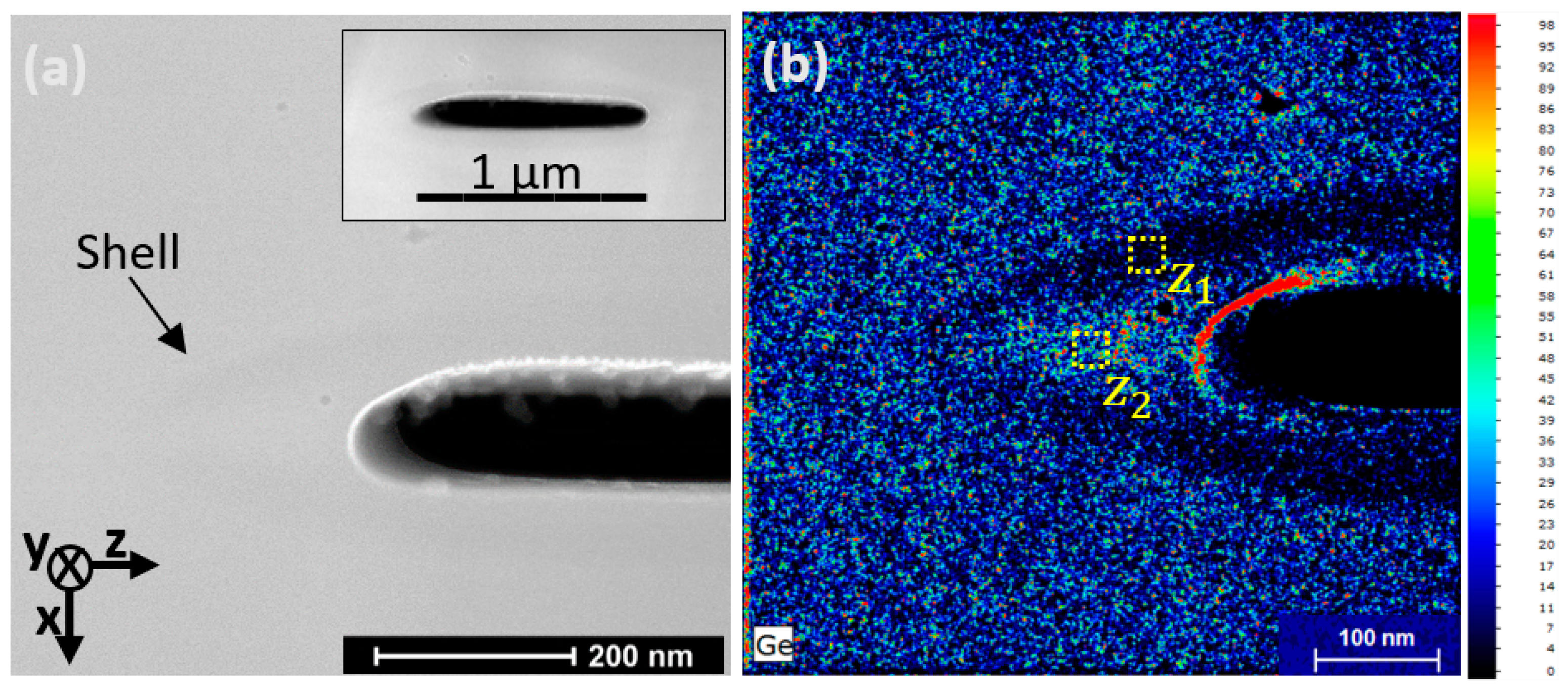
3.1. Characterizations at Room Temperature
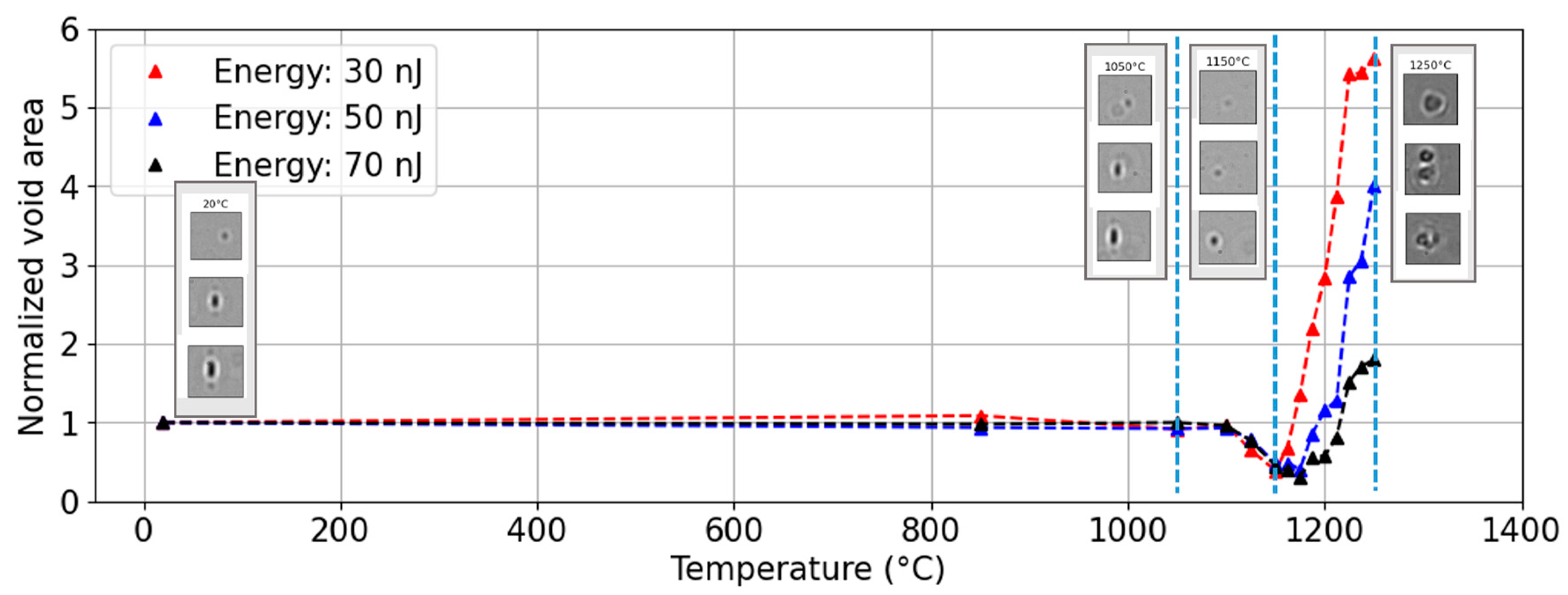
3.2. High-Temperature Behavior
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mihailov, S.J. Fiber Bragg Grating Sensors for Harsh Environments. Sensors 2012, 12, 1898–1918. [Google Scholar] [CrossRef] [PubMed]
- Mihailov, S.; Grobnic, D.; Hnatovsky, C.; Walker, R.; Lu, P.; Coulas, D.; Ding, H. Extreme Environment Sensing Using Femtosecond Laser-Inscribed Fiber Bragg Gratings. Sensors 2017, 17, 2909. [Google Scholar] [CrossRef] [PubMed]
- He, J.; Xu, B.; Xu, X.; Liao, C.; Wang, Y. Review of Femtosecond-Laser-Inscribed Fiber Bragg Gratings: Fabrication Technologies and Sensing Applications. Photonic Sens. 2021, 11, 203–226. [Google Scholar] [CrossRef]
- Laffont, G.; Cotillard, R.; Roussel, N.; Desmarchelier, R.; Rougeault, S. Temperature Resistant Fiber Bragg Gratings for On-Line and Structural Health Monitoring of the Next-Generation of Nuclear Reactors. Sensors 2018, 18, 1791. [Google Scholar] [CrossRef] [PubMed]
- Development and Performance Verification of Fiber Optic Temperature Sensors in High Temperature Engine Environments. AIAA Propulsion and Energy Forum. Available online: https://arc.aiaa.org/doi/10.2514/6.2014-3922 (accessed on 5 March 2024).
- Maurin, L.; Roussel, N.; Laffont, G. Optimally Temperature Compensated FBG-Based Sensor Dedicated to Non-Intrusive Pipe Internal Pressure Monitoring. Front. Sens. 2022, 3, 835140. Available online: https://www.frontiersin.org/articles/10.3389/fsens.2022.835140 (accessed on 5 March 2024). [CrossRef]
- Dutz, F.J.; Boje, S.; Orth, U.; Koch, A.W.; Roths, J. High-Temperature Profile Monitoring in Gas Turbine Exhaust-Gas Diffusors with Six-Point Fiber-Optic Sensor Array. Int. J. Turbomach. Propuls. Power 2020, 5, 25. [Google Scholar] [CrossRef]
- Alla, D.R.; Neelakandan, D.P.; Mumtaz, F.; Gerald, R.E.; Bartlett, L.; O’Malley, R.J.; Smith, J.D.; Huang, J. Cascaded Sapphire Fiber Bragg Gratings Inscribed by Femtosecond Laser for Molten Steel Studies. IEEE Trans. Instrum. Meas. 2024, 73, 1–8. [Google Scholar] [CrossRef]
- Canning, J. Fibre gratings and devices for sensors and lasers. Laser Photonics Rev. 2008, 2, 275–289. [Google Scholar] [CrossRef]
- Cavillon, M.; Lancry, M.; Poumellec, B.; Wang, Y.; Canning, J.; Cook, K.; Hawkins, T.; Dragic, P.; Ballato, J. Overview of high temperature fibre Bragg gratings and potential improvement using highly doped aluminosilicate glass optical fibres. J. Phys. Photonics 2019, 1, 042001. [Google Scholar] [CrossRef]
- Smelser, C.W.; Mihailov, S.J.; Grobnic, D. Formation of Type I-IR and Type II-IR gratings with an ultrafast IR laser and a phase mask. Opt. Express 2005, 13, 5377–5386. [Google Scholar] [CrossRef]
- Åslund, M.L.; Canning, J.; Stevenson, M.; Cook, K. Thermal stabilization of Type I fiber Bragg gratings for operation up to 600 °C. Opt. Lett. 2010, 35, 586–588. [Google Scholar] [CrossRef] [PubMed]
- Yoshino, T.; Ozeki, Y.; Matsumoto, M.; Itoh, K. In situ Micro-Raman Investigation of Spatio-Temporal Evolution of Heat in Ultrafast Laser Microprocessing of Glass. Jpn. J. Appl. Phys. 2012, 51, 102403. [Google Scholar] [CrossRef]
- Rudenko, A.; Moloney, J.V.; Polynkin, P. Ionization clamping in ultrafast optical breakdown of transparent solids. Phys. Rev. Appl. 2023, 20, 064035. [Google Scholar] [CrossRef]
- Gamaly, E.G.; Juodkazis, S.; Nishimura, K.; Misawa, H.; Luther-Davies, B.; Hallo, L.; Nicolai, P.; Tikhonchuk, V.T. Laser-matter interaction in the bulk of a transparent solid: Confined microexplosion and void formation. Phys. Rev. B 2006, 73, 214101. [Google Scholar] [CrossRef]
- Rolle, J.; Bergé, L.; Duchateau, G.; Skupin, S. Filamentation of ultrashort laser pulses in silica glass and KDP crystals: A comparative study. Phys. Rev. A 2014, 90, 023834. [Google Scholar] [CrossRef]
- Grobnic, D.; Smelser, C.W.; Mihailov, S.J.; Walker, R.B. Long-term thermal stability tests at 1000 °C of silica fibre Bragg gratings made with ultrafast laser radiation. Meas. Sci. Technol. 2006, 17, 1009. [Google Scholar] [CrossRef]
- Martinez, A.; Khrushchev, I.Y.; Bennion, I. Thermal properties of fibre Bragg gratings inscribed point-by-point by infrared femtosecond laser. Electron. Lett. 2005, 41, 176–178. [Google Scholar] [CrossRef]
- Lerner, A.; Blanchet, T.; Cotillard, R.; Sosa, M.; Roussel, N.; Bouwmans, G.; Laffont, G. High temperature annealing behavior of femtosecond written FBGs in Ge-doped fused silica optical fibers. In Proceedings of the European Workshop on Optical Fibre Sensors (EWOFS 2023), Mons, Belgium, 23–26 May 2023; SPIE: Bellingham WA, USA; pp. 433–436. [Google Scholar] [CrossRef]
- Bressel, L.; de Ligny, D.; Sonneville, C.; Martinez, V.; Mizeikis, V.; Buividas, R.; Juodkazis, S. Femtosecond laser induced density changes in GeO2 and SiO2 glasses: Fictive temperature effect [Invited]. Opt. Mater. Express 2011, 1, 605–613. [Google Scholar] [CrossRef]
- Mermillod-Blondin, A.; Burakov, I.M.; Stoian, R.; Rosenfeld, A.; Audouard, E.; Bulgakova, N.M.; Hertel, I.V. Direct observation of femtosecond laser induced modifications in the bulk of fused silica by phase contrast microscopy. J. Laser Micro/Nanoeng. 2006, 1, 155. [Google Scholar] [CrossRef]
- Mauclair, C.; Mermillod-Blondin, A.; Landon, S.; Huot, N.; Rosenfeld, A.; Hertel, I.V.; Audouard, E.; Myiamoto, I.; Stoian, R. Single-pulse ultrafast laser imprinting of axial dot arrays in bulk glasses. Opt. Lett. 2011, 36, 325–327. [Google Scholar] [CrossRef]
- Martinez, A.; Dubov, M.; Khrushchev, I.; Bennion, I. Photoinduced Modifications in Fiber Gratings Inscribed Directly by Infrared Femtosecond Irradiation. IEEE Photonics Technol. Lett. 2006, 18, 2266–2268. [Google Scholar] [CrossRef]
- Williams, R.J.; Krämer, R.G.; Nolte, S.; Withford, M.J.; Steel, M.J. Detuning in apodized point-by-point fiber Bragg gratings: Insights into the grating morphology. Opt. Express 2013, 21, 26854. [Google Scholar] [CrossRef] [PubMed]
- Juodkazis, S.; Misawa, H.; Hashimoto, T.; Gamaly, E.G.; Luther-Davies, B. Laser-induced microexplosion confined in a bulk of silica: Formation of nanovoids. Appl. Phys. Lett. 2006, 88, 201909. [Google Scholar] [CrossRef]
- Bellair, C.J.; Curl, C.L.; Allman, B.E.; Harris, P.J.; Roberts, A.; Delbridge, L.M.D.; Nugent, K.A. Quantitative phase amplitude microscopy IV: Imaging thick specimens. J. Microsc. 2004, 214, 62–69. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Hu, D.; Mescall, R.; You, G.; Basov, D.N.; Dai, Q.; Liu, M. Modern Scattering-Type Scanning Near-Field Optical Microscopy for Advanced Material Research. Adv. Mater. 2019, 31, 1804774. [Google Scholar] [CrossRef] [PubMed]
- Németh, G.; Datz, D.; Tóháti, H.M.; Pekker, Á.; Kamarás, K. Scattering near-field optical microscopy on metallic and semiconducting carbon nanotube bundles in the infrared. Phys. Status Solidi B 2016, 253, 2413–2416. [Google Scholar] [CrossRef]
- Lancry, M.; Régnier, E.; Poumellec, B. Fictive temperature in silica-based glasses and its application to optical fiber manufacturing. Prog. Mater. Sci. 2012, 57, 63–94. [Google Scholar] [CrossRef]
- Poumellec, B.; Niay, P.; Douay, M.; Bayon, J.F. The UV-induced refractive index grating in Ge: Preforms: Additional CW experiments and the macroscopic origin of the change in index. J. Phys. D Appl. Phys. 1996, 29, 1842. [Google Scholar] [CrossRef]
- Vlugter, P.; Bellouard, Y. Elastic properties of self-organized nanogratings produced by femtosecond laser exposure of fused silica. Phys. Rev. Mater. 2020, 4, 023607. [Google Scholar] [CrossRef]
- Hashimoto, T.; Juodkazis, S.; Misawa, H. Void recording in silica. Appl. Phys. A 2006, 83, 337–340. [Google Scholar] [CrossRef]
- Beuton, R.; Chimier, B.; Quinoman, P.; González Alaiza de Martínez, P.; Nuter, R.; Duchateau, G. Numerical studies of dielectric material modifications by a femtosecond Bessel–Gauss laser beam. Appl. Phys. A 2021, 127, 334. [Google Scholar] [CrossRef]
- Rouxel, T. Some strange things about the mechanical properties of glass. Comptes Rendus. Phys. 2023, 24, 99–112. [Google Scholar] [CrossRef]
- Varkentina, N.; Dussauze, M.; Royon, A.; Ramme, M.; Petit, Y.; Canioni, L. High repetition rate femtosecond laser irradiation of fused silica studied by Raman spectroscopy. Opt. Mater. Express 2016, 6, 79. [Google Scholar] [CrossRef]
- Bressel, L.; De Ligny, D.; Gamaly, E.G.; Rode, A.V.; Juodkazis, S. Observation of O2 inside voids formed in GeO2 glass by tightly-focused fs-laser pulses. Opt. Mater. Express 2011, 1, 1150. [Google Scholar] [CrossRef]
- Cavillon, M.; Wang, Y.; Poumellec, B.; Brisset, F.; Lancry, M. Erasure of nanopores in silicate glasses induced by femtosecond laser irradiation in the Type II regime. Appl. Phys. A 2020, 126, 876. [Google Scholar] [CrossRef]
- Wang, Y.; Wei, S.; Cavillon, M.; Sapaly, B.; Poumellec, B.; Peng, G.-D.; Canning, J.; Lancry, M. Thermal Stability of Type II Modifications Inscribed by Femtosecond Laser in a Fiber Drawn from a 3D Printed Preform. Appl. Sci. 2021, 11, 600. [Google Scholar] [CrossRef]
- Li, Y.; Yang, M.; Wang, D.N.; Lu, J.; Sun, T.; Grattan, K.T. Fiber Bragg gratings with enhanced thermal stability by residual stress relaxation. Opt. Express 2009, 17, 19785. [Google Scholar] [CrossRef]
- Cornet, A.; Martinez, V.; de Ligny, D.; Champagnon, B.; Martinet, C. Relaxation processes of densified silica glass. J. Chem. Phys. 2017, 146, 094504. [Google Scholar] [CrossRef]
- Xie, Q.; Cavillon, M.; Poumellec, B.; Lancry, M. Upper temperature limit for nanograting survival in oxide glasses. Appl. Opt. 2023, 62, 6794–6801. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sosa, M.; Cavillon, M.; Blanchet, T.; Nemeth, G.; Borondics, F.; Laffont, G.; Lancry, M. Micro-to-Nanoscale Characterization of Femtosecond Laser Photo-Inscribed Microvoids. Nanomaterials 2024, 14, 1228. https://doi.org/10.3390/nano14141228
Sosa M, Cavillon M, Blanchet T, Nemeth G, Borondics F, Laffont G, Lancry M. Micro-to-Nanoscale Characterization of Femtosecond Laser Photo-Inscribed Microvoids. Nanomaterials. 2024; 14(14):1228. https://doi.org/10.3390/nano14141228
Chicago/Turabian StyleSosa, Matilde, Maxime Cavillon, Thomas Blanchet, Gergely Nemeth, Ferenc Borondics, Guillaume Laffont, and Matthieu Lancry. 2024. "Micro-to-Nanoscale Characterization of Femtosecond Laser Photo-Inscribed Microvoids" Nanomaterials 14, no. 14: 1228. https://doi.org/10.3390/nano14141228
APA StyleSosa, M., Cavillon, M., Blanchet, T., Nemeth, G., Borondics, F., Laffont, G., & Lancry, M. (2024). Micro-to-Nanoscale Characterization of Femtosecond Laser Photo-Inscribed Microvoids. Nanomaterials, 14(14), 1228. https://doi.org/10.3390/nano14141228






