Temperature-Dependent Anisotropic Refractive Index in β-Ga2O3: Application in Interferometric Thermometers
Abstract
1. Introduction
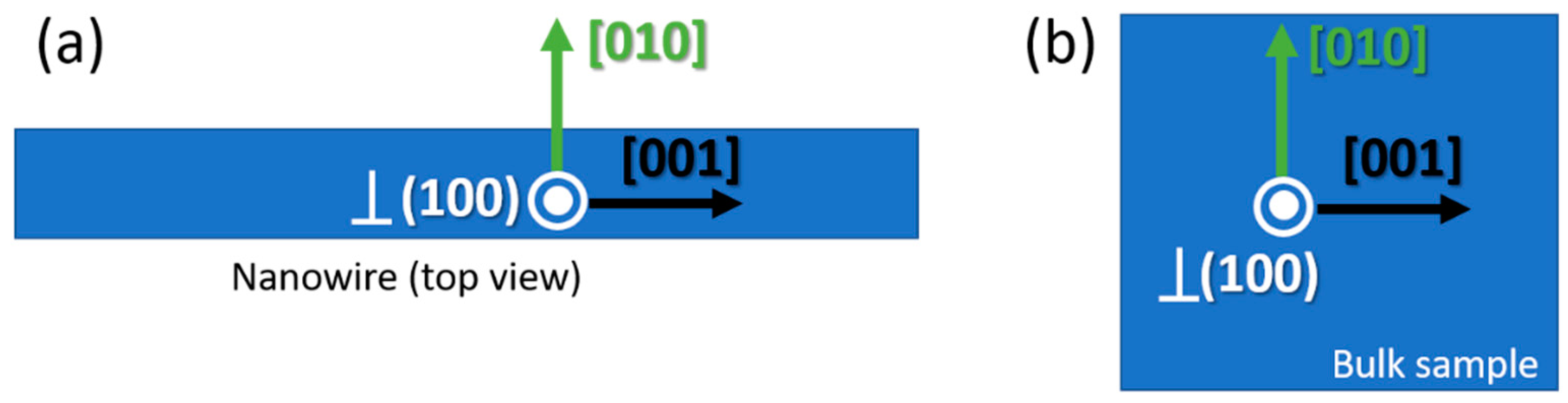
2. Materials and Methods
3. Results and Discussion
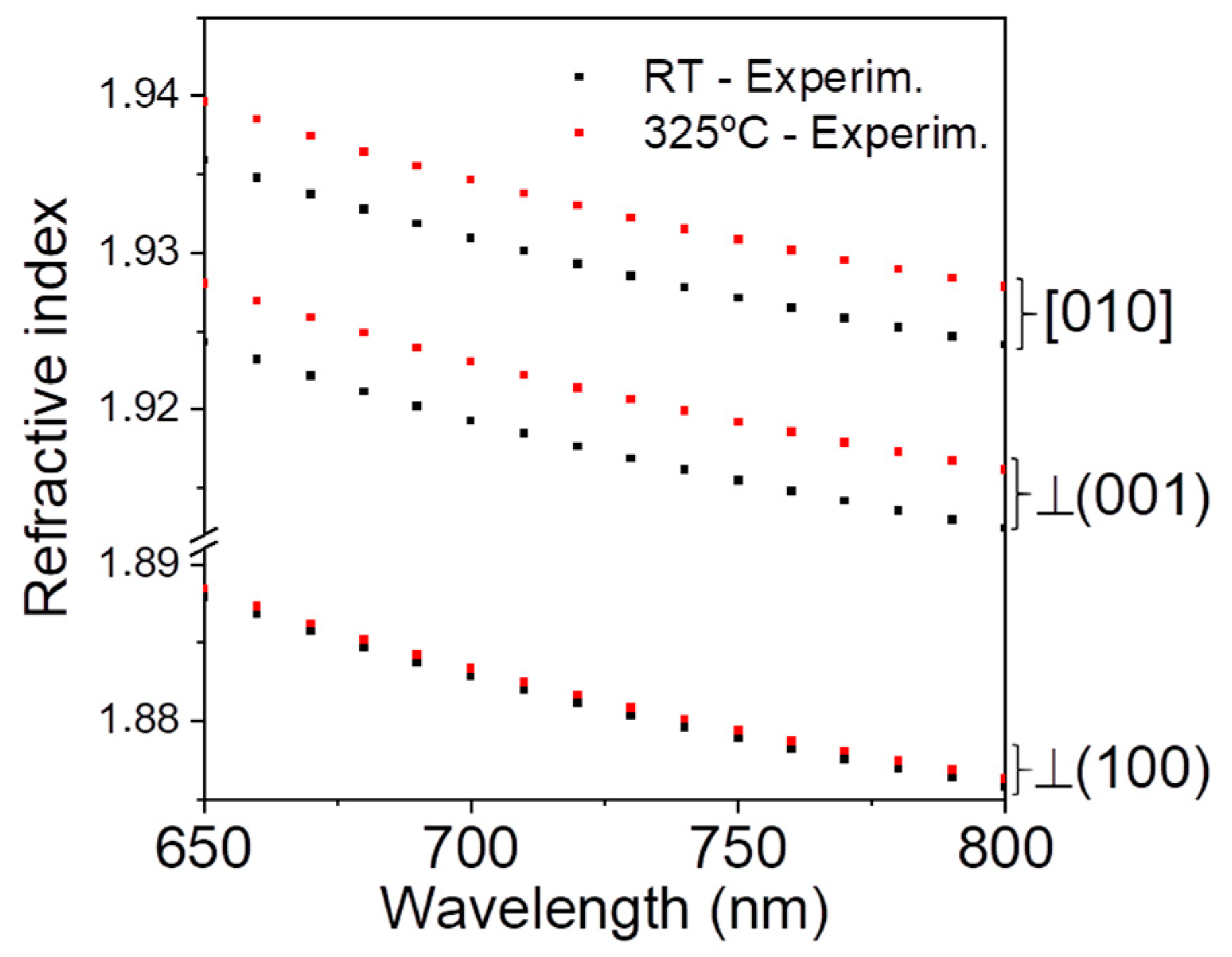
3.1. Temperature Dependence of the Refractive Index
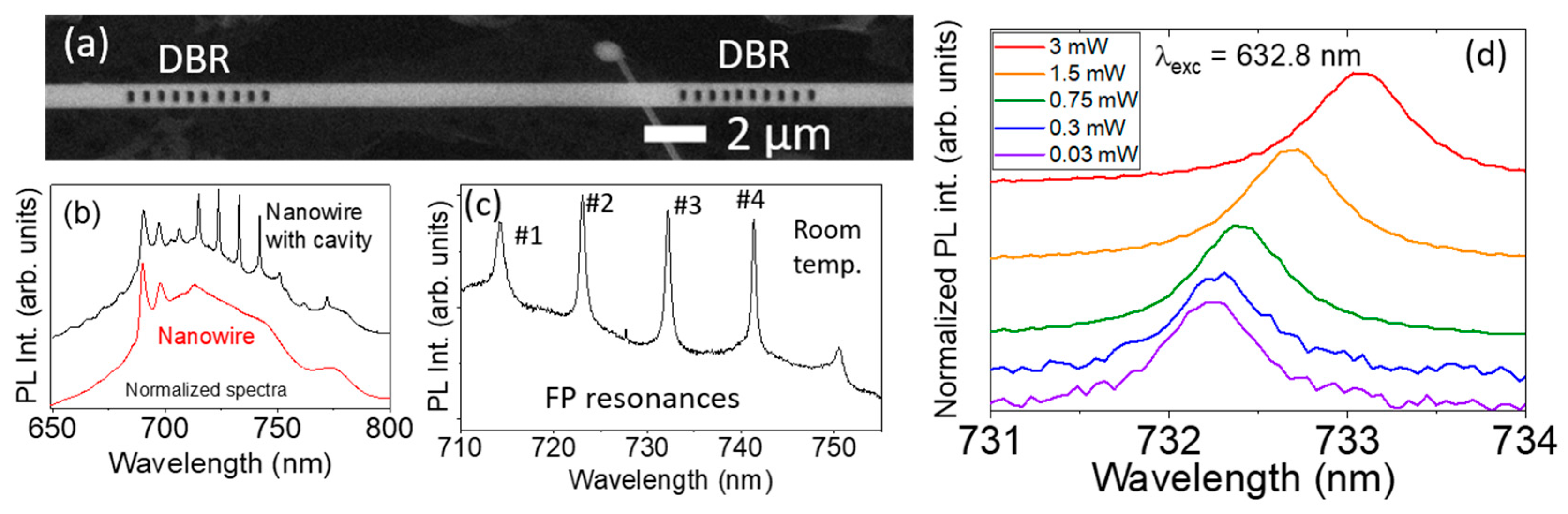
3.2. Fabry–Perot Resonances in Ga2O3 Optical Cavities
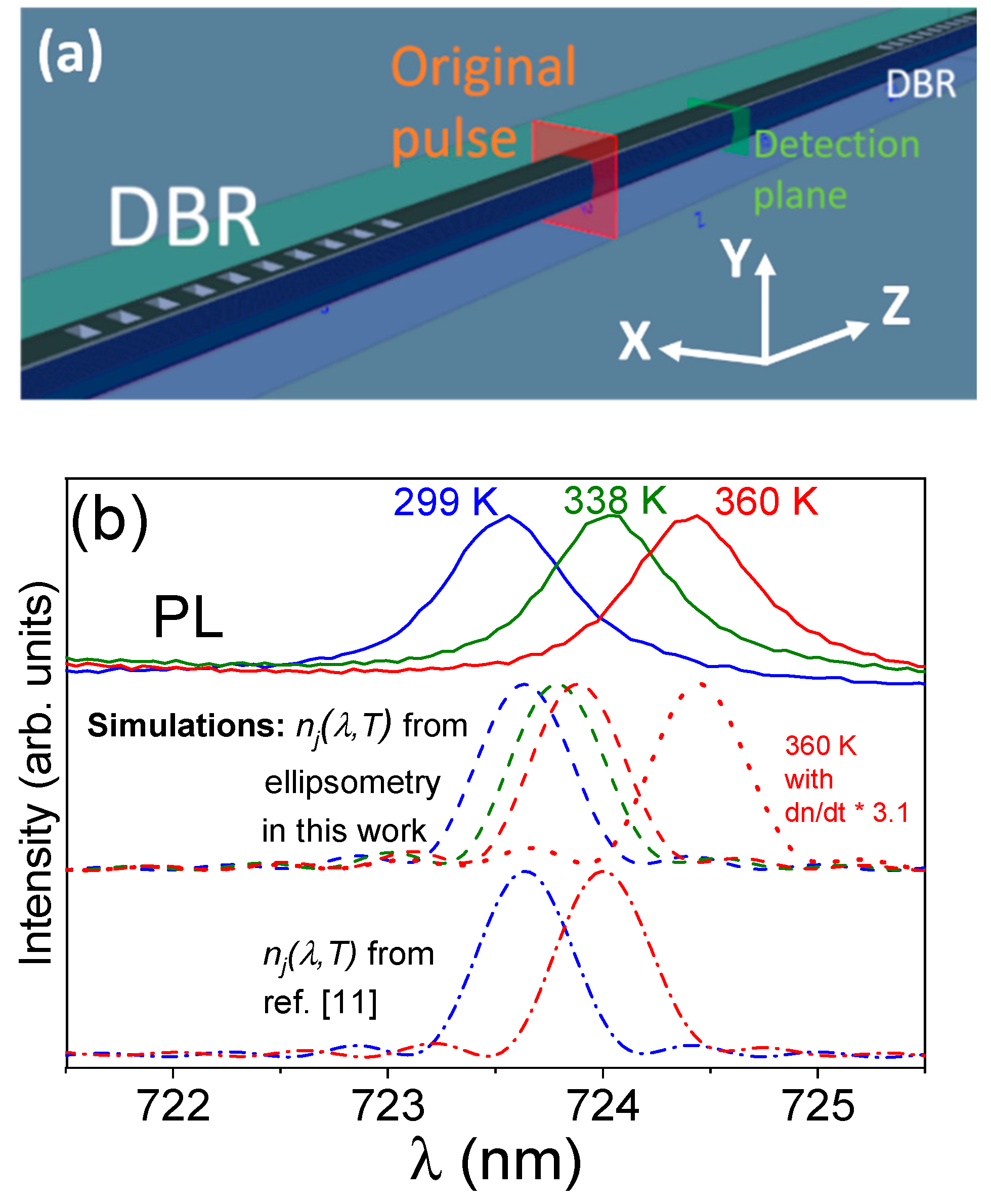
3.3. FDTD Simulation of the Temperature-Dependent F-P Resonances’ Positions
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pearton, S.J.; Yang, J.; Cary, P.H.; Kim, J.; Tadjer, M.J.; Mastro, M.A. A review of Ga2O3 materials, processing, and devices. Appl. Phys. Rev. 2018, 5, 011301. [Google Scholar] [CrossRef]
- Tadjer, M.J. Toward gallium oxide power electronics. Science 2022, 378, 724. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.; Wu, F.; Hu, H.; Wang, S.; Liu, A.; Guo, D. Review of self-powered solar-blind photodetectors based on Ga2O3. Mater. Today Phys. 2022, 28, 100883. [Google Scholar] [CrossRef]
- Miyata, T.; Nakatani, T.; Minami, T. Gallium oxide as host material for multicolor emitting phosphors. J. Lumin. 2000, 87–89, 1183–1185. [Google Scholar] [CrossRef]
- Gollakota, P.; Dhawan, A.; Wellenius, P.; Lunardi, L.M.; Muth, J.F.; Saripalli, Y.N.; Peng, H.Y.; Everitt, H.O. Optical characterization of Eu-doped β-Ga2O3 thin films. App. Phys. Lett. 2006, 88, 221906. [Google Scholar] [CrossRef]
- Nogales, E.; Lopez, I.; Mendez, B.; Piqueras, J.; Lorenz, K.; Alves, E.; Garcia, J.A. Doped gallium oxide nanowires for photonics. Proc. SPIE Int. Soc. Opt. Eng. 2012, 8263, 82630B. [Google Scholar]
- Alonso-Orts, M.; Nogales, E.; San Juan, J.M.; No, M.L.; Piqueras, J.; Mendez, B. Modal Analysis of β-Ga2O3∶Cr Widely Tunable Luminescent Optical Microcavities. Phys. Rev. Appl. 2018, 9, 064004. [Google Scholar] [CrossRef]
- Alonso-Orts, M.; Chilla, G.; Hotzel, R.; Nogales, E.; San Juan, J.M.; No, M.L.; Eickhoff, M.; Mendez, B. Near-UV optical cavities in Ga2O3 nanowires. Opt. Lett. 2021, 46, 278. [Google Scholar] [CrossRef] [PubMed]
- Alonso-Orts, M.; Carrasco, D.; San Juan, J.M.; Nó, M.L.; de Andrés, A.; Nogales, E.; Mendez, B. Wide Dynamic Range Thermometer Based on Luminescent. Optical Cavities in Ga2O3:Cr Nanowires. Small 2022, 18, 2105355. [Google Scholar] [CrossRef] [PubMed]
- Bhaumik, I.; Bhatt, R.; Ganesamoorthy, S.; Saxena, A.; Karnal, A.K.; Gupta, P.K.; Sinha, A.K.; Deb, S.K. Temperature-dependent index of refraction of monoclinic Ga2O3 single crystal. Appl. Opt. 2011, 50, 6006. [Google Scholar] [CrossRef] [PubMed]
- Sturm, C.; Schmidt-Grund, R.; Zviagin, V.; Grundmann, M. Temperature dependence of the dielectric tensor of monoclinic Ga2O3 single crystals in the spectral range 1.0–8.5 eV. Appl. Phys. Lett. 2017, 111, 082102. [Google Scholar] [CrossRef]
- Mu, W.; Jia, Z.; Yin, Y.; Hu, Q.; Li, Y.; Wu, B.; Zhang, J.; Tao, X. High quality crystal growth and anisotropic physical characterization of β-Ga2O3 single crystals grown by EFG method. J. Alloys Compd. 2017, 714, 453. [Google Scholar] [CrossRef]
- McCloy, J.S.; Jesenovec, J.; Dutton, B.; Pansegrau, C.; Remple, C.; Weber, M.; Swain, S.; McCluskey, M.; Scarpulla, M. Growth and defect characterization of doped and undoped β-Ga2O3 crystals. In Proceedings of the Proc. SPIE, 12002 SPIE OPTO: Oxide-based Materials and Devices XIII, San Francisco, CA, USA, 22 January–28 February 2022; p. 1200205. [Google Scholar]
- Schubert, M.; Korlacki, R.; Knight, S.; Hofmann, T.; Schöche, S.; Darakchieva, V.; Janzén, E.; Monemar, B.; Gogova, D.; Thieu, Q.-T.; et al. Anisotropy, phonon modes, and free charge carrier parameters in monoclinic β-gallium oxide single crystals. Phys. Rev. B 2016, 93, 125209. [Google Scholar] [CrossRef]
- Sturm, C.; Furthmüller, J.; Bechstedt, F.; Schmidt-Grund, R.; Grundmann, M. Dielectric tensor of monoclinic Ga2O3 single crystals in the spectral range 0.5–8.5 eV. APL Mater. 2015, 3, 106106. [Google Scholar] [CrossRef]
- Wei, J.; Murray, J.M.; Barnes, J.O.; Krein, D.M.; Schunemann, P.G.; Guha, S. Temperature dependent Sellmeier equation for the refractive index of GaP. Opt. Mater. Express. 2018, 8, 485. [Google Scholar] [CrossRef]
- Nogales, E.; García, J.A.; Méndez, B.; Piqueras, J. Red luminescence of Cr in β-Ga2O3 nanowires. J. Appl. Phys. 2007, 101, 033517. [Google Scholar] [CrossRef]
- Remple, C.; Barmore, L.M.; Jesenovec, J.; McCloy, J.S.; McCluskey, M.D. Photoluminescence spectroscopy of Cr3+ in β-Ga2O3 and (Al0.1Ga0.9)2O3. J. Vac. Sci. Technol. A 2023, 41, 022702. [Google Scholar] [CrossRef]
- Orlandi, F.; Mezzadri, F.; Calestani, G.; Boschi, F.; Fornari, R. Thermal expansion coefficients of β-Ga2O3 single crystals. Appl. Phys. Express 2015, 8, 111101. [Google Scholar] [CrossRef]
- Golz, C.; Galazka, Z.; Lähnemann, J.; Hortelano, V.; Hatami, F.; Masselink, W.T.; Bierwagen, O. Electrical conductivity tensor of β−Ga2O3 analyzed by van der Pauw measurements: Inherent anisotropy, off-diagonal element, and the impact of grain boundaries. Phys. Rev. Mater. 2019, 3, 124604. [Google Scholar] [CrossRef]
- Caffrey, D.; Norton, E.; Coileáin, C.Ó.; Smith, C.M.; Bulfin, B.; Farrell, L.; Shvets, I.V.; Fleischer, K. Decoupling the refractive index from the electrical properties of transparent conducting oxides via periodic superlattices. Sci. Rep. 2016, 6, 33006. [Google Scholar] [CrossRef] [PubMed]
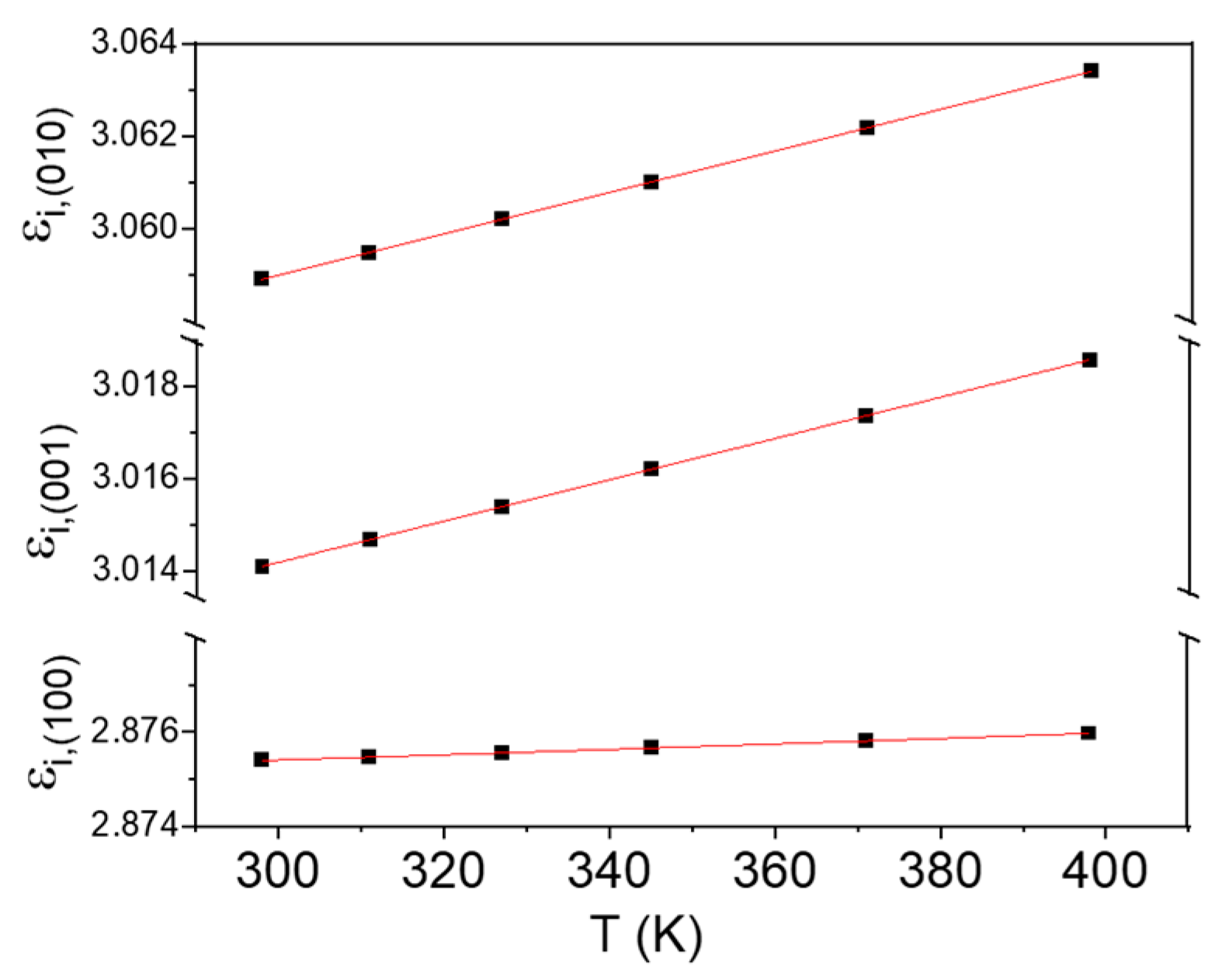
| Coefficient | Quadratic Dependence with T | A | λi (μm) |
|---|---|---|---|
| εi,(100)(T) | 2.874 + 3.199 × 10−6 T + 3.732 × 10−9 T2 | 0.57 | 0.27 |
| εi,(010)(T) | 3.046 + 4.416 × 10−5 T + 1.197 × 10−9 T2 | 0.57 | 0.27 |
| εi,(001)(T) | 3.001 + 4.418 × 10−5 T + 7.600 × 10−10 T2 | 0.57 | 0.27 |
| Temperature is in K. | |||
| Peak # | T (K) | Center (nm) | Width (nm) |
|---|---|---|---|
| 299 | 732.207 ± 0.002 | 0.648 ± 0.008 | |
| 3 | 338 | 732.6845 ± 0.0014 | 0.652 ± 0.007 |
| 360 | 733.066 ± 0.002 | 0.688 ± 0.009 | |
| 299 | 741.404 ± 0.002 | 0.531 ± 0.011 | |
| 4 | 338 | 741.880 ± 0.002 | 0.550 ± 0.010 |
| 360 | 742.262 ± 0.002 | 0.592 ± 0.011 |
| δ (K−1) | Method | Temperature Range (K) | Reference |
|---|---|---|---|
| ≈3.7 × 10−5 | Prism coupling | 298–448 | [10] |
| ≈1.8 × 10−5 | Optical interferometry | 150–400 | [9] |
| ≈6 × 10−6 | Ellipsometry | 10–300 | [11] |
| ≈5.7 × 10−6 | Ellipsometry | 295–595 K | This work |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carrasco, D.; Nieto-Pinero, E.; Alonso-Orts, M.; Serna, R.; San Juan, J.M.; Nó, M.L.; Jesenovec, J.; McCloy, J.S.; Nogales, E.; Méndez, B. Temperature-Dependent Anisotropic Refractive Index in β-Ga2O3: Application in Interferometric Thermometers. Nanomaterials 2023, 13, 1126. https://doi.org/10.3390/nano13061126
Carrasco D, Nieto-Pinero E, Alonso-Orts M, Serna R, San Juan JM, Nó ML, Jesenovec J, McCloy JS, Nogales E, Méndez B. Temperature-Dependent Anisotropic Refractive Index in β-Ga2O3: Application in Interferometric Thermometers. Nanomaterials. 2023; 13(6):1126. https://doi.org/10.3390/nano13061126
Chicago/Turabian StyleCarrasco, Daniel, Eva Nieto-Pinero, Manuel Alonso-Orts, Rosalía Serna, Jose M. San Juan, María L. Nó, Jani Jesenovec, John S. McCloy, Emilio Nogales, and Bianchi Méndez. 2023. "Temperature-Dependent Anisotropic Refractive Index in β-Ga2O3: Application in Interferometric Thermometers" Nanomaterials 13, no. 6: 1126. https://doi.org/10.3390/nano13061126
APA StyleCarrasco, D., Nieto-Pinero, E., Alonso-Orts, M., Serna, R., San Juan, J. M., Nó, M. L., Jesenovec, J., McCloy, J. S., Nogales, E., & Méndez, B. (2023). Temperature-Dependent Anisotropic Refractive Index in β-Ga2O3: Application in Interferometric Thermometers. Nanomaterials, 13(6), 1126. https://doi.org/10.3390/nano13061126








