A Study of the Mechanical Behaviour of Boron Nitride Nanosheets Using Numerical Simulation
Abstract
1. Introduction
2. Materials and Methods
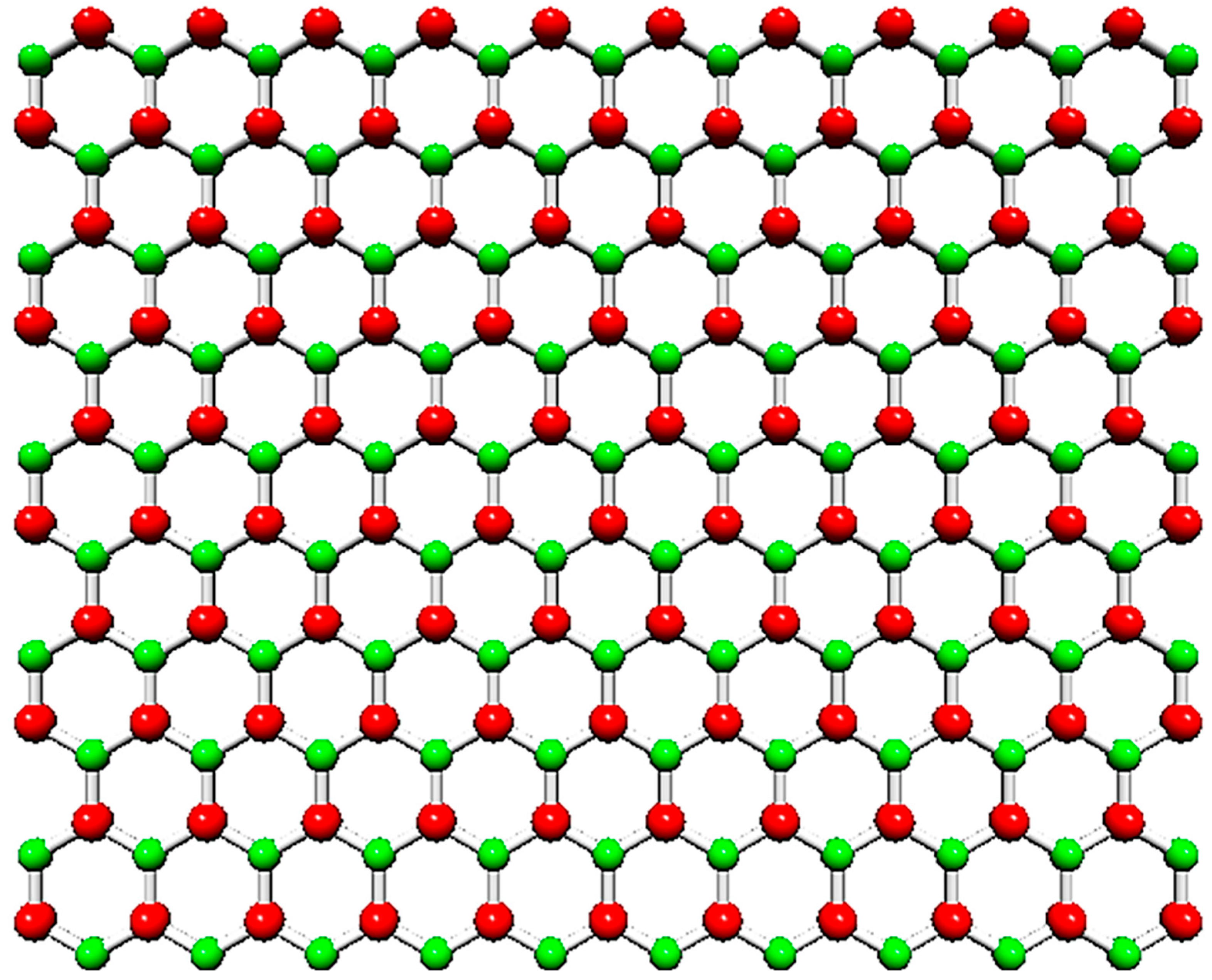
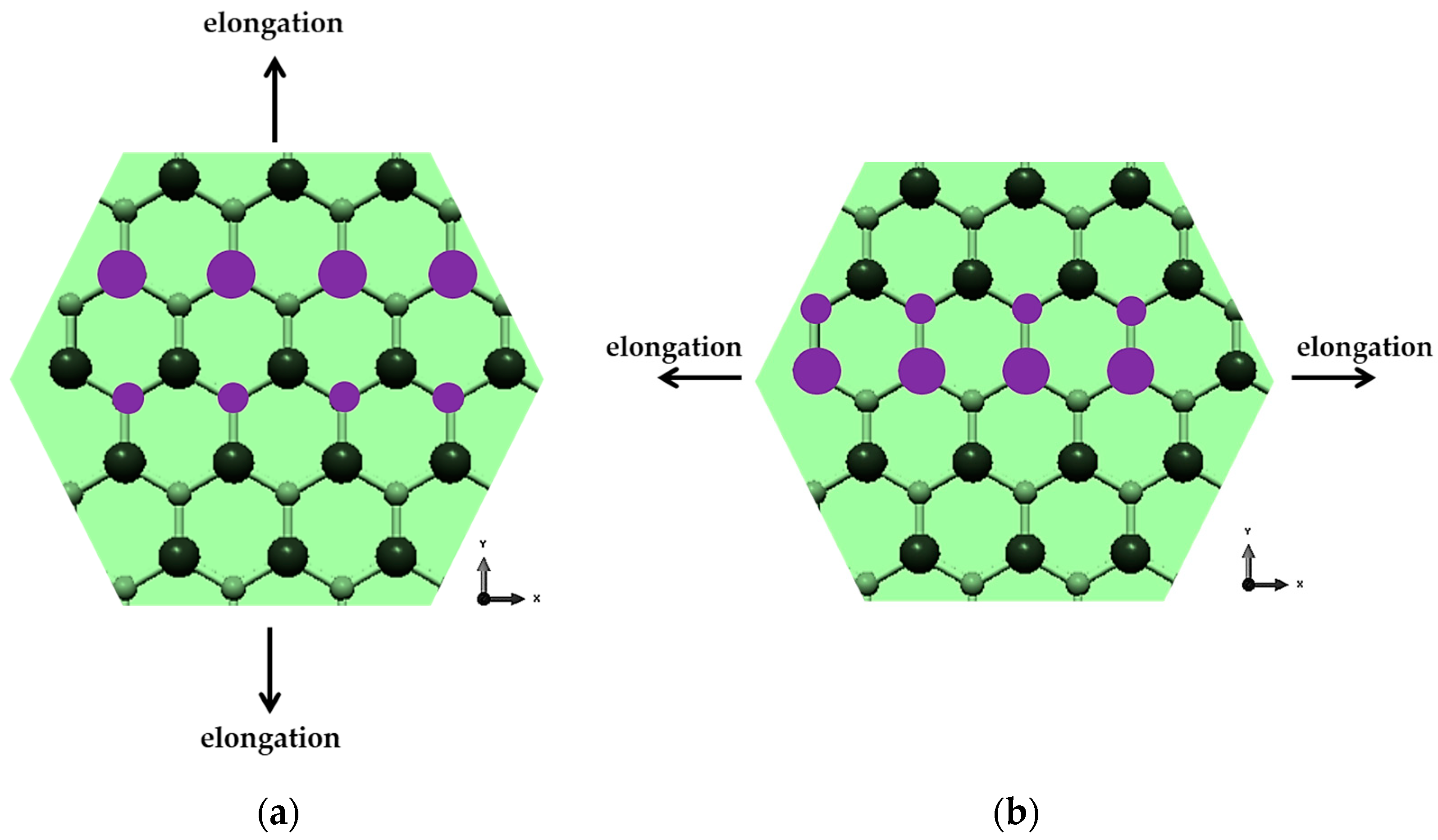
2.1. Geometrical Characteristics of BNNSs and BNNRs
2.2. Input Parameters for the FE Models of BNNSs and BNNRs
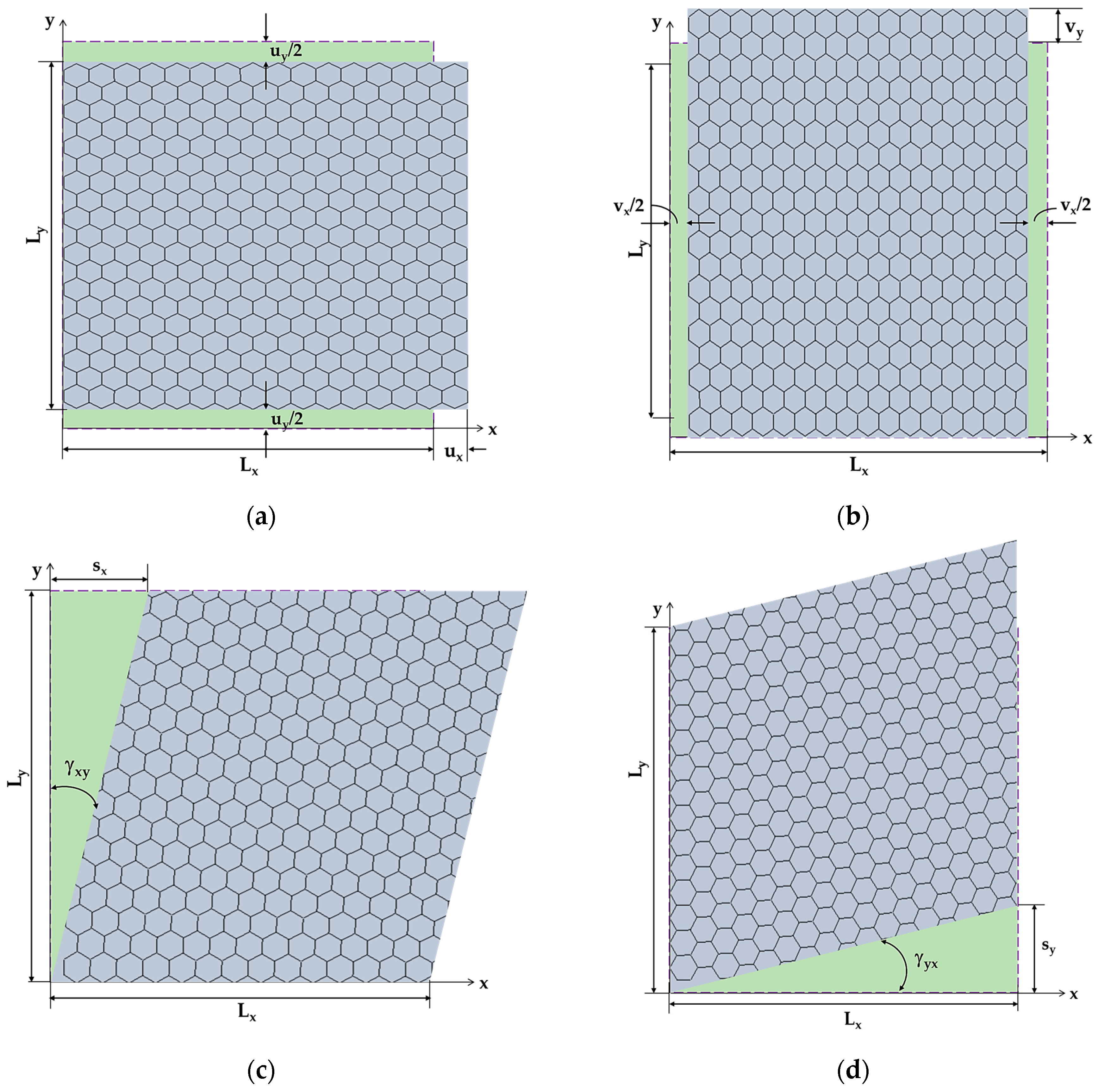
2.3. Finite Element Analysis and Elastic Properties of BNNSs and BNNRs
3. Results and Discussion
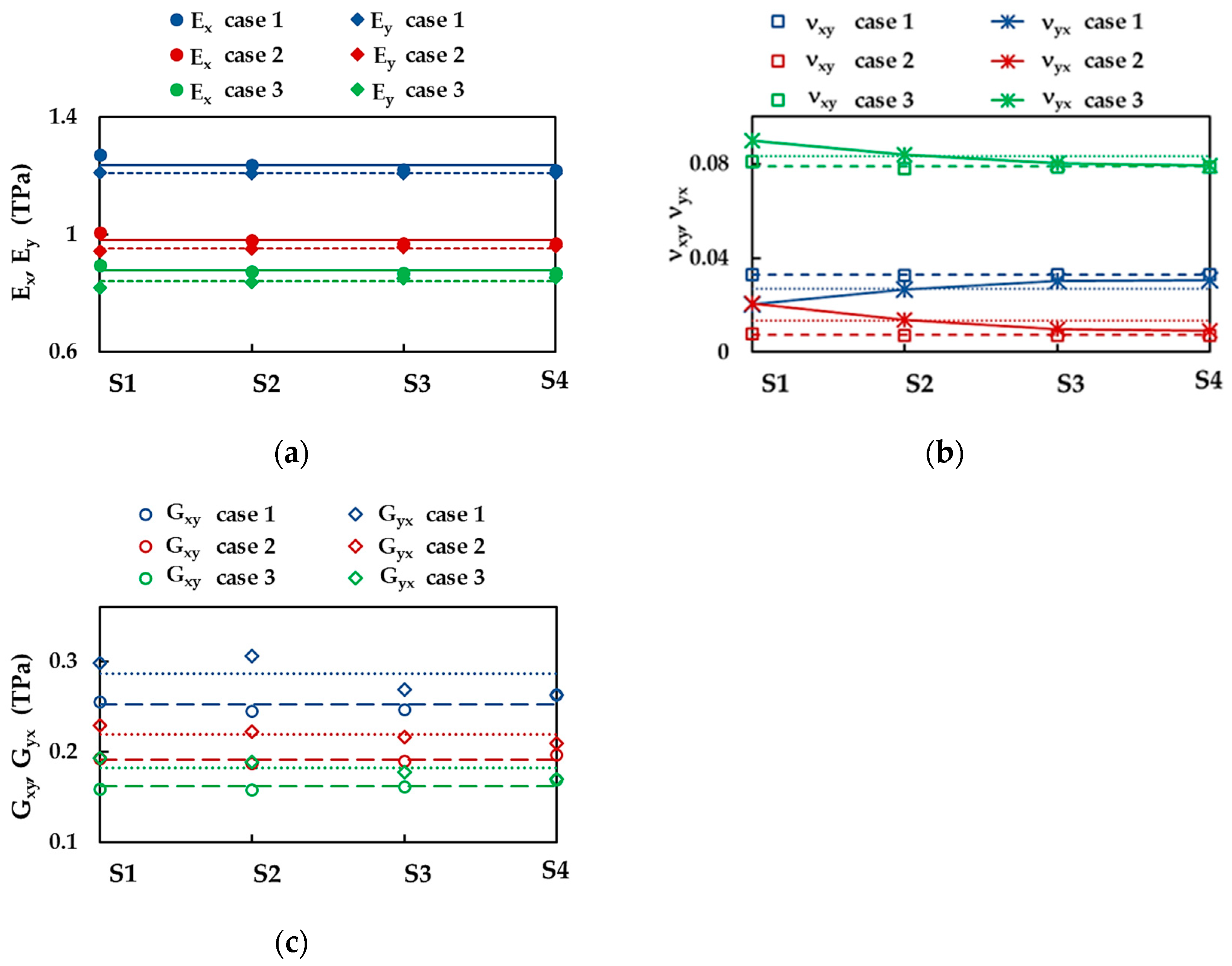
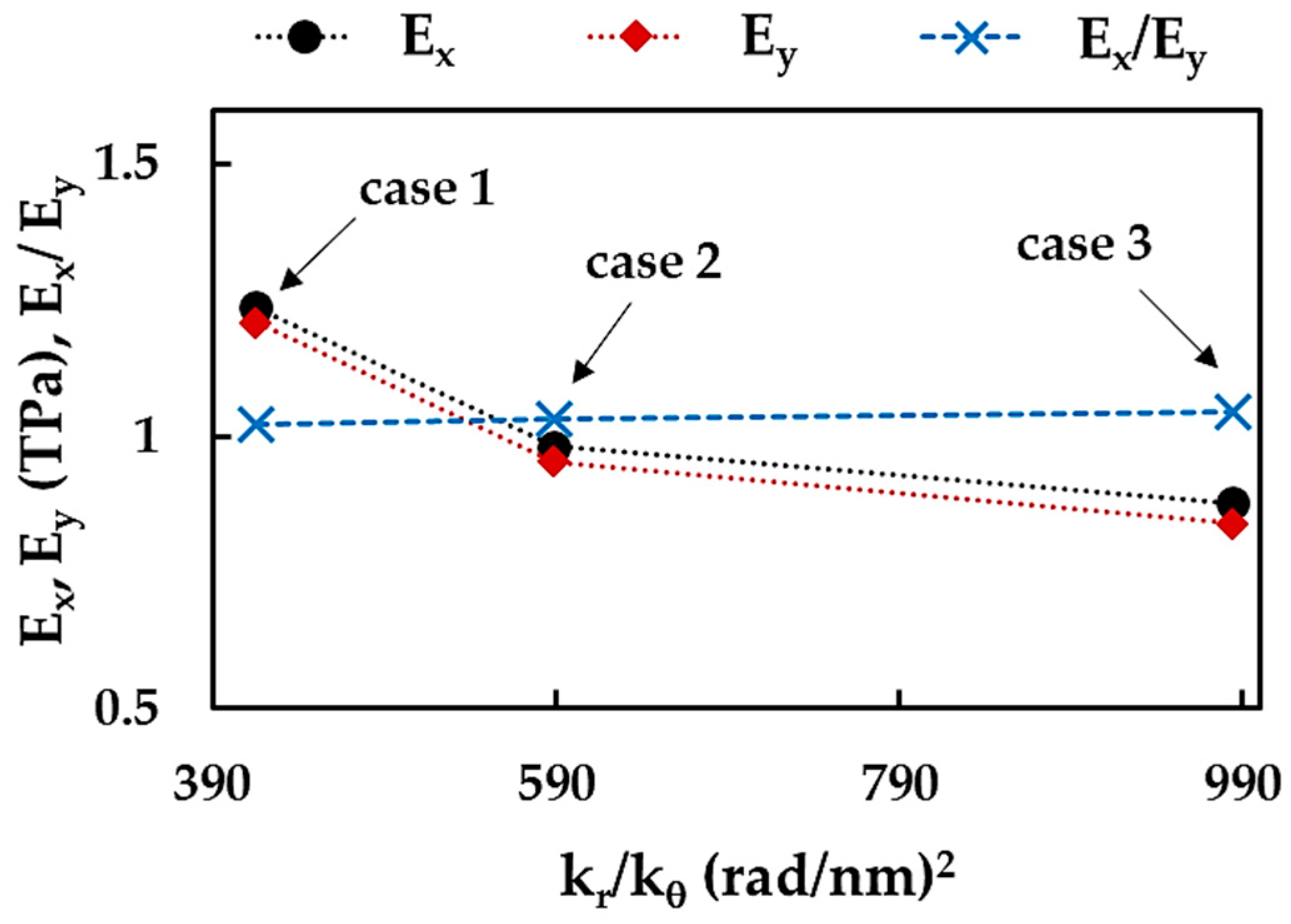
3.1. Effect of Size and Aspect Ratio on Elastic Properties of Boron Nitride Nanosheets
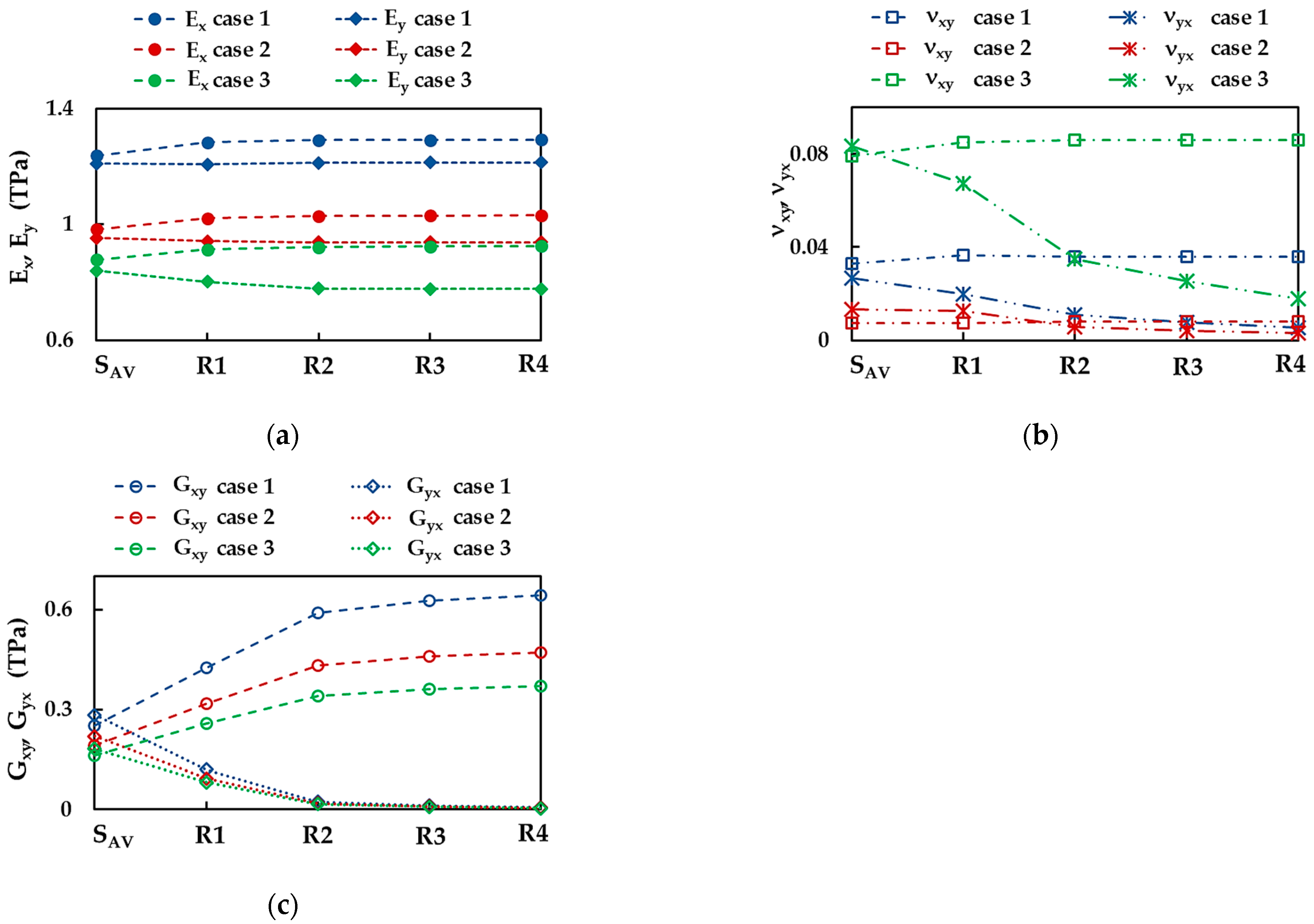
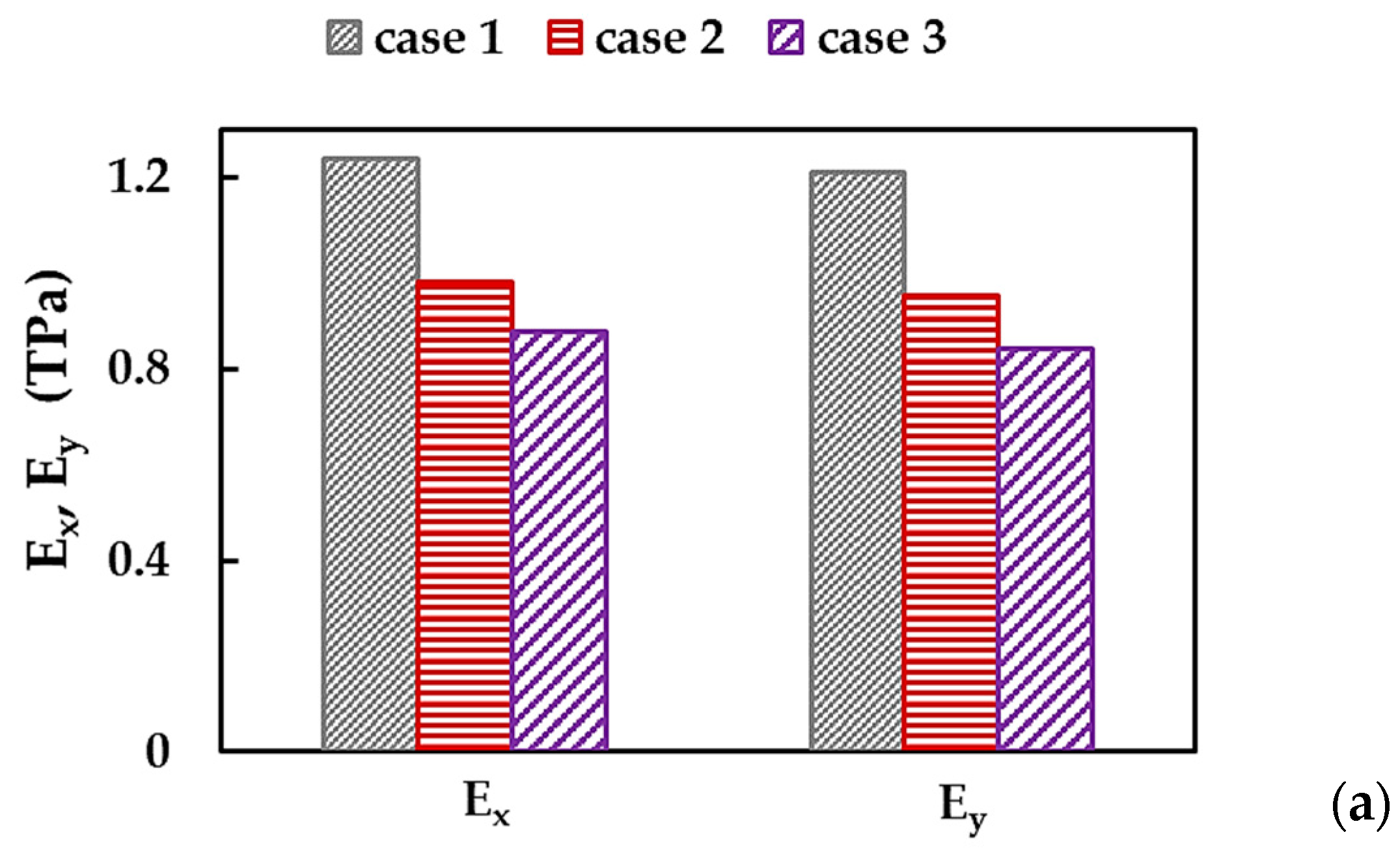
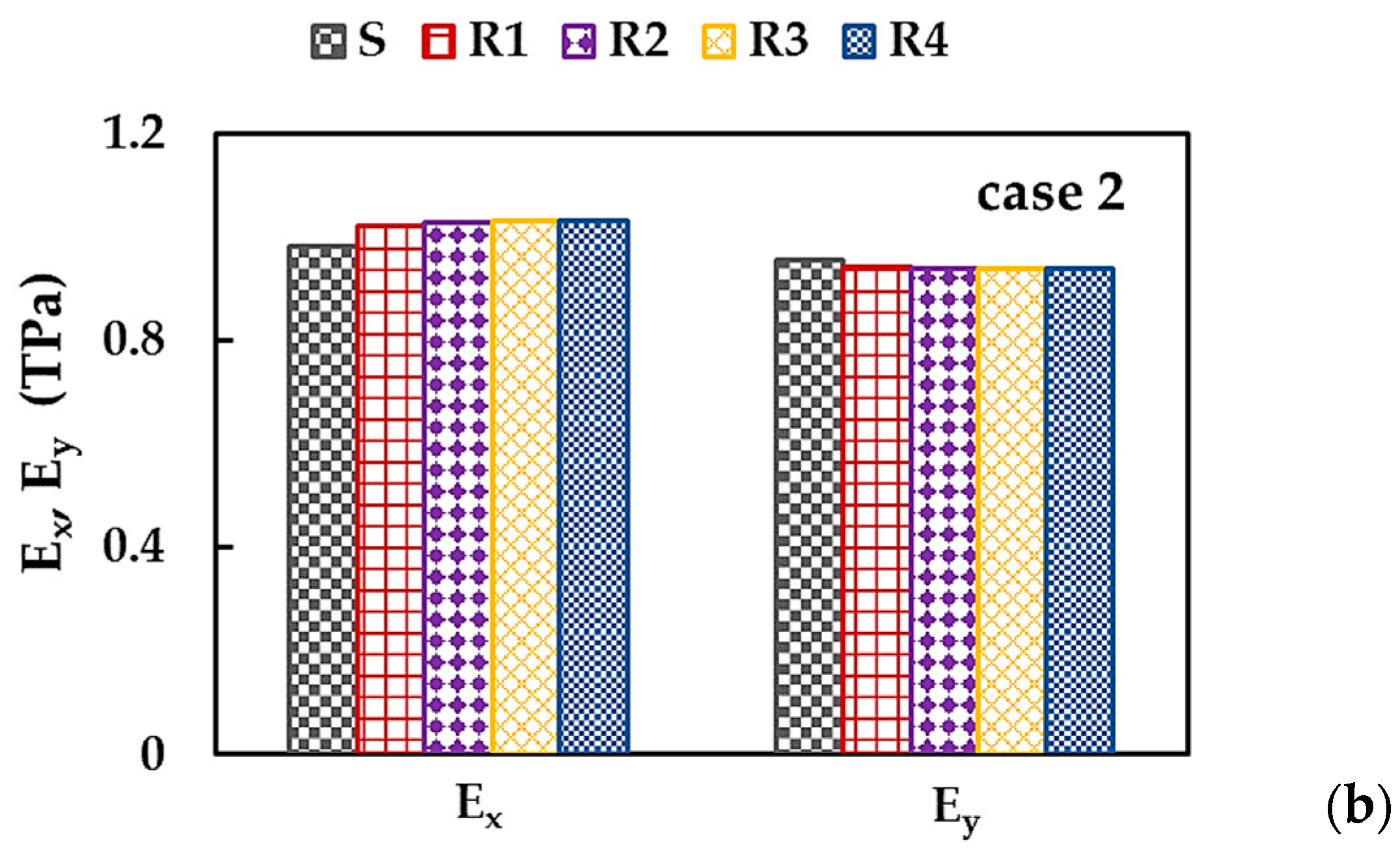
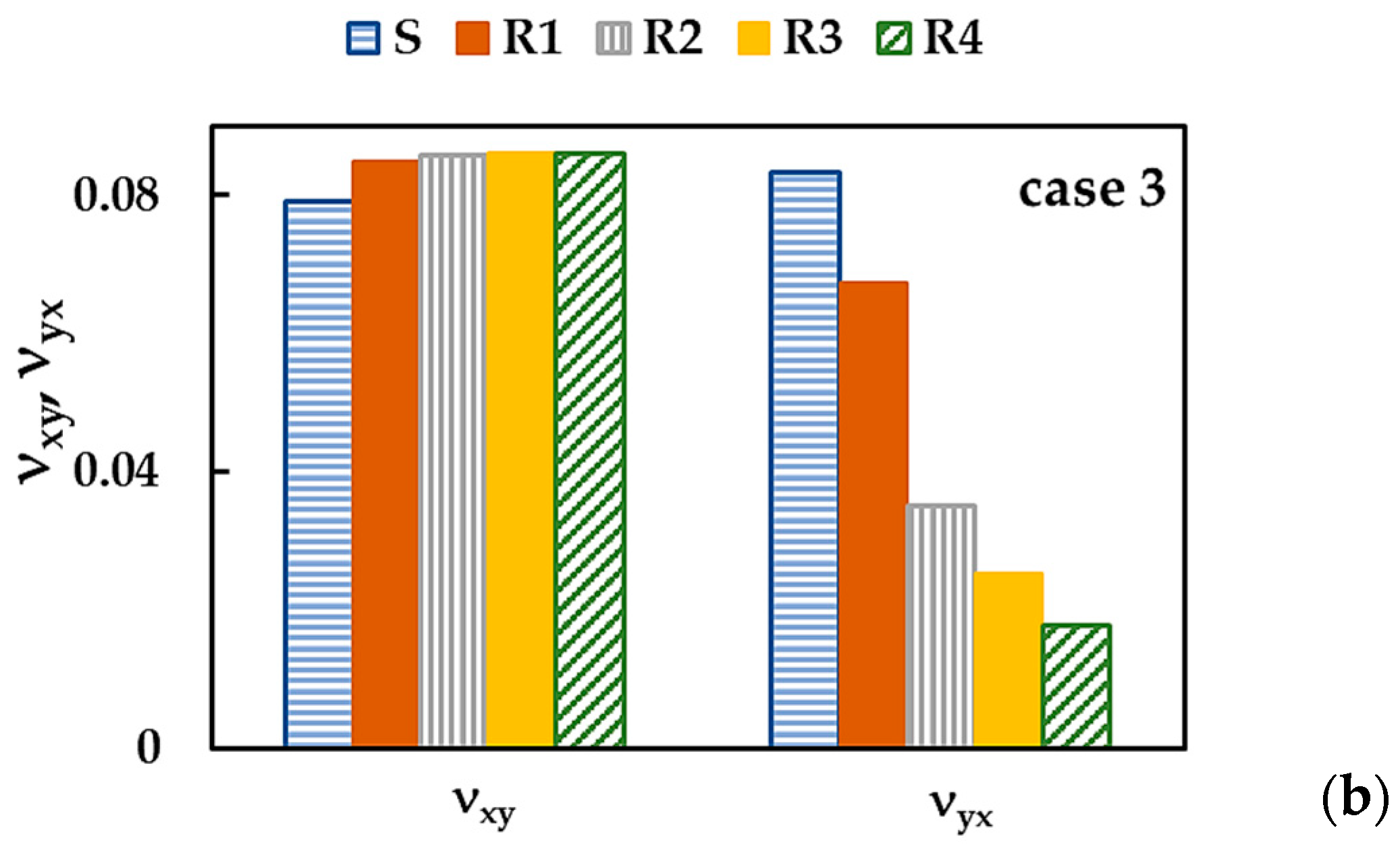
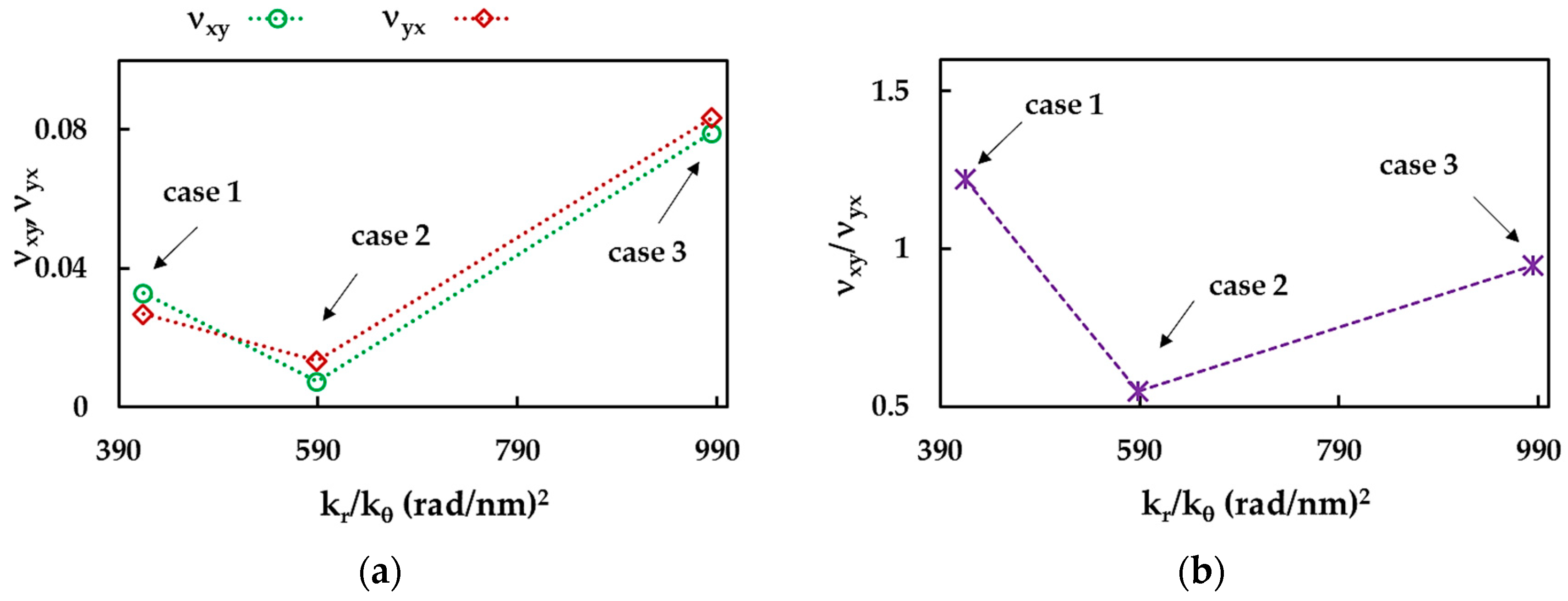
3.2. Young’s Moduli and Poisson’s Ratio of BNNSs and BNNRs
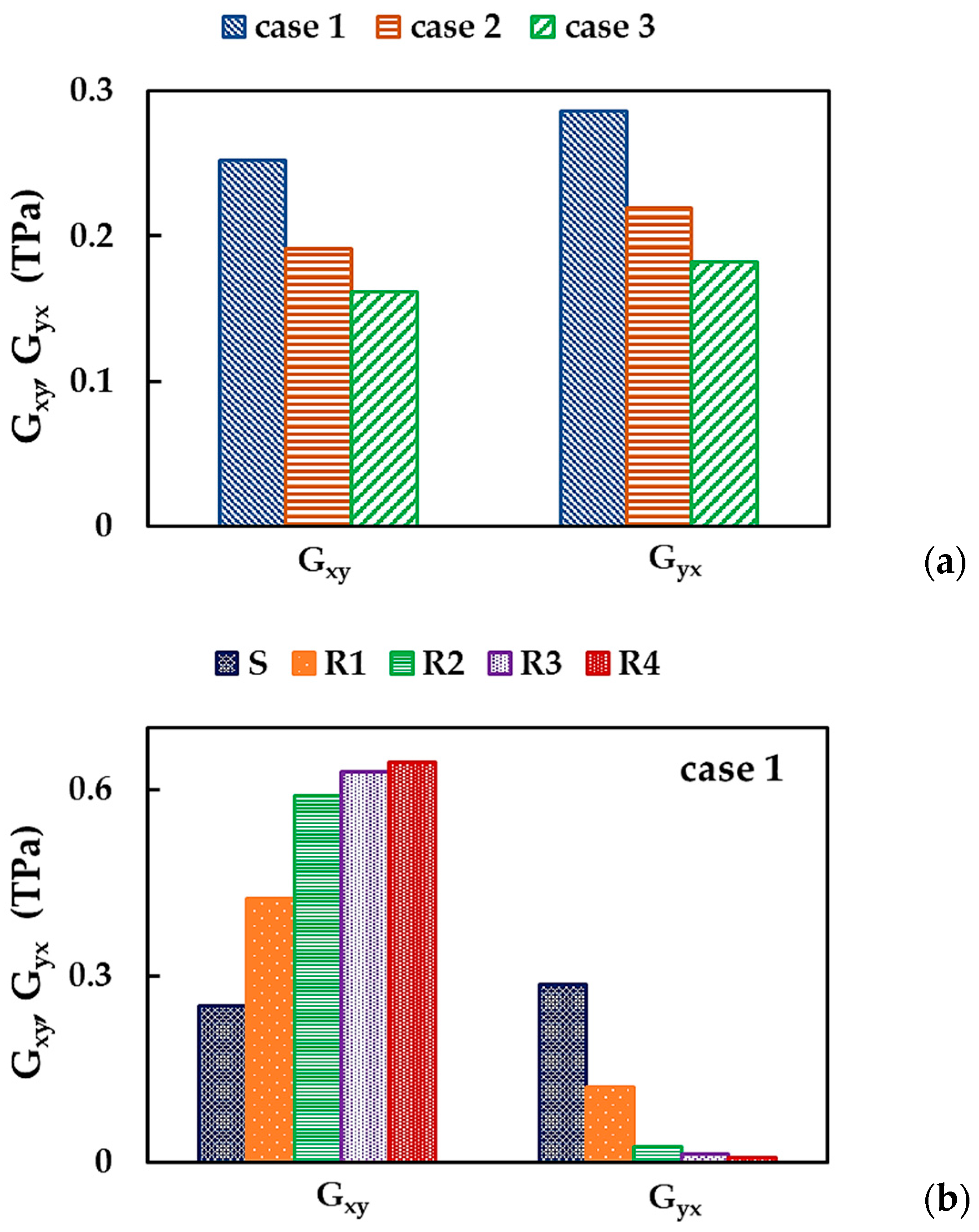
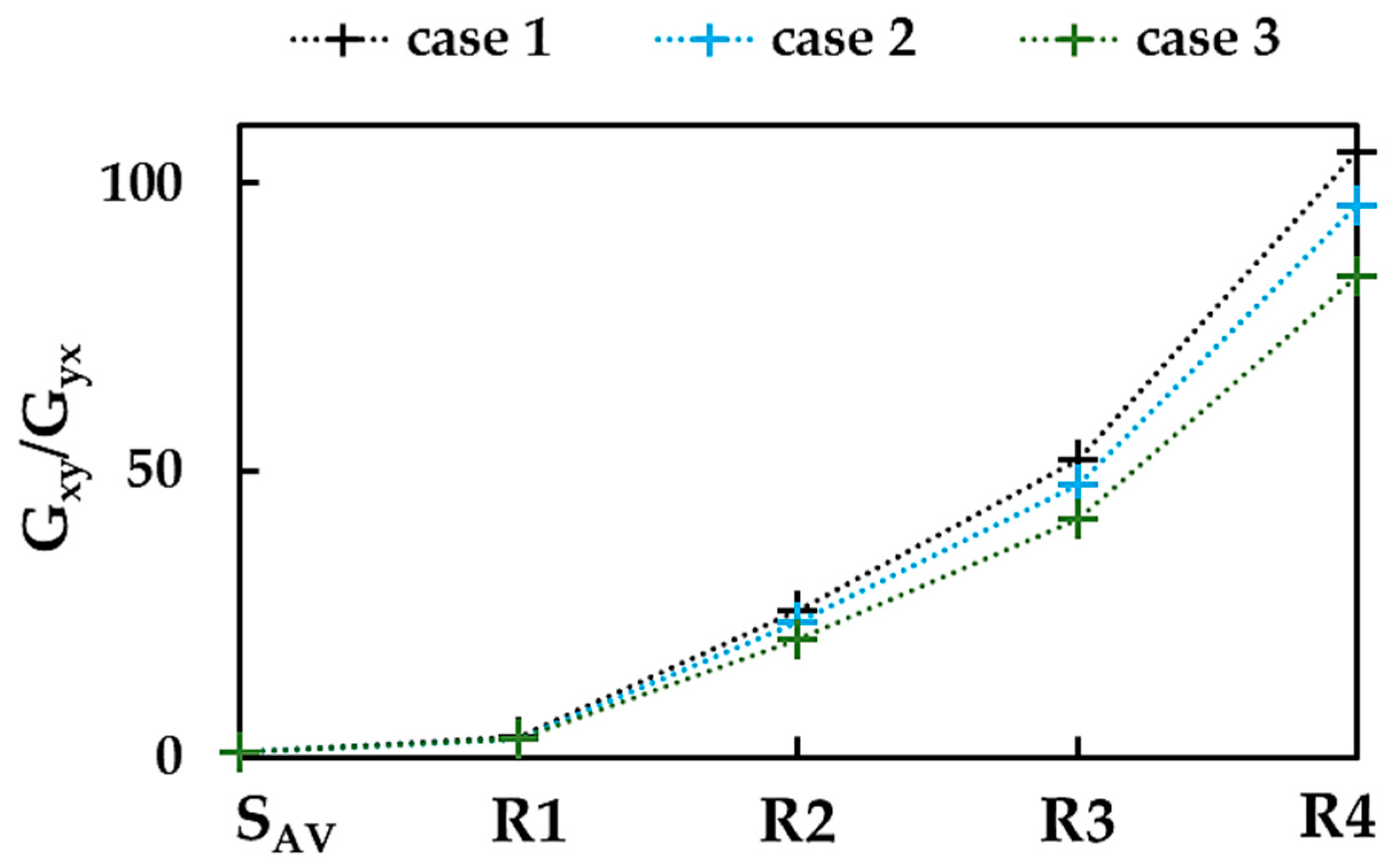
3.3. Shear Moduli of BNNSs and BNNRs
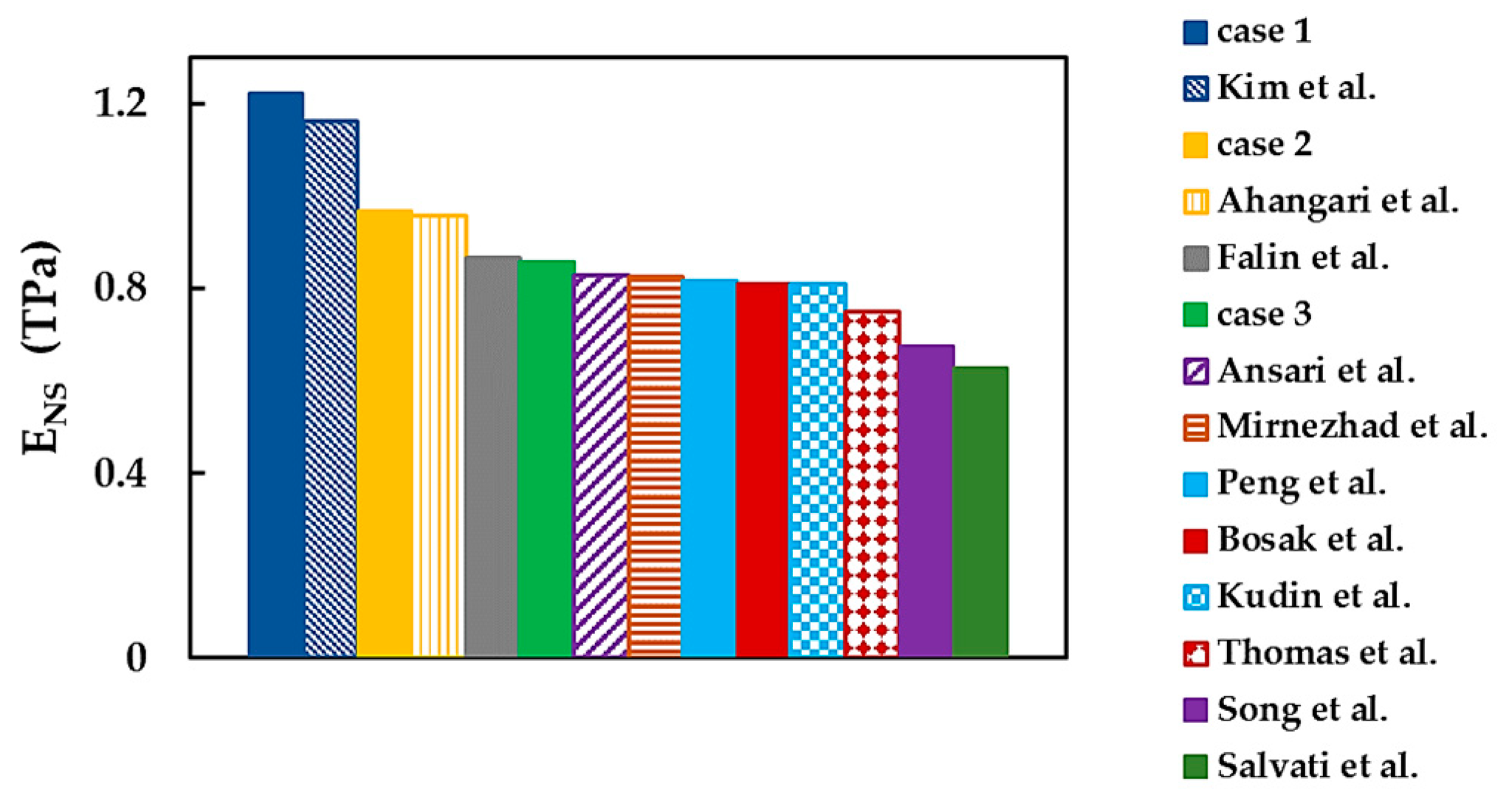
3.4. Comparison with the Literature Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Novoselov, K.S.; Jiang, D.; Schedin, F.; Booth, T.J.; Khotkevich, V.V.; Morozov, S.V.; Geim, A.K. Two-dimensional atomic crystals. Proc. Natl. Acad. Sci. USA 2005, 102, 10451–10453. [Google Scholar] [CrossRef] [PubMed]
- Zeng, H.; Zhi, C.; Zhang, Z.; Wei, X.; Wang, X.; Guo, W.; Bando, Y.; Golberg, D. “White Graphenes”: Boron Nitride Nanoribbons via Boron Nitride Nanotube Unwrapping. Nano Lett. 2010, 10, 5049–5055. [Google Scholar] [CrossRef]
- Huang, Z.; Lü, T.-Y.; Wang, H.-Q.; Yang, S.-W.; Zheng, J.-C. Electronic and thermoelectric properties of the group-III nitrides (BN, AlN and GaN) atomic sheets under biaxial strains. Comput. Mater. Sci. 2017, 130, 232–241. [Google Scholar] [CrossRef]
- Nadeem, A.; Ali Raza, M.; Maqsood, M.F.; Ilyas, M.T.; Westwood, A.; Rehman, Z.U. Characterization of boron nitride nanosheets synthesized by boron-ammonia reaction. Ceram. Int. 2020, 46, 20415–20422. [Google Scholar] [CrossRef]
- Dean, C.R.; Young, A.F.; Meric, I.; Lee, C.; Wang, L.; Sorgenfrei, S.; Watanabe, K.; Taniguchi, T.; Kim, P.; Shepard, K.L.; et al. Boron nitride substrates for high-quality graphene electronics. Nat. Nanotechnol. 2010, 5, 722–726. [Google Scholar] [CrossRef] [PubMed]
- Falin, A.; Cai, Q.; Santos, E.J.G.; Scullion, D.; Qian, D.; Zhang, R.; Yang, Z.; Huang, S.; Watanabe, K.; Taniguchi, T.; et al. Mechanical properties of atomically thin boron nitride and the role of interlayer interactions. Nat. Commun. 2017, 8, 15815. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhou, V.; Xie, Y.; Zheng, X.-Q.; Feng, P.X.-L. Optical contrast signatures of hexagonal boron nitride on a device platform. Opt. Mater. Express. 2019, 9, 1223–1232. [Google Scholar] [CrossRef]
- Liu, Y.; Weiss, N.O.; Duan, X.; Cheng, H.-C.; Huang, Y.; Duan, X. Van der Waals heterostructures and devices. Nat. Rev. Mater. 2016, 1, 16042. [Google Scholar] [CrossRef]
- Zheng, X.-Q.; Lee, J.; Feng, P.X.-L. Hexagonal boron nitride nanomechanical resonators with spatially visualized motion. Microsyst. Nanoeng. 2017, 3, 17038. [Google Scholar] [CrossRef]
- Zhang, Y.; Shi, Q.; Liu, Y.; Wang, Y.; Meng, Z.; Xiao, C.; Deng, K.; Rao, D.; Lu, R. Hexagonal boron nitride with designed nanopores as a high-efficiency membrane for separating gaseous hydrogen from methane. J. Phys. Chem. C 2015, 119, 19826–19831. [Google Scholar] [CrossRef]
- Gao, H.; Shi, Q.; Rao, D.; Zhang, Y.; Su, J.; Liu, Y.; Wang, Y.; Deng, K.; Lu, R. Rational design and strain engineering of nanoporous boron nitride nanosheet membranes for water desalination. J. Phys. Chem. C 2017, 121, 22105–22113. [Google Scholar] [CrossRef]
- Khan, A.A.; Ahmad, R.; Ahmad, I. Silicon carbide and III-Nitrides nanosheets: Promising anodes for Mg-ion batteries. Mater. Chem. Phys. 2021, 257, 123785. [Google Scholar] [CrossRef]
- Kong, X.; Li, L.; Li, M.; Xia, J.; Wang, Y.; Wei, X.; Xiong, S.; Gong, P.; Pan, Z.; Wu, X.; et al. Two-Dimensional Hexagonal Boron Nitride Nanosheets as Lateral Heat Spreader with High Thermal Conductivity. Front. Mater. 2022, 8, 817061. [Google Scholar] [CrossRef]
- Song, L.; Ci, L.; Lu, H.; Sorokin, P.B.; Jin, C.; Ni, J.; Kvashnin, A.G.; Kvashnin, D.G.; Lou, J.; Yakobson, B.I.; et al. Large scale growth and characterization of atomic hexagonal boron nitride layers. Nano Lett. 2010, 10, 3209–3215. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, S.; Hibino, H. Chemical vapor deposition of hexagonal boron nitride. e-J. Surf. Sci. Nanotech. 2012, 10, 133–138. [Google Scholar] [CrossRef][Green Version]
- Tay, R.Y.; Tsang, S.H.; Loeblein, M.; Chow, W.L.; Loh, G.C.; Toh, J.W.; Ang, S.L.; Teo, E.H.T. Direct growth of nanocrystalline hexagonal boron nitride films on dielectric substrates. Appl. Phys. Lett. 2015, 106, 101901. [Google Scholar] [CrossRef]
- Pacilé, D.; Meyer, J.C.; Girit, Ç.O.; Zettl, A. The two-dimensional phase of boron nitride: Few-atomic layer sheets and suspended membranes. Appl. Phys. Lett. 2008, 92, 133107. [Google Scholar] [CrossRef]
- An, L.; Gu, R.; Zhong, B.; Yu, Y.; Zhang, J. Water-icing-triggered scalable and controllable exfoliation of hexagonal boron nitride nanosheets. Cell. Rep. Phys. Sci. 2022, 3, 100941. [Google Scholar] [CrossRef]
- Mirzaee, M.; Rashidi, A.; Zolriasatein, A.; Abadchi, M.R. A simple, low cost, and template-free method for synthesis of boron nitride using different precursors. Ceram. Int. 2021, 47, 5977–5984. [Google Scholar] [CrossRef]
- Li, T.; Li, C.; Cai, Y.; Lin, J.; Long, X.; Wang, L.; Xu, Y.; Sun, J.; Tang, L.; Zhang, Y.W.; et al. Highly Efficient Mass Production of Boron Nitride Nanosheets via a Borate Nitridation Method. J. Phys. Chem. C 2018, 122, 17370–17377. [Google Scholar] [CrossRef]
- Kudin, K.N.; Scuseria, G.E.; Yakobson, B.I. C2F, BN, and C nanoshell elasticity from ab initio computations. Phys. Rev. B 2001, 64, 235406. [Google Scholar] [CrossRef]
- Wu, J.; Wang, B.; Wei, Y.; Yang, R.; Dresselhaus, M. Mechanics and Mechanically Tunable Band Gap in Single-Layer Hexagonal Boron-Nitride. Mater. Res. Lett. 2013, 1, 200–206. [Google Scholar] [CrossRef]
- Ahangari, M.G.; Fereidoon, A.; Mashhadzadeh, A.H. Interlayer interaction and mechanical properties in multi-layer graphene, Boron-Nitride, Aluminum-Nitride and Gallium-Nitride graphene-like structure: A quantum-mechanical DFT study. Superlattices Microstruct. 2017, 112, 30–45. [Google Scholar] [CrossRef]
- Peng, Q.; Ji, W.; De, S. Mechanical properties of the hexagonal boron nitride monolayer: Ab initio study. Comput. Mater. Sci. 2012, 56, 11–17. [Google Scholar] [CrossRef]
- Mirnezhad, M.; Ansari, R.; Shahabodini, A. Temperature effect on Young’s modulus of boron nitride sheets. J. Therm. Stresses 2013, 36, 152–159. [Google Scholar] [CrossRef]
- Le, M.-Q. Atomistic Study on the tensile properties of hexagonal AlN, BN, GaN, InN and SiC sheets. J. Comput. Theor. Nanosci. 2014, 11, 1458–1464. [Google Scholar] [CrossRef]
- Zhao, S.; Xue, J. Mechanical properties of hybrid graphene and hexagonal boron nitride sheets as revealed by molecular dynamic simulations. J. Phys. D Appl. Phys. 2013, 46, 13530. [Google Scholar] [CrossRef]
- Han, T.; Luo, Y.; Wang, C. Effects of temperature and strain rate on the mechanical properties of hexagonal boron nitride nanosheets. J. Phys. D Appl. Phys. 2014, 47, 025303. [Google Scholar] [CrossRef]
- Verma, V.; Jindal, V.K.; Dharamvir, K. Elastic moduli of a boron nitride nanotube. Nanotechnology 2007, 18, 435711. [Google Scholar] [CrossRef]
- Los, J.H.; Kroes, J.M.H.; Albe, K.; Gordillo, R.M.; Katsnelson, M.I.; Fasolino, A. Extended Tersoff potential for boron nitride: Energetics and elastic properties of pristine and defective h-BN. Phys. Rev. B 2017, 96, 184108. [Google Scholar] [CrossRef]
- Thomas, S.; Ajith, K.M.; Valsakumar, M.C. Directional anisotropy, finite size effect and elastic properties of hexagonal boron nitride. J. Phys. Condens. Matter 2016, 28, 295302. [Google Scholar] [CrossRef]
- Salavati, M.; Mojahedin, A.; Hossein, A.; Shirazi, N. Mechanical responses of pristine and defective hexagonal boron-nitride nanosheets: A molecular dynamics investigation. Front. Struct. Civ. Eng. 2020, 14, 623–631. [Google Scholar] [CrossRef]
- Eshkalak, K.E.; Sadeghzadeh, S.; Jalaly, M. Mechanical properties of defective hybrid graphene-boron nitride nanosheets: A molecular dynamics study. Comput. Mater. Sci. 2018, 149, 170–181. [Google Scholar] [CrossRef]
- Mortazavi, B.; Rémond, Y. Investigation of tensile response and thermal conductivity of boron-nitride nanosheets using molecular dynamics simulations. Physica E 2012, 44, 1846–1852. [Google Scholar] [CrossRef]
- Vijayaraghavan, V.; Zhang, L. Effective Mechanical Properties and Thickness Determination of Boron Nitride Nanosheets Using Molecular Dynamics Simulation. Nanomaterials 2018, 8, 546. [Google Scholar] [CrossRef] [PubMed]
- Qu, W.; Bagchi, S.; Chen, X.; Chew, H.B.; Ke, C. Bending and interlayer shear moduli of ultrathin boron nitride nanosheet. J. Phys. D Appl. Phys. 2019, 52, 465301. [Google Scholar] [CrossRef]
- Le, M.Q.; Nguyen, D.T. Determination of elastic properties of hexagonal sheets by atomistic finite element method. J. Comput. Theor. Nanosci. 2015, 12, 566–574. [Google Scholar] [CrossRef]
- Georgantzinos, S.K.; Kariotis, K.; Giannopoulos, G.I.; Anifantis, N.K. Mechanical properties of hexagonal boron nitride monolayers: Finite element and analytical predictions. Proc. IMechE C J. Mech. Eng. Sci. 2020, 234, 4126–4135. [Google Scholar] [CrossRef]
- Tapia, A.; Cab, C.; Hernández-Pérez, A.; Villanueva, C.; Peñuñuri, F.; Avilés, F. The bond force constants and elastic properties of boron nitride nanosheets and nanoribbons using a hierarchical modeling approach. Physica E 2017, 89, 183–193. [Google Scholar] [CrossRef]
- Qin, H.; Liang, Y.; Huang, J. Size and temperature effect of Young’s modulus of boron nitride nanosheet. J. Phys. Condens. Matter 2020, 32, 035302. [Google Scholar] [CrossRef]
- Ansari, R.; Mirnezhad, M.; Sahmani, S. Prediction of chirality- and size-dependent elastic properties of single-walled boron nitride nanotubes based on an accurate molecular mechanics model. Superlattice Microst. 2015, 80, 196–205. [Google Scholar] [CrossRef]
- Bosak, A.; Serrano, J.; Krisch, M.; Watanabe, K.; Taniguchi, T.; Kanda, H. Elasticity of hexagonal boron nitride: Inelastic X-ray scattering measurements. Phys. Rev. B Condens. Matter Mater. Phys. 2006, 73, 041402. [Google Scholar] [CrossRef]
- Kim, S.M.; Hsu, A.; Park, M.H.; Chae, S.H.; Yun, S.J.; Lee, J.S.; Cho, D.H.; Fang, W.; Lee, C.; Palacios, T.; et al. Synthesis of large-area multilayer hexagonal boron nitride for high material performance. Nat. Commun. 2015, 6, 8662. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Chou, T.W. A structural mechanics approach for the analysis of carbon nanotubes. Int. J. Solids Struct. 2003, 40, 2487–2499. [Google Scholar] [CrossRef]
- Sakharova, N.A.; Antunes, J.M.; Pereira, A.F.G.; Chaparro, B.M.; Fernandes, J.V. On the determination of elastic properties of single-walled boron nitride nanotubes by numerical simulation. Materials 2021, 14, 3183. [Google Scholar] [CrossRef]
- Rappé, A.K.; Casewit, C.J.; Colwell, K.S.; Goddard, W.A.; Skid, W.M. UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations. J. Am. Chem. Soc. 1992, 114, 10024–10039. [Google Scholar] [CrossRef]
- Şahin, H.; Cahangirov, S.; Topsakal, M.; Bekaroglu, E.; Akturk, E.; Senger, R.T.; Ciraci, S. Monolayer honeycomb structures of group-IV elements and III-V binary compounds: First-principles calculations. Phys. Rev. B 2009, 80, 155453. [Google Scholar] [CrossRef]
- Genoese, A.; Genoese, A.; Rizzi, N.L.; Salerno, G. Force constants of BN, SiC, AlN and GaN sheets through discrete homogenization. Meccanica 2018, 53, 593–611. [Google Scholar] [CrossRef]
- Ansari, R.; Rouhi, S.; Mirnezhad, M.; Aryayi, M. Stability characteristics of single-walled boron nitride nanotubes. Arch. Civ. Mech. Eng. 2015, 15, 162–170. [Google Scholar] [CrossRef]
- Chen, Y.; Chadderton, L.T.; Gerald, J.F.; Williams, J.S. A solid state process for formation of boron nitride nanotubes. Appl. Phys. Lett. 1999, 74, 2960–2962. [Google Scholar] [CrossRef]





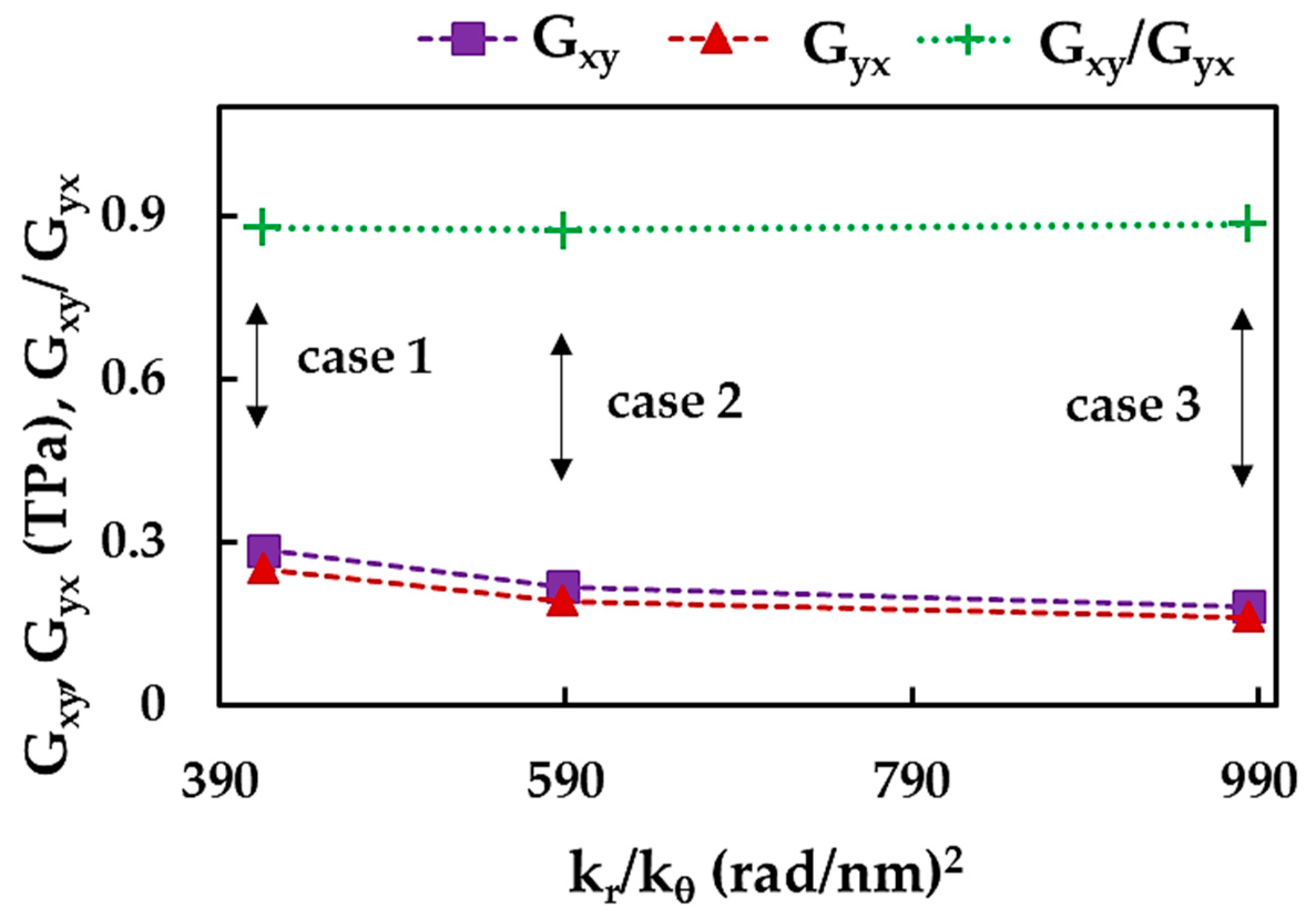
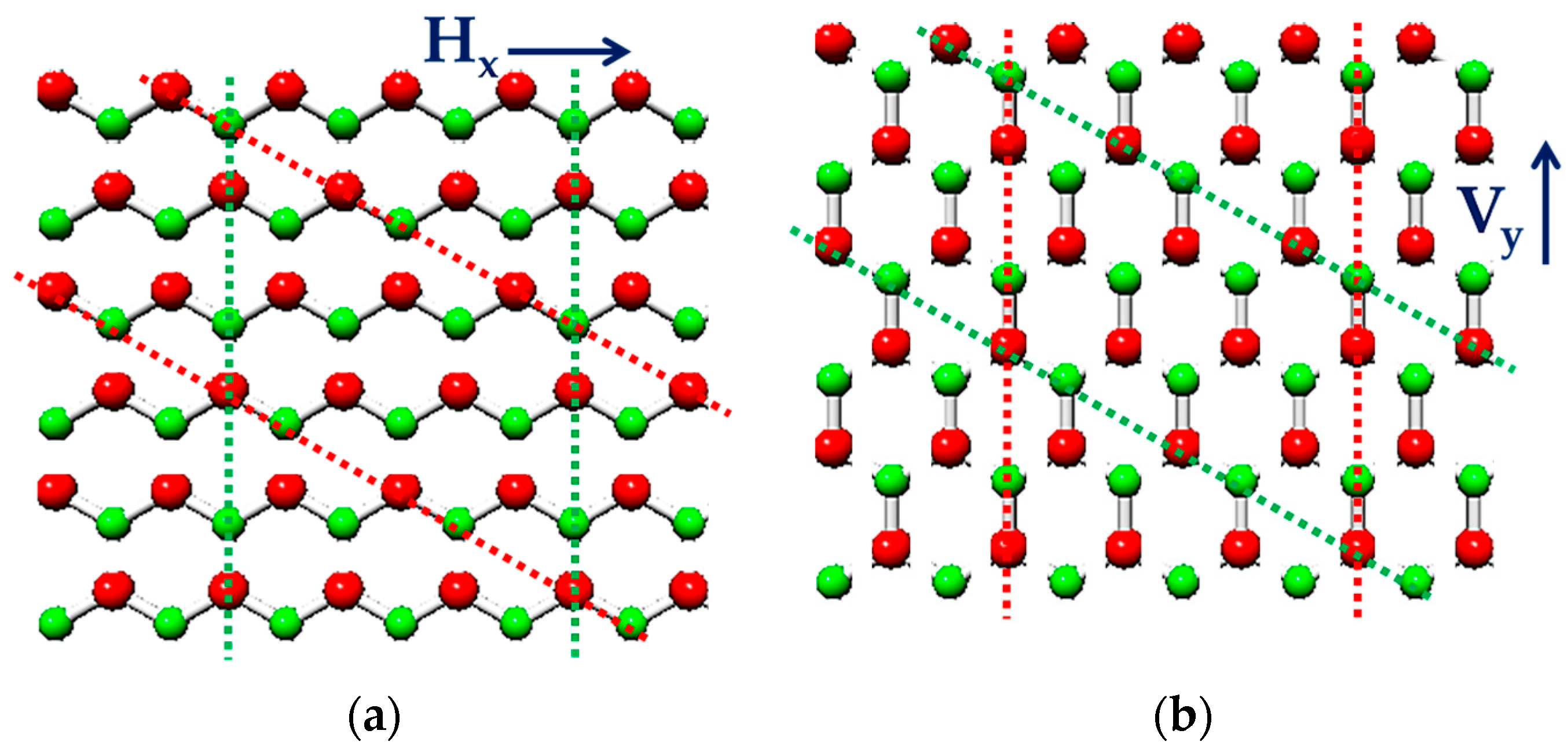
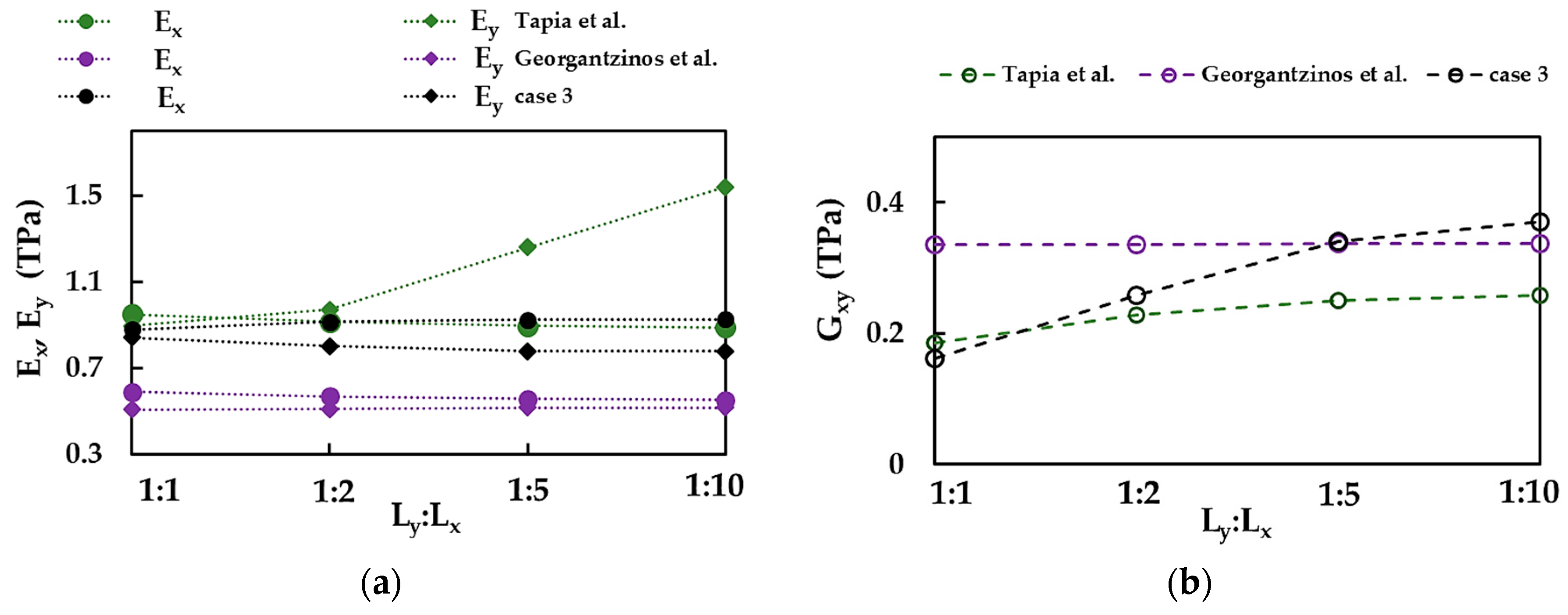
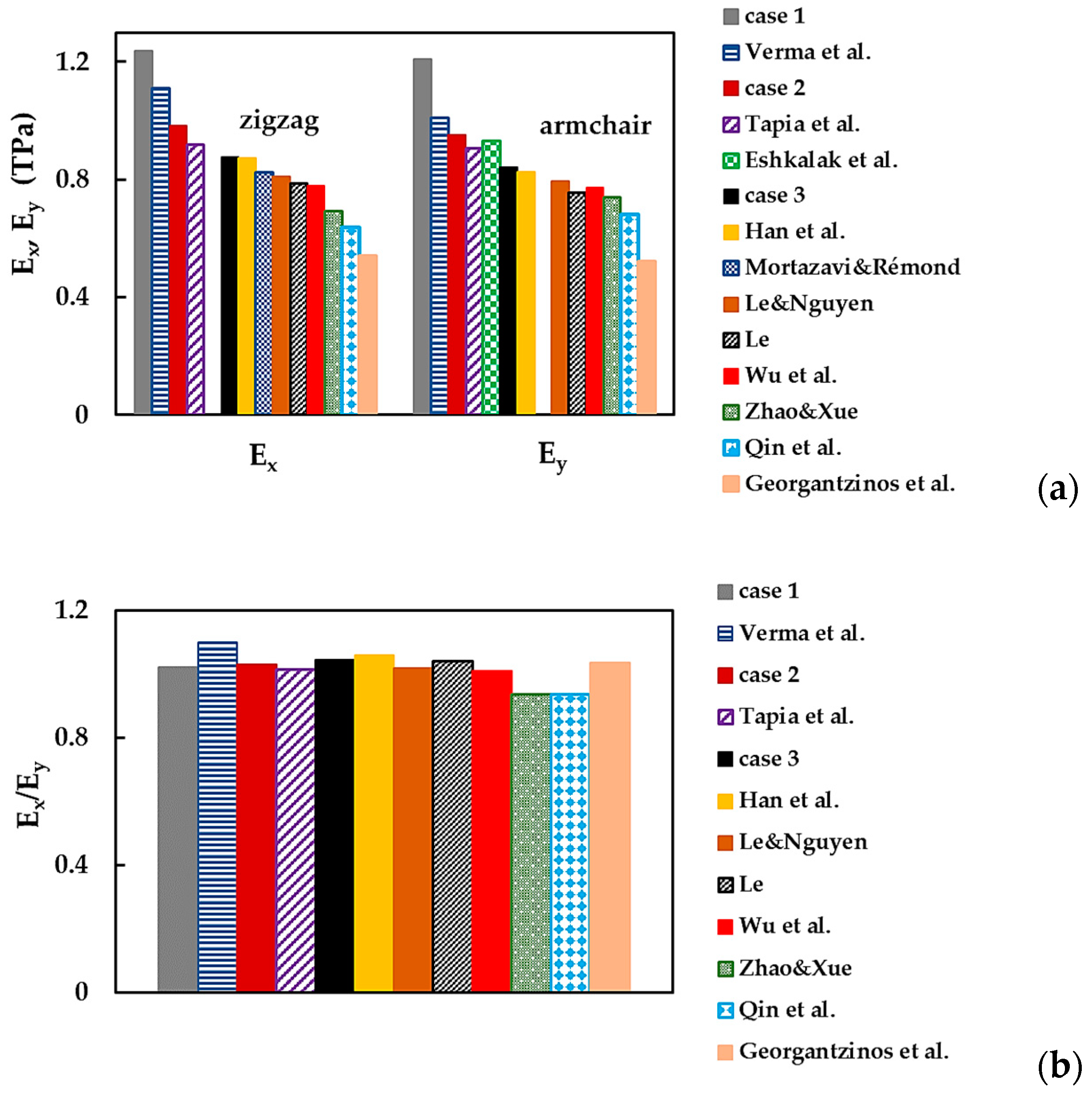

| Designation | Lx, nm | Ly, nm | Aspect Ratio, | Number of Elements | Number of Nodes |
|---|---|---|---|---|---|
| S1 | 2.04 | 2.06 | 1:1 | 237 | 170 |
| S2 | 4.07 | 4.26 | 1:1 | 954 | 660 |
| S3 | 10.18 | 9.98 | 1:1 | 5503 | 3726 |
| S4 | 14.26 | 13.94 | 1:1 | 10,728 | 7232 |
| R1 | 4.07 | 2.06 | 1:2 | 469 | 330 |
| R2 | 10.18 | 2.06 | 1:5 | 1165 | 810 |
| R3 | 14.26 | 2.06 | 1:7 | 1629 | 1130 |
| R4 | 20.37 | 2.06 | 1:10 | 2325 | 1610 |
| Case | Method | Force Field Constants | l, nm | d, nm | Eb, GPa | Gb, GPa | νb |
|---|---|---|---|---|---|---|---|
| 1 | 1 UFF | = 676 nN/nm = 1.627 nN·nm/rad2 2 = 2.470 nN·nm/rad2 | 0.145 | 0.1962 | 3243 | 2462 | 0.10 |
| 2 | 1 DFT + MM | = 585 nN/nm = 0.994 nN·nm/rad2 2 = 2.470 nN·nm/rad2 | 0.1648 | 3977 | 4941 | 0.21 | |
| 3 | 3 DFT | = 617 nN/nm = 0.627 nN·nm/rad2 = 0.132 nN·nm/rad2 | 1.447 | 0.1275 | 6989 | 737 | 0.38 |
| Case | , TPa | , TPa | , TPa | , TPa | ||
|---|---|---|---|---|---|---|
| 1 | 1.237 | 1.209 | 0.252 | 0.286 | 0.033 | 0.027 |
| 2 | 0.982 | 0.953 | 0.191 | 0.219 | 0.007 | 0.013 |
| 3 | 0.877 | 0.840 | 0.162 | 0.182 | 0.079 | 0.083 |
| NS/NR | Case | , TPa | , TPa | ||||
|---|---|---|---|---|---|---|---|
| SAV | 1 | 1.237 | 1.209 | 1.02 | 0.033 | 0.027 | 1.22 |
| 2 | 0.982 | 0.953 | 1.03 | 0.007 | 0.013 | 0.55 | |
| 3 | 0.877 | 0.840 | 1.04 | 0.079 | 0.083 | 0.95 | |
| R1 | 1 | 1.282 | 1.207 | 1.06 | 0.036 | 0.020 | 1.84 |
| 2 | 1.021 | 0.942 | 1.08 | 0.007 | 0.012 | 0.58 | |
| 3 | 0.913 | 0.802 | 1.14 | 0.085 | 0.067 | 1.26 | |
| R2 | 1 | 1.290 | 1.212 | 1.06 | 0.036 | 0.011 | 3.30 |
| 2 | 1.029 | 0.938 | 1.10 | 0.008 | 0.006 | 1.36 | |
| 3 | 0.922 | 0.778 | 1.18 | 0.086 | 0.035 | 2.45 | |
| R3 | 1 | 1.291 | 1.213 | 1.06 | 0.036 | 0.008 | 4.58 |
| 2 | 1.030 | 0.938 | 1.10 | 0.008 | 0.004 | 1.90 | |
| 3 | 0.923 | 0.777 | 1.19 | 0.086 | 0.025 | 3.39 | |
| R4 | 1 | 1.293 | 1.213 | 1.07 | 0.036 | 0.005 | 6.55 |
| 2 | 1.032 | 0.938 | 1.10 | 0.008 | 0.003 | 2.70 | |
| 3 | 0.925 | 0.777 | 1.19 | 0.086 | 0.018 | 4.84 |
| NS/NR | Case | , TPa | , TPa | |
|---|---|---|---|---|
| SAV | 1 | 0.252 | 0.286 | 0.88 |
| 2 | 0.191 | 0.219 | 0.87 | |
| 3 | 0.162 | 0.182 | 0.89 | |
| R1 | 1 | 0.425 | 0.120 | 3.55 |
| 2 | 0.318 | 0.094 | 3.39 | |
| 3 | 0.258 | 0.082 | 3.15 | |
| R2 | 1 | 0.590 | 0.023 | 25.4 |
| 2 | 0.433 | 0.018 | 23.4 | |
| 3 | 0.340 | 0.016 | 20.6 | |
| R3 | 1 | 0.628 | 0.012 | 51.8 |
| 2 | 0.460 | 0.010 | 47.5 | |
| 3 | 0.360 | 0.009 | 41.6 | |
| R4 | 1 | 0.643 | 0.006 | 105.6 |
| 2 | 0.472 | 0.005 | 96.2 | |
| 3 | 0.370 | 0.004 | 83.8 |
| Reference | Method | , nm | , TPa | , TPa | , TPa | Size, nm2 | ||
|---|---|---|---|---|---|---|---|---|
| Atomistic approach: | ||||||||
| Kudin et al. [21] | ab initio DFT | 0.335 | 0.810 | – | 0.334 | 0.211 | – | |
| Wu et al. [22] | 0.330 | 0.780 | 0.773 | 1.01 | – | – | 1.500 × 1.732 | |
| Ahangari et al. [23] | 0.320 | 0.956 | – | – | – | 1.005 × 1.132 | ||
| Peng et al. [24] | – | 0.818 1 | – | – | – | – | ||
| Mirnezhad et al. [25] | DFT + QHA | – | 0.825 1 | – | – | – | – | |
| Zhao and Xue [27] | MD: Tersoff potential | 0.330 | 0.692 | 0.739 | 0.94 | – | – | 12.00 × 12.00 |
| Thomas et al. [31] | 0.334 | 0.750 | – | – | 0.297 | 10,000 atoms | ||
| Eshkalak et al. [33] | 0.340 | – | 0.930 | – | – | – | 5.30 × 5.60 | |
| Mortazavi and Rémond [34] | 0.330 | 0.824 | – | – | – | – | – | |
| Le [26] | MD: Tersoff and Tersoff-like potentials | 0.335 | 0.786 | 0.756 | 1.04 | – | – | 10.36 × 10.22 |
| Han et al. [28] | MD: Tersoff-like potential | 0.333 | 0.874 | 0.825 | 1.06 | – | 10.00 × 10.00 | |
| Verma et al. [29] | MD: Tersoff-Berner potential | 0.333 | 1.110 | 1.010 | 1.10 | – | – | 8.67 × 10.22 |
| Salvati et al. [32] | MD: modified Tersoff potential | 0.340 | 0.628 | – | – | – | 30.00 × 30.00 | |
| NCM/MSM approach: | ||||||||
| Le and Nguyen [37] | 2-node stretching and 3-node angle bending elements | 0.335 | 0.809 | 0.794 | 1.02 | 0.340 | 0.226; 0.222 | 10.42 × 10.29 |
| Ansari et al. [41] | analytical solution | 0.340 | 0.829 | – | – | – | – | |
| Georgantzinos et al. [38] | springs | 0.340 | 0.540 | 0.522 | 1.03 | 0.338; 0.346 2 | 0.420; 0.418 | from 2.00 × 2.00 to 20.00 × 20.00 |
| Tapia et al. [39] | beams | 0.106 | 0.920 | 0.908 | 1.01 | 0.188 | 0.822 | 3.76 × 3.76 7.27 × 7.24 14.79 × 14.71 |
| Qin et al. [40] | – | 0.637 1 | 0.681 1 | 0.94 | – | – | 9.00 × 9.00 | |
| Current study | 0.340 | 1.237 | 1.209 | 1.02 | 0.252; 0.286 2 | 0.033; 0.027 | 2.04 × 2.06 4.07 × 4.26 10.18 × 9.98 14.26 × 13.94 | |
| 0.982 | 0.953 | 1.03 | 0.191; 0.219 2 | 0.007; 0.013 | ||||
| 0.877 | 0.840 | 1.04 | 0.162; 0.182 2 | 0.079; 0.083 | ||||
| Experimental: | ||||||||
| Bosak et al. [42] | X-ray scattering measurements | – | 0.811 | – | – | – | – | |
| Song et al. [14] | nanoindentation + AFM | 0.330 | 0.676 | – | – | – | 7.85 × 104 (circular) | |
| Falin et al. [6] | nanoindentation | 0.334 | 0.865 ± 0.073 | – | – | – | – | |
| Kim et al. [43] | nanoindentation + AFM | – | 1.16 ± 0.1 | – | – | – | – | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sakharova, N.A.; Pereira, A.F.G.; Antunes, J.M. A Study of the Mechanical Behaviour of Boron Nitride Nanosheets Using Numerical Simulation. Nanomaterials 2023, 13, 2759. https://doi.org/10.3390/nano13202759
Sakharova NA, Pereira AFG, Antunes JM. A Study of the Mechanical Behaviour of Boron Nitride Nanosheets Using Numerical Simulation. Nanomaterials. 2023; 13(20):2759. https://doi.org/10.3390/nano13202759
Chicago/Turabian StyleSakharova, Nataliya A., André F. G. Pereira, and Jorge M. Antunes. 2023. "A Study of the Mechanical Behaviour of Boron Nitride Nanosheets Using Numerical Simulation" Nanomaterials 13, no. 20: 2759. https://doi.org/10.3390/nano13202759
APA StyleSakharova, N. A., Pereira, A. F. G., & Antunes, J. M. (2023). A Study of the Mechanical Behaviour of Boron Nitride Nanosheets Using Numerical Simulation. Nanomaterials, 13(20), 2759. https://doi.org/10.3390/nano13202759








