Abstract
Transition-metal-doped clusters have long been attracting great attention due to their unique geometries and interesting physical and/or chemical properties. In this paper, the geometries of the lowest- and lower-energy CoKn (n = 2–12) clusters have been screened out using particle swarm optimization and first principles relaxation. The results show that except for CoK2 the other CoKn (n = 3–12) clusters are all three-dimensional structures, and CoK7 is the transition structure from which the lowest energy structures are cobalt atom-centered cage-like structures. The stability, the electronic structures, and the magnetic properties of CoKn clusters (n = 2–12) clusters are further investigated using the first principles method. The results show that the medium-sized clusters whose geometries are cage-like structures are more stable than smaller-sized clusters. The electronic configuration of CoKn clusters could be described as 1S1P1D according to the spherical jellium model. The main components of petal-shaped D molecular orbitals are Co-d and K-s states or Co-d and Co-s states, and the main components of sphere-like S molecular orbitals or spindle-like P molecular orbitals are K-s states or Co-s states. Co atoms give the main contribution to the total magnetic moments, and K atoms can either enhance or attenuate the total magnetic moments. CoKn (n = 5–8) clusters have relatively large magnetic moments, which has a relation to the strong Co-K bond and the large amount of charge transfer. CoK4 could be a magnetic superatom with a large magnetic moment of 5 μB.
1. Introduction
During the past decades, clusters have drawn significant attention due to their unique geometries, interesting physical and/or chemical properties originating from quantum size effects, and their wide application in catalysts [1], superatoms [2], and so on [3,4,5,6]. For example, Cheng et al. fabricated single platinum atoms and clusters using the atomic layer deposition (ALD) technique and then investigated the activity of hydrogen evolution reaction (HER). The results show that the platinum single atoms and clusters supported on nitrogen-doped graphene nanosheets have greater activity for HER due to the high utilization of nearly all the platinum atoms [1]. Hence, a large number of investigations have been performed to explore the geometries, stabilities, electronic structures, and physical properties of clusters [7,8,9,10] using such methods as the first principles investigation [11,12,13], molecular dynamics [14,15], bionics algorithm [16,17,18], and machine learning [19,20,21], among which kinds of bionics algorithm are on the rise.
The structures and physical properties of transition-metal-doped clusters including the transition-metal oxides and hydroxides nanoclusters are one of the hotspots [22,23,24,25]. Wang et al. investigated the total and local magnetic moments of the most stable [TM13@Au20]− clusters using density functional theory implemented in the DMol3 package, and they pointed out that the transition-metal atom could enhance or attenuate the total magnetic moments [26]. Zhao et al. investigated the geometries and electronic structures of YnAl (n = 1–14) clusters and found that doping with an Al atom could attenuate the magnetic moments but enhance the stabilities of the yttrium framework [27]. Our previous work predicted the geometries of the lowest energy and their isomers of ScKn (n = 2–12) clusters using particle swarm optimization and first principles geometry optimization, and we have also investigated the electronic structures and magnetic properties using the first principles calculation. The results showed that the doping of Sc atoms can improve the magnetic properties and stability of the Kn clusters, and the ScK12 cluster may be a magnetic superatom with a high magnetic moment of 5 μB [28]. The VIIIB atom (Fe, Co, and Ni)-doped clusters including VIIIB transition-metal oxides and hydroxides nanoclusters have also attracted great attention due to their interesting electronic structures, physical and chemical properties, and their wide application. For example, Milan Babu Poudel et al. reported that the hierarchical heterostructure comprising ternary metal sulfides covered by nickel–cobalt layered double hydroxide could be used as binder-free cathode material for supercapacitor application [29], and they also reported a superior bifunctional electrocatalyst for oxygen evolution reaction (OER) and hydrogen evolution reaction (HER), which contains both cobalt and nickel atoms [30]. As for the VIIIB atom (Fe, Co, and Ni)-doped clusters, our group has investigated the geometries, electronic structures, and magnetic properties of GenCo (n = 2–12) clusters using the first principles method, and the results show that the total magnetic moments of GenCo (n = 2–12) clusters does not quench, and the doping of the Co atom is beneficial to enhance the stability of host Gen clusters [31]. The electronic structures and magnetic moments of the core-shell clusters Co13@TM20 (TM = Mn, Fe, Co, and Ni) have also been investigated using the first-principles method, and the results show that these clusters have huge magnetic moments, especially for the Co13@Mn20 cluster, whose magnetic moment is as large as 113 μB [32]. After investigating the geometries and electronic structures using the first-principles method implemented in the Vienna Ab Initio Simulation Package (VASP) and Orca code, Hao et al. pointed out that doping of the Co atom in Bn clusters significantly changes their structures, and the Co2B and Co2B7 clusters have a large magnetic moment of 3 μB [33]. A systematic theoretical investigation of the structure, stability, and electronic properties of LinCo clusters showed that the doping with the cobalt atom could enhance the stabilities of host clusters, and greater electron transfer from Li-2s to Co-3d can help to strengthen the bond length of Li-Co [34].
Inspired by the unique structures, interesting electronic properties, and wide application of transition-metal-doped clusters, the authors are going to investigate the growth pattern, electronic structures, and magnetic moments of other VIIIB atom-doped alkali clusters. In this paper, the authors have investigated the geometries of CoKn (n = 2–12) clusters predicted by the particle swarm optimization (PSO) algorithm along with first principles relaxation. The results show that the CoKn (n = 3–12) clusters are all three-dimensional structures, and CoK7 is the transition structure from which the lowest energy structures are cobalt atom-centered cage-like structures. The stabilities, the magnetic moments, and the electronic structures are also investigated using the first principles calculation. The results show that the cobalt atom-centered cage-like clusters are more stable than smaller-sized clusters. In addition, the electronic configuration of CoKn clusters could be described as 1S1P1D according to the spherical jellium model. According to the results of the projected density of states, the main components of petal-shaped D molecular orbitals are Co-d and K-s states or Co-d and Co-s states. The main components of sphere-like S molecular orbitals or spindle-like P molecular orbitals are K-s states or Co-s states. Co atoms give the main contribution to the total magnetic moments, and K atoms can either enhance or attenuate the total magnetic moments. CoKn (n = 5–8) clusters have relatively large magnetic moments, which has a relation with the strong Co-K bond and a large amount of charge transfer. CoK4 could be a magnetic superatom with a large magnetic moment of 5 μB.
2. Computational Details
In this paper, the particle swarm optimization method implemented in CALYPSO code [16,35,36] along with the first principles calculation implemented in the Vienna Ab Initio Simulation Package (VASP) code [37,38] are used to screen out the potential candidates of CoKn (n = 2–12) clusters. The CALYPSO code has been widely used to predict the ground state structure of clusters and crystals [39,40,41]. Using this powerful structure search method combined with first-principles calculations, Tang et al. have identified a planar CoB6 monolayer as a stable two-dimensional ferromagnet [42], and our group has also investigated the geometries of transition-metal-doped clusters [43].
During the workflow of cluster structure prediction, the candidate clusters of the first generation are randomly generated by CALYPSO code, and then 80% of candidate clusters of the next generation are inherited from the previous generation. The remaining 20% of candidate clusters are still randomly generated. The population size, i.e., the total number of structures per generation, is set to be 20 for CoKn (n < 9) and 30 for CoKn (n ≥ 9) clusters. The maximum number of generations is set as more than 20 (for n < 9) and 30 (for n ≥ 9), that is to say, more than 400 (for n < 9) and 900 (for n ≥ 9) candidate isomers are generated and optimized to get the lowest-energy clusters. The geometry optimization is performed using the VASP code [35,36]. During the calculation, the projected augmented wave method and the Perdew–Burke–Ernzerhof (PBE) exchange-correlation functional [44] under generalized gradient approximation (GGA) are used. The plane-wave cutoff energy is set as 300 eV. The global break condition for the electronic self-consistency (SC) loop is set as 1 × 10−5 eV. The maximum number of electronic SC steps is set as 500, and the maximum number of ionic steps is set as 200. A conjugate gradient algorithm is used to relax the ions into their instantaneous ground state. To avoid the interaction of atoms located in neighbor cells, the CoKn clusters are placed in a cubic super lattice of 12 × 12 × 12 angstroms (for n < 9) and 15 × 15 × 15 angstroms (for n ≥ 9).
Once the convergence criterion is obtained, the PSO performance will be stopped, and then some candidates are chosen to be further optimized using the first principles Gaussian09 code. During Gaussian09 calculation [45], the geometry optimization and frequency calculation of CoKn (n = 2–12) clusters with different spin are carried out to ensure that the obtained structures are the lowest-energy structures. The Gaussian09 calculation is performed using B3LYP [46] functional at a 6-31G** level for the Co atom and a 6-311G** [47] level for K atoms. The authors have carefully checked out the harmonic vibrational frequencies of each lowest- and lower-energy clusters to ensure the obtained clusters are stable clusters without imaginary frequencies. The population analysis of CoKn clusters is studied using the Multiwfn3.8 program [48,49].
3. Results and Discussion
3.1. The Geometries of Lowest-Energy Clusters
Using the method described above, the geometries of the lowest-energy clusters and their meta stable isomers are obtained. Figure 1 gives the geometries of the lowest-energy and the meta stable isomers of CoKn (n = 2–12) clusters along with the bond length of Co-K bonds. As shown in Figure 1, except for CoK2 clusters whose geometries of lowest-energy and their isomer are planar triangular structures, the geometries of the other CoKn (n = 3–12) clusters are all three-dimensional structures. The geometries of the ground state and meta stable state of CoK3 cluster are a slightly distorted quadrangle with C2V symmetry. The bipyramid structures were found in the lowest energy structures of CoKn (n = 4–6) clusters. The lowest energy structure of CoK4 is a triangular bipyramid structure with a C3V point group. The lowest energy structure of cluster CoK5 is a tetragonal bipyramid structure with a C4V point group. The CoK6 is a twisted pentagonal bipyramid structure with a C1 point group. The ground state structure of the CoK7 cluster is a Co-atom-centered K-atom-capped tetragonal bipyramid structure with a C3V point group. Noting that from the CoK7 cluster, the lowest-energy structure becomes a Co-atom-centered polyhedron. The lowest-energy structure of the CoK8 cluster is a Co-atom-centered K-capped pentagonal bipyramid with a Cs point group. At first glance, the lowest-energy structure of the CoK9 cluster looks like a Co-atom-centered K-atom-capped square antiprism, but actually, it is a Co-atom-centered three-K-atom-capped trigonal prism because its point group is D3h. The lowest-energy structure of the CoK10 cluster is a Co-atom-centered two-K-atom-capped square antiprism. It can also be described as a Co-atom-centered 1-4-4-1-layered structure. The lowest-energy structure of the CoK11 cluster is a distorted Co-atom-centered cage-like structure. The lowest energy structure of the CoK12 cluster is a distorted Co-atom-centered icosahedral structure with a C1 point group.
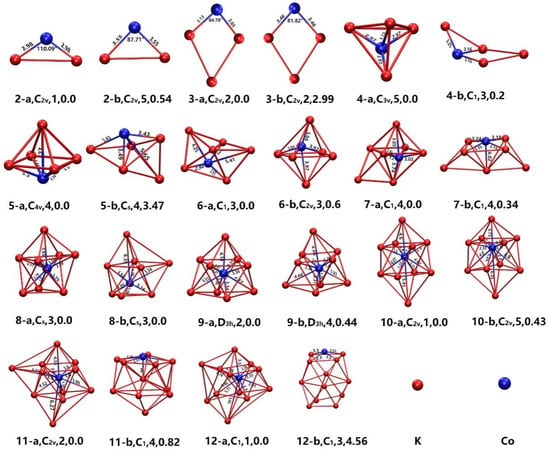
Figure 1.
The ground state structure of CoKn (n = 2–12) clusters (marked as n-a, such as 12-a) and their meta-stable isomers (marked as n-b, such as 12-b). The text below the image also gives the point group, magnetic moment (in μB), and the relative energy (in eV) compared with the ground state.
In a word, along with the increased size of clusters, the lowest-energy structures transform from planar geometry to dense packing structures, and the Co atom moves from the apex position (n < 7) to the central position of cage-like structures (n ≥ 7). A similar growth pattern can also be found in other VIIIB atom (Fe, Co, and Ni)-doped clusters. For GenCo (n = 1–13) clusters, the geometries of the most stable GenCo (n = 1–3) clusters are planar geometries. The geometries of most stable medium-sized GenCo (n = 4–13) clusters are three-dimensional configurations, and from the Ge9Co cluster, the dopant cobalt atom encapsulated geometry becomes the lowest-energy structure. As for LinCo (n = 1–12) clusters, the smallest LinCo (n = 1–3) clusters also adopt planar geometries, and the medium-sized LinCo (n = 4–12) clusters adopt three-dimensional configurations. Like the results shown in this paper, from the Li7Co cluster, the most stable LinCo clusters adopt cobalt atom-centered cage-like structures.
3.2. Relative Stability
The stability of CoKn (n = 2–12) clusters is further evaluated by the binding energy per atom (Eb), the second-order difference of energies (Δ2E), and fragmentation energies (Ef), which are defined as follows:
where E represents the total energy of the cluster or atoms marked in parentheses.
As shown in Figure 2, the binding energy per atom gradually increases until the CoK9 cluster has the largest binding energy per atom, and then size dependence becomes smooth for n = 9~12. The results show that the large-sized clusters are more stable than small clusters.
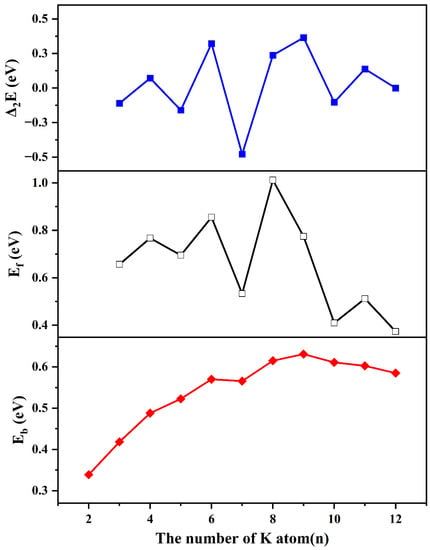
Figure 2.
The binding energy per atom (Eb), the second-order difference of energies (Δ2E), and fragmentation energies (Ef) of CoKn (n = 2–12) clusters.
As for the second-order difference of energies (Δ2E) and fragmentation energies (Ef), they own similar curves, as shown in Figure 2. The local peaks of Δ2E localized at n = 4, 6, 9, and the local peaks of Ef are found at n = 4, 6, 8, 11, implying these clusters are more stable than their neighbors.
According to the obtained results shown in Figure 2, the authors believe the CoK4, CoK6, CoK8, and CoK9 clusters are more stable than their neighbors. The relatively strong stability may have a relation with the relatively smaller bond length and relatively strong atomic interactions. For example, the bond lengths of Co-K in CoK4 are 2.97, 2.97, 2.97, and 3.73 angstrom, respectively, which are smaller than the bond length of Co-K in CoK5 (about 3.20, 3.20, 3.34, 3.34, and 4.60 angstrom). The bond lengths of Co-K in CoK6 are 2.94, 2.97, 3.00, 4.25, and 5.41 angstrom, which are also smaller than their neighbor clusters. Noting that although the cage-like clusters have relatively large bond lengths, the dense packing cage-like structures make these clusters have a relatively large binding energy per atom. Similar conclusions can also be found in other VIIIB atom-doped clusters.
3.3. Magnetic Properties
It is interesting to investigate the magnetic properties of transition-metal atom-doped clusters because the doping of a transition-metal atom can enhance or attenuate total magnetic moments [26,31,32], and the stable cluster can also be used as a superatom with giant or enhanced magnetic moments [28,50]. Herein, the total magnetic moments of CoKn (n = 2–12) clusters are obtained using the Gaussian09 calculation at the B3LYP/6-31G**(Co) and B3LYP/6-311G**(K) levels. The obtained total magnetic moments of CoKn (n = 2–12) clusters are shown in Figure 3 and Table 1. As shown in Figure 3 and Table 1, the magnetic moment of CoKn (n = 2–4) rapidly increases from 1 μB to 5 μB, and then gradually decreases to 1 μB, except for CoK7 and CoK11, whose magnetic moments are 4 μB and 2 μB, respectively. The magnetic moments of CoKn (n = 4–12) are 5 μB (CoK4), 4 μB (CoK5), 3 μB (CoK6), 4 μB (CoK7), 3 μB (CoK8), 2 μB (CoK9), 1 μB (CoK10), 2 μB (CoK11), and 1 μB (CoK12), respectively.
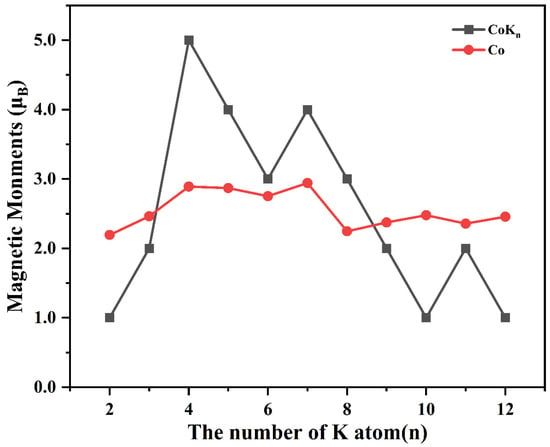
Figure 3.
The total magnetic moments of CoKn (n = 2–12) clusters (black) and local magnetic moments of Co atom in CoKn (n = 2–12) clusters (red).

Table 1.
The natural electron configuration of Co atom (NEC(Co)), the magnetic moments of CoKn clusters (m(CoKn)), Co atom (m(Co)), K atoms (m(K)), the Mulliken atomic charges of Co (q(Co)), and the average bond length of Co-K bond (R(Co-K)).
To deeply understand the atomic contribution to the total magnetic moments, the local magnetic moments of cobalt and potassium atoms are further analyzed by the natural electronic configuration (NEC) and Mulliken population analysis. The obtained local magnetic moments of cobalt and potassium atoms are listed in Figure 3 and Table 1. As shown in Figure 3 and Table 1, for all CoKn (n = 2–12) clusters, the atomic magnetic moment of the Co atom is in the range of 2.1937 μB to 2.9430 μB, indicating that the Co atom plays an important role in determining the total magnetic moment. As for K atoms, they can enhance (as in the case of CoK4, CoK5, CoK6, CoK7, and CoK8) or attenuate (as in the case of CoK2, CoK3, CoK9, CoK10, CoK11, and CoK12) the total magnetic moments of CoKn clusters.
As described above, the CoK4 cluster exhibits the largest magnetic moment among all these clusters, hence the authors would investigate the molecular orbitals to dig out the origination of the largest magnetic moment. The obtained molecular orbitals are shown in Figure 4. For comparison, the molecular orbitals of CoK5 are also investigated. As shown in Figure 4, the molecular orbitals look like sphere-like s orbitals, spindle-like p orbitals, and petal-shaped d orbitals. For those petal-shaped orbitals, the electrons localize around the Co atom, and the sphere-like and spindle-like electrons delocalize around all atoms. According to the data shown in Figure 4, the authors believe their electrons can be described as 1S21P31D8 (for CoK4) and 1S21P41D8 (for CoK5) according to the spherical jellium model [45,46].
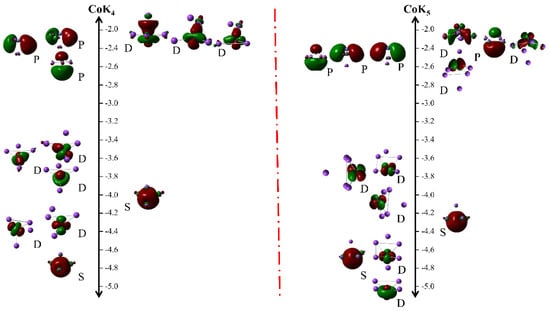
Figure 4.
The molecular orbitals of CoK4 (left) and CoK5 (right) clusters.
The projected density of states (PDOS) is also utilized to investigate the atomic interaction and atomic contribution to the molecular orbitals of CoKn clusters. Figure 5 gives the spin-polarized projected density of states of CoK4 and CoK5 clusters. Take CoK4, for example. As shown in Figure 4, the molecular orbitals of CoK4 are found in the energy range of −2.0~−2.8 eV (spindle-like spin-up molecular orbitals), −3.4~−4.6 eV (petal-shaped spin-up molecular orbitals), −4.8 eV (sphere-like spin up molecular orbital), −2.0~−2.4 eV (petal-shaped spin-down molecular orbitals), and −4.0 eV (sphere-like spin-down molecular orbitals). As shown in Figure 5, in the energy range of −2.0~−2.8 eV, there are K-s, Co-s, and Co-p states (for spin-up states), and K-s, Co-d states (for spin-down states). That is to say, the hybrid molecular orbitals coming from the Co-K interaction are found in this energy range, and the K-s states play an important role in forming the spindle-like spin-up molecular orbitals. The Co-d and K-s atomic states give the main contribution to forming the spin-down petal-shaped molecular orbitals. In the energy range of −3.0~−4.0 eV, there are mainly the Co-d and K-s states in the spin-up states, indicating the spin-up petal-shaped molecular orbitals are mainly coming from the Co-d and K-s atomic states. While there are only Co-s states found nearby −4 eV in spin-down molecular orbitals, indicating the Co-s states give the main contribution to determining the spin-down molecular orbitals. There are Co-d and Co-s states found in the energy range of −4.0~−4.6 eV in the spin-up molecular orbitals, and there are mainly Co-s states found in the spin-up molecular orbitals nearby −4.8 eV. So, the Co-d and Co-s states give the main contribution in forming the spin-up petal-shaped molecular orbitals in the energy range of −4.0~−4.6 eV, and Co-s states determine the spin-up spherical molecular orbitals nearby −4.8 eV. In a word, as for the CoK4 cluster, the main components of petal-shaped D molecular orbitals come from Co-d and K-s states (such as D molecular orbitals in the energy range of −2.0~−2.4 eV) or Co-d and Co-s states (such as D molecular orbitals in the energy range of −4.0~−4.6 eV). In addition, the main components of sphere-like S molecular orbitals or spindle-like P molecular orbitals are K-s states (such as P molecular orbitals in the energy range of −2.0~−2.8 eV) or Co-s states (such as S molecular orbitals nearby −4.8 eV). Similar conclusions can also be found in the CoK5 cluster. The main components of spindle-like P molecular orbitals in the energy range of −2.0~−2.8 eV are K-s states. The main components of spherical S molecular orbitals nearby −4.3 eV and −4.7 eV are Co-s states. The main components of petal-shaped D molecular orbitals in the energy range of −3.6~−5.0 eV are Co-d and K-s states (for D orbitals in the energy range of −3.6~−4.2 eV) and Co-d and Co-s states (for D molecular orbitals in the energy range of −4.6~−5.0 eV).
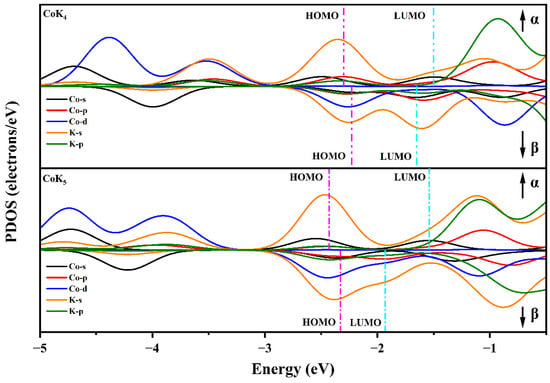
Figure 5.
The projected density of states (PDOS) of CoK4 (upper) and CoK5 (bottom) clusters.
The NEC and Mulliken atomic charges show that the Co atom has negative atomic charges ranging from −0.2175 e to −0.9731 e, indicating the Co atom is a charge acceptor, and K atoms are charge donors. Although both K and Co atoms are metal elements, the latter has larger Pauling’s electronegativity (1.88 for the Co atom, and 0.82 for the K atom) which makes the Co atom accept electrons transferred from K atoms. Note that the CoK4 cluster has the shortest average bond length of the Co-K bond and a relatively large atomic charge of the Co atom (about −0.8717 e). The electronic configuration of the isolated Co atom is [Ar]3d74s2. In the CoKn clusters, the spd hybridization was found (as discussed above) and the hybridization makes the electron transfer from the Co-4s states and K-2s states to the Co-3d states and Co-4p states (shown in the NEC results listed in Table 1, and the spin-polarized projected density of states shown in Figure 5). The strong Co-K interaction and a large amount of charge transfer result in the enhanced magnetic moment of the CoK4 cluster. Similar to the CoK4 cluster, enhanced magnetic moments are also found in CoKn (n = 5–8) clusters. The relatively weak interaction of Co-K coming from the relatively large bond length of Co-K bond in other CoKn clusters (especially the medium-sized cage-like clusters) makes these clusters have relatively smaller magnetic moments.
4. Conclusions
In this paper, the geometries of CoKn (n = 2–12) clusters are predicted using the PSO method joined with the first-principles geometries optimization, and then the electronic structures and magnetic moments are further investigated using the DFT calculation. The results show that the lowest-energy structures transform from planar geometry to dense packing structures, and the Co atom moves from the apex position (n < 7) to the central position of cage-like structures (n ≥ 7). Medium-sized clusters with cage-like geometries are more stable than small clusters, and CoK4, CoK6, CoK8, and CoK9 clusters are more stable than their neighbors. The electronic configuration of CoKn clusters can be described as 1S1P1D according to the spherical jellium model. The main components of petal-shaped D molecular orbitals are Co-d and K-s states or Co-d and Co-s states. The main components of sphere-like S molecular orbitals or spindle-like P molecular orbitals are K-s states or Co-s states. The Co atom plays an important role in determining the total magnetic moments, and K atoms can either enhance or attenuate the total magnetic moments. CoKn (n = 5–8) clusters have relatively large magnetic moments which originate from the strong interaction of Co-K and a large amount of charge transferring from K to Co atoms. CoK4 could be a magnetic superatom with a large magnetic moment of 5 μB.
Author Contributions
Y.J.: Conceptualization, Formal analysis, Writing. M.A.: PSO and DFT calculation, Formal analysis, Writing—Original Draft. X.L.: Visualization. X.J.: Investigation. J.L.: Project administration. X.C.: Project administration. H.D.: Resources. Q.J.: Supervision, Writing—Review & Editing. and H.C.: Software. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Natural Science Foundation of China (Grants Nos. 51962033, 11664038).
Data Availability Statement
The datasets generated and/or analysed during the current study are available from the corresponding author on reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cheng, N.; Stambula, S.; Wang, D.; Banis, M.N.; Liu, J.; Riese, A.; Xiao, B.; Li, R.; Sham, T.K.; Liu, L.M.; et al. Platinum single-atom and cluster catalysis of the hydrogen evolution reaction. Nat. Commun. 2016, 7, 13638. [Google Scholar] [CrossRef] [PubMed]
- Tofanelli, M.A.; Ackerson, C.J. Superatom electron configuration predicts thermal stability of Au25(SR)18 nanoclusters. J. Am. Chem. Soc. 2012, 134, 16937–16940. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Du, Q.; Zhou, S.; Kumar, V. Endohedrally doped cage clusters. Chem. Rev. 2020, 120, 9021–9163. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.J.; Huang, X.M.; Jin, P.; Chen, Z.F. Magnetic properties of atomic clusters and endohedral metallofullerenes. Coord. Chem. Rev. 2015, 289, 315–340. [Google Scholar] [CrossRef]
- Kibsgaard, J.; Jaramillo, T.F.; Besenbacher, F. Building an appropriate active-site motif into a hydrogen-evolution catalyst with thiomolybdate [Mo3S13]2− clusters. Nat. Chem. 2014, 6, 248–253. [Google Scholar] [CrossRef]
- Hu, Q.; Gao, K.; Wang, X.; Zheng, H.; Cao, J.; Mi, L.; Huo, Q.; Yang, H.; Liu, J.; He, C. Subnanometric Ru clusters with upshifted D band center improve performance for alkaline hydrogen evolution reaction. Nat. Commun. 2022, 13, 3958. [Google Scholar] [CrossRef]
- Luo, Z.; Castleman, A.W., Jr.; Khanna, S.N. Reactivity of metal clusters. Chem. Rev. 2016, 116, 14456–14492. [Google Scholar] [CrossRef]
- Chakraborty, I.; Pradeep, T. Atomically precise clusters of noble metals: Emerging link between atoms and nanoparticles. Chem. Rev. 2017, 117, 8208–8271. [Google Scholar] [CrossRef]
- Wu, X.; Liao, R.; Liang, X.; Sai, L.; Liu, Y.; Yang, G.; Zhao, J. Pivotal role of the B12-core in the structural evolution of B52–B64 clusters. Nanoscale 2023, 15, 10430–10436. [Google Scholar] [CrossRef]
- Yang, H.; Hu, Y.-F.; Yuan, Y.-Q.; Ding, J.-J. Probing the structural evolution and stabilities of CsBn0/− (n = 2–12) clusters. Phys. B Condens. Matter 2023, 652, 414628. [Google Scholar] [CrossRef]
- Xie, Q.; Pan, M.; Wang, Z.; Si, W.; Zhang, R.; Shu, Y.; Sun, G.; Jing, Q.; Shen, Y.; Uyama, H. Enhancing the oxygen reduction activity by constructing nanocluster-scaled Fe2O3/Cu interfaces. Nanoscale 2023, 15, 4388–4396. [Google Scholar] [CrossRef] [PubMed]
- Li, C.-G.; Cui, Y.-Q.; Tian, H.; Shen, Z.-G.; Shao, Q.-Q.; Ding, Y.-L.; Ren, B.-Z. Theoretical investigations on the structures and electronic and optical properties of neutral and anionic M2-doped B24 clusters (M = Li, Na, and K). New J. Chem. 2023, 47, 6612–6620. [Google Scholar] [CrossRef]
- Ge, G.X.; Han, Y.; Wan, J.G.; Zhao, J.J.; Wang, G.H. First-principles prediction of magnetic superatoms in 4d-transition-metal-doped magnesium clusters. J. Chem. Phys. 2013, 139, 174309. [Google Scholar] [CrossRef]
- Li, H.S.; Wei, D.; Zhao, X.; Ren, X.; Zhang, D.; Ju, W. Thermal stability of Ag13− clusters studied by ab initio molecular dynamics simulations. J. Phys. Chem. A 2020, 124, 4325–4332. [Google Scholar] [CrossRef]
- Liu, J.T.; Duan, H.M. Molecular dynamics simulation of structures and melting behaviours of iridium clusters with different potentials. Acta Phys. Sin. 2009, 58, 4826–4834. [Google Scholar]
- Lv, J.; Wang, Y.; Zhu, L.; Ma, Y. Particle-swarm structure prediction on clusters. J. Chem. Phys. 2012, 137, 084104. [Google Scholar] [CrossRef] [PubMed]
- Lyakhov, A.O.; Oganov, A.R.; Stokes, H.T.; Zhu, Q. New developments in evolutionary structure prediction algorithm USPEX. Comput. Phys. Commun. 2013, 184, 1172–1182. [Google Scholar] [CrossRef]
- Jorgensen, M.S.; Groves, M.N.; Hammer, B. Combining evolutionary algorithms with clustering toward rational global structure optimization at the atomic scale. J. Chem. Theory Comput. 2017, 13, 1486–1493. [Google Scholar] [CrossRef]
- Fronzi, M.; Amos, R.D.; Kobayashi, R.; Matsumura, N.; Watanabe, K.; Morizawa, R.K. Evaluation of machine learning interatomic potentials for the properties of gold nanoparticles. Nanomaterials 2022, 12, 3891. [Google Scholar] [CrossRef]
- Tong, Q.; Xue, L.; Lv, J.; Wang, Y.; Ma, Y. Accelerating CALYPSO structure prediction by data-driven learning of a potential energy surface. Faraday Discuss. 2018, 211, 31–43. [Google Scholar] [CrossRef]
- Ceriotti, M. Unsupervised machine learning in atomistic simulations, between predictions and understanding. J. Chem. Phys. 2019, 150, 150901. [Google Scholar] [CrossRef] [PubMed]
- Barroso, J.; Pan, S.; Merino, G. Structural transformations in boron clusters induced by metal doping. Chem. Soc. Rev. 2022, 51, 1098–1123. [Google Scholar] [CrossRef] [PubMed]
- Chauhan, V.; Sen, P. Electronic and magnetic properties of 3d transition metal-doped strontium clusters: Prospective magnetic superatoms. Chem. Phys. 2013, 417, 37–44. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, J.; Feng, X.; Zhang, H.; Zhao, L.; Luo, Y.; Cao, W. Magnetic superatoms in VLin (n = 1–13) clusters: A first-principles prediction. J. Phys. Chem. A 2013, 117, 13025–13036. [Google Scholar] [CrossRef]
- Lu, S.-J.; Wu, L.-S.; Lin, F. Structural, bonding, and superhalogen properties of Au4X−/04 (X = F, Cl, Br, and I) clusters. Theor. Chem. Acc. 2019, 138, 51. [Google Scholar] [CrossRef]
- Wang, J.; Bai, J.; Jellinek, J.; Zeng, X.C. Gold-coated transition-metal anion [Mn13@Au20]− with ultrahigh magnetic moment. J. Am. Chem. Soc. 2007, 129, 4110. [Google Scholar] [CrossRef]
- Zhao, G.F.; Zhang, J.; Jing, Q.; Luo, Y.H.; Wang, Y.X. A density functional study of YnAl (n = 1–14) clusters. J. Chem. Phys. 2007, 127, 234312. [Google Scholar] [CrossRef]
- Aireti, M.; Jiang, Y.; Cao, H.; Duan, H.; Cui, X.; Jing, Q.; Xue, X. The cage-like structure enhanced magnetic moment in ScKn (n = 2–12) clusters: A first-principles jointed particle swarm optimization investigation. Int. J. Quantum Chem. 2021, 121, e26654. [Google Scholar] [CrossRef]
- Poudel, M.B.; Kim, A.A.; Lohani, P.C.; Yoo, D.J.; Kim, H.J. Assembling zinc cobalt hydroxide/ternary sulfides hetereostructure and iron oxide nanorods on three-dimensional hollow porous carbon nanofiber as high energy density hybrid supercapacitor. J. Energy Storage 2023, 60, 106713. [Google Scholar] [CrossRef]
- Poudel, M.B.; Logeshwaran, N.; Kim, A.R.; Karthikeyan, S.C.; Vijayapradeep, S.; Yoo, D.J. Integrated core-shell assembly of Ni3S2 nanowires and CoMoP nanosheets as highly efficient bifunctional electrocatalysts for overall water splitting. J. Alloys Compd. 2023, 960, 170678. [Google Scholar] [CrossRef]
- Jing, Q.; Tian, F.Y.; Wang, Y.X. No quenching of magnetic moment for the GenCo (n = 1–13) clusters: First-principles calculations. J. Chem. Phys. 2008, 128, 124319. [Google Scholar] [CrossRef] [PubMed]
- Jing, Q.; Cao, H.B.; Ge, G.X.; Wang, Y.X.; Yan, H.X.; Zhang, Z.Y.; Liu, Y.H. Giant magnetic moment of the core-shell Co13@Mn20 clusters: First-principles calculations. J. Comput. Chem. 2011, 32, 2474. [Google Scholar] [CrossRef] [PubMed]
- Hao, A.; Xue, H.; Jia, J. Geometries, stabilities, and magnetic properties of Co2Bn (n = 1–10) clusters. J. Mol. Model. 2019, 25, 27. [Google Scholar] [CrossRef]
- Song, Z. First-principle investigation on growth patterns and properties of cobalt-doped lithium nanoclusters. J. Mol. Model. 2016, 22, 133. [Google Scholar] [CrossRef]
- Wang, Y.; Lv, J.; Zhu, L.; Ma, Y. Crystal structure prediction via particle-swarm optimization. Phys. Rev. B 2010, 82, 094116. [Google Scholar] [CrossRef]
- Wang, Y.; Lv, J.; Zhu, L.; Ma, Y. CALYPSO: A method for crystal structure prediction. Comput. Phys. Commun. 2012, 183, 2063–2070. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B Condens. Matter 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Sun, W.G.; Wang, J.J.; Lu, C.; Xia, X.X.; Kuang, X.Y.; Hermann, A. Evolution of the structural and electronic properties of medium-sized sodium clusters: A honeycomb-like Na20 Cluster. Inorg. Chem. 2017, 56, 1241–1248. [Google Scholar] [CrossRef]
- Lu, C.; Li, Q.; Ma, Y.; Chen, C. Extraordinary indentation strain stiffening produces superhard tungsten nitrides. Phys. Rev. Lett. 2017, 119, 115503. [Google Scholar] [CrossRef]
- Lu, C.; Amsler, M.; Chen, C. Unraveling the structure and bonding evolution of the newly discovered iron oxide FeO2. Phys. Rev. B 2018, 98, 054102. [Google Scholar] [CrossRef]
- Tang, X.; Sun, W.G.; Gu, Y.T.; Lu, C.; Kou, L.Z.; Chen, C.F. CoB6 monolayer: A robust two-dimensional ferromagnet. Phys. Rev. B 2019, 99, 045445. [Google Scholar] [CrossRef]
- Liu, H.; Cao, H.; Cui, X.; Duan, H.; Jing, Q.; Wang, Q. The geometry, electronic and magnetic properties of VLin (n = 2–13) clusters using the first-principles and PSO method. Mol. Phys. 2020, 118, e1791990. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09; Revision E.01; Gaussian Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B Condens. Matter 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Krishnan, R.; Binkley, J.S.; Seeger, R.; Pople, J.A. Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions. J. Chem. Phys. 1980, 72, 650–654. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F.W. Calculation of Molecular Orbital Composition. Acta Chim. Sin. 2011, 69, 2393–2406. [Google Scholar]
- Lu, T.; Chen, F.-W. Meaning and Functional Form of the Electron Localization Function. Acta Phys.-Chim. Sin. 2011, 27, 2786–2792. [Google Scholar]
- Li, L.; Cui, X.-H.; Cao, H.-B.; Jiang, Y.; Duan, H.-M.; Jing, Q.; Liu, J.; Wang, Q. Structural evolution and magnetic properties of ScLin (n = 2–13) clusters: A PSO and DFT investigation. Chin. Phys. B 2020, 29, 077101. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).