Generation of a Focused THz Vortex Beam from a Spintronic THz Emitter with a Helical Fresnel Zone Plate
Abstract
1. Introduction
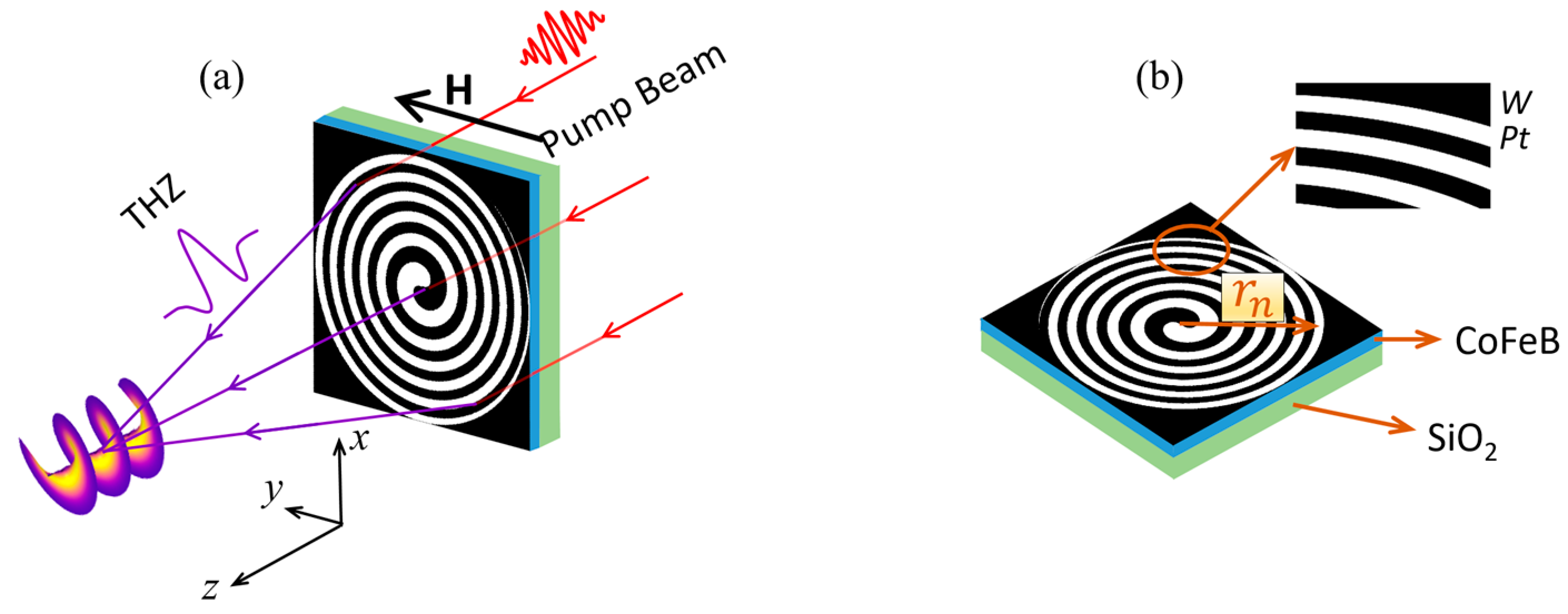
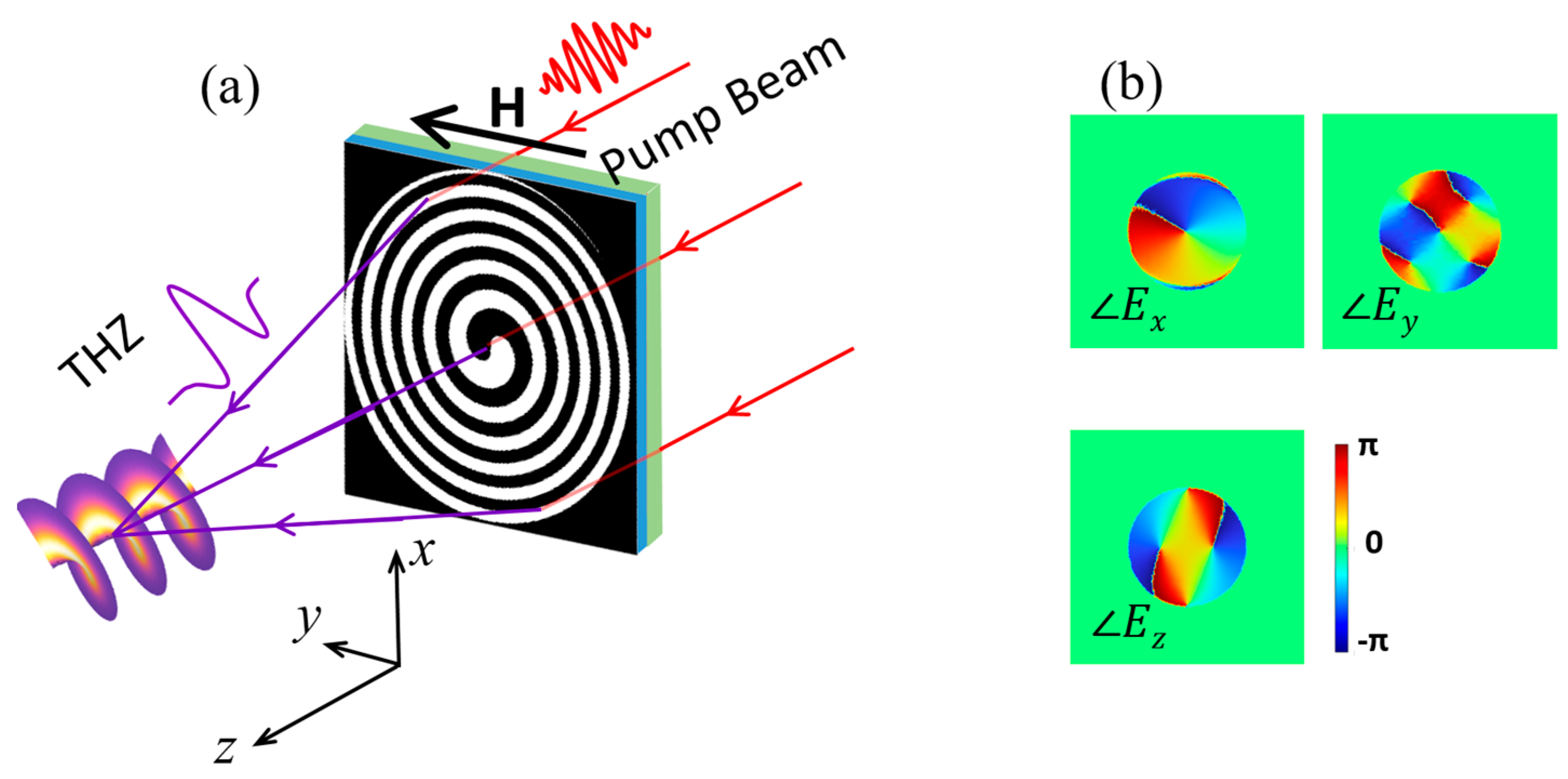
2. Theoretical Design
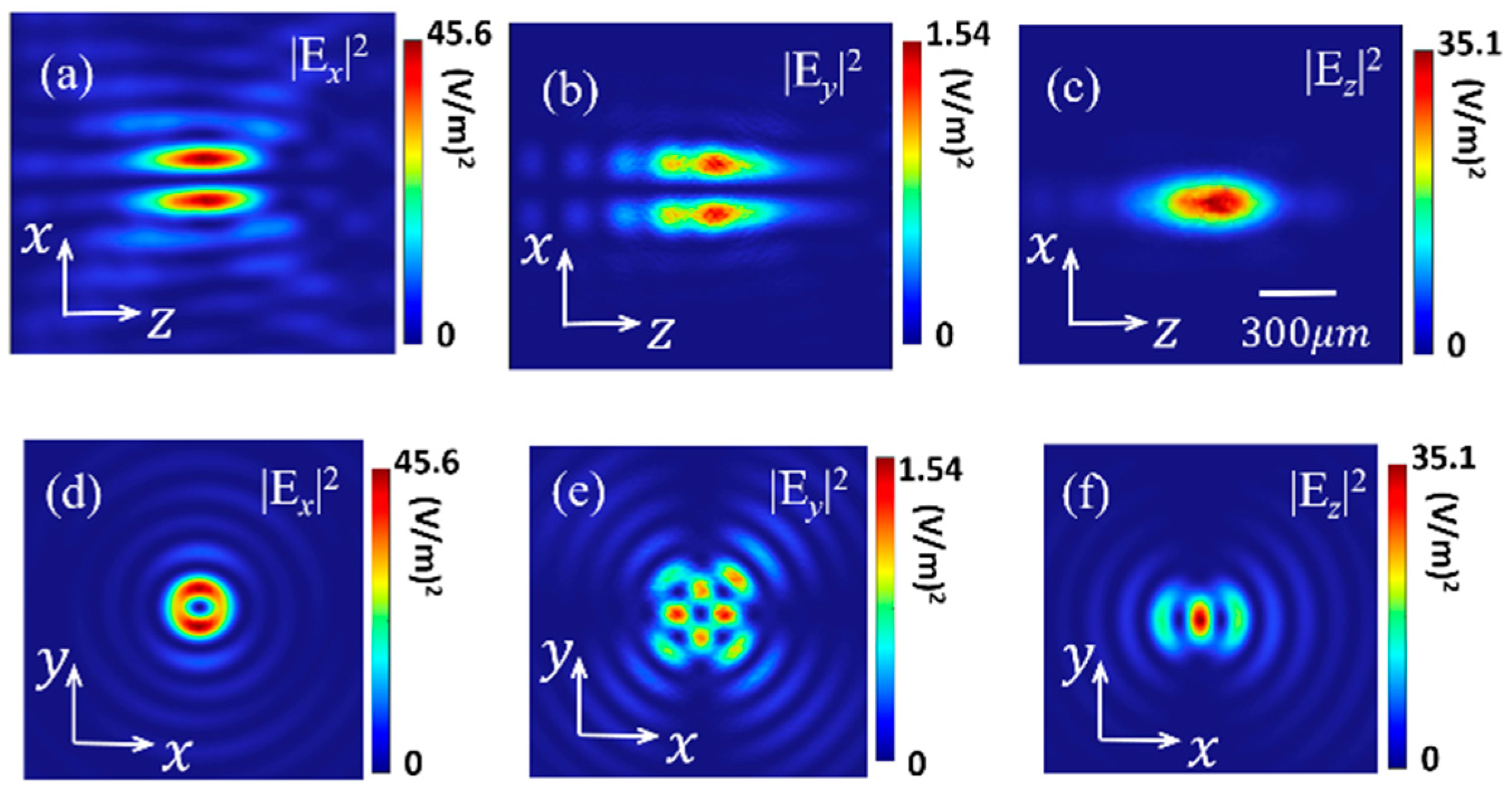
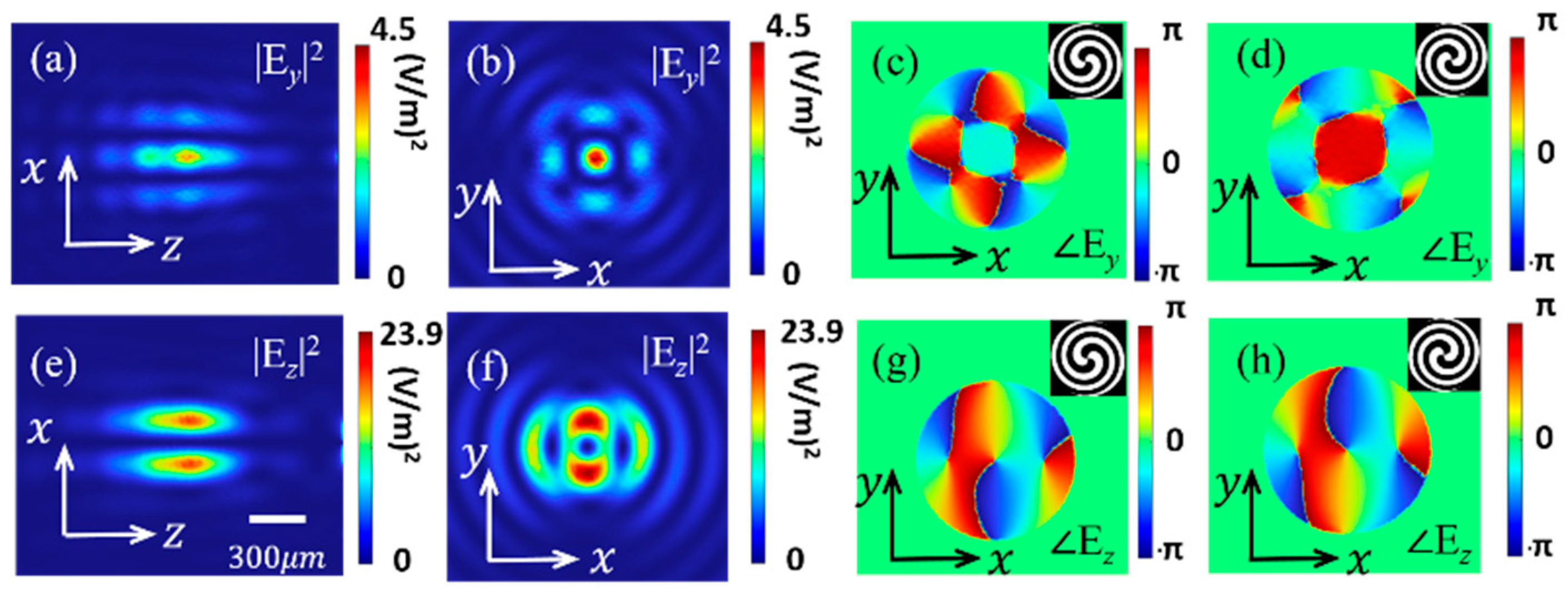
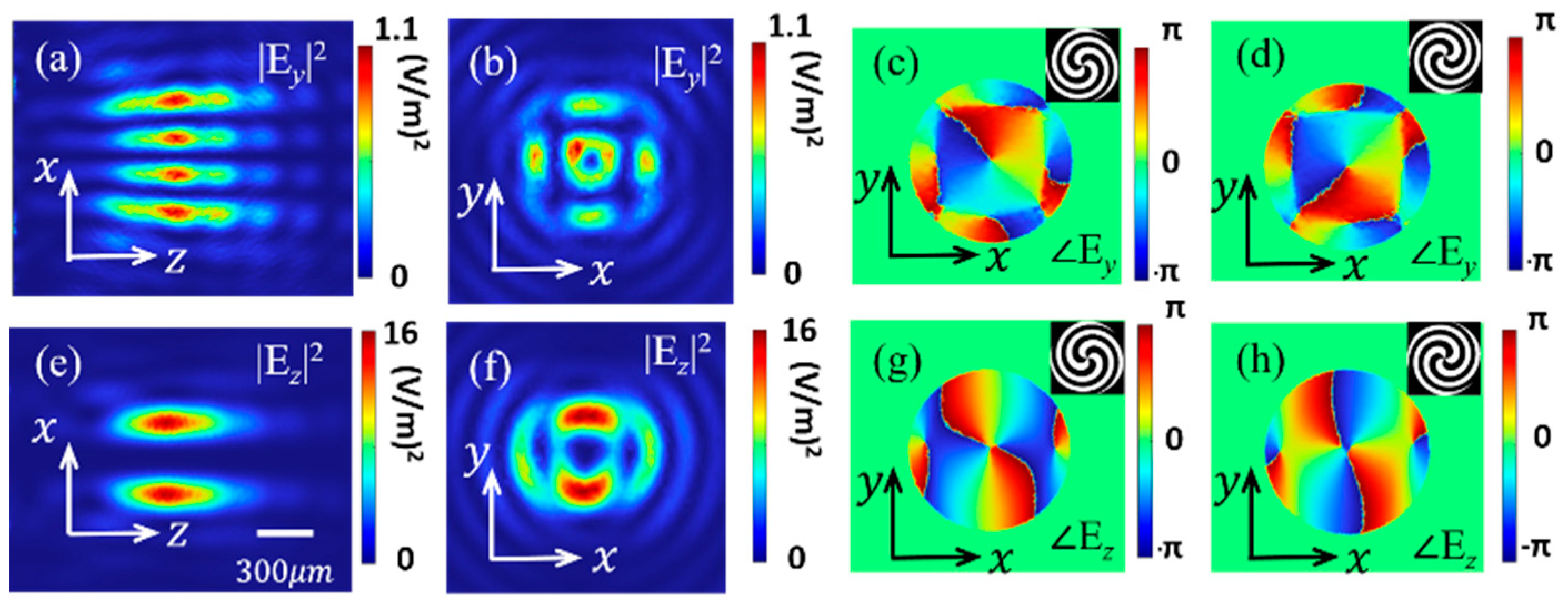
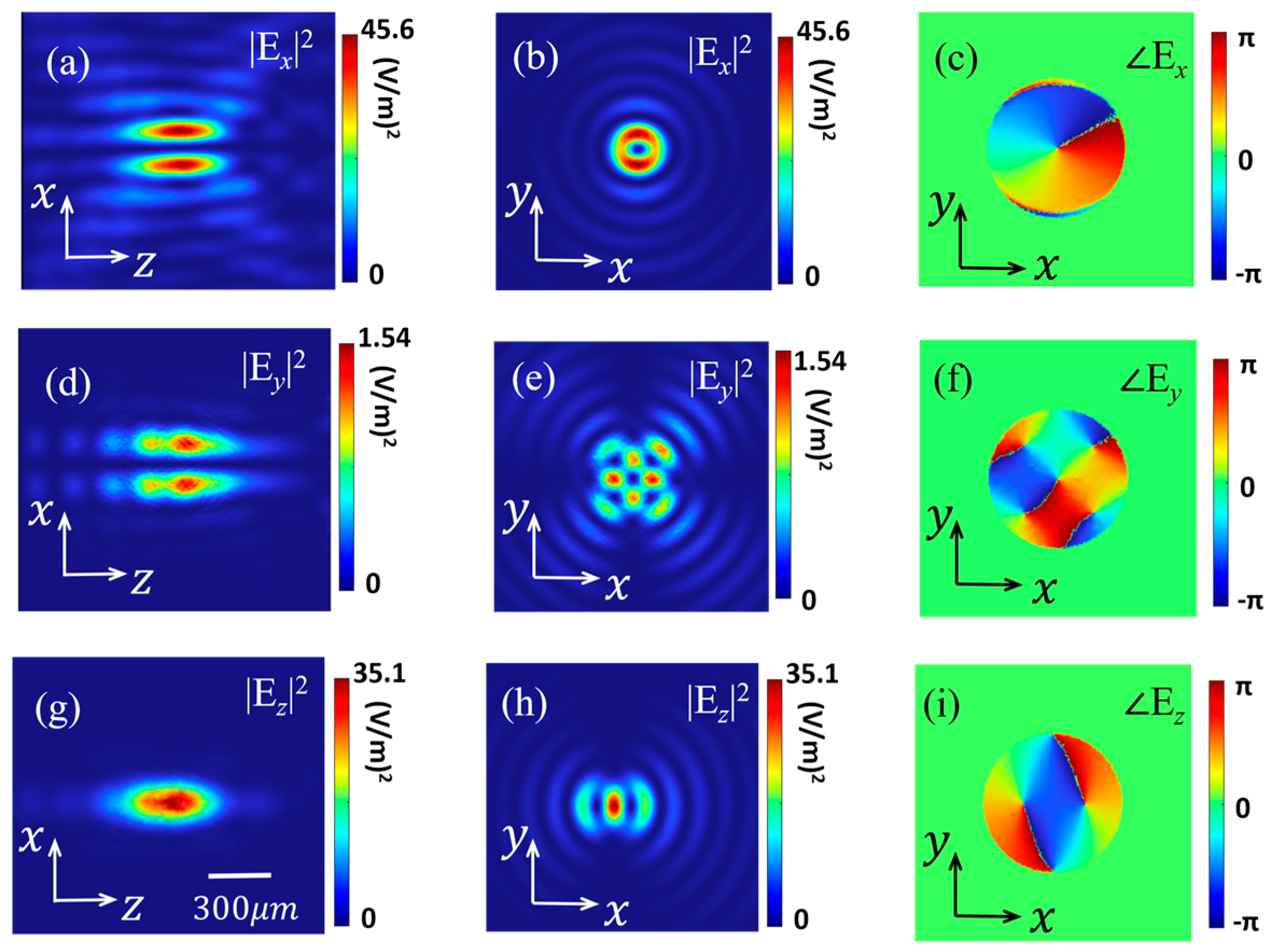
3. Results and Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef] [PubMed]
- Yao, A.M.; Padgett, M.J. Orbital angular momentum: Origins, behavior and applications. Adv. Opt. Photon. 2011, 3, 161–204. [Google Scholar] [CrossRef]
- Shen, Y.J.; Wang, X.J.; Xie, Z.W.; Min, C.J.; Fu, X.; Liu, Q.; Gong, M.L.; Yuan, X.C. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities. Light Sci. Appl. 2019, 8, 90. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.Q.; Wang, A.T.; Chen, R.S.; Zhou, Y.; Ming, H.; Zhan, Q.W. Generation and Conversion of Higher Order Optical Vortices in Optical Fiber with Helical Fiber Bragg Gratings. J. Light. Technol. 2016, 34, 2413–2418. [Google Scholar] [CrossRef]
- Zhang, X.Q.; Chen, R.S.; Wang, A.T. Focusing properties of cylindrical vector vortex beams. Opt. Commun. 2018, 414, 10–15. [Google Scholar]
- Nagatsuma, T.; Ducournau, G.; Renaud, C.C. Advances in terahertz communications accelerated by photonics. Nat. Photonics 2016, 10, 371–379. [Google Scholar] [CrossRef]
- Chen, S.C.; Feng, Z.; Li, J.; Tian, W.; Du, L.H.; Cai, J.W.; Ma, Y.C.; He, K.; Ding, H.F.; Zhai, Z.H.; et al. Ghost spintronic THz-emitter-array microscope. Light Sci. Appl. 2020, 9, 99. [Google Scholar] [CrossRef]
- Yue, X.Y.; Wang, C.W.; Zhang, B.; Zhang, Z.Y.; Xiong, Z.; Zu, X.Z.; Liu, Z.Z.; Hu, Z.P.; Odunmbaku, G.O.; Zheng, Y.J.; et al. Real-time observation of the buildup of polaron in α-FAPbI3. Nat. Commun. 2023, 14, 917. [Google Scholar] [CrossRef]
- Sirenko, A.A.; Marsik, P.; Bugnon, L.; Soulier, M.; Bernhard, C.; Stanislavchuk, T.N.; Xu, X.H.; Cheong, S.W. Total Angular Momentum Dichroism of the Terahertz Vortex Beams at the Antiferromagnetic Resonances. Phys. Rev. L 2021, 126, 157401. [Google Scholar] [CrossRef]
- Sirenko, A.A.; Marsik, P.; Bugnon, L.; Bernhard, C.; Stanislavchuk, T.N.; Kiryukhin, V.; Cheong, S.W. Terahertz Vortex Beam as a Spectroscopic Probe of Magnetic Excitations. Phys. Rev. L 2019, 122, 237401. [Google Scholar] [CrossRef]
- Pinnock, S.W.; Roh, S.; Biesner, T.; Pronin, A.V.; Dressel, M. Generation of THz Vortex Beams and Interferometric Determination of Their Topological Charge. IEEE Trans. Terahertz Sci. Technol. 2023, 13, 44–49. [Google Scholar] [CrossRef]
- Wang, Q.W.; Zhang, X.Q.; Xu, Q.; Feng, X.; Lu, Y.; Niu, L.C.; Niu, L.; Chen, X.Y.; Plum, E.; Gu, J.Q.; et al. Nonlinear Terahertz Generation: Chiral and Achiral Meta-Atom Coupling. Adv. Funct. Mater. 2023, 33, 2300639. [Google Scholar] [CrossRef]
- Lu, Y.C.; Feng, X.; Wang, Q.W.; Zhang, X.Q.; Fang, M.; Sha, W.E.I.; Huang, Z.X.; Xu, Q.; Niu, L.; Chen, X.Y.; et al. Integrated Terahertz Generator-Manipulators Using Epsilon-nearZero-Hybrid Nonlinear Metasurfaces. Nano Lett. 2021, 21, 7699–7707. [Google Scholar] [CrossRef]
- Zhang, H.F.; Zhang, X.Q.; Xu, Q.; Wang, Q.; Xu, Y.H.; Wei, M.G.; Li, Y.F.; Gu, J.Q.; Tian, Z.; Ouyang, C.M.; et al. Polarization-independent all-silicon dielectric metasurfaces in the terahertz regime. Photon. Res. 2018, 6, 24–29. [Google Scholar] [CrossRef]
- Jiang, Y.Q.; Li, H.Q.; Zhang, X.Q.; Zhang, F.; Xu, Y.; Xiao, Y.G.; Liu, F.G.; Wang, A.T.; Zhan, Q.W.; Zhao, W.S. Promoting spintronic terahertz radiation via Tamm plasmon coupling. Photon. Res. 2023, 11, 1057–1066. [Google Scholar] [CrossRef]
- Jiang, Y.Q.; Zhang, X.Q.; Liu, Y.S.; Vallobra, P.; Eimer, S.; Zhang, F.; Du, Y.C.; Liu, F.G.; Xu, Y.; Zhao, W.S. Spintronic terahertz emitter with integrated electromagnetic control. Chin. Opt. Lett. 2022, 20, 43201. [Google Scholar] [CrossRef]
- Katyba, G.M.; Raginov, N.I.; Khabushev, E.M.; Zhelnov, V.A.; Gorodetsky, A.; Ghazaryan, D.A.; Mironov, M.S.; Krasnikov, D.V.; Gladush, Y.G.; James, L.H.; et al. Tunable THz flat zone plate based on stretchable single-walled carbon nanotube thin film. Optica 2023, 10, 53–61. [Google Scholar] [CrossRef]
- Minerbi, E.; Zur, S.K.; Ellenbogen, T. Nonlinear Metasurface Fresnel Zone Plates for Terahertz Generation and Manipulation. Nano Lett. 2019, 19, 6072–6077. [Google Scholar] [CrossRef]
- Jung, H.; Hale, L.L.; Gennaro, S.D.; Briscoe, J.; Iyer, P.P.; Doiron, C.F.; Harris, C.T.; Luk, T.S.; Addamane, S.J.; Reno, J.L.; et al. Terahertz Pulse Generation with Binary Phase Control in Nonlinear InAs Metasurface. Nano Lett. 2022, 22, 9077–9083. [Google Scholar] [CrossRef]
- Feng, X.; Chen, X.Y.; Lu, Y.C.; Wang, Q.W.; Niu, L.; Xu, Q.; Zhang, X.Q.; Han, J.G.; Zhang, W.L. Direct Emission of Focused Terahertz Vortex Beams Using Indium-Tin-Oxide-Based Fresnel Zone Plates. Adv. Opt. Mater. 2022, 11, 2201628. [Google Scholar] [CrossRef]
- Seifert, T.; Jaiswal, S.; Martens, U.; Hannegan, J.; Braun, L.; Maldonado, P.; Freimuth, F.; Kronenberg, A.; Henrizi, J.; Radu, I.; et al. Efficient metallic spintronic emitters of ultrabroadband terahertz radiation. Nat. Photonics 2016, 10, 483–490. [Google Scholar] [CrossRef]
- Zhang, X.Q.; Jiang, Y.Q.; Xu, Y.; Liu, F.G.; Rui, G.H.; Wang, A.T.; Zhao, W.S. Unidirectional spintronic terahertz emitters with high efficiency. Opt. Lett. 2022, 47, 6381–6384. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Wang, H.C.; Liu, J.Y.; Zhang, M.X.; Chen, P.; Li, P.Y.; Liu, Z.K.; Han, X.F.; Wan, C.H.; Yu, H.M.; et al. Simultaneous Terahertz Pulse Generation and Manipulation with Spintronic Coding Surface. Adv. Opt. Mater. 2023, 11, 2300899. [Google Scholar] [CrossRef]
- Li, H.Q.; Jiang, Y.Q.; Zhang, X.Q.; Zhang, F.; Xiao, Y.G.; Tang, M.H.; Xu, Y.; Liu, F.G.; Zhao, W.S. Spintronic terahertz polarization programmable system for information encoding. Opt. Laser Technol. 2023, 167, 109717. [Google Scholar] [CrossRef]
- Brown, B.R.; Lohmann, A.W. Complex spatial filtering with binary masks. Appl. Opt. 1966, 5, 967–969. [Google Scholar] [CrossRef]
- Tong, M.Y.; Hu, Y.Z.; He, W.B.; Hu, S.Y.; Cheng, X.A.; Jiang, T. Light-Driven Spintronic Heterostructures for Coded Terahertz Emission. ACS Nano 2022, 16, 8294–8300. [Google Scholar] [CrossRef]
- Cao, G.Y.; Gan, X.S.; Lin, H.; Jia, B.H. An accurate design of graphene oxide ultrathin flat lens based on Rayleigh-Sommerfeld theory. Opto-Electron. Adv. 2018, 1, 180012. [Google Scholar] [CrossRef]
- Geints, Y.E.; Panina, E.K.; Minin, I.V.; Minin, O.V. Study of focusing parameters of wavelength-scale binary phase Fresnel zone plate. J. Opt. 2021, 23, 65101. [Google Scholar] [CrossRef]
- Zhang, X.Q.; Rui, G.H.; Xu, Y.; Zhang, F.; Du, Y.C.; Lian, M.T.; Lin, X.Y.; Wang, A.T.; Ming, H.; Zhao, W.S. Multi-layer magnetic recording driven by a tunable laser. Chin. Opt. Lett. 2020, 18, 102501. [Google Scholar] [CrossRef]
- Zhan, Q.W. Cylindrical vector beams: From mathematical concepts to applications. Adv. Opt. Photonics 2009, 1, 1–57. [Google Scholar] [CrossRef]
- Yang, R.; Jiang, X.T.; Yu, J.J.; Han, J.; Li, Z.G.; Zhang, D.Y.; Shi, Q.; Zhu, L.W. Controllable perfect optical vortex generated by complex amplitude encoding. Opt. Lett. 2022, 47, 2101–2104. [Google Scholar] [CrossRef] [PubMed]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Xu, Y.; Hong, B.; Zhang, F.; Wang, A.; Zhao, W. Generation of a Focused THz Vortex Beam from a Spintronic THz Emitter with a Helical Fresnel Zone Plate. Nanomaterials 2023, 13, 2037. https://doi.org/10.3390/nano13142037
Zhang X, Xu Y, Hong B, Zhang F, Wang A, Zhao W. Generation of a Focused THz Vortex Beam from a Spintronic THz Emitter with a Helical Fresnel Zone Plate. Nanomaterials. 2023; 13(14):2037. https://doi.org/10.3390/nano13142037
Chicago/Turabian StyleZhang, Xiaoqiang, Yong Xu, Bin Hong, Fan Zhang, Anting Wang, and Weisheng Zhao. 2023. "Generation of a Focused THz Vortex Beam from a Spintronic THz Emitter with a Helical Fresnel Zone Plate" Nanomaterials 13, no. 14: 2037. https://doi.org/10.3390/nano13142037
APA StyleZhang, X., Xu, Y., Hong, B., Zhang, F., Wang, A., & Zhao, W. (2023). Generation of a Focused THz Vortex Beam from a Spintronic THz Emitter with a Helical Fresnel Zone Plate. Nanomaterials, 13(14), 2037. https://doi.org/10.3390/nano13142037






