Resonant Excitation of the Ferroelectric Soft Mode by a Narrow-Band THz Pulse
Abstract
1. Introduction
2. Materials and Methods
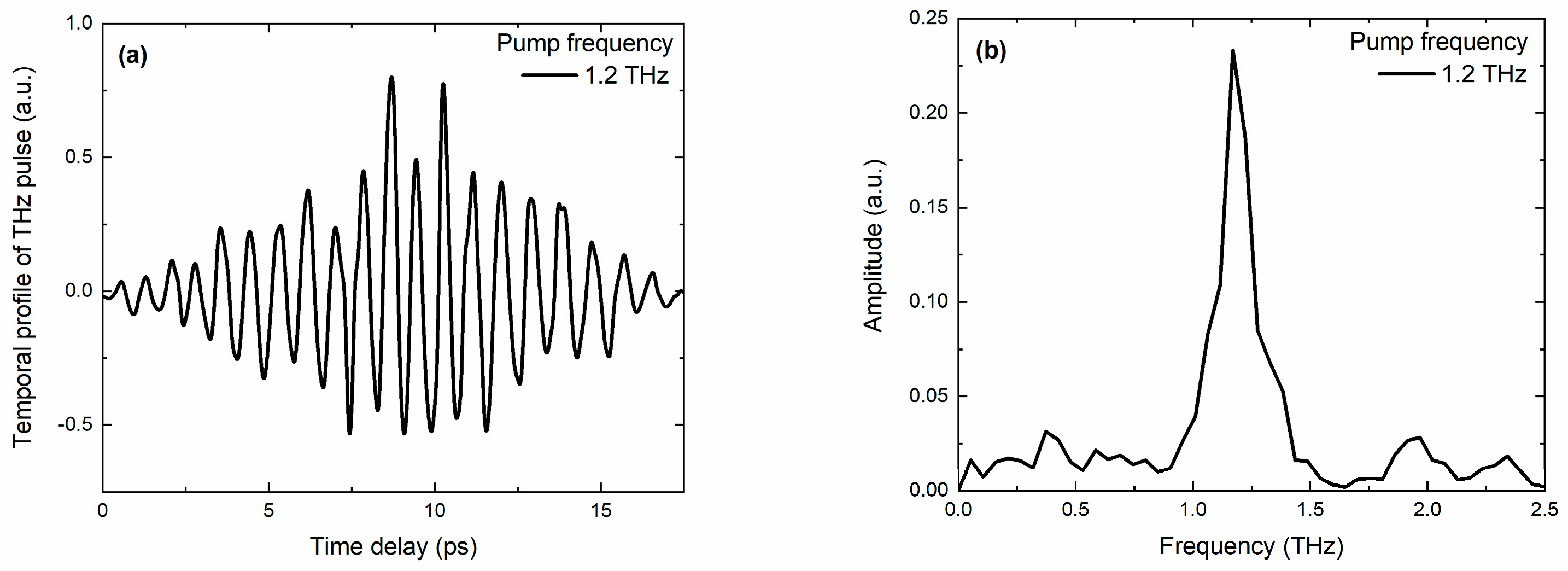
3. Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kim, D.-Y.; Moon, S.E.; Kim, E.-K.; Lee, S.-J.; Choi, J.-J.; Kim, H.-E. Electro-optic characteristics of (001)-oriented Ba0.6Sr0.4TiO3 thin films. Appl. Phys. Lett. 2003, 82, 1455–1457. [Google Scholar] [CrossRef]
- Mukhortov, V.M.; Masychev, S.I.; Golovko, Y.I.; Chub, A.V.; Mukhortov, V.M. Application of nanodimensional barium-strontium titanate films in tunable microwave devices. Tech. Phys. 2006, 51, 1359–1361. [Google Scholar] [CrossRef]
- Brekhov, K.A.; Lavrov, S.D. Electro-optic properties of Ba0.8Sr0.2TiO3 thin film. Ceram. Int. 2020, 47, 3122–3126. [Google Scholar] [CrossRef]
- Eltes, F.; Mai, C.; Caimi, D.; Kroh, M.; Popoff, Y.; Winzer, G.; Petousi, D.; Lischke, S.; Ortmann, J.E.; Czornomaz, L.; et al. A BaTiO3-Based Electro-Optic Pockels Modulator Monolithically Integrated on an Advanced Silicon Photonics Platform. J. Light. Technol. 2019, 37, 1456–1462. [Google Scholar] [CrossRef]
- Stanciu, C.D.; Hansteen, F.; Kimel, A.V.; Kirilyuk, A.; Tsukamoto, A.; Itoh, A.; Rasing, T. All-optical magnetic recording with circularly polarized light. Phys. Rev. Lett. 2007, 99, 047601. [Google Scholar] [CrossRef]
- Vahaplar, K.; Kalashnikova, A.M.; Kimel, A.V.; Gerlach, S.; Hinzke, D.; Nowak, U.; Chantrell, R.; Tsukamoto, A.; Itoh, A.; Kirilyuk, A.; et al. All-optical magnetization reversal by circularly polarized laser pulses: Experiment and multiscale modeling. Phys. Rev. B 2012, 85, 104402. [Google Scholar] [CrossRef]
- Blank, T.G.H.; Grishunin, K.A.; Ivanov, B.A.; Mashkovich, E.A.; Afanasiev, D.; Kimel, A.V. Empowering Control of Antiferromagnets by THz-induced Spin Coherence. arXiv 2022, arXiv:2212.09532. [Google Scholar]
- Blank, T.G.H.; Grishunin, K.A.; Zvezdin, K.A.; Hai, N.T.; Wu, J.C.; Su, S.-H.; Huang, J.-C.A.; Zvezdin, A.K.; Kimel, A.V. Two-dimensional THz spectroscopy of nonlinear phononics in the topological insulator MnBi2Te4. arXiv 2022, arXiv:2212.07532. [Google Scholar]
- Mashkovich, E.A.; Grishunin, K.A.; Zvezdin, A.K.; Blank, T.G.H.; Zavyalov, A.G.; van Loosdrecht, P.H.M.; Kalashnikova, A.M.; Kimel, A.V. Terahertz-driven magnetization dynamics of bismuth-substituted yttrium iron-gallium garnet thin film near a compensation point. Phys. Rev. B 2022, 106, 184425. [Google Scholar] [CrossRef]
- Kalashnikova, A.M.; Kimel, A.V.; Pisarev, R.V.; Gridnev, V.N.; Kirilyuk, A.; Rasing, T. Impulsive Generation of Coherent Magnons by Linearly Polarized Light in the Easy-Plane Antiferromagnet FeBO3. Phys. Rev. Lett. 2007, 99, 167205. [Google Scholar] [CrossRef]
- Kalashnikova, A.M.; Kimel, A.V.; Pisarev, R.V.; Gridnev, V.N.; Usachev, P.A.; Kirilyuk, A.; Rasing, T. Impulsive excitation of coherent magnons and phonons by subpicosecond laser pulses in the weak ferromagnet FeBO3. Phys. Rev. B 2008, 78, 104301. [Google Scholar] [CrossRef]
- Subkhangulov, R.R.; Henriques, A.B.; Rappl, P.H.O.; Abramof, E.; Rasing, T.; Kimel, A.V. All-optical manipulation and probing of the d–f exchange interaction in EuTe. Sci. Rep. 2014, 4, 4368. [Google Scholar] [CrossRef] [PubMed]
- Mikhaylovskiy, R.V.; Hendry, E.; Secchi, A.; Mentink, J.H.; Eckstein, M.; Wu, A.; Pisarev, R.V.; Kruglyak, V.V.; Katsnelson, M.I.; Rasing, T.; et al. Ultrafast optical modification of exchange interactions in iron oxides. Nat. Commun. 2015, 6, 8190. [Google Scholar] [CrossRef] [PubMed]
- Yukalov, V.I.; Yukalova, E.P. Ultrafast polarization switching in ferroelectrics. Phys. Rev. Res. 2019, 1, 033136. [Google Scholar] [CrossRef]
- Caputo, J.-G.; Kazantseva, E.V.; Maimistov, A.I. Electromagnetically induced switching of ferroelectric thin films. Phys. Rev. B 2007, 75, 014113. [Google Scholar] [CrossRef]
- Chen, P.; Paillard, C.; Zhao, H.J.; Íñiguez, J.; Bellaiche, L. Deterministic control of ferroelectric polarization by ultrafast laser pulses. Nat. Commun. 2022, 13, 2566. [Google Scholar] [CrossRef] [PubMed]
- Abalmasov, V.A. Ultrafast reversal of the ferroelectric polarization by a midinfrared pulse. Phys. Rev. B 2020, 101, 014102. [Google Scholar] [CrossRef]
- Zhilyaev, P.; Starykh, E.; Brekhov, K.; Mishina, E. Modeling of ultrafast polarization switching in PbTiO3. Materialia 2023, 27, 101681. [Google Scholar] [CrossRef]
- Brekhov, K.A.; Grishunin, K.A.; Afanas’ev, D.V.; Semin, S.V.; Sherstyuk, N.E.; Kitaeva, G.K.; Mishina, E.D.; Rasing, T.; Kimel, A.V. Photoinduced dynamics and femtosecond excitation of phonon modes in ferroelectric semiconductor Sn2P2S6. JETP Lett. 2015, 102, 372–377. [Google Scholar] [CrossRef]
- Brekhov, K.A.; Grishunin, K.A.; Afanas’ev, D.V.; Semin, S.V.; Sherstyuk, N.E.; Mishina, E.D.; Kimel, A.V.D. Optical second harmonic generation and its photoinduced dynamics in ferroelectric semiconductor Sn2P2S6. Phys. Solid State 2018, 60, 31–36. [Google Scholar] [CrossRef]
- Brekhov, K.A.; Ilyin, N.A.; Mishina, E.D.; Prudkovskii, P.A.; Kitaeva, G.K. The temperature dependence of the photoinduced soft mode in Sn2P2S6 crystal. Int. J. Mod. Phys. B 2019, 33, 1950061. [Google Scholar] [CrossRef]
- Hoffmann, M.C.; Kozina, M.E. Terahertz-pump experiments on complex solids at X-ray FELs. In Proceedings of the Terahertz Emitters, Receivers, and Applications IX; Razeghi, M., Baranov, A.N., Eds.; SPIE: Philadelphia, PA, USA, 2018; p. 12. [Google Scholar]
- Grübel, S.; Johnson, J.A.; Beaud, P.; Dornes, C.; Ferrer, A.; Haborets, V.; Huber, L.; Huber, T.; Kohutych, A.; Kubacka, T.; et al. Ultrafast X-ray diffraction of a ferroelectric soft mode driven by broadband terahertz pulses. arXiv 2016, arXiv:1602.05435. [Google Scholar]
- Kozina, M.; van Driel, T.; Chollet, M.; Sato, T.; Glownia, J.M.; Wandel, S.; Radovic, M.; Staub, U.; Hoffmann, M.C. Ultrafast X-ray diffraction probe of terahertz field-driven soft mode dynamics in SrTiO3. Struct. Dyn. 2017, 4, 054301. [Google Scholar] [CrossRef]
- Li, X.; Qiu, T.; Zhang, J.; Baldini, E.; Lu, J.; Rappe, A.M.; Nelson, K.A. Terahertz field–induced ferroelectricity in quantum paraelectric SrTiO3. Science 2019, 364, 1079–1082. [Google Scholar] [CrossRef]
- Miyamoto, T.; Yada, H.; Yamakawa, H.; Okamoto, H. Ultrafast modulation of polarization amplitude by terahertz fields in electronic-type organic ferroelectrics. Nat. Commun. 2013, 4, 2586. [Google Scholar] [CrossRef] [PubMed]
- Chen, F.; Zhu, Y.; Liu, S.; Qi, Y.; Hwang, H.Y.; Brandt, N.C.; Lu, J.; Quirin, F.; Enquist, H.; Zalden, P.; et al. Ultrafast terahertz-field-driven ionic response in ferroelectric BaTiO3. Phys. Rev. B 2016, 94, 180104. [Google Scholar] [CrossRef]
- Bilyk, V.; Mishina, E.; Sherstyuk, N.; Bush, A.; Ovchinnikov, A.; Agranat, M. Transient Polarization Reversal using an Intense THz Pulse in Silicon-Doped Lead Germanate. Phys. Status Solidi–Rapid Res. Lett. 2021, 15, 2000460. [Google Scholar] [CrossRef]
- Prosandeev, S.; Grollier, J.; Talbayev, D.; Dkhil, B.; Bellaiche, L. Ultrafast Neuromorphic Dynamics Using Hidden Phases in the Prototype of Relaxor Ferroelectrics. Phys. Rev. Lett. 2021, 126, 027602. [Google Scholar] [CrossRef]
- Mankowsky, R.; von Hoegen, A.; Först, M.; Cavalleri, A. Ultrafast Reversal of the Ferroelectric Polarization. Phys. Rev. Lett. 2017, 118, 197601. [Google Scholar] [CrossRef]
- Grishunin, K.A.; Ilyin, N.A.; Sherstyuk, N.E.; Mishina, E.D.; Kimel, A.; Mukhortov, V.M.; Ovchinnikov, A.V.; Chefonov, O.V.; Agranat, M.B. THz Electric Field-Induced Second Harmonic Generation in Inorganic Ferroelectric. Sci. Rep. 2017, 7, 687. [Google Scholar] [CrossRef]
- Grishunin, K.; Bilyk, V.; Sherstyuk, N.; Mukhortov, V.; Ovchinnikov, A.; Chefonov, O.; Agranat, M.; Mishina, E.; Kimel, A.V. Transient Second Harmonic Generation Induced by Single Cycle THz pulses in Ba0.8Sr0.2TiO3/MgO. Sci. Rep. 2019, 9, 697. [Google Scholar] [CrossRef] [PubMed]
- Bilyk, V.; Ilyin, N.; Mishina, E.; Ovchinnikov, A.; Chefonov, O.; Mukhortov, V. Nonlinear terahertz pulse induced polarization dynamics in ferroelectric Ba0.8Sr0.2TiO3 thin film. Scr. Mater. 2022, 214, 114687. [Google Scholar] [CrossRef]
- Shirokov, V.B.; Biryukov, S.V.; Mukhortov, V.M.; Yuzyuk, Y.I. Polarization of thin barium-strontium titanate films by an external electric field. Tech. Phys. 2011, 56, 1175–1180. [Google Scholar] [CrossRef]
- Zinchenko, S.P.; Stryukov, D.V.; Pavlenko, A.V.; Mukhortov, V.M. The Effect of a Ba0.2Sr0.8TiO3 Sublayer on the Structure and Electric Characteristics of Lead Zirconate Titanate Films on the Si(001) Substrate. Tech. Phys. Lett. 2020, 46, 1196–1199. [Google Scholar] [CrossRef]
- García, R.; Gonzalo, J.A. Dynamic Critical Behavior of Ferroelectric Triglycine Sulfate from Dielectric Loss Measurements. Phys. Rev. Lett. 1983, 50, 1501–1504. [Google Scholar] [CrossRef]
- Vorotilov, K.A.; Sigov, A.S. Ferroelectric memory. Phys. Solid State 2012, 54, 894–899. [Google Scholar] [CrossRef]
- Ngo, T.Q.; Posadas, A.B.; McDaniel, M.D.; Hu, C.; Bruley, J.; Yu, E.T.; Demkov, A.A.; Ekerdt, J.G. Epitaxial c-axis oriented BaTiO3 thin films on SrTiO3-buffered Si(001) by atomic layer deposition. Appl. Phys. Lett. 2014, 104, 082910. [Google Scholar] [CrossRef]
- Vaithyanathan, V.; Lettieri, J.; Tian, W.; Sharan, A.; Vasudevarao, A.; Li, Y.L.; Kochhar, A.; Ma, H.; Levy, J.; Zschack, P.; et al. c-axis oriented epitaxial BaTiO3 films on (001) Si. J. Appl. Phys. 2006, 100, 024108. [Google Scholar] [CrossRef]
- Anokhin, A.S.; Biryukov, S.V.; Golovko, Y.I.; Mukhortov, V.M. Structural and Electric Characteristics of Two-Layer Bi4Ti3O12/(Ba,Sr)TiO3 Thin Films Deposited on a Silicon Substrate by Radio-Frequency Sputtering at Increased Oxygen Pressures. Phys. Solid State 2019, 61, 139–144. [Google Scholar] [CrossRef]
- Sharma, S.; Tomar, M.; Puri, N.K.; Gupta, V. Ultraviolet Radiation Detection by Barium Titanate Thin Films Grown by Sol-gel Hydrothermal Method. Procedia Eng. 2014, 87, 1172–1175. [Google Scholar] [CrossRef]
- Pavlov, D.P.; Batalov, R.I.; Leontyev, A.V.; Zharkov, D.K.; Migachev, S.A.; Lunev, I.V.; Mukhortov, V.M.; Shaposhnikova, T.S.; Mamin, R.F. Investigation of the barium strontium titanate films on the silicon substrate. Ferroelectrics 2021, 575, 117–122. [Google Scholar] [CrossRef]
- Stryukov, D.V.; Pavlenko, A.V. Unit-Cell Deformation under Discontinuous Deposition of Barium–Strontium Niobate Films. Tech. Phys. Lett. 2019, 45, 1191–1193. [Google Scholar] [CrossRef]
- Mukhortov, V.M.; Golovko, Y.I.; Pavlenko, A.V.; Stryukov, D.V.; Biryukov, S.V.; Kovtun, A.P.; Zinchenko, S.P. The Field Effect in a Metal–Ferroelectric–Semiconductor System of Multilayer Ferroelectric Films with Various Structure Types. Phys. Solid State 2018, 60, 1786–1792. [Google Scholar] [CrossRef]
- Stryukov, D.V.; Mukhortov, V.M.; Golovko, Y.I.; Biryukov, S.V. Specific features of the ferroelectric state in two-layer barium strontium titanate-based heterostructures. Phys. Solid State 2018, 60, 115–119. [Google Scholar] [CrossRef]
- Ovchinnikov, A.V.; Chefonov, O.V.; Agranat, M.B.; Fortov, V.E.; Jazbinsek, M.; Hauri, C.P. Generation of strong-field spectrally tunable terahertz pulses. Opt. Express 2020, 28, 33921. [Google Scholar] [CrossRef]
- Zainullin, F.A.; Khusyainov, D.I.; Kozintseva, M.V.; Buryakov, A.M. Polarization analysis of THz radiation using a wire grid polarizer and ZnTe crystal. Russ. Technol. J. 2022, 10, 74–84. [Google Scholar] [CrossRef]
- Mishina, E.; Bilyk, V.; Sherstyuk, N.; Sigov, A. Ferroelectric switching by (sub)-picosecond electromagnetic pulse. Ferroelectrics 2021, 577, 1–12. [Google Scholar] [CrossRef]
- Yuzyuk, Y.I.; Zakharchenko, I.N.; Alyoshin, V.A.; Leont’ev, I.N.; Rabkin, L.M.; Mukhortov, V.M.; Simon, P. Influence of the growth mechanism and thermoelastic stresses on the lattice dynamics of heteroepitaxial films of barium strontium titanate. Phys. Solid State 2007, 49, 1759–1765. [Google Scholar] [CrossRef]
- Anokhin, A.S.; Yuzyuk, Y.I.; Lyanguzov, N.V.; Razumnaya, A.G.; Stryukov, D.V.; Bunina, O.A.; Golovko, Y.I.; Shirokov, V.B.; Mukhortov, V.M.; El Marssi, M. Direct transition from the rhombohedral ferroelectric to the paraelectric phase in a (Ba,Sr)TiO3 thin film on a (111)MgO substrate. EPL Europhys. Lett. 2015, 112, 47001. [Google Scholar] [CrossRef]
- Mishina, E.; Grishunin, K.; Bilyk, V.; Sherstyuk, N.; Sigov, A.; Mukhortov, V.; Ovchinnikov, A.; Kimel, A. Ultrafast polarization switching of (BaSr)TiO3 thin film by a single-period terahertz pulse in a vicinity of phase transition. Ferroelectrics 2018, 532, 199–207. [Google Scholar] [CrossRef]
- Lu, X.; Chen, Z.; Cao, Y.; Tang, Y.; Xu, R.; Saremi, S.; Zhang, Z.; You, L.; Dong, Y.; Das, S.; et al. Mechanical-force-induced non-local collective ferroelastic switching in epitaxial lead-titanate thin films. Nat. Commun. 2019, 10, 3951. [Google Scholar] [CrossRef] [PubMed]
- Qi, T.; Shin, Y.-H.; Yeh, K.-L.; Nelson, K.A.; Rappe, A.M. Collective Coherent Control: Synchronization of Polarization in Ferroelectric PbTiO3 by Shaped THz Fields. Phys. Rev. Lett. 2009, 102, 247603. [Google Scholar] [CrossRef] [PubMed]




| Ba0.8Sr0.2TiO3/ MgO(001) | Ba0.8Sr0.2TiO3/ Si(001) | Ba0.8Sr0.2TiO3/ MgO(111) | |
|---|---|---|---|
| Crystal structure | Single crystal | Polycrystalline | Single crystal |
| Crystallographic orientation | (001) | (001, 011) | (111) |
| Thickness d, nm | 375 | 375 | 800 |
| Geometry | Transmission, 0° | Reflection, 45° | Transmission, 0° |
 |  |  | |
| Coherence length, nm | 1630 ± 90 nm | 67 ± 2 nm | 1350 ± 90 nm |
| THz field, kV/cm | 700 ÷ 1400 | 700 ÷ 1400 | 320 ÷ 560 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brekhov, K.; Bilyk, V.; Ovchinnikov, A.; Chefonov, O.; Mukhortov, V.; Mishina, E. Resonant Excitation of the Ferroelectric Soft Mode by a Narrow-Band THz Pulse. Nanomaterials 2023, 13, 1961. https://doi.org/10.3390/nano13131961
Brekhov K, Bilyk V, Ovchinnikov A, Chefonov O, Mukhortov V, Mishina E. Resonant Excitation of the Ferroelectric Soft Mode by a Narrow-Band THz Pulse. Nanomaterials. 2023; 13(13):1961. https://doi.org/10.3390/nano13131961
Chicago/Turabian StyleBrekhov, Kirill, Vladislav Bilyk, Andrey Ovchinnikov, Oleg Chefonov, Vladimir Mukhortov, and Elena Mishina. 2023. "Resonant Excitation of the Ferroelectric Soft Mode by a Narrow-Band THz Pulse" Nanomaterials 13, no. 13: 1961. https://doi.org/10.3390/nano13131961
APA StyleBrekhov, K., Bilyk, V., Ovchinnikov, A., Chefonov, O., Mukhortov, V., & Mishina, E. (2023). Resonant Excitation of the Ferroelectric Soft Mode by a Narrow-Band THz Pulse. Nanomaterials, 13(13), 1961. https://doi.org/10.3390/nano13131961







