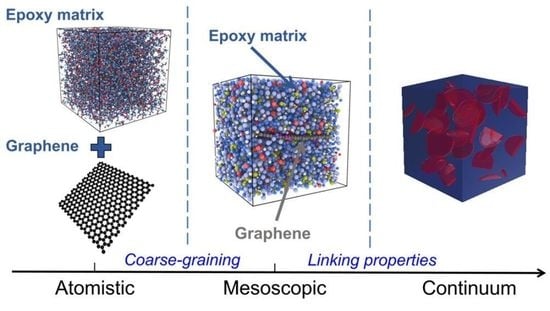
Atomistic to Mesoscopic Modelling of Thermophysical Properties of Graphene-Reinforced Epoxy Nanocomposites
Abstract
:1. Introduction
2. Materials and Methods
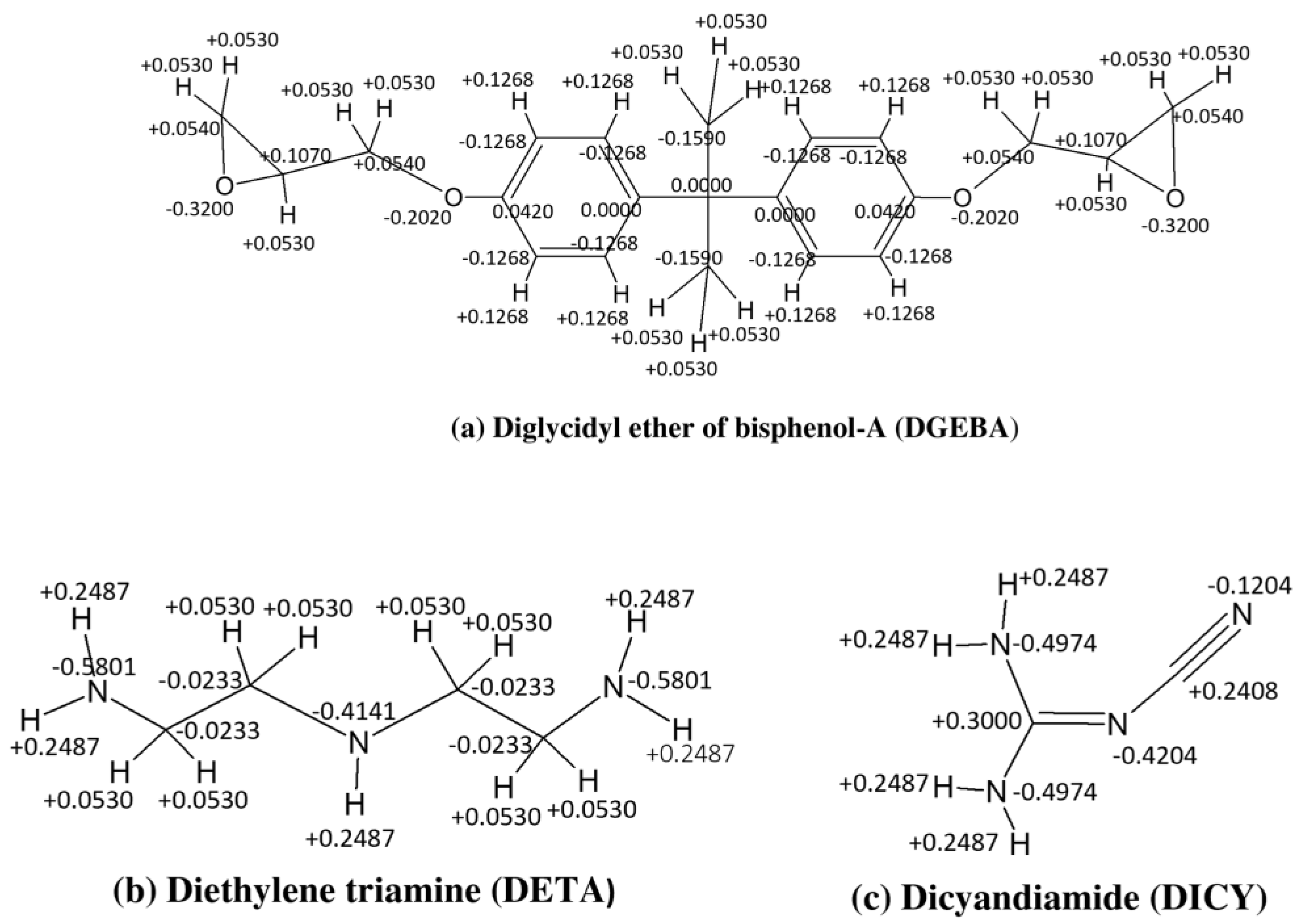
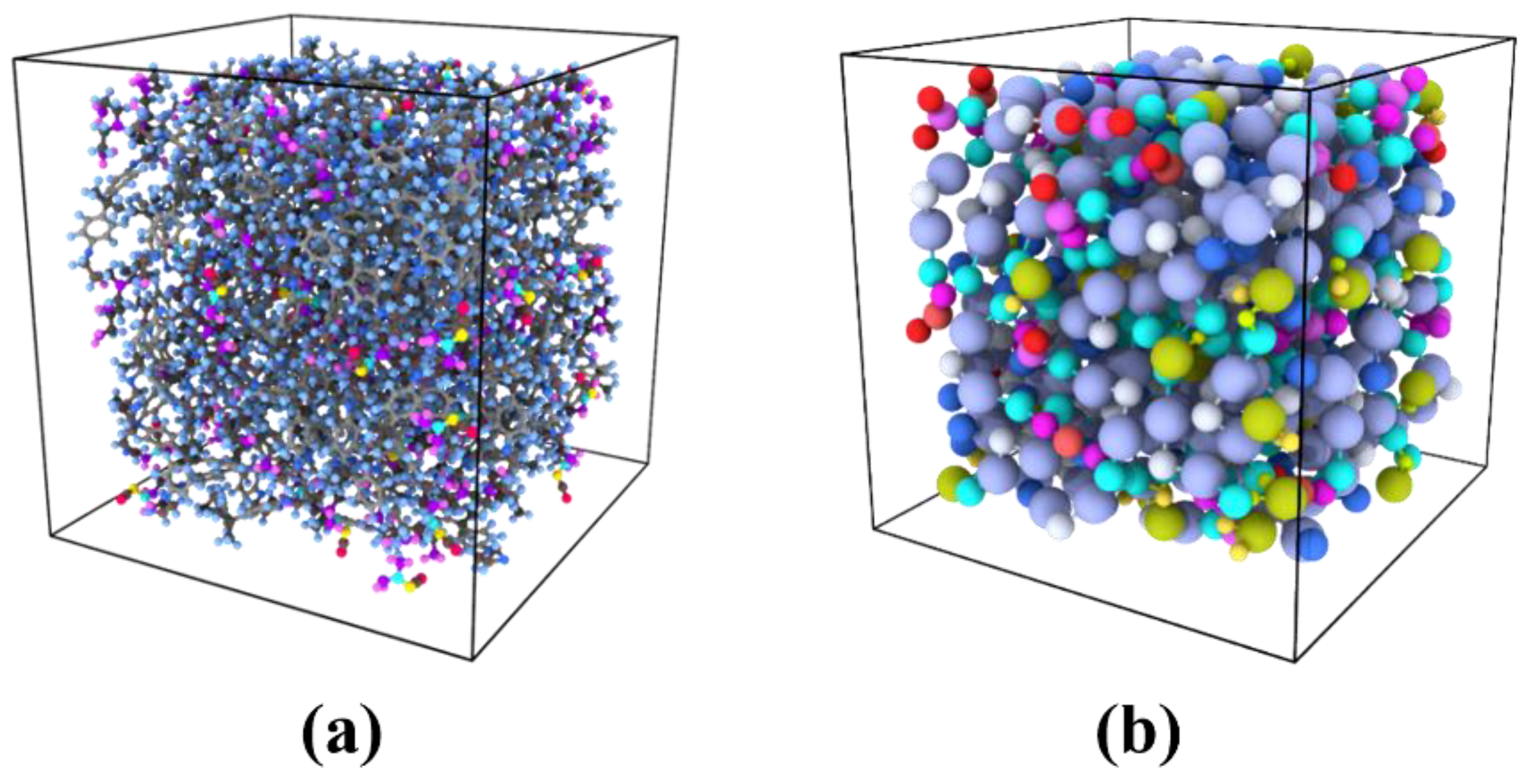
2.1. Atomistic Model of Epoxy
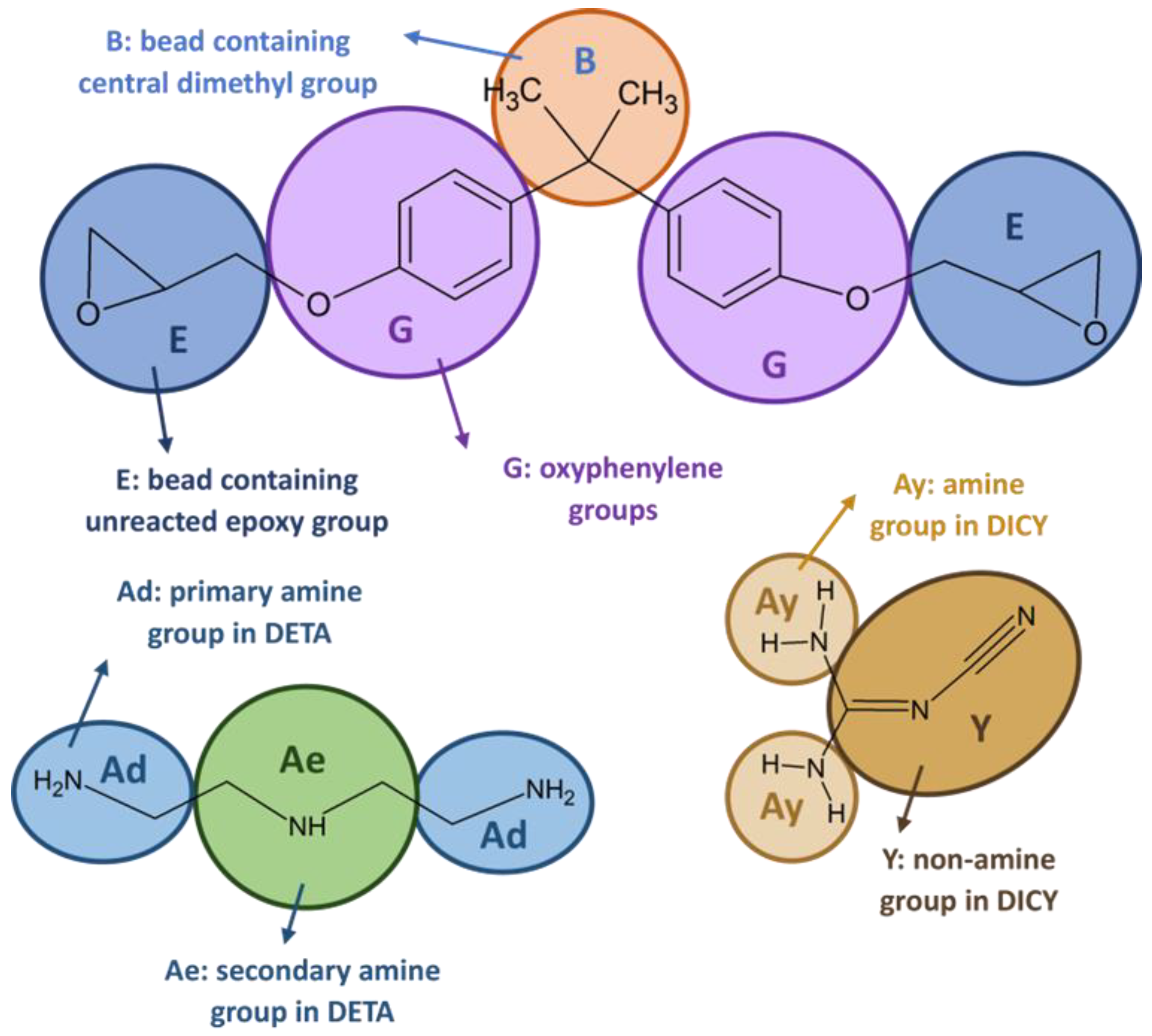
2.2. Mesoscopic Model of Epoxy
2.3. Coarse-Graining by Iterative Boltzmann Inversion
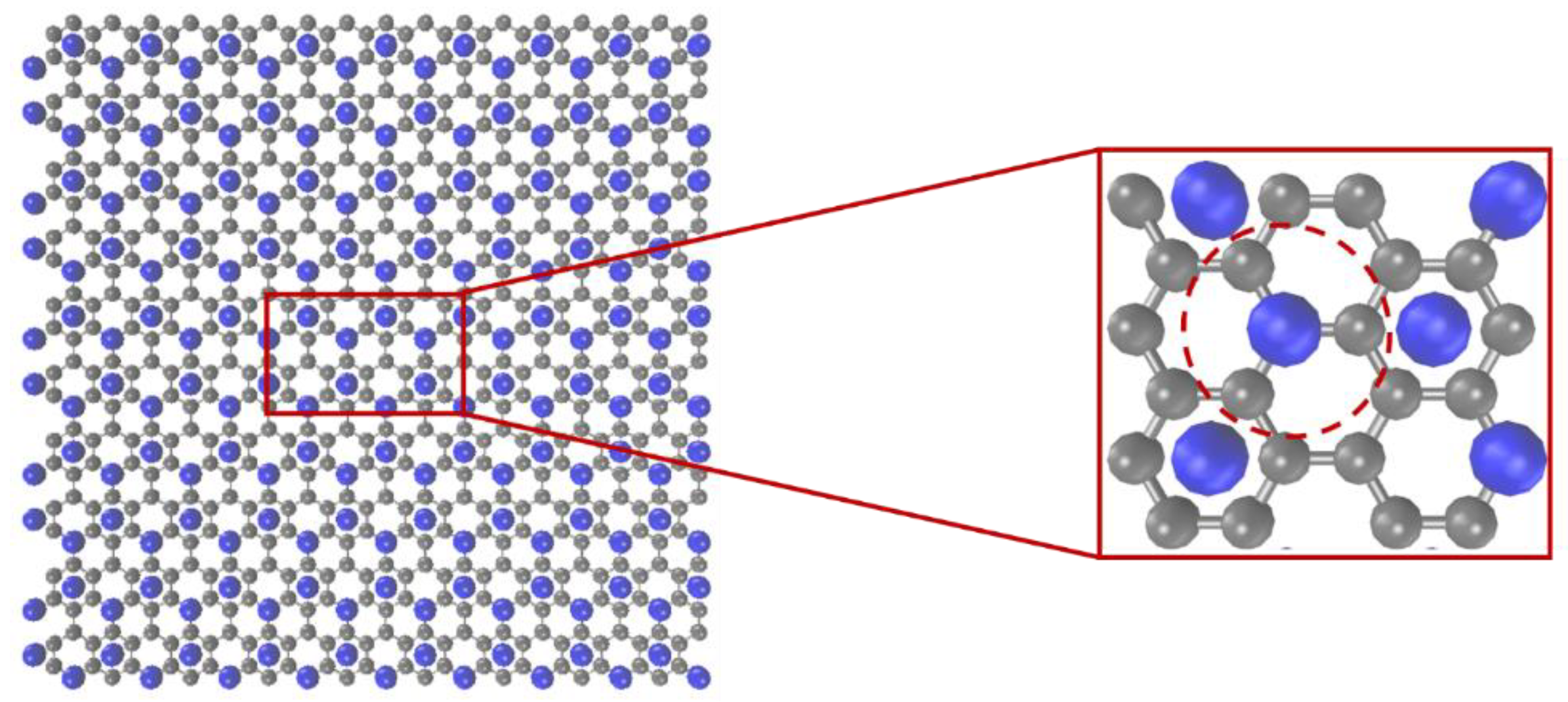
2.4. Mesoscopic Model of Graphene
2.5. Simulation Protocol for Atomistic and Mesoscopic Simulations
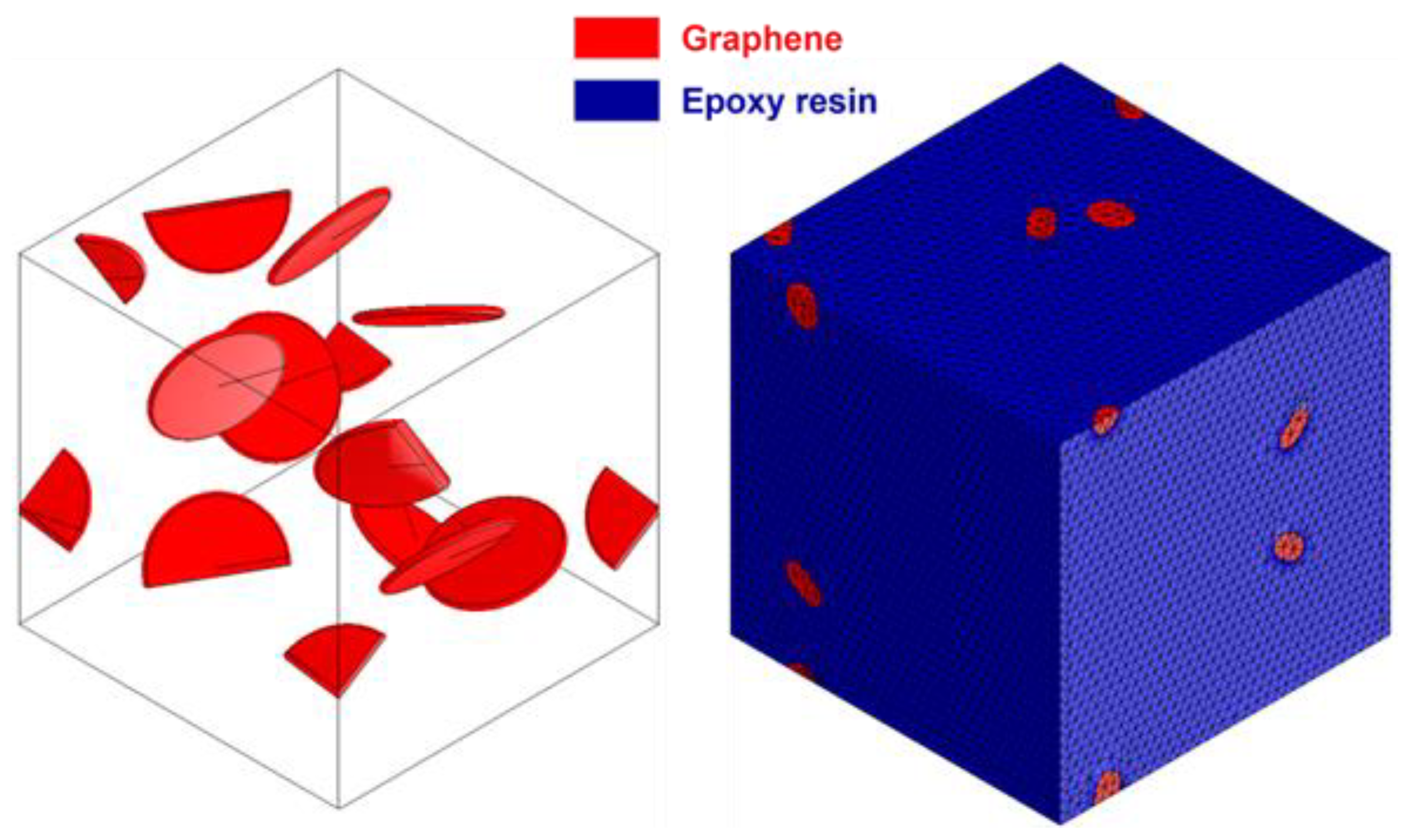
2.6. Continuum Models of Epoxy/Gr Composites
3. Results and Discussion
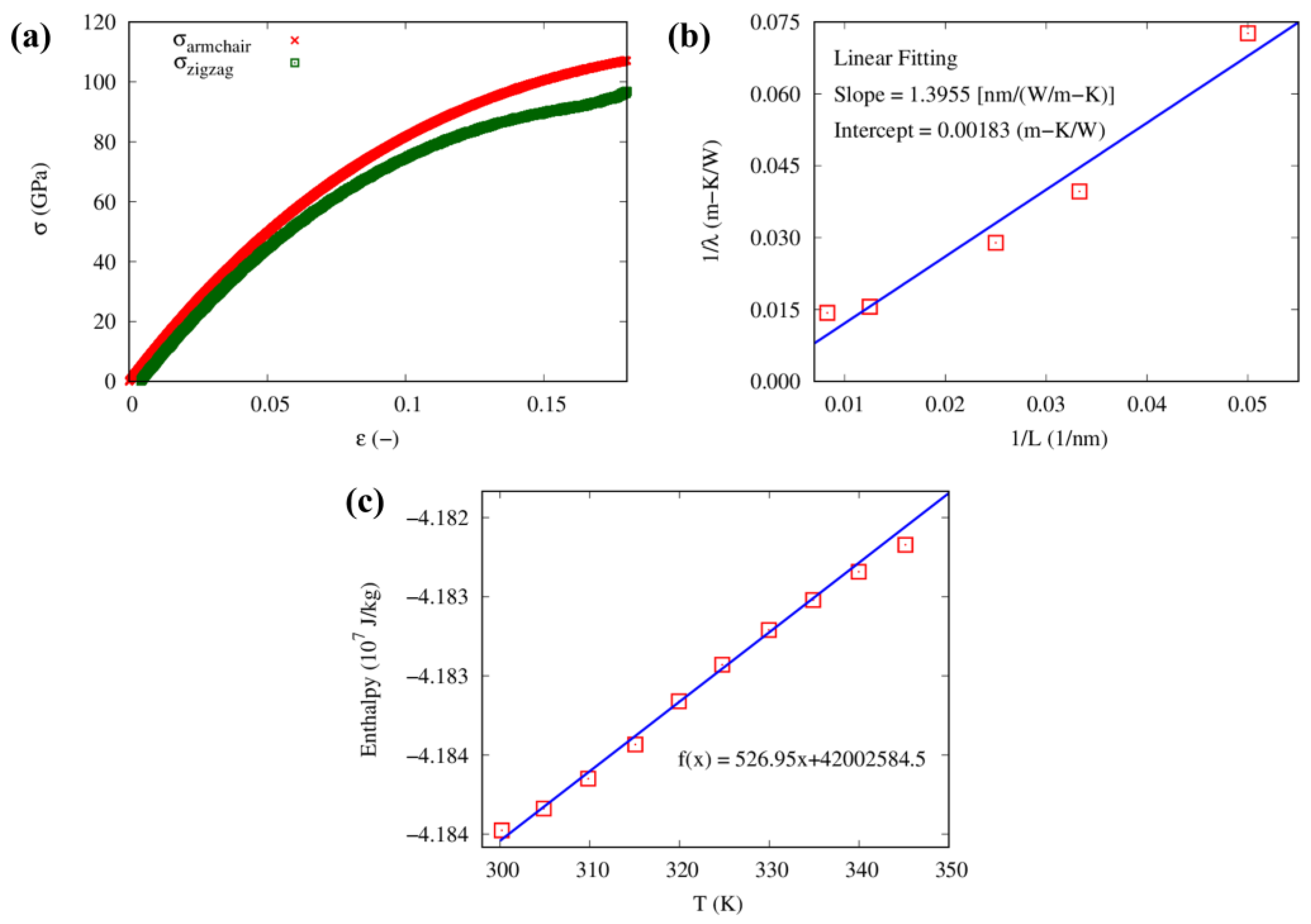
3.1. Atomistic Simulation of Epoxy
3.2. Coarse-Grained Potentials Determination
3.3. Mesoscopic Simulation of Epoxy
3.4. Mesoscopic Simulation of Graphene
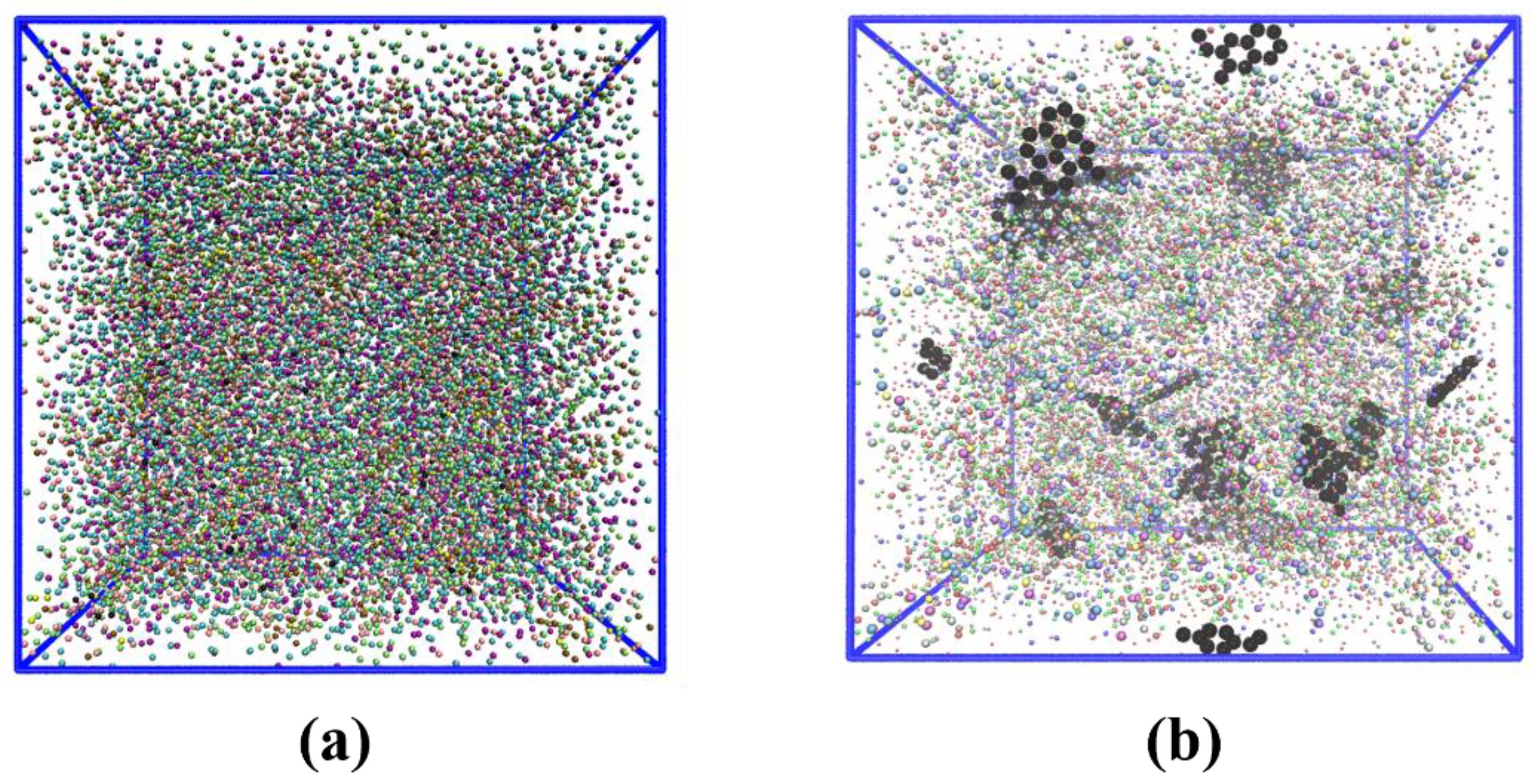
3.5. Coarse-Grained and Continuum Simulation of Epoxy/Gr Composites
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, S.; Chevali, V.S.; Xu, Z.; Hui, D.; Wang, H. A Review of Extending Performance of Epoxy Resins Using Carbon Nanomaterials. Compos. B Eng. 2018, 136, 197–214. [Google Scholar] [CrossRef]
- Zotti, A.; Zuppolini, S.; Borriello, A.; Zarrelli, M. Thermal and Mechanical Characterization of an Aeronautical Graded Epoxy Resin Loaded with Hybrid Nanoparticles. Nanomaterials 2020, 10, 1388. [Google Scholar] [CrossRef] [PubMed]
- Ribezzo, A.; Falciani, G.; Bergamasco, L.; Fasano, M.; Chiavazzo, E. An Overview on the Use of Additives and Preparation Procedure in Phase Change Materials for Thermal Energy Storage with a Focus on Long Term Applications. J. Energy Storage 2022, 53, 105140. [Google Scholar] [CrossRef]
- Gu, H.; Tadakamalla, S.; Zhang, X.; Huang, Y.; Jiang, Y.; Colorado, H.A.; Luo, Z.; Wei, S.; Guo, Z. Epoxy Resin Nanosuspensions and Reinforced Nanocomposites from Polyaniline Stabilized Multi-Walled Carbon Nanotubes. J. Mater. Chem. C Mater. 2013, 1, 729–743. [Google Scholar] [CrossRef]
- Bao, C.; Guo, Y.; Song, L.; Kan, Y.; Qian, X.; Hu, Y. In Situ Preparation of Functionalized Graphene Oxide/Epoxy Nanocomposites with Effective Reinforcements. J. Mater. Chem. 2011, 21, 13290–13298. [Google Scholar] [CrossRef]
- Jeyranpour, F.; Alahyarizadeh, G.; Minuchehr, A. The Thermo-Mechanical Properties Estimation of Fullerene-Reinforced Resin Epoxy Composites by Molecular Dynamics Simulation—A Comparative Study. Polymer 2016, 88, 9–18. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, S.; Ye, S.; Feng, J. A Feasible Route to Balance the Mechanical Properties of Epoxy Thermosets by Reinforcing a PCL-PPC-PCL Toughened System with Reduced Graphene Oxide. Compos. Sci. Technol. 2016, 125, 108–113. [Google Scholar] [CrossRef]
- Zhu, J.; Wei, S.; Ryu, J.; Budhathoki, M.; Liang, G.; Guo, Z. In Situ Stabilized Carbon Nanofiber (CNF) Reinforced Epoxy Nanocomposites. J. Mater. Chem. 2010, 20, 4937–4948. [Google Scholar] [CrossRef]
- Mishra, S.; Srivastava, R.; Muhammad, A.; Amit, A.; Chiavazzo, E.; Fasano, M.; Asinari, P. The Impact of Physicochemical Features of Carbon Electrodes on the Capacitive Performance of Supercapacitors: A Machine Learning Approach. Sci. Rep. 2023, 13, 6494. [Google Scholar] [CrossRef]
- Ye, Z.; Wu, P.; Wang, H.; Jiang, S.; Huang, M.; Lei, D.; Wu, F. Multimode Tunable Terahertz Absorber Based on a Quarter Graphene Disk Structure. Results Phys. 2023, 48, 106420. [Google Scholar] [CrossRef]
- Lai, R.; Shi, P.; Yi, Z.; Li, H.; Yi, Y. Triple-Band Surface Plasmon Resonance Metamaterial Absorber Based on Open-Ended Prohibited Sign Type Monolayer Graphene. Micromachines 2023, 14, 953. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Yi, Y.; Yang, H.; Cheng, S.; Yang, W.; Zhang, H.; Yi, Z.; Yi, Y.; Li, H. Active Tunable Terahertz Bandwidth Absorber Based on Single Layer Graphene. Commun. Theor. Phys. 2023, 75, 045503. [Google Scholar] [CrossRef]
- Fu, Y.; Michopoulos, J.; Song, J.-H. Coarse-Grained Molecular Dynamics Simulations of Epoxy Resin during the Curing Process. Comput. Mater. Sci. 2015, 107, 24–32. [Google Scholar] [CrossRef]
- Yang, S.; Cui, Z.; Qu, J. A Coarse-Grained Model for Epoxy Molding Compound. J. Phys. Chem. B 2014, 118, 1660–1669. [Google Scholar] [CrossRef]
- Baptista, R.; Mendão, A.; Guedes, M.; Marat-Mendes, R. An Experimental Study on Mechanical Properties of Epoxy-Matrix Composites Containing Graphite Filler. Procedia Struct. Integr. 2016, 1, 74–81. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Barrera, E.V. Asymmmetric Diamino Functionalization of Nanotubes Assisted by BOC Protection and Their Epoxy Nanocomposites. Adv. Funct. Mater. 2010, 20, 3039–3044. [Google Scholar] [CrossRef]
- Ma, P.-C.; Mo, S.-Y.; Tang, B.-Z.; Kim, J.-K. Dispersion, Interfacial Interaction and Re-Agglomeration of Functionalized Carbon Nanotubes in Epoxy Composites. Carbon 2010, 48, 1824–1834. [Google Scholar] [CrossRef]
- Wang, Z.; Luo, J.; Zhao, G. Dielectric and Microwave Attenuation Properties of Graphene Nanoplatelet–Epoxy Composites. AIP Adv. 2014, 4, 017139. [Google Scholar] [CrossRef] [Green Version]
- Wang, F.; Drzal, L.T.; Qin, Y.; Huang, Z. Mechanical Properties and Thermal Conductivity of Graphene Nanoplatelet/Epoxy Composites. J. Mater. Sci. 2015, 50, 1082–1093. [Google Scholar] [CrossRef]
- Gavrielides, A.; Duguet, T.; Aufray, M.; Lacaze-Dufaure, C. Model of the DGEBA-EDA Epoxy Polymer: Experiments and Simulation Using Classical Molecular Dynamics. Int. J. Polym. Sci. 2019, 2019, 9604714. [Google Scholar] [CrossRef] [Green Version]
- Bandyopadhyay, A.; Valavala, P.K.; Clancy, T.C.; Wise, K.E.; Odegard, G.M. Molecular Modeling of Crosslinked Epoxy Polymers: The Effect of Crosslink Density on Thermomechanical Properties. Polymer 2011, 52, 2445–2452. [Google Scholar] [CrossRef]
- Li, C.; Strachan, A. Molecular Dynamics Predictions of Thermal and Mechanical Properties of Thermoset Polymer EPON862/DETDA. Polymer 2011, 52, 2920–2928. [Google Scholar] [CrossRef]
- Mohammad Nejad, S.; Srivastava, R.; Bellussi, F.M.; Chávez Thielemann, H.; Asinari, P.; Fasano, M. Nanoscale Thermal Properties of Carbon Nanotubes/Epoxy Composites by Atomistic Simulations. Int. J. Therm. Sci. 2021, 159, 106588. [Google Scholar] [CrossRef]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and Testing of a General Amber Force Field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Mayo, S.L.; Olafson, B.D.; Goddard, W.A. DREIDING: A Generic Force Field for Molecular Simulations. J. Phys. Chem. 1990, 94, 8897–8909. [Google Scholar] [CrossRef]
- Shelley, J.C.; Shelley, M.Y.; Reeder, R.C.; Bandyopadhyay, S.; Klein, M.L. A Coarse Grain Model for Phospholipid Simulations. J. Phys. Chem. B 2001, 105, 4464–4470. [Google Scholar] [CrossRef]
- Vettorel, T.; Meyer, H. Coarse Graining of Short Polythylene Chains for Studying Polymer Crystallization. J. Chem. Theory Comput. 2006, 2, 616–629. [Google Scholar] [CrossRef]
- Fukunaga, H.; Takimoto, J.; Doi, M. A Coarse-Graining Procedure for Flexible Polymer Chains with Bonded and Nonbonded Interactions. J. Chem. Phys. 2002, 116, 8183–8190. [Google Scholar] [CrossRef]
- Li, Y.; Tang, S.; Abberton, B.C.; Kröger, M.; Burkhart, C.; Jiang, B.; Papakonstantopoulos, G.J.; Poldneff, M.; Liu, W.K. A Predictive Multiscale Computational Framework for Viscoelastic Properties of Linear Polymers. Polymer 2012, 53, 5935–5952. [Google Scholar] [CrossRef]
- Marrink, S.J.; de Vries, A.H.; Mark, A.E. Coarse Grained Model for Semiquantitative Lipid Simulations. J. Phys. Chem. B 2004, 108, 750–760. [Google Scholar] [CrossRef] [Green Version]
- Marrink, S.J.; Risselada, H.J.; Yefimov, S.; Tieleman, D.P.; de Vries, A.H. The MARTINI Force Field: Coarse Grained Model for Biomolecular Simulations. J. Phys. Chem. B 2007, 111, 7812–7824. [Google Scholar] [CrossRef] [Green Version]
- Komarov, P.V.; Yu-Tsung, C.; Shih-Ming, C.; Khalatur, P.G.; Reineker, P. Highly Cross-Linked Epoxy Resins: An Atomistic Molecular Dynamics Simulation Combined with a Mapping/Reverse Mapping Procedure. Macromolecules 2007, 40, 8104–8113. [Google Scholar] [CrossRef]
- Srivastava, R.; Fasano, M.; Mohammad Nejad, S.; Chávez Thielemann, H.; Chiavazzo, E.; Asinari, P. 3 Modeling Carbon-Based Smart Materials; Charitidis, C.A., Koumoulos, E.P., Dragatogiannis, D.A., Eds.; De Gruyter: Berlin, Germany, 2020; pp. 33–80. ISBN 9783110479133. [Google Scholar]
- Verma, A.K.; Srivastava, R. Chapter 22—Multiscale Modeling Approach for Removal of Heavy Metal Ions from Water: A Review. In Current Directions in Water Scarcity Research; Tiwari, A.K., Kumar, A., Singh, A.K., Singh, T.N., Suozzi, E., Matta, G., Lo Russo, S., Eds.; Elsevier: Amsterdam, The Netherlands, 2022; Volume 5, pp. 439–457. ISSN 2542-7946. [Google Scholar]
- Yu, J.; Huang, X.; Wang, L.; Peng, P.; Wu, C.; Wu, X.; Jiang, P. Preparation of Hyperbranched Aromatic Polyamide Grafted Nanoparticles for Thermal Properties Reinforcement of Epoxy Composites. Polym. Chem. 2011, 2, 1380. [Google Scholar] [CrossRef]
- Kotch, T.G.; Lees, A.J.; Fuerniss, S.J.; Papathomas, K.I. Luminescent Organometallic Complexes as Visible Probes in the Isothermal Curing of Epoxy Resins. Chem. Mater. 1992, 4, 675–683. [Google Scholar] [CrossRef]
- Golaz, B.; Michaud, V.; Leterrier, Y.; Månson, J.-A.E. UV Intensity, Temperature and Dark-Curing Effects in Cationic Photo-Polymerization of a Cycloaliphatic Epoxy Resin. Polymer 2012, 53, 2038–2048. [Google Scholar] [CrossRef]
- Arcos-Casarrubias, J.A.; Vázquez-Torres, H.; Granados-Olvera, J.A.; Cedeño, A.J.; Cervantes-Uc, J.M. Viscoelastic Behavior and Toughness of the DGEBA Epoxy Resin with 1,2-Diaminocyclohexane: Effect of Functionalized Poly(Dimethylsiloxane), Diglycidyl Ether, PDMS-DGE, Pre-Reacted with 1,2-Diaminocyclohexane. Polym. Bull. 2022, 79, 2871–2901. [Google Scholar] [CrossRef]
- Sun, H. COMPASS: An Ab Initio Force-Field Optimized for Condensed-Phase ApplicationsOverview with Details on Alkane and Benzene Compounds. J. Phys. Chem. B 1998, 102, 7338–7364. [Google Scholar] [CrossRef]
- Mirzoev, A.; Lyubartsev, A. Multiscale Simulations of Soft Matter: Systematic Structure-Based Coarse-Graining Approach; Stockholm University: Stockholm, Sweden, 2013. [Google Scholar]
- Henderson, R.L. A Uniqueness Theorem for Fluid Pair Correlation Functions. Phys. Lett. A 1974, 49, 197–198. [Google Scholar] [CrossRef]
- Glagolev, M.; Glova, A.; Mezhenskaia, D.; Falkovich, S.; Larin, S.; Vasilevskaya, V.; Lyulin, S. Coarse-Grained A-Graft-B Model of Poly(Lactic Acid) for Molecular Dynamics Simulations. J. Polym. Sci. B Polym. Phys. 2018, 56, 604–612. [Google Scholar] [CrossRef]
- Garg, R.; Dutta, N.; Choudhury, N. Work Function Engineering of Graphene. Nanomaterials 2014, 4, 267–300. [Google Scholar] [CrossRef] [Green Version]
- Ruiz, L.; Xia, W.; Meng, Z.; Keten, S. A Coarse-Grained Model for the Mechanical Behavior of Multi-Layer Graphene. Carbon 2015, 82, 103–115. [Google Scholar] [CrossRef]
- Crisafulli, A.; Khodayari, A.; Mohammadnejad, S.; Fasano, M. Sliding Dynamics of Parallel Graphene Sheets: Effect of Geometry and Van Der Waals Interactions on Nano-Spring Behavior. Crystals 2018, 8, 149. [Google Scholar] [CrossRef] [Green Version]
- Mohammad Nejad, S.; Bozorg Bigdeli, M.; Srivastava, R.; Fasano, M. Heat Transfer at the Interface of Graphene Nanoribbons with Different Relative Orientations and Gaps. Energies 2019, 12, 796. [Google Scholar] [CrossRef] [Green Version]
- Shang, J.-J.; Yang, Q.-S.; Liu, X. New Coarse-Grained Model and Its Implementation in Simulations of Graphene Assemblies. J. Chem. Theory Comput. 2017, 13, 3706–3714. [Google Scholar] [CrossRef]
- Tersoff, J. Empirical Interatomic Potential for Carbon, with Applications to Amorphous Carbon. Phys. Rev. Lett. 1988, 61, 2879–2882. [Google Scholar] [CrossRef] [Green Version]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; in ’t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS—A Flexible Simulation Tool for Particle-Based Materials Modeling at the Atomic, Meso, and Continuum Scales. Comput. Phys. Commun. 2022, 271, 108171. [Google Scholar] [CrossRef]
- Jang, C.; Sirk, T.W.; Andzelm, J.W.; Abrams, C.F. Comparison of Crosslinking Algorithms in Molecular Dynamics Simulation of Thermosetting Polymers. Macromol. Theory Simul. 2015, 24, 260–270. [Google Scholar] [CrossRef]
- Sirk, T.W.; Khare, K.S.; Karim, M.; Lenhart, J.L.; Andzelm, J.W.; McKenna, G.B.; Khare, R. High Strain Rate Mechanical Properties of a Cross-Linked Epoxy across the Glass Transition. Polymer 2013, 54, 7048–7057. [Google Scholar] [CrossRef]
- Müller-Plathe, F. A Simple Nonequilibrium Molecular Dynamics Method for Calculating the Thermal Conductivity. J. Chem. Phys. 1997, 106, 6082–6085. [Google Scholar] [CrossRef]
- Mori, T.; Tanaka, K. Average Stress in Matrix and Average Elastic Energy of Materials with Misfitting Inclusions. Acta Metall. 1973, 21, 571–574. [Google Scholar] [CrossRef]
- Eshelby, J.D. The Determination of the Elastic Field of an Ellipsoidal Inclusion, and Related Problems. Proc. R. Soc. Lond. A Math. Phys. Sci. 1957, 241, 376–396. [Google Scholar] [CrossRef]
- Liu, C.; Ning, W.; Tam, L.; Yu, Z. Understanding Fracture Behavior of Epoxy-Based Polymer Using Molecular Dynamics Simulation. J. Mol. Graph. Model. 2020, 101, 107757. [Google Scholar] [CrossRef] [PubMed]
- Feng, R.; Farris, R.J. The Characterization of Thermal and Elastic Constants for an Epoxy Photoresist SU8 Coating. J. Mater. Sci. 2002, 37, 4793–4799. [Google Scholar] [CrossRef]
- Yu, H.; Balogun, O.; Li, B.; Murray, T.W.; Zhang, X. Building Embedded Microchannels Using a Single Layered SU-8, and Determining Young’s Modulus Using a Laser Acoustic Technique. J. Micromech. Microeng. 2004, 14, 1576. [Google Scholar] [CrossRef] [Green Version]
- Al-Halhouli, A.T.; Kampen, I.; Krah, T.; Büttgenbach, S. Nanoindentation Testing of SU-8 Photoresist Mechanical Properties. Microelectron. Eng. 2008, 85, 942–944. [Google Scholar] [CrossRef]
- Lorenz, H.; Laudon, M.; Renaud, P. Mechanical Characterization of a New High-Aspect-Ratio near UV-Photoresist. Microelectron. Eng. 1998, 41–42, 371–374. [Google Scholar] [CrossRef]
- Tay, F.E.H.; van Kan, J.A.; Watt, F.; Choong, W.O. A Novel Micro-Machining Method for the Fabrication of Thick-Film SU-8 Embedded-Channels. J. Micromech. Microeng. 2001, 11, 27. [Google Scholar] [CrossRef]
- Hammacher, J.; Fuelle, A.; Flaemig, J.; Saupe, J.; Loechel, B.; Grimm, J. Stress Engineering and Mechanical Properties of SU-8-Layers for Mechanical Applications. Microsyst. Technol. 2008, 14, 1515–1523. [Google Scholar] [CrossRef]
- Wang, Z.; Cheng, Y.; Yang, M.; Huang, J.; Cao, D.; Chen, S.; Xie, Q.; Lou, W.; Wu, H. Dielectric Properties and Thermal Conductivity of Epoxy Composites Using Core/Shell Structured Si/SiO2/Polydopamine. Compos. B Eng. 2018, 140, 83–90. [Google Scholar] [CrossRef]
- Ren, J.; Li, Q.; Yan, L.; Jia, L.; Huang, X.; Zhao, L.; Ran, Q.; Fu, M. Enhanced Thermal Conductivity of Epoxy Composites by Introducing Graphene@boron Nitride Nanosheets Hybrid Nanoparticles. Mater. Des. 2020, 191, 108663. [Google Scholar] [CrossRef]
- Ackermann, A.C.; Fischer, M.; Wick, A.; Carosella, S.; Fox, B.L.; Middendorf, P. Mechanical, Thermal and Electrical Properties of Epoxy Nanocomposites with Amine-Functionalized Reduced Graphene Oxide via Plasma Treatment. J. Compos. Sci. 2022, 6, 153. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Q.; Gao, L.; Jia, Y. Effects of Key Thermophysical Properties on the Curing Uniformity of Carbon Fiber Reinforced Resin. Composites 2018, 18, 19–26. [Google Scholar] [CrossRef]
- Feng, B.; Fan, L.-W.; Zeng, Y.; Ding, J.-Y.; Shao, X.-F. Atomistic Insights into the Effects of Hydrogen Bonds on the Melting Process and Heat Conduction of Erythritol as a Promising Latent Heat Storage Material. Int. J. Therm. Sci. 2019, 146, 106103. [Google Scholar] [CrossRef]
- Zheng, M.; Jaramillo-Botero, A.; Ju, X.; Goddard, W.A. Coarse-Grained Force-Field for Large Scale Molecular Dynamics Simulations of Polyacrylamide and Polyacrylamide-Gels Based on Quantum Mechanics. Phys. Chem. Chem. Phys. 2021, 23, 10909–10918. [Google Scholar] [CrossRef]
- González, M.G.; Cabanelas, J.C.; Baselga, J. Applications of FTIR on Epoxy Resins—Identification, Monitoring the Curing Process, Phase Separation and Water Uptake. In Infrared Spectroscopy; Theophanides, T., Ed.; IntechOpen: Rijeka, Croatia, 2012; p. 13. [Google Scholar]
- Ardham, V.R.; Leroy, F. Communication: Is a Coarse-Grained Model for Water Sufficient to Compute Kapitza Conductance on Non-Polar Surfaces? J. Chem. Phys. 2017, 147, 151102. [Google Scholar] [CrossRef] [Green Version]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Li, M.; Deng, T.; Zheng, B.; Zhang, Y.; Liao, Y.; Zhou, H. Effect of Defects on the Mechanical and Thermal Properties of Graphene. Nanomaterials 2019, 9, 347. [Google Scholar] [CrossRef] [Green Version]
- Zhan, N.; Chen, B.; Li, C.; Shen, P.K. Molecular Dynamics Simulations of the Thermal Conductivity of Graphene for Application in Wearable Devices. Nanotechnology 2019, 30, 025705. [Google Scholar] [CrossRef]
- Li, Q.-Y.; Xia, K.; Zhang, J.; Zhang, Y.; Li, Q.; Takahashi, K.; Zhang, X. Measurement of Specific Heat and Thermal Conductivity of Supported and Suspended Graphene by a Comprehensive Raman Optothermal Method. Nanoscale 2017, 9, 10784–10793. [Google Scholar] [CrossRef]
- Balandin, A.A. Phononics of Graphene and Related Materials. ACS Nano 2020, 14, 5170–5178. [Google Scholar] [CrossRef]
- Balandin, A.A. Thermal Properties of Graphene and Nanostructured Carbon Materials. Nat. Mater. 2011, 10, 569–581. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Wu, Q.; Mishra, C.; Kang, J.; Zhang, H.; Cho, K.; Cai, W.; Balandin, A.A.; Ruoff, R.S. Thermal Conductivity of Isotopically Modified Graphene. Nat. Mater. 2012, 11, 203–207. [Google Scholar] [CrossRef]
- Yu, C.; Zhang, G. Impacts of Length and Geometry Deformation on Thermal Conductivity of Graphene Nanoribbons. J. Appl. Phys. 2013, 113, 044306. [Google Scholar] [CrossRef]
- Cao, A. Molecular Dynamics Simulation Study on Heat Transport in Monolayer Graphene Sheet with Various Geometries. J. Appl. Phys. 2012, 111, 083528. [Google Scholar] [CrossRef]
- Wang, L.; Sun, H. Thermal Conductivity of Silicon and Carbon Hybrid Monolayers: A Molecular Dynamics Study. J. Mol. Model. 2012, 18, 4811–4818. [Google Scholar] [CrossRef]
- Böer, K.W.; Pohl, U.W. Phonon-Induced Thermal Properties. In Semiconductor Physics; Springer International Publishing: Cham, Switzerland, 2020; pp. 1–29. [Google Scholar]
- Lewis, J.S.; Barani, Z.; Magana, A.S.; Kargar, F.; Balandin, A.A. Thermal and Electrical Conductivity Control in Hybrid Composites with Graphene and Boron Nitride Fillers. Mater. Res. Express 2019, 6, 085325. [Google Scholar] [CrossRef] [Green Version]
- Barani, Z.; Mohammadzadeh, A.; Geremew, A.; Huang, C.; Coleman, D.; Mangolini, L.; Kargar, F.; Balandin, A.A. Thermal Properties of the Binary-Filler Hybrid Composites with Graphene and Copper Nanoparticles. Adv. Funct. Mater. 2020, 30, 1904008. [Google Scholar] [CrossRef]
- Shenogina, N.B.; Tsige, M.; Patnaik, S.S.; Mukhopadhyay, S.M. Molecular Modeling Approach to Prediction of Thermo-Mechanical Behavior of Thermoset Polymer Networks. Macromolecules 2012, 45, 5307–5315. [Google Scholar] [CrossRef]
- Li, C.; Medvedev, G.A.; Lee, E.-W.; Kim, J.; Caruthers, J.M.; Strachan, A. Molecular Dynamics Simulations and Experimental Studies of the Thermomechanical Response of an Epoxy Thermoset Polymer. Polymer 2012, 53, 4222–4230. [Google Scholar] [CrossRef]
- Feng, T.; He, J.; Rai, A.; Hun, D.; Liu, J.; Shrestha, S.S. Size Effects in the Thermal Conductivity of Amorphous Polymers. Phys. Rev. Appl. 2020, 14, 044023. [Google Scholar] [CrossRef]
- Duan, K.; He, Y.; Li, Y.; Liu, J.; Zhang, J.; Hu, Y.; Lin, R.; Wang, X.; Deng, W.; Li, L. Machine-Learning Assisted Coarse-Grained Model for Epoxies over Wide Ranges of Temperatures and Cross-Linking Degrees. Mater. Des. 2019, 183, 108130. [Google Scholar] [CrossRef]
- Odegard, G.M.; Patil, S.U.; Deshpande, P.P.; Kanhaiya, K.; Winetrout, J.J.; Heinz, H.; Shah, S.P.; Maiaru, M. Molecular Dynamics Modeling of Epoxy Resins Using the Reactive Interface Force Field. Macromolecules 2021, 54, 9815–9824. [Google Scholar] [CrossRef]
- Giuntoli, A.; Hansoge, N.K.; van Beek, A.; Meng, Z.; Chen, W.; Keten, S. Systematic Coarse-Graining of Epoxy Resins with Machine Learning-Informed Energy Renormalization. NPJ Comput. Mater. 2021, 7, 168. [Google Scholar] [CrossRef]
- Mousavi, A.A.; Arash, B.; Rolfes, R. Optimization Assisted Coarse-Grained Modeling of Agglomerated Nanoparticle Reinforced Thermosetting Polymers. Polymer 2021, 225, 123741. [Google Scholar] [CrossRef]
- Shoji, N.; Sasaki, K.; Uedono, A.; Taniguchi, Y.; Hayashi, K.; Matsubara, N.; Kobayashi, T.; Yamashita, T. Effect of Conversion on Epoxy Resin Properties: Combined Molecular Dynamics Simulation and Experimental Study. Polymer 2022, 254, 125041. [Google Scholar] [CrossRef]
- Orselly, M.; Devemy, J.; Bouvet-Marchand, A.; Dequidt, A.; Loubat, C.; Malfreyt, P. Molecular Simulations of Thermomechanical Properties of Epoxy-Amine Resins. ACS Omega 2022, 7, 30040–30050. [Google Scholar] [CrossRef]
- Thomas, S.; Ajith, K.M.; Lee, S.U.; Valsakumar, M.C. Assessment of the mechanical properties of monolayer graphene using the energy and strain-fluctuation methods. RSC Adv. 2018, 8, 27283–27292. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef]
- Cao, Q.; Geng, X.; Wang, H.; Wang, P.; Liu, A.; Lan, Y.; Peng, Q. A Review of Current Development of Graphene Mechanics. Crystals 2018, 8, 357. [Google Scholar] [CrossRef] [Green Version]
- Politano, A.; Chiarello, G. Probing the Young’s modulus and Poisson’s ratio in graphene/metal interfaces and graphite: A comparative study. Nano Res. 2015, 8, 1847–1856. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muhammad, A.; Sáenz Ezquerro, C.; Srivastava, R.; Asinari, P.; Laspalas, M.; Chiminelli, A.; Fasano, M. Atomistic to Mesoscopic Modelling of Thermophysical Properties of Graphene-Reinforced Epoxy Nanocomposites. Nanomaterials 2023, 13, 1960. https://doi.org/10.3390/nano13131960
Muhammad A, Sáenz Ezquerro C, Srivastava R, Asinari P, Laspalas M, Chiminelli A, Fasano M. Atomistic to Mesoscopic Modelling of Thermophysical Properties of Graphene-Reinforced Epoxy Nanocomposites. Nanomaterials. 2023; 13(13):1960. https://doi.org/10.3390/nano13131960
Chicago/Turabian StyleMuhammad, Atta, Carlos Sáenz Ezquerro, Rajat Srivastava, Pietro Asinari, Manuel Laspalas, Agustín Chiminelli, and Matteo Fasano. 2023. "Atomistic to Mesoscopic Modelling of Thermophysical Properties of Graphene-Reinforced Epoxy Nanocomposites" Nanomaterials 13, no. 13: 1960. https://doi.org/10.3390/nano13131960
APA StyleMuhammad, A., Sáenz Ezquerro, C., Srivastava, R., Asinari, P., Laspalas, M., Chiminelli, A., & Fasano, M. (2023). Atomistic to Mesoscopic Modelling of Thermophysical Properties of Graphene-Reinforced Epoxy Nanocomposites. Nanomaterials, 13(13), 1960. https://doi.org/10.3390/nano13131960