Remote Sensing of the Nano-Rheological Properties of Soft Materials Using Magnetic Nanoparticles and Magnetic AC Susceptometry
Abstract
:1. Introduction
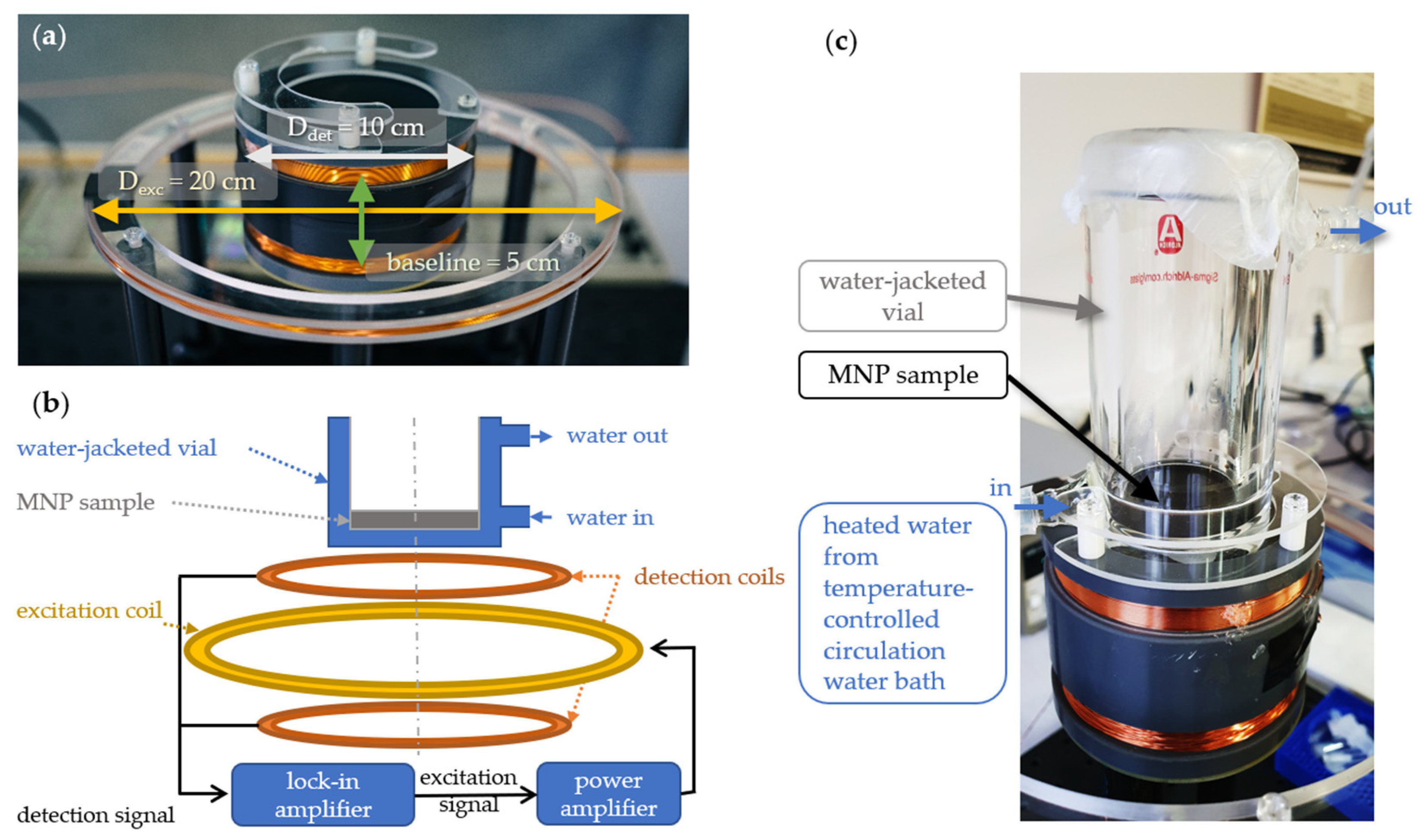
2. Materials and Methods
3. Results and Discussion
3.1. Field Amplitude and Distance
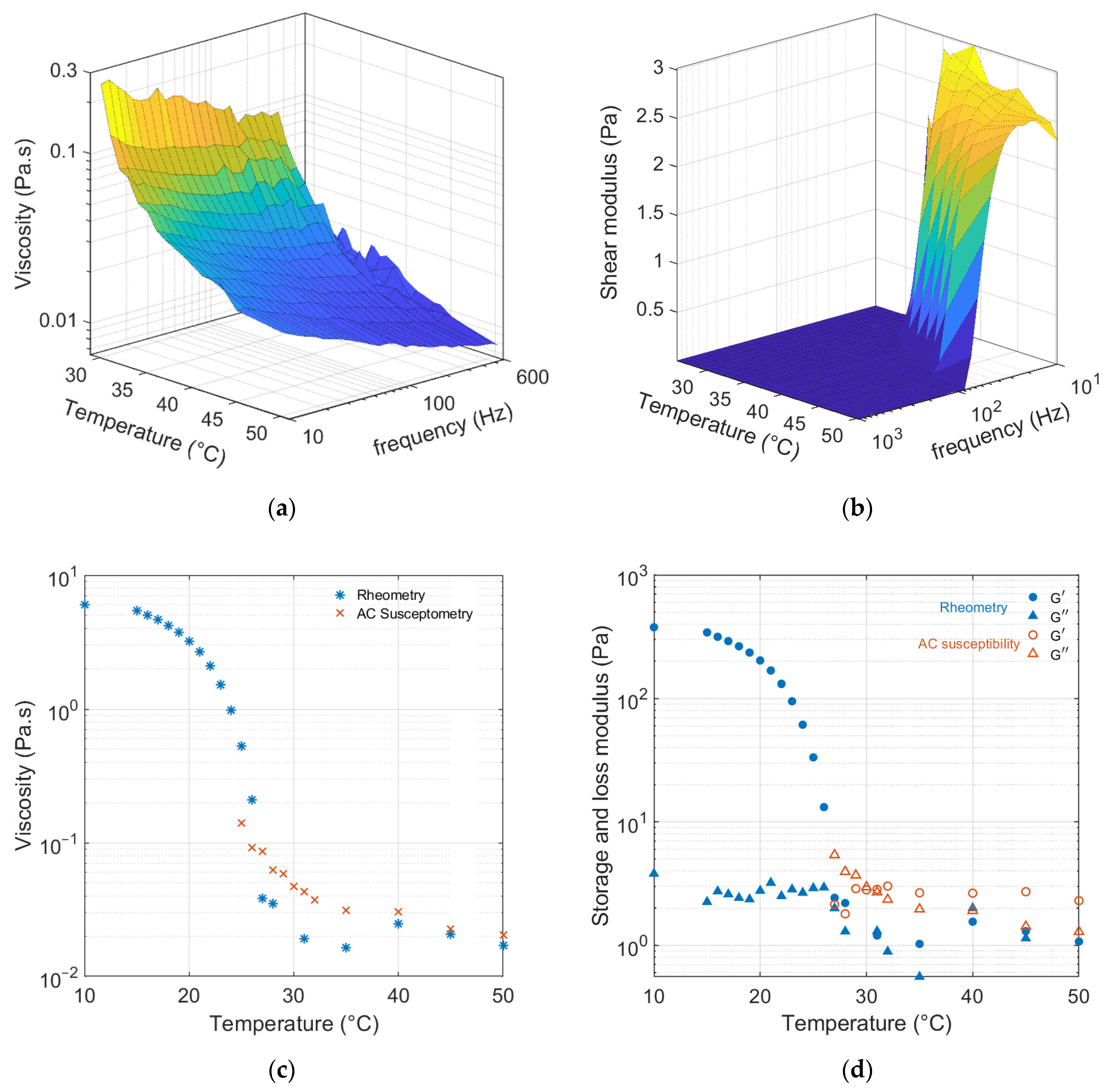
3.2. Temperature Dependence
3.3. Gelatin Solution
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mezger, T. The Rheology Handbook: For Users of Rotational and Oscillatory Rheometers; Vincentz Network: Hannover, Germany, 2020; ISBN 978-3-7486-0370-2. [Google Scholar]
- Funami, T. In Vivo and Rheological Approaches for Characterizing Food Oral Processing and Usefulness of Polysaccharides as Texture Modifiers-A Review. Food Hydrocoll. 2017, 68, 2–14. [Google Scholar] [CrossRef]
- Takahashi, J.; Nakazawa, F. Palatal Pressure Patterns of Gelatin Gels in the Mouth. J. Texture Stud. 1991, 22, 1–11. [Google Scholar] [CrossRef]
- Kohyama, K.; Nishi, M. Direct Measurement of Biting Pressures for Crackers Using a Multiple-Point Sheet Sensor. J. Texture Stud. 1997, 28, 605–617. [Google Scholar] [CrossRef]
- Qazi, W.M.; Ekberg, O.; Wiklund, J.; Mansoor, R.; Stading, M. Simultaneous X-Ray Video-Fluoroscopy and Pulsed Ultrasound Velocimetry Analyses of the Pharyngeal Phase of Swallowing of Boluses with Different Rheological Properties. Dysphagia 2020, 35, 898–906. [Google Scholar] [CrossRef] [Green Version]
- Panouillé, M.; Saint-Eve, A.; Souchon, I. Instrumental Methods for Bolus Characterization during Oral Processing to Understand Food Perceptions. Curr. Opin. Food Sci. 2016, 9, 42–49. [Google Scholar] [CrossRef]
- Sierra-Bermúdez, S.; Maldonado-Camargo, L.P.; Orange, F.; Guinel, M.J.-F.; Rinaldi, C. Assessing Magnetic Nanoparticle Aggregation in Polymer Melts by Dynamic Magnetic Susceptibility Measurements. J. Magn. Magn. Mater. 2015, 378, 64–72. [Google Scholar] [CrossRef]
- Ludwig, F.; Remmer, H. Rotational Dynamics of Magnetic Nanoparticles in Different Matrix Systems. Phys. Sci. Rev. 2020, 7, 981–1008. [Google Scholar] [CrossRef]
- Sriviriyakul, T.; Bogren, S.; Schaller, V.; Jonasson, C.; Blomgren, J.; Ahrentorp, F.; Lopez-Sanchez, P.; Berta, M.; Grüttner, C.; Zeng, L.; et al. Nanorheological Studies of Xanthan/Water Solutions Using Magnetic Nanoparticles. J. Magn. Magn. Mater. 2019, 473, 268–271. [Google Scholar] [CrossRef]
- Remmer, H.; Dieckhoff, J.; Tschöpe, A.; Roeben, E.; Schmidt, A.M.; Ludwig, F. Dynamics of CoFe2O4 Single-Core Nanoparticles in Viscoelastic Media. Phys. Procedia 2015, 75, 1150–1157. [Google Scholar] [CrossRef] [Green Version]
- Remmer, H.; Roeben, E.; Schmidt, A.M.; Schilling, M.; Ludwig, F. Dynamics of Magnetic Nanoparticles in Viscoelastic Media. J. Magn. Magn. Mater. 2017, 427, 331–335. [Google Scholar] [CrossRef]
- Barrera, C.; Florián-Algarin, V.; Acevedo, A.; Rinaldi, C. Monitoring Gelation Using Magnetic Nanoparticles. Soft Matter 2010, 6, 3662. [Google Scholar] [CrossRef]
- Calero-DdelC, V.L.; Santiago-Quiñonez, D.I.; Rinaldi, C. Quantitative Nanoscale Viscosity Measurements Using Magnetic Nanoparticles and SQUID AC Susceptibility Measurements. Soft Matter 2011, 7, 4497. [Google Scholar] [CrossRef]
- Roeben, E.; Roeder, L.; Teusch, S.; Effertz, M.; Deiters, U.K.; Schmidt, A.M. Magnetic Particle Nanorheology. Colloid Polym. Sci. 2014, 292, 2013–2023. [Google Scholar] [CrossRef]
- Ilg, P.; Evangelopoulos, A.E. Magnetic Susceptibility, Nanorheology, and Magnetoviscosity of Magnetic Nanoparticles in Viscoelastic Environments. Phys. Rev. E 2018, 97, 032610. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pankhurst, Q.A.; Connolly, J.; Jones, S.K.; Dobson, J. Applications of Magnetic Nanoparticles in Biomedicine. J. Phys. Appl. Phys. 2003, 36, R167–R181. [Google Scholar] [CrossRef] [Green Version]
- Khandhar, A.P.; Ferguson, R.M.; Krishnan, K.M. Monodispersed Magnetite Nanoparticles Optimized for Magnetic Fluid Hyperthermia: Implications in Biological Systems. J. Appl. Phys. 2011, 109, 07B310. [Google Scholar] [CrossRef] [Green Version]
- Ahrentorp, F.; Astalan, A.; Blomgren, J.; Jonasson, C.; Wetterskog, E.; Svedlindh, P.; Lak, A.; Ludwig, F.; Van Ijzendoorn, L.J.; Westphal, F.; et al. Effective Particle Magnetic Moment of Multi-Core Particles. J. Magn. Magn. Mater. 2015, 380, 221–226. [Google Scholar] [CrossRef]
- Bogren, S.; Fornara, A.; Ludwig, F.; del Puerto Morales, M.; Steinhoff, U.; Hansen, M.; Kazakova, O.; Johansson, C. Classification of Magnetic Nanoparticle Systems—Synthesis, Standardization and Analysis Methods in the NanoMag Project. Int. J. Mol. Sci. 2015, 16, 20308–20325. [Google Scholar] [CrossRef] [Green Version]
- Blomgren, J.; Ahrentorp, F.; Ilver, D.; Jonasson, C.; Sepehri, S.; Kalaboukhov, A.; Winkler, D.; Zardán Gómez de la Torre, T.; Strømme, M.; Johansson, C. Development of a Sensitive Induction-Based Magnetic Nanoparticle Biodetection Method. Nanomaterials 2018, 8, 887. [Google Scholar] [CrossRef] [Green Version]
- DiMarzio, E.A.; Bishop, M. Connection between the Macroscopic Electric and Mechanical Susceptibilities. J. Chem. Phys. 1974, 60, 3802–3811. [Google Scholar] [CrossRef]
- Hess, M.; Roeben, E.; Rochels, P.; Zylla, M.; Webers, S.; Wende, H.; Schmidt, A.M. Size Effects on Rotational Particle Diffusion in Complex Fluids as Probed by Magnetic Particle Nanorheology. Phys. Chem. Chem. Phys. 2019, 21, 26525–26539. [Google Scholar] [CrossRef]
- Raikher, Y.L.; Rusakov, V.V.; Coffey, W.T.; Kalmykov, Y.P. Dynamic Susceptibilities of an Assembly of Dipolar Particles in an Elastic Environment. Phys. Rev. E 2001, 63, 031402. [Google Scholar] [CrossRef] [PubMed]
- Yoshida, T.; Enpuku, K. Simulation and Quantitative Clarification of AC Susceptibility of Magnetic Fluid in Nonlinear Brownian Relaxation Region. Jpn. J. Appl. Phys. 2009, 48, 127002. [Google Scholar] [CrossRef]
- Kestin, J.; Sokolov, M.; Wakeham, W.A. Viscosity of Liquid Water in the Range −8 °C to 150 °C. J. Phys. Chem. Ref. Data 1978, 7, 941–948. [Google Scholar] [CrossRef] [Green Version]
- Ludwig, F.; Kazakova, O.; Barquin, L.F.; Fornara, A.; Trahms, L.; Steinhoff, U.; Svedlindh, P.; Wetterskog, E.; Pankhurst, Q.A.; Southern, P.; et al. Magnetic, Structural, and Particle Size Analysis of Single- and Multi-Core Magnetic Nanoparticles. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef]



| MNP System | 100 nm | 80 nm | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Temperature (°C) | 20.1 | 23.5 | 27.5 | 33.5 | 35.5 | 40.5 | 45.5 | 20.9 | 24.9 | 32.9 | 37.2 |
| Particle median diameter (nm) | 144 | 142 | 140 | 139 | 141 | 139 | 137 | 97 | 95 | 97 | 100 |
| Geometrical standard deviation (nm) | 48 | 49 | 46 | 44 | 45 | 47 | 45 | 24 | 28 | 30 | 31 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sepehri, S.; Andersson, J.; Schaller, V.; Grüttner, C.; Stading, M.; Johansson, C. Remote Sensing of the Nano-Rheological Properties of Soft Materials Using Magnetic Nanoparticles and Magnetic AC Susceptometry. Nanomaterials 2023, 13, 67. https://doi.org/10.3390/nano13010067
Sepehri S, Andersson J, Schaller V, Grüttner C, Stading M, Johansson C. Remote Sensing of the Nano-Rheological Properties of Soft Materials Using Magnetic Nanoparticles and Magnetic AC Susceptometry. Nanomaterials. 2023; 13(1):67. https://doi.org/10.3390/nano13010067
Chicago/Turabian StyleSepehri, Sobhan, Johanna Andersson, Vincent Schaller, Cordula Grüttner, Mats Stading, and Christer Johansson. 2023. "Remote Sensing of the Nano-Rheological Properties of Soft Materials Using Magnetic Nanoparticles and Magnetic AC Susceptometry" Nanomaterials 13, no. 1: 67. https://doi.org/10.3390/nano13010067
APA StyleSepehri, S., Andersson, J., Schaller, V., Grüttner, C., Stading, M., & Johansson, C. (2023). Remote Sensing of the Nano-Rheological Properties of Soft Materials Using Magnetic Nanoparticles and Magnetic AC Susceptometry. Nanomaterials, 13(1), 67. https://doi.org/10.3390/nano13010067








