Broadband and Incident-Angle-Modulation Near-Infrared Polarizers Based on Optically Anisotropic SnSe
Abstract
1. Introduction
2. Materials and Methods
2.1. Absorption Coefficient and Penetration Depth
2.2. Net Phase Shift of s Light
2.3. Theoretical CSalculations by the 4 × 4 Matrix Method
2.4. Numerical Simulations Using the Finite-Difference Time-Domain (FDTD) Method
3. Results and Discussion
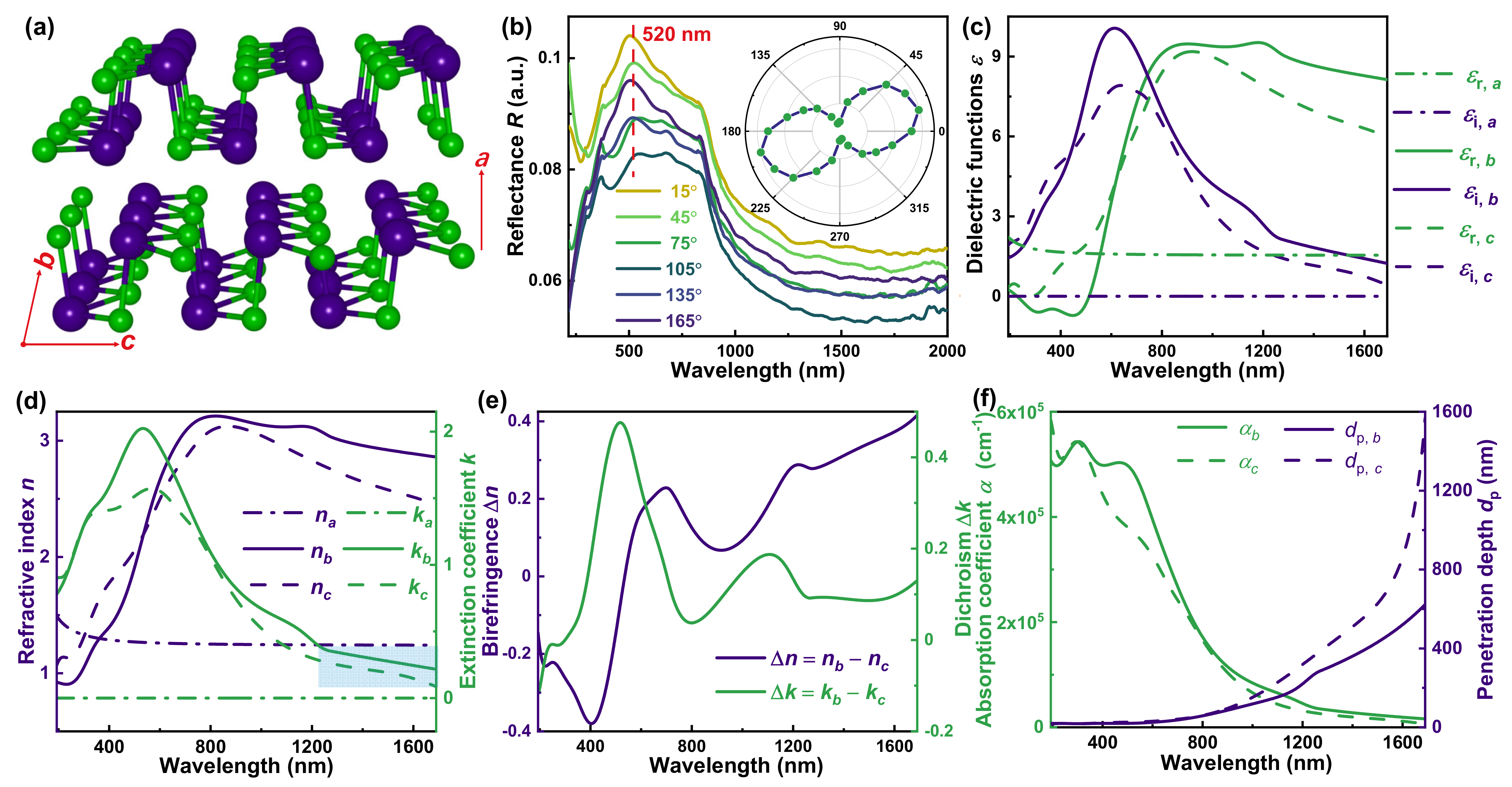
3.1. Optical Anisotropy of SnSe
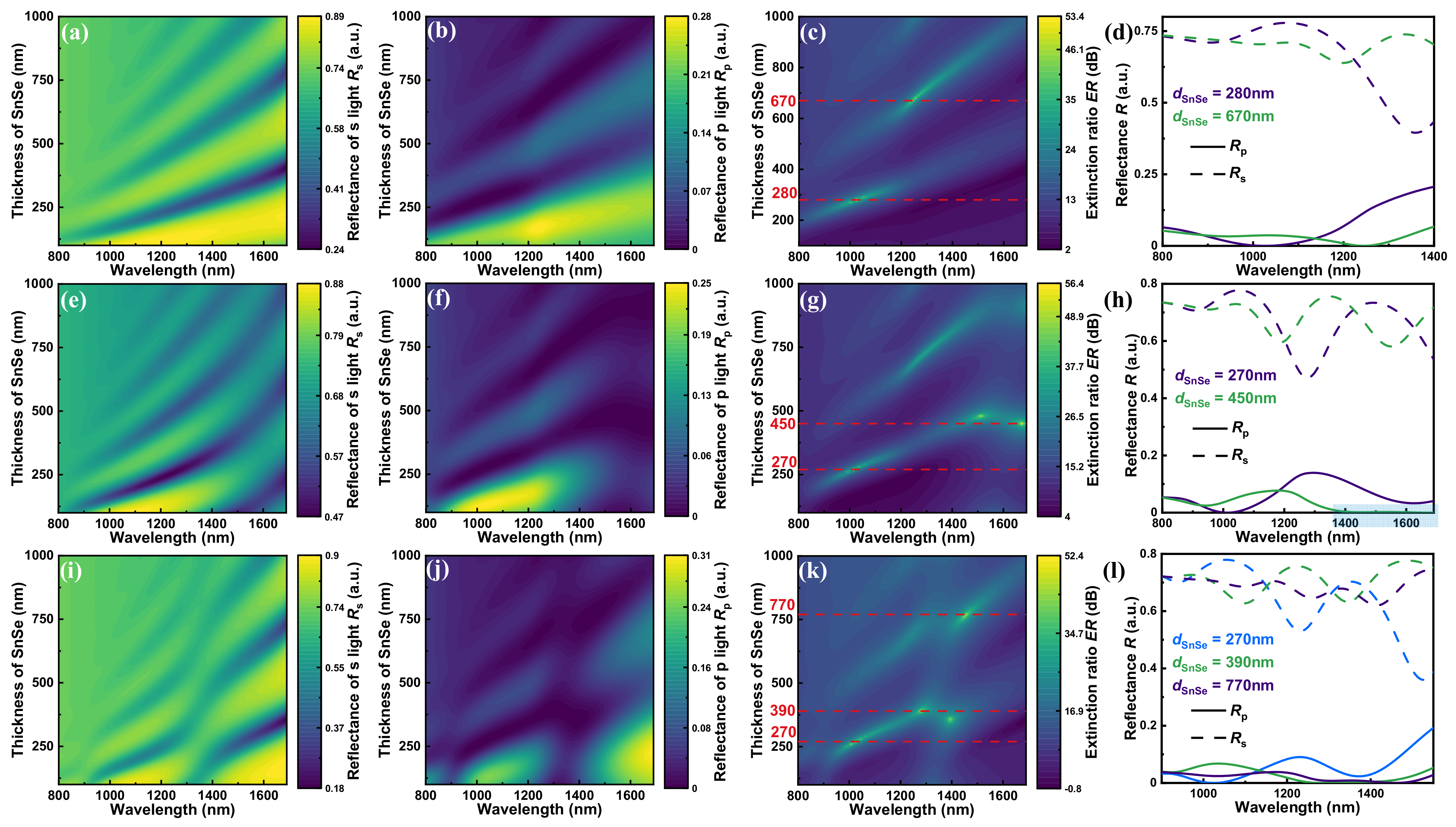
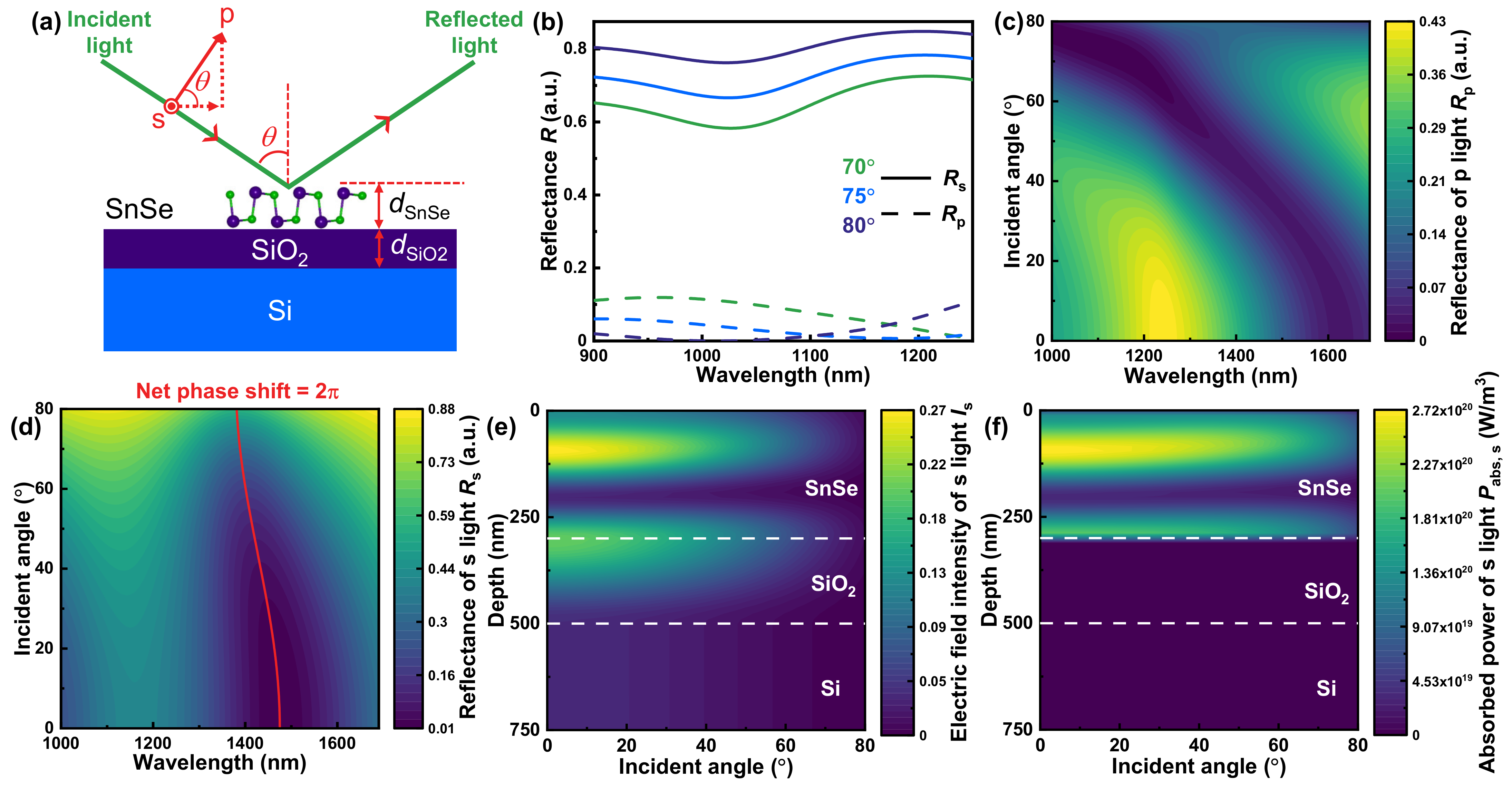
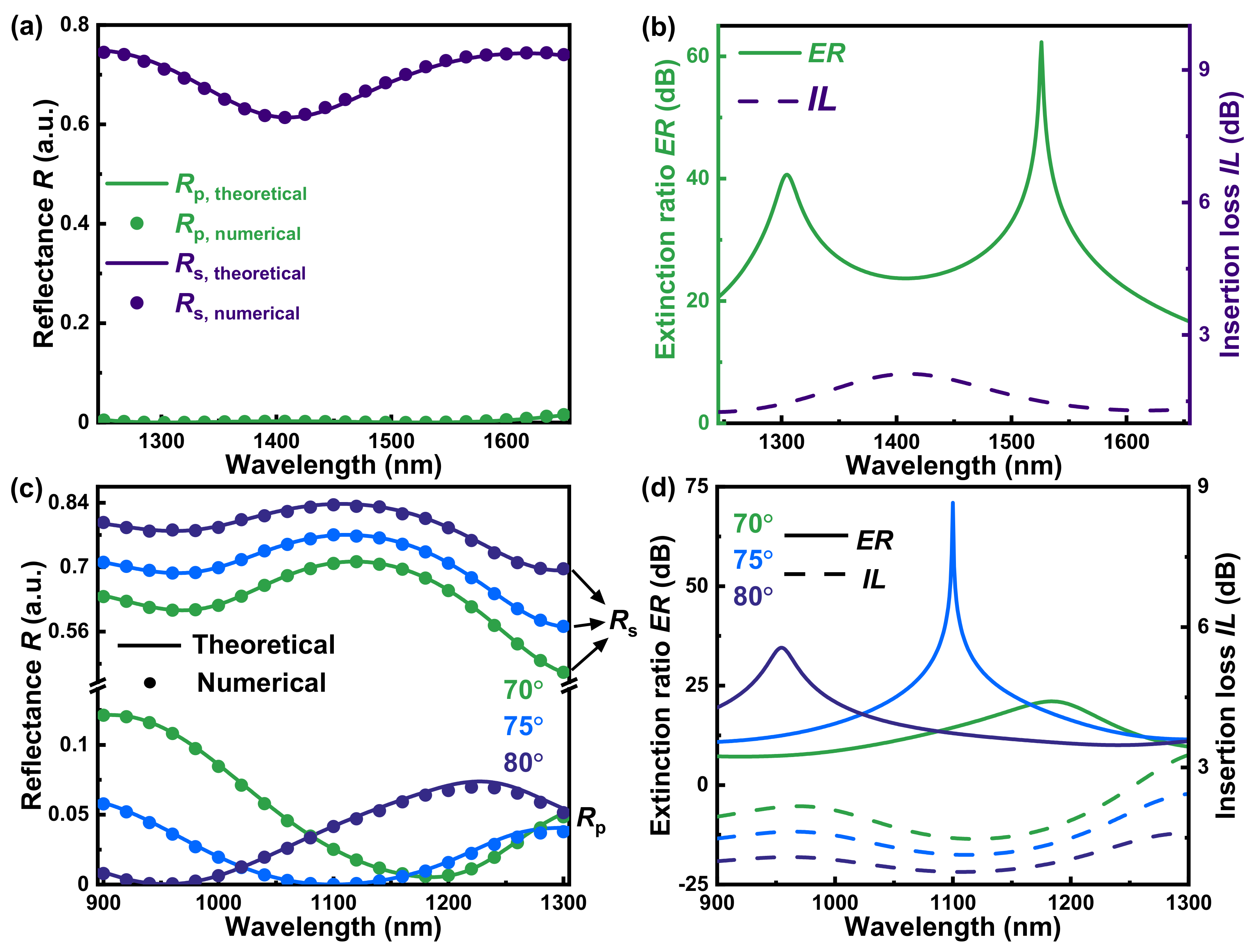
3.2. Design of Broadband and Incident-Angle-Modulation Near-Infrared Polarizers
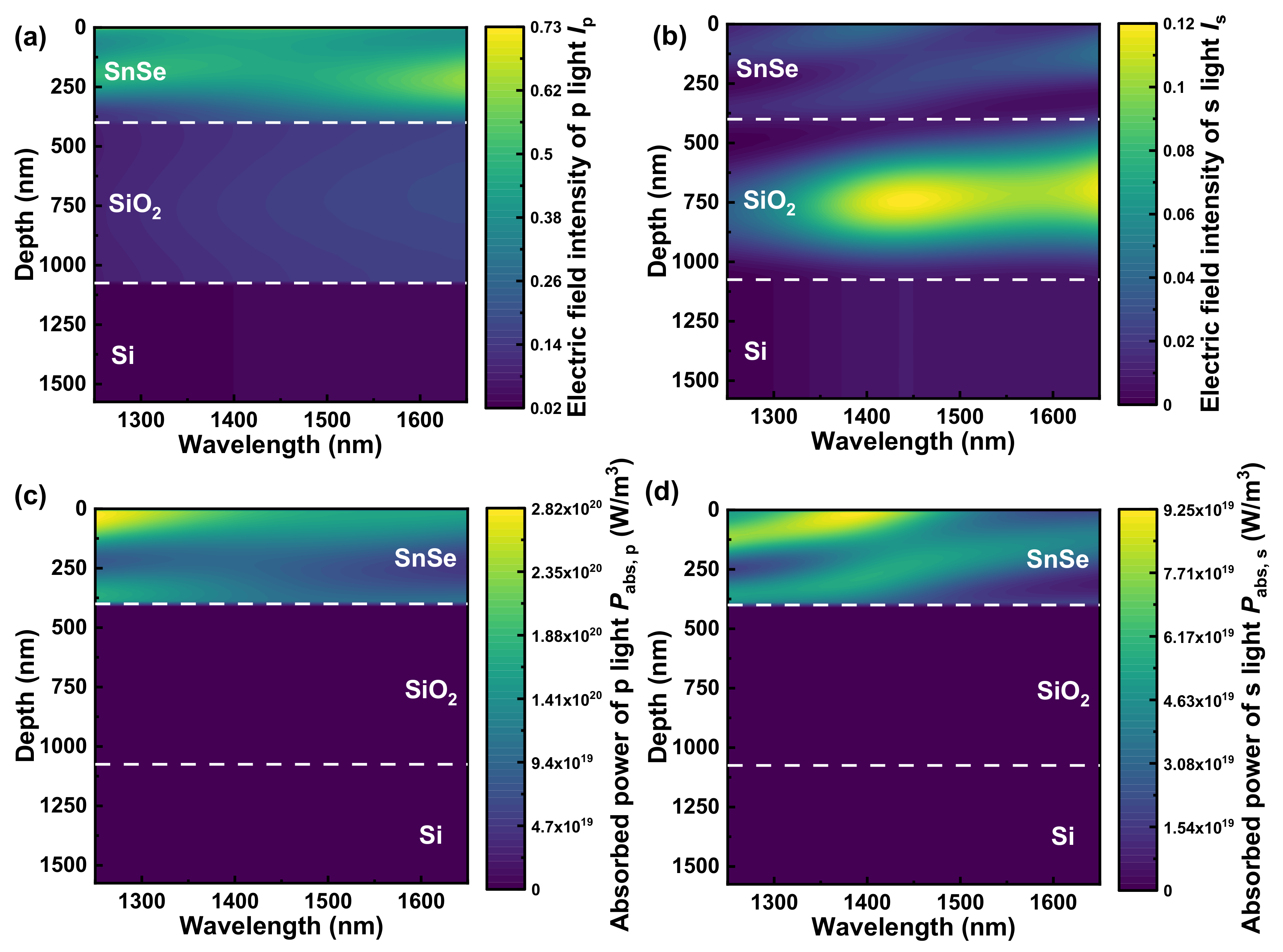
3.3. Mechanism for Broadband and Incident-Angle-Modulation Near-Infrared Polarizers
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Mueller Matrix Spectroscopic Ellipsometry Analysis
Appendix B. Thickness-Dependent Bandgap of SnSe

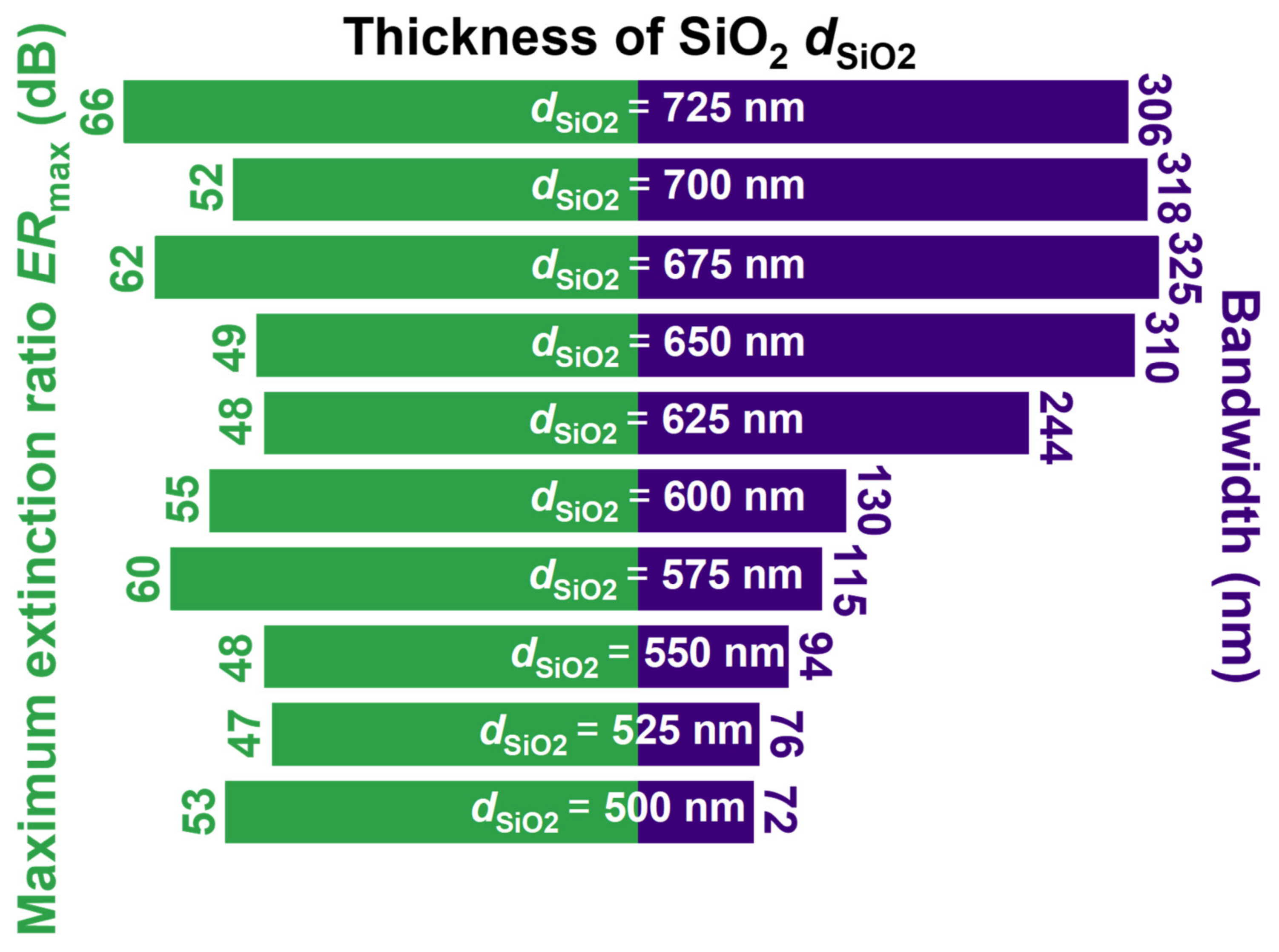
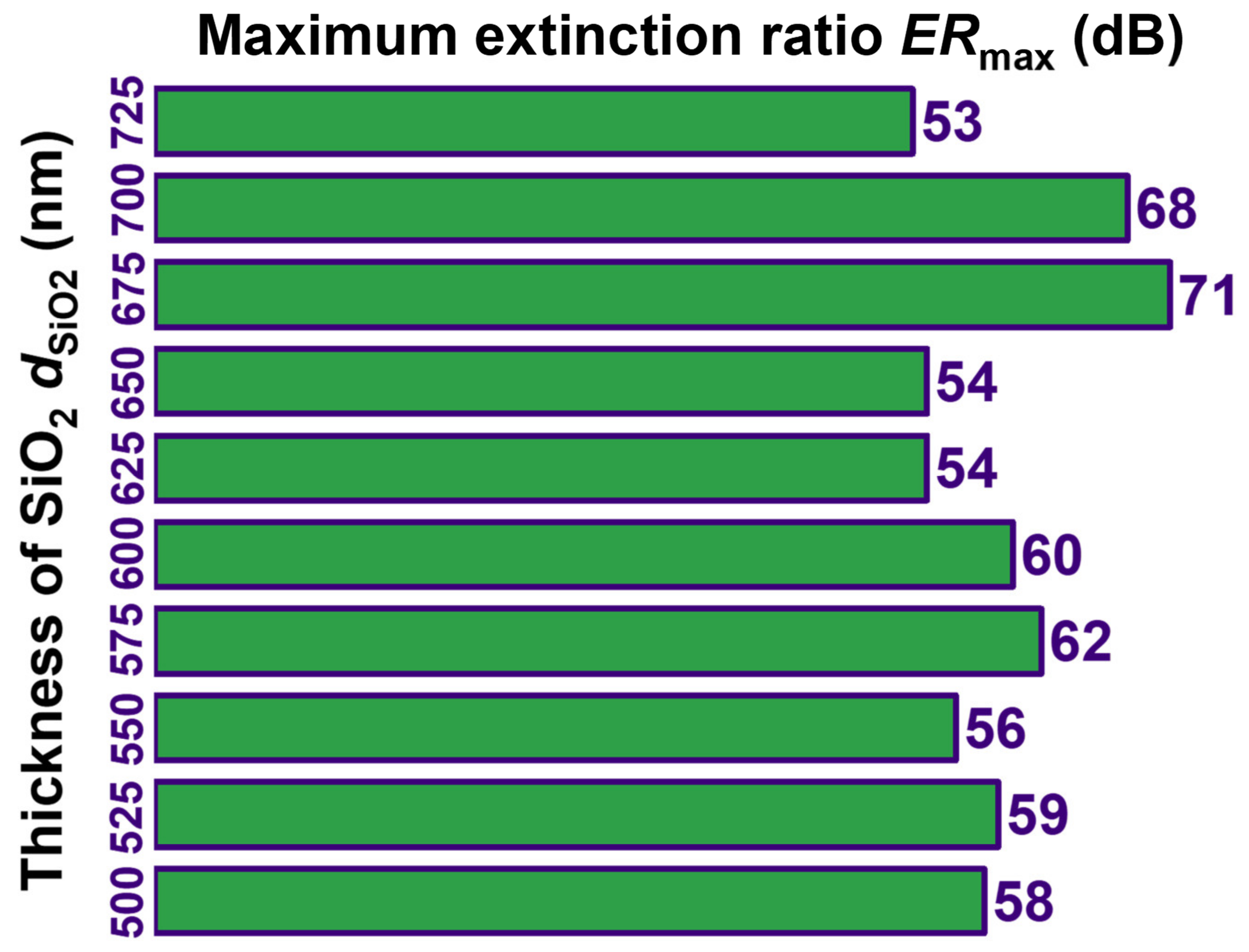
Appendix C. Optimization of the Thickness of SnSe and SiO2
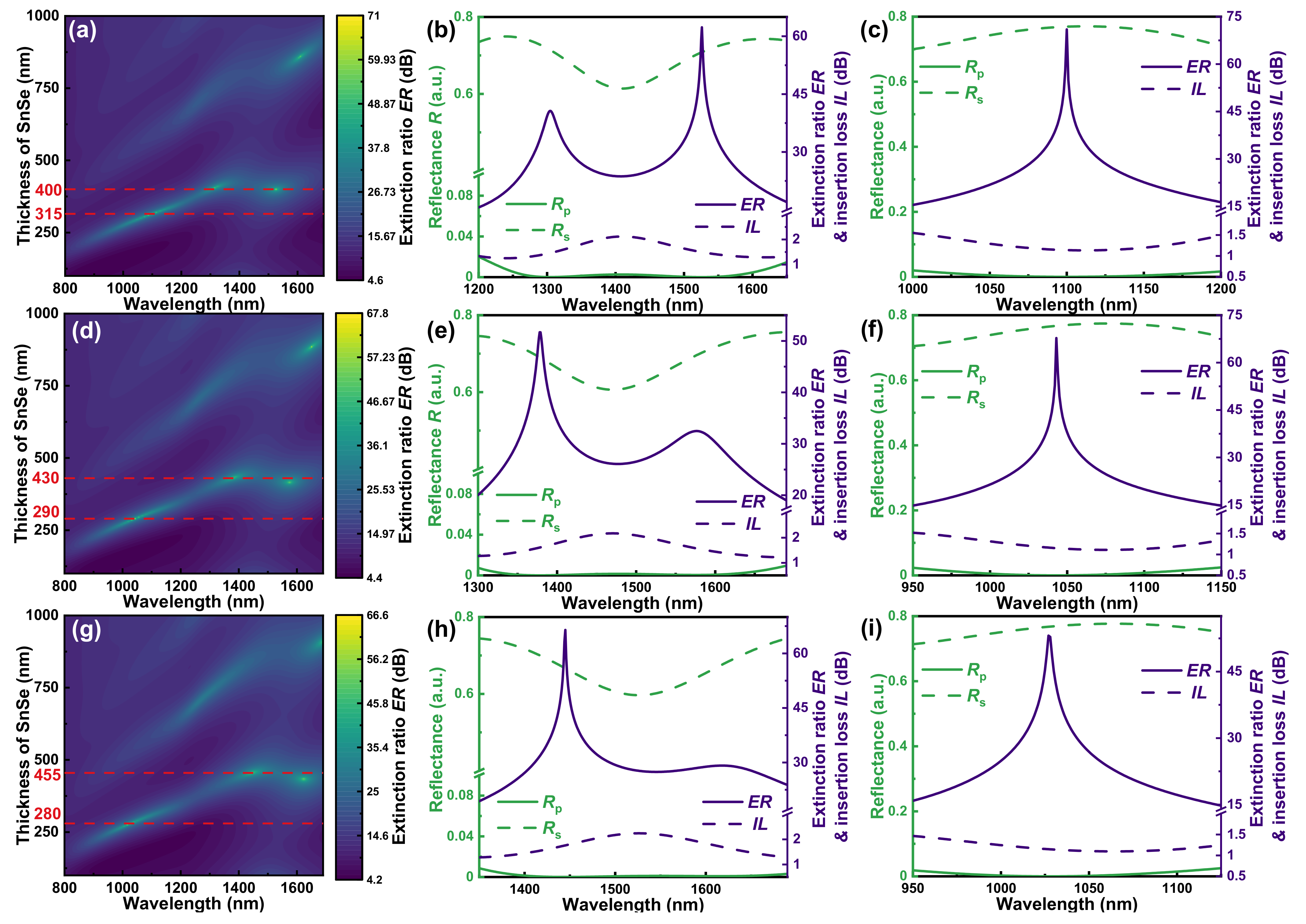
| Thickness of SiO2 [nm] | Thickness of SnSe [nm] | Wavelength Region 1 [nm] | Bandwidth [nm] | Maximum Extinction Ratio ERmax [dB] | Average Insertion Loss ILave [dB] |
|---|---|---|---|---|---|
| 675 | 400 | 1262−1586 | 324 | 62 | 1.7 |
| 700 | 430 | 1325−1642 | 317 | 52 | 1.7 |
| 725 | 455 | 1383−1688 | 305 | 66 | 1.8 |
| Thickness of SiO2 [nm] | Thickness of SnSe [nm] | Wavelength 1 [nm] | Maximum Extinction Ratio ERmax [dB] | Insertion Loss IL [dB] |
|---|---|---|---|---|
| 675 | 315 | 1100 | 71 | 1.1 |
| 700 | 290 | 1043 | 68 | 1.2 |
| 725 | 280 | 1027 | 53 | 1.1 |
Appendix D. Distribution of Horizontal Component of p Light’s Electric Field Intensity Ix
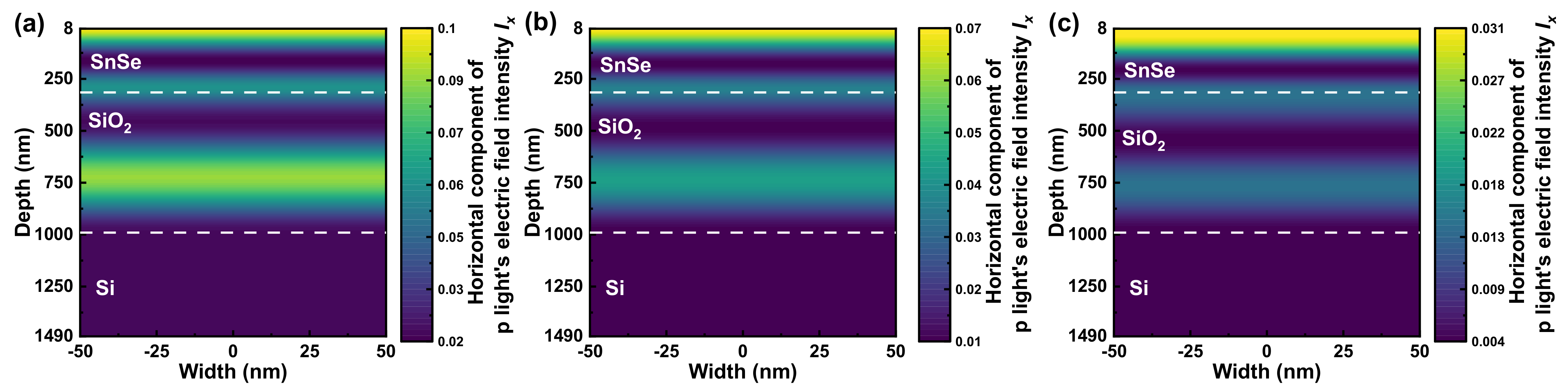
References
- Zhao, L.-D.; Lo, S.-H.; Zhang, Y.; Sun, H.; Tan, G.; Uher, C.; Wolverton, C.; Dravid, V.P.; Kanatzidis, M.G. Ultralow thermal conductivity and high thermoelectric figure of merit in SnSe crystals. Nature 2014, 508, 373–377. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.-G.; Shi, X.; Zhao, L.-D.; Zou, J. High-performance SnSe thermoelectric materials: Progress and future challenge. Prog. Mater. Sci. 2018, 97, 283–346. [Google Scholar] [CrossRef]
- Yan, Q.; Kanatzidis, M.G. High-performance thermoelectrics and challenges for practical devices. Nat. Mater. 2022, 21, 503–513. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Wang, W.; Yang, J.; Li, S. Recent Advances of Layered Thermoelectric Materials. Adv. Sustain. Syst. 2018, 2, 1800046. [Google Scholar] [CrossRef]
- Pejjai, B.; Minnam Reddy, V.R.; Gedi, S.; Park, C. Status review on earth-abundant and environmentally green Sn-X (X = Se, S) nanoparticle synthesis by solution methods for photovoltaic applications. Int. J. Hydrog. Energy 2017, 42, 2790–2831. [Google Scholar] [CrossRef]
- Minnam Reddy, V.R.; Gedi, S.; Pejjai, B.; Park, C. Perspectives on SnSe-based thin film solar cells: A comprehensive review. J. Mater. Sci. Mater. Electron. 2016, 27, 5491–5508. [Google Scholar] [CrossRef]
- Yang, S.; Liu, Y.; Wu, M.; Zhao, L.-D.; Lin, Z.; Cheng, H.-c.; Wang, Y.; Jiang, C.; Wei, S.-H.; Huang, L.; et al. Highly-anisotropic optical and electrical properties in layered SnSe. Nano Res. 2018, 11, 554–564. [Google Scholar] [CrossRef]
- Yu, Y.; Xiong, T.; Guo, Z.; Hou, S.; Yang, J.; Liu, Y.-Y.; Gu, H.; Wei, Z. Wide-spectrum polarization-sensitive and fast-response photodetector based on 2D group IV-VI semiconductor tin selenide. Fundam. Res. 2022, 2, 985–992. [Google Scholar] [CrossRef]
- Mao, Y.; Xu, C.; Yuan, J.; Zhao, H. A two-dimensional GeSe/SnSe heterostructure for high performance thin-film solar cells. J. Mater. Chem. A 2019, 7, 11265–11271. [Google Scholar] [CrossRef]
- Shi, W.; Gao, M.; Wei, J.; Gao, J.; Fan, C.; Ashalley, E.; Li, H.; Wang, Z. Tin Selenide (SnSe): Growth, Properties, and Applications. Adv. Sci. 2018, 5, 1700602. [Google Scholar] [CrossRef]
- Yuan, H.; Liu, X.; Afshinmanesh, F.; Li, W.; Xu, G.; Sun, J.; Lian, B.; Curto, A.G.; Ye, G.; Hikita, Y.; et al. Polarization-sensitive broadband photodetector using a black phosphorus vertical p–n junction. Nat. Nanotechnol. 2015, 10, 707–713. [Google Scholar] [CrossRef]
- Car, R.; Ciucci, G.; Quartapelle, L. Electronic band structure of SnSe. Phys. Status Solidi B 1978, 86, 471–478. [Google Scholar] [CrossRef]
- Brown, A.; Rundqvist, S. Refinement of the crystal structure of black phosphorus. Acta Crystallogr. 1965, 19, 684–685. [Google Scholar] [CrossRef]
- Niu, S.; Joe, G.; Zhao, H.; Zhou, Y.; Orvis, T.; Huyan, H.; Salman, J.; Mahalingam, K.; Urwin, B.; Wu, J.; et al. Giant optical anisotropy in a quasi-one-dimensional crystal. Nat. Photonics 2018, 12, 392–396. [Google Scholar] [CrossRef]
- Tudi, A.; Han, S.; Yang, Z.; Pan, S. Potential optical functional crystals with large birefringence: Recent advances and future prospects. Coord. Chem. Rev. 2022, 459, 214380. [Google Scholar] [CrossRef]
- Qiao, J.; Kong, X.; Hu, Z.-X.; Yang, F.; Ji, W. High-mobility transport anisotropy and linear dichroism in few-layer black phosphorus. Nat. Commun. 2014, 5, 4475. [Google Scholar] [CrossRef]
- Zhang, H.; Ni, Z.; Stevens, C.E.; Bai, A.; Peiris, F.; Hendrickson, J.R.; Wu, L.; Jariwala, D. Cavity-enhanced linear dichroism in a van der Waals antiferromagnet. Nat. Photonics 2022, 16, 311–317. [Google Scholar] [CrossRef]
- Ma, J.; Ye, X.; Jin, B. Structure and application of polarizer film for thin-film-transistor liquid crystal displays. Displays 2011, 32, 49–57. [Google Scholar] [CrossRef]
- Wang, Q.-H.; Ji, C.-C.; Li, L.; Deng, H. Dual-view integral imaging 3D display by using orthogonal polarizer array and polarization switcher. Opt. Express 2016, 24, 9–16. [Google Scholar] [CrossRef]
- Xu, H.; Dai, D.; Shi, Y. Silicon integrated nanophotonic devices for on-chip multi-mode interconnects. Appl. Sci. 2020, 10, 6365. [Google Scholar] [CrossRef]
- Dai, D.; Bauters, J.; Bowers, J.E. Passive technologies for future large-scale photonic integrated circuits on silicon: Polarization handling, light non-reciprocity and loss reduction. Light Sci. Appl. 2012, 1, e1. [Google Scholar] [CrossRef]
- Fujiwara, H. Spectroscopic Ellipsometry: Principles and Applications; John Wiley & Sons: Chichester, UK, 2007. [Google Scholar]
- Zhang, P.; Tan, Y.; Liu, W.; Chen, W. Methods for optical phase retardation measurement: A review. Sci. China Technol. Sci. 2013, 56, 1155–1164. [Google Scholar] [CrossRef]
- Kaiho, T. Industrial applications of organic polyiodides. Arkivoc 2021, 2021, 66–78. [Google Scholar] [CrossRef]
- Xuan, Z.; Li, J.; Liu, Q.; Yi, F.; Wang, S.; Lu, W. Artificial Structural Colors and Applications. Innovation 2021, 2, 100081. [Google Scholar] [CrossRef] [PubMed]
- Bao, Q.; Zhang, H.; Wang, B.; Ni, Z.; Lim, C.H.Y.X.; Wang, Y.; Tang, D.Y.; Loh, K.P. Broadband graphene polarizer. Nat. Photonics 2011, 5, 411–415. [Google Scholar] [CrossRef]
- Heidari, M.; Faramarzi, V.; Sharifi, Z.; Hashemi, M.; Bahadori-Haghighi, S.; Janjan, B.; Abbott, D. A high-performance TE modulator/TM-pass polarizer using selective mode shaping in a VO2-based side-polished fiber. Nanophotonics 2021, 10, 3451–3463. [Google Scholar] [CrossRef]
- Li, X.; Lin, Z.; He, S. Ultrahigh extinction ratio and ultra-low insertion loss silicon TE polarizer covering 1260–1675 nm bandwidth. Opt. Lett. 2022, 47, 2065–2068. [Google Scholar] [CrossRef]
- Han, X.; Chen, L.; Jiang, Y.; Frigg, A.; Xiao, H.; Nguyen, T.G.; Boes, A.; Yang, J.; Ren, G.; Su, Y.; et al. Integrated Subwavelength Gratings on a Lithium Niobate on Insulator Platform for Mode and Polarization Manipulation. Laser Photonics Rev. 2022, 16, 2200130. [Google Scholar] [CrossRef]
- Shen, W.; Hu, C.; Huo, S.; Sun, Z.; Fan, S.; Liu, J.; Hu, X. Wavelength tunable polarizer based on layered black phosphorus on Si/SiO2 substrate. Opt. Lett. 2018, 43, 1255–1258. [Google Scholar] [CrossRef]
- Shen, W.; Hu, C.; Huo, S.; Sun, Z.; Fan, G.; Liu, J.; Sun, L.; Hu, X.J.N. Black phosphorus nano-polarizer with high extinction ratio in visible and near-infrared regime. Nanomaterials 2019, 9, 168. [Google Scholar] [CrossRef]
- Mccall, M.W.; Hodgkinson, I.J.; Wu, Q. Birefringent Thin Films And Polarizing Elements, 2nd ed.; World Scientific Publishing Company: Singapore, 2014. [Google Scholar]
- Guo, F.; Chen, L.; Gao, Z.; Sun, Y.; Zhai, Z.; Tao, X. Novel Polarized Crystal BaTeW2O9: Crystal Growth, Characterization, and Wide-Band Polarized Prism. Cryst. Growth Des. 2022, 22, 2587–2593. [Google Scholar] [CrossRef]
- Li, Y.; Huang, S.; Zhou, P.; Liu, S.; Lu, J.; Li, X.; Su, Y. Polymer-Stabilized Blue Phase Liquid Crystals for Photonic Applications. Adv. Mater. Technol. 2016, 1, 1600102. [Google Scholar] [CrossRef]
- Won, Y.; Shin, H.S.; Jo, M.; Lim, Y.J.; Manda, R.; Lee, S.H. An electrically switchable dye-doped liquid crystal polarizer for organic light emitting-diode displays. J. Mol. Liq. 2021, 333, 115922. [Google Scholar] [CrossRef]
- Kats, M.A.; Capasso, F. Optical absorbers based on strong interference in ultra-thin films. Laser Photonics Rev. 2016, 10, 735–749. [Google Scholar] [CrossRef]
- Kim, J.-H.; Jung, S.-Y.; Jeong, I.-K. Optical Modeling for Polarization-dependent Optical Power Dissipation of Thin-film Organic Solar Cells at Oblique Incidence. J. Opt. Soc. Korea 2012, 16, 6–12. [Google Scholar] [CrossRef]
- Guo, Z.; Gu, H.; Fang, M.; Song, B.; Wang, W.; Chen, X.; Zhang, C.; Jiang, H.; Wang, L.; Liu, S. Complete Dielectric Tensor and Giant Optical Anisotropy in Quasi-One-Dimensional ZrTe5. ACS Mater. Lett. 2021, 3, 525–534. [Google Scholar] [CrossRef]
- Dong, D.; Liu, Y.; Fu, Y. Critical Coupling and Perfect Absorption Using α-MoO3 Multilayers in the Mid-Infrared. Ann. Phys. 2021, 533, 2000512. [Google Scholar] [CrossRef]
- Kane, Y. Numerical solution of initial boundary value problems involving maxwell’s equations in isotropic media. IEEE Trans. Antennas Propag. 1966, 14, 302–307. [Google Scholar] [CrossRef]
- Sullivan, D.M. Electromagnetic Simulation Using the FDTD Method; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Song, B.; Gu, H.; Zhu, S.; Jiang, H.; Chen, X.; Zhang, C.; Liu, S. Broadband optical properties of graphene and HOPG investigated by spectroscopic Mueller matrix ellipsometry. Appl. Surf. Sci. 2018, 439, 1079–1087. [Google Scholar] [CrossRef]
- Gu, H.; Song, B.; Fang, M.; Hong, Y.; Chen, X.; Jiang, H.; Ren, W.; Liu, S. Layer-dependent dielectric and optical properties of centimeter-scale 2D WSe2: Evolution from a single layer to few layers. Nanoscale 2019, 11, 22762–22771. [Google Scholar] [CrossRef]
- Lee, S.-Y.; Yee, K.-J. Black phosphorus phase retarder based on anisotropic refractive index dispersion. 2D Mater. 2021, 9, 015020. [Google Scholar] [CrossRef]
- Yang, H.; Jussila, H.; Autere, A.; Komsa, H.-P.; Ye, G.; Chen, X.; Hasan, T.; Sun, Z. Optical Waveplates Based on Birefringence of Anisotropic Two-Dimensional Layered Materials. ACS Photonics 2017, 4, 3023–3030. [Google Scholar] [CrossRef]
- Andres-Penares, D.; Brotons-Gisbert, M.; Bonato, C.; Sánchez-Royo, J.F.; Gerardot, B.D. Optical and dielectric properties of MoO3 nanosheets for van der Waals heterostructures. Appl. Phys. Lett. 2021, 119, 223104. [Google Scholar] [CrossRef]
- Manifacier, J.C.; Gasiot, J.; Fillard, J.P. A simple method for the determination of the optical constants n, k and the thickness of a weakly absorbing thin film. J. Phys. E Sci. Instrum. 1976, 9, 1002–1004. [Google Scholar] [CrossRef]
- Dong, J.; Lu, R. Characterization of weakly absorbing thin films by multiple linear regression analysis of absolute unwrapped phase in angle-resolved spectral reflectometry. Opt. Express 2018, 26, 12291–12305. [Google Scholar] [CrossRef]
- Wang, D.; Li, M.; Lu, R.; Zhang, C. Multilayer Thin Film Based Structural Color Filters: Principle, Fabrication and Applications. J. Synth. Cryst. 2021, 50, 1287–1306. [Google Scholar]
- Yang, Z.; Ji, C.; Liu, D.; Guo, L.J. Enhancing the Purity of Reflective Structural Colors with Ultrathin Bilayer Media as Effective Ideal Absorbers. Adv. Opt. Mater. 2019, 7, 1900739. [Google Scholar] [CrossRef]
- Akhavan, A.; Abdolhosseini, S.; Ghafoorifard, H.; Habibiyan, H. Narrow Band Total Absorber at Near-Infrared Wavelengths Using Monolayer Graphene and Sub-Wavelength Grating Based on Critical Coupling. J. Light. Technol. 2018, 36, 5593–5599. [Google Scholar] [CrossRef]
- Dong, D.; Liu, Y.; Fei, Y.; Fan, Y.; Li, J.; Feng, Y.; Fu, Y. Designing a nearly perfect infrared absorber in monolayer black phosphorus. Appl. Opt. 2019, 58, 3862–3869. [Google Scholar] [CrossRef]
- Yang, M.; Xiong, L.; Li, Q.; Cheng, S.; Ye, Y.; Liu, Z.; Hu, W.; Guo, D. van der Waals forces enhanced light–graphene interaction in optical microfiber polarizer. AIP Adv. 2022, 12, 045027. [Google Scholar] [CrossRef]
- Dai, S.; Yu, W.; Zhao, Y.; Li, M.; Li, J.; Zhang, Z.; Liu, J. Broadband and Compact TE-Pass Polarizer Based on Hybrid Plasmonic Grating on LNOI Platform. IEEE Photonics J. 2021, 13, 1–9. [Google Scholar] [CrossRef]
- Jin, W.; Chiang, K.S. Leaky-mode long-period grating on a lithium-niobate-on-insulator waveguide. Optica 2021, 8, 1624–1631. [Google Scholar] [CrossRef]
- Zhao, B.; Sakurai, A.; Zhang, Z.M. Polarization Dependence of the Reflectance and Transmittance of Anisotropic Metamaterials. J. Thermophys. Heat Transf. 2015, 30, 240–246. [Google Scholar] [CrossRef]
- Petrik, P.; Fried, M.; Lohner, T.; Berger, R.; Bíró, L.P.; Schneider, C.; Gyulai, J.; Ryssel, H. Comparative study of polysilicon-on-oxide using spectroscopic ellipsometry, atomic force microscopy, and transmission electron microscopy. Thin Solid Films 1998, 313, 259–263. [Google Scholar] [CrossRef]
- Xue, F.-N.; Zhao, Z.-H.; Zhang, Y.; Liu, T.; Lu, Y.; Zhang, J.-C. Layer-dependent electronic structure, dynamic stability, and phonon properties of few-layer SnSe. Phys. Rev. B 2022, 106, 104301. [Google Scholar] [CrossRef]
- Kats, M.A.; Blanchard, R.; Genevet, P.; Capasso, F. Nanometre optical coatings based on strong interference effects in highly absorbing media. Nat. Mater. 2013, 12, 20–24. [Google Scholar] [CrossRef]
- Li, Z.; Butun, S.; Aydin, K. Large-Area, Lithography-Free Super Absorbers and Color Filters at Visible Frequencies Using Ultrathin Metallic Films. ACS Photonics 2015, 2, 183–188. [Google Scholar] [CrossRef]

| Polarizers | Extinction Ratio ER [dB] | Insertion Loss IL [dB] | Working Wavelength (Range) [nm] | References |
|---|---|---|---|---|
| Graphene fiber | ~19 ± 2.5 | ~5 | 1530−1630 (100) | [26] |
| Graphene microfiber | 31 | - | 1550 | [53] |
| Subwavelength grating on SOI platform | >35 | <0.6 | 1260−1390 (130) & 1520−1600 (80) | [28] |
| Subwavelength gratings on LNOI platform | >30 | <3.1 | 1550 | [29] |
| Hybrid plasmonic grating on LNOI platform | 20 | <2.3 | 1470−1700 (230) | [54] |
| Long-period grating on LNOI waveguide | 20 | <2 | 1430−1700 (270) | [55] |
| Broadband polarizer based on optically anisotropic SnSe | >23 (Maximum: 62) | <2.1 (Average: 1.7) | 1262−1586 (324) | This work |
| Polarizer dynamically and reversibly modulated by high incident angle | 21 & 71 & 35 | 1.7 & 1.1 & 1.1 | 1184 & 1100 & 955 | This work |
| Incident Angle [°] | ERmax Wavelength [nm] | Ip [a. u.] | Ip/Is | Pabs,p/1020 [W/m3] | Pabs,p/Pabs,s |
|---|---|---|---|---|---|
| 70 | 1184 | 0.45 | 15 | 2.29 | 2.75 |
| 75 | 1100 | 0.32 | 32 | 2.57 | 4.02 |
| 80 | 955 | 0.18 | 36 | 2.83 | 4.22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Z.; Gu, H.; Yu, Y.; Wei, Z.; Liu, S. Broadband and Incident-Angle-Modulation Near-Infrared Polarizers Based on Optically Anisotropic SnSe. Nanomaterials 2023, 13, 134. https://doi.org/10.3390/nano13010134
Guo Z, Gu H, Yu Y, Wei Z, Liu S. Broadband and Incident-Angle-Modulation Near-Infrared Polarizers Based on Optically Anisotropic SnSe. Nanomaterials. 2023; 13(1):134. https://doi.org/10.3390/nano13010134
Chicago/Turabian StyleGuo, Zhengfeng, Honggang Gu, Yali Yu, Zhongming Wei, and Shiyuan Liu. 2023. "Broadband and Incident-Angle-Modulation Near-Infrared Polarizers Based on Optically Anisotropic SnSe" Nanomaterials 13, no. 1: 134. https://doi.org/10.3390/nano13010134
APA StyleGuo, Z., Gu, H., Yu, Y., Wei, Z., & Liu, S. (2023). Broadband and Incident-Angle-Modulation Near-Infrared Polarizers Based on Optically Anisotropic SnSe. Nanomaterials, 13(1), 134. https://doi.org/10.3390/nano13010134






