Electrohydrodynamics Analysis of Dielectric 2D Nanofluids
Abstract
:1. Introduction
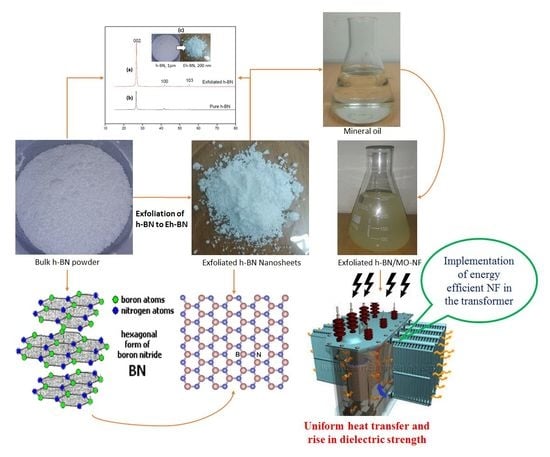
2. Experimental Methods
2.1. Characterization of NPs and MO
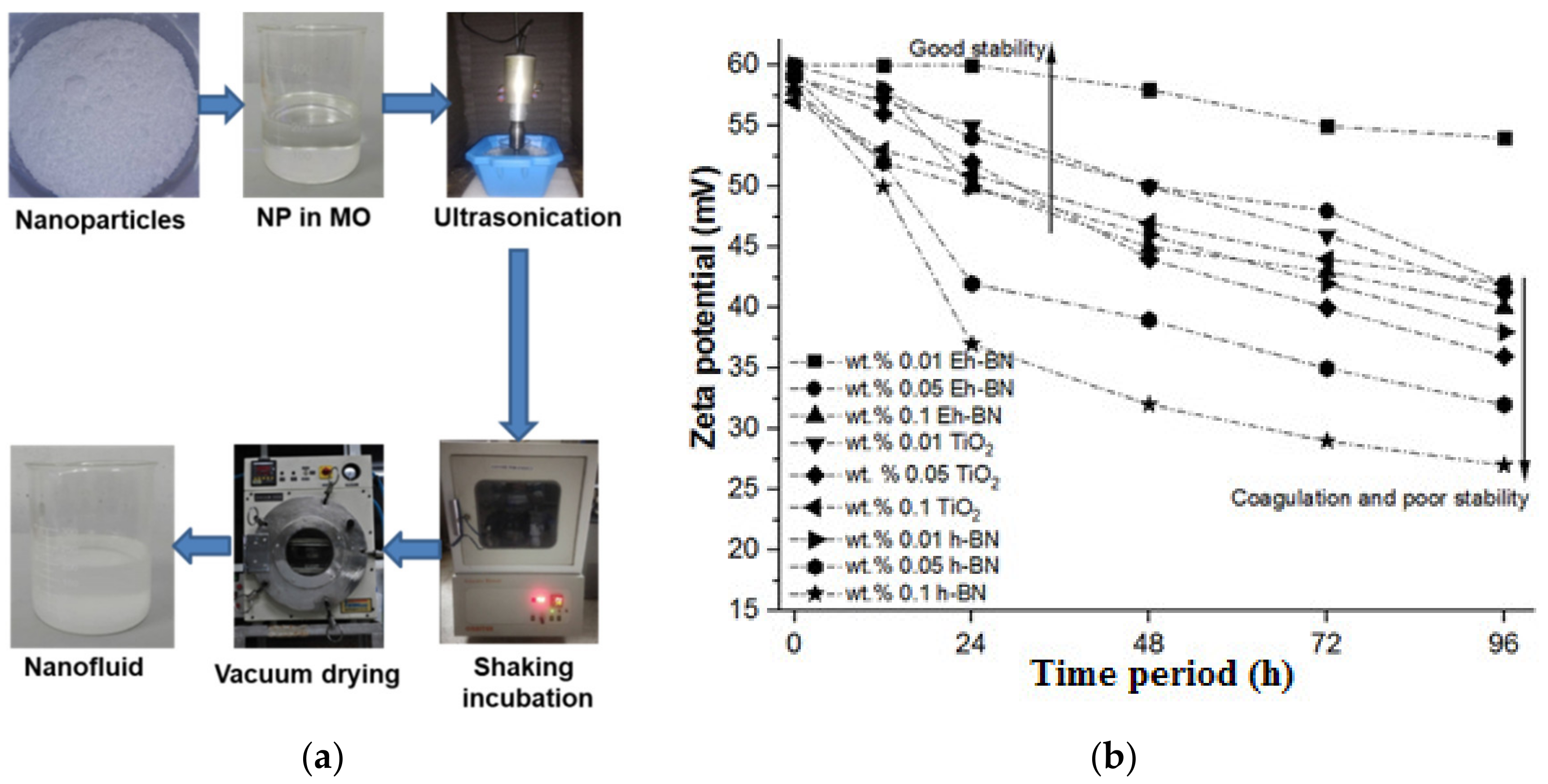
2.2. Preparation of NFs
2.3. Measurement Error of Instrument
3. Results and Discussion
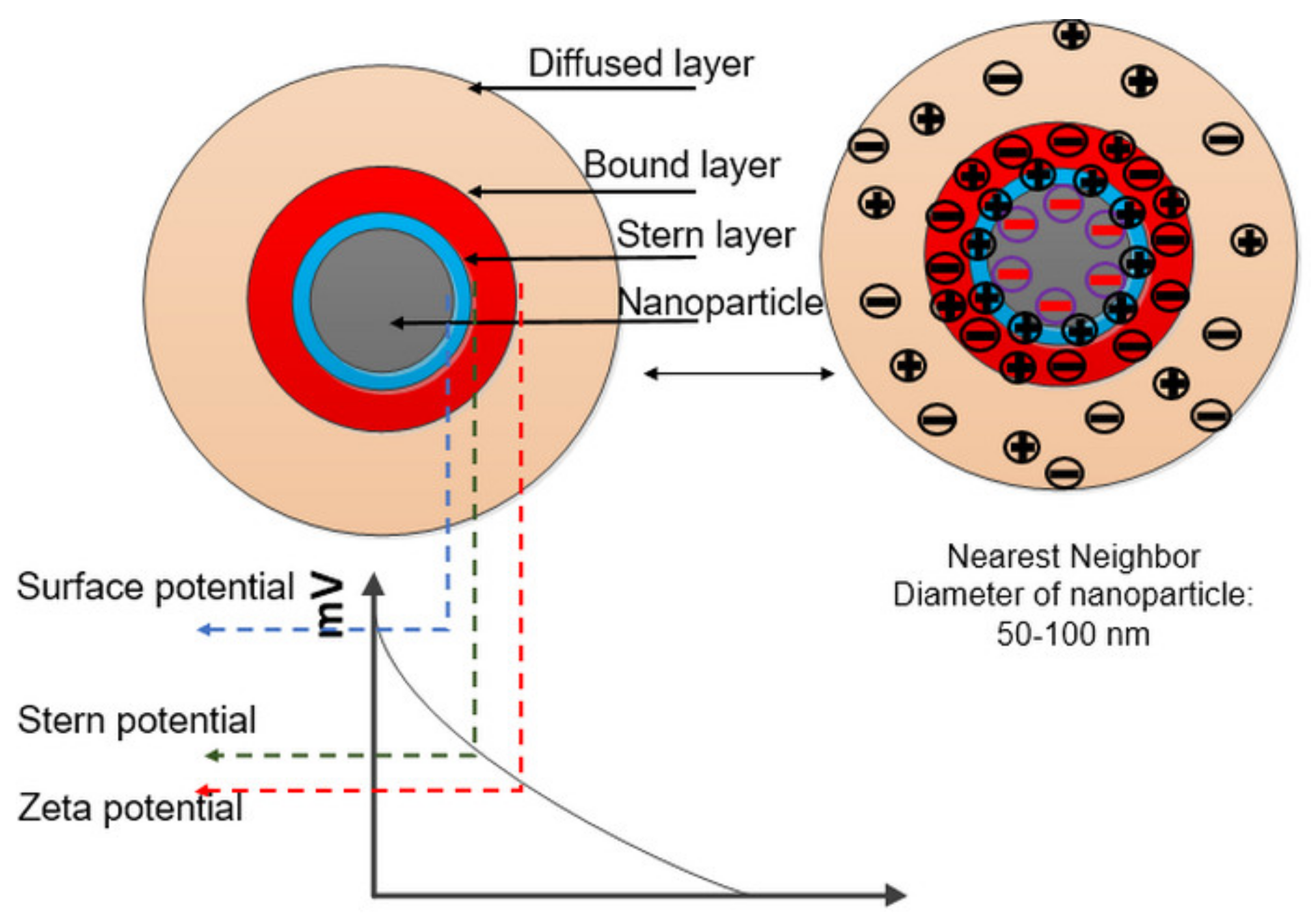
3.1. Stability Analysis by Zeta Potential
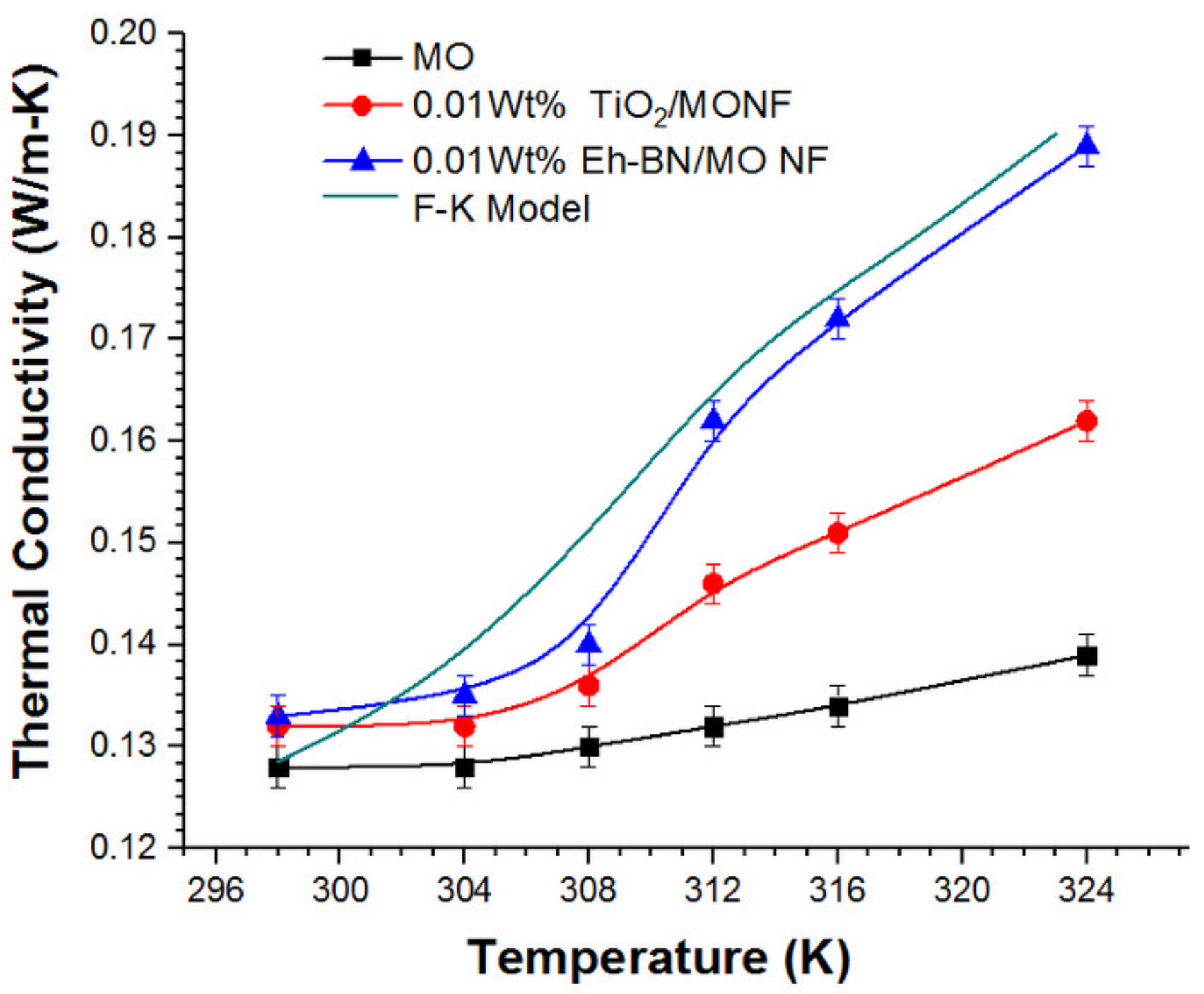
3.2. Thermal Conductivity
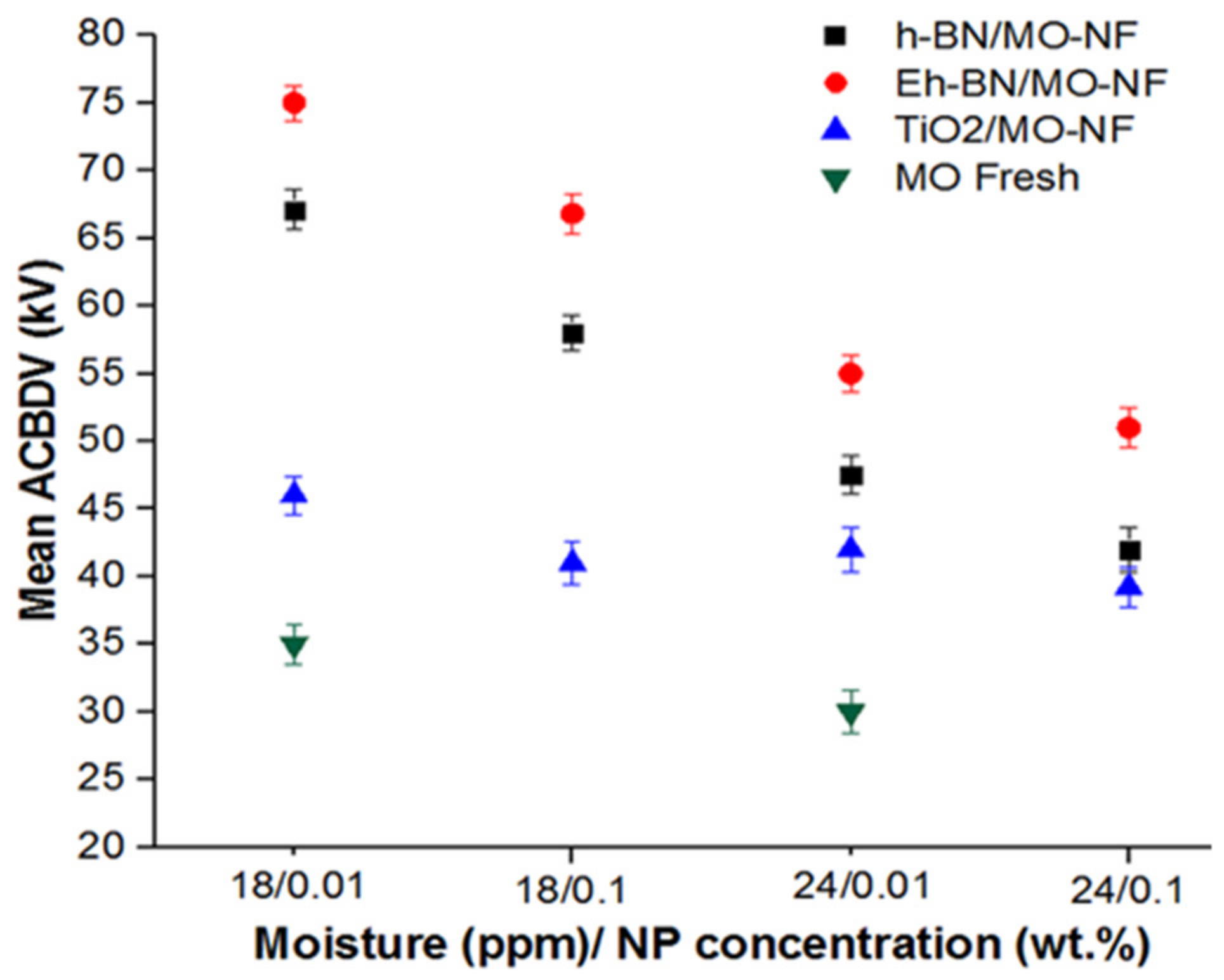
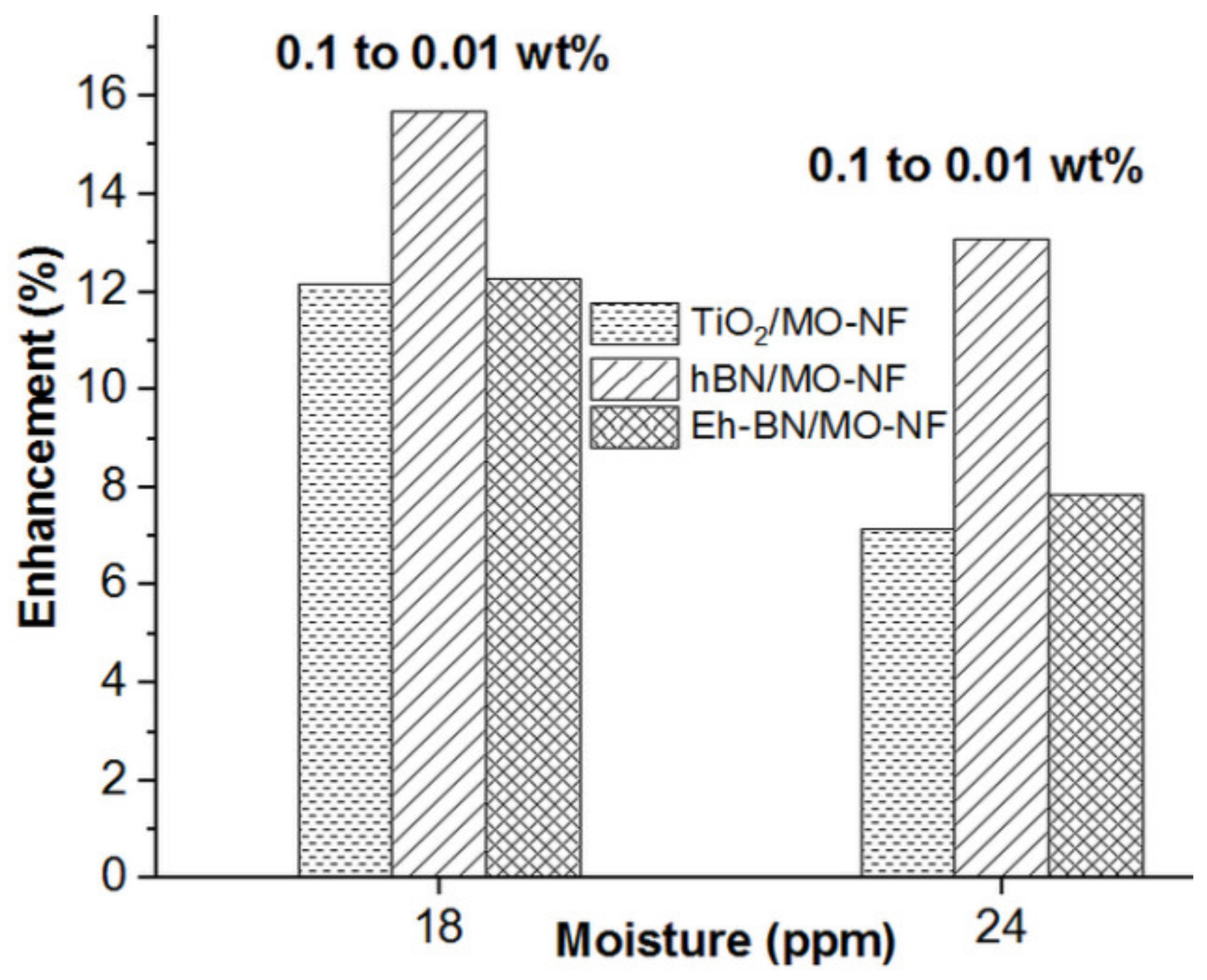
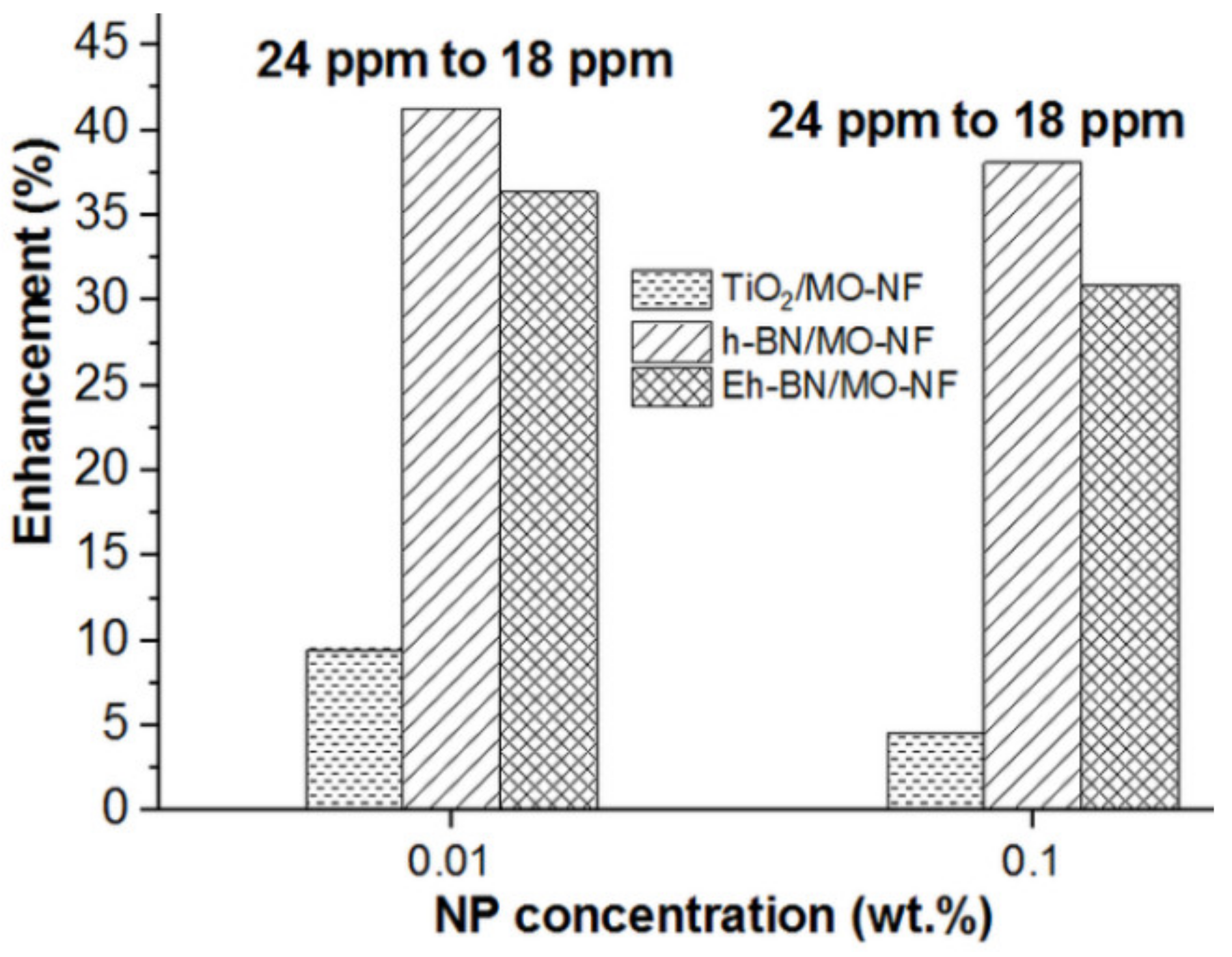
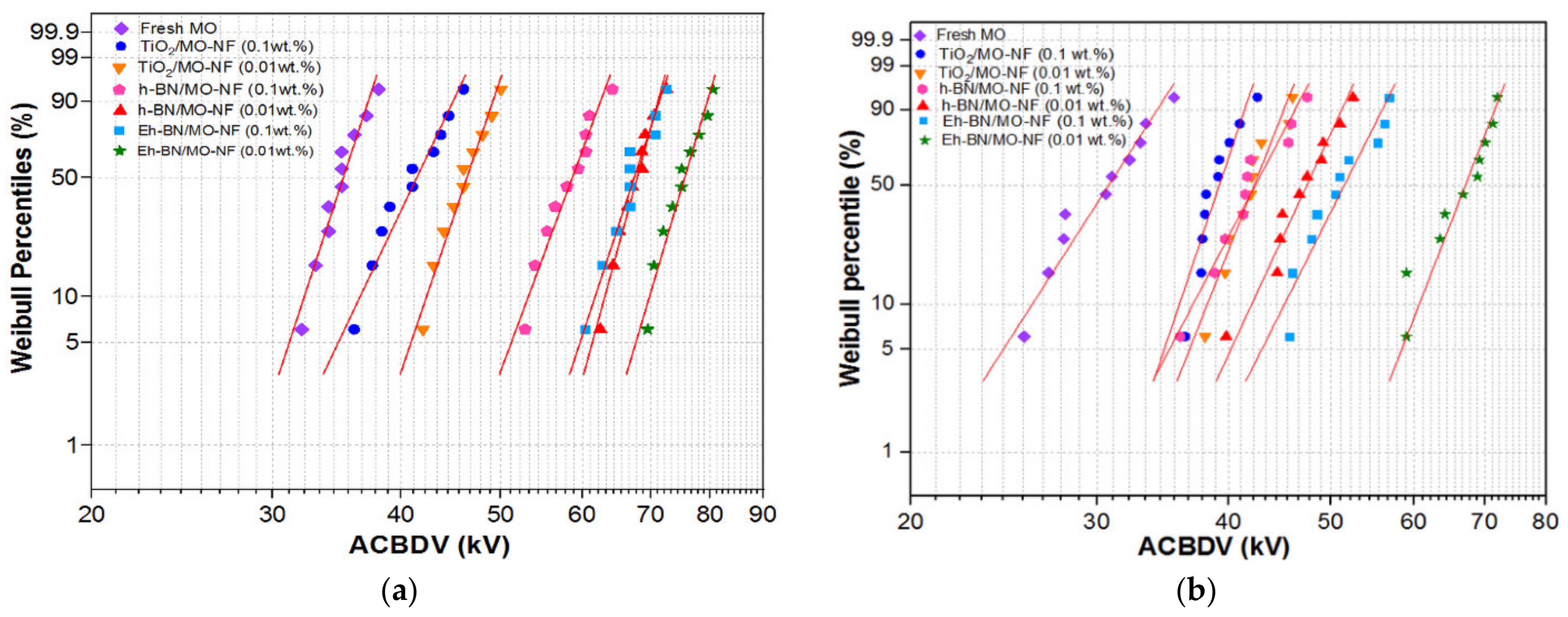
3.3. AC Breakdown Voltage (ACBDV)
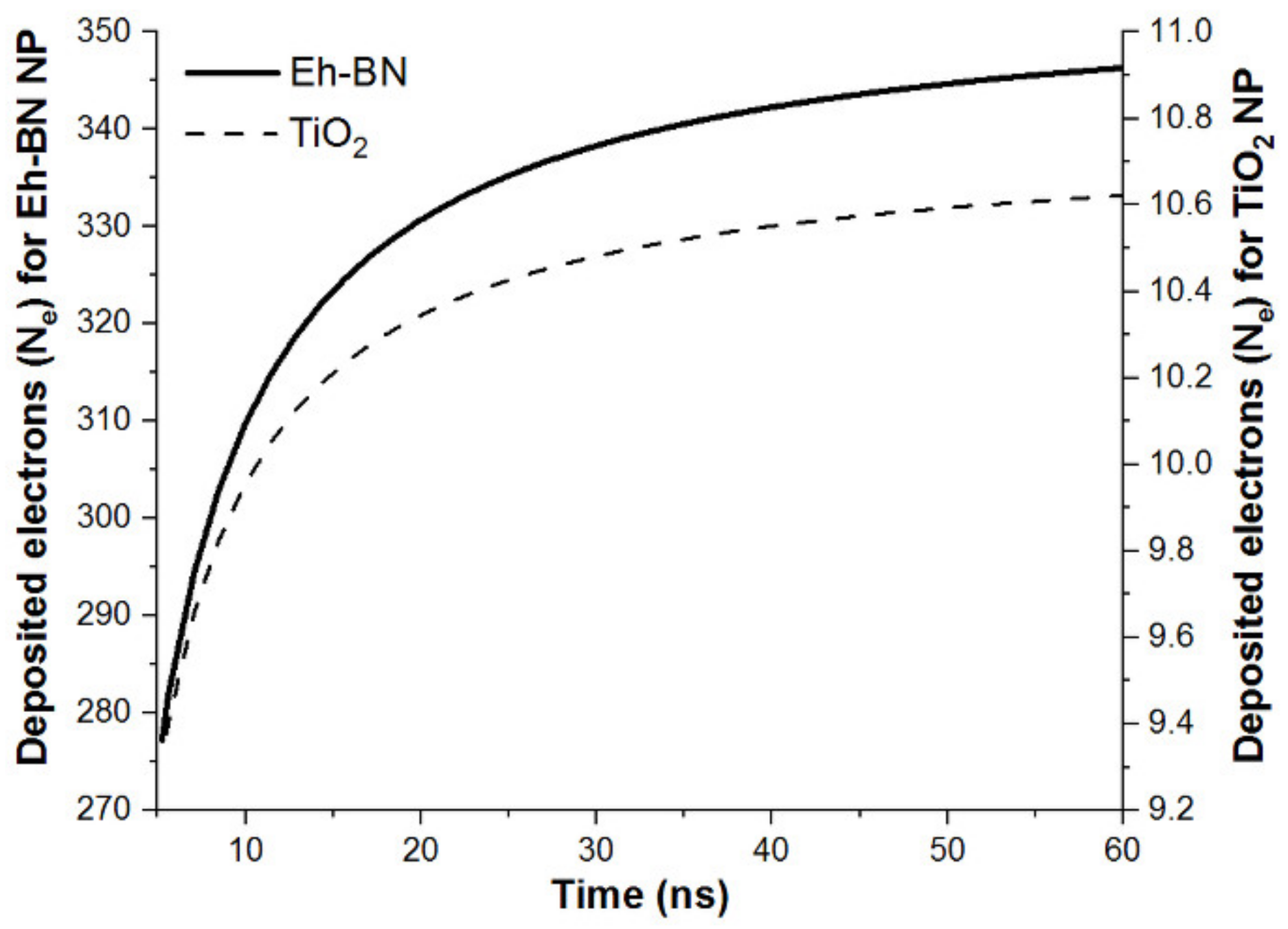
4. Charging Dynamics
5. Conclusions
- The dispersion of 0.01 wt.% of Eh-BN NP is observed to be stable for a longer period.
- The high aspect ratio and greater surface charges in Eh-BN NP are largely responsible for higher thermal conductivity in Eh-BN/MO NF.
- Higher moisture contamination in the MO and NFs reduces the ACBDV. However, Eh-BN NP has a minimal affinity towards moisture and augments the ACBDV compared to MO and other batches of NFs.
- From the charge-dynamics analysis, it is observed that the Eh-BN NP scavenges a higher number of free electrons compared to other NPs, and hence the initiation of the streamer is arrested, which leads to enhancement in the ACBDV for Eh-BN/MO-NF compared to MO and other NFs.
Author Contributions
Funding
Conflicts of Interest
References
- Oommen, T.V. Moisture equilibrium charts for transformer insulation drying practice. IEEE Trans. Power Appar. Syst. 1984, 103, 3062–3067. [Google Scholar] [CrossRef]
- Hwang, J.G.; Zahn, M.; O’Sullivan, F.M.; Pettersson, L.A.A.; Hjortstam, O.; Liu, R. Effects of nanoparticle charging on streamer development in transformer oil-based nanofluids. J. Appl. Phys. 2010, 107, 14310–14317. [Google Scholar] [CrossRef] [Green Version]
- Choi, C.; Yoo, S.H.; Oh, J.M. Preparation and heat transfer properties of nanoparticle-in-transformer oil dispersions as advanced energy efficient coolants. J. Curr. Appl. Phys. 2008, 8, 710–712. [Google Scholar] [CrossRef]
- UmerIlyasa, S.; Pendyalaa, R.; Naraharib, M.; Susin, L. Stability, rheology and thermal analysis of functionalized alumina- thermal oil-based nanofluids for advanced cooling systems. Energy Convers. Manag. 2017, 142, 215–229. [Google Scholar]
- Hussain, M.; Mir, F.A.; Ansari, M.A. Nanofluid transformer oil for cooling and insulating applications: A brief review. Appl. Surf. Sci. Adv. 2022, 8, 100223. [Google Scholar] [CrossRef]
- Rajnak, M.; Wu, Z.; Dolnik, B.; Paulovicova, K.; Tothova, J.; Cimbala, R.; Kurimský, J.; Kopcansky, P.; Sunden, B.; Wadsö, L.; et al. Magnetic Field Effect on Thermal, Dielectric, and Viscous Properties of a Transformer Oil-Based Magnetic Nanofluid. Energies 2019, 12, 4532. [Google Scholar] [CrossRef] [Green Version]
- Baruah, N.; Maharana, M.; Nayak, S.K. Performance Analysis of Vegetable Oil based Nanofluids used in Transformers. IET Sci. Meas. Technol. 2019, 13, 995–1002. [Google Scholar] [CrossRef]
- Duangthongsuk, W.; Wongwises, S. An experimental study on the heat transfer performance and pressure drop of TiO2–water nanofluids flowing under a turbulent flow regime. Int. J. Heat Mass Transf. 2010, 53, 334–344. [Google Scholar] [CrossRef]
- Jin, H.; Andritsch, T.; Tsekmes, I.A.; Kochetov, R.; Morshuis, P.; Smit, J.J. Properties of mineral oil based silica nanofluids. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 1100–1108. [Google Scholar]
- Lewis, T.J. Nanometric dielectrics. IEEE Trans. Dielectr. Electr. Insul. 1994, 1, 812–825. [Google Scholar] [CrossRef]
- Atiya, E.G.; Mansour, D.E.A.; Khattab, R.M.; Azmy, A.M. Dispersion behavior and breakdown strength of transformer oil filled with TiO2 nanoparticles. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 2463–2471. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, Y.; Lu, W.; Peng, N.; Chen, W. The Impact of TiO2 Nanoparticle Concentration Levels on Impulse Breakdown Performance of Mineral Oil-Based Nanofluids. Nanomaterials 2019, 9, 627. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Maharana, M.; Baruah, N.; Nayak, S.K.; Sahoo, N. Effect of oxidative ageing on the thermophysical and electrical properties of the nanofluid with statistical analysis of AC breakdown voltage. IET Sci. Meas. Technol. 2018, 12, 1074–1081. [Google Scholar] [CrossRef]
- Thabet, A.; Allam, M.; Shaaban, S.A. Investigation on enhancing breakdown voltages of transformer oil nanofluids using multi-nanoparticles technique. IET Gener. Transm. Distrib. 2018, 12, 1171–1176. [Google Scholar] [CrossRef]
- Šárpataky, M.; Kurimský, J.; Rajňák, M. Dielectric Fluids for Power Transformers with Special Emphasis on Biodegradable Nanofluids. Nanomaterials 2021, 11, 2885. [Google Scholar] [CrossRef]
- Maharana, M.; Bordeori, M.M.; Nayak, S.K.; Sahoo, N. Nanofluid-based transformer oil: Effect of ageing on thermal, electrical and physicochemical properties. IET Sci. Meas. Technol. 2018, 12, 878–885. [Google Scholar] [CrossRef]
- Choi, S.U.S. Nanofluids: From vision to reality through research. J. Heat Transf. 2009, 131, 033106. [Google Scholar] [CrossRef]
- Zhi, C.; Xu, Y.; Bando, Y.; Golberg, D. Highly thermoconductive fluid with boron nitride nanofillers. ACS Nano 2011, 5, 6571–6577. [Google Scholar] [CrossRef]
- Taha-Tijerina, J.; Narayanan, T.N.; Gao, G.; Rohde, M.; Tsentalovich, D.A.; Pasquali, M.; Ajayan, P.M. Electrically insulating thermal nano-oils using 2d fillers. ACS Nano 2012, 6, 1214–1220. [Google Scholar] [CrossRef]
- Coleman, J.N.; Lotya, M.; O’Neill, A.; Bergin, S.D.; King, P.J.; Khan, U.; Young, K.; Gaucher, A.; De, S.; Smith, R.J.; et al. Two-dimensional nanosheets produced by liquid exfoliation of layered materials. Science 2011, 331, 568–571. [Google Scholar] [CrossRef] [Green Version]
- Pakdel, A.; Zhi, C.; Bando, Y.; Nakayama, T.; Golberg, D. Boron nitride nanosheet coatings with controllable water repellency. ACS Nano 2011, 56, 507–6515. [Google Scholar] [CrossRef]
- Pate, K.; Safier, P. Chemical metrology methods for CMP quality. In Advances in Chemical Mechanical Planarization (CMP); Woodhead Publishing: Sawston, UK, 2022; pp. 355–383. [Google Scholar]
- Kleinstreuer, C.; Feng, Y. Experimental and theoretical studies of nanofluid thermal conductivity enhancement: A review. Nanoscale Res. Lett. 2011, 6, 229. [Google Scholar] [CrossRef] [Green Version]
- Dong, M.; Dai, J.; Li, Y.; Xie, J.; Ren, M.; Dang, Z. Insight into the dielectric response of transformer oil-based nanofluids. AIP Adv. 2017, 7, 025307. [Google Scholar] [CrossRef] [Green Version]
- Katiyar, A.; Dhar, P.; Nandi, T.; Maganti, L.S.; Das, S.K. Enhanced breakdown performance of Anatase and Rutile Titania based Nano-oils. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 3494–3503. [Google Scholar] [CrossRef]
- Rarani, E.M.; Etesami, N.; Esfahany, M.N. Influence of the uniform electric field on viscosity of magnetic nanofluid (Fe3O4-EG). J. Appl. Phys. 2012, 112, 094903. [Google Scholar] [CrossRef]
- Delgado, A.V.; González-Caballero, F.; Hunter, R.J.; Koopal, L.K.; Lyklema, J. Measurement and interpretation of electrokinetic phenomena. Pure Appl. Chem. 2005, 77, 1753–1805. [Google Scholar] [CrossRef] [Green Version]
- Dhar, P.; Katiyar, A.; Maganti, L.S.; Pattamatta, A.; Das, S.K. Superior dielectric breakdown strength of graphene and carbon nanotube infused nano-oils. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 943–956. [Google Scholar] [CrossRef] [Green Version]

| Characteristic | Specification |
|---|---|
| Formula | CnH2n+2 |
| Density (gm/cc) | 0.828 |
| Kinematic viscosity at (cSt) | 0.0123 |
| Interfacial tension (IFT)at (N/m) | 0.047 |
| Flash point in (°C) | 146 |
| Pour point in (°C) | −18 |
| Tan delta at 90 °C (Max). | 0.0085 |
| Water content (ppm) | 25 |
| AC breakdown voltage (kV) | 30 |
| Thermal conductivity (W/m-K) | 0.128 |
| Characteristic | Specification | |
|---|---|---|
| TiO2 | Eh-BN | |
| Purity (%) | 99.5 | 98 |
| Size (nm) | 21 | 0.1 |
| Density (g/cm3) | 3.9 | 2.29 |
| Dielectric constant | 31 | 3–4 |
| Thermal conductivity (W/m-K) | 11 | 300 |
| Electrical resistivity (Ω-cm) | 1014 | 1015 |
| Thermal expansion coefficient (°C) | 11.5 × 10−6 | 4 × 10−6 |
| Source of Uncertainty | % Error (±) |
|---|---|
| Instrument accuracy (U1) | 0.916 |
| Gap gauge (U2) | 0.44 |
| Electrode (U3) | 0.168 |
| Combined uncertainty (Uc) | 1.03 |
| Source of Uncertainty | % Error (±) |
|---|---|
| Instrument accuracy (U1) | 0.5 |
| Electrical probe (U2) | 0.2 |
| Measurement (U3) | 0.1 |
| Combined uncertainty (Uc) | 0.547 |
| Oil Samples | |||||||
|---|---|---|---|---|---|---|---|
| 18 ppm | |||||||
| MO | TiO2 0.01 | TiO2 0.1 | h-BN 0.01 | h-BN 0.1 | Eh-BN 0.01 | Eh-BN 0.1 | |
| α | 35.7 | 47.1 | 42.4 | 68.8 | 59.8 | 76.6 | 68.5 |
| β | 21.5 | 20.8 | 14.8 | 25.8 | 19 | 23.38 | 21.5 |
| 24 ppm | |||||||
| α | 31.7 | 43.1 | 39.8 | 48.5 | 43.5 | 68.4 | 52.8 |
| β | 11.3 | 18.4 | 21.6 | 15.6 | 13.8 | 18.7 | 14.4 |
| Moisture Level | Oil Samples | 63.2% | 50% | ||
|---|---|---|---|---|---|
| KV | % Rise | kV | % Rise | ||
| 18 | MO | 35 | 118.5 | 35 | 114.2 |
| TiO2-0.01 | 47 | 62.7 | 46 | 63 | |
| TiO2-0.1 | 43 | 77.9 | 41 | 82.9 | |
| h-BN-0.01 | 68.6 | 11.5 | 68 | 10.3 | |
| h-BN-0.1 | 60.5 | 16.4 | 58.5 | 28.2 | |
| Eh-BN-0.01 | 76.5 | 0 | 75 | 0 | |
| Eh-BN-0.1 | 66.8 | 14.5 | 66.8 | 12.2 | |
| 24 | MO | 32.2 | 114.9 | 30.8 | 119.1 |
| TiO2-0.01 | 42.1 | 64.3 | 42 | 60.7 | |
| TiO2-0.1 | 39.2 | 76.5 | 38.5 | 75.3 | |
| h-BN-0.01 | 49 | 41.2 | 47 | 43.6 | |
| h-BN-0.1 | 42 | 64.7 | 41.5 | 62.6 | |
| Eh-BN-0.01 | 69.2 | 0 | 67.5 | 0 | |
| Eh-BN-0.1 | 52 | 33 | 50.5 | 33.6 | |
| NPs | Qs per NP × 10−18 (C) | Ne per NP | Nnp in 100 gm of MO × 1019 | Total Ne × 1019 |
|---|---|---|---|---|
| TiO2/MO | −1.72 | 11 | 7.54 | 83 |
| Eh-BN/MO | −5.675 | 354 | 2.43 | 860.22 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maharana, M.; Baruah, N.; Nayak, S.K.; Sahoo, N.; Wu, K.; Goswami, L. Electrohydrodynamics Analysis of Dielectric 2D Nanofluids. Nanomaterials 2022, 12, 1489. https://doi.org/10.3390/nano12091489
Maharana M, Baruah N, Nayak SK, Sahoo N, Wu K, Goswami L. Electrohydrodynamics Analysis of Dielectric 2D Nanofluids. Nanomaterials. 2022; 12(9):1489. https://doi.org/10.3390/nano12091489
Chicago/Turabian StyleMaharana, Mrutyunjay, Niharika Baruah, Sisir Kumar Nayak, Niranjan Sahoo, Kai Wu, and Lalit Goswami. 2022. "Electrohydrodynamics Analysis of Dielectric 2D Nanofluids" Nanomaterials 12, no. 9: 1489. https://doi.org/10.3390/nano12091489
APA StyleMaharana, M., Baruah, N., Nayak, S. K., Sahoo, N., Wu, K., & Goswami, L. (2022). Electrohydrodynamics Analysis of Dielectric 2D Nanofluids. Nanomaterials, 12(9), 1489. https://doi.org/10.3390/nano12091489