Unexpected Anisotropy of the Electron and Hole Landé g-Factors in Perovskite CH3NH3PbI3 Polycrystalline Films
Abstract
:1. Introduction
2. Materials and Methods
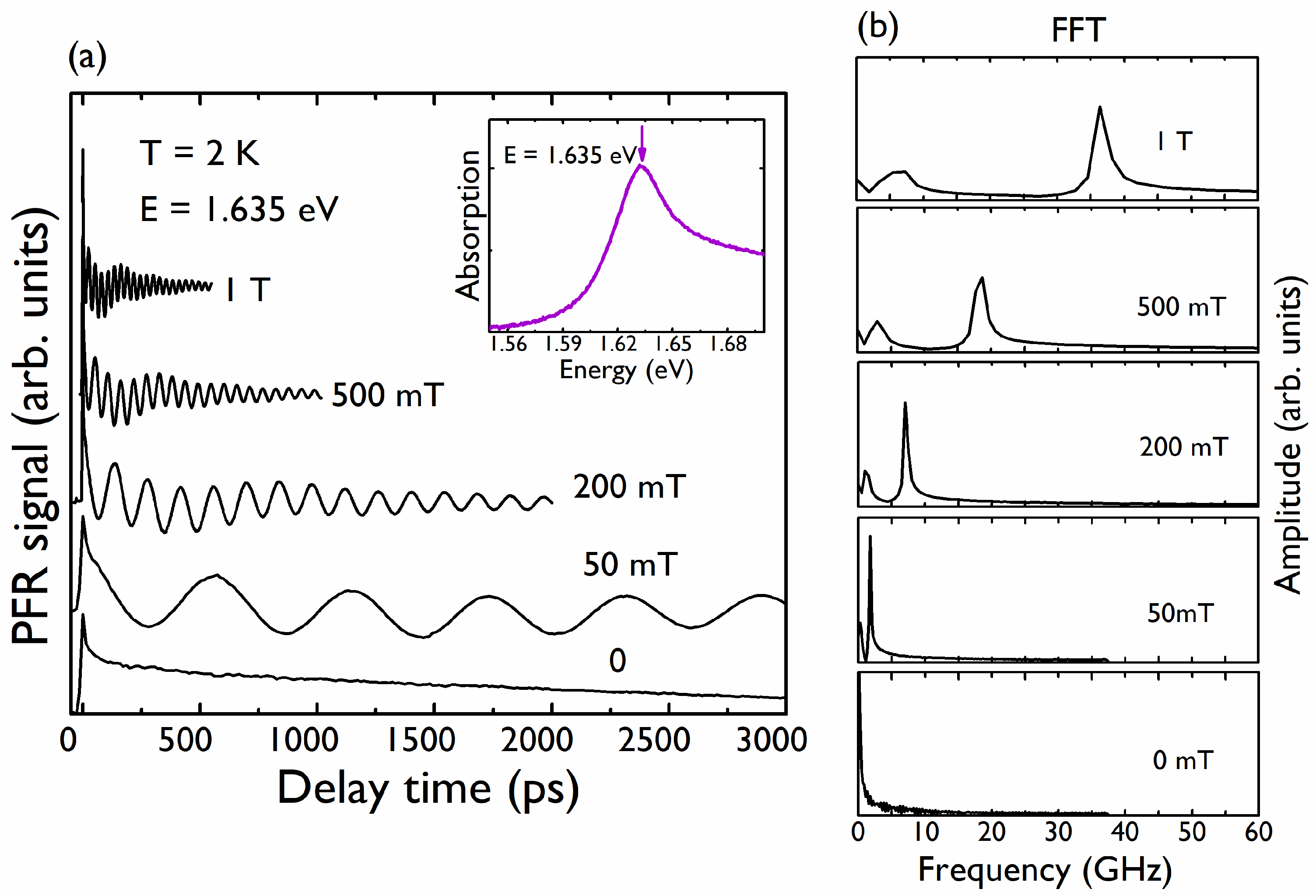
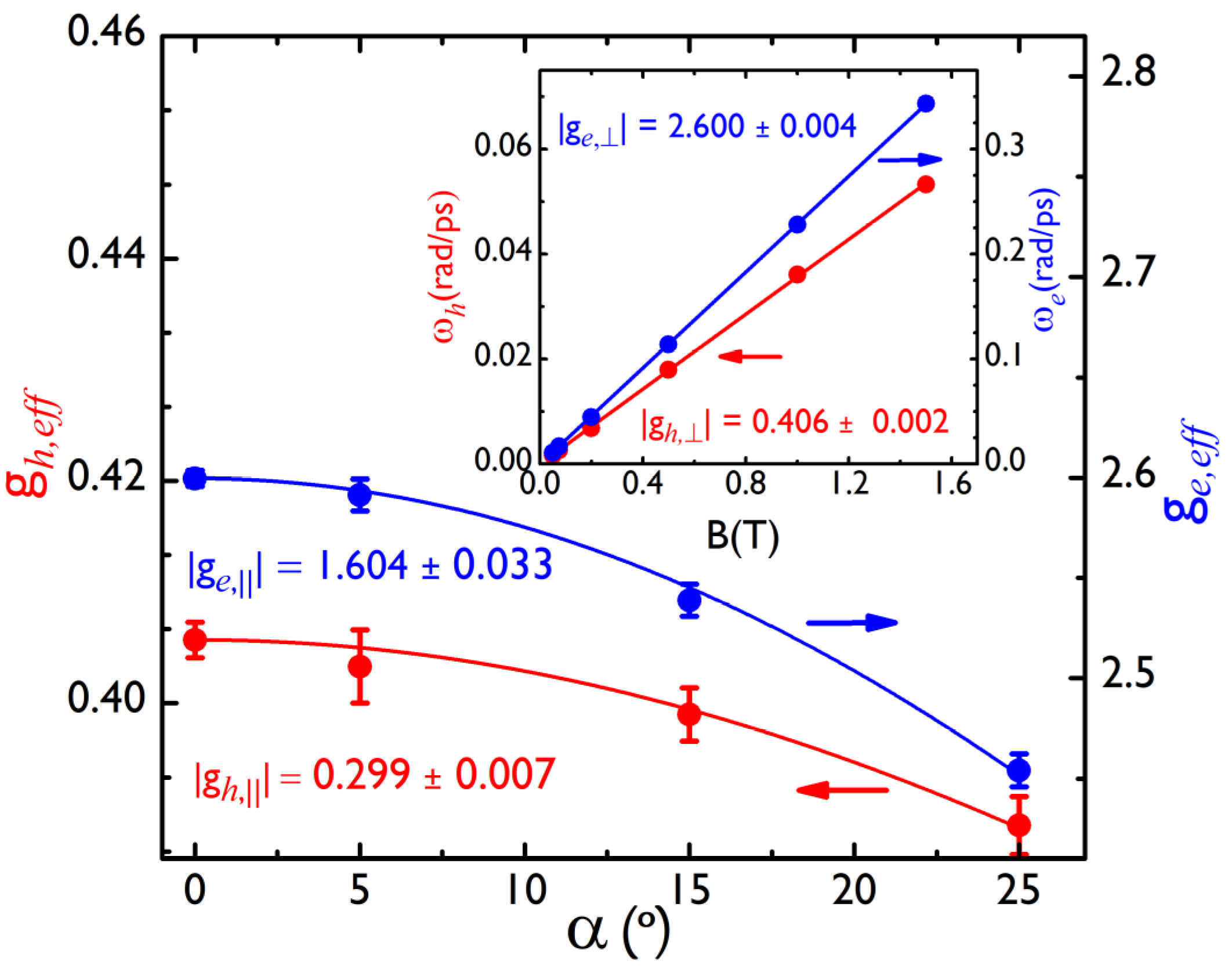
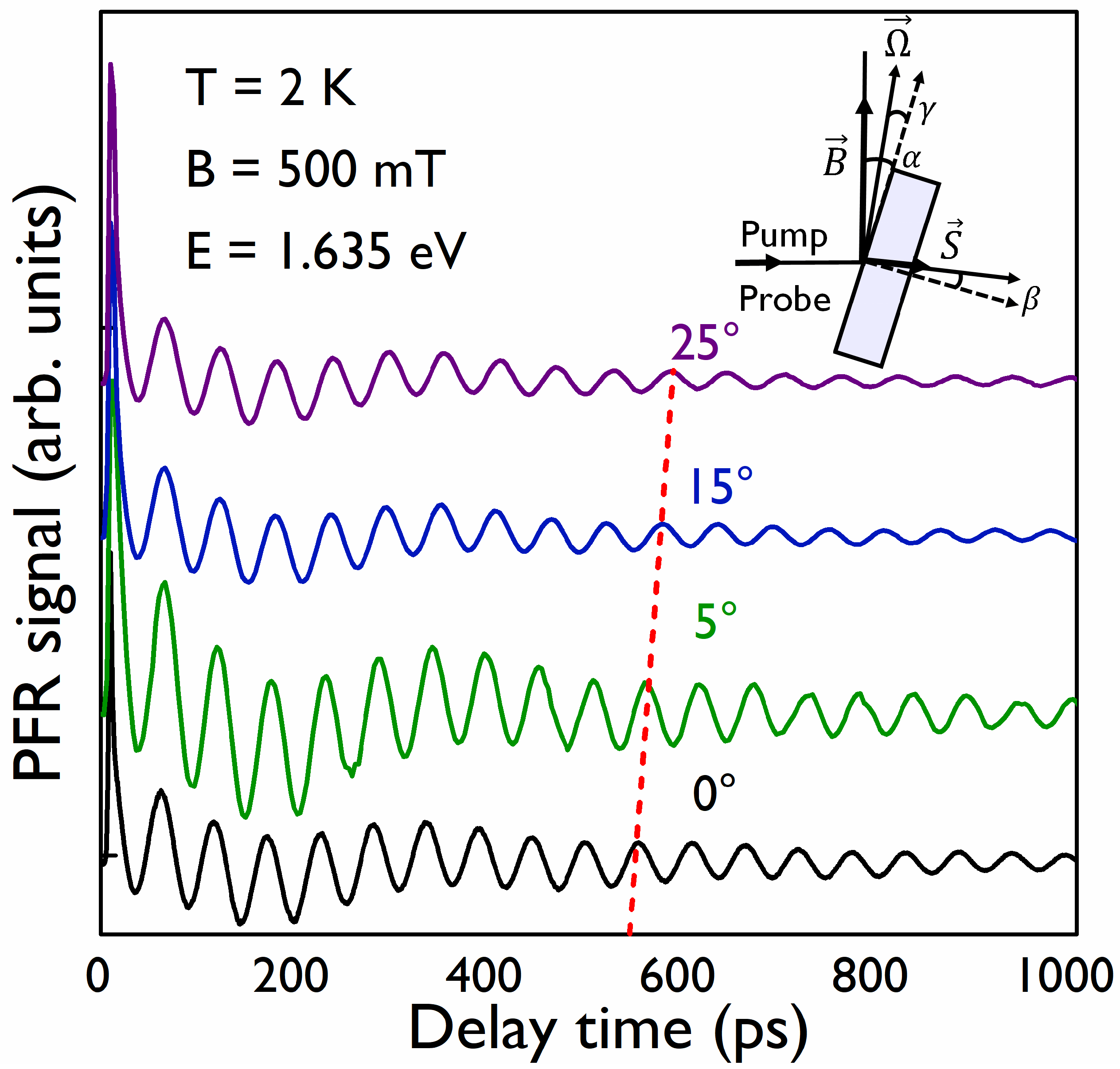
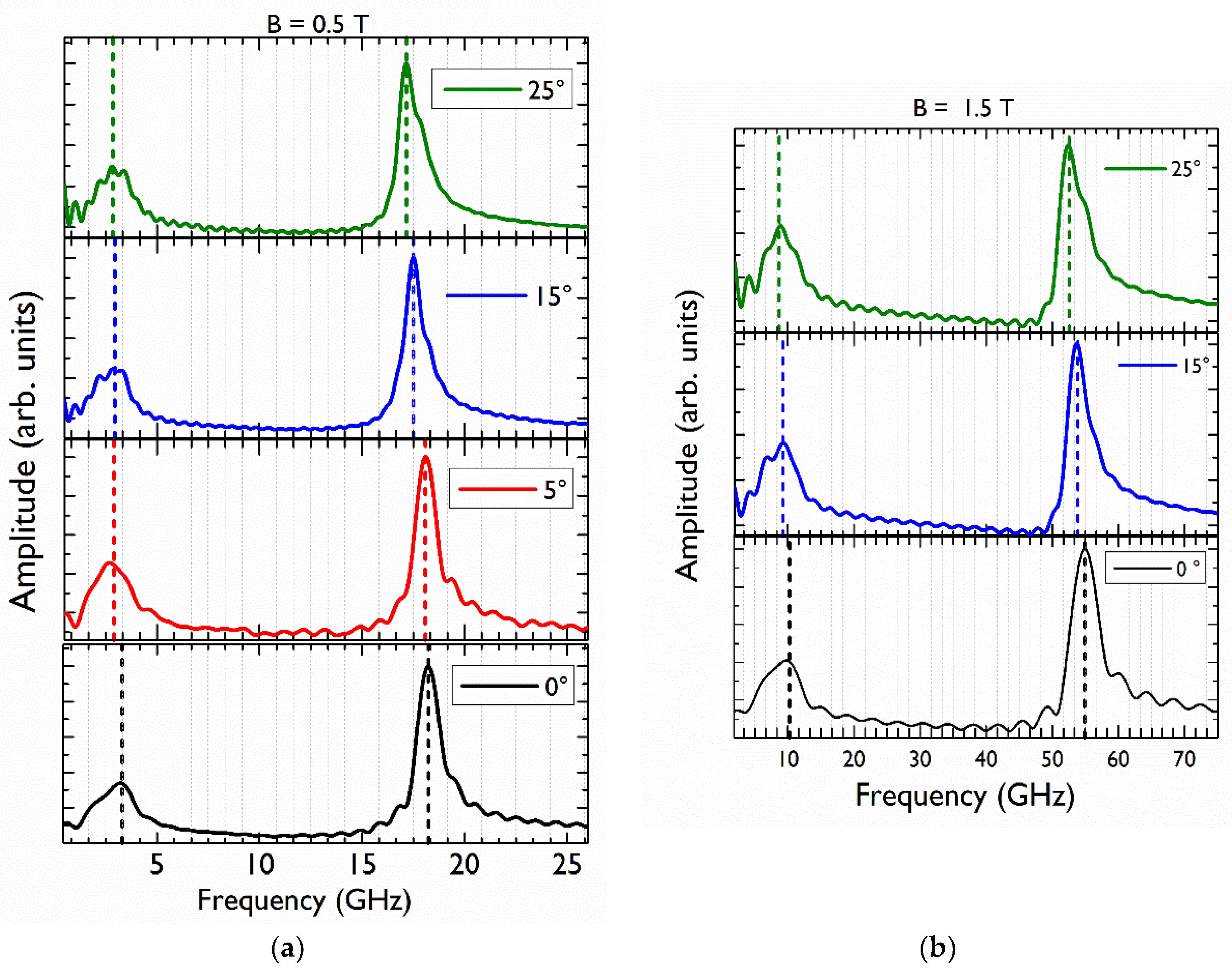
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stoumpos, C.C.; Malliakas, C.D.; Peters, J.A.; Liu, Z.; Sebastian, M.; Im, J.; Chasapis, T.C.; Wibowo, A.C.; Chung, D.Y.; Freeman, A.J.; et al. Crystal Growth of the perovskite semiconductor CsPbBr3: A material for high energy radiation detection. Cryst. Growth Des. 2013, 13, 2722–2727. [Google Scholar] [CrossRef]
- Lee, M.M.; Teuscher, J.; Miyasaka, T.; Murakami, T.N.; Snaith, H.J. Efficient hybrid solar cells based on mesosuperstructured organometal halide perovskites. Science 2012, 338, 643–647. [Google Scholar] [CrossRef] [Green Version]
- Manser, J.S.; Christians, J.A.; Kamat, P.V. Intriguing optoelectronic properties of metal halide perovskites. Chem. Rev. 2016, 116, 12956–13008. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Rocca Rivarola, F.W.; Davis, N.J.J.L.; Bai, S.; Jellicoe, T.C.; de la Peña, F.; Hou, S.; Ducatin, C.; Gao, F.; Friend, R.H.; et al. Highly efficient perovskite nanocrystals light-emitting diodes enabled by a universal crosslink method. Adv. Mater. 2016, 28, 3528–3534. [Google Scholar] [CrossRef] [PubMed]
- Cho, H.; Jeong, S.H.; Park, Y.H.; Kim, M.H.; Wolf, C.; Lee, C.L.; Heo, J.H.; Sadhanala, A.; Myoung, N.S.; Yoo, S.; et al. Overcoming the electroluminescence efficiency limitations of perovskite light- emitting diodes. Science 2015, 350, 1222–1225. [Google Scholar] [CrossRef] [PubMed]
- Dursun, I.; Shen, C.; Parida, M.R.; Pan, J.; Sarmah, S.P.; Priante, D.; Alyami, N.; Liu, J.; Saidaminov, M.I.; Alias, M.S.; et al. Perovskite nanocrystals as a color converter for visible light communication. ACS Photonics 2016, 3, 1150–1156. [Google Scholar] [CrossRef] [Green Version]
- Jana, S.; Carlos, E.; Panigrahi, S.; Martins, R.; Fortunato, E. Toward stable solution-processed high-mobility p-type thin film transistors based on halide perovskites. ACS Nano 2020, 14, 14790–14797. [Google Scholar] [CrossRef]
- Panigrahi, S.; Jana, S.; Calmeiro, T.; Nunes, D.; Martins, R.; Fortunato, E. Imaging the anomalous charge distribution inside CsPbBr3 perovskite quantum dots sensitized solar cells. ACS Nano 2017, 11, 10214–10221. [Google Scholar] [CrossRef]
- Panigrahi, S.; Jana, S.; Calmeiro, T.; Nunes, D.; Deuermeier, J.; Martins, R.; Fortunato, E. Mapping the space charge carrier dynamics in plasmon-based perovskite solar cells. J. Mater. Cham. 2019, 7, 19811–19819. [Google Scholar] [CrossRef]
- Kepenekian, M.; Robles, R.; Katan, C.; Sapori, D.; Pedesseau, L.; Even, J. Rashba and Dresselhaus effects in hybrid organic-inorganic perovskites: From basics to devices. ACS Nano 2015, 9, 1157–11567. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, C.; Liu, H.; McLaughlin, R.; Zhai, Y.; Vardeny, S.R.; Liu, X.; McGill, S.; Semenov, D.; Guo, H.; et al. Spin opto-electronic devices based in hybrid organic-inorganic trihalide perovskites. Nat. Commun. 2019, 10, 129. [Google Scholar] [CrossRef] [Green Version]
- Giovanni, D.; Ma, H.; Chua, J.; Grätzel, M.; Ramesh, R.; Mhaisalkar, S.; Mathews, N.; Sum, T.C. Highly spin- polarized carrier dynamics and ultralarge photoinduced magnetization in CH3NH3PbI3 perovskite thin films. Nano Lett. 2015, 15, 1553–1558. [Google Scholar] [CrossRef]
- Odenthal, P.; Talmadge, W.; Gundlach, N.; Wang, R.; Zhang, C.; Sun, D.; Yu, Z.G.; Vardeny, Z.V.; Li, Y.S. Spin- polarized carrier dynamics and ultralarge photoinduced magnetization in CH3NH3PbI3 perovskite thin films. Nature Phys 2017, 13, 894–899. [Google Scholar] [CrossRef]
- Belykh, V.V.; Yakovlev, D.R.; Glazov, M.M.; Grigoryev, P.S.; Hussain, M.; Rautert, J.; Dirin, D.N.; Kovalenko, M.V.; Bayer, M. Coherent spin dynamics of electrons and holes in CsPbBr3 perovskite crystals. Nat. Commun. 2019, 10, 673. [Google Scholar] [CrossRef]
- Garcia-Arellano, G.; Trippé-Allard, G.; Legrand, L.; Barisien, T.; Garrot, D.; Deleporte, E.; Bernardot, F.; Testelin, C.; Chamarro, M. Energy tunning of electronic spin coherent evolution in methylammonium lead iodide perovskites. J. Phys. Chem. Lett. 2021, 12, 8272–8279. [Google Scholar] [CrossRef]
- Billing, D.G.; Lemmerer, A. Bis [(S)-β-phenetylammonium] tribromoplumbate (II). Acta Cryst. 2003, 59, m381–m383. [Google Scholar]
- Ma, J.; Chen, C.; Jin, L.; Wang, J.; Wang, S.; Tang, J.; Li, D. Chiral 2D perovskites with a high degree of circularly polarized luminiscence. ACS Nano 2019, 13, 3659–3665. [Google Scholar] [CrossRef]
- Chen, C.; Gao, L.; Gao, W.; Ge, C.; Du, X.; Li, Z.; Yang, Y.; Niu, G.D.; Tang, J. Circularly polarized light detection using chiral hybrid perovskites. Nat. Commun. 2019, 10, 1927–1934. [Google Scholar] [CrossRef]
- Niesner, D.; Wilhelm, M.; Levchuk, I.; Osvet, A.; Shrestha, S.; Batentschuk, M.; Brabec, C.; Fauster, T. Giant Rashba splitting in CH3NH3PbBr3 organic-inorganic perovskites. Phys. Rev. Lett. 2016, 117, 126401. [Google Scholar] [CrossRef] [Green Version]
- Bekenstein, Y.; Koscher, B.A.; Eaton, S.W.; Yang, P.; Alivisatos, A.P. Highly luminescent colloidal nanoplatelets of perovskite cesium lead halide and their oriented assemblies. J. Am. Chem. Soc. 2015, 137, 16008–16011. [Google Scholar] [CrossRef] [Green Version]
- Gonzalez-Carrero, S.; Galian, R.E.; Pérez-Prieto, J. Maximazing the emissive properties of CH3NH3PbBr3 perovskite nanoparticles. J. Mat. Chem. A 2015, 3, 9187–9193. [Google Scholar] [CrossRef]
- Steinmetz, V.; Ramade, J.; Legrand, L.; Barisien, T.; Bernardot, F.; Lhuillier, E.; Bernard, M.; Vabre, M.; Saïdi, I.; Ghribi, A.; et al. Anisotropic shape of CsPbBr3 colloidal nanocrystals: From 1D to 2D confinement effects. Nanoscale 2020, 12, 18978–18986. [Google Scholar] [CrossRef] [PubMed]
- Miyata, A.; Mitioglu, A.; Plochocka, P.; Portugall, O.; Tse-Wei Wang, J.; Stranks, S.D.; Snaith, H.J.; Nicholas, R.J. Direct measurement of the exciton binding energy and effective masses for charge carriers in an organic-inorganic tri-halide perovskite. Nat. Phys. 2015, 11, 582–587. [Google Scholar] [CrossRef] [Green Version]
- Baranowski, M.; Plochocka, P. Excitons in metal halide perovskites. Adv. Energy Mat. 2020, 10, 1903659. [Google Scholar] [CrossRef]
- Hirasawa, M.; Ishihara, T.; Goto, T.; Uchida, K.; Miura, N. Magnetoabsorption of the lowest exciton in perovskite- type compound (CH3NH3)PbI3. Phys. B 1994, 201, 427–430. [Google Scholar] [CrossRef]
- Tanaka, K.; Takahashi, T.; Ban, T.; Kondo, T.; Uchida, K.; Noboru, M. Comparative study on the excitons in lead- halide-based perovskite-type crystals CH3NH3PbBr3 CH3NH3PbI3. Solid State Comm. 2003, 127, 619–623. [Google Scholar] [CrossRef]
- Zhang, C.; Su, D.; Yu, Z.G.; Sheng, C.X.; McGill, S.; Semenov, D.; Vardeny, Z.V. Field induced spin splitting and anomalous photoluminescence circular polarization in CH3NH3PbI3 films at high magnetic field. Phys. Rev. B 2018, 97, 134412. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Surrente, A.; Galkowski, K.; Bruyant, N.; Maude, D.K.; Haghighirad, A.A.; Snaith, H.J.; Plochocka, P.; Nicholas, R.J. Unraveling the exciton binding energy and the dielectric constant in single-crystal methylammonium lead triiodide perovskite. J. Phys. Chem. Lett. 2017, 8, 1851–1855. [Google Scholar] [CrossRef] [Green Version]
- Chamarro, M.; Bernardot, F.; Testelin, C. Spin decoherence and relaxation processes in zero-dimensional semiconductor nanostructures. J. Phys. Condens. Matter 2007, 19, 445007. [Google Scholar] [CrossRef]
- Kirstein, E.; Yakovlev, D.R.; Glazov, M.M.; Evers, E.; Zhukov, E.A.; Belykh, V.V.; Kopteva, D.; Kudlacik, N.E.; Nazarenko, O.; Dirin, D.N.; et al. Lead-dominated hyperfine interaction impacting the carrier spin dynamics in halide perovskites. Adv. Mater. 2021, 34, 2105263. [Google Scholar] [CrossRef]
- Diab, H.; Allard-Trippé, G.; Lédée, F.; Jemli, K.; Vilar, C.; Bouchez, G.; Jacques, V.L.R.; Tejeda, A.; Even, J.; Lauret, J.-S.; et al. Narrow linewidth excitonic emission in organic-inorganic lead iodide perovskite single crystals. J. Phys. Chem. Lett. 2016, 7, 5093–5100. [Google Scholar] [CrossRef]
- Yu, Z.G. Effective mass model and magneto-optical properties in hybrid perovskites. Sci. Rep. 2016, 6, 28576. [Google Scholar] [CrossRef] [Green Version]
- Kirstein, E.; Yakovlev, D.R.; Glazov, M.M.; Zhukov, E.A.; Kudlacik, D.; Kalitukha, I.V.; Sapega, V.F.; Dimitriev, G.S.; Semina, M.A.; Nestoklon, M.O.; et al. The Lande factors of electrons and holes in lead halide perovskites: Universal dependence on the band gap. arXiv 2021, arXiv:2112.15384v1. [Google Scholar]
- Brenner, T.M.; Rakita, Y.; Orr, Y.; Klein, E.; Feldman, I.; Elbaum, M.; Cahen, D.; Hodes, G. Conversion of single crystalline PbI2 to CH3NH3PbI3: Structural relations and transformation dynamics. Chem. Mater. 2016, 28, 6501–6510. [Google Scholar] [CrossRef]
- Oesinghaus, L.; Schlipf, J.; Giesbrecht, N.; Song, L.; Hu, Y.; Bein, T.; Docampo, P.; Müller-Buschbaum, P. Towards tailored film morphologies: The origin of crystal orientation of hybrid perovskite thin films. Adv. Mater. Interfaces 2016, 3, 1600403. [Google Scholar] [CrossRef] [Green Version]
- Zhao, J.; Deng, Y.; Wei, H.; Zheng, X.; Yu, Z.; Shao, Y.; Shield, J.E.; Huang, J. Strained hybrid perovskite thin films and their impact on the intrinsic stability of perovskite solar cells. Sci. Adv. 2017, 3, 5616. [Google Scholar] [CrossRef] [Green Version]
- Zhu, C.; Niu, X.; Fu, Y.; Li, N.; Hu, C.; Chen, Y.; He, X.; Na, G.; Liu, P.; Zai, H.; et al. Strain engineering in perovskite solar cells and its impacts on carrier dynamics. Nat. Commun. 2019, 10, 815. [Google Scholar] [CrossRef] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garcia-Arellano, G.; Trippé-Allard, G.; Campos, T.; Bernardot, F.; Legrand, L.; Garrot, D.; Deleporte, E.; Testelin, C.; Chamarro, M. Unexpected Anisotropy of the Electron and Hole Landé g-Factors in Perovskite CH3NH3PbI3 Polycrystalline Films. Nanomaterials 2022, 12, 1399. https://doi.org/10.3390/nano12091399
Garcia-Arellano G, Trippé-Allard G, Campos T, Bernardot F, Legrand L, Garrot D, Deleporte E, Testelin C, Chamarro M. Unexpected Anisotropy of the Electron and Hole Landé g-Factors in Perovskite CH3NH3PbI3 Polycrystalline Films. Nanomaterials. 2022; 12(9):1399. https://doi.org/10.3390/nano12091399
Chicago/Turabian StyleGarcia-Arellano, Guadalupe, Gaëlle Trippé-Allard, Thomas Campos, Frédérick Bernardot, Laurent Legrand, Damien Garrot, Emmanuelle Deleporte, Christophe Testelin, and Maria Chamarro. 2022. "Unexpected Anisotropy of the Electron and Hole Landé g-Factors in Perovskite CH3NH3PbI3 Polycrystalline Films" Nanomaterials 12, no. 9: 1399. https://doi.org/10.3390/nano12091399
APA StyleGarcia-Arellano, G., Trippé-Allard, G., Campos, T., Bernardot, F., Legrand, L., Garrot, D., Deleporte, E., Testelin, C., & Chamarro, M. (2022). Unexpected Anisotropy of the Electron and Hole Landé g-Factors in Perovskite CH3NH3PbI3 Polycrystalline Films. Nanomaterials, 12(9), 1399. https://doi.org/10.3390/nano12091399






