Unraveling the Structural, Dielectric, Magnetic, and Optical Characteristics of Nanostructured La2NiMnO6 Double Perovskites
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Synthesis
2.2. Sample Characterization
3. Results and Discussion
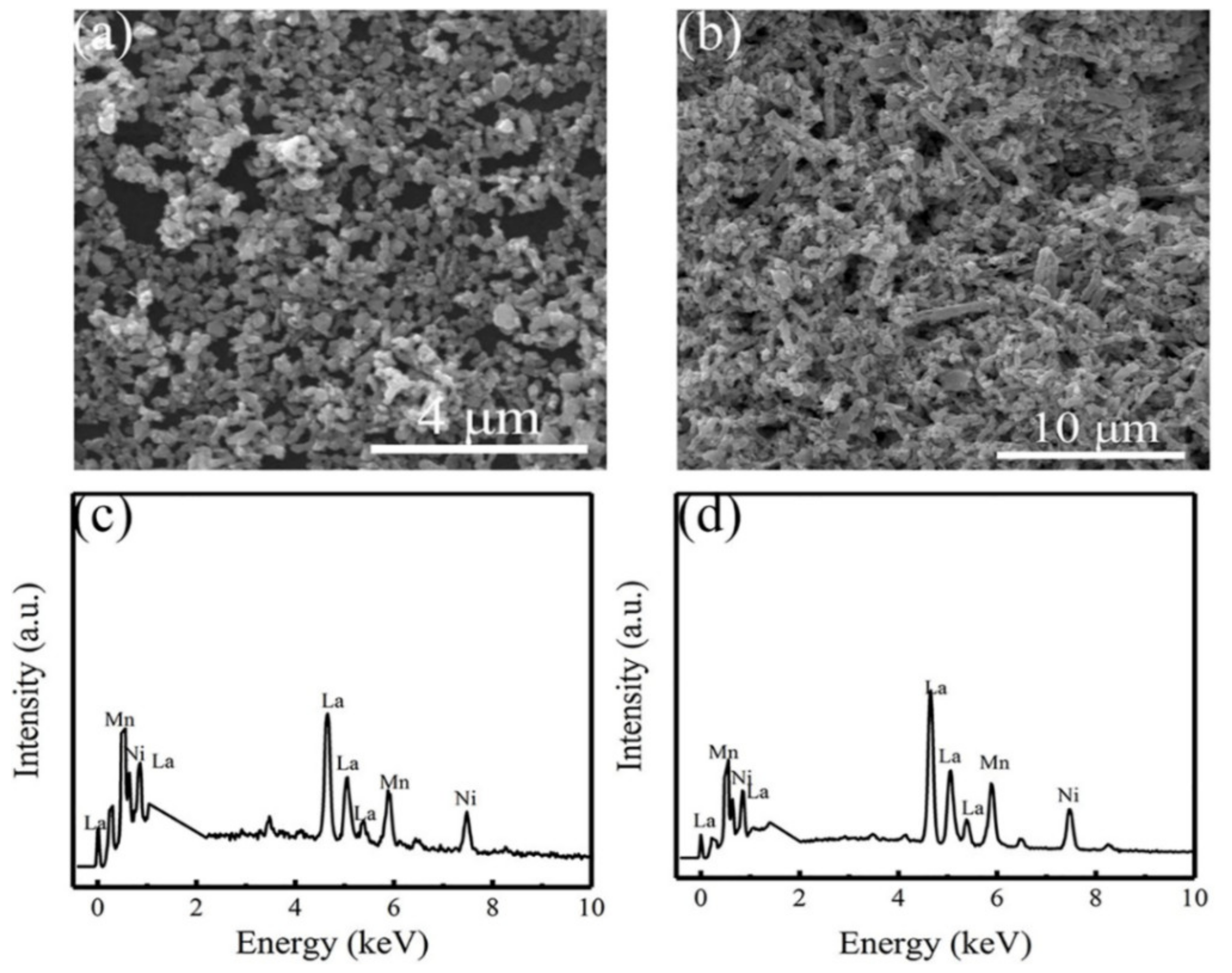
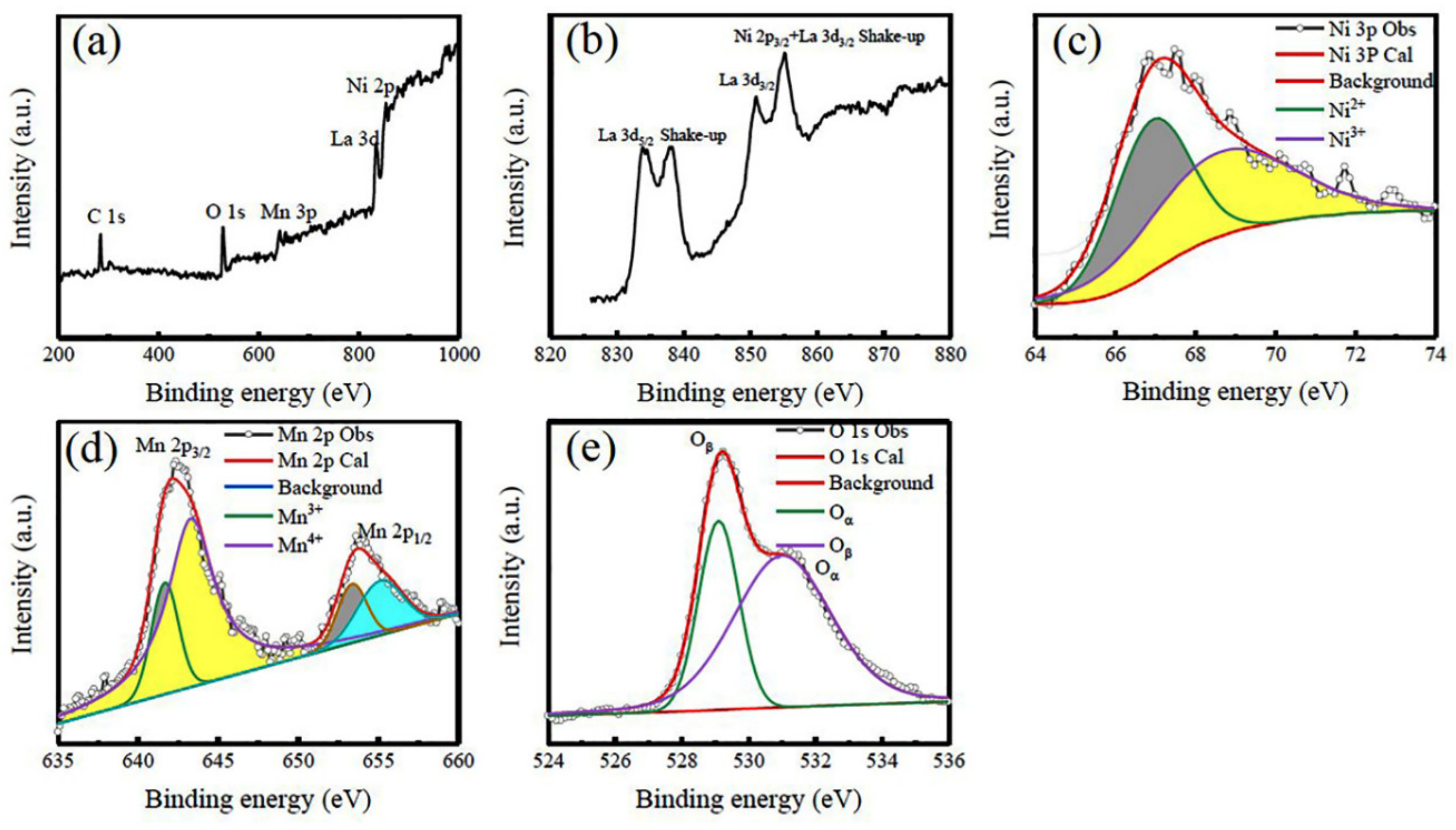
3.1. Structural Characterization
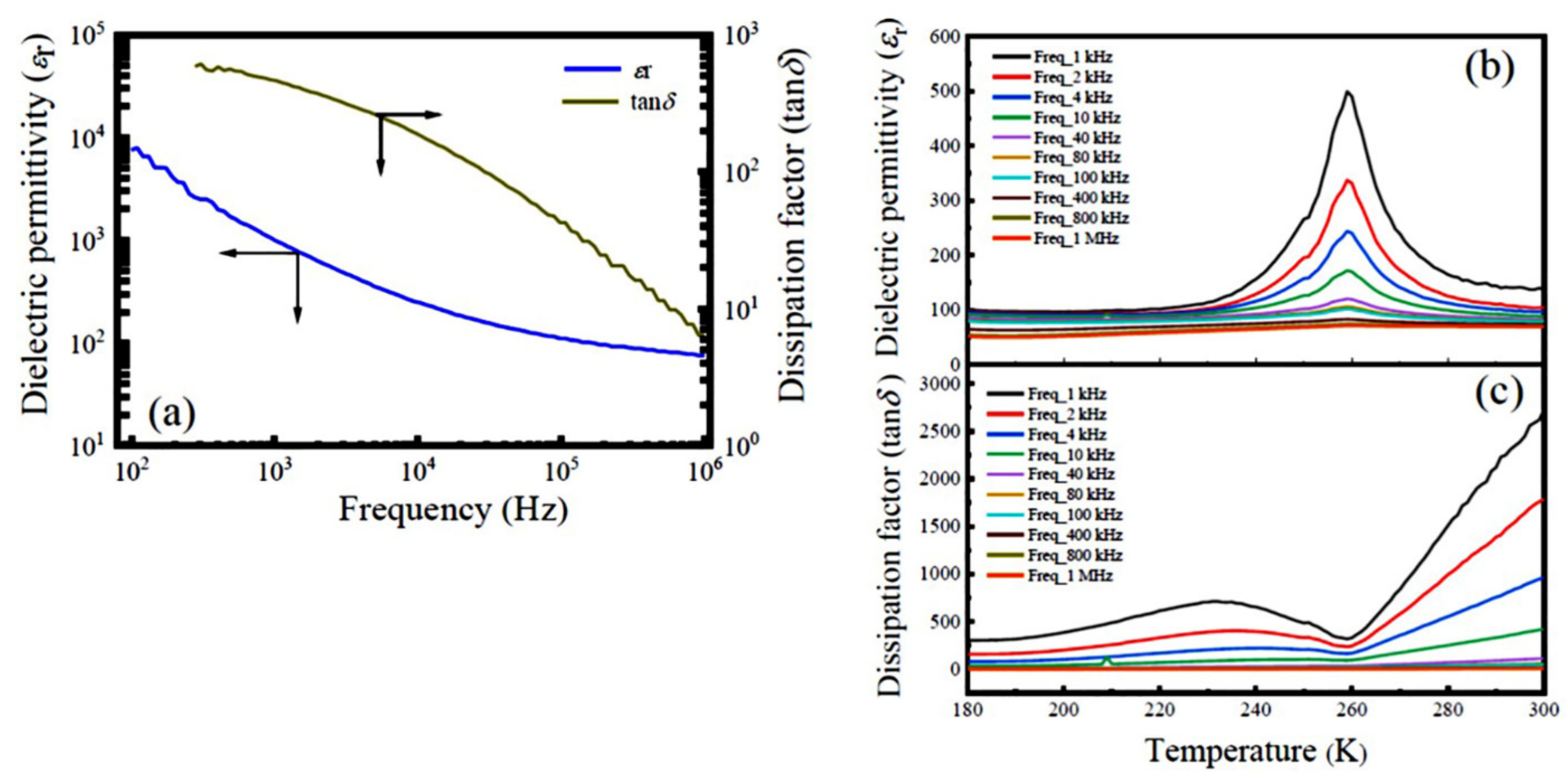
3.2. Dielectric Properties
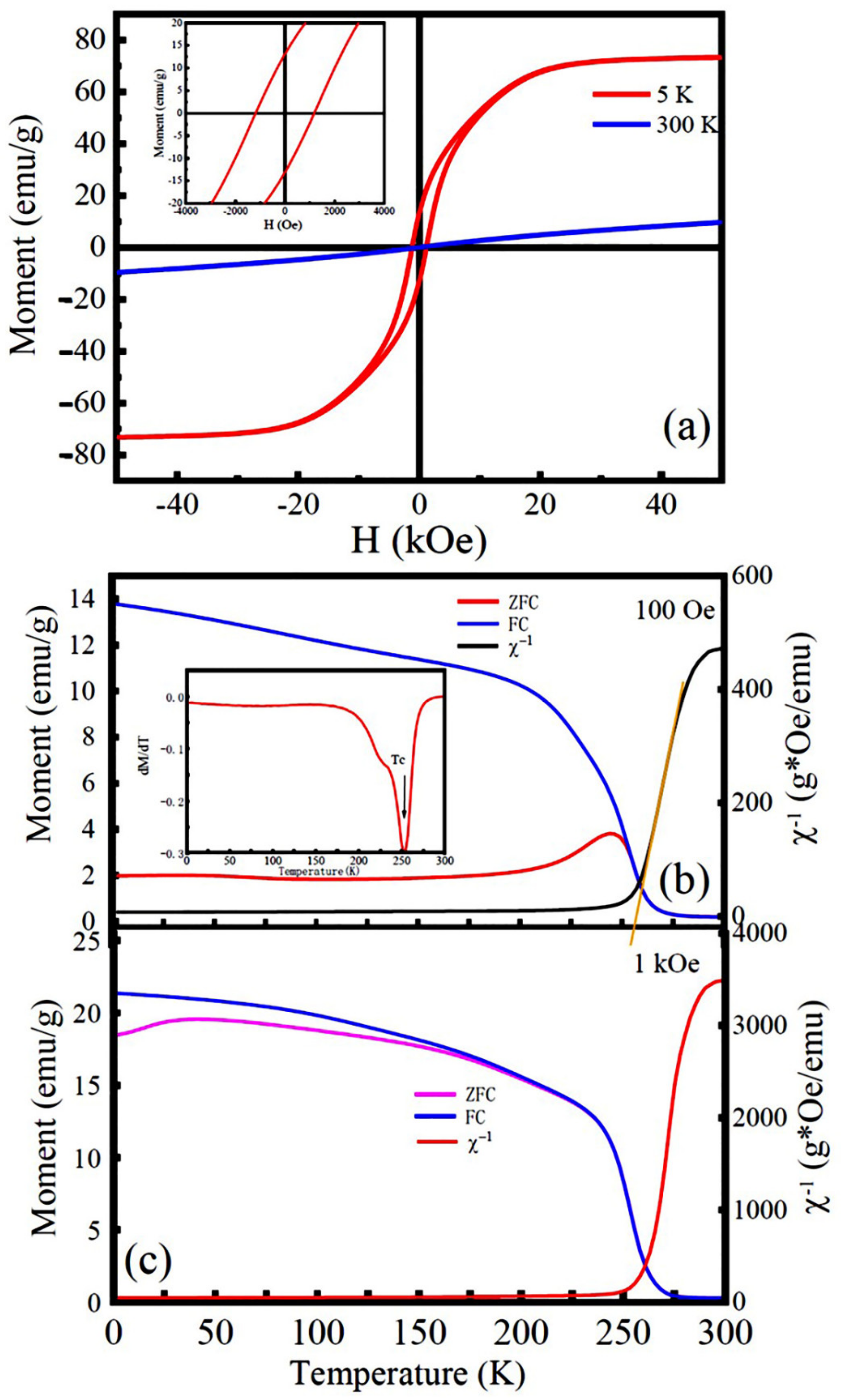
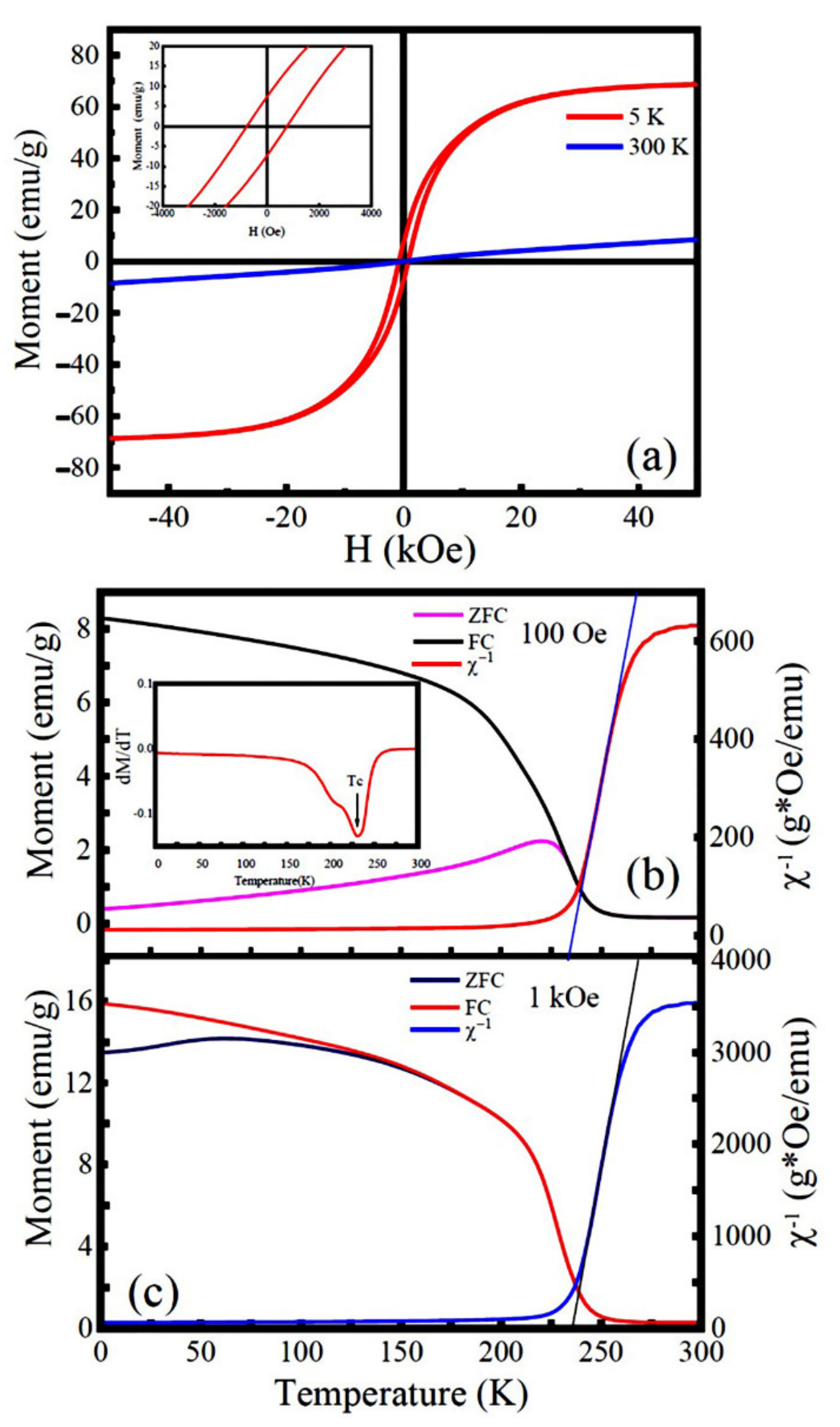
3.3. Magnetic Properties
3.4. Optical Properties
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Retuerto, M.; Muñoz, Á.; Martínez-Lope, M.J.; Alonso, J.A.; Mompeán, F.J.; Fernández-Díaz, M.T.; Sánchez-Benítez, J. Magnetic Interactions in the Double Perovskites R2NiMnO6 (R = Tb, Ho, Er, Tm) Investigated by Neutron Diffraction. Inorg. Chem. 2015, 54, 10890–10900. [Google Scholar] [CrossRef] [PubMed]
- Kakarla, D.C.; Jyothinagaram, K.M.; Das, A.K.; Adyam, V. Dielectric and Magnetodielectric Properties of R2NiMnO6 (R = Nd, Eu, Gd, Dy, and Y). J. Am. Ceram. Soc. 2014, 97, 2858–2866. [Google Scholar] [CrossRef]
- Rogado, N.S.; Li, J.; Sleight, A.W.; Subramanian, M.A. Magnetocapacitance and Magnetoresistance near Room Temperature in a Ferromagnetic Semiconductor: La2NiMnO6. Adv. Mater. 2005, 17, 2225–2227. [Google Scholar] [CrossRef]
- Nasir, M.; Kumar, S.; Patra, N.; Bhattacharya, D.; Jha, S.N.; Basaula, D.R.; Bhatt, S.; Khan, M.; Liu, S.W.; Biring, S.; et al. Role of Antisite Disorder, Rare-Earth Size, and Superexchange Angle on Band Gap, Curie Temperature, and Magnetization of R2NiMnO6 Double Perovskites. ACS Appl. Electron. Mater. 2019, 1, 141–153. [Google Scholar] [CrossRef]
- Sobolev, A.V.; Glazkova, I.S.; Akulenko, A.A.; Sergueev, I.; Chumakov, A.I.; Yi, W.; Belik, A.A.; Presniakov, I.A. Ni-61 Nuclear Forward Scattering Study of Magnetic Hyperfine Interactions in Double Perovskites A2NiMnO6 (A = Sc, in, Tl). J. Phys. Chem. C 2019, 123, 23628–23634. [Google Scholar] [CrossRef]
- Anderson, M.T.; Greenwood, K.B.; Taylor, G.A.; Poeppelmeier, K.R. B-Cation Arrangements in Double Perov skites. Prog. Solid State Chem. 1993, 22, 197–233. [Google Scholar] [CrossRef]
- Nasir, M.; Khan, M.; Kumar, S.; Bhatt, S.; Patra, N.; Bhattacharya, D.; Jha, S.N.; Biring, S.; Sen, S. The Effect of High Temperature Annealing on the Antisite Defects in Ferromagnetic La2NiMnO6 Double Perovskite. J. Magn. Magn. Mater. 2019, 483, 114–123. [Google Scholar] [CrossRef]
- Dass, R.I.; Goodenough, J.B. Multiple Magnetic Phases of La2CoMnO6-δ (0 <~δ <~0.05). Phys. Rev. B 2003, 67, 014401. [Google Scholar] [CrossRef]
- Choudhury, D.; Mandal, P.; Mathieu, R.; Hazarika, A.; Rajan, S.; Sundaresan, A.; Waghmare, U.V.; Knut, R.; Karis, O.; Nordblad, P.; et al. Near-Room-Temperature Colossal Magnetodielectricity and Multiglass Properties in Partially Disordered La2NiMnO6. Phys. Rev. Lett. 2012, 108, 127201. [Google Scholar] [CrossRef]
- Wang, T.; Wu, H.Y.; Sun, Y.B.; Xing, R.; Xv, B.; Zhao, J.J. Physical Properties of Sr-Doped Double Perovskite La2NiMnO6. J. Supercond. Nov. Magn. 2020, 33, 727–739. [Google Scholar] [CrossRef]
- Chakraborty, T.; Nhalil, H.; Yadav, R.; Wagh, A.A.; Elizabeth, S. Magnetocaloric Properties of R2NiMnO6 (R=Pr, Nd, Tb, Ho and Y) Double Perovskite Family. J. Magn. Magn. Mater. 2017, 428, 59–63. [Google Scholar] [CrossRef]
- Matte, D.; de Lafontaine, M.; Ouellet, A.; Balli, M.; Fournier, P. Tailoring the Magnetocaloric Effect in La2NiMnO6 Thin Films. Phys. Rev. Appl. 2018, 9, 054042. [Google Scholar] [CrossRef]
- Gauvin-Ndiaye, C.; Baker, T.E.; Karan, P.; Masse, E.; Balli, M.; Brahiti, N.; Eskandari, M.A.; Fournier, P.; Tremblay, A.M.S.; Nourafkan, R. Electronic and Magnetic Properties of the Candidate Magnetocaloric-Material Double Perovskites La2NiCoO6, La2NiMnO6, and La2NiFeO6. Phys. Rev. B 2018, 98, 125132. [Google Scholar] [CrossRef]
- Yi, W.; Princep, A.J.; Guo, Y.; Johnson, R.D.; Khalyavin, D.; Manuel, P.; Senyshyn, A.; Presniakav, I.A.; Sobolev, A.V.; Matsushita, Y.; et al. Sc2NiMnO6: A Double-Perovskite with a Magnetodielectric Response Driven by Multiple Magnetic Orders. Inorg. Chem. 2015, 54, 8012–8021. [Google Scholar] [CrossRef] [PubMed]
- Dass, R.I.; Yan, J.Q.; Goodenough, J.B. Oxygen Stoichiometry, Ferromagnetism, and Transport Properties of La2-xNiMnO6+δ. Phys. Rev. B 2003, 68, 064415. [Google Scholar] [CrossRef]
- Asai, K.; Sekizawa, H.; Iida, S. Magnetization Measurements and 55Mn NMR Studies of LaNi0.5Mn0.5O3. J. Phys. Soc. Jpn. 1979, 47, 1054–1060. [Google Scholar] [CrossRef]
- Blasse, G. Ferromagnetic Interactions in Non-Metallic Perovskites. J. Phys. Chem. Solids. 1965, 26, 1969–1971. [Google Scholar] [CrossRef]
- Kanamori, J. Superexchange Interaction and Symmetry Properties of Electron Orbitals. J. Phys. Chem. Solids 1959, 10, 87–98. [Google Scholar] [CrossRef]
- Nasir, M.; Khan, M.; Bhatt, S.; Bera, A.K.; Furquan, M.; Kumar, S.; Yusuf, S.M.; Patra, N.; Bhattacharya, D.; Jha, S.N.; et al. Influence of Cation Order and Valence States on Magnetic Ordering in La2Ni1-XMn1+XO6. Phys. Status Solidi 2019, 256, 1900019. [Google Scholar] [CrossRef]
- Chandrasekhar, K.D.; Das, A.K.; Mitra, C.; Venimadhav, A. The Extrinsic Origin of the Magnetodielectric Effect in the Double Perovskite La2NiMnO6. J. Phys.: Condens. Matter. 2012, 24, 495901. [Google Scholar] [CrossRef]
- Bernal-Salamanca, M.; Konstantinovic, Z.; Balcells, L.; Pannunzio-Miner, E.; Sandiumenge, F.; Lopez-Mir, L.; Bozzo, B.; Herrero-Martin, J.; Pomar, A.; Frontera, C.; et al. Nonstoichiometry Driven Ferromagnetism in Double Perovskite La2Ni1-XMn1+XO6 Insulating Thin Films. Cryst. Growth Des. 2019, 19, 2765–2771. [Google Scholar] [CrossRef]
- Joly, V.L.J.; Joy, P.A.; Date, S.K.; Gopinath, C.S. Two Ferromagnetic Phases with Different Spin States of Mn and Ni in LaMn0.5Ni0.5O3. Phys. Rev. B 2002, 65, 184416. [Google Scholar] [CrossRef]
- Bull, C.L.; Gleeson, D.; Knight, K.S. Determination of B-Site Ordering and Structural Transformations in the Mixed Transition Metal Perovskites La2NiCoO6 and La2NiMnO6. J. Phys. Condens. Matter. 2003, 15, 4927–4936. [Google Scholar] [CrossRef]
- Iliev, M.N.; Gospodinov, M.M.; Singh, M.P.; Meen, J.; Truong, K.D.; Fournier, P.; Jandl, S. Growth, Magnetic Properties, and Raman Scattering of La2NiMnO6 Single Crystals. J. Appl. Phys. 2009, 106, 023515. [Google Scholar] [CrossRef]
- Singh, M.P.; Truong, K.D.; Jandl, S.; Fournier, P. Long-Range Ni/Mn Structural Order in Epitaxial DoublePerovskite La2NiMnO6 Thin Films. Phys. Rev. B 2009, 79, 224421. [Google Scholar] [CrossRef]
- Pal, S.; Govinda, S.; Goyal, M.; Mukherjee, S.; Pal, B.; Saha, R.; Sundaresan, A.; Jana, S.; Karis, O.; Freeland, J.W.; et al. Effect of Anti-Site Disorder on Magnetism in La2NiMnO6. Phys. Rev. B 2018, 97, 165137. [Google Scholar] [CrossRef]
- Yuan, X.; Li, Q.; Hu, J.; Xu, M. Unusual Dynamic Magnetic Behavior of Polycrystalline La2NiMnO6. Phys. B 2013, 424, 73–78. [Google Scholar] [CrossRef]
- Das, H.; Waghmare, U.V.; Saha-Dasgupta, T.; Sarma, D.D. Electronic Structure, Phonons, and Dielectric Anomaly in Ferromagnetic Insulating Double Pervoskite La2NiMnO6. Phys. Rev. Lett. 2008, 100, 186402. [Google Scholar] [CrossRef]
- Zhao, S.; Shi, L.; Zhou, S.; Zhao, J.; Yang, H.; Guo, Y. Size-Dependent Magnetic Properties and Raman Spectra of La2NiMnO6 Nanoparticles. J. Appl. Phys. 2009, 106, 123901. [Google Scholar] [CrossRef]
- Masud, M.G.; Ghosh, A.; Sannigrahi, J.; Chaudhuri, B.K. Observation of Relaxor Ferroelectricity and Multiferroic Behaviour in Nanoparticles of the Ferromagnetic Semiconductor La2NiMnO6. J. Phys. Condens. Matter 2012, 24, 295902. [Google Scholar] [CrossRef]
- Hossain, A.; Atique Ullah, A.K.M.; Sarathi Guin, P.; Roy, S. An Overview of La2NiMnO6 Double Perovskites: Synthesis, Structure, Properties, and Applications. J. Sol-Gel Sci. Technol. 2020, 93, 479–494. [Google Scholar] [CrossRef]
- Booth, R.J.; Fillman, R.; Whitaker, H.; Nag, A.; Tiwari, R.M.; Ramanujachary, K.V.; Gopalakrishnan, J.; Lofland, S.E. An Investigation of Structural, Magnetic and Dielectric Properties of R2NiMnO6 (R = Rare Earth, Y). Mater. Res. Bull. 2009, 44, 1559–1564. [Google Scholar] [CrossRef]
- Kumar, P.; Ghara, S.; Rajeswaran, B.; Muthu, D.V.S.; Sundaresan, A.; Sood, A.K. Temperature Dependent Magnetic, Dielectric and Raman Studies of Partially Disordered La2NiMnO6. Solid State Commun. 2014, 184, 47–51. [Google Scholar] [CrossRef]
- Islam, S.A.U.; Andrabi, F.A.; Mohmed, F.; Sultan, K.; Ikram, M.; Asokan, K. Ba Doping Induced Modifications in the Structural, Morphological and Dielectric Properties of Double Perovskite La2NiMnO6 Ceramics. J. Solid State Chem. 2020, 20, 121597. [Google Scholar] [CrossRef]
- Nasir, M.; Khan, M.; Rini, E.G.; Agbo, S.A.; Sen, S. Exploring the Role of Fe Substitution on Electronic, Structural, and Magnetic Properties of La2NiMnO6 Double Perovskites. Appl. Phys. A 2021, 127, 208. [Google Scholar] [CrossRef]
- Lan, C.; Zhao, S.; Xu, T.; Ma, J.; Hayase, S.; Ma, T. Investigation on Structures, Band Gaps, and Electronic Structures of Lead Free La2NiMnO6 Double Perovskite Materials for Potential Application of Solar Cell. J. Alloys Compd. 2016, 655, 208–214. [Google Scholar] [CrossRef]
- Sheikh, M.S.; Ghosh, D.; Dutta, A.; Bhattacharyya, S.; Sinha, T.P. Lead Free Double Perovskite Oxides Ln2NiMnO6 (Ln = La, Eu, Dy, Lu), A New Promising Material for Photovoltaic Application. Mater. Sci. Eng. B 2017, 226, 10–17. [Google Scholar] [CrossRef]
- Biswal, A.K.; Ray, J.; Babu, P.D.; Siruguri, V.; Vishwakarma, P.N. Dielectric Relaxations in La2NiMnO6 with Signatures of Griffiths Phase. J. Appl. Phys. 2014, 115, 194106. [Google Scholar] [CrossRef]
- Sayed, F.N.; Achary, S.N.; Jayakumar, O.D.; Deshpande, S.K.; Krishna, P.S.R.; Chatterjee, S.; Ayyub, P.; Tyagi, A.K. Role of Annealing Conditions on the Ferromagnetic and Dielectric Properties of La2NiMnO6. J. Mater. Res. 2011, 26, 567–577. [Google Scholar] [CrossRef]
- Gaikwad, V.M.; Yadav, K.K.; Lofland, S.E.; Ramanujachary, K.V.; Chakraverty, S.; Ganguli, A.K.; Jha, M. New Low Temperature Process for Stabilization of Nanostructured La2NiMnO6 and Their Magnetic Properties. J. Magn. Magn. Mater. 2019, 471, 8–13. [Google Scholar] [CrossRef]
- Wu, Z.Y.; Ma, C.B.; Tang, X.G.; Li, R.; Liu, Q.X.; Chen, B.T. Double-Perovskite Magnetic La2NiMnO6 Nanoparticles for Adsorption of Bovine Serum Albumin Applications. Nanoscale Res. Lett. 2013, 8, 207. [Google Scholar] [CrossRef] [PubMed]
- Mao, Y.B.; Parsons, J.; McCloy, J.S. Magnetic properties of double perovskite La2BMnO6 (B = Ni or Co) nanoparticles. Nanoscale. 2013, 5, 4720–4728. [Google Scholar] [CrossRef] [PubMed]
- Mao, Y.B. Facile Molten-Salt Synthesis of Double Perovskite La2BMnO6 nanoparticles. RSC Adv. 2012, 2, 12675–12678. [Google Scholar] [CrossRef]
- Yang, D.X.; Jiang, R.; Zhang, Y.H.; Zhang, H.; Lei, S.L.; Yang, T.; Hu, X.S.; Huang, S.; Ge, J.Y.; Su, K.P.; et al. Effect of B-Site Ordering on the Magnetic Order in Multifunctional La2NiMnO6 Double Perovskite. Chin. Phys. Lett. 2020, 37, 106201. [Google Scholar] [CrossRef]
- De Azevedo Filho, J.B.; Souza, R.F.; Queiroz, J.C.A.; Costa, T.H.C.; Sena, C.P.S.; Fonseca, S.G.C.; da Silva, A.O.; Oliveira, J.B.L. Theoretical and Experimental Investigation of the Structural and Magnetic Properties of La2NiMnO6. J. Magn. Magn. Mater. 2021, 527, 167770. [Google Scholar] [CrossRef]
- Gaikwad, V.M.; Yadav, K.K.; Sunaina Chakraverty, S.; Lofland, S.E.; Ramanujachary, K.V.; Nishanthi, S.T.; Ganguli, A.K.; Jha, M. Design of Process for Stabilization of La2NiMnO6 Nanorods and Their Magnetic Properties. J. Magn. Magn. Mater. 2019, 492, 165652. [Google Scholar] [CrossRef]
- McGuire, S.C.; Koenigsmann, C.; Chou, C.C.; Tong, X.; Wong, S.S. Lanthanum-based double perovskite nanoscale motifs as support media for the methanol oxidation reaction. Catal. Sci. Technol. 2021, 12, 613–629. [Google Scholar] [CrossRef]
- Das, H.; Waghmare, U.V.; Saha-Dasgupta, T.; Sarma, D.D. Theoretical Evidence and Chemical Origin of the Mag netism-Dependent Electrostructural Coupling in La2NiMnO6. Phys. Rev. B 2009, 79, 144403. [Google Scholar] [CrossRef]
- Sheikh, M.S.; Sakhya, A.P.; Dutta, A.; Sinha, T.P. Origin of Narrow Band Gap and Optical Anisotropy in Solar Cell Absorbers L2NiMnO6 (L La, Eu): A comparative DFT study. Comput. Mater. Sci. 2019, 161, 293–299. [Google Scholar] [CrossRef]
- Pacheco, J.M.; Gueorguiev, G.K.; Martins, J.L. First-Principles Study of the Possibility of Condensed Phases of En dohedral Silicon Cage Clusters. Phys. Rev. B 2002, 66, 033401. [Google Scholar] [CrossRef]
- Oliveira, M.I.A.; Rivelino, R.; Mota, F.D.; Gueorguiev, G.K. Optical Properties and Quasiparticle Band Gaps of Transition-Metal Atoms Encapsulated by Silicon Cages. J. Phys. Chem. C 2014, 118, 5501–5509. [Google Scholar] [CrossRef]
- Oliveira, M.J.T.; Medeiros, P.V.C.; Sousa, J.R.F.; Nogueira, F.; Gueorguiev, G.K. Optical and Magnetic Excitations of Metal-Encapsulating Si Cages: A Systematic Study by Time-Dependent Density Functional Theory. J. Phys. Chem. C 2014, 118, 11377–11384. [Google Scholar] [CrossRef]
- Shannon, R.D. Revised Effective Ionic-Radii and Systematic Studies of Interatomic Distances in Halides and Chacogenides. Acta Cryst. 1976, 32, 751–767. [Google Scholar] [CrossRef]
- Tokura, Y.; Tomioka, Y. Colossal Magnetoresistive Manganites. J. Magn. Magn. Mater. 1999, 200, 1–23. [Google Scholar] [CrossRef]
- Mickevicius, S.; Grebinskij, S.; Bondarenka, V.; Vengalis, B.; Sliuziene, K.; Orlowski, B.A.; Osinniy, V.; Drube, W. Investigation of Epitaxial LaNiO3-X Thin Films by High-Energy XPS. J. Alloys Compd. 2006, 423, 107–111. [Google Scholar] [CrossRef]
- Stojanovic, M.; Haverkamp, R.G.; Mims, C.A.; Moudallal, H.; Jacobson, A.J. Synthesis and Characterization of LaCr1-xNixO3 Perovskite Oxide Catalysts. J. Catal. 1997, 166, 315–323. [Google Scholar] [CrossRef]
- Arca, E.; Kehoe, A.B.; Veal, T.D.; Shmeliov, A.; Scanlon, D.O.; Downing, C.; Daly, D.; Mullarkey, D.; Shvets, I.V.; Nicolosi, V.; et al. Valence Band Modification of Cr2O3 by Ni-Doping: Creating a High Figure of Merit P-Type Tco. J. Mater. Chem. C 2017, 5, 12610–12618. [Google Scholar] [CrossRef]
- An, Z.; Zhuo, Y.; Xu, C.; Chen, C. Influence of the TiO2 Crystalline Phase of MnOx/TiO2 Catalysts for No Oxidation. Chin. J. Catal. 2014, 35, 120–126. [Google Scholar] [CrossRef]
- Ichimura, K.; Inoue, Y.; Yasumori, I. Catalysis by Mixed Oxide Perovskites. I. Hydrogenolysis of Ethylene and Ethane on LaCoO3. Bull. Chem. SOC. Jpn. 1980, 53, 3044–3049. [Google Scholar] [CrossRef]
- Yamazoe, N.; Teraoka, Y.; Seiyama, T. TPD and XPS Study on Thermal Behavior of Absorbed Oxygen in La1-xSrxCoO3. Chem. Lett. 1981, 10, 1767–1770. [Google Scholar] [CrossRef]
- Tabata, K.; Matsumoto, I.; Kohiki, S. Surface Characterization and Catalytic Properties of La1-xSrxCoO3. J. Mater. Sci. 1987, 22, 1882–1886. [Google Scholar] [CrossRef]
- Tabata, K.; Matsumoto, I.; Kohiki, S. Effect of Thermal Treatment on Catalytic Properties of La0.9Ce0.1CoO3. J. Mater. Sci. 1987, 22, 3037–3040. [Google Scholar] [CrossRef]
- Tejuca, L.G.; Fierro, J.L.G.; Tascón, J.M.D. Structure and Reactivity of Perovskite-Type Oxides. Adv. Catal. 1989, 36, 237–328. [Google Scholar] [CrossRef]
- Richiter, L.; Bader, S.D.; Brodsky, M.B. Ultraviolet, X-Ray-Photoelectron, and Electron-Energy-Loss Spectroscopy Studies of LaCoO3 and Oxygen Chemisorbed on LaCoO3. Phys. Rev. B 1980, 22, 3059–3064. [Google Scholar] [CrossRef]
- Dupin, J.C.; Gonbeau, D.; Vinatier, P.; Levasseur, A. Systematic XPS Studies of Metal Oxides, Hydroxides and Peroxides. Phys. Chem. Chem. Phys. 2000, 2, 1319–1324. [Google Scholar] [CrossRef]
- Kitamura, M.; Ohkubo, I.; Matsunami, M.; Horiba, K.; Kumigashira, H.; Matsumoto, Y.; Koinuma, H.; Oshima, M. Electronic Structure Characterization of La2NiMnO6 Epitaxial Thin Films Using Synchrotron-Radiation Photoelectron Spectroscopy and Optical Spectroscopy. Appl. Phys. Lett. 2009, 94, 262503. [Google Scholar] [CrossRef]
- Mohanty, S.; Choudhary, R.N.P.; Padhee, R.; Parida, B.N. Dielectric and Impedance Spectroscopy of BiFeO3–NaTaO3 Multiferroics. Ceram. Int. 2014, 40, 9017–9025. [Google Scholar] [CrossRef]
- Cross, L.E. Relaxor Ferroelectrics: An Review. Ferroelectrics 1994, 151, 305–320. [Google Scholar] [CrossRef]
- Yang, W.Z.; Liu, X.Q.; Zhao, H.J.; Lin, Y.Q.; Chen, X.M. Structure, Magnetic, and Dielectric Characteristics of Ln2NiMnO6 (Ln = Nd and Sm) Ceramics. J. Appl. Phys. 2012, 112, 064104. [Google Scholar] [CrossRef]
- Rivera, I.; Kumar, A.; Ortega, N.; Katiyar, R.S.; Lushnikov, S. Divide Line between Relaxor, Diffused Ferroelectric, Ferroelectric and Dielectric. Solid State Commun. 2009, 149, 172–176. [Google Scholar] [CrossRef]
- Glass, A.M. Dielectric, Thermal, and Pyroelectric Properties of Ferroelectric LiTaO3. Phys. Rev. 1968, 172, 564–571. [Google Scholar] [CrossRef]
- Uchino, K.; Nomura, S. Critical Exponents of the Dielectric Constants in Diffused Phase Transition Crystals. Ferroelectr. Lett. Sect. 1982, 44, 55–61. [Google Scholar] [CrossRef]
- Chen, X.; Chen, J.; Huang, G.; Ma, D.; Zhou, L.H. Relaxor Behaviour and Dielectric Properties of Bi(Zn2/3Nb1/3)O3-Modified BaTiO3 ceramics. J. Electron. Mater. 2015, 44, 4804–4810. [Google Scholar] [CrossRef]
- Bensemma, N.; Taïbi, K. Relaxor Behaviour in Lead-Free Ba(Ti1-xScx/2Nbx/2)O3 Ceramics. J. Asian Ceram. Soc. 2014, 2, 132–137. [Google Scholar] [CrossRef][Green Version]
- Reddy, M.P.; Shakoor, R.A.; Mohamed, A.M.A. Structural and Magnetic Studies of La2BMnO6 (B=Ni and Co) Nanoparticles Prepared by Microwave Sintering Approach. Mater. Chem. Phys. 2016, 177, 346–352. [Google Scholar] [CrossRef]
- Kittel, C. Introduction to Solid State Physics, 8th ed.; John Wiley and Sons: New York, NY, USA, 2004; pp. 323–355. ISBN 978-0471415268. [Google Scholar]
- Taguchi, H. Relationship between Crystal Structure and Electrical Properties of Nd(Cr1-XFeX)O3. J. Solid State Chem. 1997, 131, 108–114. [Google Scholar] [CrossRef]
- Coey, J.M.D. Magnetism and Magnetic Materials; Cambridge University Press: Cambridge, UK, 2010; p. 115. ISBN 978-0-471-41526-8. [Google Scholar]
- Choudhary, N.; Verma, M.K.; Sharma, N.D.; Sharma, S.; Singh, D. Correlation between Magnetic and Transport Properties of Rare Earth Doped Perovskite Manganites La0.6R0.1Ca0.3MnO3 (R = La, Nd, Sm, Gd, and Dy) Synthesized by Pechini Process. Mater. Chem. Phys. 2020, 242, 122482. [Google Scholar] [CrossRef]
- Tauc, J.; Grigorov, R.; Vancu, A. Optical Properties and Electronic Structure of Amorphous Germanium. Phys. Status Solidi 1966, 15, 627–637. [Google Scholar] [CrossRef]
- Moritomo, Y.; Shimamoto, N.; Xu, S.; Machida, A.; Nishibori, E.; Takata, M.; Sakata, M.; Nakamura, A. Effects of B-Site Disorder in Sr2FeMoO6 with Double Perovskite Structure. Jpn. J. Appl. Phys. 2001, 40, L672–L674. [Google Scholar] [CrossRef]
- Arima, T.; Tokura, Y.; Torrance, J.B. Variation of Optical Gaps in Perovskite-Type 3d Transition-Metal Oxides. Phys. Rev. B 1993, 48, 17006–17009. [Google Scholar] [CrossRef]
- Hissariya, R.; Babu, S.; Ram, S.; Mishra, S.K. Spin-up conversion, exchange-interactions, and tailored magnetic properties in core-shell La2NiMnO6 of small crystallites. Nanotechnology. 2021, 32, 435702. [Google Scholar] [CrossRef] [PubMed]
- Tiwary, S.; Kuila, S.; Sahoo, M.R.; Barik, A.; Babu, P.D.; Vishwakarma, P.N. Magnetoelectricity in La2NiMnO6 and its PVDF impregnated derivative. J. Appl. Phys. 2018, 124, 044101. [Google Scholar] [CrossRef]




| Materials | Space Group | Unit Cell Parameters | Average Bond Length (Å) <Mn-O> | Average Bond Length (Å) <Ni-O> | Bond Angle (°) Ni-Oi-Mn (i = 1–3) <Ni-O-Mn> | Structural Tolerance Factor (t) | Fitting Parameters |
|---|---|---|---|---|---|---|---|
| LNMO NPs | P21/n | a = 5.5060(6) Å | 1.9656(2) | 1.9656(2) | 158.217(4) 162.550(3) 161.192(4) 160.653(3) | 0.901 | Rp = 8.93% Rwp=12.0% |
| b = 5.4482(5) Å | |||||||
| c = 7.7569(9)Å | |||||||
| β = 89.91(3)° | |||||||
| V = 232.691(5) Å3 | |||||||
| LNMO NRs | a = 5.5087(6) Å | 1.9670(2) | 1.9670(2) | 158.253(3) 162.533(2) 161.160(3) 160.648(3) | 0.905 | Rp = 8.54% Rwp=11.72% | |
| b = 5.4455(3) Å | |||||||
| c = 7.7736(8) Å | |||||||
| β = 89.85(2) °V = 232.193(5) Å3 |
| Material | Tirr (K) | Tc (K) | θp (K) | C (emu⋅K/mol) | μeff (μB) | μcal (μB) | Mr (emu/g) | HC (Oe) | MSexp (μB/f.u.) | MScal (μB/f.u.) | ASD Content |
|---|---|---|---|---|---|---|---|---|---|---|---|
| LNMO NPs | @ 100 Oe | 5.51 | 13.1 | 1141 | 6.20 | 6.18 | 0.02% | ||||
| 258.4 | 252.0 | 257.0 | 3.64(5) | 5.39(4) | |||||||
| @ 1000 Oe | |||||||||||
| 239.5 | 253.0 | 262.0 | 3.75(5) | 5.47(4) | |||||||
| LNMO NWs | @ 100 Oe | 5.35 | 7.36 | 763 | 5.68 | 5.99 | 2.59% | ||||
| 234.5 | 232.0 | 235.8 | 4.43(5) | 5.95(4) | |||||||
| @ 1000 Oe | |||||||||||
| 185.5 | 227.0 | 235.6 | 2.48(1) | 4.45(1) | |||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yi, K.; Tang, Q.; Wu, Z.; Zhu, X. Unraveling the Structural, Dielectric, Magnetic, and Optical Characteristics of Nanostructured La2NiMnO6 Double Perovskites. Nanomaterials 2022, 12, 979. https://doi.org/10.3390/nano12060979
Yi K, Tang Q, Wu Z, Zhu X. Unraveling the Structural, Dielectric, Magnetic, and Optical Characteristics of Nanostructured La2NiMnO6 Double Perovskites. Nanomaterials. 2022; 12(6):979. https://doi.org/10.3390/nano12060979
Chicago/Turabian StyleYi, Kang, Qingkai Tang, Zhiwei Wu, and Xinhua Zhu. 2022. "Unraveling the Structural, Dielectric, Magnetic, and Optical Characteristics of Nanostructured La2NiMnO6 Double Perovskites" Nanomaterials 12, no. 6: 979. https://doi.org/10.3390/nano12060979
APA StyleYi, K., Tang, Q., Wu, Z., & Zhu, X. (2022). Unraveling the Structural, Dielectric, Magnetic, and Optical Characteristics of Nanostructured La2NiMnO6 Double Perovskites. Nanomaterials, 12(6), 979. https://doi.org/10.3390/nano12060979






