Nanoparticle Aggregation and Thermophoretic Particle Deposition Process in the Flow of Micropolar Nanofluid over a Stretching Sheet
Abstract
:1. Introduction
- What is the influence of nanoparticles with and without aggregation on porosity parameter over a velocity profile?
- What is the impact of nanoparticles with and without aggregation over a thermal distribution?
- What is the effect of HS/S parameter, thermophoretic parameter, bioconvection Peclet number and bioconvection Lewis number on respective profiles?
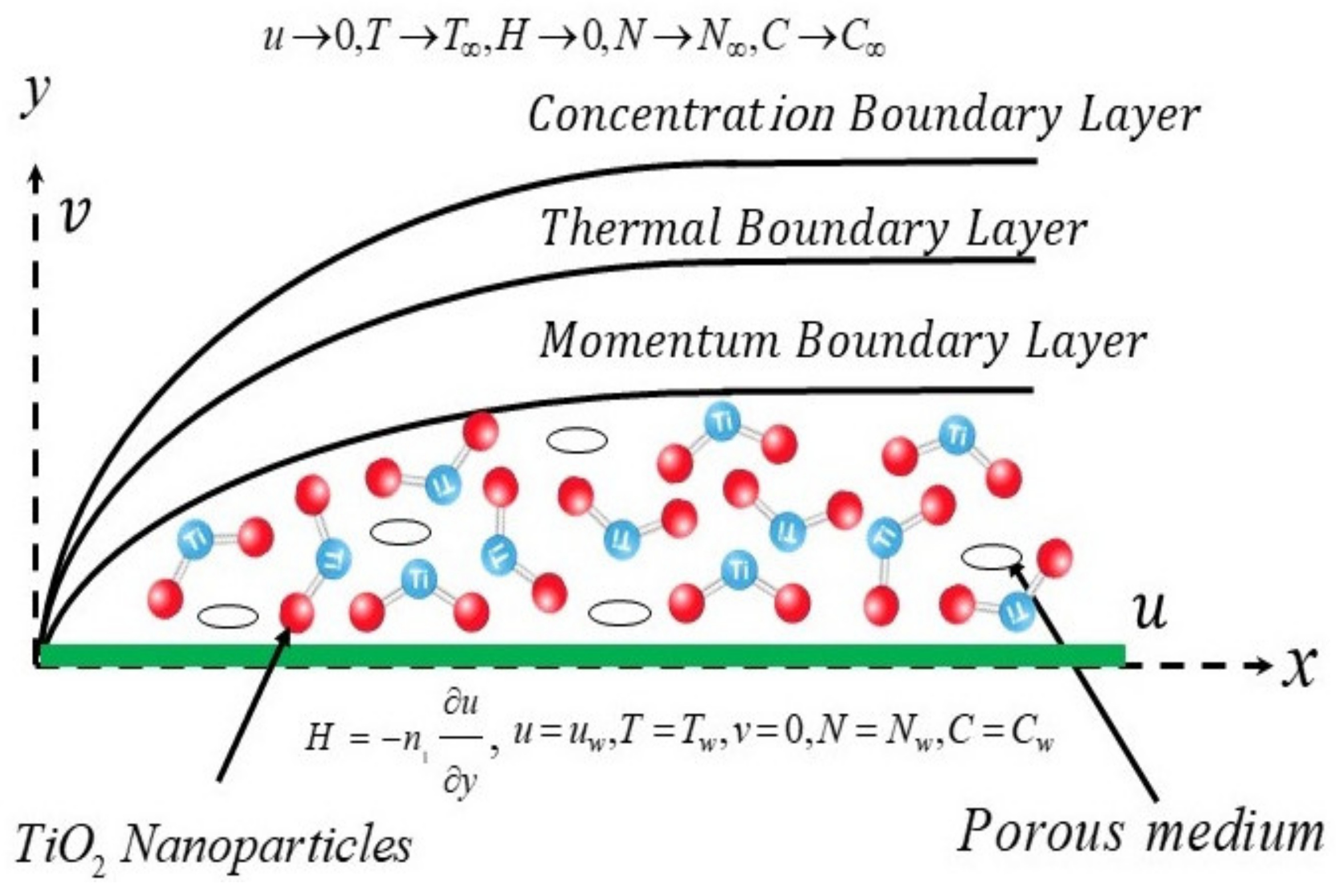
2. Mathematical Formulation
3. Numerical Process and Authentication of Code
4. Analysis of Results
5. Concluding Remarks
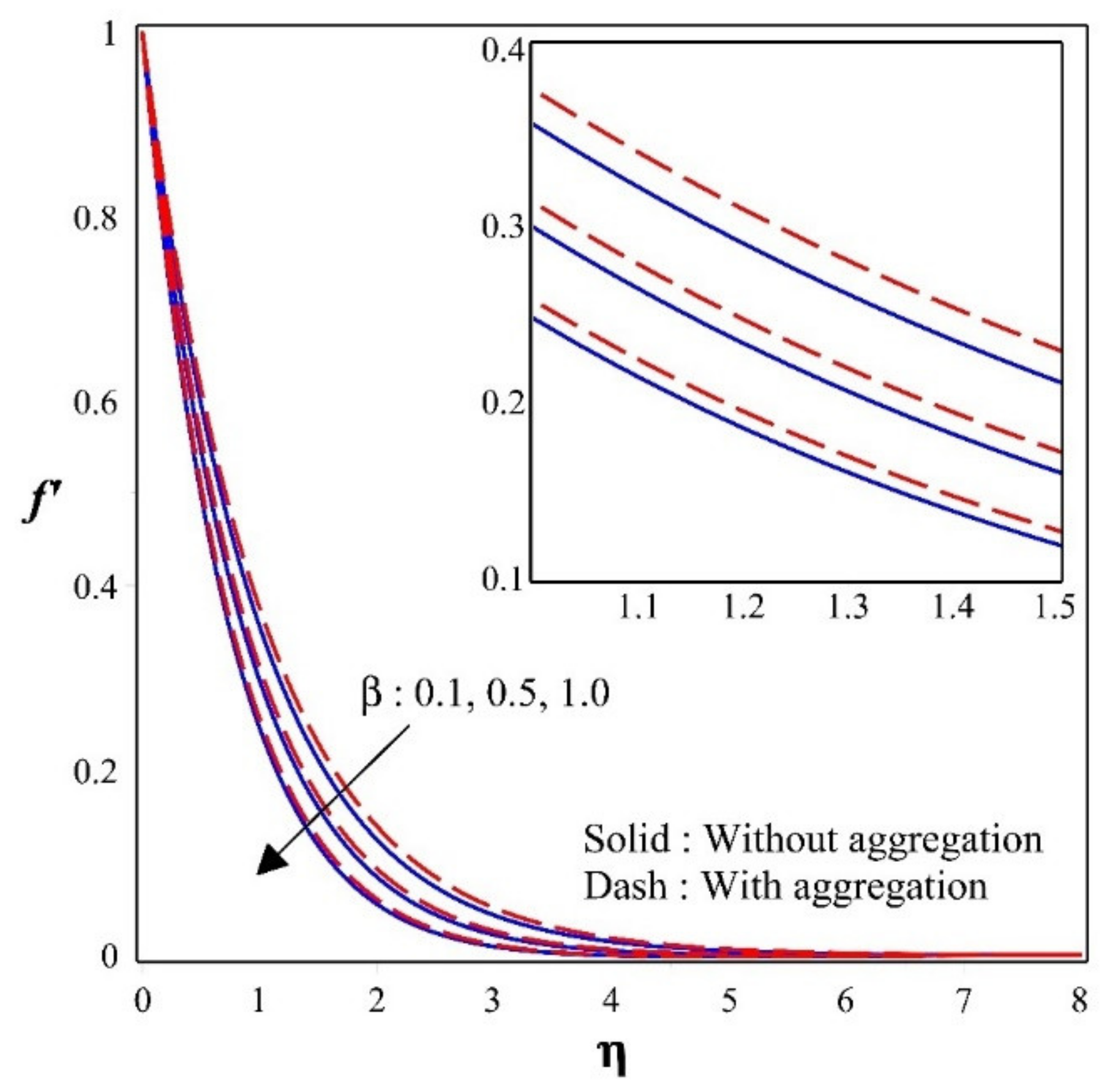
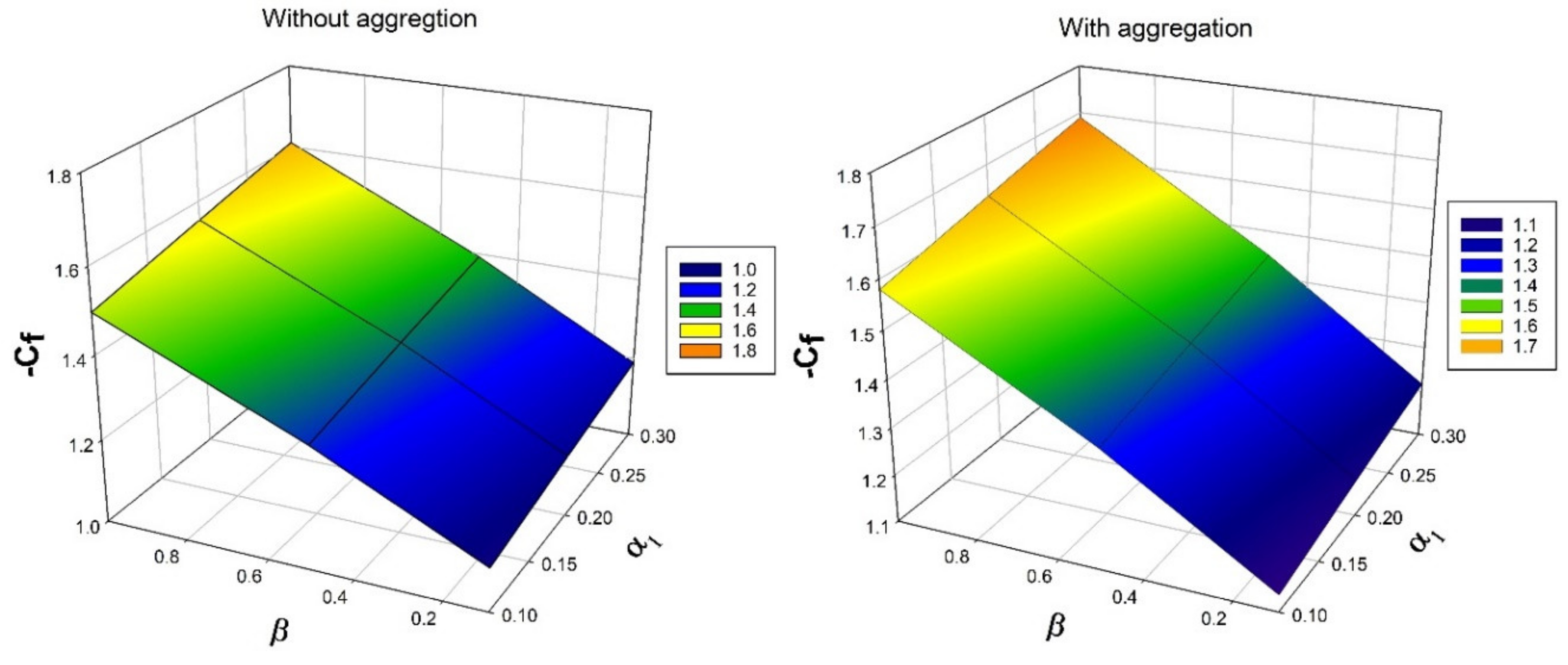
- Enhancement in the porous parameter will diminishes the velocity profile due to presence of porous medium which drags the fluid motion.
- For escalating values of velocity is more in the presence of aggregation than absence of aggregation in but, reverse trend is seen in .
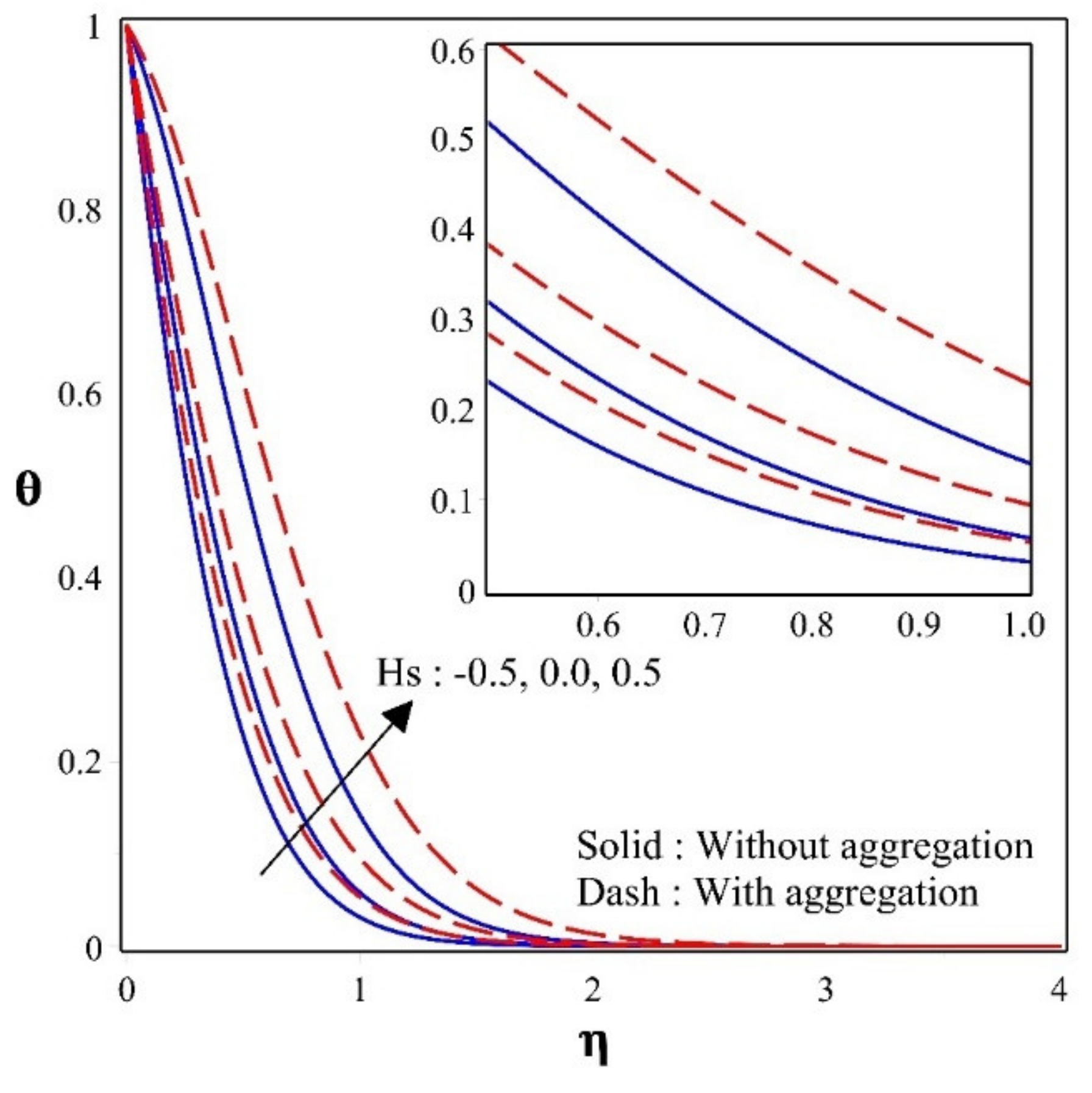
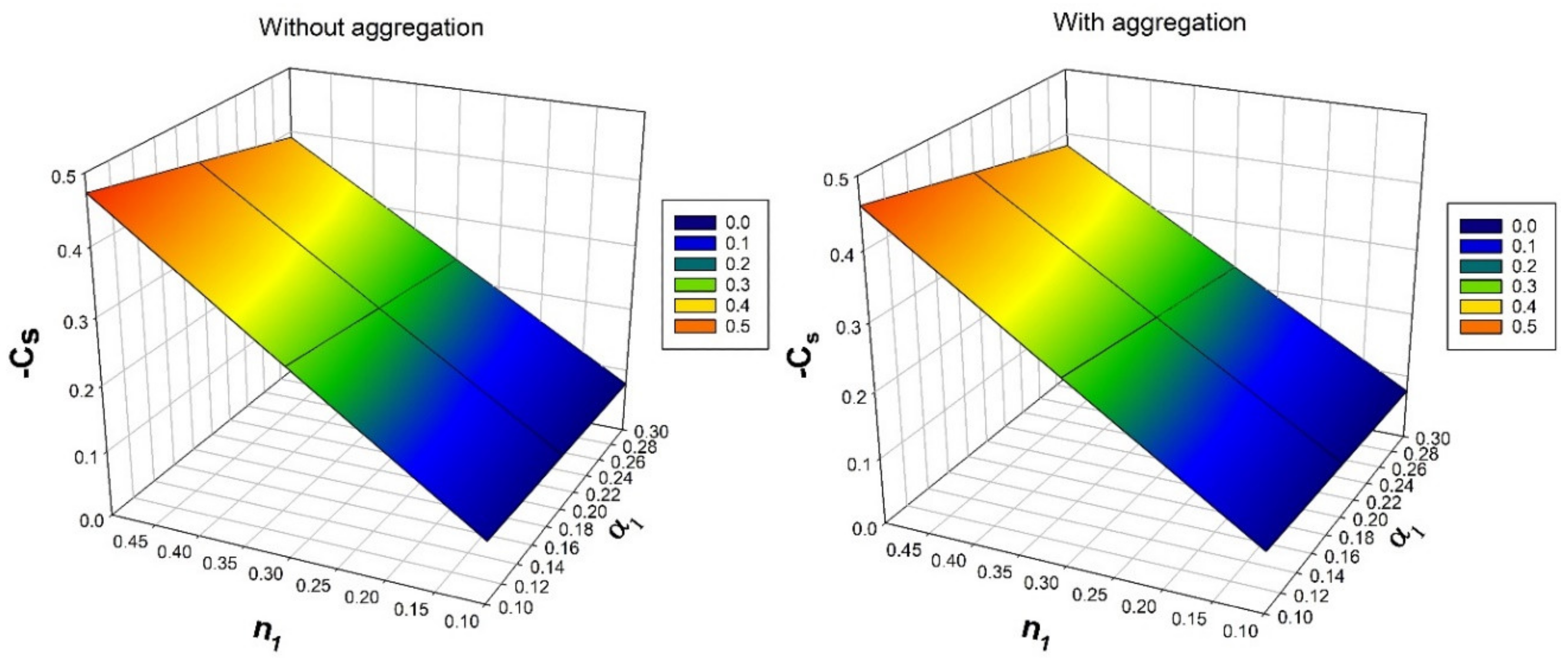
- Improvement in the values of will improve the profiles of temperature and heat transfer rate. Heat transfer gradually increases from heat sink to source.
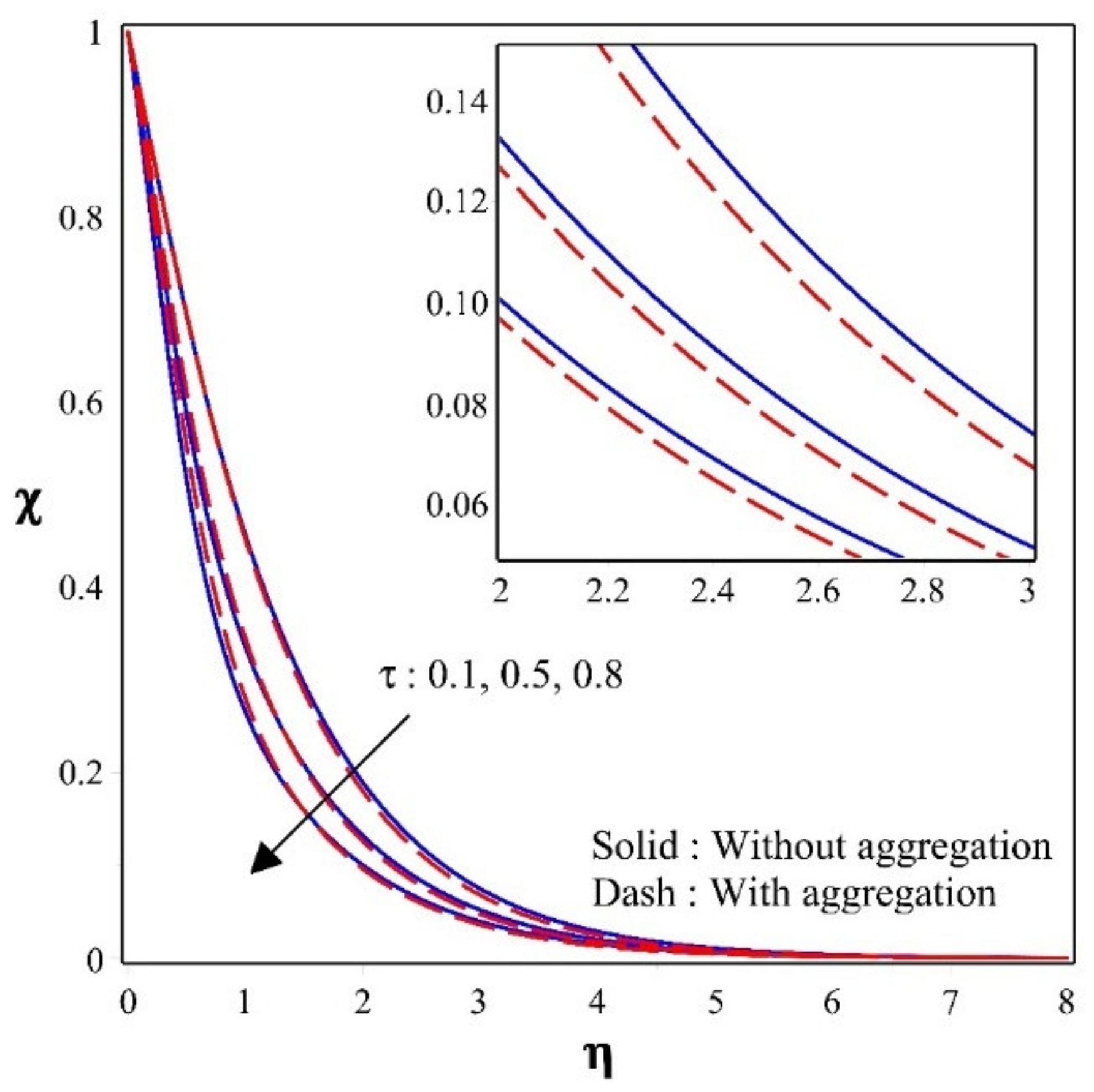
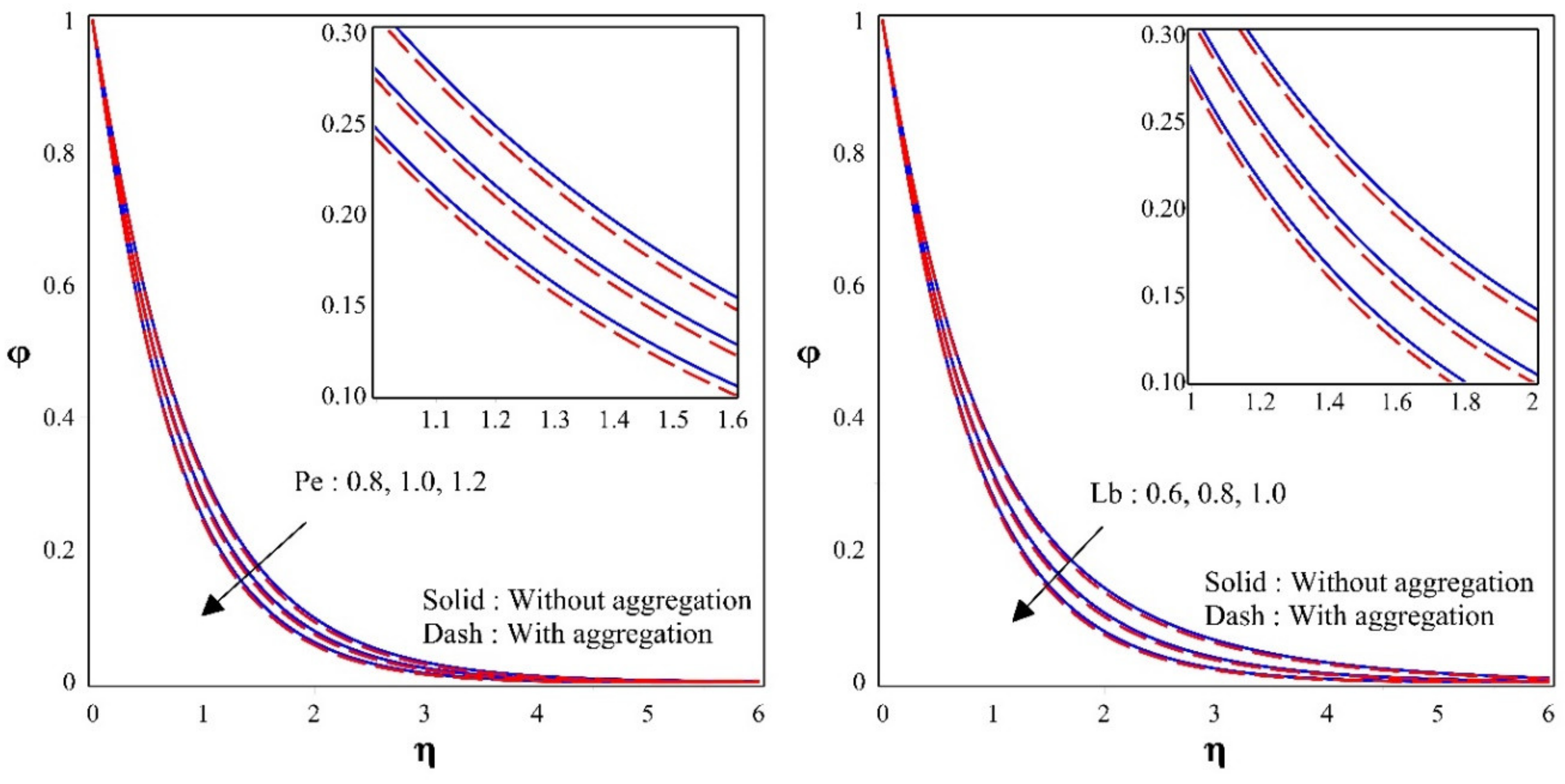
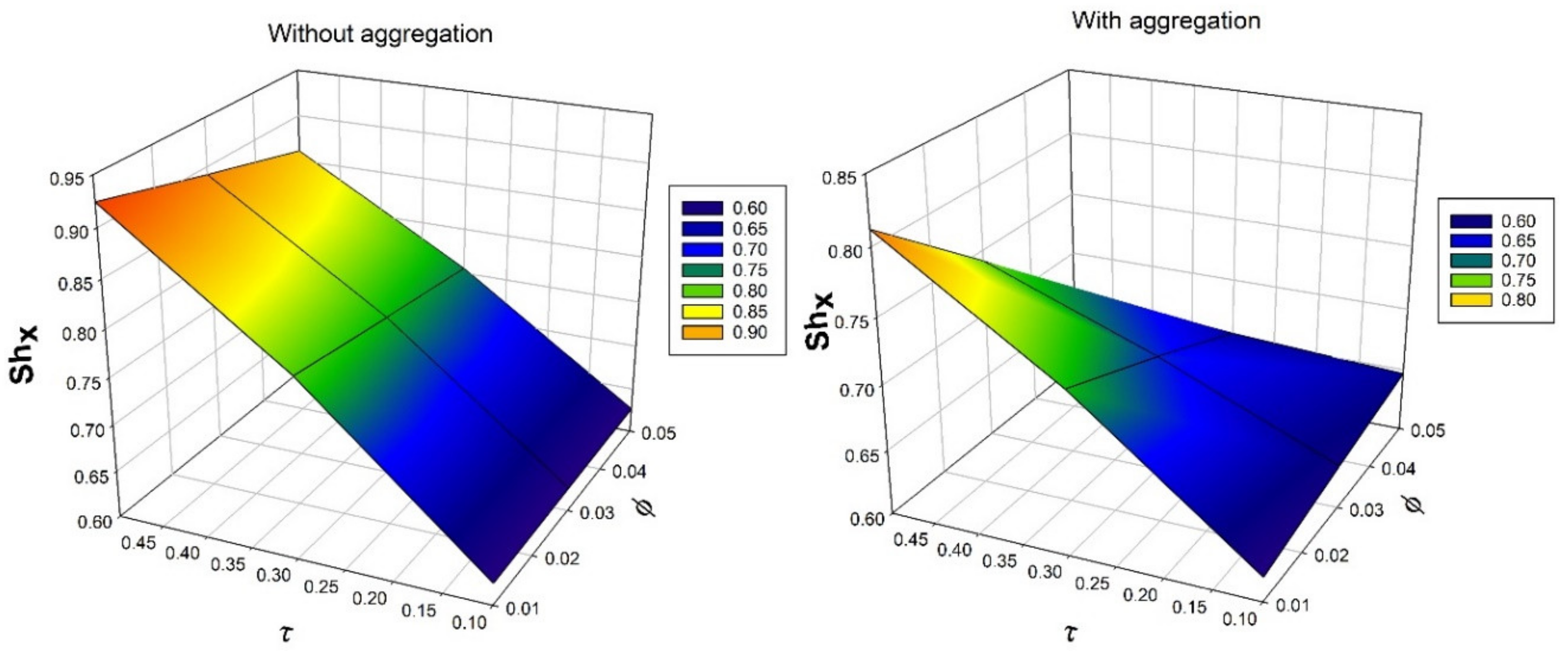
- Nanoparticles with aggregation have a lower concentration than nanoparticles without aggregation in the presence of thermophoretic parameter.
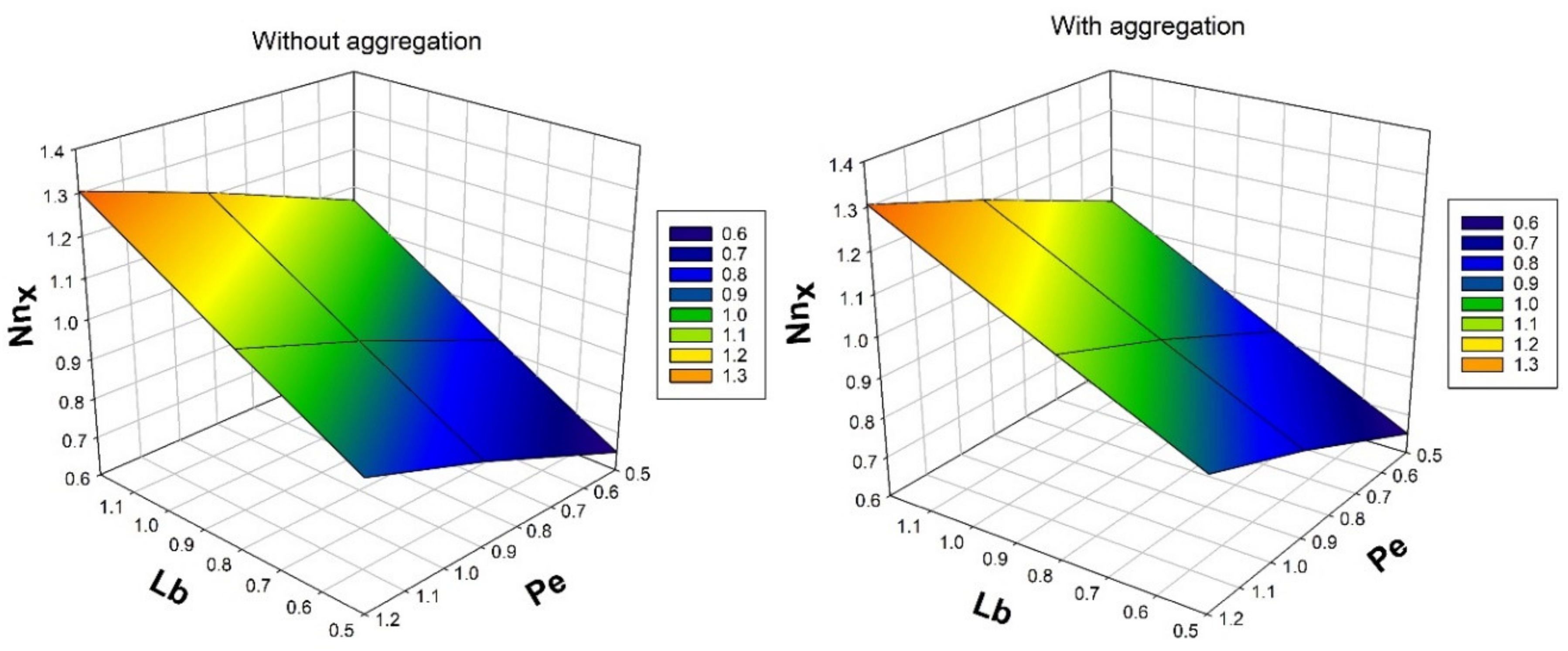
- Density number of motile microorganisms will be decreased by improved values of .
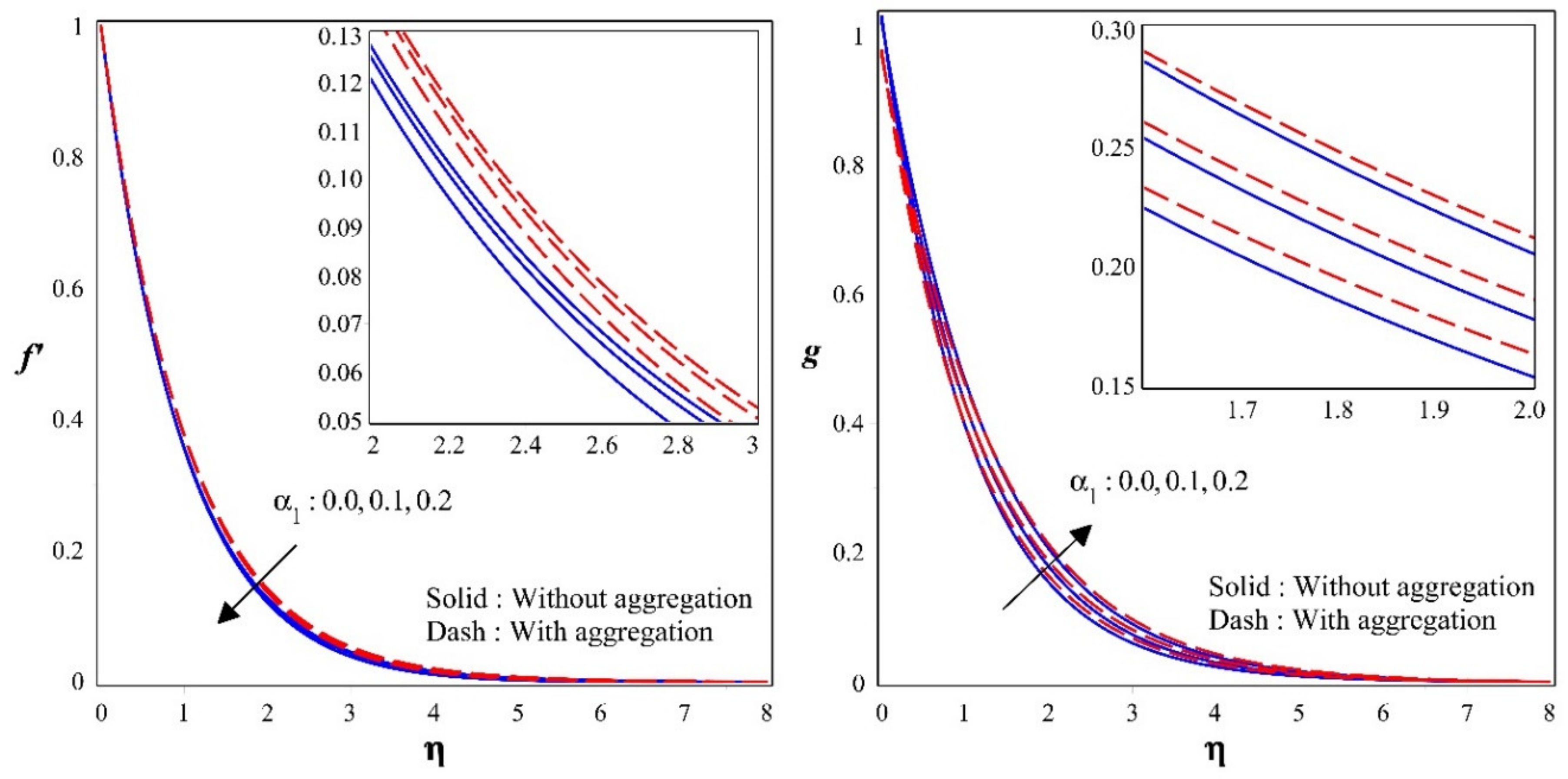
- Nanoparticle with aggregation is lesser impact in velocity profile but shows more impact in temperature, concentration and bioconvection profiles.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Stretching Constant | Microrotation Parameter | ||
| Concentration | The density of motile microorganisms at the wall | ||
| Wall and ambient concentration | The ambient density of motile microorganisms | ||
| Specific heat | Density number of motile microorganisms | ||
| Skin friction | Nusselt number | ||
| Wall couple stress factor | Bioconvection Peclet number | ||
| Diffusivity | Prandtl number | ||
| Fractal index | Radii of aggregates | ||
| Dimensionless velocity profile | Radii of nanoparticle | ||
| Dimensionless microrotation velocity profile | local Reynolds number | ||
| Heat source/sink constraint | Schmidt number | ||
| Microinertia density | Sherwood number | ||
| Thermal conductivity | Temperature | ||
| Thermal aggregation conductivity | Reference temperature | ||
| Coefficient of vortex viscosity | Wall and ambient temperature | ||
| Thermophoretic constant | Uniform velocity | ||
| Permeability of porous media | Thermophoretic velocity | ||
| Bioconvection Lewis number | Velocity components | ||
| The density of motile microorganism | Coordinate axis | ||
| Greek symbols | |||
| Spin gradient viscosity | Micropolar parameter | ||
| Porous parameter | Thermophoretic parameter | ||
| Kinematic viscosity | Concentration difference parameter | ||
| Dynamic viscosity | Density | ||
| Extreme volume fraction | Effective volume fraction of aggregates | ||
| Similarity variable | Stream function | ||
| Dimensionless temperature profile | Dimensionless bioconvection profile | ||
| Dimensionless concentration profile | Solid volume fraction | ||
| Subscripts | |||
| aggregates | Nanoparticle | ||
| Fluid | Nanofluid | ||
References
- Mehmood, R.; Rana, S.; Akbar, N.; Nadeem, S. Non-aligned stagnation point flow of radiating Casson fluid over a stretching surface. Alex. Eng. J. 2018, 57, 939–946. [Google Scholar] [CrossRef]
- Eringen, A.C. Theory of Micropolar Fluids. J. Math. Mech. 1966, 16, 1–18. [Google Scholar] [CrossRef]
- Habib, D.; Abdal, S.; Ali, R.; Baleanu, D.; Siddique, I. On bioconvection and mass transpiration of micropolar nanofluid dynamics due to an extending surface in existence of thermal radiations. Case Stud. Therm. Eng. 2021, 27, 101239. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, U.; Khan, I.; Baleanu, D.; Nisar, K.S. Stability Analysis and Dual Solutions of Micropolar Nanofluid over the Inclined Stretching/Shrinking Surface with Convective Boundary Condition. Symmetry 2020, 12, 74. [Google Scholar] [CrossRef] [Green Version]
- Madhukesh, J.K.; Prasannakumara, B.C.; Kumar, R.S.V.; Rauf, A.; Shehzad, S.A. Flow of hydromagnetic micropolar-casson nanofluid over porous disks influenced by cattaneo-christov theory and slip effects. J. Porous Media 2022, 25, 35–49. [Google Scholar] [CrossRef]
- Mabood, F.; Shamshuddin; Mishra, S. Characteristics of thermophoresis and Brownian motion on radiative reactive micropolar fluid flow towards continuously moving flat plate: HAM solution. Math. Comput. Simul. 2021, 191, 187–202. [Google Scholar] [CrossRef]
- Zaib, A.; Khan, U.; Shah, Z.; Kumam, P.; Thounthong, P. Optimization of entropy generation in flow of micropolar mixed convective magnetite (Fe3O4) ferroparticle over a vertical plate. Alex. Eng. J. 2019, 58, 1461–1470. [Google Scholar] [CrossRef]
- Khan, M.I.; Waqas, H.; Khan, S.U.; Imran, M.; Chu, Y.-M.; Abbasi, A.; Kadry, S. Slip flow of micropolar nanofluid over a porous rotating disk with motile microorganisms, nonlinear thermal radiation and activation energy. Int. Commun. Heat Mass Transf. 2021, 122, 105161. [Google Scholar] [CrossRef]
- Bahiraei, M.; Naseri, M.; Monavari, A. A second law analysis on flow of a nanofluid in a shell-and-tube heat exchanger equipped with new unilateral ladder type helical baffles. Powder Technol. 2021, 394, 234–249. [Google Scholar] [CrossRef]
- Bahiraei, M.; Naseri, M.; Monavari, A. Thermal-hydraulic performance of a nanofluid in a shell-and-tube heat exchanger equipped with new trapezoidal inclined baffles: Nanoparticle shape effect. Powder Technol. 2021, 395, 348–359. [Google Scholar] [CrossRef]
- Khan, U.; Zaib, A.; Abu Bakar, S.; Ishak, A. Unsteady stagnation-point flow of a hybrid nanofluid over a spinning disk: Analysis of dual solutions. Neural Comput. Appl. 2022, 89, 1–18. [Google Scholar] [CrossRef]
- Kumar, R.N.; Suresha, S.; Gowda, R.J.P.; Megalamani, S.B.; Prasannakumara, B.C. Exploring the impact of magnetic dipole on the radiative nanofluid flow over a stretching sheet by means of KKL model. Pramana-J. Phys. 2021, 95, 180. [Google Scholar] [CrossRef]
- Alhadhrami, A.; Alzahrani, H.A.H.; Kumar, R.N.; Gowda, R.J.P.; Sarada, K.; Prasanna, B.M.; Madhukesh, J.K.; Madhukeshwara, N. Impact of thermophoretic particle deposition on Glauert wall jet slip flow of nanofluid. Case Stud. Therm. Eng. 2021, 28, 101404. [Google Scholar] [CrossRef]
- Madhukesh, J.K.; Ramesh, G.K.; Prasannakumara, B.C.; Shehzad, S.A.; Abbasi, F.M. Bio-Marangoni convection flow of Casson nanoliquid through a porous medium in the presence of chemically reactive activation energy. Appl. Math. Mech.-Engl. Ed. 2021, 42, 1191–1204. [Google Scholar] [CrossRef]
- Muhammad, N.; Nadeem, S. Ferrite nanoparticles Ni-ZnFe2O4, Mn-ZnFe2O4 and Fe2O4 in the flow of ferromagnetic nanofluid. Eur. Phys. J. Plus 2017, 132, 377. [Google Scholar] [CrossRef]
- Guo, S.-Z.; Li, Y.; Jiang, J.-S.; Xie, H.-Q. Nanofluids Containing γ-Fe2O3 Nanoparticles and Their Heat Transfer Enhancements. Nanoscale Res. Lett. 2010, 5, 1222–1227. [Google Scholar] [CrossRef] [Green Version]
- Xie, H.; Wang, J.; Xi, T.; Liu, Y.; Ai, F.; Wu, Q. Thermal conductivity enhancement of suspensions containing nanosized alumina particles. J. Appl. Phys. 2002, 91, 4568–4572. [Google Scholar] [CrossRef]
- Wolthers, W.; Duits, M.H.G.; ven den Ende, D.; Mellema, J. Shear history dependence of the viscosity of aggregated colloidal dispersions. J. Rheol. 1996, 40, 799–811. [Google Scholar] [CrossRef]
- Mackolil, J.; Mahanthesh, B. Sensitivity analysis of Marangoni convection in TiO2–EG nanoliquid with nanoparticle aggregation and temperature-dependent surface tension. J. Therm. Anal. 2021, 143, 2085–2098. [Google Scholar] [CrossRef]
- Mahanthesh, B.; Thriveni, K.; Rana, P.; Muhammad, T. Radiative heat transfer of nanomaterial on a convectively heated circular tube with activation energy and nanoparticle aggregation kinematic effects. Int. Commun. Heat Mass Transf. 2021, 127, 105568. [Google Scholar] [CrossRef]
- Kolsi, L.; Oztop, H.F.; Ghachem, K.; Almeshaal, M.A.; Mohammed, H.A.; Babazadeh, H.; Abu-Hamdeh, N. Numerical Study of Periodic Magnetic Field Effect on 3D Natural Convection of MWCNT-Water/Nanofluid with Consideration of Aggregation. Processes 2019, 7, 957. [Google Scholar] [CrossRef] [Green Version]
- Mackolil, J.; Mahanthesh, B. Inclined magnetic field and nanoparticle aggregation effects on thermal Marangoni convection in nanoliquid: A sensitivity analysis. Chin. J. Phys. 2021, 69, 24–37. [Google Scholar] [CrossRef]
- Saleh, B.; Madhukesh, J.K.; Kumar, R.S.V.; Afzal, A.; Abdelrhman, Y.; Aly, A.A.; Gowda, R.J.P. Aspects of magnetic dipole and heat source/sink on the Maxwell hybrid nanofluid flow over a stretching sheet. Proc. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2022, 09544089211056243. [Google Scholar] [CrossRef]
- Madhukesh, J.; Ramesh, G.; Aly, E.H.; Chamkha, A.J. Dynamics of water conveying SWCNT nanoparticles and swimming microorganisms over a Riga plate subject to heat source/sink. Alex. Eng. J. 2021, 61, 2418–2429. [Google Scholar] [CrossRef]
- Sajid, T.; Jamshed, W.; Shahzad, F.; Eid, M.R.; Alshehri, H.M.; Goodarzi, M.; Akgül, E.K.; Nisar, K.S. Micropolar fluid past a convectively heated surface embedded with nth order chemical reaction and heat source/sink. Phys. Scr. 2021, 96, 104010. [Google Scholar] [CrossRef]
- Khan, S.U.; Shehzad, S.A.; Rauf, A.; Ali, N. Mixed convection flow of couple stress nanofluid over oscillatory stretching sheet with heat absorption/generation effects. Results Phys. 2018, 8, 1223–1231. [Google Scholar] [CrossRef]
- Chu, Y.-M.; Khan, U.; Shafiq, A.; Zaib, A. Numerical Simulations of Time-Dependent Micro-Rotation Blood Flow Induced by a Curved Moving Surface Through Conduction of Gold Particles with Non-uniform Heat Sink/Source. Arab. J. Sci. Eng. 2021, 46, 2413–2427. [Google Scholar] [CrossRef]
- Shehzad, S.; Mabood, F.; Rauf, A.; Tlili, I. Forced convective Maxwell fluid flow through rotating disk under the thermophoretic particles motion. Int. Commun. Heat Mass Transf. 2020, 116, 104693. [Google Scholar] [CrossRef]
- Kumar, R.N.; Gowda, R.J.P.; Madhukesh, J.K.; Prasannakumara, B.C.; Ramesh, G.K. Impact of thermophoretic particle deposition on heat and mass transfer across the dynamics of Casson fluid flow over a moving thin needle. Phys. Scr. 2021, 96, 075210. [Google Scholar] [CrossRef]
- Shankaralingappa, B.M.; Madhukesh, J.K.; Sarris, I.E.; Gireesha, B.J.; Prasannakumara, B.C. Influence of Thermophoretic Particle Deposition on the 3D Flow of Sodium Alginate-Based Casson Nanofluid over a Stretching Sheet. Micromachines 2021, 12, 1474. [Google Scholar] [CrossRef]
- Hafeez, A.; Khan, M.; Ahmed, J. Oldroyd-B fluid flow over a rotating disk subject to Soret–Dufour effects and thermophoresis particle deposition. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 235, 2408–2415. [Google Scholar] [CrossRef]
- Chen, S.-B.; Shahmir, N.; Ramzan, M.; Sun, Y.-L.; Aly, A.A.; Malik, M.Y. Thermophoretic particle deposition in the flow of dual stratified Casson fluid with magnetic dipole and generalized Fourier’s and Fick’s laws. Case Stud. Therm. Eng. 2021, 26, 101186. [Google Scholar] [CrossRef]
- Ali, B.; Shafiq, A.; Manan, A.; Wakif, A.; Hussain, S. Bioconvection: Significance of mixed convection and mhd on dynamics of Casson nanofluid in the stagnation point of rotating sphere via finite element simulation. Math. Comput. Simul. 2021, 194, 254–268. [Google Scholar] [CrossRef]
- Alqarni, M.S.; Waqas, H.; Alghamdi, M.; Muhammad, T. Importance of bioconvection in 3D viscoelastic nanofluid flow due to exponentially stretching surface with nonlinear radiative heat transfer and variable thermal conductivity. J. Therm. Anal. 2021, 147, 4805–4819. [Google Scholar] [CrossRef]
- Wakif, A.; Animasaun, I.L.; Khan, U.; Alshehri, A.M. Insights into the Generalized Fourier’s and Fick’s Laws for Simulating Mixed Bioconvective Flows of Radiative-Reactive Walters-B Fluids Conveying Tiny Particles subject to Lorentz Force. Preprint 2021. [Google Scholar] [CrossRef]
- Farooq, U.; Waqas, H.; Khan, M.I.; Khan, S.U.; Chu, Y.-M.; Kadry, S. Thermally radioactive bioconvection flow of Carreau nanofluid with modified Cattaneo-Christov expressions and exponential space-based heat source. Alex. Eng. J. 2021, 60, 3073–3086. [Google Scholar] [CrossRef]
- Naganthran, K.; Basir, F.M.; Thumma, T.; Ige, E.O.; Nazar, R.; Tlili, I. Scaling group analysis of bioconvective micropolar fluid flow and heat transfer in a porous medium. J. Therm. Anal. 2021, 143, 1943–1955. [Google Scholar] [CrossRef]
- Kumar, T.; Kumar, B.R.; Makinde, O.D.; Kumar, A.V. Magneto-Convective Heat Transfer in Micropolar Nanofluid over a Stretching Sheet with Non-Uniform Heat Source/Sink. Defect Diffus. Forum 2018, 387, 78–90. [Google Scholar] [CrossRef]
- Alam Khan, N.; Sultan, F.; Alam Khan, N. Heat and Mass Transfer of Thermophoretic MHD Flow of Powell–Eyring Fluid over a Vertical Stretching Sheet in the Presence of Chemical Reaction and Joule Heating. Int. J. Chem. React. Eng. 2015, 13, 37–49. [Google Scholar] [CrossRef]
- Mahanthesh, B. Flow and heat transport of nanomaterial with quadratic radiative heat flux and aggregation kinematics of nanoparticles. Int. Commun. Heat Mass Transf. 2021, 127, 105521. [Google Scholar] [CrossRef]
- Chen, J.; Zhao, C.; Wang, B. Effect of nanoparticle aggregation on the thermal radiation properties of nanofluids: An experimental and theoretical study. Int. J. Heat Mass Transf. 2020, 154, 119690. [Google Scholar] [CrossRef]
- Mahanthesh, B.; Thriveni, K. Nanoparticle aggregation effects on radiative heat transport of nanoliquid over a vertical cylinder with sensitivity analysis. Appl. Math. Mech.-Engl. Ed. 2021, 42, 331–346. [Google Scholar] [CrossRef]
- Ellahi, R.; Hassan, M.; Zeeshan, A. Aggregation effects on water base Al2O3-nanofluid over permeable wedge in mixed convection: Aggregation effects on water base Al2O3. Asia-Pacific J. Chem. Eng. 2016, 11, 179–186. [Google Scholar] [CrossRef]
- Chen, H.; Witharana, S.; Jin, Y.; Kim, C.; Ding, Y. Predicting thermal conductivity of liquid suspensions of nanoparticles (nanofluids) based on rheology. Particuology 2009, 7, 151–157. [Google Scholar] [CrossRef]
- Chen, H.; Ding, Y.; He, Y.; Tan, C. Rheological behaviour of ethylene glycol based titania nanofluids. Chem. Phys. Lett. 2007, 444, 333–337. [Google Scholar] [CrossRef]
- Pal, D.; Mandal, G. Thermal radiation and MHD effects on boundary layer flow of micropolar nanofluid past a stretching sheet with non-uniform heat source/sink. Int. J. Mech. Sci. 2017, 126, 308–318. [Google Scholar] [CrossRef]
- Fauzi, E.L.A.; Ahmad, S.; Pop, I. Flow over a permeable stretching sheet in micropolar nanofluids with suction. In Proceedings of the AIP Conference Proceedings, American Institute of Physics, Penang, Malaysia, 10 July 2014; Volume 1605, pp. 428–433. [Google Scholar] [CrossRef]
- Nazar, R.; Amin, N.; Filip, D.; Pop, I. Stagnation point flow of a micropolar fluid towards a stretching sheet. Int. J. Non-linear Mech. 2004, 39, 1227–1235. [Google Scholar] [CrossRef]

| S. No | Properties | Expressions for Nanofluid |
|---|---|---|
| 01 | Viscosity | |
| 02 | Density | |
| 03 | Heat capacity | |
| 04 | Thermal conductivity |
| Properties | Titanium Dioxide | Water |
|---|---|---|
| 4250 | 997.1 | |
| 686.2 | 4179 | |
| 8.9538 | 0.613 | |
| Pr | - | 6.2 |
| Present Study | ||
|---|---|---|
| 0.0 | 0.0 | −1.0000 |
| - | 1.0 | −1.3678 |
| - | 2.0 | −1.6211 |
| - | 4.0 | −2.0040 |
| 0.5 | 0.0 | −1.0000 |
| - | 1.0 | −1.2246 |
| - | 2.0 | −1.4140 |
| - | 4.0 | −1.7319 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Y.; Madhukesh, J.K.; Khan, U.; Zaib, A.; Abdel-Aty, A.-H.; Yahia, I.S.; Alqahtani, M.S.; Wang, F.; Galal, A.M. Nanoparticle Aggregation and Thermophoretic Particle Deposition Process in the Flow of Micropolar Nanofluid over a Stretching Sheet. Nanomaterials 2022, 12, 977. https://doi.org/10.3390/nano12060977
Yu Y, Madhukesh JK, Khan U, Zaib A, Abdel-Aty A-H, Yahia IS, Alqahtani MS, Wang F, Galal AM. Nanoparticle Aggregation and Thermophoretic Particle Deposition Process in the Flow of Micropolar Nanofluid over a Stretching Sheet. Nanomaterials. 2022; 12(6):977. https://doi.org/10.3390/nano12060977
Chicago/Turabian StyleYu, Yangyang, Javali K. Madhukesh, Umair Khan, Aurang Zaib, Abdel-Haleem Abdel-Aty, Ibrahim S. Yahia, Mohammed S. Alqahtani, Fuzhang Wang, and Ahmed M. Galal. 2022. "Nanoparticle Aggregation and Thermophoretic Particle Deposition Process in the Flow of Micropolar Nanofluid over a Stretching Sheet" Nanomaterials 12, no. 6: 977. https://doi.org/10.3390/nano12060977
APA StyleYu, Y., Madhukesh, J. K., Khan, U., Zaib, A., Abdel-Aty, A.-H., Yahia, I. S., Alqahtani, M. S., Wang, F., & Galal, A. M. (2022). Nanoparticle Aggregation and Thermophoretic Particle Deposition Process in the Flow of Micropolar Nanofluid over a Stretching Sheet. Nanomaterials, 12(6), 977. https://doi.org/10.3390/nano12060977









