Micromagnetic Design of Skyrmionic Materials and Chiral Magnetic Configurations in Patterned Nanostructures for Neuromorphic and Qubit Applications
Abstract
1. Introduction
2. Materials and Methods
2.1. General Issues about Skyrmions
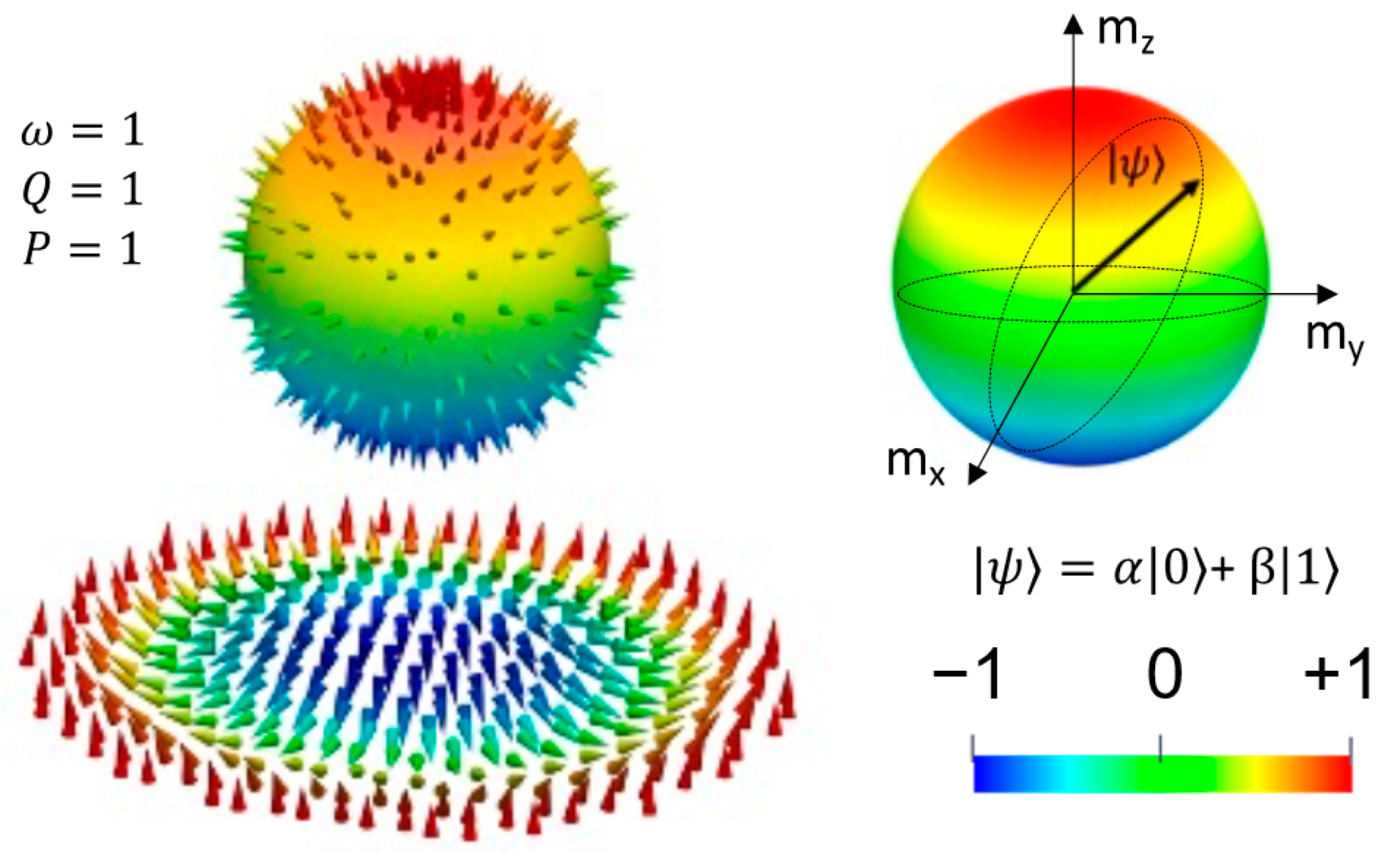
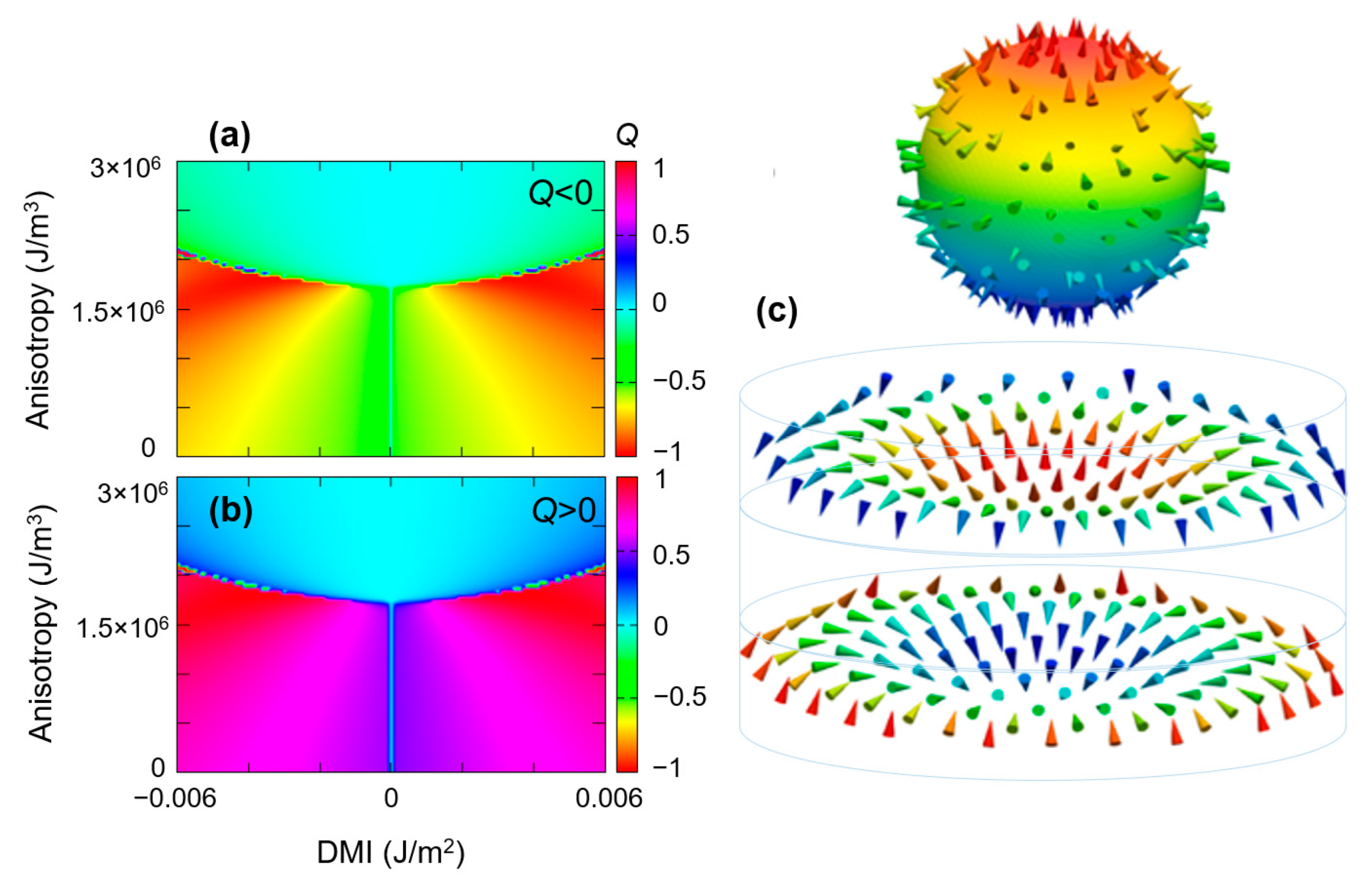
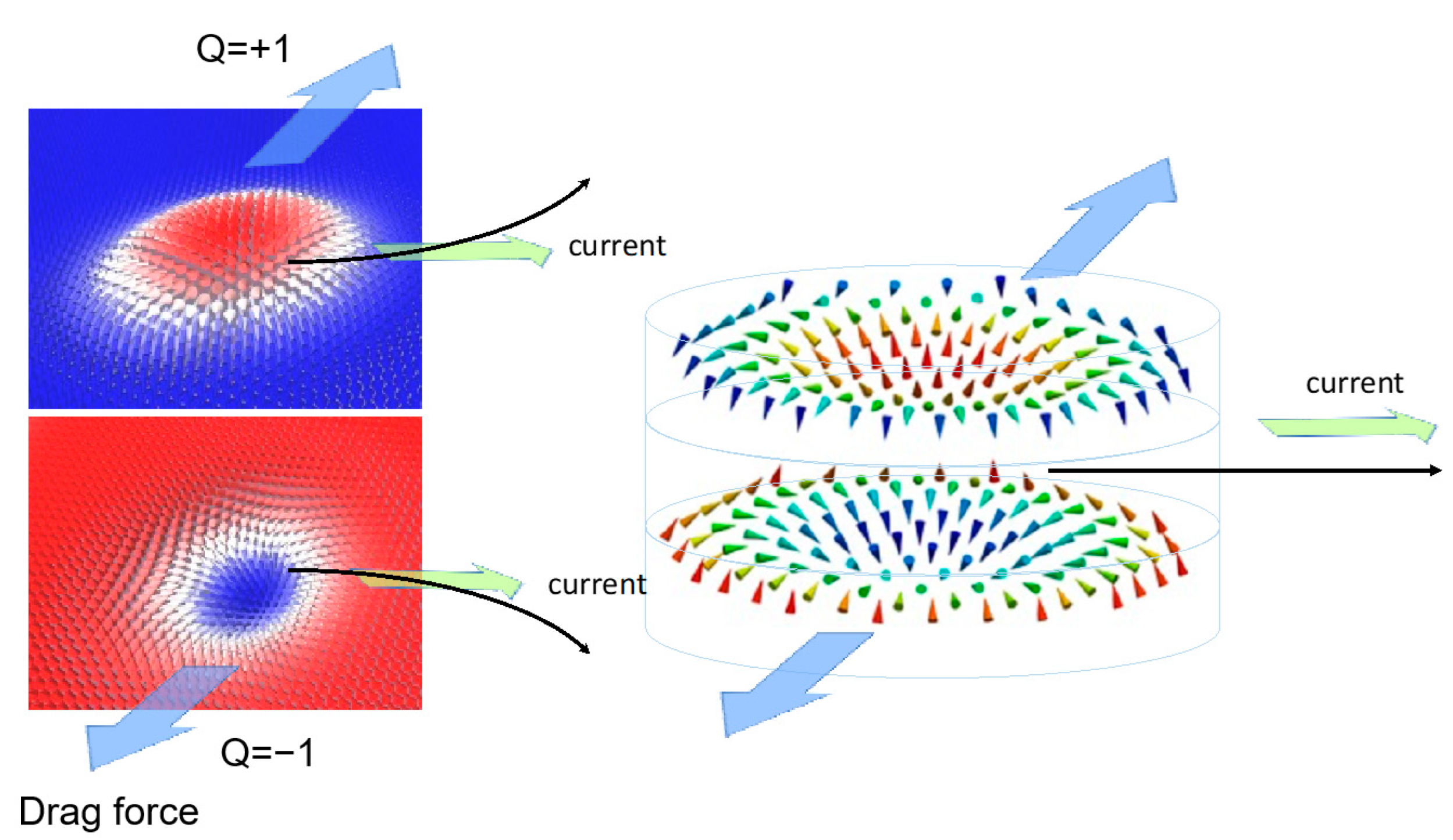
- The topological charge or the winding number Q = |1| that describes how many times the magnetization vector m can be mapped onto a sphere: . In saturated magnetic states Q = 0, Q = |0.5|for magnetic vortices, and more complex structures that wrapping the Bloch sphere multiple times Q >|1|.
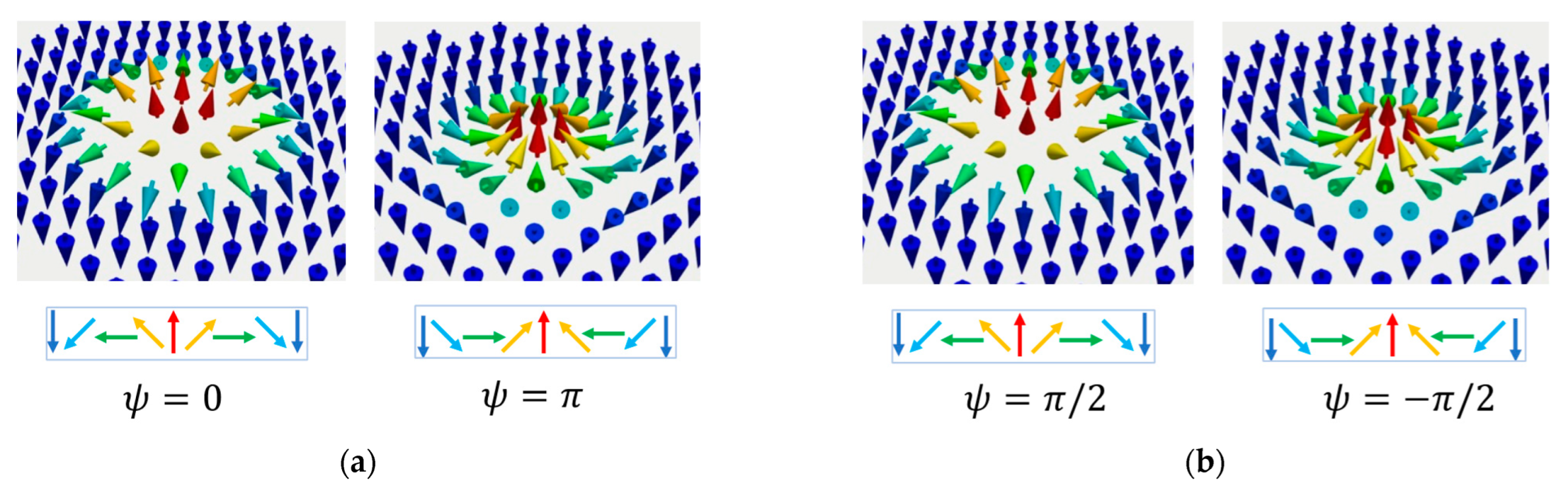
- The vorticity (chirality) ω = +/−1; ω = ((end) − θ(start))/2π. The sign of ω and Q are directly related to the orientation of the skyrmion core: P = ω·Q = 1/−1 for up/down, respectively; topological charge calculated from vorticity .
- The helicity is uniquely determined by the type of DMI that occurs in the energetic competition (bulk or surface): for a Néel skyrmion and for a Bloch skyrmion.
2.2. Ab-Initio Calculations of Magnetic Properties
2.3. Micromagnetic Modeling Tools
3. Results
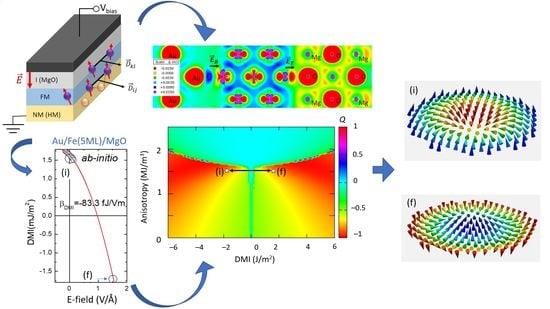
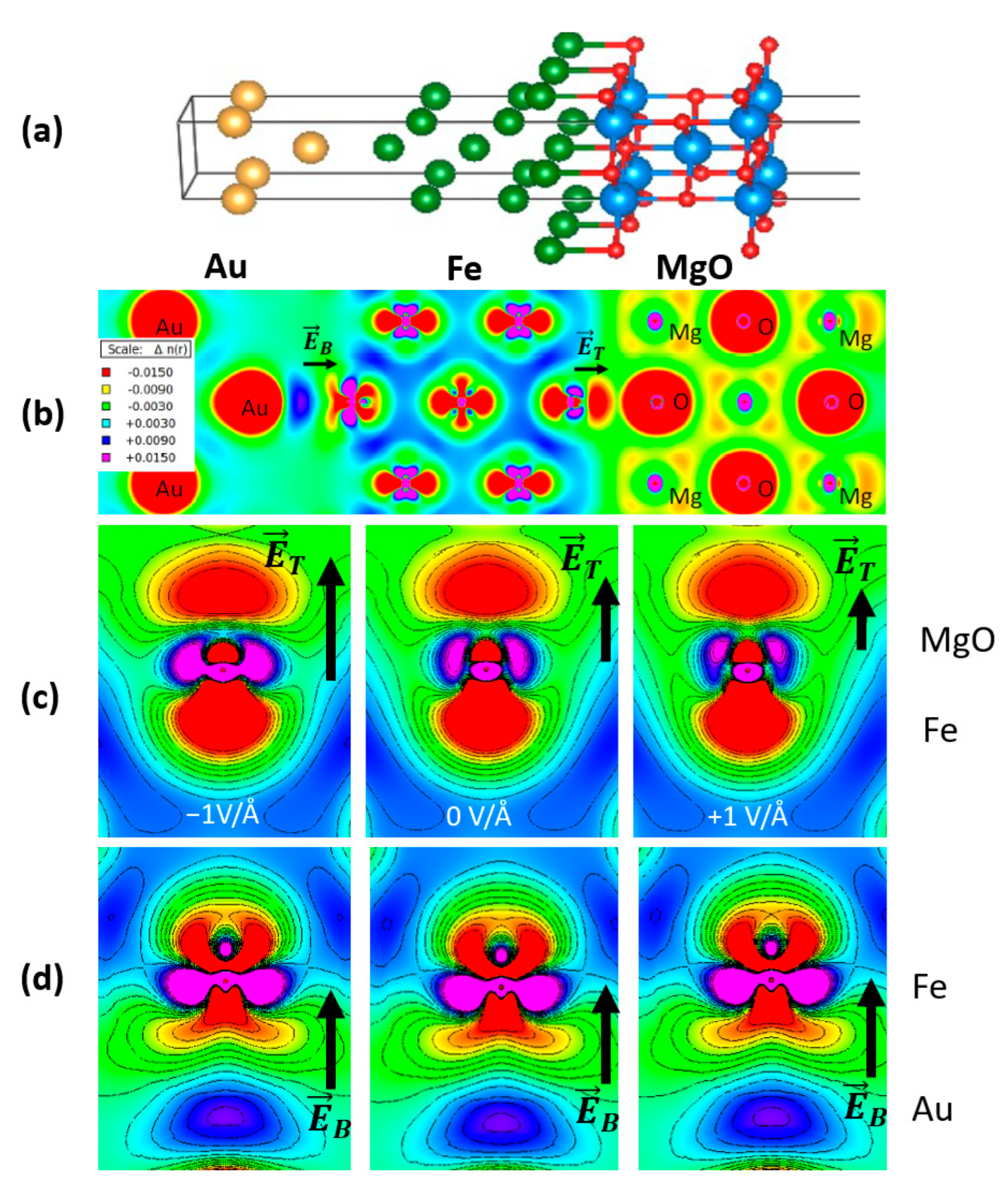
3.1. Ab-initio Calculations of Multilayer Stacks
3.2. Micromagnetic Design of Skyrmionic Materials
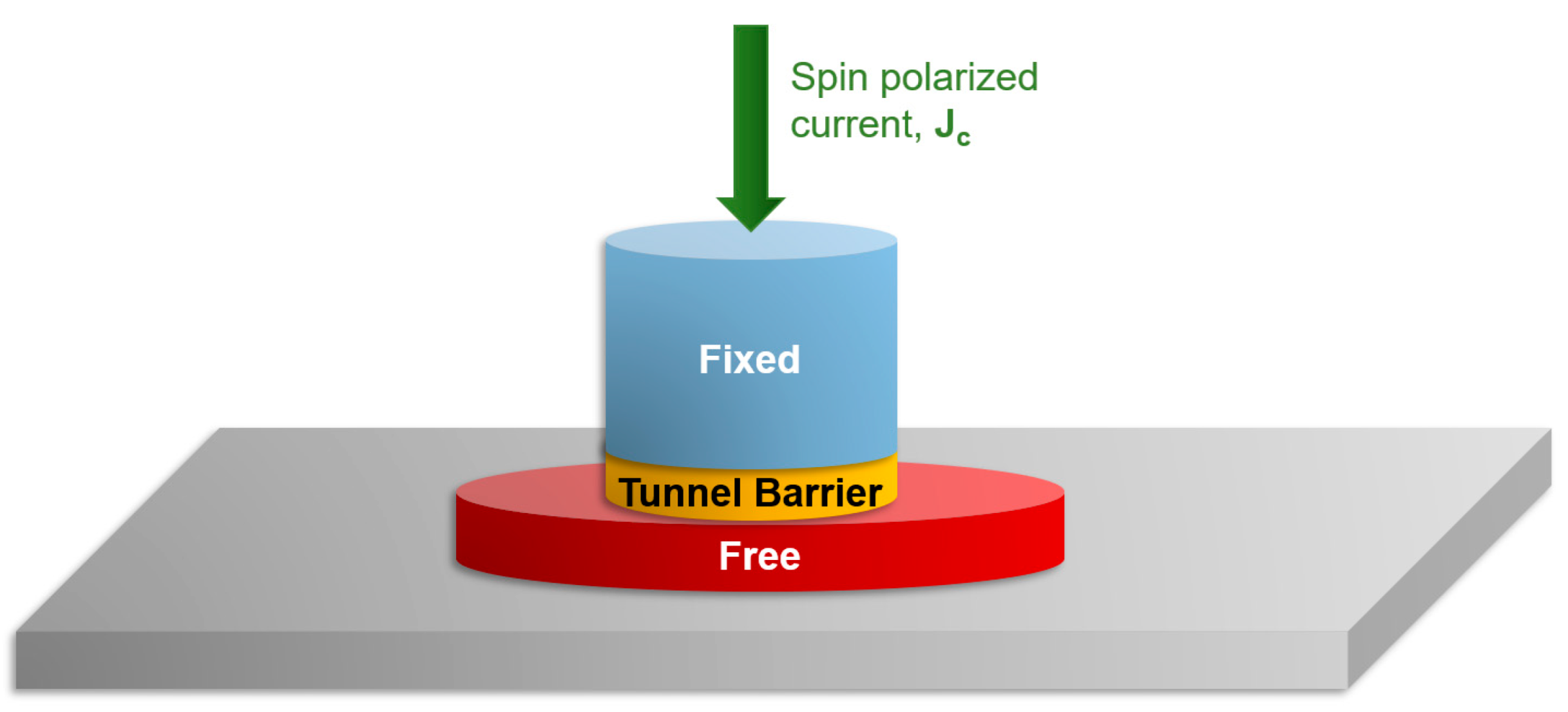
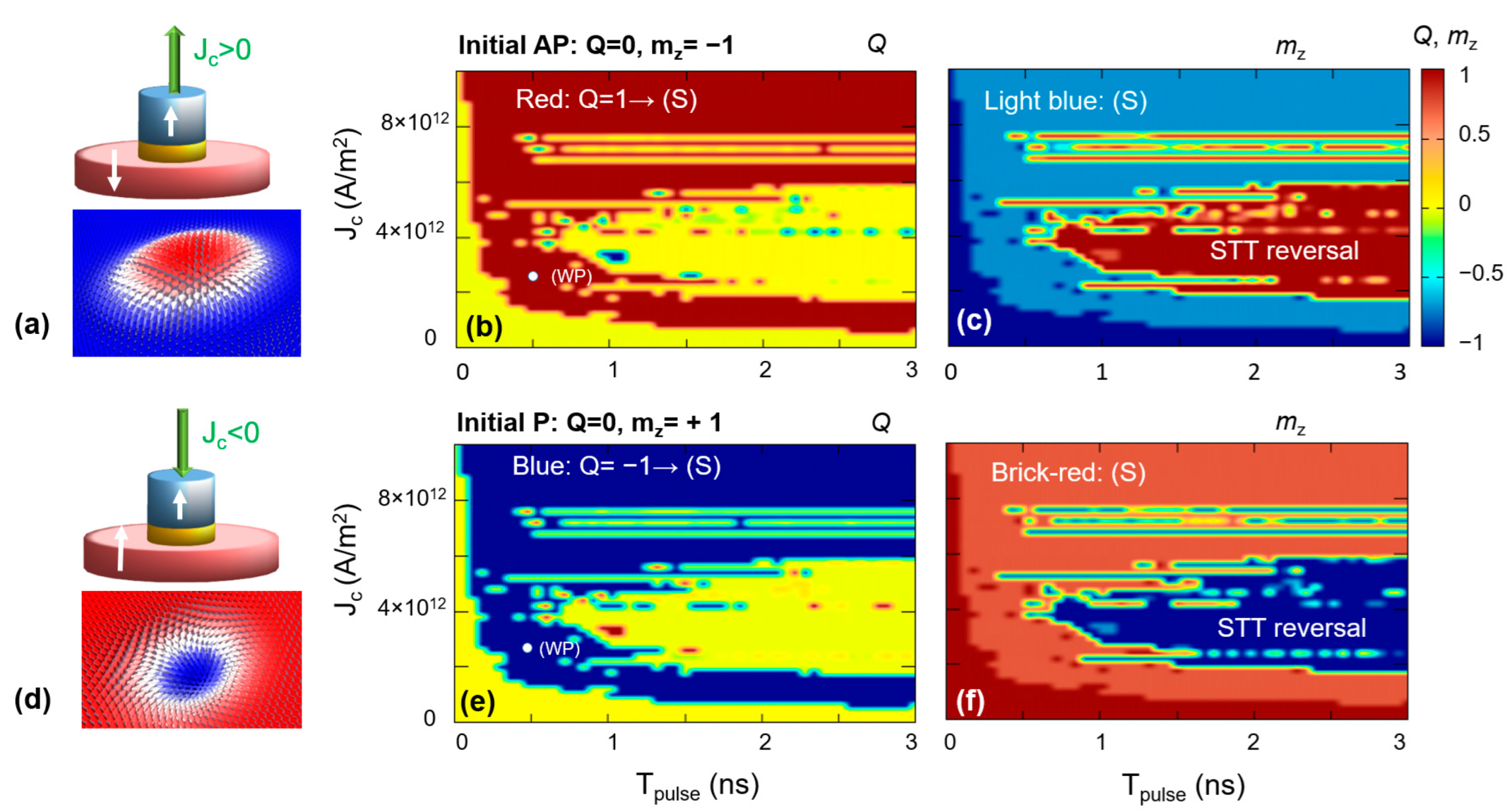
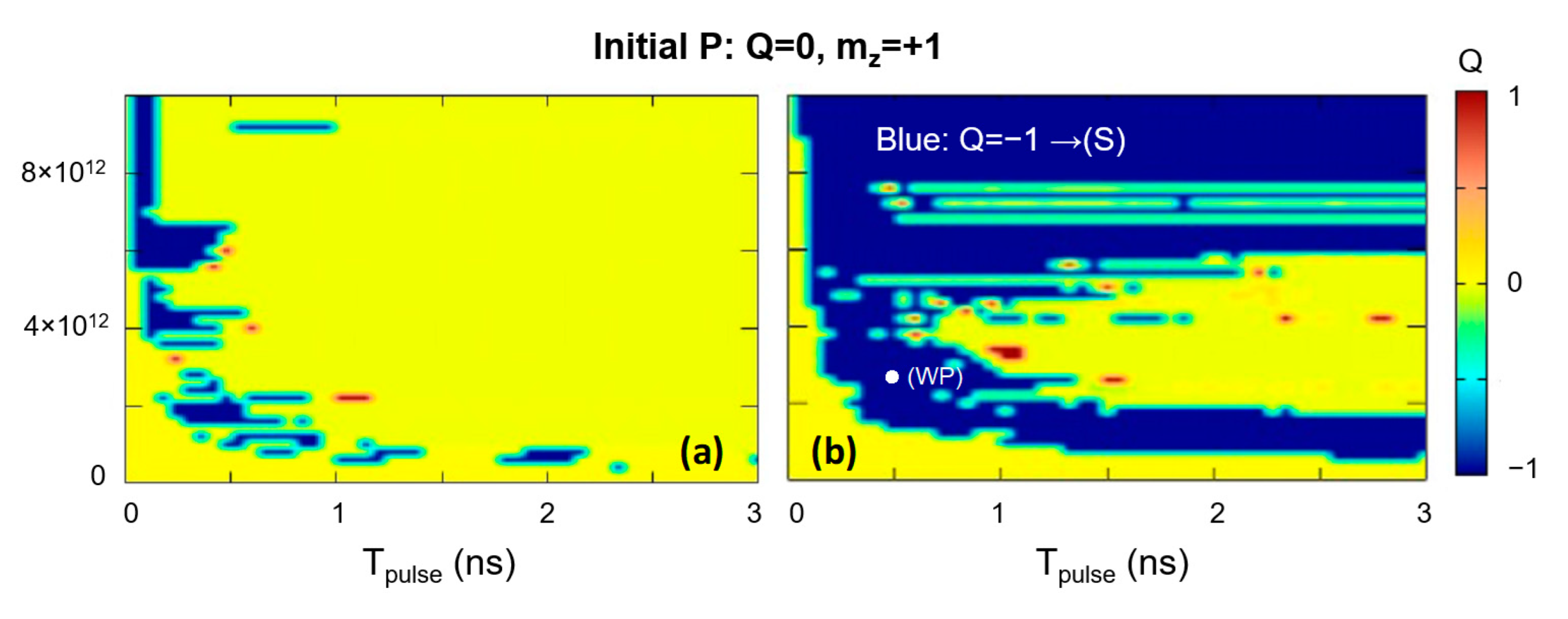
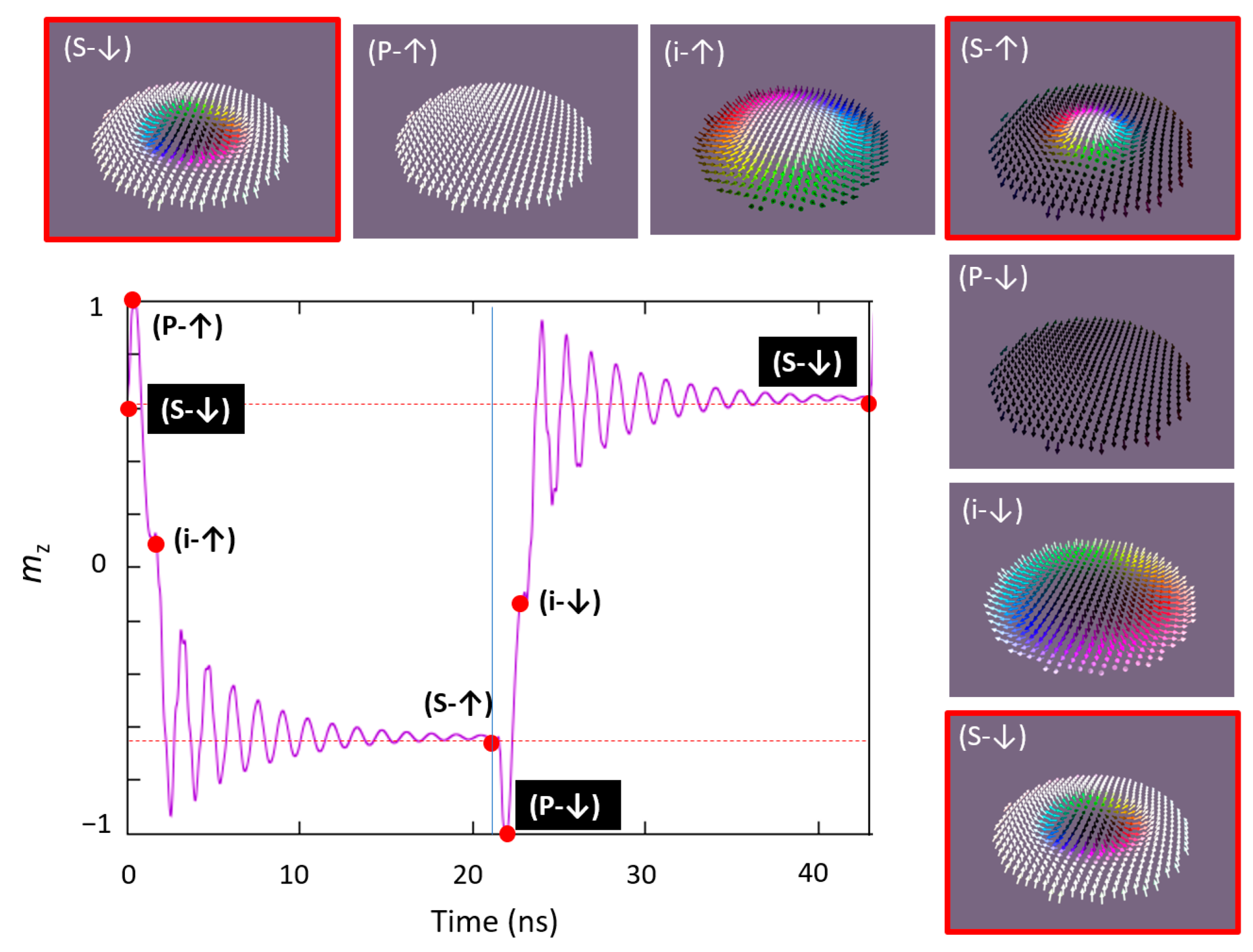
3.2.1. Injection of Skyrmions by STT in Patterned Nanodisks
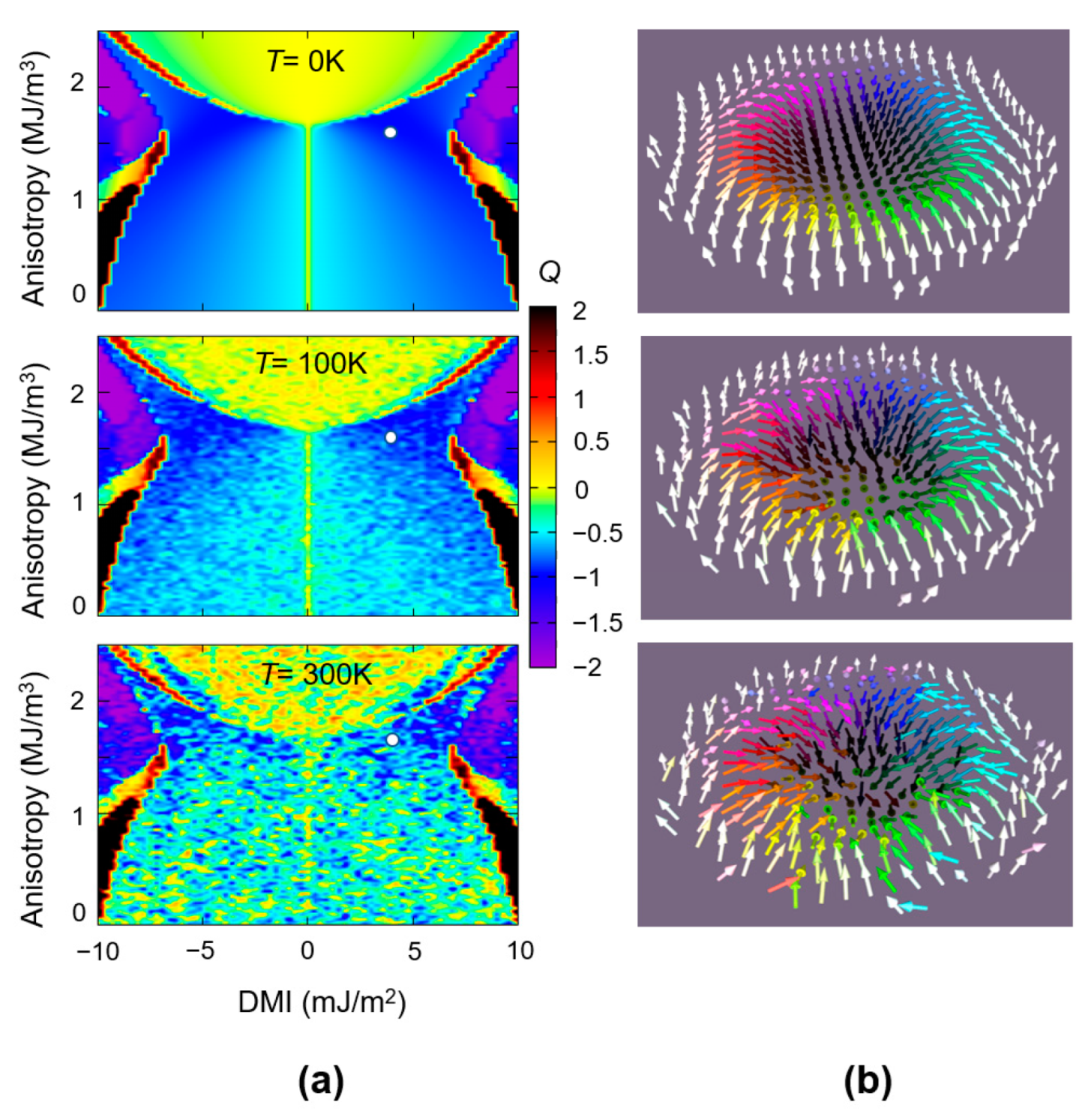
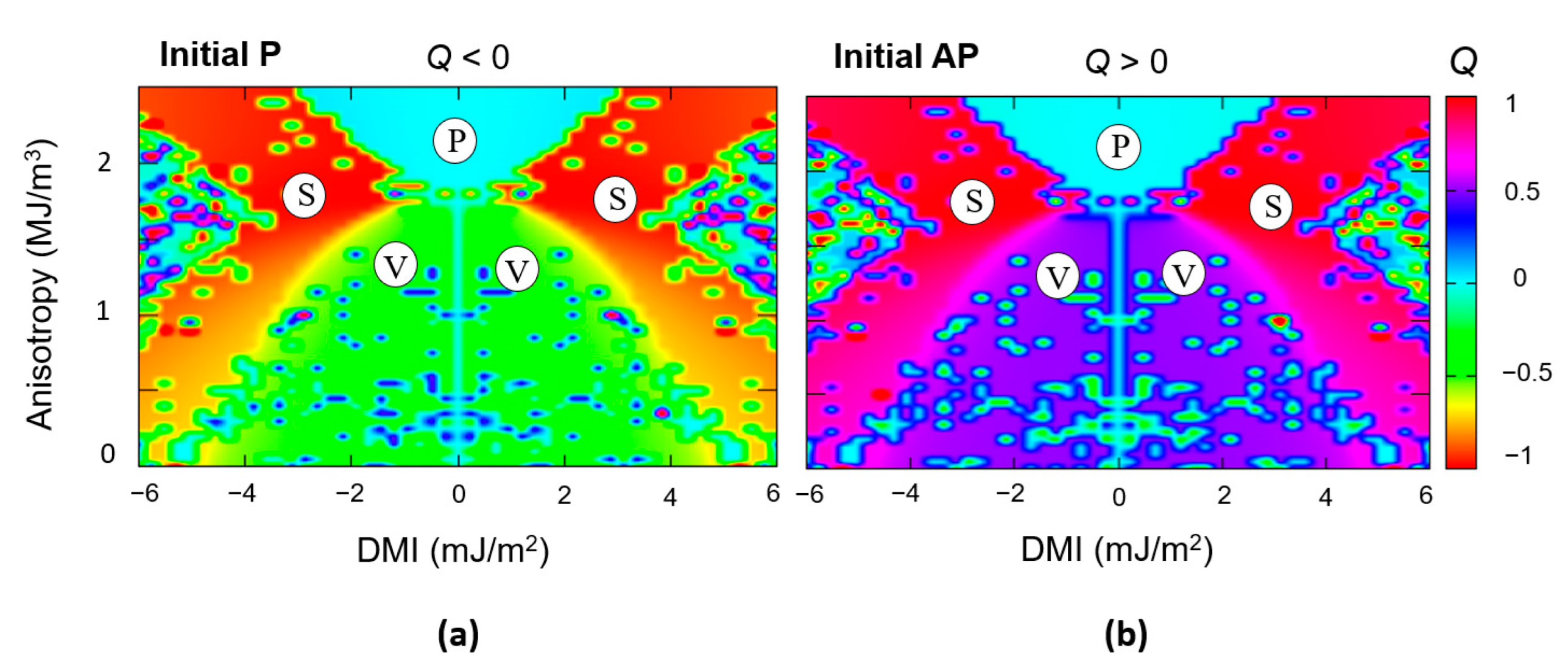
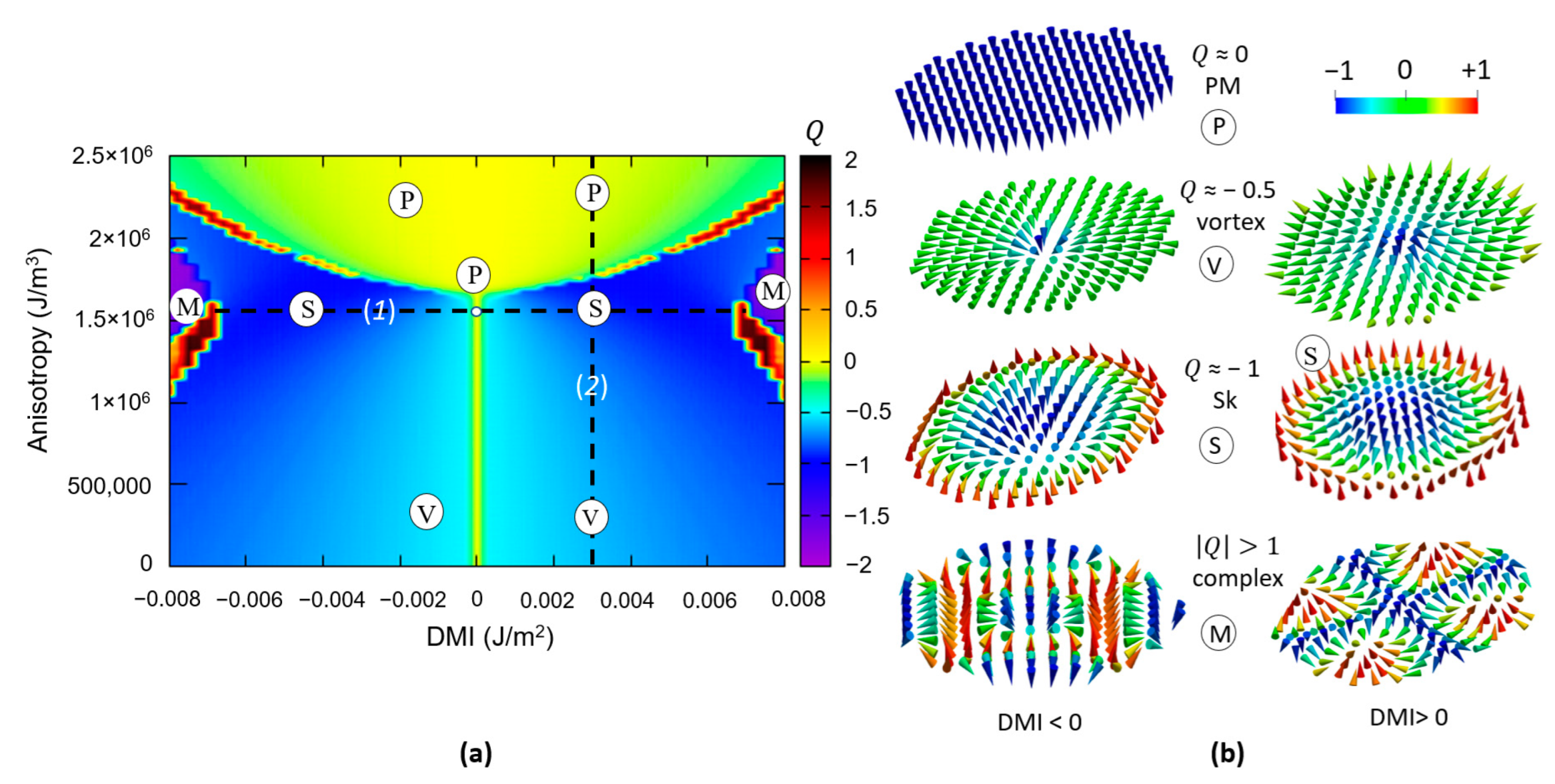
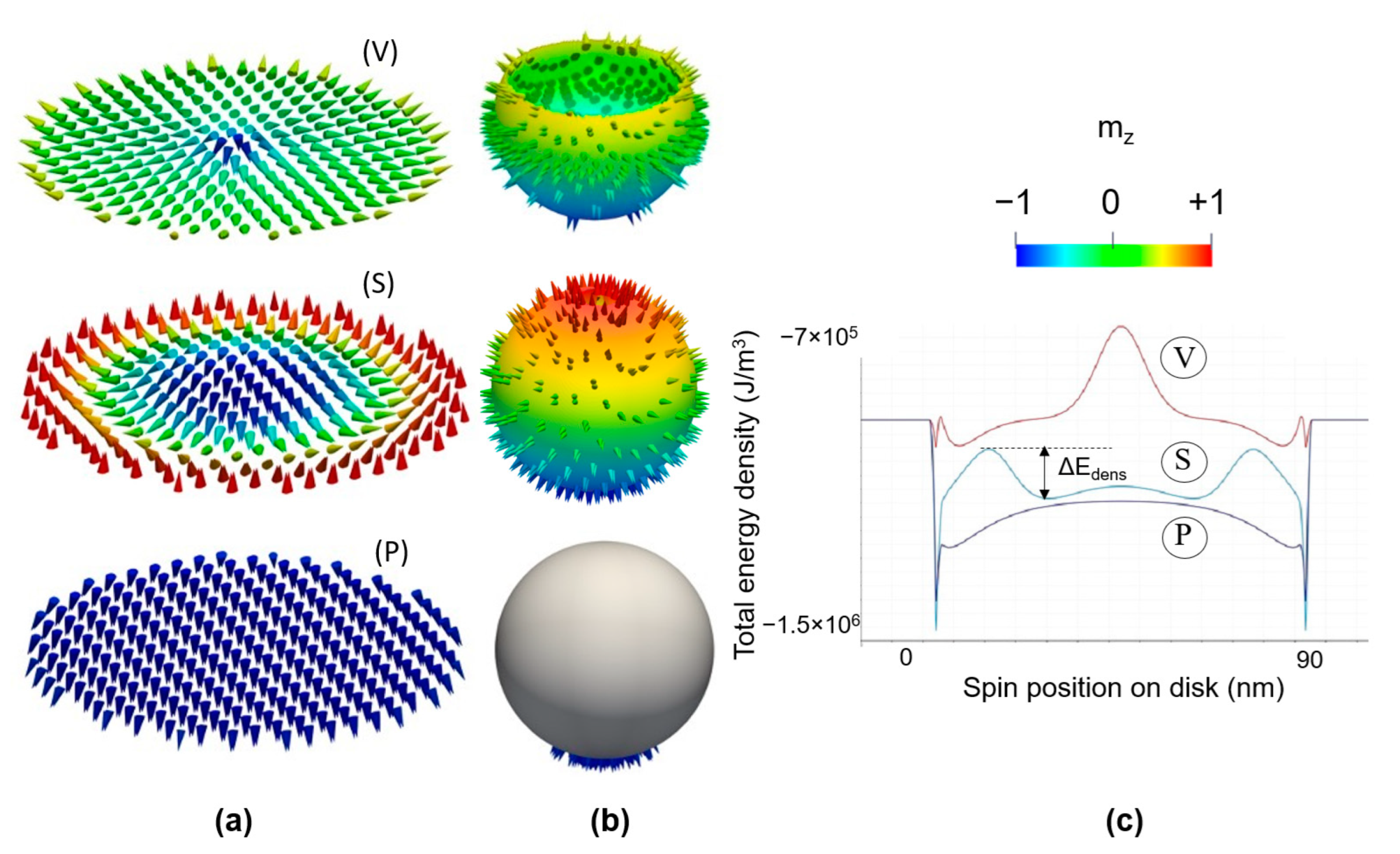
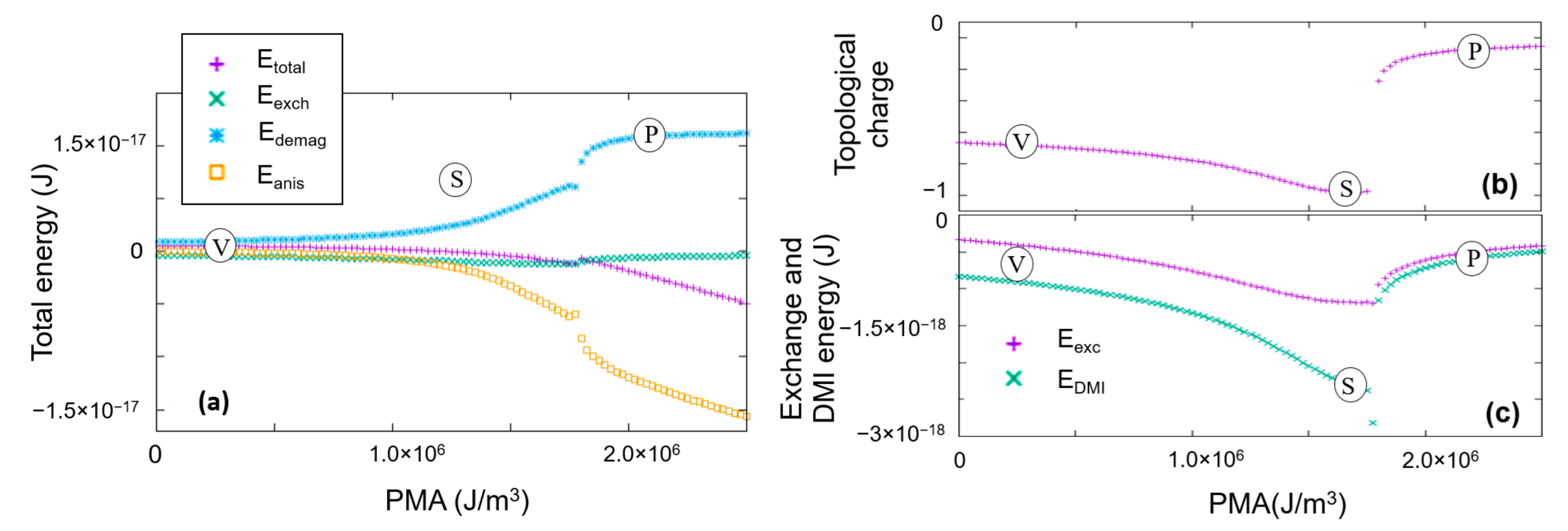
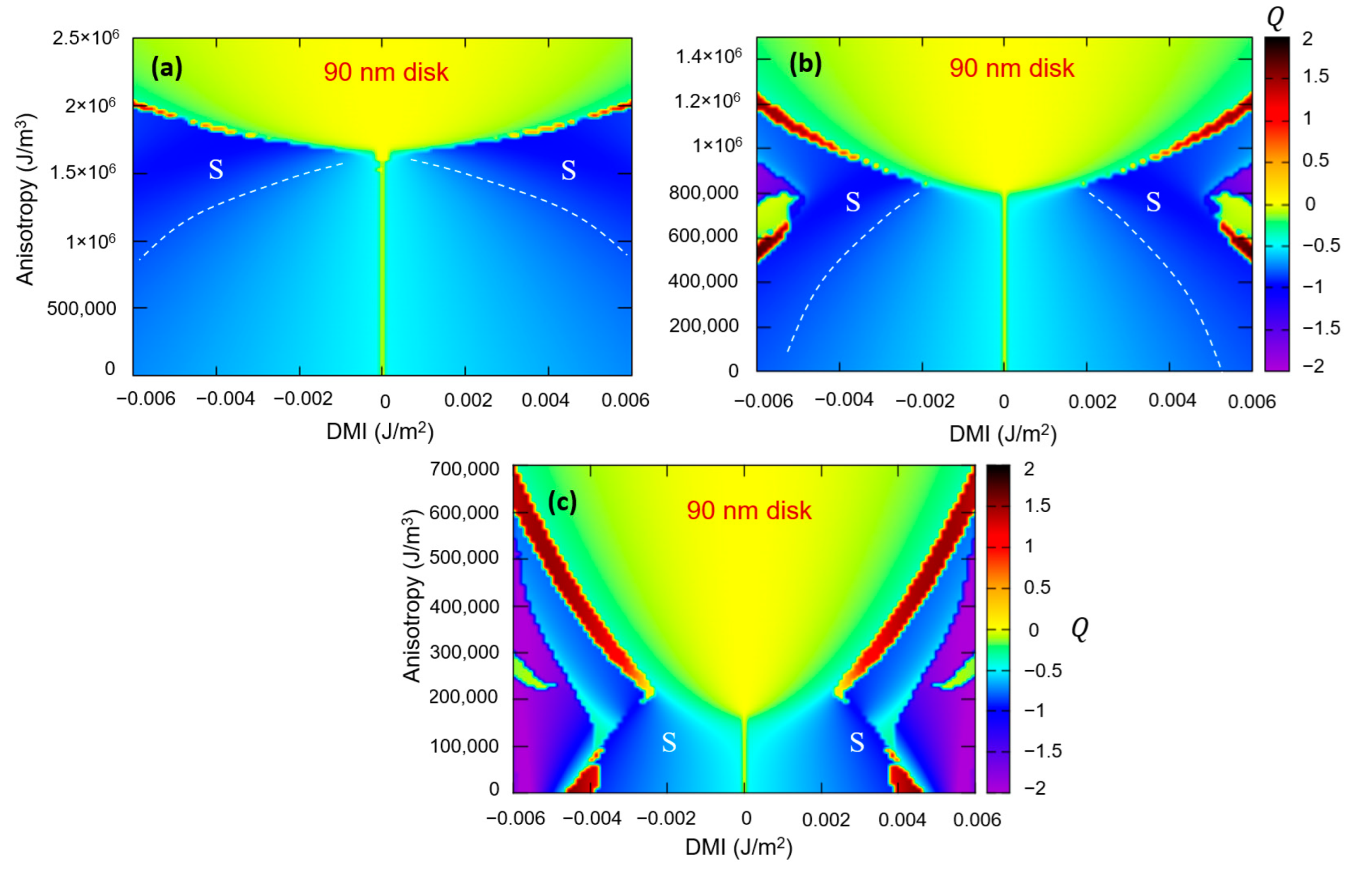
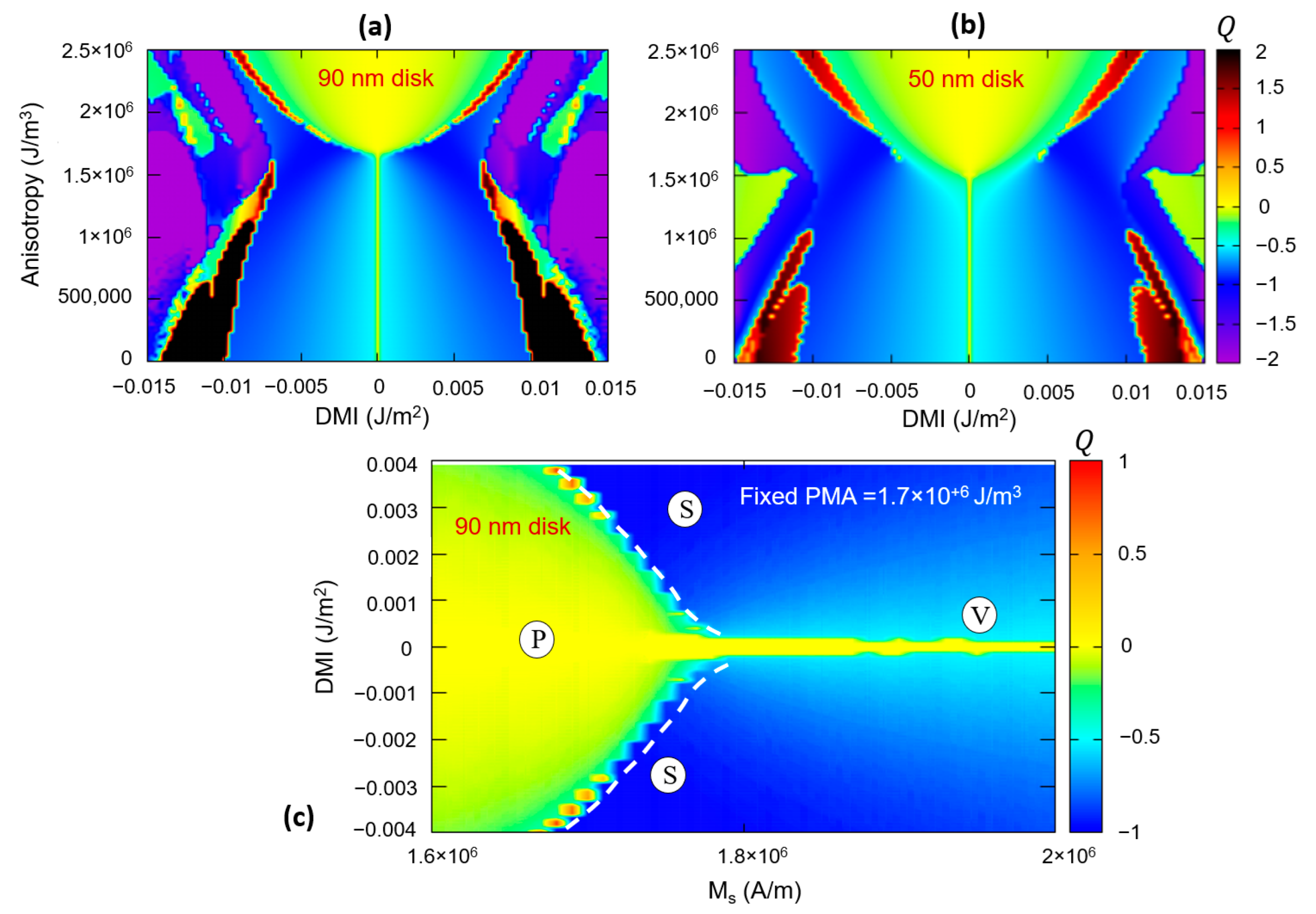
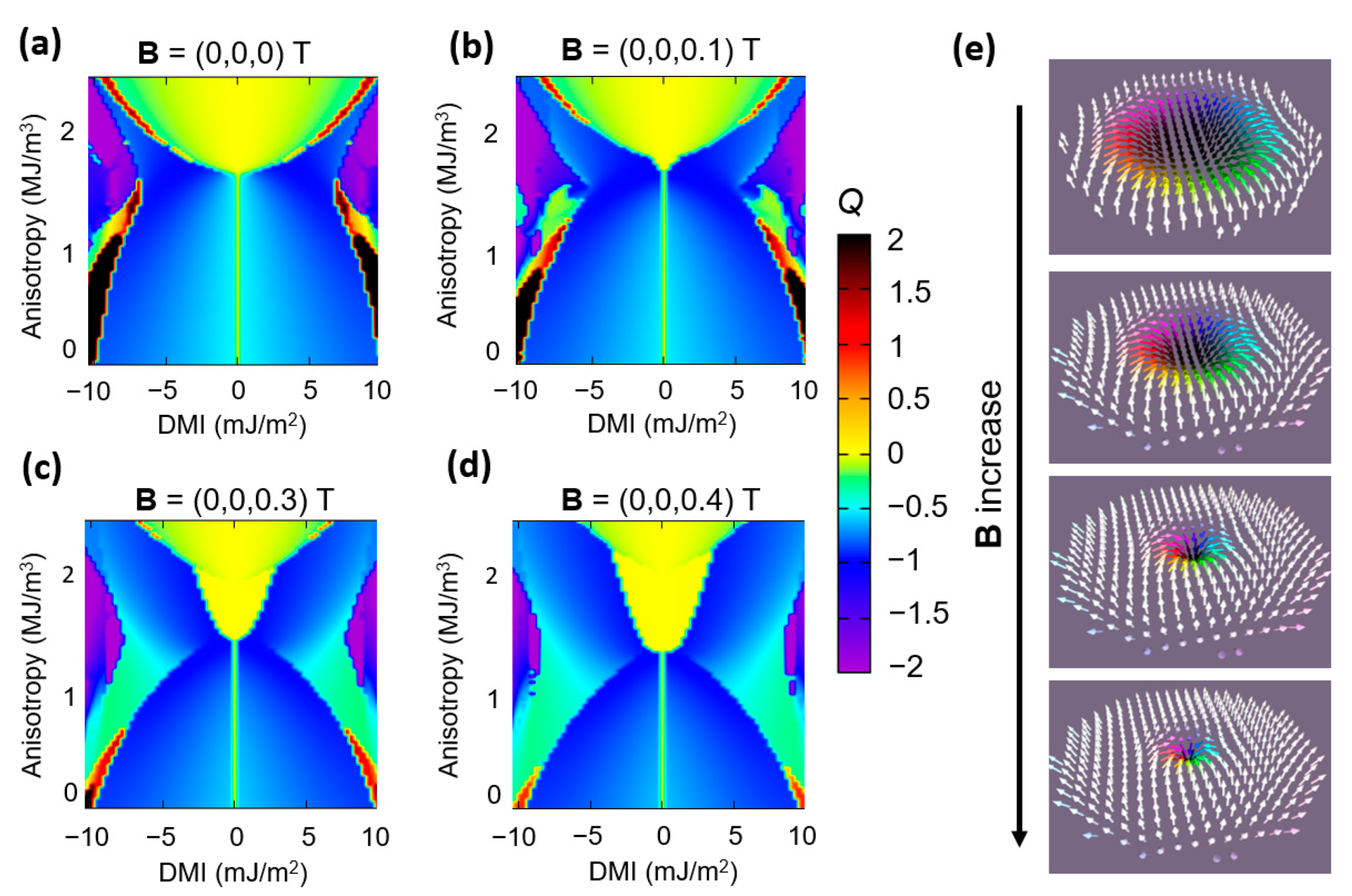
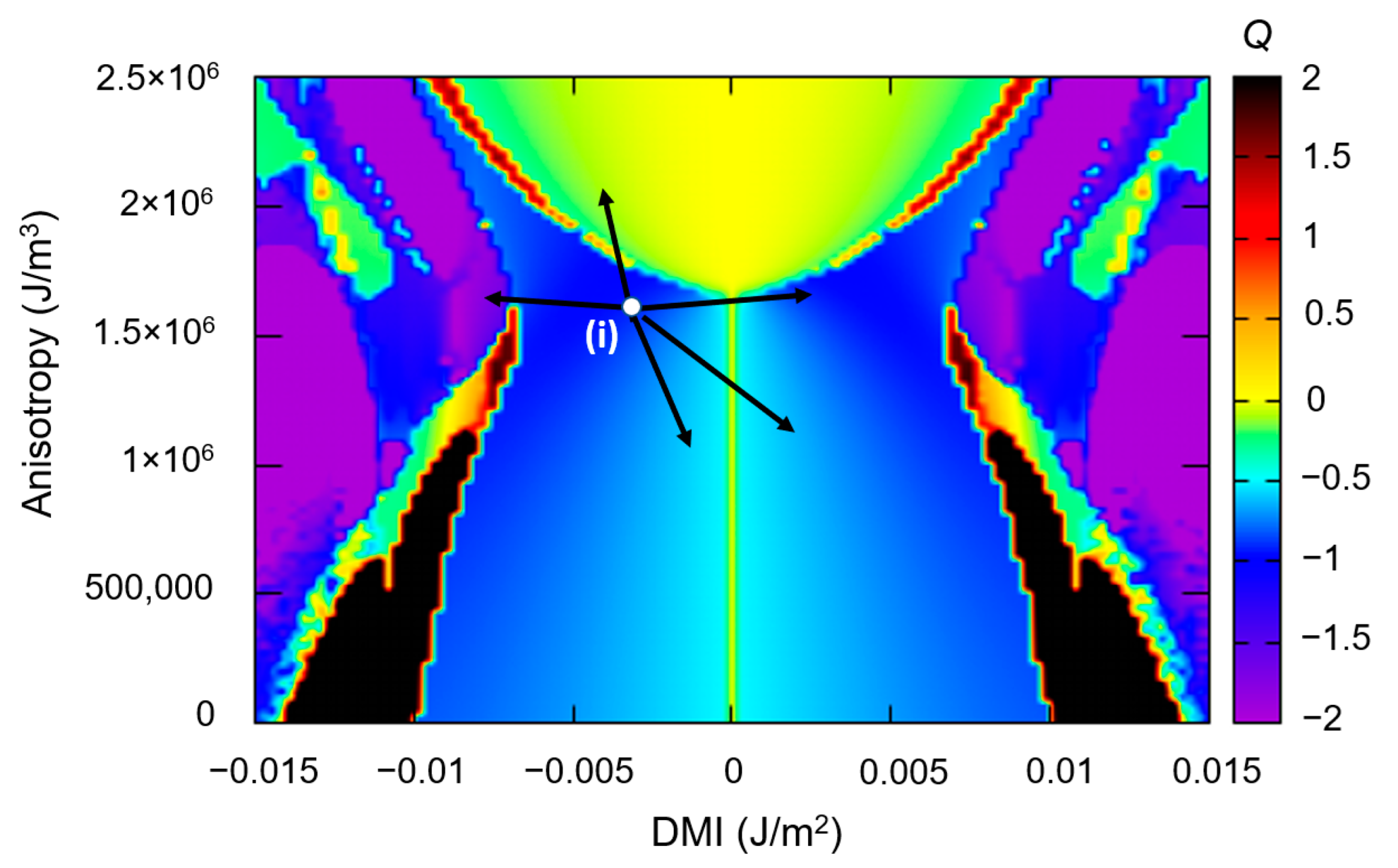
3.2.2. Skyrmionic Ground States in Patterned Nanodisks
- At a fixed DMI, at small PMA values, the ground state is vortex-like, with Q ≈ −0.5; when the PMA increases, within a certain range whose extension increases with the value of the DMI, the ground state becomes skyrmionic Q ≈ −1; above a threshold maximum value of the PMA, the ground state will be a saturated monodomain.
- Within the skyrmionic window, the skyrmion’s diameter progressively decreases with the PMA increase. The narrow transition from a skyrminonic to a saturated state implies some complex chiral states with .
- The skyrmionic states are stabilized by larger values of DMI but, above a critical value, at fixed PMA, large DMI will favour configurations within a PMA window increasing with the increase in the DMI.
- In conclusion, an optimum window of PMA and DMI values is required to stabilize a skyrmionic ground state.
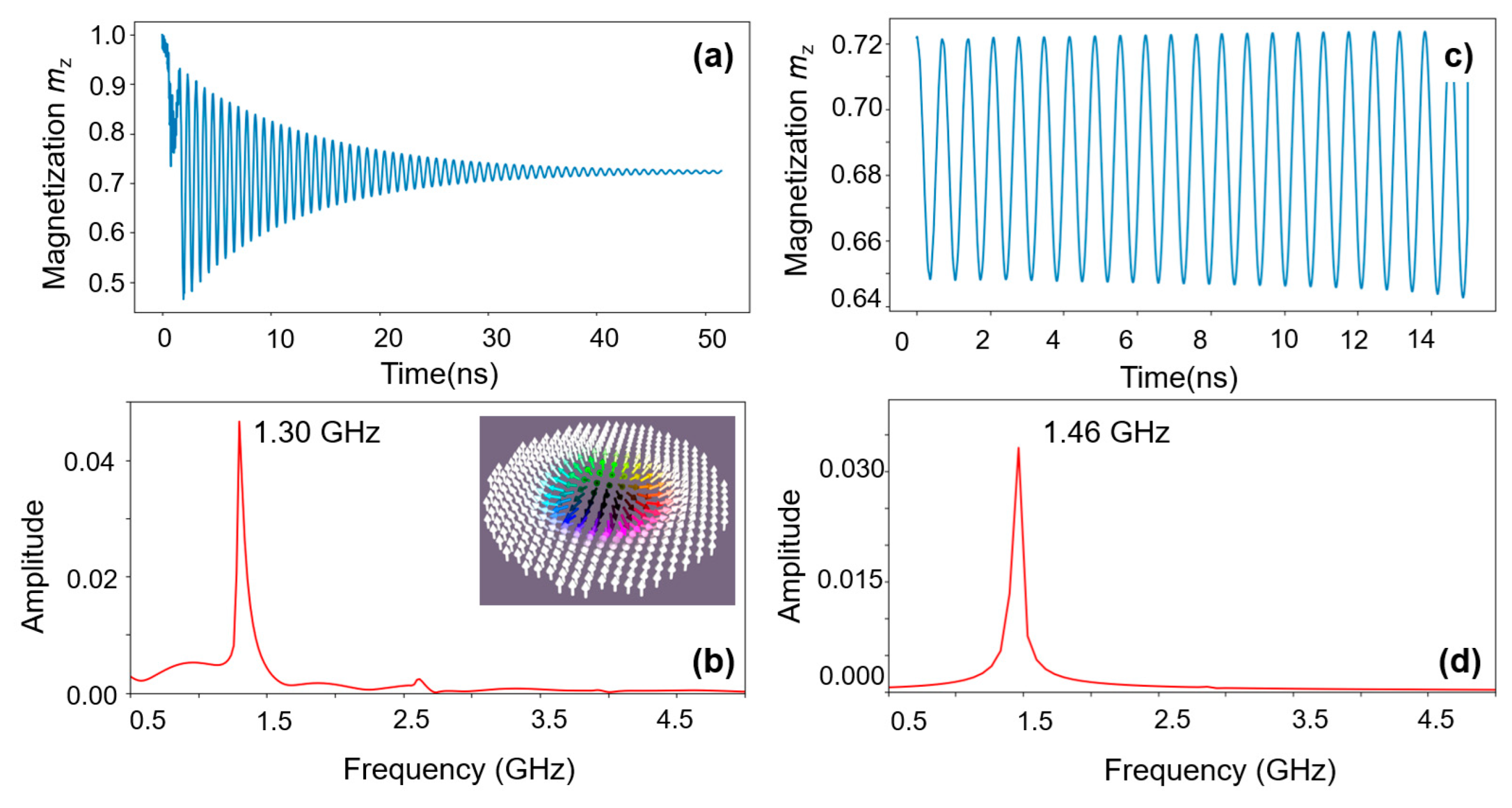
3.2.3. Skyrmionic Nano-Oscillators
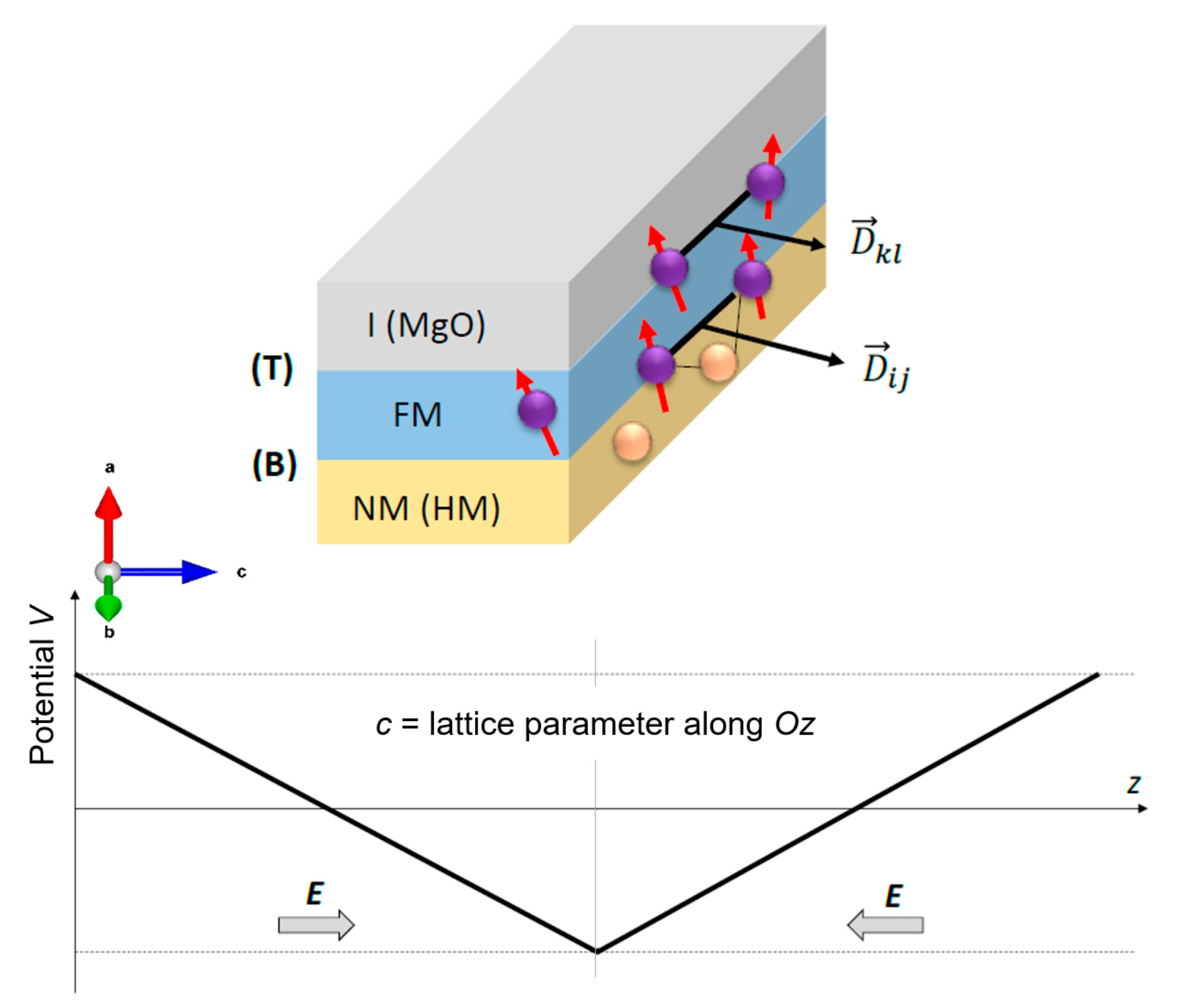
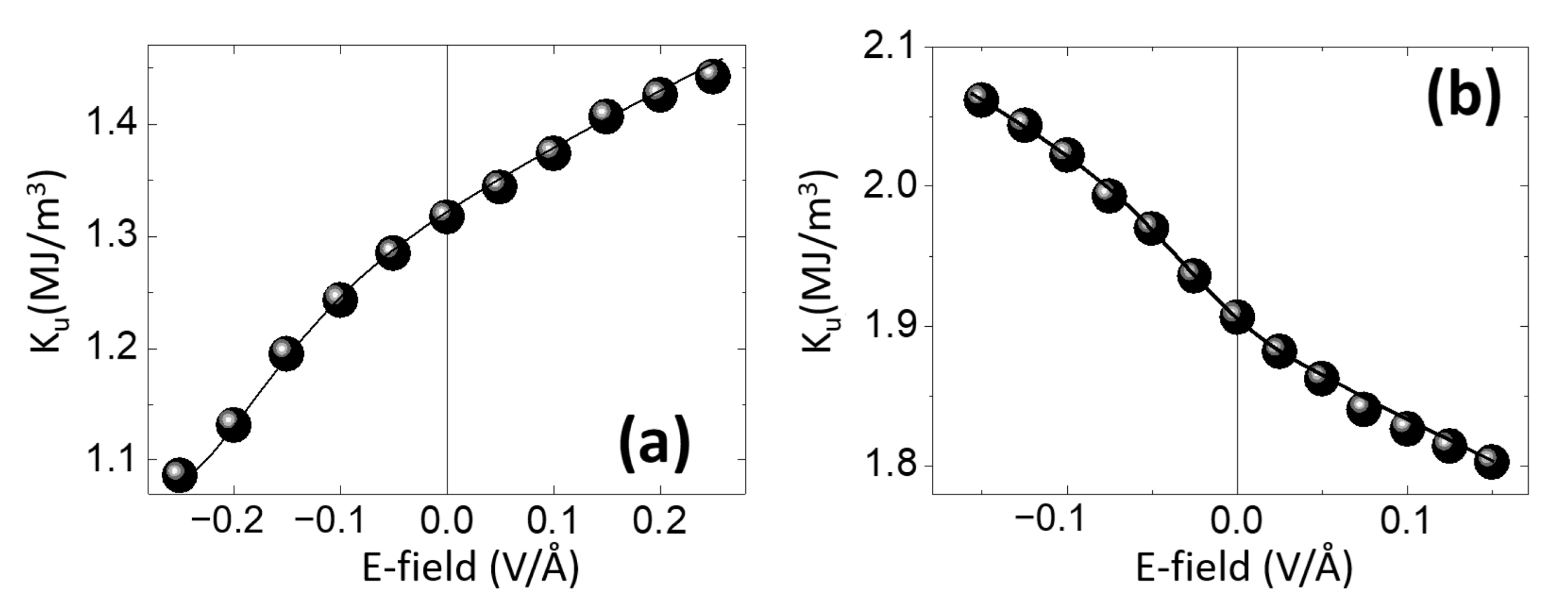
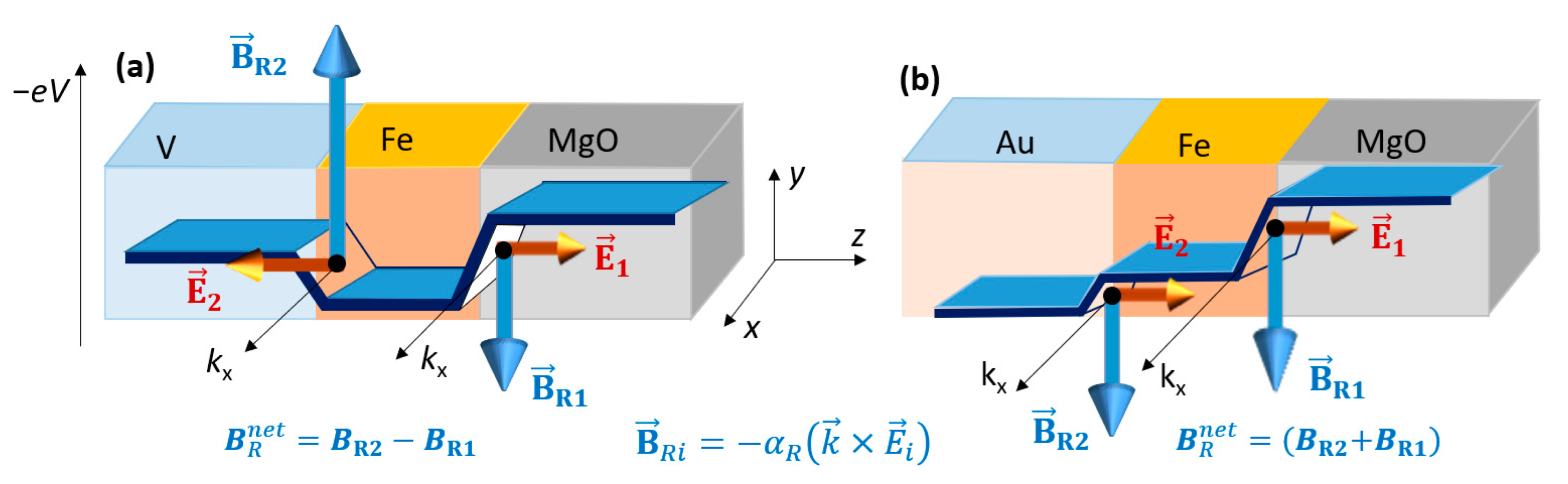
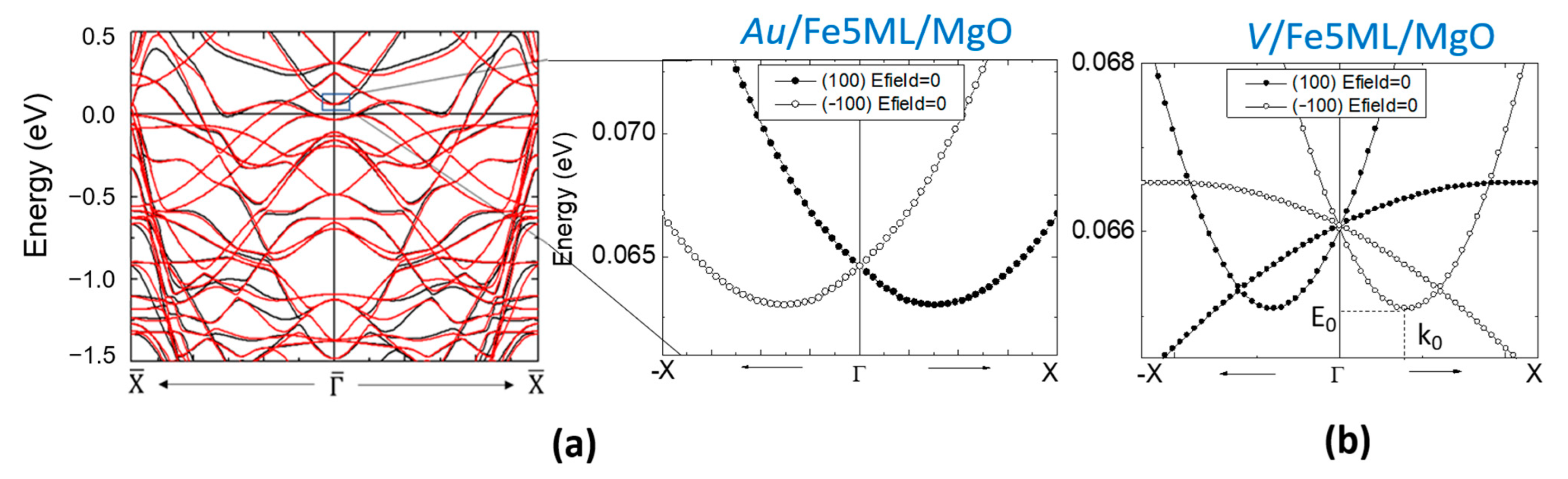
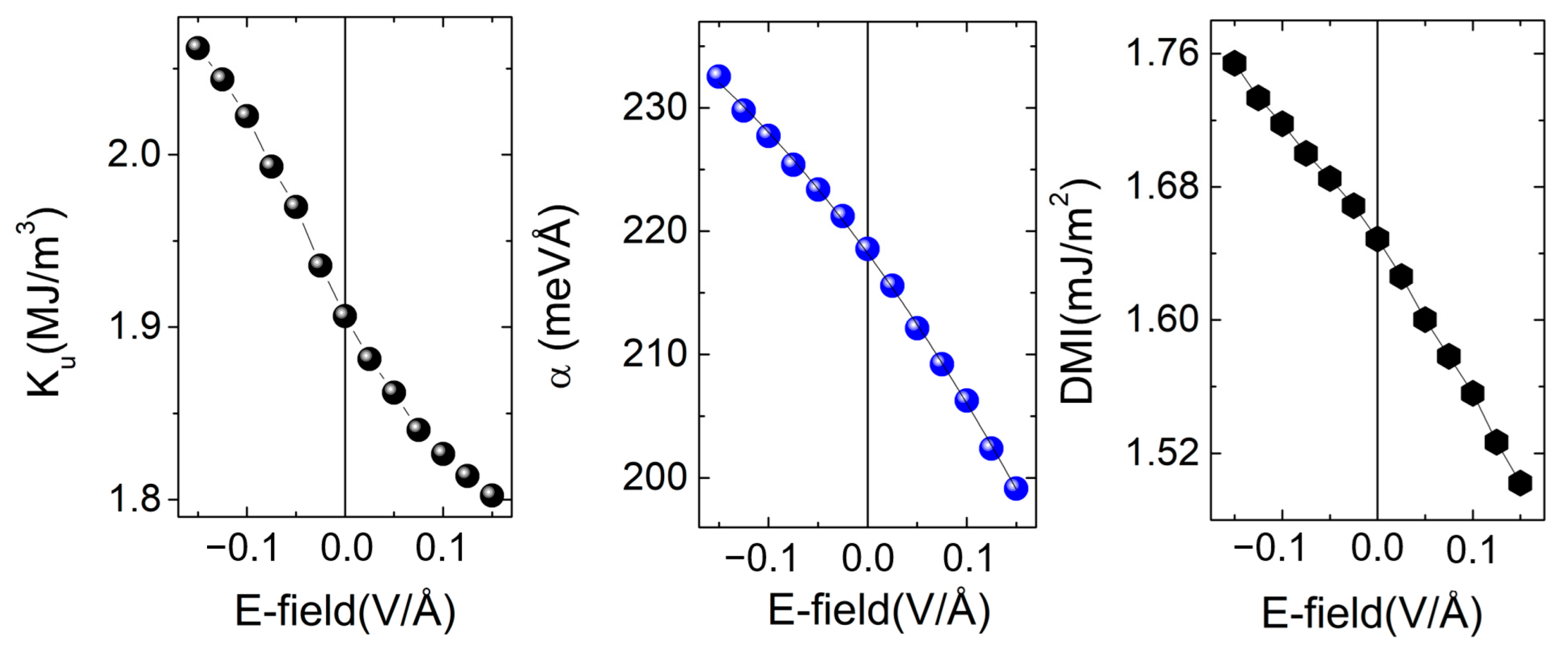
3.2.4. Skyrmion Manipulation by Electric Fields
4. Discussion
4.1. Multiscale Modeling of Skyrmionic Nanomaterials
4.2. Experimental Issues on Magnetic Skyrmionic Nano-Materials

5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
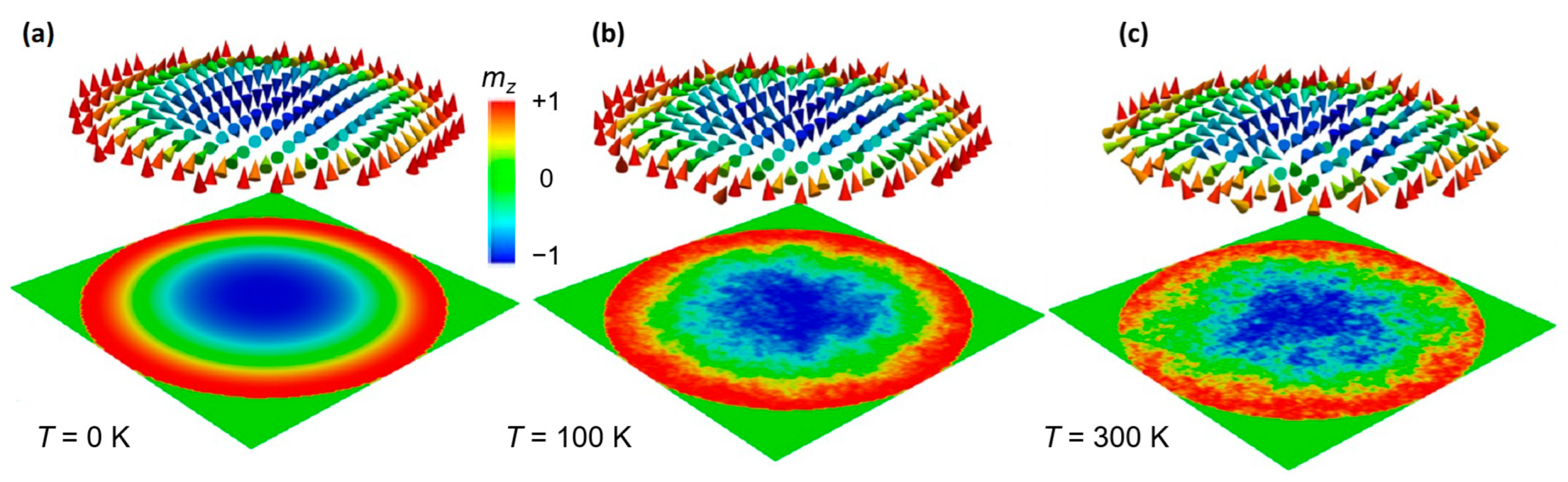
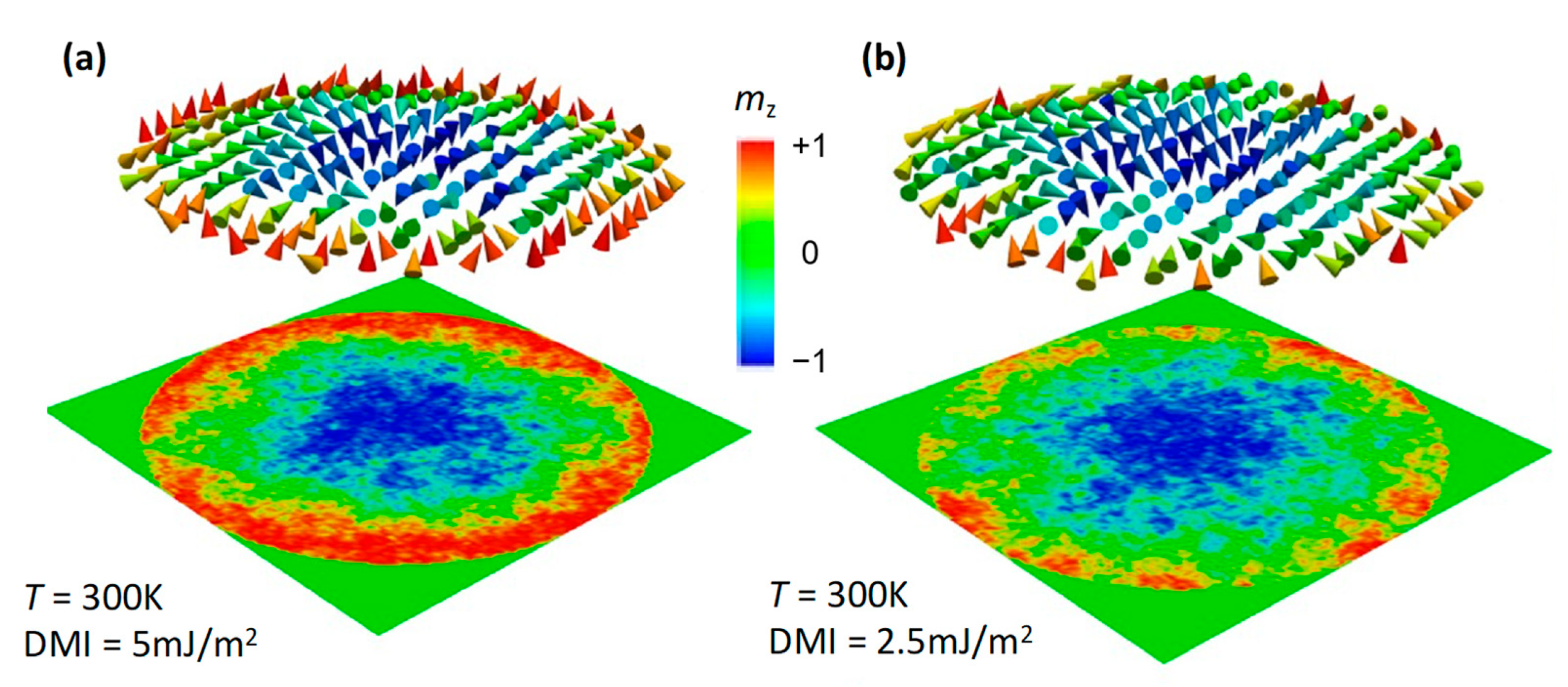
The Influence of Thermal Fluctuations at Finite Temperature
References
- Jones, N. How to stop data centres from gobbling up the world’s electricity. Nature 2018, 561, 163–166. [Google Scholar] [CrossRef] [PubMed]
- Vopson, M.M. The information catastrophe. AIP Adv. 2020, 10, 085014. [Google Scholar] [CrossRef]
- Bogdanov, A.; Hubert, A. Thermodynamically stable magnetic vortex states in magnetic crystals. J. Magn. Magn. Mater. 1994, 138, 255–269. [Google Scholar] [CrossRef]
- Dzyaloshinskii, I.E. Theory of Helicoidal Structures in Antiferromagnets. I. Nonmetals. Sov. Phys. JETP 1964, 19, 960. [Google Scholar]
- Coey, J.M.D. Magnetism and Magnetic Materials; Cambridge University Press: Cambridge, UK, 2010; pp. 139–140. [Google Scholar]
- Woo, S.; Litzius, K.; Krueger, B.; Im, M.-Y.; Caretta, L.; Richter, K.; Mann, M.; Krone, A.; Reeve, R.; Weigand, M.; et al. Observation of room-temperature magnetic skyrmions and their current-driven dynamics in ultrathin metallic ferromagnets. Nat. Mater. 2016, 15, 501–506. [Google Scholar] [CrossRef] [PubMed]
- Boulle, O.; Vogel, J.; Yang, H.; Pizzini, S.; Chaves, D.D.S.; Locatelli, A.; Menteş, T.O.; Sala, A.; Buda-Prejbeanu, L.D.; Klein, O.; et al. Room-temperature chiral magnetic skyrmions in ultrathin magnetic nanostructures. Nat. Nanotechnol. 2016, 11, 449–454. [Google Scholar] [CrossRef] [PubMed]
- Meyer, S.; Perini, M.; von Malottki, S.; Kubetzka, A.; Wiesendanger, R.; von Bergmann, K.; Heinze, S. Isolated zero field sub-10 nm skyrmions in ultrathin Co films. Nat. Commun. 2019, 10, 3823. [Google Scholar] [CrossRef] [PubMed]
- Moreau-Luchaire, C.; Mouta, S.C.; Reyren, N.; Sampaio, J.; Vaz, C.A.; Van Horne, N.; Bouzehouane, K.; Garcia, K.; Deranlot, C.; Warnicke, P.; et al. Additive interfacial chiral interaction in multilayers for stabilization of small individual skyrmions at room temperature. Nat. Nanotechnol. 2016, 11, 444–448. [Google Scholar] [CrossRef]
- Litzius, K.; Lemesh, I.; Krueger, B.; Bassirian, P.; Caretta, L.; Richter, K.; Büttner, F.; Sato, K.; Tretiakov, O.A.; Förster, J.; et al. Skyrmion Hall effect revealed by direct time-resolved X-ray microscopy. Nat. Phys. 2016, 13, 170–175. [Google Scholar] [CrossRef]
- Lemesh, I.; Litzius, K.; Böttcher, M.; Bassirian, P.; Kerber, N.; Heinze, D.; Zázvorka, J.; Büttner, F.; Caretta, L.; Mann, M.; et al. Current-induced Skyrmion generation through morphological thermal transitions in chiral ferromagnetic Heterostructures. Adv. Mater. 2018, 30, 1805461. [Google Scholar] [CrossRef]
- Litzius, K.; Leliaert, J.; Bassirian, P.; Rodrigues, D.R.S.D.R.; Kromin, S.; Lemesh, I.; Zazvorka, J.; Lee, K.-J.; Mulkers, J.; Kerber, N.; et al. The role of temperature and drive current in skyrmion dynamics. Nat. Electron. 2020, 3, 30–36. [Google Scholar] [CrossRef]
- Litzius, K. Spin-Orbit-Induced Dynamics of Chiral Magnetic Structures. Ph.D. Thesis, Johannes Gutenberg-Universitat Mainz, Mainz, Germany, 2018. [Google Scholar]
- Jaiswal, S.; Litzius, K.; Lemesh, I.; Büttner, F.; Finizio, S.; Raabe, J.; Weigand, M.; Lee, K.; Langer, J.; Ocker, B.; et al. Investigation of the Dzyaloshinskii-Moriya interaction and room temperature skyrmions in W/CoFeB/MgO thin films and microwires. Appl. Phys. Lett. 2017, 111, 022409. [Google Scholar] [CrossRef]
- Zázvorka, J.; Jakobs, F.; Heinze, D.; Keil, N.; Kromin, S.; Jaiswal, S.; Litzius, K.; Jakob, G.; Virnau, P.; Pinna, D.; et al. Thermal skyrmion diffusion used in a reshuffler device. Nat. Nanotechnol. 2019, 14, 658–661. [Google Scholar] [CrossRef] [PubMed]
- Tomasello, R.; Martinez, E.; Zivieri, R.; Torres, L.; Carpentieri, M.; Finocchio, G. A strategy for the design of skyrmion racetrack memories. Sci. Rep. 2014, 4, 6784. [Google Scholar] [CrossRef] [PubMed]
- Schott, M.; Bernand-Mantel, A.; Ranno, L.; Pizzini, S.; Vogel, J.; Béa, H.; Baraduc, C.; Auffret, S.; Gaudin, G.; Givord, D. The Skyrmion Switch: Turning Magnetic Skyrmion Bubbles on and off with an Electric Field. Nano Lett. 2017, 17, 3006–3012. [Google Scholar] [CrossRef]
- Grollier, J.; Querlioz, D.; Camsari, K.Y.; Everschor-Sitte, K.; Fukami, S.; Stiles, M.D. Neuromorphic spintronics. Nat. Electron. 2020, 3, 360–370. [Google Scholar] [CrossRef]
- Psaroudaki, C.; Panagopoulos, C. Skyrmion Qubits: A New Class of Quantum Logic Elements Based on Nanoscale Magnetization. Phys. Rev. Lett. 2021, 127, 067201. [Google Scholar] [CrossRef]
- Parkin, S.S.P.; Hayashi, M.; Thomas, L. Magnetic Domain-Wall Racetrack Memory. Science 2008, 320, 190–194. [Google Scholar] [CrossRef]
- Fillion, C.-E.; Fischer, J.; Kumar, R.; Fassatoui, A.; Pizzini, S.; Ranno, L.; Ourdani, D.; Belmeguenai, M.; Roussigné, Y.; Chérif, S.-M.; et al. Gate-controlled skyrmion and domain wall chirality. Nat. Commun. 2022, 13, 5257. [Google Scholar] [CrossRef]
- Wang, X.S.; Yuan, H. A theory on skyrmion size. Commun. Phys. 2018, 1, 31. [Google Scholar] [CrossRef]
- Blaha, P.; Schwarz, K.; Tran, F.; Laskowski, R.; Madsen, G.K.H.; Marks, L.D. WIEN2k: An APW+lo program for calculating the properties of solids. J. Chem. Phys. 2020, 152, 074101. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Wang, D.-S.; Wu, R.; Freeman, A. Validity of the force theorem for magnetocrystalline anisotropy. J. Magn. Magn. Mater. 1996, 159, 337–341. [Google Scholar] [CrossRef]
- Yang, H.; Boulle, O.; Cros, V.; Fert, A.; Chshiev, M. Controlling Dzyaloshinskii-Moriya Interaction via Chirality Dependent Atomic-Layer Stacking, Insulator Capping and Electric Field. Sci. Rep. 2018, 8, 12356. [Google Scholar] [CrossRef] [PubMed]
- Stahn, J.; Pietsch, U.; Blaha, P.; Schwarz, K. Electric-field-induced charge-density variations in covalently bonded binary compounds. Phys. Rev. B 2001, 63, 165205. [Google Scholar] [CrossRef]
- One, R.-A.; Mican, S.; Tiusan, C. Perpendicular Magnetic Anisotropy and Its Electric Field Manipulation in Magnetic Multilayered Heterostructures. Stud. Univ. Babeș- Bolyai Phys. 2021, 66, 91–110. [Google Scholar] [CrossRef]
- Vansteenkiste, A.; Leliaert, J.; Dvornik, M.; Helsen, M.; Garcia-Sanchez, F.; Van Waeyenberge, B. The design and verification of MuMax3. AIP Adv. 2014, 4, 107133. [Google Scholar] [CrossRef]
- Ibrahim, F.; Yang, H.X.; Hallal, A.; Dieny, B.; Chshiev, M. Anatomy of electric field control of perpendicular magnetic anisotropy at Fe/MgO interfaces. Phys. Rev. B 2016, 93, 014429. [Google Scholar] [CrossRef]
- Barnes, S.E.; Ieda, J.; Maekawa, S. Rashba Spin-Orbit Anisotropy and the Electric Field Control of Magnetism. Sci. Rep. 2014, 4, 4105. [Google Scholar] [CrossRef]
- Chen, G. Skyrmion Hall effect. Nat. Phys. 2017, 13, 112–113. [Google Scholar] [CrossRef]
- Garcia-Sanchez, F.; Sampaio, J.; Reyren, N.; Cros, V.; Kim, J.-V. A skyrmion-based spin-torque nano-oscillator. New J. Phys. 2016, 18, 075011. [Google Scholar] [CrossRef]
- Jing, X.; Zong-Yi, H.; Yi-Fan, S.; Wen-Jing, J.; Liu-Rong, L.; Xi-Chao, Z.; Xiao-Xi, L.; Yan, Z. Overview of magnetic skyrmion-based devices and applications. Acta Phys. Sin. 2018, 67, 137505. [Google Scholar] [CrossRef]
- Petit-Watelot, S.; Kim, J.-V.; Ruotolo, A.; Otxoa, R.M.; Bouzehouane, K.; Grollier, J.; Vansteenkiste, A.; VandeWiele, B.; Cros, V.; Devolder, T. Commensurability and chaos in magnetic vortex oscillations. Nat. Phys. 2012, 8, 682–687. [Google Scholar] [CrossRef]
- Nikonov, D.E.; Csaba, G.; Porod, W.; Shibata, T.; Voils, D.; Hammerstrom, D.; Young, I.A.; Bourianoff, G.I. Coupled-Oscillator Associative Memory Array Operation for Pattern Recognition. IEEE J. Explor. Solid-State Comput. Devices Circuits 2015, 1, 85–93. [Google Scholar] [CrossRef]
- One, R.-A.; Béa, H.; Mican, S.; Joldos, M.; Veiga, P.B.; Dieny, B.; Buda-Prejbeanu, L.D.; Tiusan, C. Route towards efficient magnetization reversal driven by voltage control of magnetic anisotropy. Sci. Rep. 2021, 11, 8801. [Google Scholar] [CrossRef]
- Legrand, W.; Maccariello, D.; Ajejas, F.; Collin, S.; Vecchiola, A.; Bouzehouane, K.; Reyren, N.; Cros, V.; Fert, A. Room-temperature stabilization of antiferromagnetic skyrmions in synthetic antiferromagnets. Nat. Mater. 2019, 19, 34–42. [Google Scholar] [CrossRef] [PubMed]
- Tsurkan, S.; Zakeri, K. Giant Dzyaloshinskii-Moriya interaction in epitaxial Co/Fe bilayers with C2v symmetry. Phys. Rev. B 2020, 102, 060406. [Google Scholar] [CrossRef]
- Ye, C.; Li, L.-L.; Shu, Y.; Li, Q.-R.; Xia, J.; Hou, Z.-P.; Zhou, Y.; Liu, X.-X.; Yang, Y.-Y.; Zhao, G.-P. Generation and manipulation of skyrmions and other topological spin structures with rare metals. Rare Met. 2022, 41, 2200–2216. [Google Scholar] [CrossRef]
- Hou, Z.; Li, L.; Liu, C.; Gao, X.; Ma, Z.; Zhou, G.; Peng, Y.; Yan, M.; Zhang, X.-X.; Liu, J. Emergence of room temperature stable skyrmionic bubbles in the rare earth based REMn2Ge2 (RE = Ce, Pr, and Nd) magnets. Mater. Today Phys. 2021, 17, 100341. [Google Scholar] [CrossRef]
- Takagi, R.; Matsuyama, N.; Ukleev, V.; Le Yu, L.; White, J.S.; Francoual, S.; Mardegan, J.R.L.; Hayami, S.; Saito, H.; Kaneko, K.; et al. Square and rhombic lattices of magnetic skyrmions in a centrosymmetric binary compound. Nat. Commun. 2022, 13, 1472. [Google Scholar] [CrossRef]
- Zuo, S.; Liu, J.; Qiao, K.; Zhang, Y.; Chen, J.; Su, N.; Liu, Y.; Cao, J.; Zhao, T.; Wang, J.; et al. Spontaneous Topological Magnetic Transitions in NdCo5 Rare-Earth Magnets. Adv. Mater. 2021, 33, 2103751. [Google Scholar] [CrossRef]
- Chen, K.; Lott, D.; Philippi-Kobs, A.; Weigand, M.; Luo, C.; Radu, F. Observation of compact ferrimagnetic skyrmions in DyCo3 film. Nanoscale 2020, 12, 18137–18143. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Liu, J.; Wang, Z.; Zhang, Q.; Xu, T.; Dong, Y.; Zhao, L.; Je, S.-G.; Im, K.X.; Zhu, J.; et al. Rare-Earth Permanent Magnet SmCo 5 for Chiral Interfacial Spin-Orbitronics. Adv. Func. Mater. 2021, 31, 2104426. [Google Scholar] [CrossRef]
- Caretta, L.; Rosenberg, E.; Büttner, F.; Fakhrul, T.; Gargiani, P.; Valvidares, M.; Chen, Z.; Reddy, P.; Muller, D.A.; Ross, C.A.; et al. Interfacial Dzyaloshinskii-Moriya interaction arising from rare-earth orbital magnetism in insulating magnetic oxides. Nat. Commun. 2020, 11, 1090. [Google Scholar] [CrossRef] [PubMed]
- Khanh, N.D.; Nakajima, T.; Yu, X.; Gao, S.; Shibata, K.; Hirschberger, M.; Yamasaki, Y.; Sagayama, H.; Nakao, H.; Peng, L.; et al. Nanometric square skyrmion lattice in a centrosymmetric tetragonal magnet. Nat. Nanotechnol. 2020, 15, 444–449. [Google Scholar] [CrossRef]
- Sampaio, J.; Cros, V.; Rohart, S.; Thiaville, A.; Fert, A. Nucleation, stability and current-induced motion of isolated magnetic skyrmions in nanostructures. Nat. Nanotechnol. 2013, 8, 839–844. [Google Scholar] [CrossRef]
- Wang, L.; Liu, C.; Mehmood, N.; Han, G.; Wang, Y.; Xu, X.; Feng, C.; Hou, Z.; Peng, Y.; Gao, X.; et al. Construction of a Room-Temperature Pt/Co/Ta Multilayer Film with Ultrahigh-Density Skyrmions for Memory Application. ACS Appl. Mater. Interfaces 2019, 11, 12098–12104. [Google Scholar] [CrossRef]





| Multilayer System | Diameter of Skyrmion Core (nm) | Temperature of Skyrmion Stability (K) | Reference | |
|---|---|---|---|---|
| Pt/Co/Ta | 75–200 | 1.3 | [5] | |
| Pt/Co/MgO | 70–130 | 2.0 | [6] | |
| Ir/Co/Pt | 25–100 | N.A. | [7] | |
| [Ir/Co/Pt]10 | 100 | 2 | [8] | |
| Pt/CoFeB/MgO | <250 | 1.35 | [9,10,11] | |
| Pd/CoFeB/MgO | <200 | 0.78 | [12] | |
| W/CoFeB/MgO | 250 | 0.3–0.7 | [13] | |
| Ta/CoFeB/MgO | 300 | 0.33 | [14] | |
| Ta/CoFeB/Ta/MgO | 1000–2000 | 0.33 | >300 | [14] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
One, R.-A.; Mican, S.; Cimpoeșu, A.-G.; Joldos, M.; Tetean, R.; Tiușan, C.V. Micromagnetic Design of Skyrmionic Materials and Chiral Magnetic Configurations in Patterned Nanostructures for Neuromorphic and Qubit Applications. Nanomaterials 2022, 12, 4411. https://doi.org/10.3390/nano12244411
One R-A, Mican S, Cimpoeșu A-G, Joldos M, Tetean R, Tiușan CV. Micromagnetic Design of Skyrmionic Materials and Chiral Magnetic Configurations in Patterned Nanostructures for Neuromorphic and Qubit Applications. Nanomaterials. 2022; 12(24):4411. https://doi.org/10.3390/nano12244411
Chicago/Turabian StyleOne, Roxana-Alina, Sever Mican, Angela-Georgiana Cimpoeșu, Marius Joldos, Romulus Tetean, and Coriolan Viorel Tiușan. 2022. "Micromagnetic Design of Skyrmionic Materials and Chiral Magnetic Configurations in Patterned Nanostructures for Neuromorphic and Qubit Applications" Nanomaterials 12, no. 24: 4411. https://doi.org/10.3390/nano12244411
APA StyleOne, R.-A., Mican, S., Cimpoeșu, A.-G., Joldos, M., Tetean, R., & Tiușan, C. V. (2022). Micromagnetic Design of Skyrmionic Materials and Chiral Magnetic Configurations in Patterned Nanostructures for Neuromorphic and Qubit Applications. Nanomaterials, 12(24), 4411. https://doi.org/10.3390/nano12244411