Organic Disordered Semiconductors as Networks Embedded in Space and Energy
Abstract
1. Introduction
2. Proposed Model: The ODS System and its Associated Network
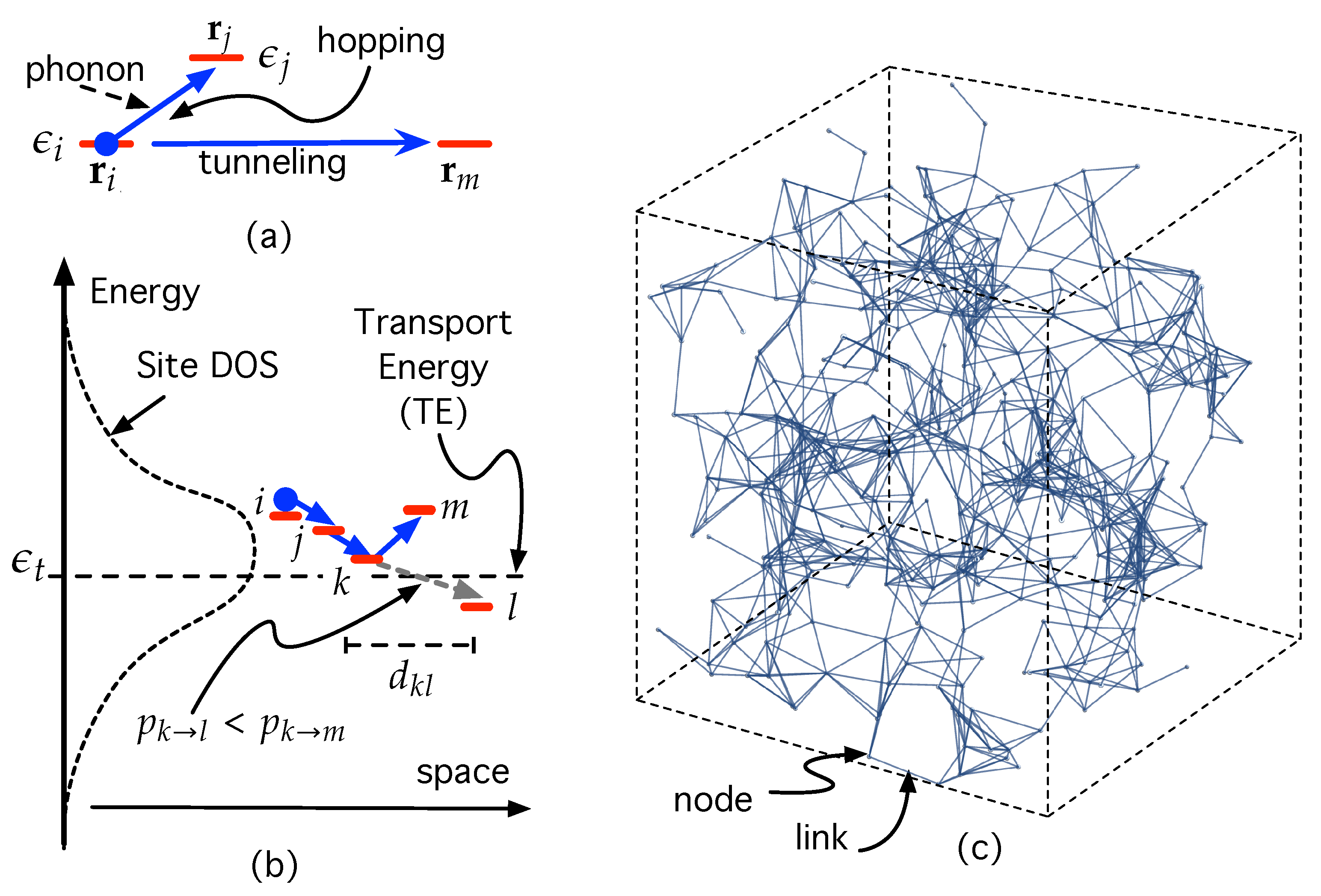
2.1. The ODS System
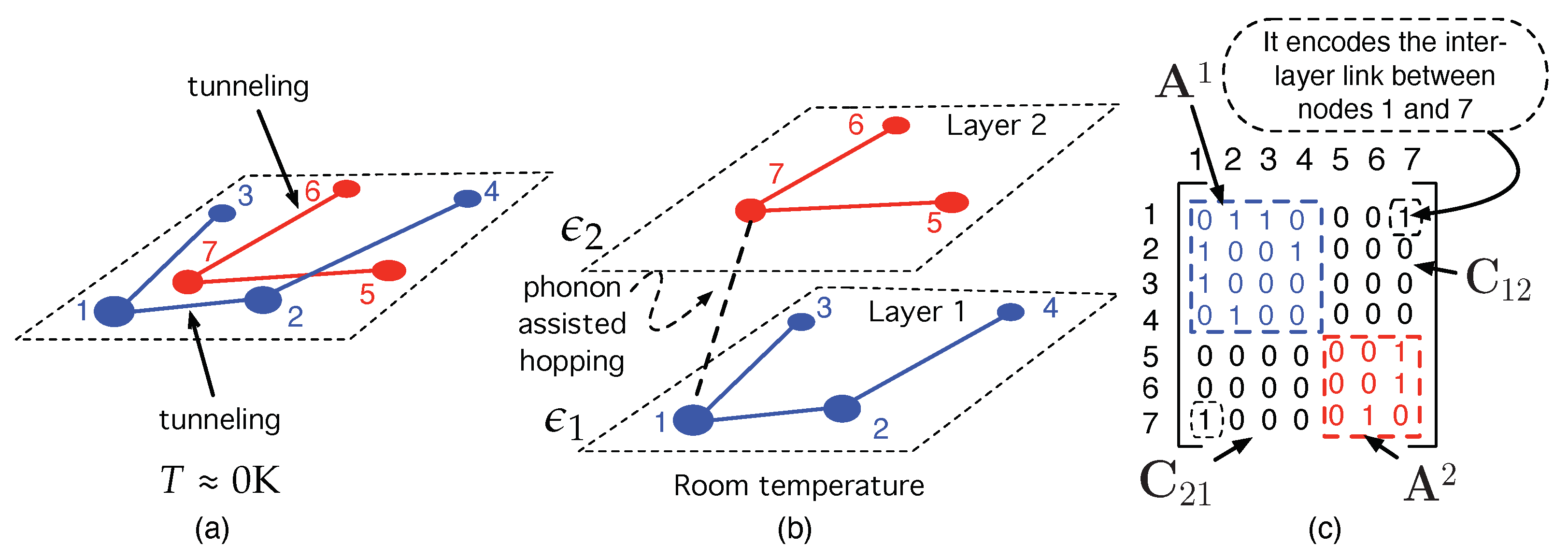
2.2. Defining the Network Associated with the ODS System
3. Simulations: Experimental Work
3.1. Methodology
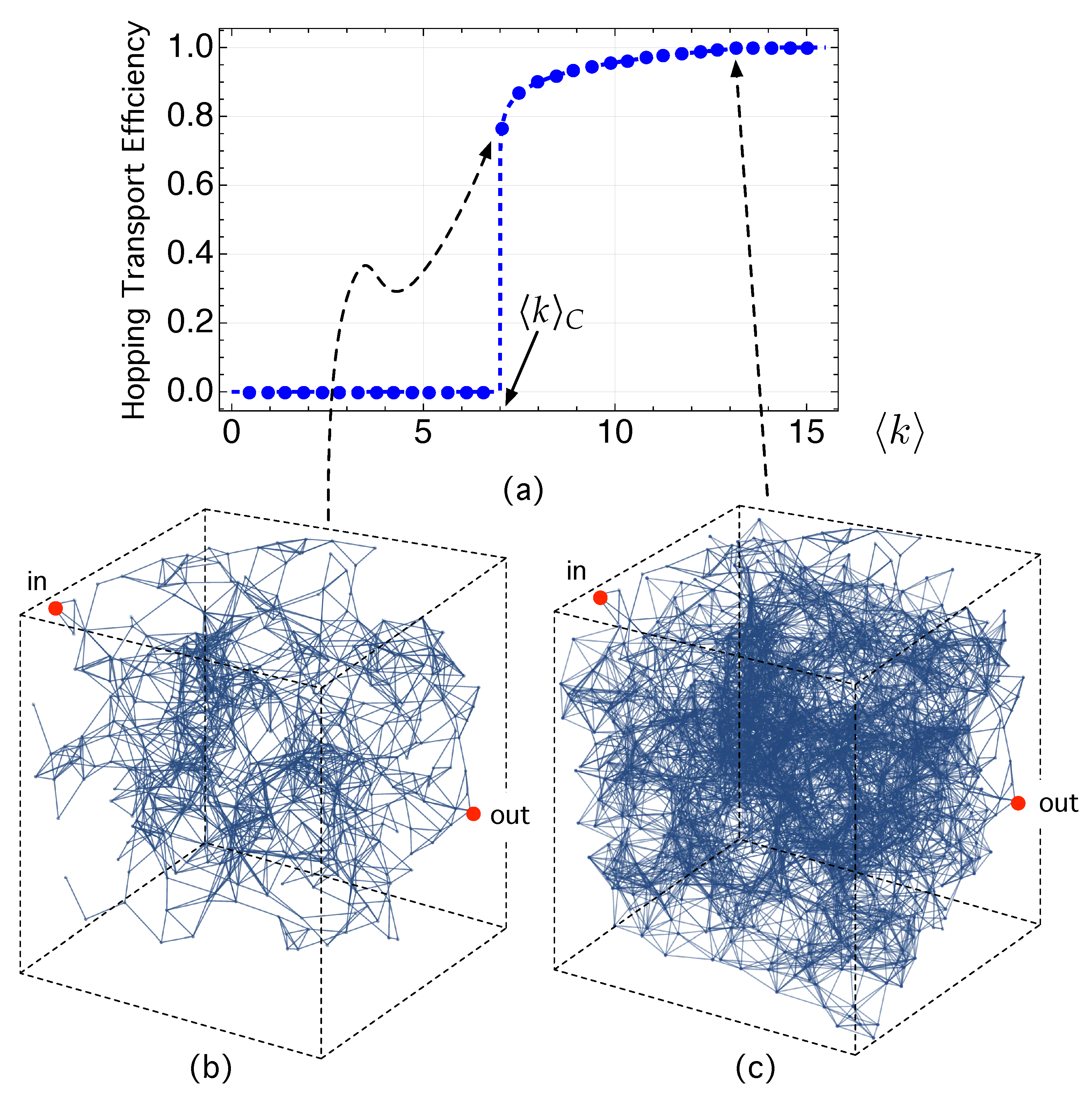
3.2. Exploring Carrier Dynamics
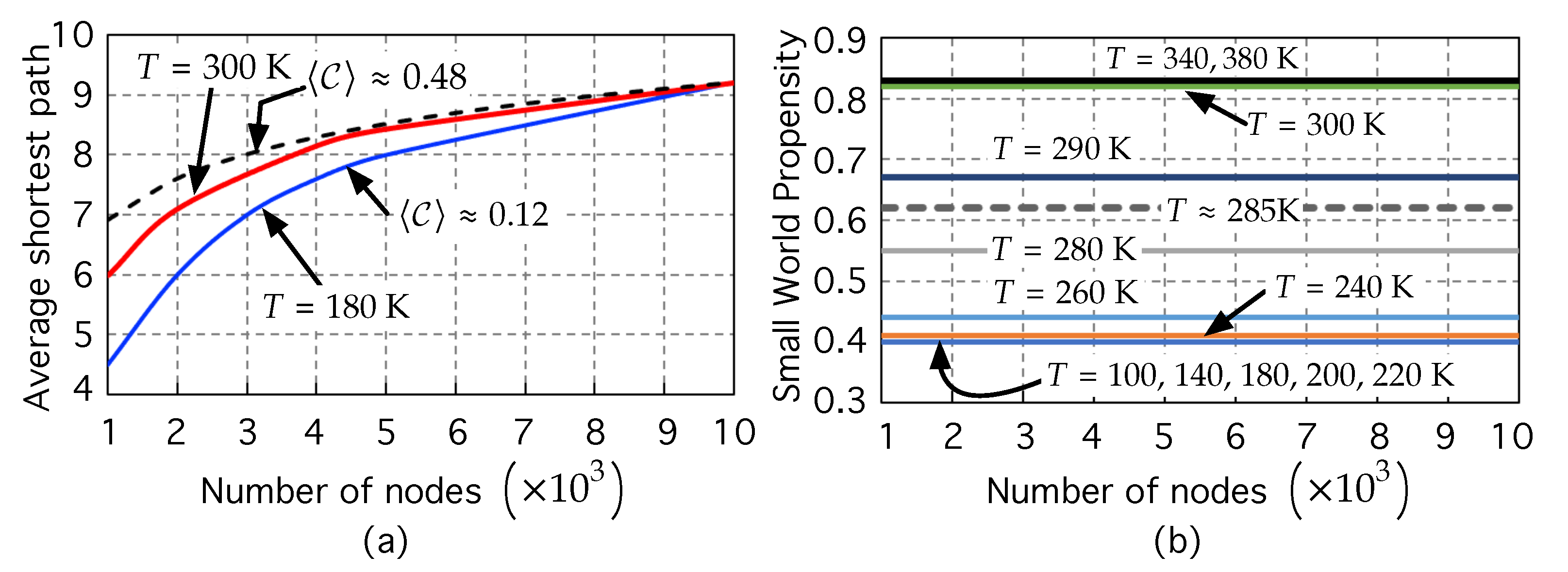
3.3. Studying the Network Structure: Navigating the Network
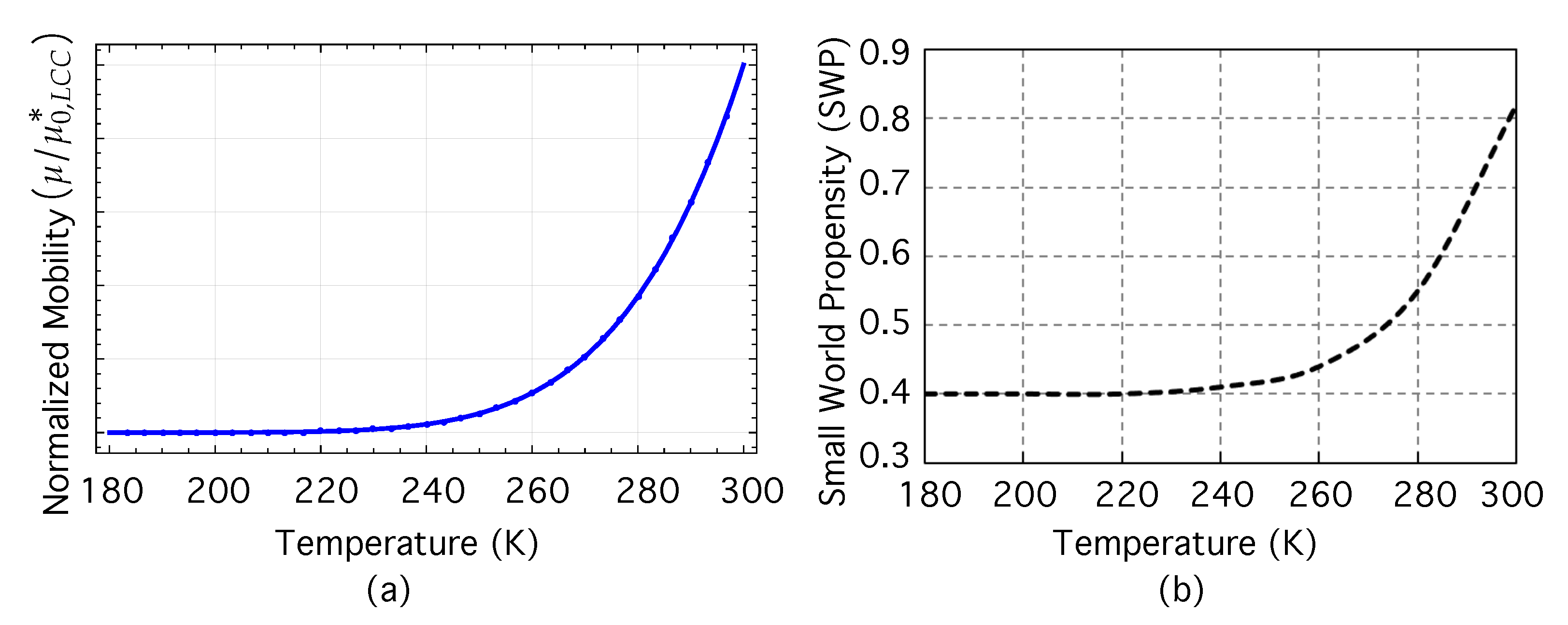
3.4. Carrier Mobility and Network Structure
4. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ARP | Average Return Probability. |
| CTQW | Continuous-Time Quantum Walks. |
| DOS | Density of States. |
| GDM | Gaussian Disorder Model. |
| MA | Miller–Abrahams. |
| NS | Network Science. |
| ODS | Organic Disordered Semiconductor |
| OFET | Organic Field-Effect Transistors. |
| OLED | Organic Light-Emitting Diodes. |
| OS | Organic Semiconductors. |
| OTFT | Organic Thin-Film Transistors. |
| QT | Quantum Transport. |
| RGG | Random Geometric Graph. |
| RN | Random Network. |
| RW | Random Walk. |
| SW | Small-World. |
| SWP | Small-World Propensity. |
| SN | Spatial Networks. |
| TE | Transport Energy. |
| VRH | Variable-Range Hopping. |
| Symbol | Definition or Meaning |
| Adjacency matrix of a graph . | |
| Element of the adjacency matrix | |
| Node degree matrix: . It is the diagonal matrix formed from the nodes degrees. | |
| Euclidean distance between any pair of nodes i and j in a network. | |
| Distance between two nodes i and j. It is the length of the shortest path (geodesic path) between them, that is, the minimum number of links when going from one node to the other. | |
| Fermi level. | |
| Energy of state i. | |
| Transport energy. | |
| Hopping transport efficiency. | |
| Graph , where is the set of nodes (), is the set of links, and is weighted adjacency matrix that emerges from our method to link formation. | |
| Attempt-to-escape frequency. | |
| Miller–Abrahams hopping rate between states i and j. | |
| Ket vector in the Hilbert space . It corresponds to the electron wave function in nanostructure (≡ site ≡ node ≡ ket) i. | |
| Bra vector in the dual space corresponding to the ket | |
| Average node degree. | |
| Thermal energy. | |
| Degree of a node i. It is the number of links connecting i to any other node. | |
| ℓ | Average path length of a network. It is the mean value of distances between any pair of nodes in the network. |
| Set of links (edges) of a network (graph). | |
| Laplacian matrix of a graph . | |
| M | Size of a graph . It is the number of links in the set . |
| Carrier hopping mobility. | |
| Carrier hopping mobility at low temperature and low carrier concentration. | |
| n | Carrier concentration. |
| N | Order of a graph . It is the number of nodes in set , that is the cardinality of set : . |
| Set of nodes (or vertices) of a graph. | |
| Site concentration. | |
| Probability for an electron to evolve between kets and in the time interval t. | |
| Average return probability | |
| Probability density function giving the probability that a randomly selected node has k links. | |
| The energy scale of the Gaussian DOS. | |
| Weighted adjacency matrix. | |
| Carrier localization length. |
References
- Fukuda, K.; Yu, K.; Someya, T. The future of flexible organic solar cells. Adv. Energy Mater. 2020, 10, 2000765. [Google Scholar] [CrossRef]
- Bronstein, H.; Nielsen, C.B.; Schroeder, B.C.; McCulloch, I. The role of chemical design in the performance of organic semiconductors. Nat. Rev. Chem. 2020, 4, 66–77. [Google Scholar] [CrossRef]
- Zojer, K. Simulation of Charge Carriers in Organic Electronic Devices: Methods with their Fundamentals and Applications. Adv. Opt. Mater. 2021, 9, 2100219. [Google Scholar] [CrossRef]
- Zhang, F.; Di, C.a. Exploring thermoelectric materials from high mobility organic semiconductors. Chem. Mater. 2020, 32, 2688–2702. [Google Scholar] [CrossRef]
- Zuo, G.; Abdalla, H.; Kemerink, M. Conjugated polymer blends for organic thermoelectrics. Adv. Electron. Mater. 2019, 5, 1800821. [Google Scholar] [CrossRef]
- Riede, M.; Spoltore, D.; Leo, K. Organic solar cells—The path to commercial success. Adv. Energy Mater. 2021, 11, 2002653. [Google Scholar] [CrossRef]
- Coropceanu, V.; Chen, X.K.; Wang, T.; Zheng, Z.; Brédas, J.L. Charge-transfer electronic states in organic solar cells. Nat. Rev. Mater. 2019, 4, 689–707. [Google Scholar] [CrossRef]
- Song, J.; Lee, H.; Jeong, E.G.; Choi, K.C.; Yoo, S. Organic light-emitting diodes: Pushing toward the limits and beyond. Adv. Mater. 2020, 32, 1907539. [Google Scholar] [CrossRef]
- Liu, Y.; Li, C.; Ren, Z.; Yan, S.; Bryce, M.R. All-organic thermally activated delayed fluorescence materials for organic light-emitting diodes. Nat. Rev. Mater. 2018, 3, 1–20. [Google Scholar] [CrossRef]
- Simonetti, O.; Giraudet, L. Transport models in disordered organic semiconductors and their application to the simulation of thin-film transistors. Polym. Int. 2019, 68, 620–636. [Google Scholar] [CrossRef]
- Virkar, A.A.; Mannsfeld, S.; Bao, Z.; Stingelin, N. Organic semiconductor growth and morphology considerations for organic thin-film transistors. Adv. Mater. 2010, 22, 3857–3875. [Google Scholar] [CrossRef] [PubMed]
- Riera-Galindo, S.; Leonardi, F.; Pfattner, R.; Mas-Torrent, M. Organic semiconductor/polymer blend films for organic field-effect transistors. Adv. Mater. Technol. 2019, 4, 1900104. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, J.; Zhang, S.; Huang, J. OFET chemical sensors: Chemical sensors based on ultrathin organic field-effect transistors. Polym. Int. 2021, 70, 414–425. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, P.; Hu, W. Organic field-effect transistor-based gas sensors. Chem. Soc. Rev. 2015, 44, 2087–2107. [Google Scholar] [CrossRef]
- Neupane, G.P.; Ma, W.; Yildirim, T.; Tang, Y.; Zhang, L.; Lu, Y. 2D organic semiconductors, the future of green nanotechnology. Nano Mater. Sci. 2019, 1, 246–259. [Google Scholar] [CrossRef]
- Dey, A.; Singh, A.; Das, D.; Iyer, P.K. Organic semiconductors: A New future of nanodevices and applications. In Thin Film Structures in Energy Applications; Springer: Berlin/Heidelberg, Germany, 2015; pp. 97–128. [Google Scholar]
- Baranovskii, S.D. Mott lecture: Description of charge transport in disordered organic semiconductors: Analytical theories and computer simulations. Phys. Status Solidi (a) 2018, 215, 1700676. [Google Scholar] [CrossRef]
- Upreti, T.; Wang, Y.; Zhang, H.; Scheunemann, D.; Gao, F.; Kemerink, M. Experimentally validated hopping-transport model for energetically disordered organic semiconductors. Phys. Rev. Appl. 2019, 12, 064039. [Google Scholar] [CrossRef]
- Wojcik, M.; Zawieja, I.; Seki, K. Charge Transport in Disordered Organic Solids: Refining the Bässler Equation with High-Precision Simulation Results. J. Phys. Chem. C 2020, 124, 17879–17888. [Google Scholar] [CrossRef]
- Bässler, H. Localized states and electronic transport in single component organic solids with diagonal disorder. Phys. Status Solidi (b) 1981, 107, 9–54. [Google Scholar] [CrossRef]
- Lee, Y.; Jung, S.; Plews, A.; Nejim, A.; Simonetti, O.; Giraudet, L.; Baranovskii, S.D.; Gebhard, F.; Meerholz, K.; Jung, S.; et al. Parametrization of the Gaussian disorder model to account for the high carrier mobility in disordered organic transistors. Phys. Rev. Appl. 2021, 15, 024021. [Google Scholar] [CrossRef]
- Nenashev, A.; Oelerich, J.; Dvurechenskii, A.; Gebhard, F.; Baranovskii, S. Fundamental characteristic length scale for the field dependence of hopping charge transport in disordered organic semiconductors. Phys. Rev. B 2017, 96, 035204. [Google Scholar] [CrossRef]
- Oelerich, J.O. Theoretical Modeling of Kinetic Phenomena of Atoms and Charge Carriers in Disordered Materials. Ph.D. Thesis, Philipps-Universität Marburg, Marburg, Germany, 2015. [Google Scholar]
- Zvyagin, I. A percolation approach to the temperature and charge carrier concentration dependence of the hopping conductivity in organic materials. Phys. Status Solidi c 2008, 5, 725–729. [Google Scholar] [CrossRef]
- Khan, M.; Nikitenko, V.; Burdakov, Y.V. An analytic modelling of charge transport in thin layers of disordered organic materials. J. Phys. Conf. Ser. 2017, 938, 012069. [Google Scholar] [CrossRef]
- Baranovskii, S. Theoretical description of charge transport in disordered organic semiconductors. Phys. Status Solidi (b) 2014, 251, 487–525. [Google Scholar] [CrossRef]
- Coehoorn, R.; Bobbert, P.A. Effects of Gaussian disorder on charge carrier transport and recombination in organic semiconductors. Phys. Status Solidi (a) 2012, 209, 2354–2377. [Google Scholar] [CrossRef]
- Shukri, S.; Deja, L. Effects of localization length and spatial disorder on a charge carrier mobility in organic disordered semiconductors. AIP Adv. 2021, 11, 095118. [Google Scholar] [CrossRef]
- Burdakov, Y.V.; Nikitenko, V. Monte-Carlo study of drift mobility in ultrathin organic layers: Miller-Abrahams and Marcus models. J. Phys. Conf. Ser. 2017, 938, 012067. [Google Scholar] [CrossRef]
- Lee, Y. Gaussian Density of States Driven Numerical Modeling of Organic Field-Effect Transistors. Ph.D. Thesis, Institut Polytechnique de Paris, Palaiseau, France, 2020. [Google Scholar]
- Shklovskii, B.I.; Efros, A.L. Variable-range hopping conduction. In Electronic Properties of Doped Semiconductors; Springer: Berlin/Heidelberg, Germany, 1984; pp. 202–227. [Google Scholar]
- Pollak, M.; Shklovskii, B. Hopping Transport in Solids; Elsevier: Amsterdam, The Netherlands, 1991. [Google Scholar]
- Ortuño, M.; Estellés-Duart, F.; Somoza, A.M. Numerical Simulations of Variable-Range Hopping. Phys. Status Solidi (b) 2022, 259, 2100340. [Google Scholar] [CrossRef]
- Miller, A.; Abrahams, E. Impurity conduction at low concentrations. Phys. Rev. 1960, 120, 745. [Google Scholar] [CrossRef]
- Marcus, R.A. Chemical and electrochemical electron-transfer theory. Annu. Rev. Phys. Chem. 1964, 15, 155–196. [Google Scholar] [CrossRef]
- Martínez, A.G.; Gómez, P.C.; de la Moya, S.; Siehl, H.U. Structural proton transfer rates in pure water according to Marcus theory and TD-DFT computations. J. Mol. Liq. 2022, 357, 119048. [Google Scholar] [CrossRef]
- Serdiuk, I.E.; Mo?ka, M.; Kozakiewicz, K.; Liberek, B.; Bojarski, P.; Park, S.Y. Vibrationally Assisted Direct Intersystem Crossing between the Same Charge-Transfer States for Thermally Activated Delayed Fluorescence: Analysis by Marcus–Hush Theory Including Reorganization Energy. J. Phys. Chem. B 2021, 125, 2696–2706. [Google Scholar] [CrossRef] [PubMed]
- Sowa, J.K.; Mol, J.A.; Briggs, G.A.D.; Gauger, E.M. Beyond Marcus theory and the Landauer-Büttiker approach in molecular junctions: A unified framework. J. Chem. Phys. 2018, 149, 154112. [Google Scholar] [CrossRef] [PubMed]
- Koch, A.; Kinzel, D.; Dröge, F.; Gräfe, S.; Kupfer, S. Photochemistry and Electron Transfer Kinetics in a Photocatalyst Model Assessed by Marcus Theory and Quantum Dynamics. J. Phys. Chem. C 2017, 121, 16066–16078. [Google Scholar] [CrossRef]
- Roy, S.; Baer, M.D.; Mundy, C.J.; Schenter, G.K. Marcus theory of ion-pairing. J. Chem. Theory Comput. 2017, 13, 3470–3477. [Google Scholar] [CrossRef] [PubMed]
- Nenashev, A.; Jansson, F.; Oelerich, J.; Huemmer, D.; Dvurechenskii, A.; Gebhard, F.; Baranovskii, S. Advanced percolation solution for hopping conductivity. Phys. Rev. B 2013, 87, 235204. [Google Scholar] [CrossRef]
- Nenashev, A.; Oelerich, J.; Baranovskii, S. Theoretical tools for the description of charge transport in disordered organic semiconductors. J. Phys. Condens. Matter 2015, 27, 093201. [Google Scholar] [CrossRef] [PubMed]
- Lesne, A.; Laguës, M. Scale Invariance: From Phase Transitions to Turbulence; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Li, M.; Liu, R.R.; Lü, L.; Hu, M.B.; Xu, S.; Zhang, Y.C. Percolation on complex networks: Theory and application. Phys. Rep. 2021, 907, 1–68. [Google Scholar] [CrossRef]
- Lee, D.; Kahng, B.; Cho, Y.; Goh, K.I.; Lee, D.S. Recent advances of percolation theory in complex networks. J. Korean Phys. Soc. 2018, 73, 152–164. [Google Scholar] [CrossRef]
- Hofacker, A. Critical charge transport networks in doped organic semiconductors. Commun. Mater. 2020, 1, 1–9. [Google Scholar] [CrossRef]
- Ambegaokar, V.; Halperin, B.; Langer, J. Hopping conductivity in disordered systems. Phys. Rev. B 1971, 4, 2612. [Google Scholar] [CrossRef]
- Pollak, M. A percolation treatment of dc hopping conduction. J. -Non-Cryst. Solids 1972, 11, 1–24. [Google Scholar] [CrossRef]
- Grünewald, M.; Thomas, P. A hopping model for activated charge transport in amorphous silicon. Phys. Status Solidi (b) 1979, 94, 125–133. [Google Scholar] [CrossRef]
- Vissenberg, M.; Matters, M. Theory of the field-effect mobility in amorphous organic transistors. Phys. Rev. B 1998, 57, 12964. [Google Scholar] [CrossRef]
- Baranovskii, S.; Zvyagin, I.; Cordes, H.; Yamasaki, S.; Thomas, P. Electronic transport in disordered organic and inorganic semiconductors. J. -Non-Cryst. Solids 2002, 299, 416–419. [Google Scholar] [CrossRef]
- Barabási, A.L. Network Science; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Spielman, D. Spectral graph theory. In Combinatorial Scientific Computing; Number 18; Chapman & Hall/CRC Computational Science: Boca Raton, FL, USA, 2012. [Google Scholar]
- Cuadra, L.; Nieto-Borge, J.C. Modeling Quantum Dot Systems as Random Geometric Graphs with Probability Amplitude-Based Weighted Links. Nanomaterials 2021, 11, 375. [Google Scholar] [CrossRef] [PubMed]
- Cuadra, L.; Nieto-Borge, J.C. Approaching disordered quantum dot systems by complex networks with spatial and physical-based constraints. Nanomaterials 2021, 11, 2056. [Google Scholar] [CrossRef]
- Cuadra, L.; Salcedo-Sanz, S.; Del Ser, J.; Jiménez-Fernández, S.; Geem, Z.W. A critical review of robustness in power grids using complex networks concepts. Energies 2015, 8, 9211–9265. [Google Scholar] [CrossRef]
- Nicosia, V.; Tang, J.; Mascolo, C.; Musolesi, M.; Russo, G.; Latora, V. Graph metrics for temporal networks. In Temporal Networks; Springer: Berlin/Heidelberg, Germany, 2013; pp. 15–40. [Google Scholar]
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D.U. Complex networks: Structure and dynamics. Phys. Rep. 2006, 424, 175–308. [Google Scholar] [CrossRef]
- Strogatz, S.H. Exploring complex networks. Nature 2001, 410, 268–276. [Google Scholar] [CrossRef]
- Li, P.; Li, K.; Wang, Y.; Zheng, Y.; Wang, D.; Yang, G.; Yu, X. A systematic mapping study for blockchain based on complex network. Concurr. Comput. Pract. Exp. 2022, 34, e5712. [Google Scholar] [CrossRef]
- Ma, X.; Zhou, H.; Li, Z. On the resilience of modern power systems: A complex network perspective. Renew. Sustain. Energy Rev. 2021, 152, 111646. [Google Scholar] [CrossRef]
- Cuadra, L.; Pino, M.D.; Nieto-Borge, J.C.; Salcedo-Sanz, S. Optimizing the structure of distribution smart grids with renewable generation against abnormal conditions: A complex networks approach with evolutionary algorithms. Energies 2017, 10, 1097. [Google Scholar] [CrossRef]
- Doyle, J.C.; Alderson, D.L.; Li, L.; Low, S.; Roughan, M.; Shalunov, S.; Tanaka, R.; Willinger, W. The “robust yet fragile” nature of the Internet. Proc. Natl. Acad. Sci. USA 2005, 102, 14497–14502. [Google Scholar] [CrossRef] [PubMed]
- Barthélemy, M. Spatial networks. Phys. Rep. 2011, 499, 1–101. [Google Scholar] [CrossRef]
- García-Sánchez, M.; Jiménez-Serra, I.; Puente-Sánchez, F.; Aguirre, J. The emergence of interstellar molecular complexity explained by interacting networks. Proc. Natl. Acad. Sci. USA 2022, 119, e2119734119. [Google Scholar] [CrossRef]
- Fan, J.; Meng, J.; Ludescher, J.; Chen, X.; Ashkenazy, Y.; Kurths, J.; Havlin, S.; Schellnhuber, H.J. Statistical physics approaches to the complex Earth system. Phys. Rep. 2021, 896, 1–84. [Google Scholar] [CrossRef]
- Wu, T.; Zhang, X.; Liu, Z. Understanding the mechanisms of brain functions from the angle of synchronization and complex network. Front. Phys. 2022, 17, 1–23. [Google Scholar] [CrossRef]
- Montoya, J.M.; Solé, R.V. Small world patterns in food webs. J. Theor. Biol. 2002, 214, 405–412. [Google Scholar] [CrossRef]
- Chimal-Eguía, J.C.; Castillo-Montiel, E.; Paez-Hernández, R.T. Properties of the vascular networks in malignant tumors. Entropy 2020, 22, 166. [Google Scholar] [CrossRef]
- Guimera, R.; Amaral, L.A.N. Functional cartography of complex metabolic networks. Nature 2005, 433, 895–900. [Google Scholar] [CrossRef] [PubMed]
- Newman, M. Networks; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
- Chung, F.R.; Graham, F.C. Spectral Graph Theory; Number 92; American Mathematical Society: Providence, RI, USA, 1997. [Google Scholar]
- Spielman, D.A. Algorithms, graph theory, and linear equations in Laplacian matrices. In Proceedings of the International Congress of Mathematicians 2010 (ICM 2010) (In 4 Volumes) Vol. I: Plenary Lectures and Ceremonies Vols. II–IV: Invited Lectures; World Scientific: Singapore, 2010; pp. 2698–2722. [Google Scholar]
- Iannelli, F.; Koher, A.; Brockmann, D.; Hövel, P.; Sokolov, I.M. Effective distances for epidemics spreading on complex networks. Phys. Rev. E 2017, 95, 012313. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Wu, X.; Niu, R.; Wu, X.; Fan, R. A new SAIR model on complex networks for analysing the 2019 novel coronavirus (COVID-19). Nonlinear Dyn. 2020, 101, 1777–1787. [Google Scholar] [CrossRef] [PubMed]
- Ding, L.; Liu, S.Y.; Yang, Q.; Xu, X.K. Uncovering the Dependence of Cascading Failures on Network Topology by Constructing Null Models. Entropy 2019, 21, 1119. [Google Scholar] [CrossRef]
- Dobson, I.; Carreras, B.A.; Lynch, V.E.; Newman, D.E. Complex systems analysis of series of blackouts: Cascading failure, critical points, and self-organization. Chaos Interdiscip. J. Nonlinear Sci. 2007, 17, 026103. [Google Scholar] [CrossRef]
- Pond, T.; Magsarjav, S.; South, T.; Mitchell, L.; Bagrow, J.P. Complex contagion features without social reinforcement in a model of social information flow. Entropy 2020, 22, 265. [Google Scholar] [CrossRef]
- Liu, W.; Liu, C.; Yang, Z.; Liu, X.; Zhang, Y.; Wei, Z. Modeling the propagation of mobile malware on complex networks. Commun. Nonlinear Sci. Numer. Simul. 2016, 37, 249–264. [Google Scholar] [CrossRef]
- Salcedo-Sanz, S.; Casillas-Pérez, D.; Del Ser, J.; Casanova-Mateo, C.; Cuadra, L.; Piles, M.; Camps-Valls, G. Persistence in complex systems. Phys. Rep. 2022, 957, 1–73. [Google Scholar] [CrossRef]
- Oliveira, C.L.; Morais, P.A.; Moreira, A.A.; Andrade, J.S., Jr. Enhanced flow in small-world networks. Phys. Rev. Lett. 2014, 112, 148701. [Google Scholar] [CrossRef]
- Backstrom, L.; Boldi, P.; Rosa, M.; Ugander, J.; Vigna, S. Four degrees of separation. In Proceedings of the 4th Annual ACM Web Science Conference, Evanston, IL, USA, 22–24 June 2012; pp. 33–42. [Google Scholar]
- Roxin, A.; Riecke, H.; Solla, S.A. Self-sustained activity in a small-world network of excitable neurons. Phys. Rev. Lett. 2004, 92, 198101. [Google Scholar] [CrossRef]
- Bassett, D.S.; Greenfield, D.L.; Meyer-Lindenberg, A.; Weinberger, D.R.; Moore, S.W.; Bullmore, E.T. Efficient physical embedding of topologically complex information processing networks in brains and computer circuits. PLoS Comput. Biol. 2010, 6, e1000748. [Google Scholar] [CrossRef] [PubMed]
- Viana, M.P.; Strano, E.; Bordin, P.; Barthelemy, M. The simplicity of planar networks. Sci. Rep. 2013, 3, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Brédas, J.L.; Beljonne, D.; Coropceanu, V.; Cornil, J. Charge-transfer and energy-transfer processes in π-conjugated oligomers and polymers: A molecular picture. Chem. Rev. 2004, 104, 4971–5004. [Google Scholar] [CrossRef]
- Rubel, O.; Baranovskii, S.; Thomas, P.; Yamasaki, S. Concentration dependence of the hopping mobility in disordered organic solids. Phys. Rev. B 2004, 69, 014206. [Google Scholar] [CrossRef]
- Ding, X.; Jiang, T. Spectral distributions of adjacency and Laplacian matrices of random graphs. Ann. Appl. Probab. 2010, 20, 2086–2117. [Google Scholar] [CrossRef]
- Masuda, N.; Porter, M.A.; Lambiotte, R. Random walks and diffusion on networks. Phys. Rep. 2017, 716, 1–58. [Google Scholar] [CrossRef]
- Mülken, O.; Blumen, A. Continuous-time quantum walks: Models for coherent transport on complex networks. Phys. Rep. 2011, 502, 37–87. [Google Scholar] [CrossRef]
- Van Kampen, N.G. Stochastic Processes in Physics and Chemistry; Elsevier: Amsterdam, The Netherlands, 1992; Volume 1. [Google Scholar]
- Kulvelis, N.; Dolgushev, M.; Mülken, O. Universality at breakdown of quantum transport on complex networks. Phys. Rev. Lett. 2015, 115, 120602. [Google Scholar] [CrossRef]
- Milgram, S. The small world problem. Psychol. Today 1967, 2, 60–67. [Google Scholar]
- Travers, J.; Milgram, S. An experimental study of the small world problem. In Social Networks; Elsevier: Amsterdam, The Netherlands, 1977; pp. 179–197. [Google Scholar]
- Muldoon, S.F.; Bridgeford, E.W.; Bassett, D.S. Small-world propensity and weighted brain networks. Sci. Rep. 2016, 6, 1–13. [Google Scholar] [CrossRef]
- Oelerich, J.; Jansson, F.; Nenashev, A.; Gebhard, F.; Baranovskii, S. Energy position of the transport path in disordered organic semiconductors. J. Phys. Condens. Matter 2014, 26, 255801. [Google Scholar] [CrossRef]
- Baranovskii, S.; Cordes, H.; Hensel, F.; Leising, G. Charge-carrier transport in disordered organic solids. Phys. Rev. B 2000, 62, 7934. [Google Scholar] [CrossRef]
- Baranovskii, S.; Faber, T.; Hensel, F.; Thomas, P. The applicability of the transport-energy concept to various disordered materials. J. Phys. Condens. Matter 1997, 9, 2699. [Google Scholar] [CrossRef]
- Baranovskii, S.; Zvyagin, I.; Cordes, H.; Yamasaki, S.; Thomas, P. Percolation approach to hopping transport in organic disordered solids. Phys. Status Solidi (b) 2002, 230, 281–288. [Google Scholar] [CrossRef]
- Kordt, P.; Speck, T.; Andrienko, D. Finite-size scaling of charge carrier mobility in disordered organic semiconductors. Phys. Rev. B 2016, 94, 014208. [Google Scholar] [CrossRef]
- Böhme, G.A. Emergence and persistence of diversity in complex networks. Eur. Phys. J. Spec. Top. 2013, 222, 3089–3169. [Google Scholar] [CrossRef]
- Kivelä, M.; Arenas, A.; Barthelemy, M.; Gleeson, J.P.; Moreno, Y.; Porter, M.A. Multilayer networks. J. Complex Netw. 2014, 2, 203–271. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cuadra, L.; Salcedo-Sanz, S.; Nieto-Borge, J.C. Organic Disordered Semiconductors as Networks Embedded in Space and Energy. Nanomaterials 2022, 12, 4279. https://doi.org/10.3390/nano12234279
Cuadra L, Salcedo-Sanz S, Nieto-Borge JC. Organic Disordered Semiconductors as Networks Embedded in Space and Energy. Nanomaterials. 2022; 12(23):4279. https://doi.org/10.3390/nano12234279
Chicago/Turabian StyleCuadra, Lucas, Sancho Salcedo-Sanz, and José Carlos Nieto-Borge. 2022. "Organic Disordered Semiconductors as Networks Embedded in Space and Energy" Nanomaterials 12, no. 23: 4279. https://doi.org/10.3390/nano12234279
APA StyleCuadra, L., Salcedo-Sanz, S., & Nieto-Borge, J. C. (2022). Organic Disordered Semiconductors as Networks Embedded in Space and Energy. Nanomaterials, 12(23), 4279. https://doi.org/10.3390/nano12234279







