Optical and Thermal Behavior of Germanium Thin Films under Femtosecond Laser Irradiation
Abstract
1. Introduction
- Stage 1 () photoionization, impact ionization;
- Stage 2 (eq) electron–electron scattering, electron-phonon scattering and carrier recombination;
- Stage 3 (eq) thermal equilibrium;
- Stage 4 (eq) thermal diffusion and re-solidification,
2. Theoretical Model
- z is the direction perpendicular to the surface;
- is the ambipolar diffusion coefficient. It represents the mobility coefficient of charge carriers when there is a diffusion driven by an electric field, such as the diffusion of electron–hole plasma induced by the laser-related electric field;
- I is the laser intensity;
- is the one-photon absorption coefficient;
- is the two-photon absorption coefficient, which can be ignored when the photon energy is higher than Ge bandgap (Eg ≈ 0.66 eV at room temperature);
- is the impact ionization factor, related to valence electrons excited by collisions with free electrons, occurring when the free electron energy exceeds the material bandgap (avalanche ionization);
- is the Auger recombination coefficient. This phenomenon is very important in fs laser interaction with semiconductors. It refers to excited free electrons recombining again with holes, and transferring their energy to other electrons in the same band by electron–electron collisions.
- ,, and are the heat capacity, the absolute temperature, and the thermal conductivity of electrons and lattice, respectively;
- G is the electron–lattice coupling coefficient;
- is the heat delivered by the laser source, defined as:
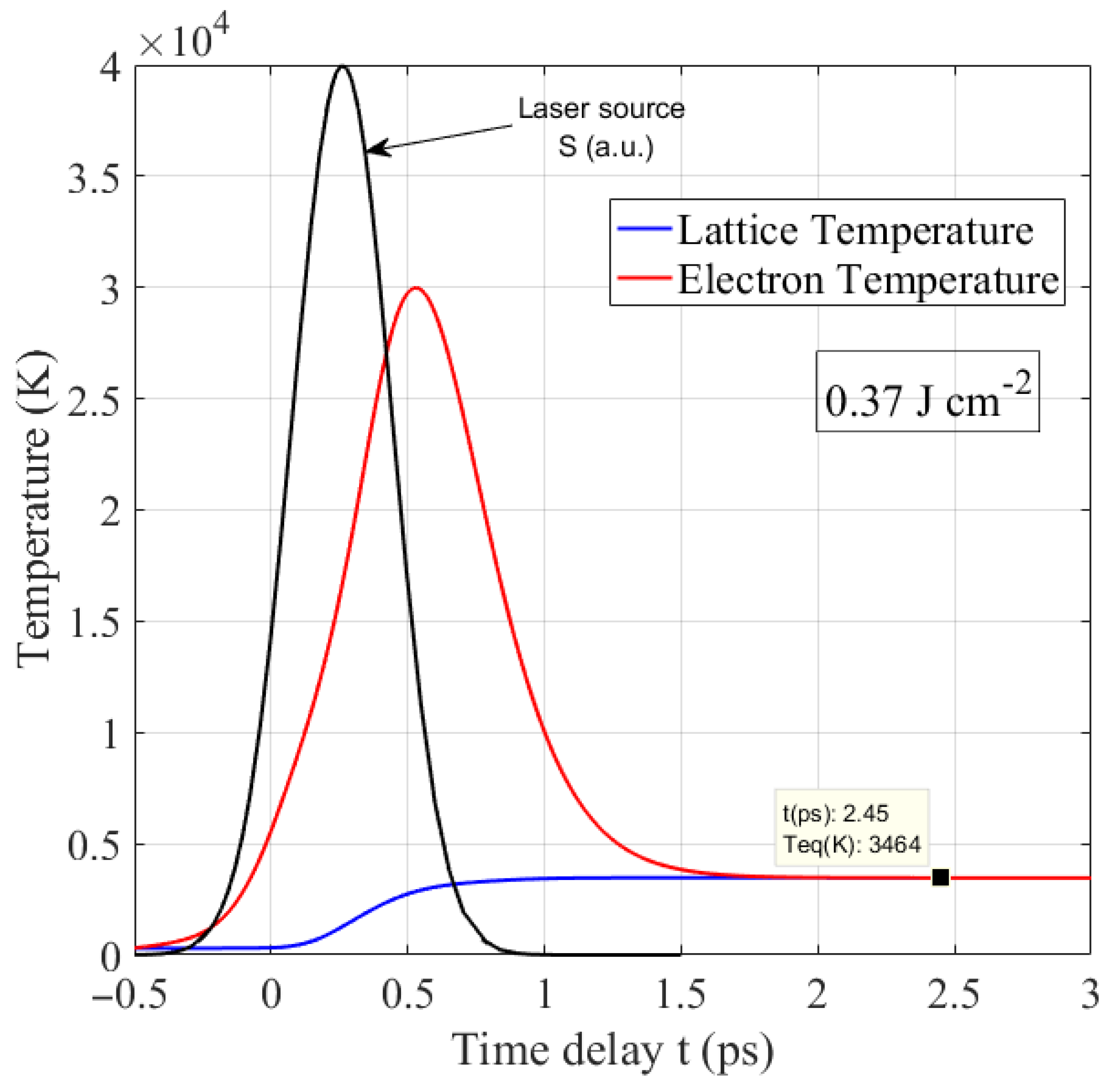
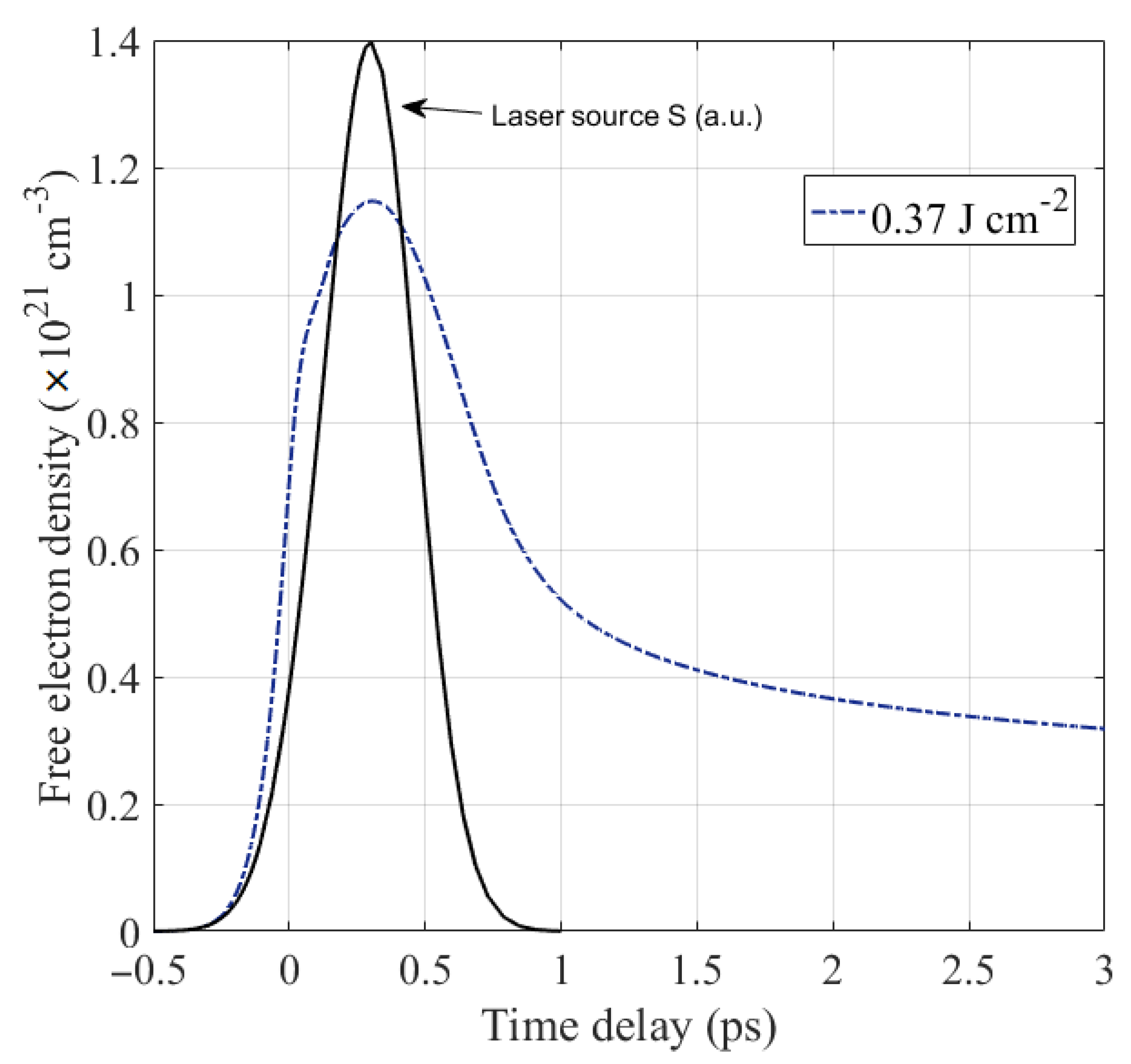
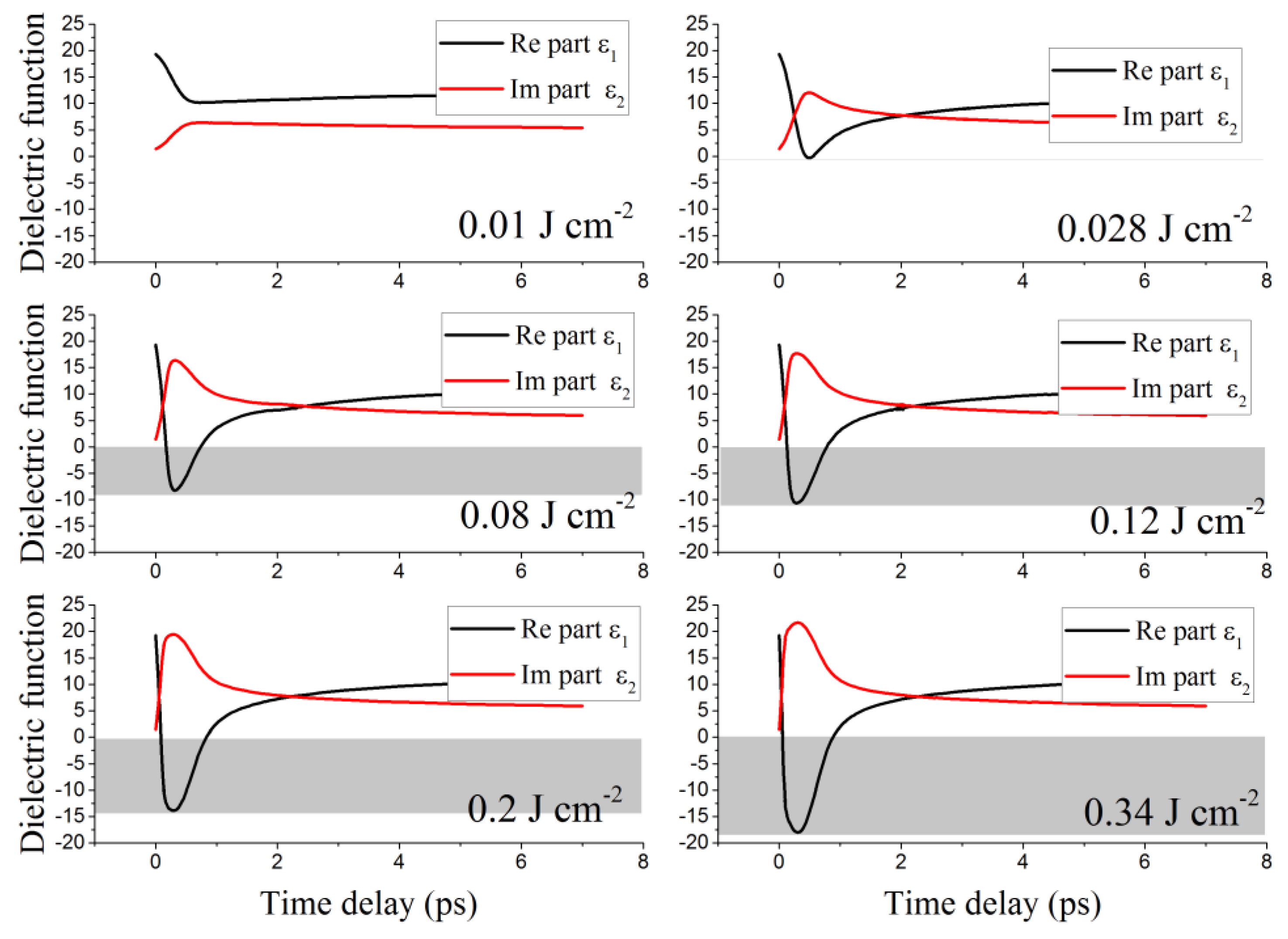
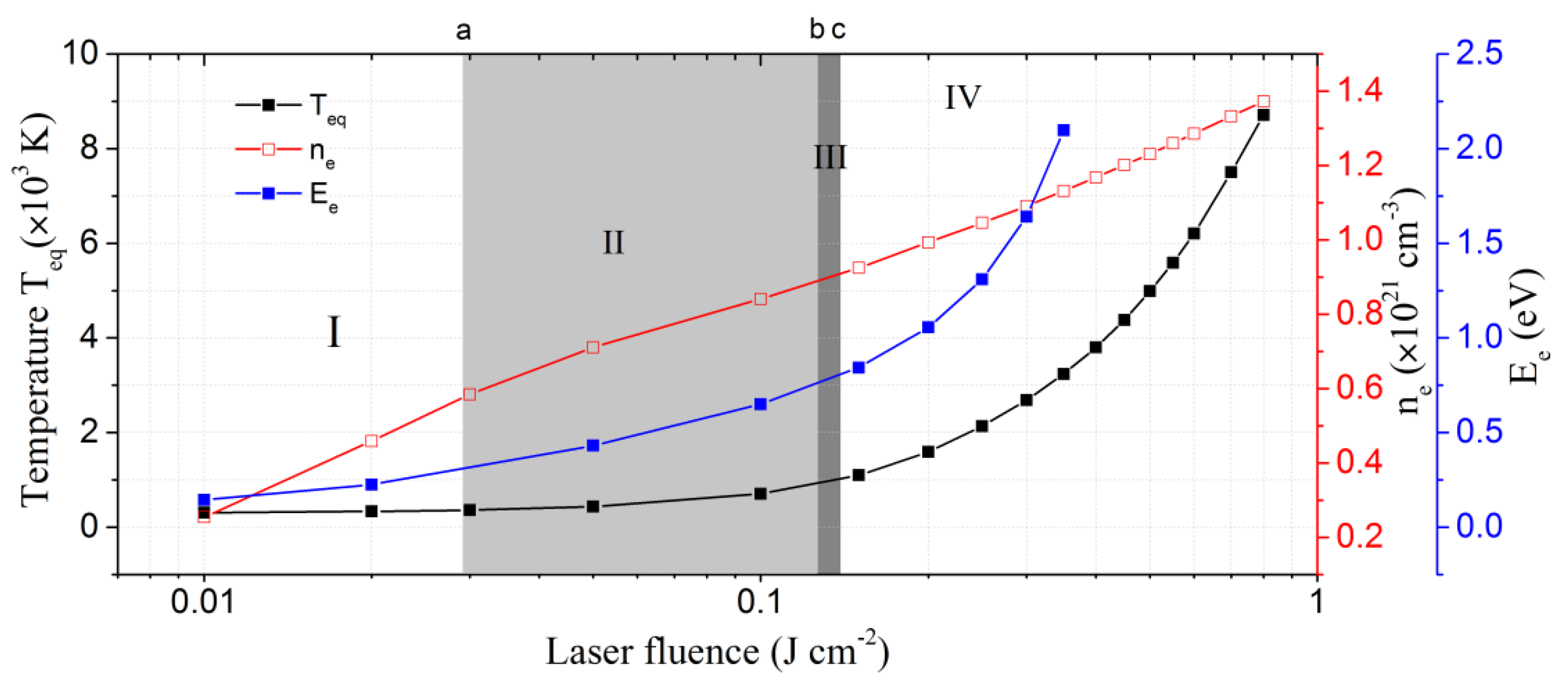
3. Results and Discussion
- Photoionization;
- Metallic state induced by photoionization (F > 0.028 J cm−2);
- Impact ionization (F > 0.12 J cm−2);
- Thermal modification (F > 0.14 J cm−2).
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Ambipolar diffusion coefficient (m2 s−1) | [11,26] | |
| One-photon absorption coefficient (m−1) | [20] | |
| Bandgap Eg (eV) | [47] | |
| Auger recombination coefficient (m6 s−1) | [11,26] | |
| Electron-electron scattering time (fs) | see Appendix B | |
| Optical effective electron mass | [26] | |
| Cross section coefficient (cm2) | [48] | |
| Impact ionization coefficient (cm2 J−1) | [48] | |
| Electronic heat capacity (J m−3 K−1) | [11] | |
| Electron-phonon scattering time (s) | [11,20] | |
| Electron-phonon coupling coefficient(J m−3 K−1 s−1) | [20] | |
| Density (kg m−3) | [20] | |
| Lattice heat capacity (J kg−1 K−1) | [20] | |
| Electron thermal conductivity (W m−1 K−1) | [20] | |
| Lattice thermal conductivity (W m−1 K−1) | [11] | |
| Free-carrier absorption cross-section (m2) | [11] | |
| Melting temperature (K) | [20,22] | |
| Critical temperature (K) | [20,22] | |
| Initial free electron density nc0 (cm−3) | [11] |
Appendix B
Appendix C
References
- von der Linde, D.; Sokolowski-Tinten, K.; Bialkowski, J. Laser–solid interaction in the femtosecond time regime. Appl. Surf. Sci. 1997, 109–110, 1–10. [Google Scholar] [CrossRef]
- Phillips, K.C.; Gandhi, H.H.; Mazur, E.; Sundaram, S.K. Ultrafast laser processing of materials: A review. Adv. Opt. Photon 2015, 7, 684–712. [Google Scholar] [CrossRef]
- Malinauskas, M.; Žukauskas, A.; Hasegawa, S.; Hayasaki, Y.; Mizeikis, V.; Buividas, R.; Juodkazis, S. Ultrafast laser processing of materials: From science to industry. Light. Sci. Appl. 2016, 5, e16133. [Google Scholar] [CrossRef] [PubMed]
- Bulgakova, N.; Bulgakov, A. Pulsed laser ablation of solids: Transition from normal vaporization to phase explosion. Appl. Phys. A 2001, 73, 199–208. [Google Scholar] [CrossRef]
- Stoian, R.; Rosenfeld, A.; Ashkenasi, D.; Hertel, I.V.; Bulgakova, N.; Campbell, E. Surface Charging and Impulsive Ion Ejection during Ultrashort Pulsed Laser Ablation. Phys. Rev. Lett. 2002, 88, 097603. [Google Scholar] [CrossRef]
- Gamaly, E.G.; Rode, A.; Luther-Davies, B.; Tikhonchuk, V.T. Ablation of solids by femtosecond lasers: Ablation mechanism and ablation thresholds for metals and dielectrics. Phys. Plasmas 2002, 9, 949–957. [Google Scholar] [CrossRef]
- Eaton, S.M.; Zhang, H.; Herman, P.R.; Yoshino, F.; Shah, L.; Bovatsek, J.; Arai, A.Y. Heat accumulation effects in femtosecond laser-written waveguides with variable repetition rate. Opt. Express 2005, 13, 4708–4716. [Google Scholar] [CrossRef]
- Abdelmalek, A.; Giakoumaki, A.; Bharadwaj, V.; Sotillo, B.; Le Phu, T.; Bollani, M.; Bedrane, Z.; Ramponi, R.; Eaton, S.; Maaza, M. Morphological Study of Nanostructures Induced by Direct Femtosecond Laser Ablation on Diamond. Micromachines 2021, 12, 583. [Google Scholar] [CrossRef]
- Bonse, J.; Baudach, S.; Krüger, J.; Kautek, W.; Lenzner, M. Femtosecond laser ablation of silicon–modification thresholds and morphology. Appl. Phys. A 2002, 74, 19–25. [Google Scholar] [CrossRef]
- Li, Z.; Fang, F.; Chen, J.; Zhang, X. Machining approach of freeform optics on infrared materials via ultra-precision turning. Opt. Express 2017, 25, 2051–2062. [Google Scholar] [CrossRef]
- Taylor, L.L.; Xu, J.; Pomerantz, M.; Smith, T.R.; Lambropoulos, J.C.; Qiao, J. Femtosecond laser polishing of germanium. Opt. Mater. Express 2019, 9, 4165–4177. [Google Scholar] [CrossRef]
- Zhang, F.; Li, S.; Chen, A.; Jiang, Y.; Li, S.; Jin, M. Ultrafast dynamical process of Ge irradiated by the femtosecond laser pulses. High Power Laser Sci. Eng. 2016, 4, E12. [Google Scholar] [CrossRef]
- Cheng, C.; Wang, S.; Chang, K.; Chen, J. Femtosecond laser ablation of copper at high laser fluence: Modeling and experimental comparison. Appl. Surf. Sci. 2016, 361, 41–48. [Google Scholar] [CrossRef]
- Sundaram, S.K.; Mazur, E. Inducing and probing non-thermal transitions in semiconductors using femtosecond laser pulses. Nat. Mater. 2002, 1, 217–224. [Google Scholar] [CrossRef]
- Abdelmalek, A.; Sotillo, B.; Bedrane, Z.; Bharadwaj, V.; Pietralunga, S.; Ramponi, R.; Amara, E.-H.; Eaton, S.M. Origin of femtosecond laser induced periodic nanostructure on diamond. AIP Adv. 2017, 7, 105105. [Google Scholar] [CrossRef]
- Miyaji, G.; Miyazaki, K. Origin of periodicity in nanostructuring on thin film surfaces ablated with femtosecond laser pulses. Opt. Express 2008, 16, 16265–16271. [Google Scholar] [CrossRef]
- Gan, Y.; Chen, J.K. Numerical Analysis of Ultrashort Pulse Laser-Induced Thermomechanical Response of Germanium Thin Films. Nanoscale Microscale Thermophys. Eng. 2012, 16, 274–287. [Google Scholar] [CrossRef]
- Anisimov, S.I.; Rethfeld, B. Theory of ultrashort laser pulse interaction with a metal. In Proceedings of the SPIE 3093, Non-resonant Laser-Matter Interaction (NLMI-9), Saint Petersburg-Pushkin, Russia, 1–3 July 1996; pp. 192–203. [Google Scholar] [CrossRef]
- Rethfeld, B.; Sokolowski-Tinten, K.; Von Der Linde, D.; Anisimov, S. Timescales in the response of materials to femtosecond laser excitation. Appl. Phys. A 2004, 79, 767–769. [Google Scholar] [CrossRef]
- Zhu, H.; Zhang, Z.; Xu, J.; Ren, Y.; Zhu, Z.; Xu, K.; Wang, Z.; Wang, C. A numerical study of picosecond laser micro-grooving of single crystalline germanium: Mechanism discussion and process simulation. J. Manuf. Process. 2021, 69, 351–367. [Google Scholar] [CrossRef]
- Sokolowski-Tinten, K.; von der Linde, D. Generation of dense electron-hole plasmas in silicon. Phys. Rev. B 2000, 61, 2643–2650. [Google Scholar] [CrossRef]
- Bonse, J.; Bachelier, G.; Siegel, J.; Solis, J. Time- and space-resolved dynamics of melting, ablation, and solidification phenomena induced by femtosecond laser pulses in germanium. Phys. Rev. B 2006, 74, 134106. [Google Scholar] [CrossRef]
- Møller, S.H.; Andersen, S.T.; Balling, P. Transient optical properties of highly excited dielectric materials: Apparent birefringence and delayed reflectivity increase. Phys. Rev. Res. 2020, 2, 043010. [Google Scholar] [CrossRef]
- Miyazaki, K.; Miyaji, G. Periodic Nanostructure Formation on Silicon Irradiated with Multiple Low-fluence Femtosecond Laser Pulses in Water. Phys. Procedia 2012, 39, 674–682. [Google Scholar] [CrossRef]
- Vaghasiya, H.; Krause, S.; Miclea, P.-T. Thermal and non-thermal ablation mechanisms in crystalline silicon by femtosecond laser pulses: Classical approach of the carrier density two temperature model. J. Phys. D Appl. Phys. 2022, 55, 175109. [Google Scholar] [CrossRef]
- Chen, J.; Tzou, D.; Beraun, J. Numerical investigation of ultrashort laser damage in semiconductors. Int. J. Heat Mass Transf. 2005, 48, 501–509. [Google Scholar] [CrossRef]
- Zhang, H.; Wolbers, S.A.; Krol, D.M.; Dijkhuis, J.I.; Van Oosten, D. Modeling and experiments of self-reflectivity under femtosecond ablation conditions. J. Opt. Soc. Am. B 2015, 32, 606–616. [Google Scholar] [CrossRef]
- Momma, C.; Nolte, S.; Chichkov, B.N.; Alvensleben, F.V.; Tünnermann, A. Precise laser ablation with ultrashort pulses. Appl. Surf. Sci. 1997, 109–110, 15–19. [Google Scholar] [CrossRef]
- Gattass, R.R.; Mazur, E. Femtosecond laser micromachining in transparent materials. Nat. Photonics 2008, 2, 219–225. [Google Scholar] [CrossRef]
- Shinoda, M.; Gattass, R.R.; Mazur, E. Femtosecond laser-induced formation of nanometer-width grooves on synthetic single-crystal diamond surfaces. J. Appl. Phys. 2009, 105, 053102. [Google Scholar] [CrossRef]
- Manickam, S.; Wang, J.; Huang, C. Laser–material interaction and grooving performance in ultrafast laser ablation of crystalline germanium under ambient conditions. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2013, 227, 1714–1723. [Google Scholar] [CrossRef]
- Cavalleri, A.; Siders, C.W.; Rose-Petruck, C.; Jimenez, R.; Tóth, C.; Squier, J.A.; Barty, C.P.J.; Wilson, K.R.; Sokolowski-Tinten, K.; von Hoegen, M.H.; et al. Ultrafast x-ray measurement of laser heating in semiconductors: Parameters determining the melting threshold. Phys. Rev. B 2001, 63, 193306. [Google Scholar] [CrossRef]
- Salihoglu, O.; Kuüruüm, U.; Yağlıoğlu, H.G.; Elmali, A.; Aydinli, A. Femtosecond laser crystallization of amorphous Ge. J. Appl. Phys. 2011, 109, 123108. [Google Scholar] [CrossRef]
- Nunley, T.N.; Fernando, N.S.; Samarasingha, N.; Moya, J.M.; Nelson, C.M.; Medina, A.A.; Zollner, S. Optical constants of germanium and thermally grown germanium dioxide from 0.5 to 6.6eV via a multisample ellipsometry investigation. J. Vac. Sci. Technol. B Nanotechnol. Microelectron. Mater. Process. Meas. Phenom. 2016, 34, 061205. [Google Scholar] [CrossRef]
- Her, T.-H.; Finlay, R.J.; Wu, C.; Deliwala, S.; Mazur, E. Microstructuring of silicon with femtosecond laser pulses. Appl. Phys. Lett. 1998, 73, 1673–1675. [Google Scholar] [CrossRef]
- Derrien, T.J.-Y.; Bulgakova, N.M. Modeling of silicon in femtosecond laser-induced modification regimes: Accounting for ambipolar diffusion. In Proceedings of the SPIE 10228, Nonlinear Optics and Applications X, SPIE Optics+Optoelectronics, Prague, Czech Republic, 24–27 April 2017; p. 102280E. [Google Scholar] [CrossRef]
- Girolami, M.; Bellucci, A.; Mastellone, M.; Orlando, S.; Valentini, V.; Montereali, R.; Vincenti, M.; Polini, R.; Trucchi, D.M. Optical characterization of double-nanotextured black diamond films. Carbon 2018, 138, 384–389. [Google Scholar] [CrossRef]
- Girolami, M.; Bellucci, A.; Mastellone, M.; Orlando, S.; Serpente, V.; Valentini, V.; Polini, R.; Sani, E.; De Caro, T.; Trucchi, D.M. Femtosecond-Laser Nanostructuring of Black Diamond Films under Different Gas Environments. Materials 2020, 13, 5761. [Google Scholar] [CrossRef] [PubMed]
- Mastellone, M.; Bellucci, A.; Girolami, M.; Serpente, V.; Polini, R.; Orlando, S.; Santagata, A.; Sani, E.; Hitzel, F.; Trucchi, D.M. Deep-Subwavelength 2D Periodic Surface Nanostructures on Diamond by Double-Pulse Femtosecond Laser Irradiation. Nano Lett. 2021, 21, 4477–4483. [Google Scholar] [CrossRef] [PubMed]
- He, W.; Yang, J. Probing ultrafast nonequilibrium dynamics in single-crystal SiC through surface nanostructures induced by femtosecond laser pulses. J. Appl. Phys. 2017, 121, 123108. [Google Scholar] [CrossRef]
- Mastellone, M.; Bellucci, A.; Girolami, M.; Montereali, R.; Orlando, S.; Polini, R.; Serpente, V.; Sani, E.; Valentini, V.; Vincenti, M.; et al. Enhanced selective solar absorption of surface nanotextured semi-insulating 6H–SiC. Opt. Mater. 2020, 107, 109967. [Google Scholar] [CrossRef]
- Girolami, M.; Criante, L.; Di Fonzo, F.; Turco, S.L.; Mezzetti, A.; Notargiacomo, A.; Pea, M.; Bellucci, A.; Calvani, P.; Valentini, V.; et al. Graphite distributed electrodes for diamond-based photon-enhanced thermionic emission solar cells. Carbon 2017, 111, 48–53. [Google Scholar] [CrossRef]
- Sánchez, M.I.; Delaporte, P.; Spiegel, Y.; Franta, B.; Mazur, E.; Sarnet, T. A Laser-Processed Silicon Solar Cell with Photovoltaic Efficiency in the Infrared. Phys. Status solidi A 2021, 218, 2000550. [Google Scholar] [CrossRef]
- Bellucci, A.; Calvani, P.; Girolami, M.; Orlando, S.; Polini, R.; Trucchi, D.M. Optimization of black diamond films for solar energy conversion. Appl. Surf. Sci. 2016, 380, 8–11. [Google Scholar] [CrossRef]
- Cai, J.; Pan, X.; Yuan, H.; Zhang, Y.; Meng, F.; Zhang, M. Experimental study of diamond ablation based on femtosecond laser. Optik 2020, 217, 164838. [Google Scholar] [CrossRef]
- Wu, M.; Guo, B.; Zhao, Q.; He, P.; Zeng, Z.; Zang, J. The influence of the ionization regime on femtosecond laser beam machining mono-crystalline diamond. Opt. Laser Technol. 2018, 106, 34–39. [Google Scholar] [CrossRef]
- Boukhatem, M.H. Carriers Temperature Dependence of Energy Band Gap for Germanium. Silicon 2016, 8, 309–312. [Google Scholar] [CrossRef]
- Wang, M.; Mei, W.; Wang, Y. Simulation of femtosecond laser ablation sapphire based on free electron density. Opt. Laser Technol. 2019, 113, 123–128. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdelmalek, A.; Kotsedi, L.; Bedrane, Z.; Amara, E.-H.; Girolami, M.; Maaza, M. Optical and Thermal Behavior of Germanium Thin Films under Femtosecond Laser Irradiation. Nanomaterials 2022, 12, 3786. https://doi.org/10.3390/nano12213786
Abdelmalek A, Kotsedi L, Bedrane Z, Amara E-H, Girolami M, Maaza M. Optical and Thermal Behavior of Germanium Thin Films under Femtosecond Laser Irradiation. Nanomaterials. 2022; 12(21):3786. https://doi.org/10.3390/nano12213786
Chicago/Turabian StyleAbdelmalek, Ahmed, Lebogang Kotsedi, Zeyneb Bedrane, El-Hachemi Amara, Marco Girolami, and Malik Maaza. 2022. "Optical and Thermal Behavior of Germanium Thin Films under Femtosecond Laser Irradiation" Nanomaterials 12, no. 21: 3786. https://doi.org/10.3390/nano12213786
APA StyleAbdelmalek, A., Kotsedi, L., Bedrane, Z., Amara, E.-H., Girolami, M., & Maaza, M. (2022). Optical and Thermal Behavior of Germanium Thin Films under Femtosecond Laser Irradiation. Nanomaterials, 12(21), 3786. https://doi.org/10.3390/nano12213786








