Crystallisation Kinetics and Associated Electrical Conductivity Dynamics of Poly(Ethylene Vinyl Acetate) Nanocomposites in the Melt State
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
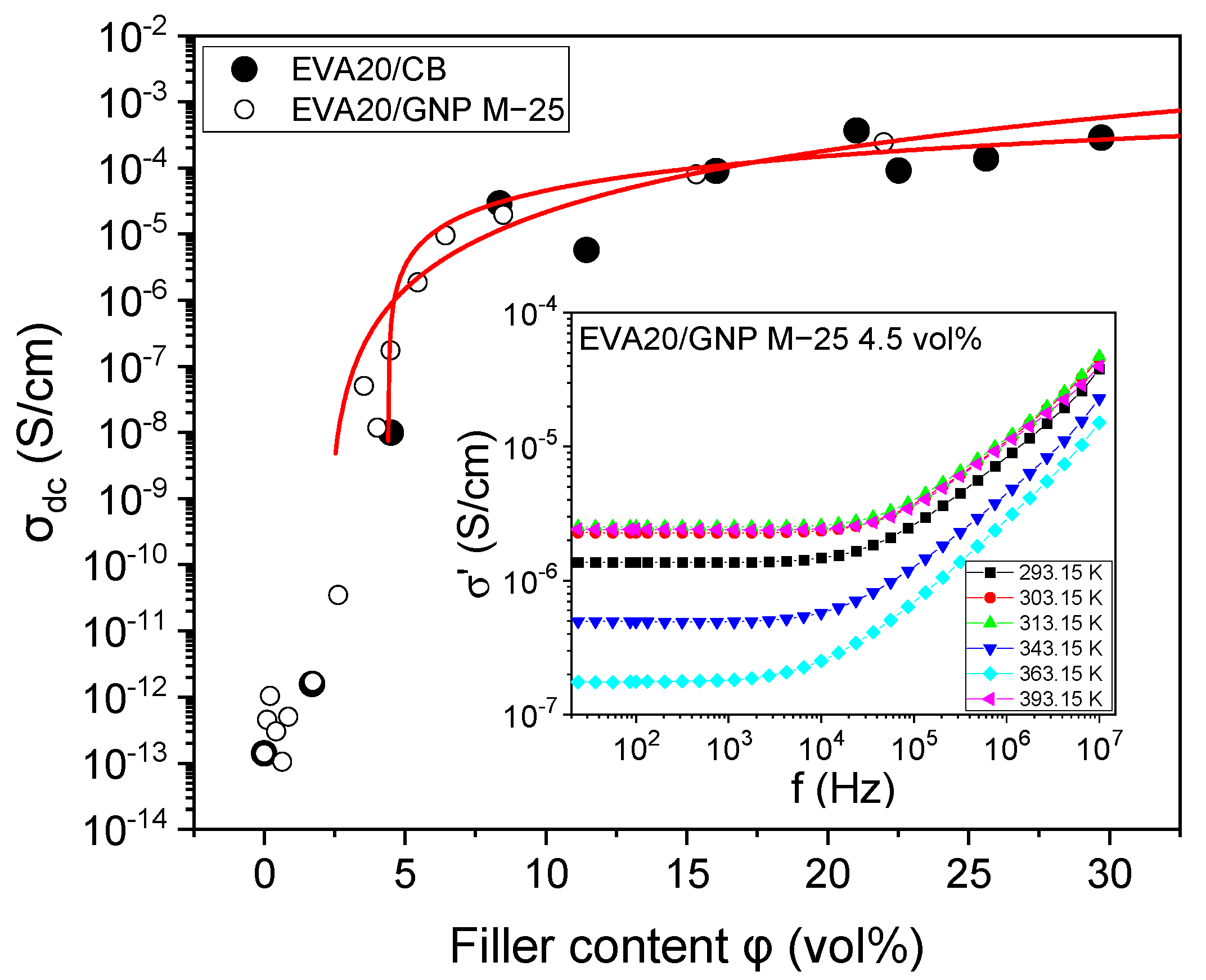
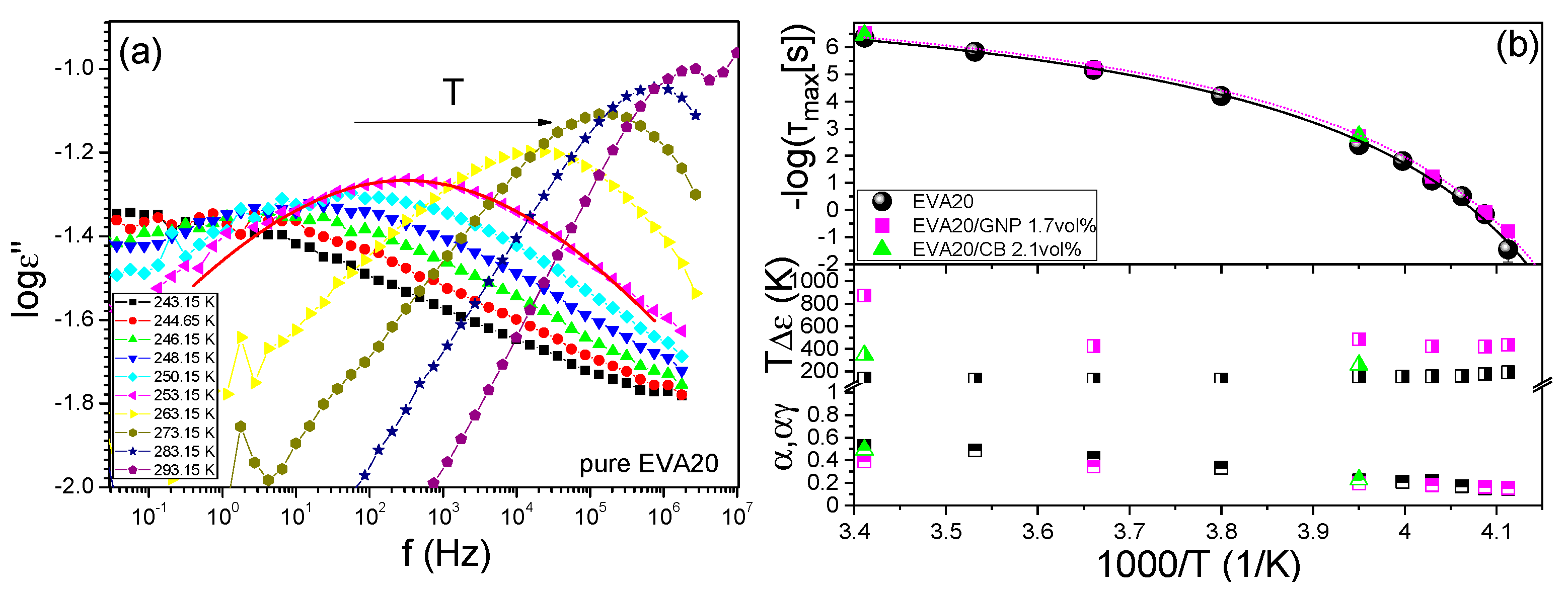
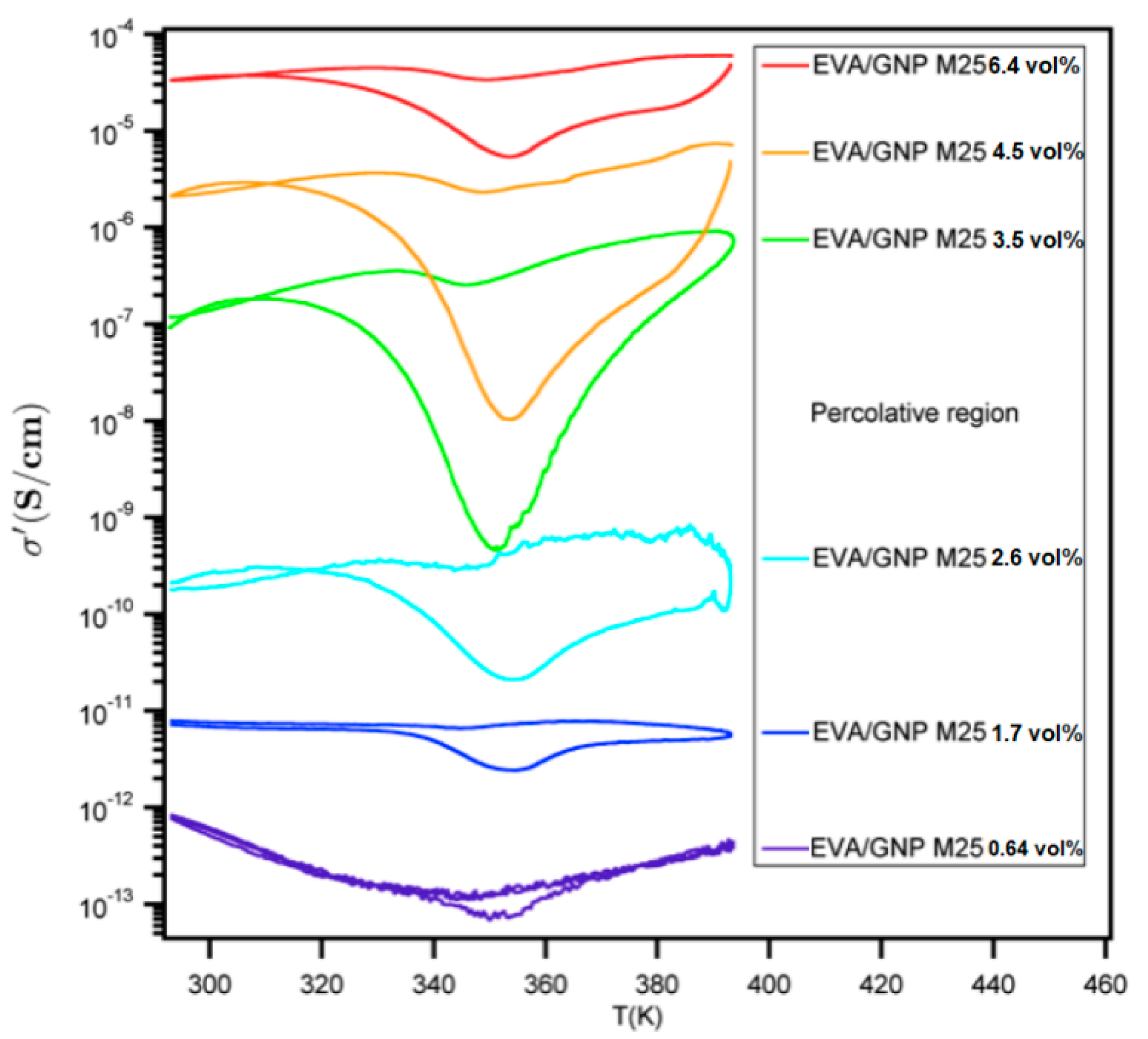
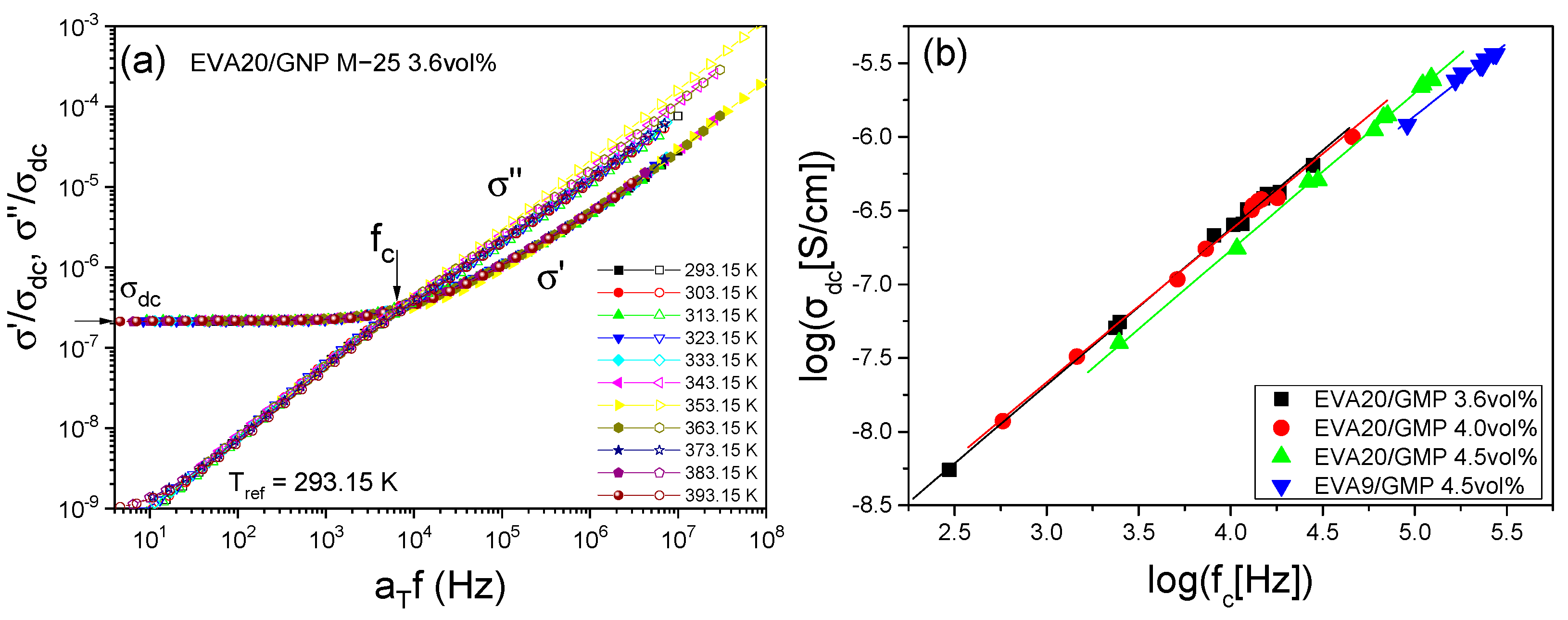
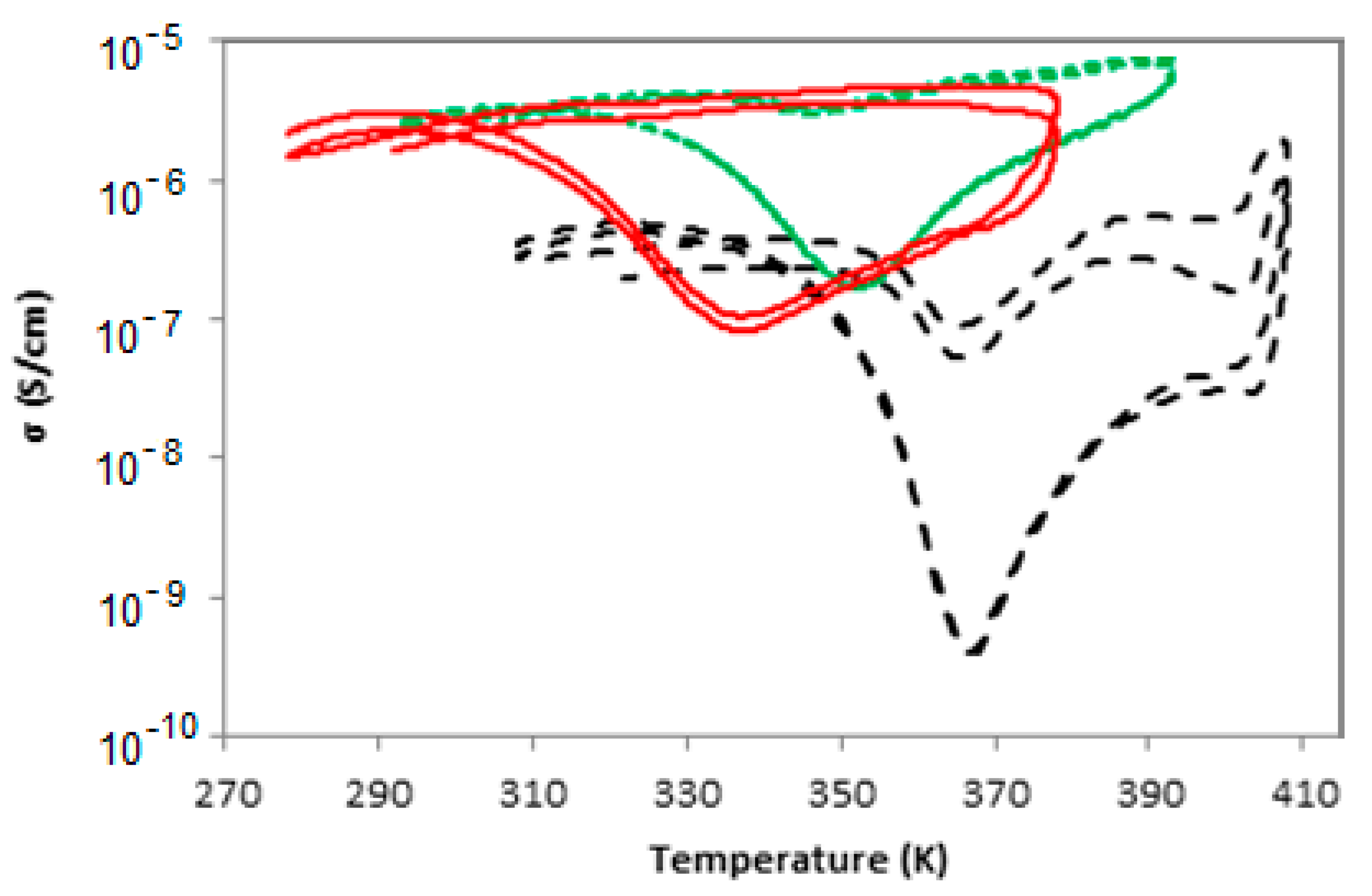
3.1. Electrical Behaviour
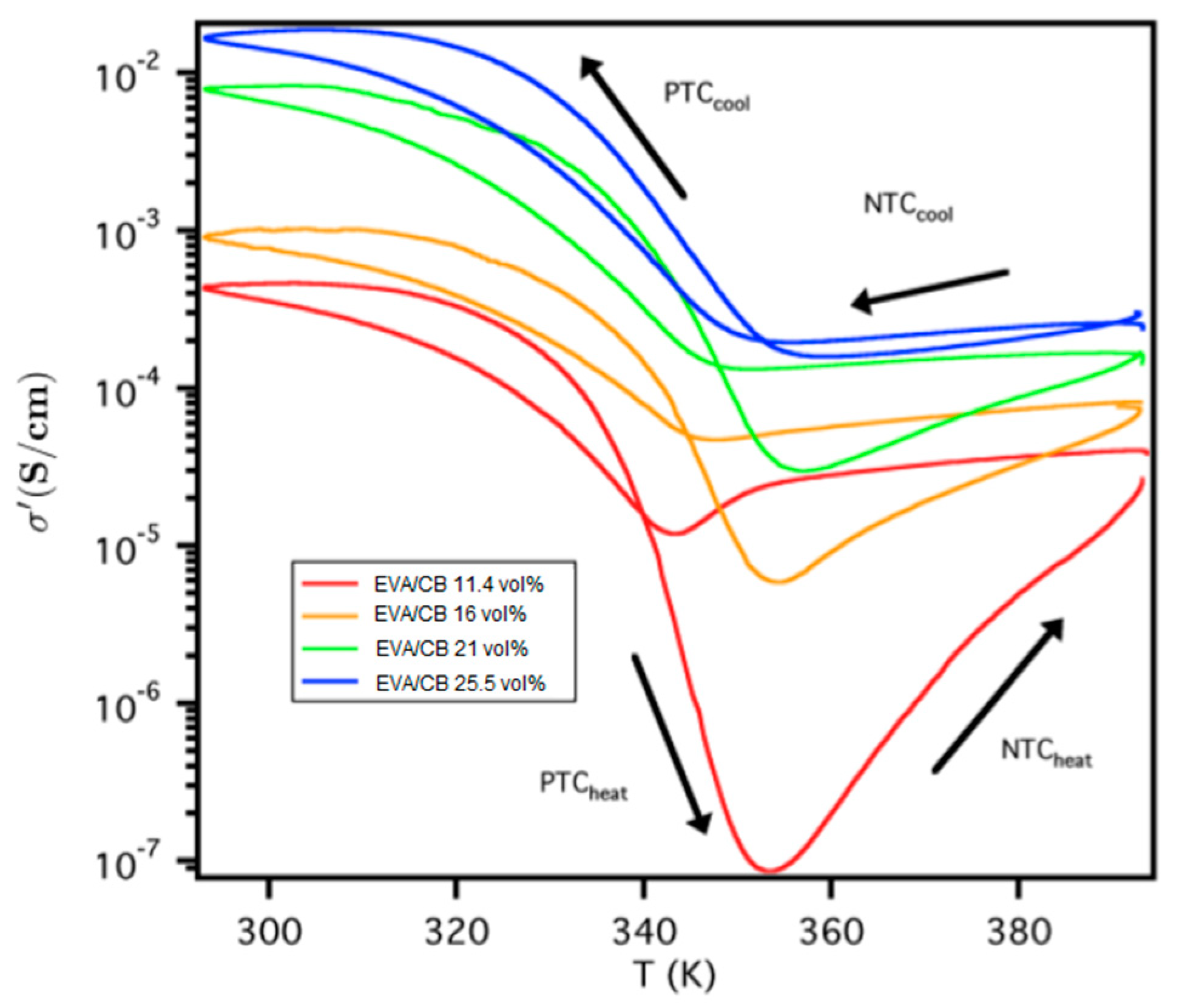
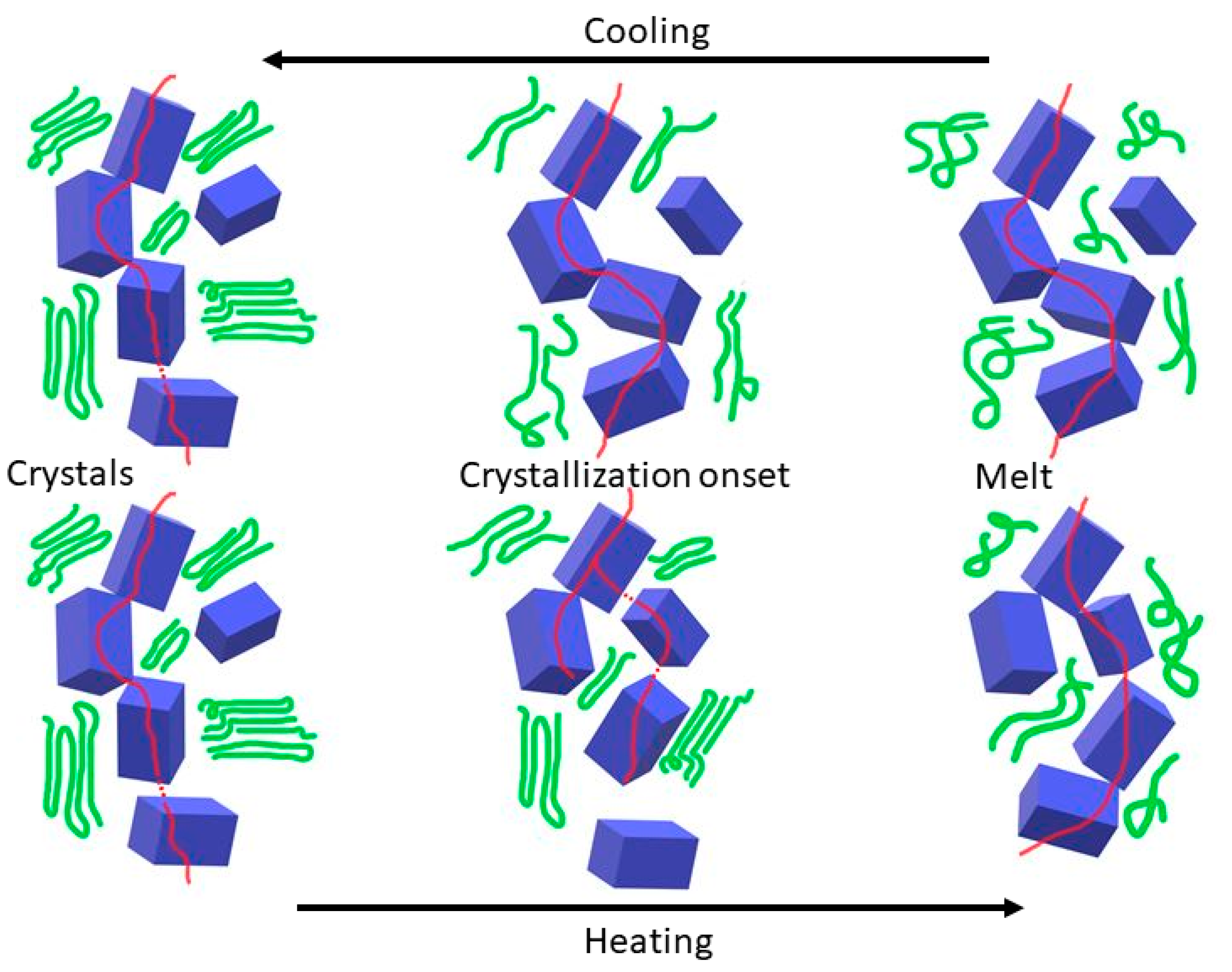
3.2. Thermal Cycling
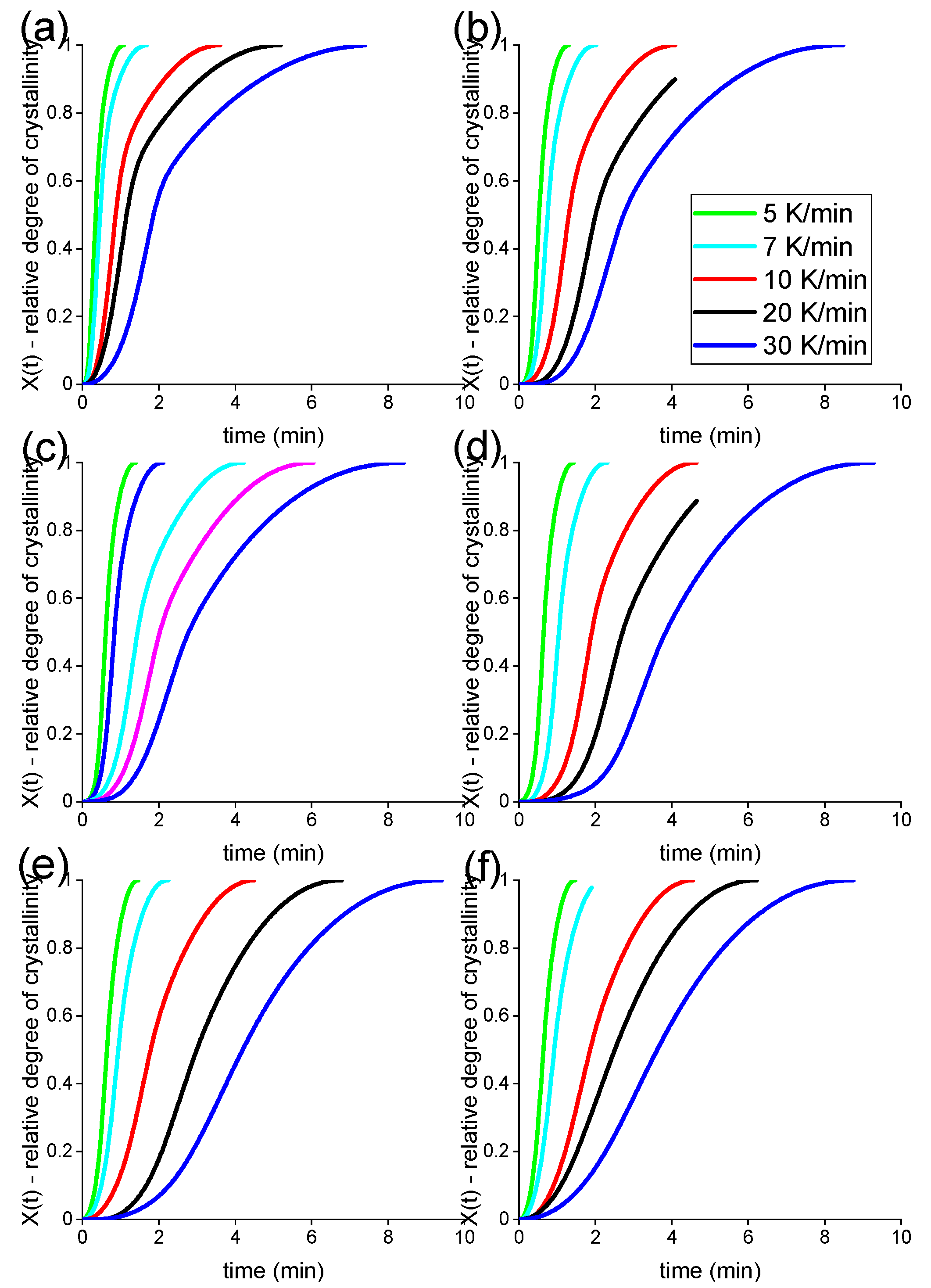
3.3. Thermal Properties
VA Content
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kim, H.; Abdala, A.A.; Macosko, C.W. Graphene/polymer nanocomposites. Macromolecules 2010, 43, 6515–6530. [Google Scholar] [CrossRef]
- Potts, J.R.; Dreyer, D.R.; Bielawski, C.W.; Ruoff, R.S. Graphene-based polymer nanocomposites. Polymer 2011, 52, 5–25. [Google Scholar] [CrossRef]
- Paul, D.R.; Robeson, L.M. Polymer nanotechnology: Nanocomposites. Polymer 2008, 49, 3187–3204. [Google Scholar] [CrossRef]
- Stankovich, S.; Dikin, D.A.; Dommett, G.H.B.; Kohlhaas, K.M.; Zimney, E.J.; Stach, E.A.; Piner, R.D.; Nguyen, S.T.; Ruoff, R.S. Graphene-based composite materials. Nature 2006, 442, 282–286. [Google Scholar] [CrossRef] [PubMed]
- Gkourmpis, T. Carbon-based high aspect ratio polymer nanocomposites. In Nanoscience and Computational Chemistry: Research Progress; Mercader, G.A., Haghi, A.K., Eds.; Apple Academic Press: Toronto, ON, Canada, 2014. [Google Scholar]
- Díez-Pascual, A.M. Development of graphene-based polymeric nanocomposites: A brief overview. Polymers 2021, 13, 2978. [Google Scholar]
- Paszkiewicz, S.; Szymczyk, A.; Pawlikowska, D.; Subocz, J.; Zenker, M.; Masztak, R. Electrically and thermally conductive low density polyethylene-based nanocomposites reinforced by MWCNT or hybrid MWCNT/graphene nanoplatelets with improved thermo-oxidative stability. Nanomaterials 2018, 8, 264. [Google Scholar] [CrossRef]
- Boland, C.S.; Khan, U.; Ryan, G.; Barwich, S.; Charifou, R.; Harvey, A.; Backes, C.; Li, Z.; Ferreira, M.S.; Möbius, M.E.; et al. Sensitive electromechanical sensors using viscoelastic graphene-polymer nanocomposites. Science 2016, 354, 1257–1260. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Qi, S.; He, J.; Duan, G. High conductivity and low percolation threshold in polyaniline/graphite nanosheets composites. J. Matter. Sci. 2010, 45, 483–489. [Google Scholar] [CrossRef]
- Chen, G.; Weng, W.; Wu, D.; Wu, C. PMMA/graphite nanosheets composite and its conducting properties. Eur. Polym. J. 2003, 39, 2329–2335. [Google Scholar] [CrossRef]
- Kalaitzidou, K.; Fukushima, H.; Drzal, L.T. A new compounding method for exfoliated graphite–polypropylene nanocomposites with enhanced flexural properties and lower percolation threshold. Compos. Sci. Technol. 2007, 67, 2045–2051. [Google Scholar] [CrossRef]
- Vadukumpully, S.; Paul, J.; Mahanta, N.; Valiyaveettil, S. Flexible conductive graphene/poly(vinyl chloride) composite thin films with high mechanical strength and thermal stability. Carbon 2011, 49, 198–205. [Google Scholar] [CrossRef]
- Kim, H.; Miura, Y.; Macosko, C.W. Graphene/polyurethane nanocomposites for improved gas barrier and electrical conductivity. Chem. Mater. 2010, 22, 3441–3450. [Google Scholar] [CrossRef]
- Papageorgiou, D.; Kinloch, I.A.; Young, R.J. Mechanical properties of graphene and graphene-based nanocomposites. Prog. Mater. Sci. 2017, 90, 75–127. [Google Scholar] [CrossRef]
- La Mantia, F.P.; Titone, V.; Milazzo, A.; Ceraulo, M.; Botta, L. Morphology, rheological and mechanical properties of isotropic and anisotropic PP/rPET/GnP nanocomposite samples. Nanomaterials 2021, 11, 3058. [Google Scholar] [CrossRef]
- Ganguli, S.; Roy, A.K.; Anderson, D.P. Improved thermal conductivity for chemically functionalized exfoliated graphite/epoxy composites. Carbon 2008, 46, 806–817. [Google Scholar] [CrossRef]
- Ansari, S.; Giannelis, E.P. Functionalized graphene sheet—Poly (vinylidene fluoride) conductive nanocomposites. J. Polym. Sci. Part B Polym. Phys. 2009, 47, 888–897. [Google Scholar] [CrossRef]
- Tang, Z.-H.; Wang, D.-Y.; Li, Y.-Q.; Huang, P.; Fu, S.-Y. Modeling the synergistic electrical percolation effect of carbon nanotube/graphene/polymer composites. Compos. Sci. Technol. 2022, 225, 109496–109502. [Google Scholar] [CrossRef]
- Gkourmpis, T. Controlling the morphology of polymers. In Multiple Scales of Structure and Processing; Mitchell, G.R., Tojeira, A., Eds.; Springer: London, UK, 2016. [Google Scholar]
- Kirkpartick, S. Percolation and conduction. Rev. Mod. Phys. 1973, 45, 574–588. [Google Scholar] [CrossRef]
- Lux, F. Models proposed to explain the electrical conductivity of mixtures made of conductive and insulating materials. J. Mater. Sci. 1993, 28, 285–301. [Google Scholar] [CrossRef]
- Zallen, P. The Physics of Amorphous Solids; Wiley: New York, NY, USA, 1983. [Google Scholar]
- Jäger, K.-M.; McQueen, D.H.; Vilcakova, J. AC conductance and capacitance of carbon black polymer composites during rhermal cycling and isothermal annealing. J. Phys. D 2002, 35, 1068–1075. [Google Scholar] [CrossRef]
- Yu, G.; Zhang, M.Q.; Zeng, H.M.; Hou, Y.H.; Zhang, H.B. Conductive polymer blends filled with carbon black: Positive temperature coefficient behaviour. Polym. Eng. Sci. 1999, 39, 1678–1688. [Google Scholar] [CrossRef]
- Tang, H.; Liu, Z.Y.; Piao, J.H.; Chen, X.F.; Lou, Y.X.; Li, S.H. Electrical behavior of carbon black-filled polymer composites: Effect of interaction between filler and matrix. J. Appl. Polym. Sci. 1994, 51, 1159–1164. [Google Scholar] [CrossRef]
- Pang, H.; Zhong, G.-J.; Xu, J.-Z.; Yan, D.-X.; Ji, X. Non-isothermal crystallization of ethylene-vinyl acetate copolymer containing a high weight fraction of graphene nanosheets and carbon nanotubes. Chin. J. Polym. Sci. 2012, 30, 879–892. [Google Scholar] [CrossRef]
- Redondo-Foj, B.; Ortiz-Serna, P.; Carsí, M.; Sanchis, M.J.; Culebras, M.; Gómez, C.M.; Cantarero, A. Electrical conductivity properties of expanded graphite–polycarbonatediol polyurethane composites. Polym. Int. 2015, 64, 284–292. [Google Scholar] [CrossRef]
- He, F.; Fan, J.; Lau, S.; Chan, L.H. Preparation, crystallization behavior, and dynamic mechanical property of nanocomposites based on poly(vinylidene fluoride) and exfoliated graphite nanoplate. J. Appl. Polym. Sci. 2011, 119, 1166–1175. [Google Scholar] [CrossRef]
- Xu, J.-Z.; Chen, C.; Wang, Y.; Tang, H.; Li, Z.-M.; Hsiao, B.S. Graphene nanosheets and shear flow induced crystallization in isotactic polypropylene nanocomposites. Macromolecules 2011, 44, 2808–2818. [Google Scholar] [CrossRef]
- Gaska, K.; Manika, G.C.; Gkourmpis, T.; Tranchida, D.; Gitsas, A.; Kádár, R. Mechanical behavior of melt-mixed 3D hierarchical graphene/polypropylene nanocomposites. Polymers 2020, 12, 1309. [Google Scholar] [CrossRef]
- Kádár, R.; Gaska, K.; Gkourmpis, T. Nonlinear “oddities” at the percolation of 3D hierarchical graphene polymer nanocomposites. Rheol. Acta 2020, 59, 333–347. [Google Scholar] [CrossRef]
- Gkourmpis, T.; Gaska, K.; Tranchida, D.; Gitsas, A.; Müller, C.; Matic, A.; Kádár, R. Melt-mixed 3D hierarchical graphene/polypropylene nanocomposites with low electrical percolation threshold. Nanomaterials 2019, 9, 1766. [Google Scholar] [CrossRef]
- Atif, R.; Shyha, I.; Inam, F. Mechanical, thermal, and electrical properties of graphene-epoxy nanocomposites—A review. Polymers 2016, 8, 281. [Google Scholar] [CrossRef]
- Persson, H.; Yao, Y.; Klement, U.; Rychwalski, R.W. A simple way of improving graphite nanoplatelets (GNP) for their incorporation into a polymer matrix. Express Polym. Lett. 2012, 6, 142–147. [Google Scholar]
- Oxfall, H.; Ariu, G.; Gkourmpis, T.; Rychwalski, R.W.; Rigdhal, M. Effect of carbon black on electrical and rheological properties of graphite nanoplatelets/poly(ethylene-butyl acrylate) composites. Express Polym. Lett. 2015, 9, 66–76. [Google Scholar] [CrossRef]
- Sullivan, E.M.; Karimineghlani, P.; Naraghi, M.; Gerhardt, R.W.; Kalaitzidou, K. The effect of nanofiller geometry and compounding method on polylactic acid nanocomposite films. Eur. Polym. J. 2016, 77, 31–42. [Google Scholar] [CrossRef]
- Smith, A.T.; LaChance, A.M.; Zeng, S.; Liu, B.; Sun, L. Synthesis, properties, and applications of graphene oxide/reduced graphene oxide and their nanocomposites. Nano Mater. Sci. 2019, 1, 31–47. [Google Scholar] [CrossRef]
- Askeland, P.A.; Fukushima, H.; Do, I.; Kalaitzidou, K.; Drzal, L.T. NSTI Nanotechnology Conference and Trade Show; Nano Science and Technology Institute: Cambridge, MA, USA, 2006; Volume 1, p. 76. [Google Scholar]
- Mallow, A.; Abdelaziz, O.; Kalaitzidou, K.; Graham, S. Investigation of the stability of paraffin–exfoliated graphite nanoplatelet composites for latent heat thermal storage systems. J. Mater. Chem. 2012, 22, 24469–24476. [Google Scholar] [CrossRef]
- Bartl, H.; Hardt, D. Addition and Condensation Polymerization Process; Platzer, N.A.J., Ed.; American Chemical Society: Washington, DC, USA, 1969. [Google Scholar]
- Floudas, G.; Paluch, M.; Grzybowski, A.; Ngai, K.L. Molecular Dynamics of Glass-Forming Systems—Effects of Pressure; Kremer, F., Ed.; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Havriliak, S.; Negami, S. A complex plane representation of dielectric and mechanical relaxation processes in some polymers. Polymer 1967, 8, 161–210. [Google Scholar] [CrossRef]
- Das, N.C.; Chaki, T.K.; Kashtgir, D. Effect of filler treatment and crosslinking on mechanical and dynamic mechanical properties and electrical conductivity of carbon black-filled ethylene–vinyl acetate copolymer composites. J. Appl. Polym. Sci. 2003, 90, 2073–2082. [Google Scholar] [CrossRef]
- Probst, C. Conducting carbon black. In Carbon Black Science and Technology; Donnet, J.-B., Bansal, R.C., Wang, M.-J., Eds.; Taylor and Francis: London, UK, 1993. [Google Scholar]
- Li, B.; Zhong, W.-H. Review on polymer/graphite nanoplatelet nanocomposites. J. Mater. Sci. 2011, 46, 5595–5614. [Google Scholar] [CrossRef]
- Kalaitzidou, K.; Fukushima, H.; Askeland, P.; Drzal, L. The nucleating effect of exfoliated graphite nanoplatelets and their influence on the crystal structure and electrical conductivity of polypropylene nanocomposites. J. Mater. Sci. 2008, 43, 2895–2907. [Google Scholar]
- Li, J.; Vaisman, L.; Marom, G.; Kim, J.-K. Br treated graphite nanoplatelets for improved electrical conductivity of polymer composites. Carbon 2007, 45, 744–750. [Google Scholar] [CrossRef]
- Kuilla, T.; Bhadra, S.; Yao, D.; Kim, N.H.; Bose, S.; Lee, J.H. Recent advances in graphene based polymer composites. Progr. Polym. Sci. 2010, 35, 1350–1375. [Google Scholar] [CrossRef]
- Buback, M.; Busch, M.; Lovis, K.; Mähling, F.-O. High-pressure free-radical copolymerization of ethene and butyl acrylate. Macromol. Chem. Phys. 1996, 197, 303–313. [Google Scholar] [CrossRef]
- Khazraei, P.K.F.; Dhib, R. Modeling of ethylene copolymerization in nonisothermal high-pressure reactors using bifunctional initiators. Polym. Eng. Sci. 2019, 59, 74–85. [Google Scholar] [CrossRef]
- Stockmayer, W.H. Dielectric dispersion in solutions of flexible polymers. Pure Appl. Chem. 1967, 15, 539–554. [Google Scholar] [CrossRef]
- Zhang, S.H.; Casalini, R.; Runt, J.; Roland, C.M. Pressure effects on the segmental dynamics of hydrogen-bonded polymer blends. Macromolecules 2003, 36, 9917–9923. [Google Scholar] [CrossRef][Green Version]
- Bistac, S.; Vallat, M.F.; Schultz, J. Study of ethylene copolymers films by dielectric spectroscopy: Influence of the polymer thickness on the glass-relaxation temperature. Prog. Org. Coat. 1999, 37, 49–56. [Google Scholar] [CrossRef]
- Vogel, H. Das Temperaturabhaengigkeitsgesetz der Viskositaet von Fluessigkeiten. Phys. Z. 1921, 22, 645–646. [Google Scholar]
- Fulcher, G.S. Analysis of recent measurements of the viscosity of glasses. J. Am. Ceram. Soc. 1925, 8, 339–355. [Google Scholar]
- Tammann, G.; Hesse, W.Z. Die Abhängigkeit der Viscosität von der Temperatur bie unterkühlten Flüssigkeiten. Anorg. Allg. Chem. 1926, 156, 245–257. [Google Scholar]
- Hallouet, B.; Desclaux, P.; Wetzel, B.; Schlarb, A.K.; Pelster, R. Analysing dielectric interphases in composites containing nano- and micro-particles. J. Phys. D App. Phys. 2009, 42, 064004. [Google Scholar] [CrossRef]
- Jäger, K.-M.; McQueen, D.H. Fractal agglomerates and electrical conductivity in carbon black polymer composites. Polymer 2001, 42, 9575–9581. [Google Scholar] [CrossRef]
- Gkourmpis, T.; Svanberg, C.; Kaliappan, S.K.; Schaffer, W.; Obadal, M.; Kandioller, G.; Tranchida, D. Improved electrical and flow properties of conductive polyolefin blends: Modification of poly(ethylene vinyl acetate) copolymer/carbon black with ethylene–propylene copolymer. Eur. Polym. J. 2013, 49, 1975–1983. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifschitz, E.M. Textbook of Theoretical Physics Vol. V Statistical Physics; Akademie-Verlag: Berlin, Germany, 1979. [Google Scholar]
- Dyre, J.C.; Schrøder, T.B. Universality of ac conduction in disordered solids. Rev. Mod. Phys. 2000, 72, 873–892. [Google Scholar] [CrossRef]
- Shi, J.; Zhang, X.M.; Jin, J.; Chen, S. Non-isothermal crystallization and melting of ethylene-vinyl acetate copolymers with different vinyl acetate contents. Express Polym. Lett. 2008, 2, 623–629. [Google Scholar] [CrossRef]
- Xu, J.Z.; Chen, T.; Yang, C.L.; Li, Z.M.; Mao, Y.M.; Zeng, B.Q.; Hsiao, B.S. Isothermal crystallization of poly(l-lactide) induced by graphene nanosheets and carbon nanotubes: A comparative study. Macromolecules 2010, 43, 5000–5008. [Google Scholar] [CrossRef]
- Wang, L.-Z.; Duan, L.-L. Isothermal crystallization of a single polyethylene chain induced by graphene: A molecular dynamics simulation. Comput. Theor. Chem. 2012, 1002, 59–63. [Google Scholar] [CrossRef]
- Rissanou, A.N.; Power, A.J.; Harmandaris, V. Structural and dynamical properties of polyethylene/graphene nanocomposites through molecular dynamics simulations. Polymers 2015, 7, 390–417. [Google Scholar] [CrossRef]
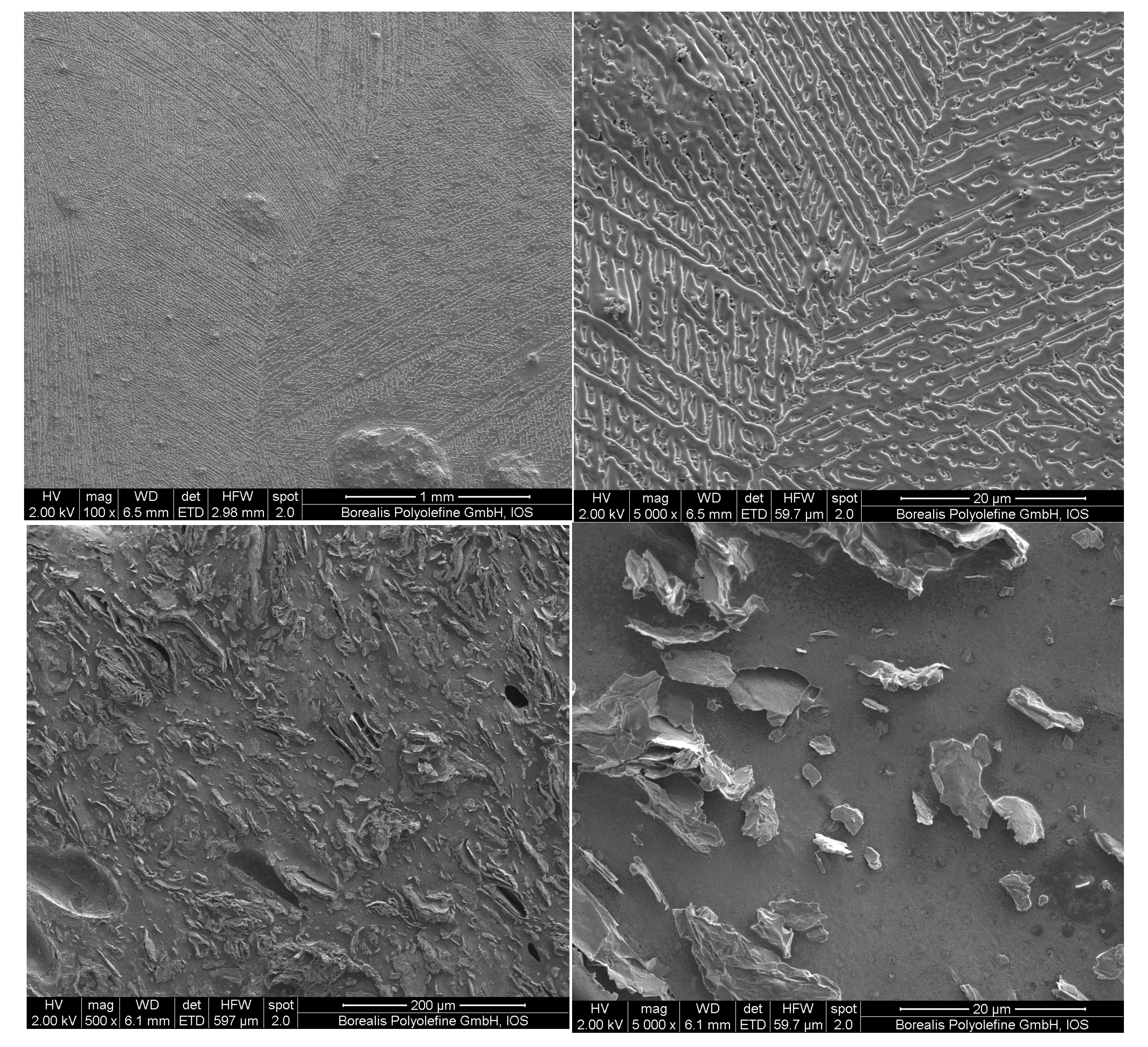
| Polymer | Sample Code | Vinyl Acetate Content (%) | Melting Temperature (°C) | Density (kg/m3) | Mw (kg/mol) | Mw/Mn |
|---|---|---|---|---|---|---|
| Escorene™ Ultra FL 00909 | EVA9 | 9 | 94 | 928 | 184 | 13.1 |
| Escorene™ Ultra UL 02020 | EVA20 | 20 | 80 | 940 | 161 | 11.5 |
| Escorene™ Ultra UL 04533EH2 | EVA33 | 33 | 61 | 956 | n.a. | 4.4 |
| CB (vol%) | NTCcool | PTCcool | NTCheat | PTCheat | ||
|---|---|---|---|---|---|---|
| 11.4 | 2 | 35 | 297 | 5398 | 1.177 × 10−5 | 138 |
| 16.0 | 1 | 19 | 12 | 174 | 4.128 × 10−5 | 8 |
| 21.0 | 1 | 57 | 6 | 276 | 1.018 × 10−4 | 4 |
| 22.5 | 1 | 47 | 4 | 173 | 1.304 × 10−4 | 3 |
| 25.5 | 1 | 84 | 2 | 119 | 3.650 × 10−5 | 1 |
| 29.7 | 2 | 110 | 1 | 13 | −2.955 × 10−4 | 1 |
| GNP (vol%) | NTCcool | PTCcool | NTCheat | PTCheat | ||
|---|---|---|---|---|---|---|
| 1.7 | 1 | 1 | 2 | 3 | 3.501 × 10−12 | 2 |
| 2.6 | 1 | 1 | 17 | 10 | 2.309 × 10−10 | 12 |
| 3.5 | 3 | 0 | 1601 | 201 | 2.537 × 10−7 | 558 |
| 4.5 | 2 | 1 | 489 | 204 | 2.473 × 10−6 | 241 |
| 5.5 | 1 | 1 | 17 | 20 | 8.176 × 10−6 | 15 |
| 6.4 | 2 | 1 | 9 | 6 | 2.419 × 10−5 | 6 |
| GNP (vol%) | 0 | 1.7 | 4.5 | 11.4 | 21 | 25.6 | |||
| Tc (K) | 340.2 | 340.8 | 340.7 | 339.9 | 338.7 | 338.6 | |||
| Tm (K) | 356.7 | 356.0 | 355.5 | 355.0 | 354.1 | 353.8 | |||
| GNP (vol%) | 0.2 | 0.4 | 0.9 | 1.7 | 2.6 | 3.5 | 4.5 | 5.5 | 6.4 |
| Tc (K) | 339.5 | 339.6 | 339.8 | 340.1 | 340.4 | 340.2 | 340.5 | 340.6 | 340.5 |
| Tm (K) | 357.2 | 357.0 | 357.4 | 357.2 | 357.1 | 356.8 | 357.0 | 357.1 | 357.1 |
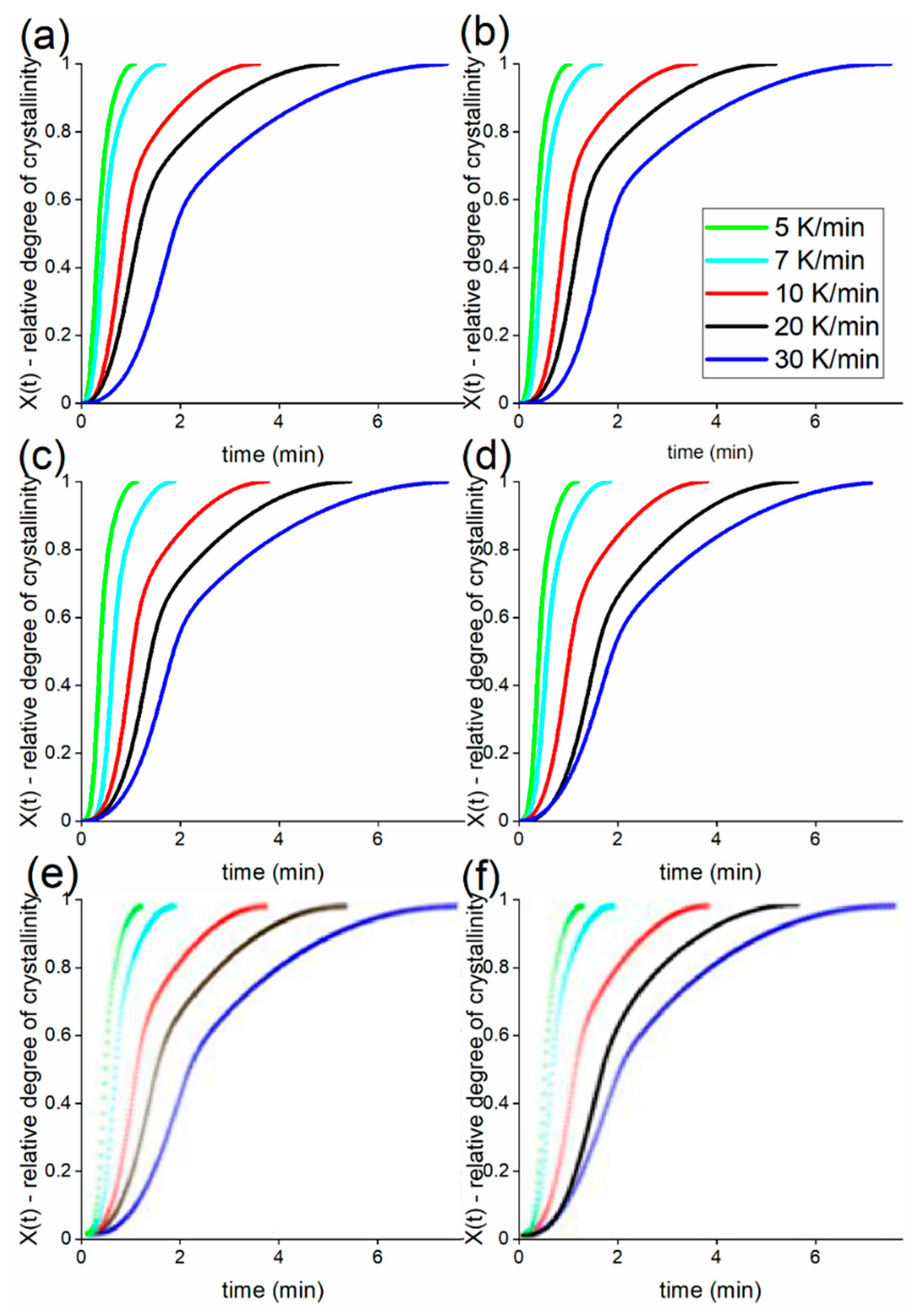
| CB (vol%) | 5 K/min (min) | 7 K/min (min) | 10 K/min (min) | 20 K/min (min) | 30 K/min (min) |
|---|---|---|---|---|---|
| 0 | 1.6 | 1.2 | 0.9 | 0.5 | 0.3 |
| 1.7 | 2.7 | 2.0 | 1.3 | 0.8 | 0.5 |
| 4.5 | 2.8 | 2.0 | 1.4 | 0.8 | 0.6 |
| 11.5 | 3.8 | 2.7 | 1.9 | 1.1 | 0.6 |
| 21.2 | 4.2 | 3.0 | 1.8 | 0.9 | 0.6 |
| 25.8 | 3.6 | 2.5 | 1.9 | 0.9 | 0.6 |
| GNP (vol%) | 5 K/min (min) | 7 K/min (min) | 10 K/min (min) | 20 K/min (min) | 30 K/min (min) |
|---|---|---|---|---|---|
| 0 | 1.6 | 1.2 | 0.9 | 0.5 | 0.3 |
| 0.2 | 1.8 | 1.2 | 0.9 | 0.5 | 0.3 |
| 1.7 | 1.9 | 1.4 | 1.0 | 0.9 | 0.4 |
| 3.6 | 1.9 | 1.6 | 1.0 | 0.6 | 0.4 |
| 4.5 | 2.2 | 1.5 | 1.1 | 0.6 | 0.4 |
| 6.5 | 2.0 | 1.8 | 1.1 | 0.6 | 0.5 |
| %VA | NTCcool | PTCcool | NTCheat | PTCheat | ||
|---|---|---|---|---|---|---|
| 9 | 3 | 16 | 843 | 4434 | 1.09 × 10−7 | 271 |
| 20 | 1 | 2 | 179 | 420 | 2.44 × 10−6 | 221 |
| 33 | 0 | 1 | 21 | 35 | 5.02 × 10−6 | 49 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stalmann, G.; Matic, A.; Jacobsson, P.; Tranchida, D.; Gitsas, A.; Gkourmpis, T. Crystallisation Kinetics and Associated Electrical Conductivity Dynamics of Poly(Ethylene Vinyl Acetate) Nanocomposites in the Melt State. Nanomaterials 2022, 12, 3602. https://doi.org/10.3390/nano12203602
Stalmann G, Matic A, Jacobsson P, Tranchida D, Gitsas A, Gkourmpis T. Crystallisation Kinetics and Associated Electrical Conductivity Dynamics of Poly(Ethylene Vinyl Acetate) Nanocomposites in the Melt State. Nanomaterials. 2022; 12(20):3602. https://doi.org/10.3390/nano12203602
Chicago/Turabian StyleStalmann, Gertrud, Aleksandar Matic, Per Jacobsson, Davide Tranchida, Antonis Gitsas, and Thomas Gkourmpis. 2022. "Crystallisation Kinetics and Associated Electrical Conductivity Dynamics of Poly(Ethylene Vinyl Acetate) Nanocomposites in the Melt State" Nanomaterials 12, no. 20: 3602. https://doi.org/10.3390/nano12203602
APA StyleStalmann, G., Matic, A., Jacobsson, P., Tranchida, D., Gitsas, A., & Gkourmpis, T. (2022). Crystallisation Kinetics and Associated Electrical Conductivity Dynamics of Poly(Ethylene Vinyl Acetate) Nanocomposites in the Melt State. Nanomaterials, 12(20), 3602. https://doi.org/10.3390/nano12203602












