Dynamical Behavior of Two Interacting Double Quantum Dots in 2D Materials for Feasibility of Controlled-NOT Operation
Abstract
1. Introduction
2. Model and Methodology
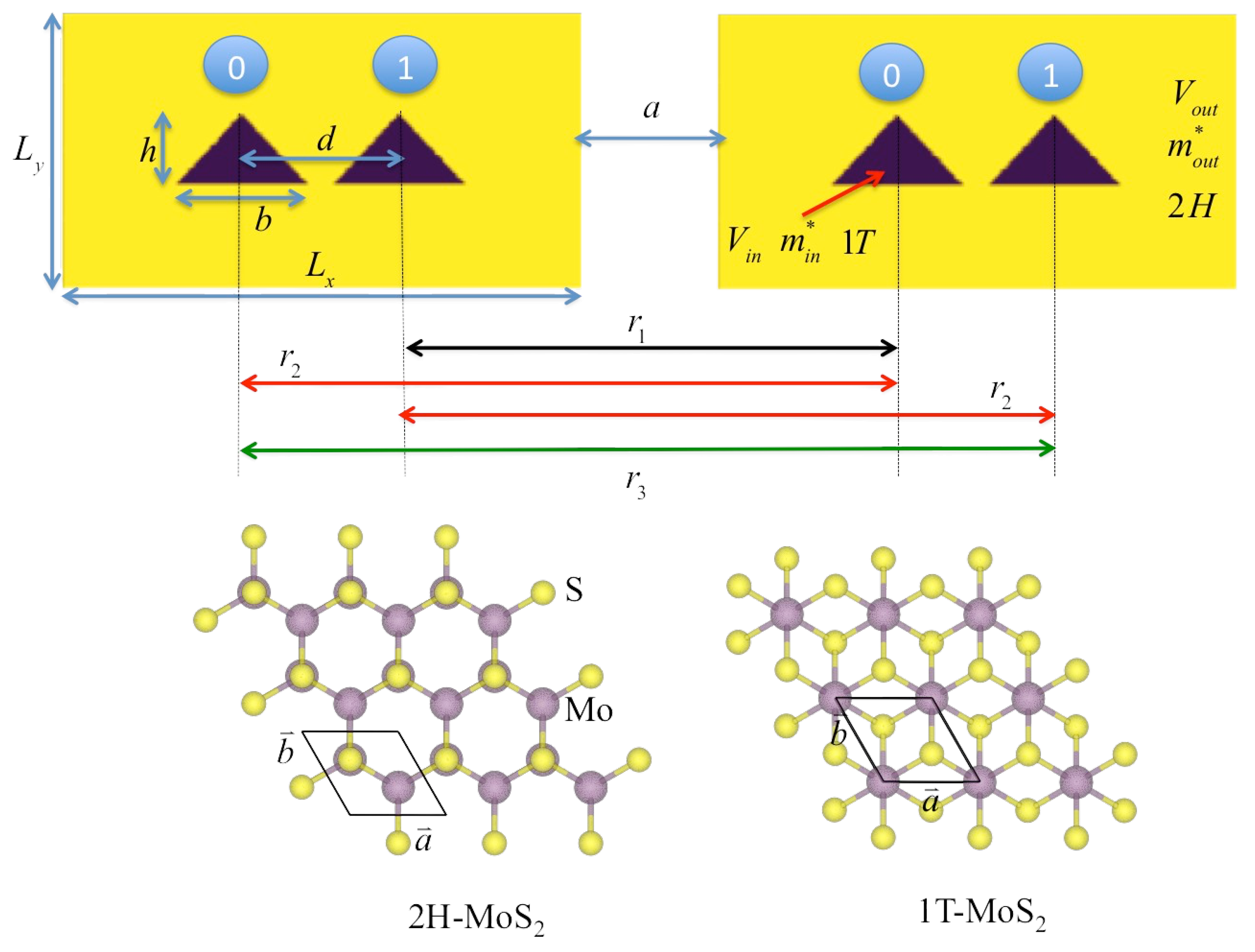
2.1. Structural Model
2.2. Electronic Potential Model
2.3. Matrix Model
2.4. Dynamics of States
2.4.1. CNOT Operation
2.4.2. Transition Probability
3. Results and Discussion
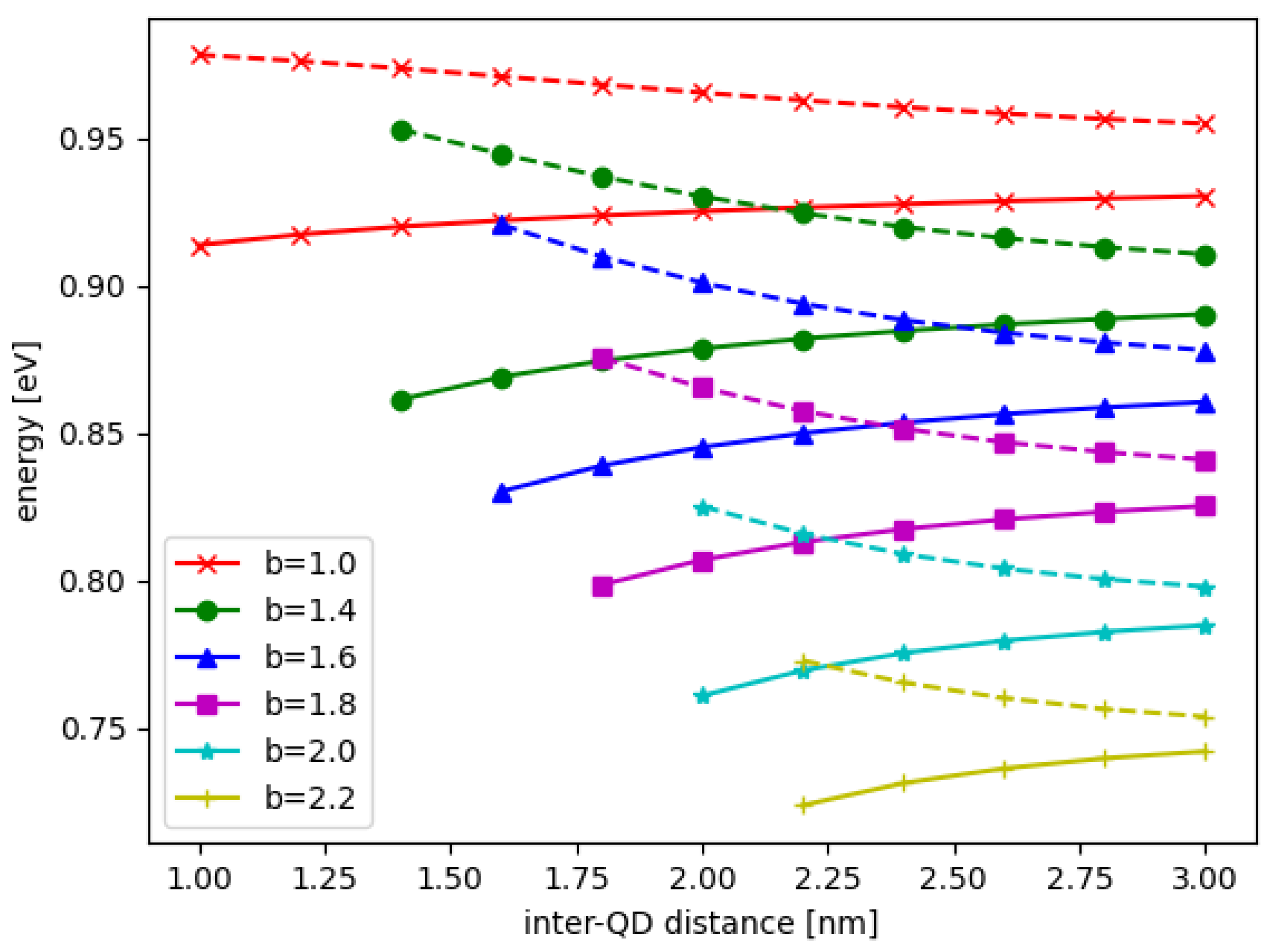
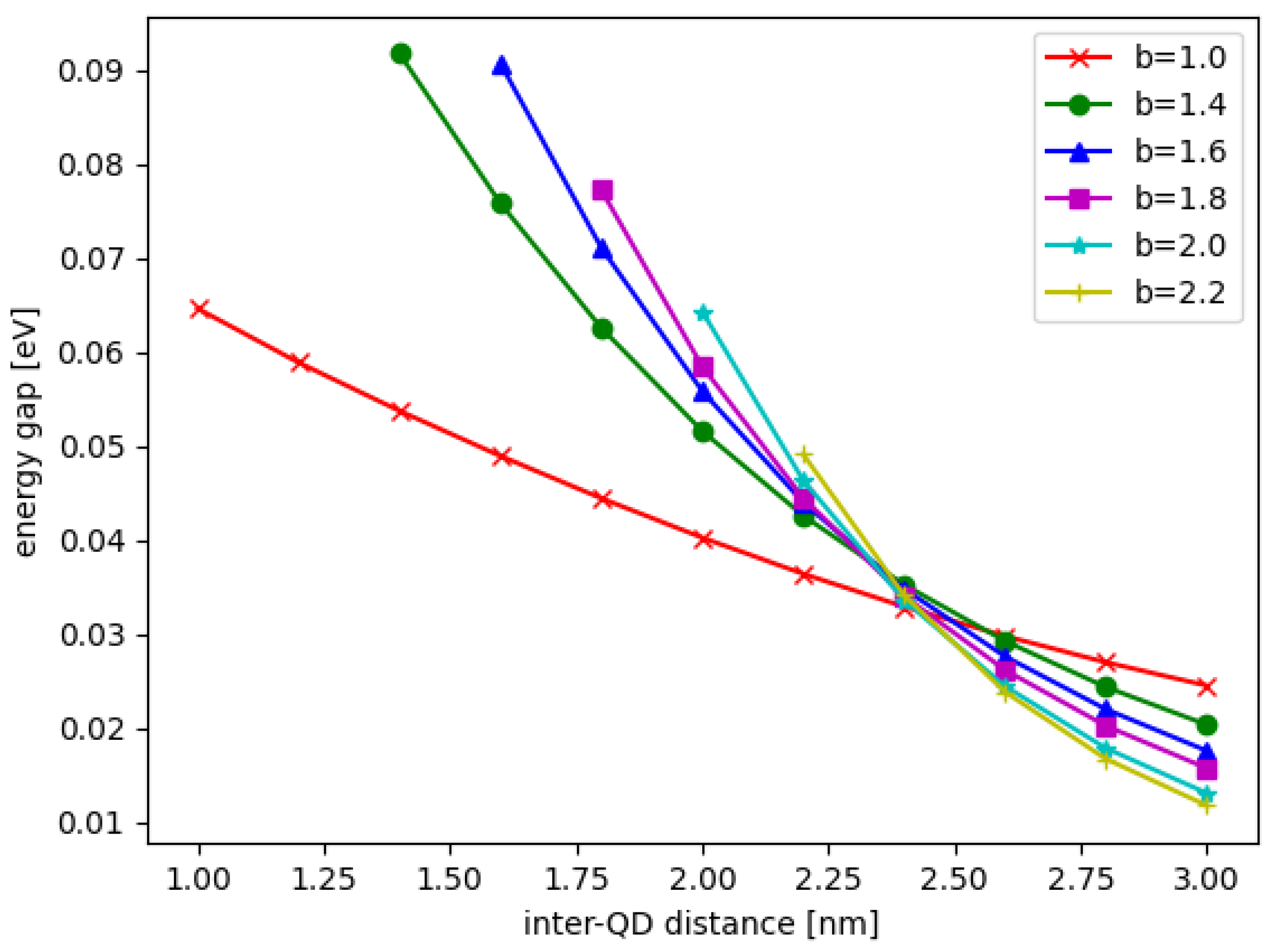
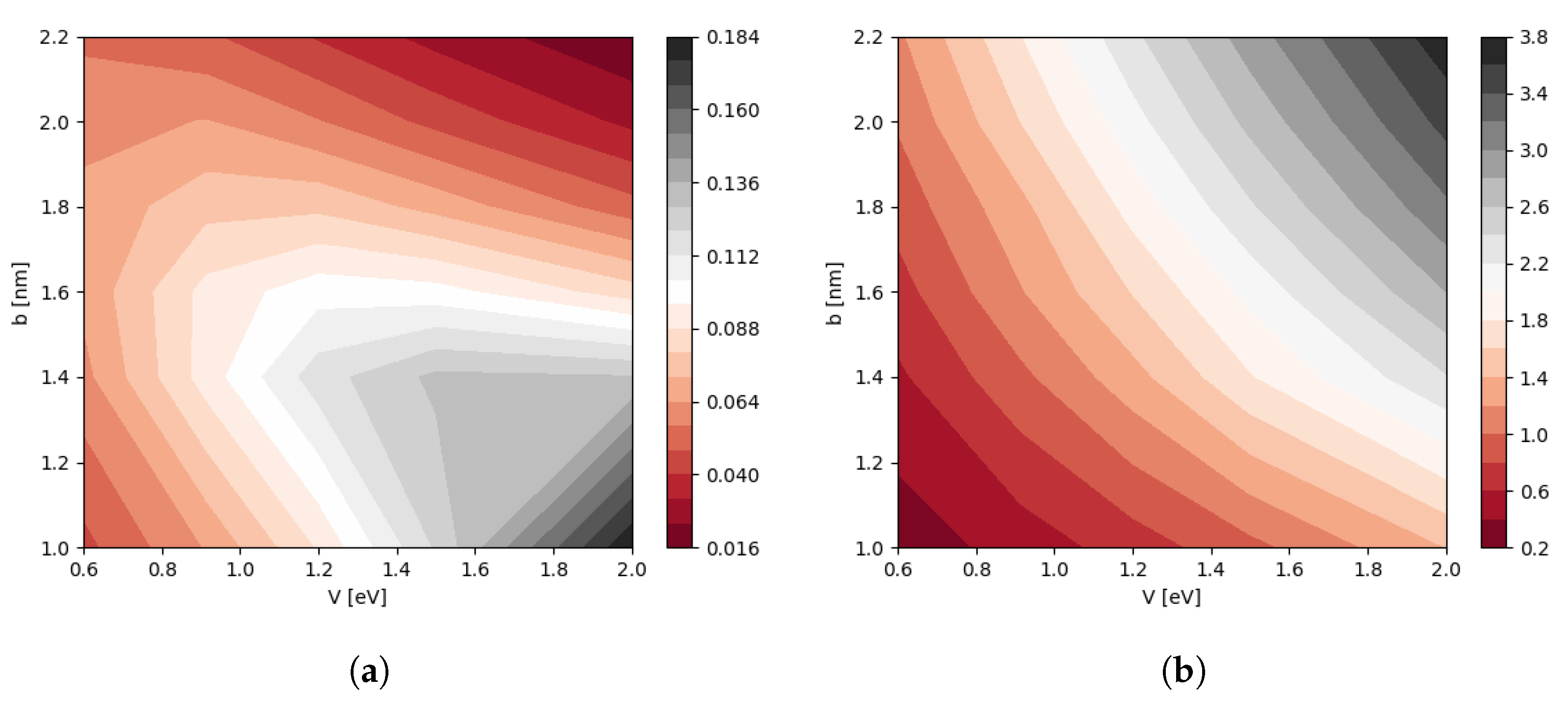
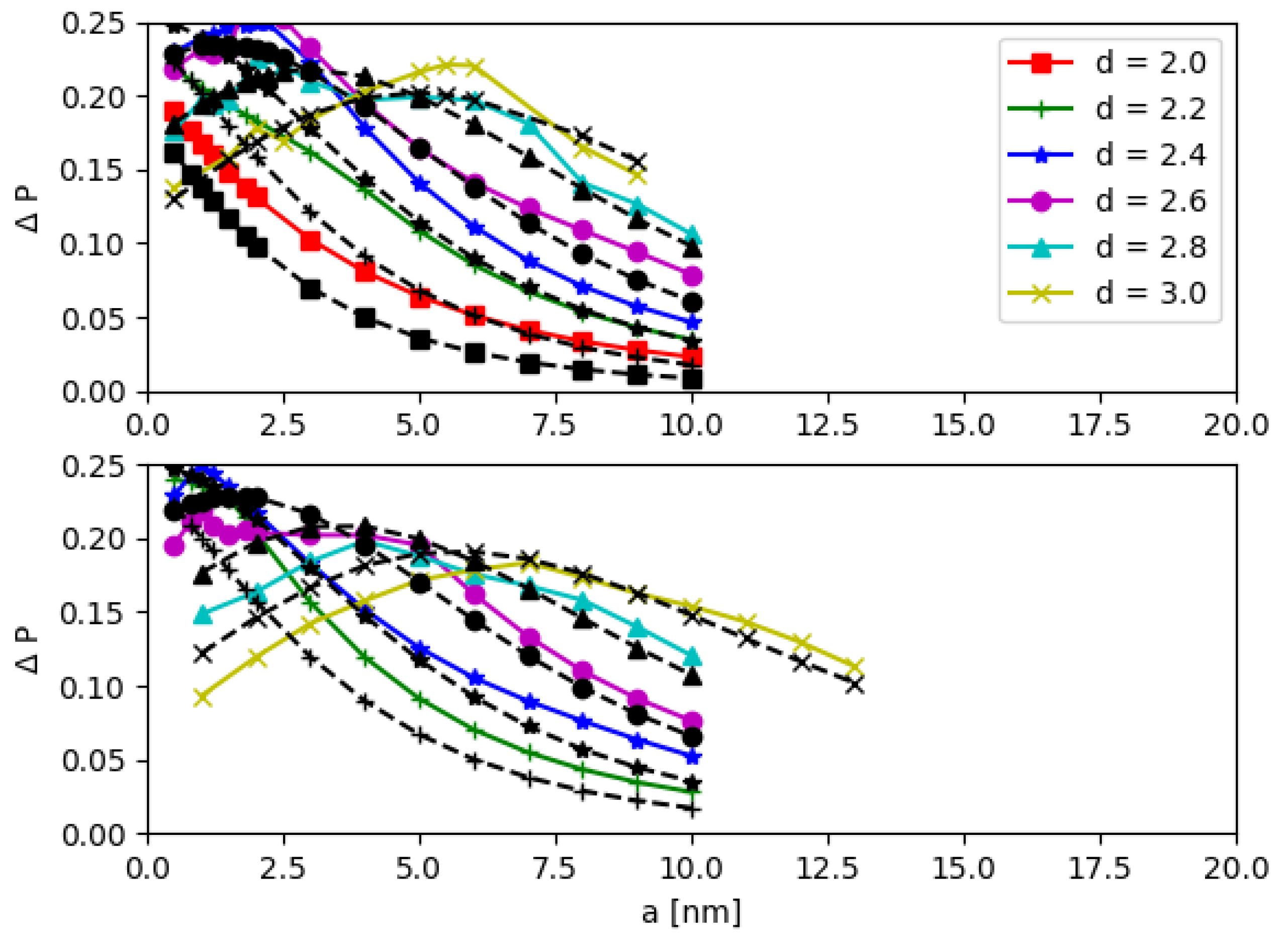
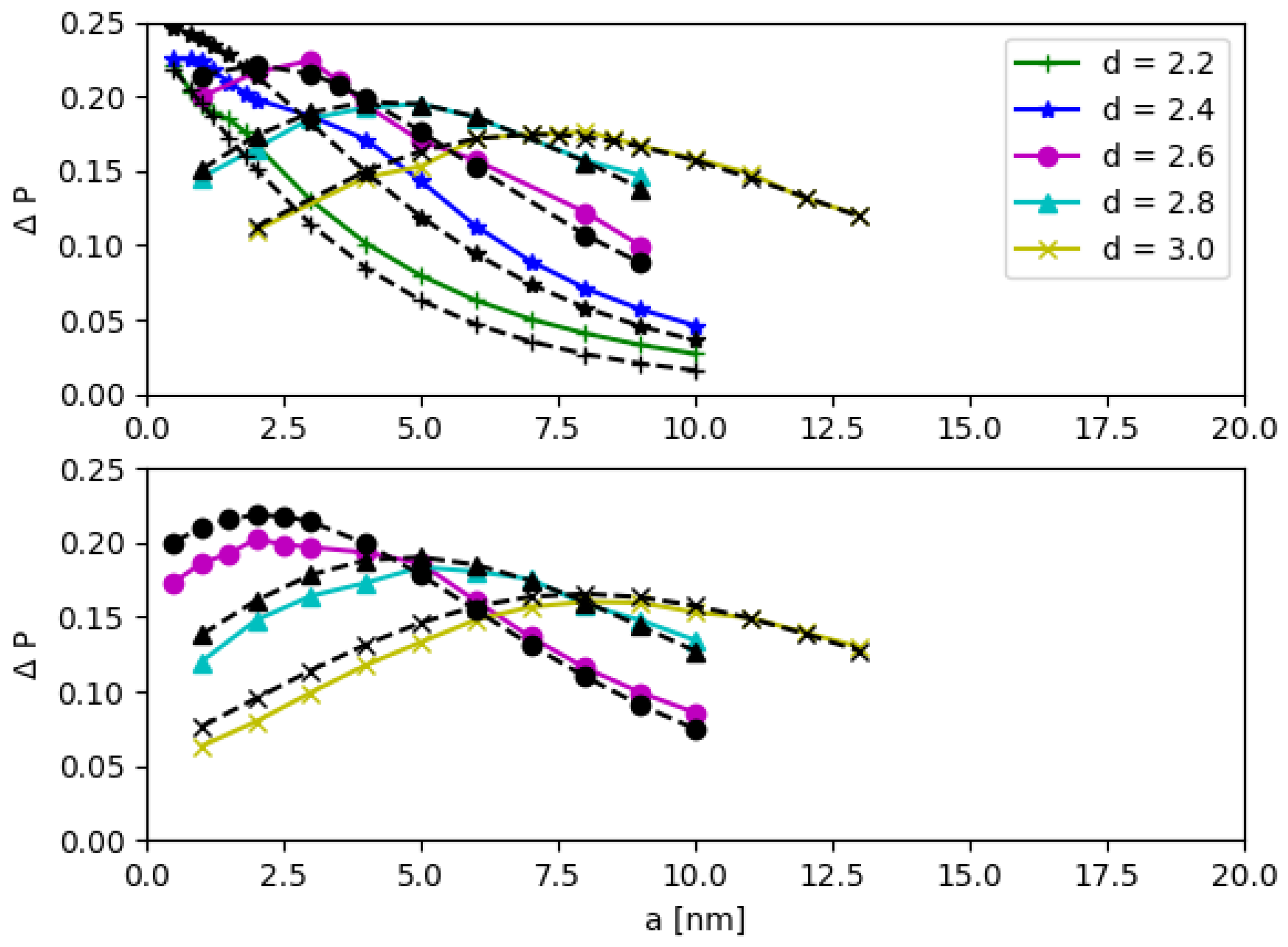
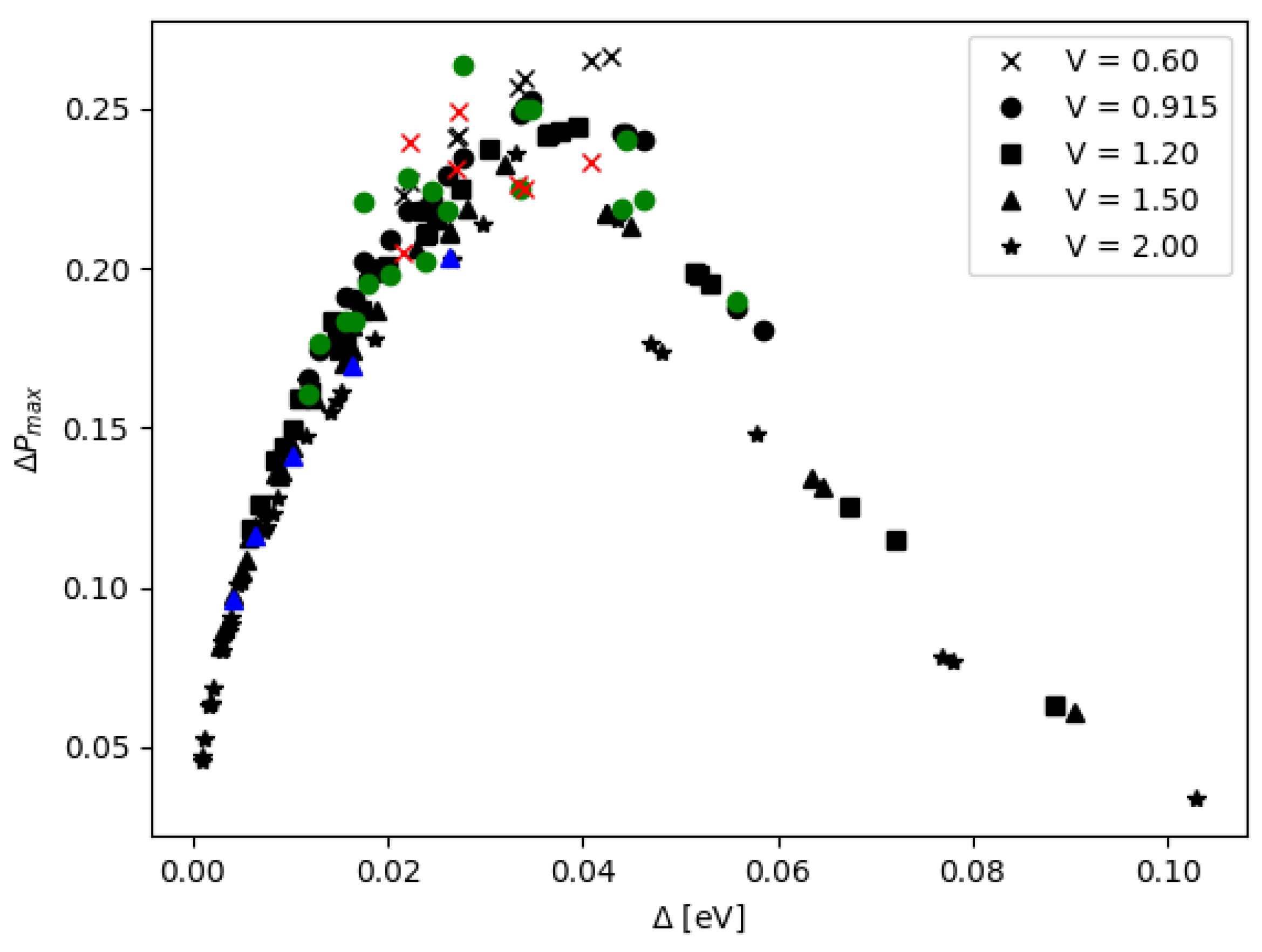
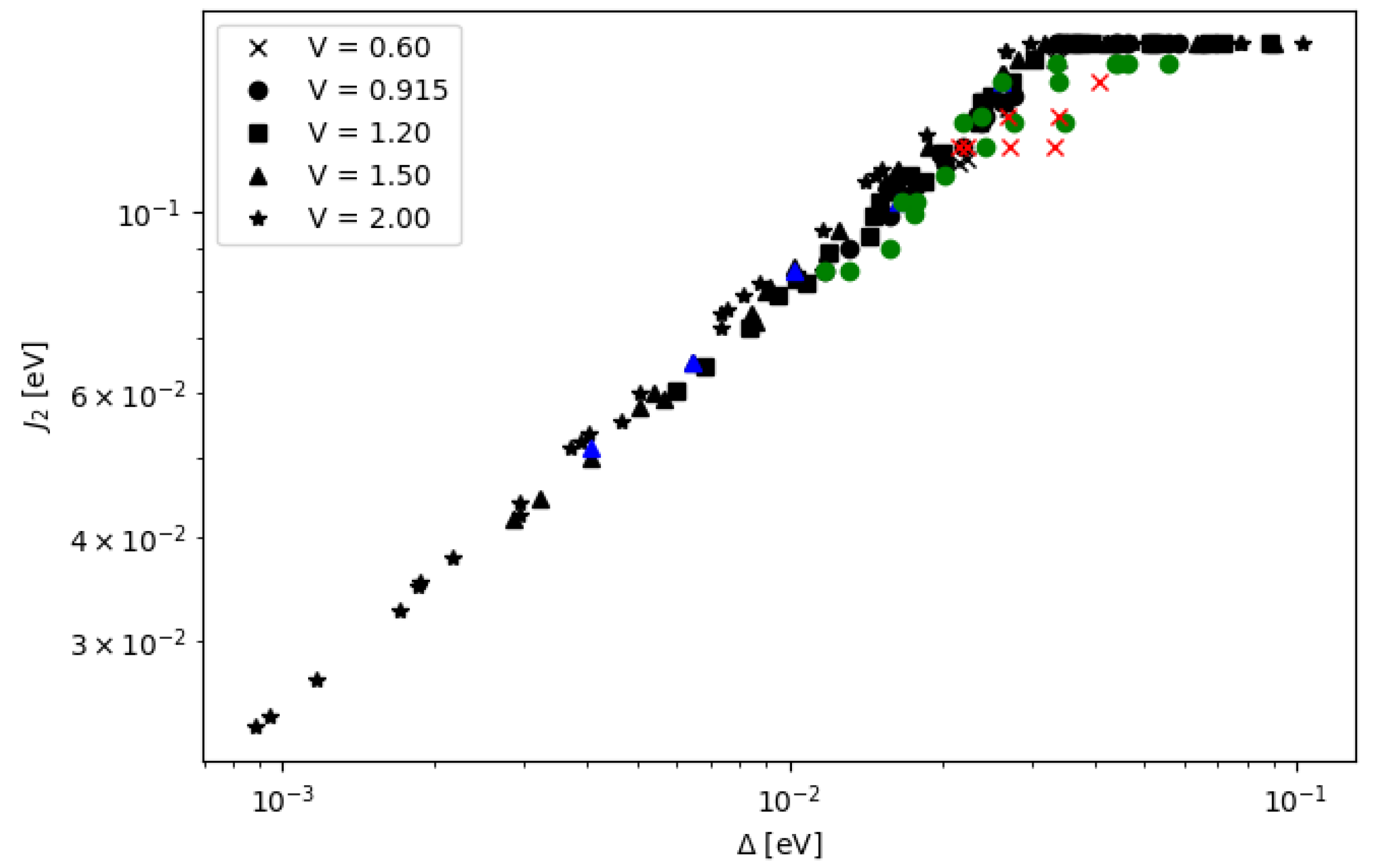
3.1. Parameter Optimization for Energy Tuning of DQD
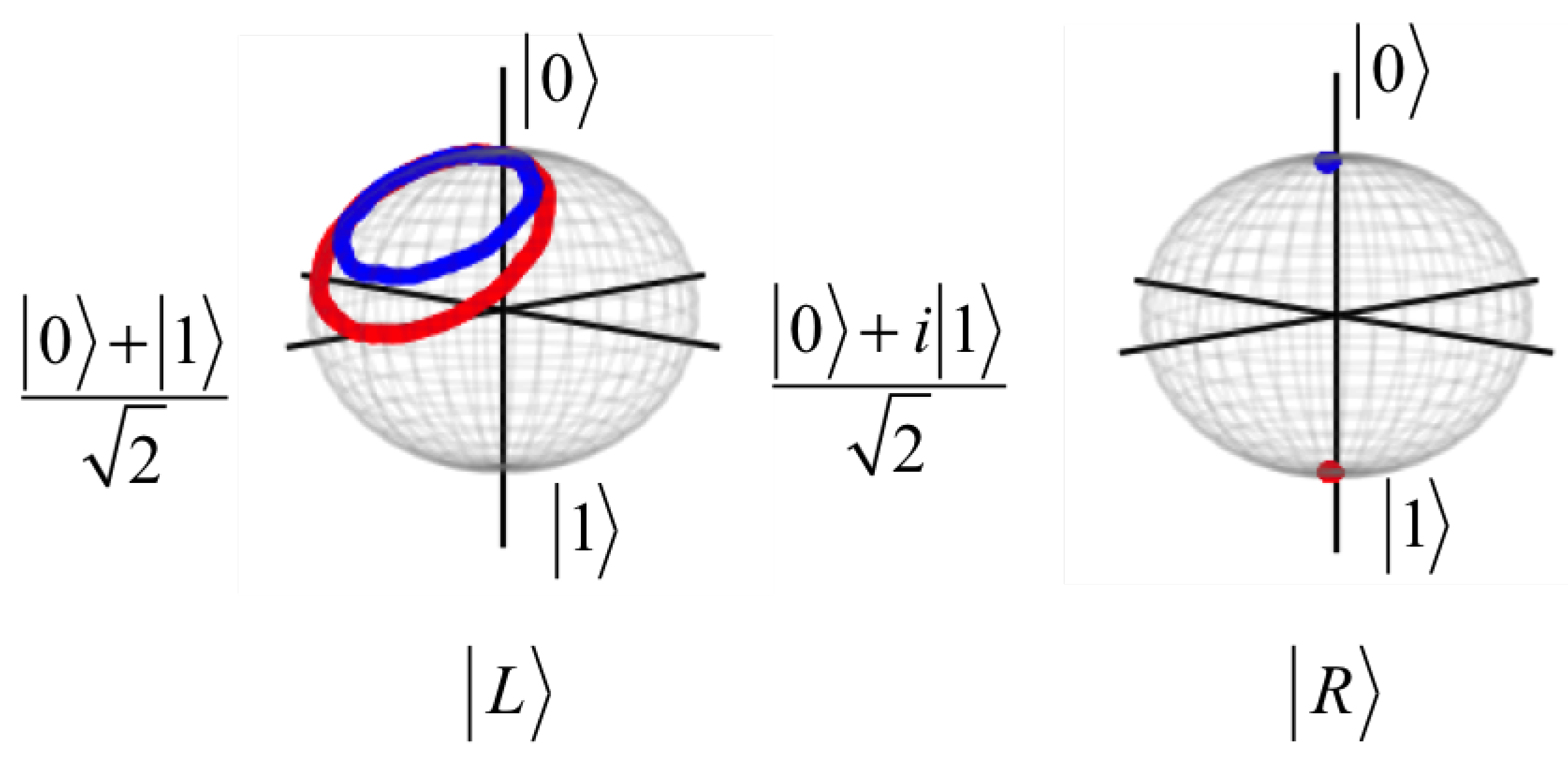
3.2. Dynamics of States on Bloch Sphere
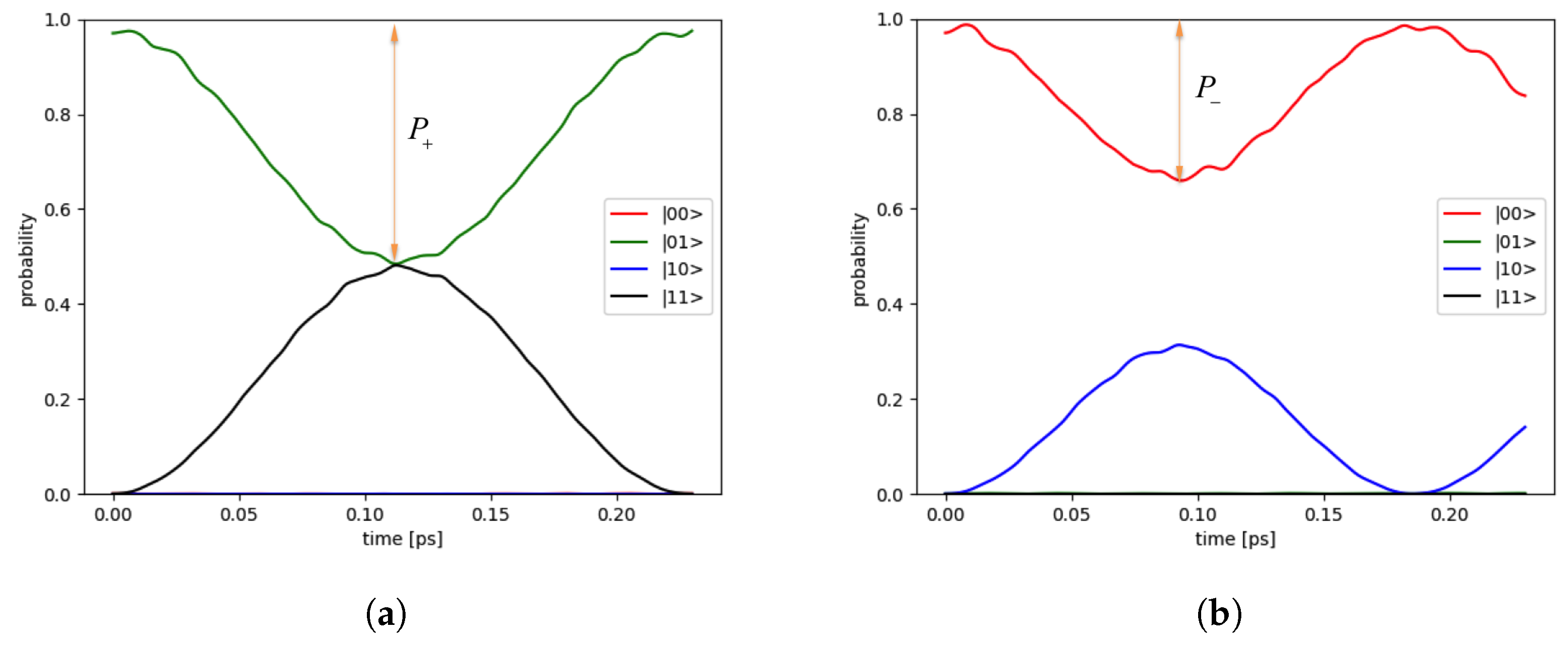
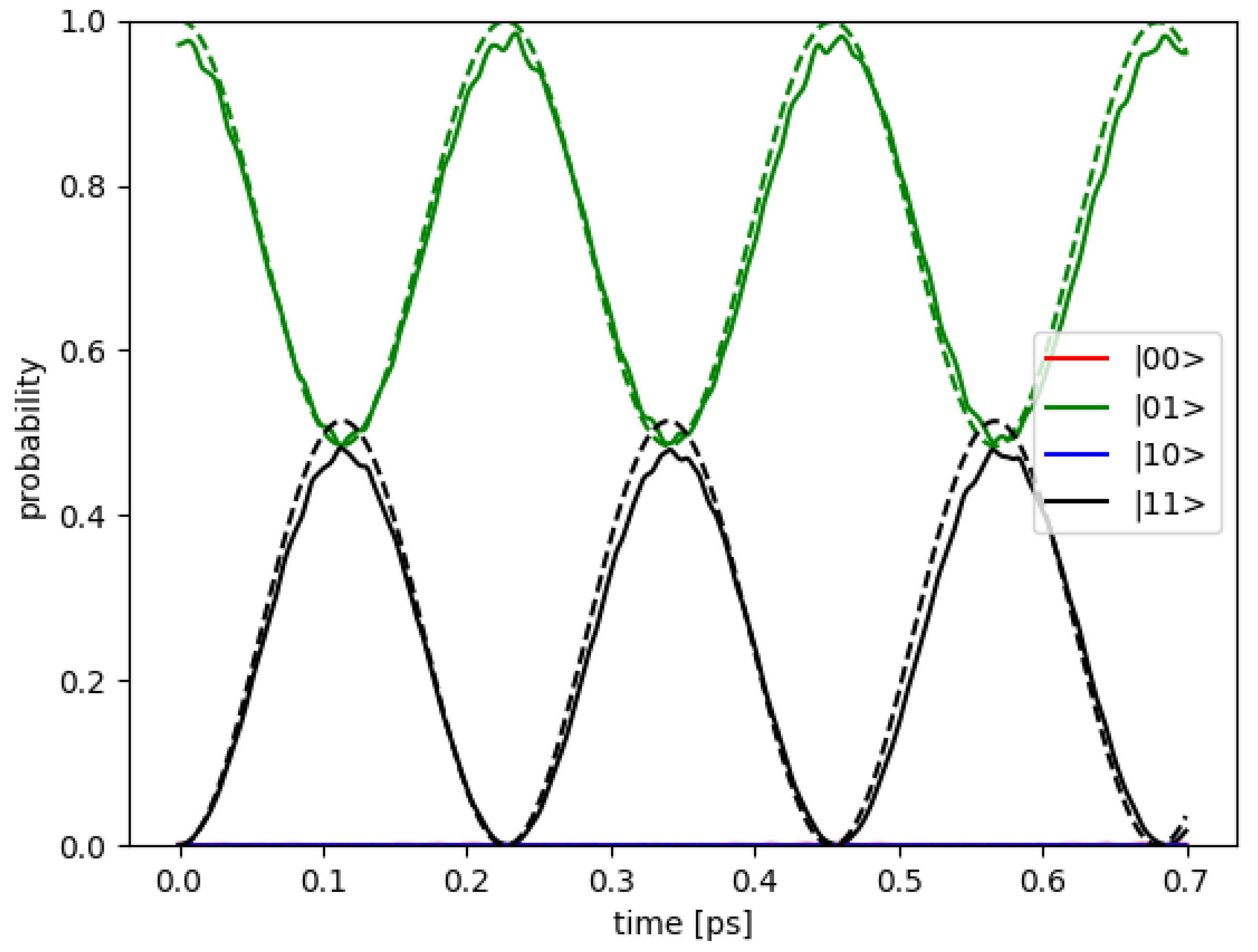
3.3. CNOT Gate Efficiency
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DQD | Double quantum dots |
| QD | Quantum dot |
| CNOT | Controlled-NOT (gate) |
| DFT | Density functional theory |
| FD | Finite difference |
| TB | Tight binding |
References
- Georgescu, I.M.; Ashhab, S.; Nori, F. Quantum simulation. Rev. Mod. Phys. 2014, 86, 153–185. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; University Press Cambridge: Cambridge, UK, 2000. [Google Scholar]
- Divincenzo, D.P. Topics in Quantum Computers. In Mesoscopic Electron Transport; Sohn, L.L., Kouwenhoven, L.P., Schön, G., Eds.; Springer: Dordrecht, The Netherlands, 1997; pp. 657–677. [Google Scholar] [CrossRef]
- Hayashi, T.; Fujisawa, T.; Cheong, H.D.; Jeong, Y.H.; Hirayama, Y. Coherent Manipulation of Electronic States in a Double Quantum Dot. Phys. Rev. Lett. 2003, 91, 226804. [Google Scholar] [CrossRef] [PubMed]
- Fujisawa, T.; Hayashi, T.; Cheong, H.; Jeong, Y.; Hirayama, Y. Rotation and phase-shift operations for a charge qubit in a double quantum dot. Phys. E 2004, 21, 1046–1052. [Google Scholar] [CrossRef]
- Gorman, J.; Hasko, D.G.; Williams, D.A. Charge-Qubit Operation of an Isolated Double Quantum Dot. Phys. Rev. Lett. 2005, 95, 090502. [Google Scholar] [CrossRef] [PubMed]
- Fujisawa, T.; Hayashi, T.; Sasaki, S. Time-dependent single-electron transport through quantum dots. Rep. Prog. Phys. 2006, 69, 759–796. [Google Scholar] [CrossRef]
- Shi, Z.; Simmons, C.B.; Ward, D.R.; Prance, J.R.; Mohr, R.T.; Koh, T.S.; Gamble, J.K.; Wu, X.; Savage, D.E.; Lagally, M.G.; et al. Coherent quantum oscillations and echo measurements of a Si charge qubit. Phys. Rev. B 2013, 88, 075416. [Google Scholar] [CrossRef]
- Petersson, K.D.; Petta, J.R.; Lu, H.; Gossard, A.C. Quantum Coherence in a One-Electron Semiconductor Charge Qubit. Phys. Rev. Lett. 2010, 105, 246804. [Google Scholar] [CrossRef] [PubMed]
- Larsson, M.; Xu, H.Q. Charge state readout and hyperfine interaction in a few-electron InGaAs double quantum dot. Phys. Rev. B 2011, 83, 235302. [Google Scholar] [CrossRef]
- Li, H.O.; Cao, G.; Yu, G.D.; Xiao, M.; Guo, G.C.; Jiang, H.W.; Guo, G.P. Conditional rotation of two strongly coupled semiconductor charge qubits. Nat. Commun. 2015, 6, 7681. [Google Scholar] [CrossRef]
- MacQuarrie, E.R.; Neyens, S.F.; Dodson, J.P.; Corrigan, J.; Thorgrimsson, B.; Holman, N.; Palma, M.; Edge, L.F.; Friesen, M.; Coppersmith, S.N.; et al. Progress toward a capacitively mediated CNOT between two charge qubits in Si/SiGe. NPJ Quantum Inf. 2020, 6, 81. [Google Scholar] [CrossRef]
- Wang, X.; Sun, G.; Li, N.; Chen, P. Quantum dots derived from two-dimensional materials and their applications for catalysis and energy. Chem. Soc. Rev. 2016, 45, 2239–2262. [Google Scholar] [CrossRef]
- Senellart, P. Deterministic light–matter coupling with single quantum dots. In Quantum Dots: Optics, Electron Transport and Future Applications; Tartakovskii, A., Ed.; Cambridge University Press: Cambridge, UK, 2012; pp. 137–152. [Google Scholar] [CrossRef]
- Laferrière, P.; Yeung, E.; Miron, I.; Northeast, D.B.; Haffouz, S.; Lapointe, J.; Korkusinski, M.; Poole, P.J.; Williams, R.L.; Dalacu, D. Unity yield of deterministically positioned quantum dot single photon sources. Sci. Rep. 2022, 12, 6376. [Google Scholar] [CrossRef] [PubMed]
- Kouwenhoven, L.P.; Marcus, C.M.; McEuen, P.L.; Tarucha, S.; Westervelt, R.M.; Wingreen, N.S. Electron Transport in Quantum Dots. In Mesoscopic Electron Transport; Sohn, L.L., Kouwenhoven, L.P., Schön, G., Eds.; Springer: Dordrecht, The Netherlands, 1997; pp. 105–214. [Google Scholar] [CrossRef]
- Kang, J.; Tongay, S.; Zhou, J.; Li, J.; Wu, J. Band offsets and heterostructures of two-dimensional semiconductors. Appl. Phys. Lett. 2013, 102, 012111. [Google Scholar] [CrossRef]
- Patra, A.; Jana, S.; Samal, P.; Tran, F.; Kalantari, L.; Doumont, J.; Blaha, P. Efficient Band Structure Calculation of Two-Dimensional Materials from Semilocal Density Functionals. J. Phys. Chem. C 2021, 125, 11206–11215. [Google Scholar] [CrossRef]
- Dev, P. Fingerprinting quantum emitters in hexagonal boron nitride using strain. Phys. Rev. Res. 2020, 2, 022050. [Google Scholar] [CrossRef]
- Hunkao, R.; Kesorn, A.; Maezono, R.; Sinsarp, A.; Sukkabot, W.; Tivakornsasithorn, K.; Suwanna, S. Density Functional Theory Study of Strain-Induced Band Gap Tunability of Two-Dimensional Layered MoS2, MoO2, WS2 and WO2. In Proceedings of the 44th Congress on Science and Technology of Thailand (STT 44), Bangkok, Thailand, 29–31 October 2018; pp. 715–722. [Google Scholar]
- Xei, X.; Kang, J.; Cao, W.; Chu, J.H.; Gong, Y.; Ajayan, P.M.; Banerjee, K. Designing artificial 2D crystals with site and size controlled quantum dots. Sci. Rep. 2017, 7, 9965. [Google Scholar]
- Guo, Y.; Ma, L.; Mao, K.; Ju, M.; Bai, Y.; Zhao, J.; Zeng, X.C. Eighteen functional monolayer metal oxides: Wide bandgap semiconductors with superior oxidation resistance and ultrahigh carrier mobility. Nanoscale Horiz. 2019, 4, 592–600. [Google Scholar] [CrossRef]
- Kakanakova-Georgieva, A.; Giannazzo, F.; Nicotra, G.; Cora, I.; Gueorguiev, G.K.; Persson, P.O.; Pécz, B. Material proposal for 2D indium oxide. Appl. Surf. Sci. 2021, 548, 149275. [Google Scholar] [CrossRef]
- Freitas, R.R.Q.; de Brito Mota, F.; Rivelino, R.; de Castilho, C.M.C.; Kakanakova-Georgieva, A.; Gueorguiev, G.K. Spin-orbit-induced gap modification in buckled honeycomb XBi and XBi3 (X = B, Al, Ga, and IN) sheets. J. Phys. Condens. Matter 2015, 27, 485306. [Google Scholar] [CrossRef]
- Woon, C.Y.; Gopir, G.; Othman, A.P. Discontinuity Mass of Finite Difference Calculation in InAs-GaAs Quantum Dots. Adv. Mater. Res. 2014, 895, 415–419. [Google Scholar]
- Kesorn, A.; Sukkabot, W.; Suwanna, S. Dynamics and Quantum Leakage of InAs/GaAs Double Quantum Dots under Finite Time-Dependent Square-Pulsed Electric Field. Adv. Mater. Res. 2016, 1131, 97–105. [Google Scholar]
- Kesorn, A.; Kalasuwan, P.; Sinsarp, A.; Sukkabot, W.; Suwanna, S. Effects of square electric field pulses with random fluctuation on state dynamics of InAs/GaAs double quantum dots. Integr. Ferroelectr. 2016, 175, 220–235. [Google Scholar] [CrossRef]
- Brill, A.R.; Kafri, A.; Mohapatra, P.K.; Ismach, A.; de Ruiter, G.; Koren, E. Modulating the Optoelectronic Properties of MoS2 by Highly Oriented Dipole-Generating Monolayers. ACS Appl. Mater. Interfaces 2021, 13, 32590–32597. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.M.; Dev, D.; Krishnaprasad, A.; Tetard, L.; Roy, T. Optoelectronic synapse using monolayer MoS2 field effect transistors. Sci. Rep. 2020, 10, 21870. [Google Scholar] [CrossRef]
- Singh, E.; Kim, K.S.; Yeom, G.Y.; Nalwa, H.S. Two-dimensional transition metal dichalcogenide-based counter electrodes for dye-sensitized solar cells. RSC Adv. 2017, 7, 28234–28290. [Google Scholar] [CrossRef]
- Ladha, D.G. A review on density functional theory–based study on two-dimensional materials used in batteries. Mater. Today Chem. 2019, 11, 94–111. [Google Scholar] [CrossRef]
- Pawłowski, J.; Bieniek, M.; Woźniak, T. Valley Two-Qubit System in a MoS2-Monolayer Gated Double Quantum dot. Phys. Rev. Appl. 2021, 15, 054025. [Google Scholar] [CrossRef]
- Sajid, A.; Thygesen, K.S. VNCB defect as source of single photon emission from hexagonal boron nitride. 2D Mater. 2020, 7, 031007. [Google Scholar] [CrossRef]
- Thompson, J.J.P.; Brem, S.; Fang, H.; Frey, J.; Dash, S.P.; Wieczorek, W.; Malic, E. Criteria for deterministic single-photon emission in two-dimensional atomic crystals. Phys. Rev. Mater. 2020, 4, 084006. [Google Scholar] [CrossRef]
- Vamivakas, A.N.; Zhao, Y.; Fält, S.; Badolato, A.; Taylor, J.M.; Atatüre, M. Nanoscale Optical Electrometer. Phys. Rev. Lett. 2011, 107, 166802. [Google Scholar] [CrossRef]
- Cui, S.; Pu, H.; Wells, S.A.; Wen, Z.; Mao, S.; Chang, J.; Hersam, M.C.; Chen, J. Ultrahigh sensitivity and layer-dependent sensing performance of phosphorene-based gas sensors. Nat. Commun. 2015, 6, 8632. [Google Scholar] [CrossRef] [PubMed]
- Tyagi, D.; Wang, H.; Huang, W.; Hu, L.; Tang, Y.; Guo, Z.; Ouyang, Z.; Zhang, H. Recent advances in two-dimensional-material-based sensing technology toward health and environmental monitoring applications. Nanoscale 2020, 12, 3535–3559. [Google Scholar] [CrossRef] [PubMed]
- Kajale, S.N.; Yadav, S.; Cai, Y.; Joy, B.; Sarkar, D. 2D material based field effect transistors and nanoelectromechanical systems for sensing applications. iScience 2021, 24, 103513. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.C.; Dumcenco, D.O.; Huang, Y.S.; Suenaga, K. Atomic mechanism of the semiconducting-to- metallic phase transition in single-layered MoS2. Nat. Nanotechnol. 2014, 9, 391–396. [Google Scholar] [CrossRef] [PubMed]
- Barenco, A.; Bennett, C.H.; Cleve, R.; DiVincenzo, D.P.; Margolus, N.; Shor, P.; Sleator, T.; Smolin, J.A.; Weinfurter, H. Elementary gates for quantum computation. Phys. Rev. A 1995, 52, 3457–3467. [Google Scholar] [CrossRef] [PubMed]
- Plantenberg, J.H.; de Groot, P.C.; Harmans, C.J.P.M.; Mooij, J.E. Demonstration of controlled-NOT quantum gates on a pair of superconducting quantum bits. Nature 2007, 447, 836–839. [Google Scholar] [CrossRef]
- Long, J.; Zhao, T.; Bal, M.; Zhao, R.; Barron, G.S.; Ku, H.s.; Howard, J.A.; Wu, X.; McRae, C.R.H.; Deng, X.H.; et al. A universal quantum gate set for transmon qubits with strong ZZ interactions. arXiv 2021, arXiv:2103.12305. [Google Scholar] [CrossRef]
- Knill, E.; Laflamme, R.; Milburn, G.J. A scheme for efficient quantum computation with linear optics. Nature 2001, 409, 46–52. [Google Scholar] [CrossRef]
- O’Brien, J.L.; Pryde, G.J.; White, A.G.; Ralph, T.C.; Branning, D. Demonstration of an all-optical quantum controlled-NOT gate. Nature 2003, 426, 264–267. [Google Scholar] [CrossRef]
- Clements, W.R.; Humphreys, P.C.; Metcalf, B.J.; Kolthammer, W.S.; Walmsley, I.A. Optimal design for universal multiport interferometers. Optica 2016, 3, 1460–1465. [Google Scholar] [CrossRef]
- Carolan, J.; Harrold, C.; Sparrow, C.; Martín-López, E.; Russell, N.J.; Silverstone, J.W.; Shadbolt, P.J.; Matsuda, N.; Oguma, M.; Itoh, M.; et al. Universal linear optics. Science 2015, 349, 711–716. [Google Scholar] [CrossRef] [PubMed]
- Ewert, F.; van Loock, P. 3/4-Efficient Bell Measurement with Passive Linear Optics and Unentangled Ancillae. Phys. Rev. Lett. 2014, 113, 140403. [Google Scholar] [CrossRef] [PubMed]
- Zeuner, J.; Sharma, A.N.; Tillmann, M.; Heilmann, R.; Gräfe, M.; Moqanaki, A.; Szameit, A.; Walther, P. Integrated-optics heralded controlled-NOT gate for polarization-encoded qubits. NPJ Quantum Inf. 2018, 4, 13. [Google Scholar] [CrossRef]
- Lee, J.M.; Lee, W.J.; Kim, M.S.; Cho, S.; Ju, J.J.; Navickaite, G.; Fernandez, J. Controlled-NOT operation of SiN-photonic circuit using photon pairs from silicon-photonic circuit. Opt. Commun. 2022, 509, 127863. [Google Scholar] [CrossRef]
- Li, L.; Chen, J.; Wu, K.; Cao, C.; Shi, S.; Cui, J. The Stability of Metallic MoS2 Nanosheets and Their Property Change by Annealing. Nanomaterials 2019, 9, 1366. [Google Scholar] [CrossRef]
- Varga, K.; Driscoll, J.A. Computational Nanoscience: Applications for Molecules, Clusters, and Solids; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Grasselli, M.; Pelinovsky, D. Numerical Mathematics; Jones and Bartlett Publishers: Sudbury, MA, USA, 2008. [Google Scholar]
- Jelic, V.; Marsiglio, F. The double-well potential in quantum mechanics: A simple, numerically exact formulation. Eur. J. Phys. 2012, 33, 1651–1666. [Google Scholar] [CrossRef]
- Griffiths, D.J. Introduction to Quantum Mechanics, 2nd ed.; Pearson Prentice Hall: Hoboken, NJ, USA, 2004. [Google Scholar]
- Santos, E.J.G.; Kaxiras, E. Electric-Field Dependence of the Effective Dielectric Constant in Graphene. Nano Lett. 2013, 13, 898–902. [Google Scholar] [CrossRef]
- Keldysh, L.V. Coulomb interaction in thin semiconductor and semimetal films. JETP Lett. 1979, 29, 658. [Google Scholar]
- Cudazzo, P.; Tokatly, I.V.; Rubio, A. Dielectric screening in two-dimensional insulators: Implications for excitonic and impurity states in graphane. Phys. Rev. B 2011, 84, 085406. [Google Scholar] [CrossRef]
- Van Tuan, D.; Yang, M.; Dery, H. Coulomb interaction in monolayer transition-metal dichalcogenides. Phys. Rev. B 2018, 98, 125308. [Google Scholar] [CrossRef]
- Pedersen, L.H.; Møller, N.M.; Mølmer, K. Fidelity of quantum operations. Phys. Lett. A 2007, 367, 47–51. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kesorn, A.; Hunkao, R.; Tivakornsasithorn, K.; Sinsarp, A.; Sukkabot, W.; Suwanna, S. Dynamical Behavior of Two Interacting Double Quantum Dots in 2D Materials for Feasibility of Controlled-NOT Operation. Nanomaterials 2022, 12, 3599. https://doi.org/10.3390/nano12203599
Kesorn A, Hunkao R, Tivakornsasithorn K, Sinsarp A, Sukkabot W, Suwanna S. Dynamical Behavior of Two Interacting Double Quantum Dots in 2D Materials for Feasibility of Controlled-NOT Operation. Nanomaterials. 2022; 12(20):3599. https://doi.org/10.3390/nano12203599
Chicago/Turabian StyleKesorn, Aniwat, Rutchapon Hunkao, Kritsanu Tivakornsasithorn, Asawin Sinsarp, Worasak Sukkabot, and Sujin Suwanna. 2022. "Dynamical Behavior of Two Interacting Double Quantum Dots in 2D Materials for Feasibility of Controlled-NOT Operation" Nanomaterials 12, no. 20: 3599. https://doi.org/10.3390/nano12203599
APA StyleKesorn, A., Hunkao, R., Tivakornsasithorn, K., Sinsarp, A., Sukkabot, W., & Suwanna, S. (2022). Dynamical Behavior of Two Interacting Double Quantum Dots in 2D Materials for Feasibility of Controlled-NOT Operation. Nanomaterials, 12(20), 3599. https://doi.org/10.3390/nano12203599







