Magnetic Concentric Hot-Circle Generation at Optical Frequencies in All-Dielectric Mesoscale Janus Particles
Abstract
:1. Introduction
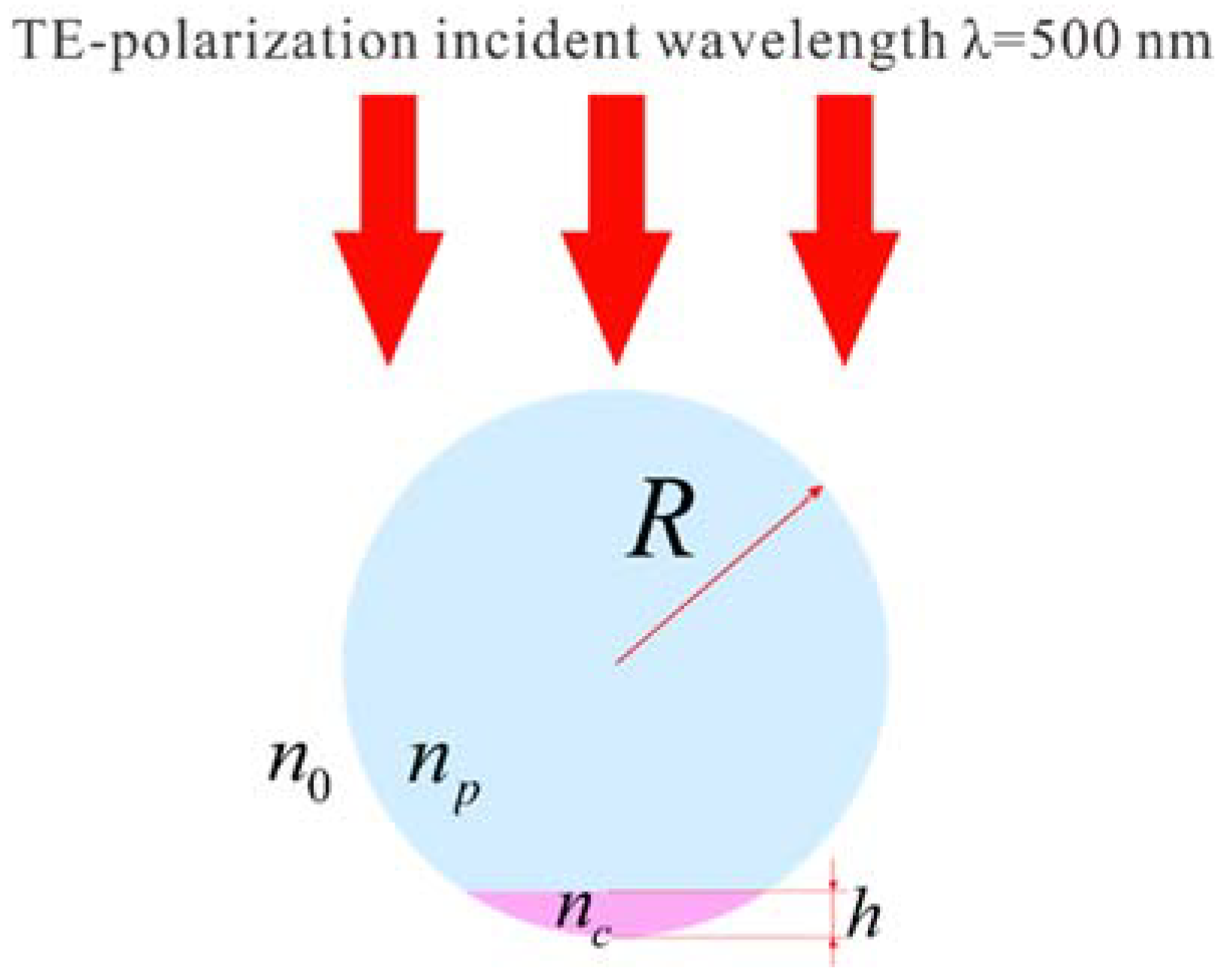
2. Computational Model
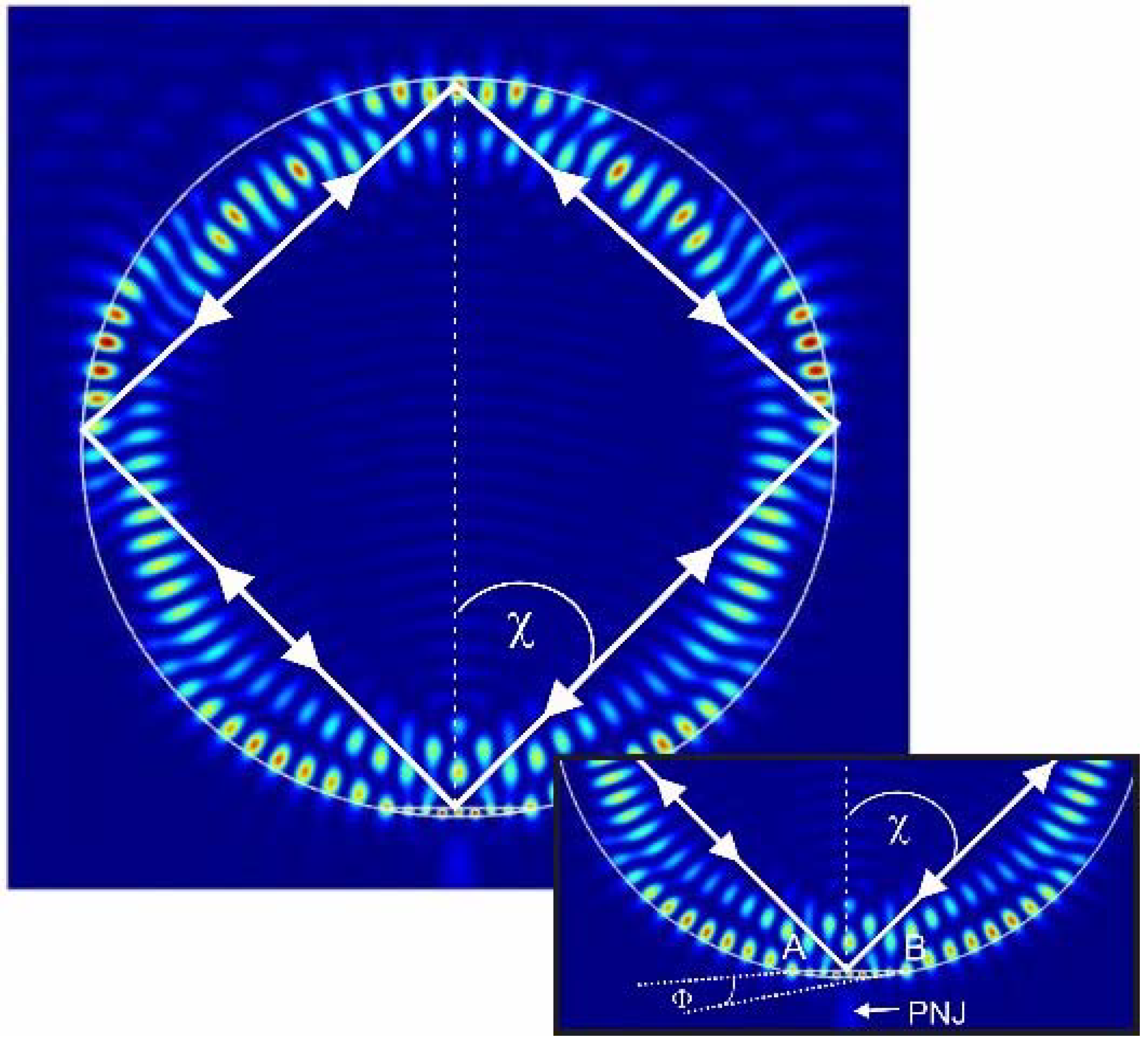
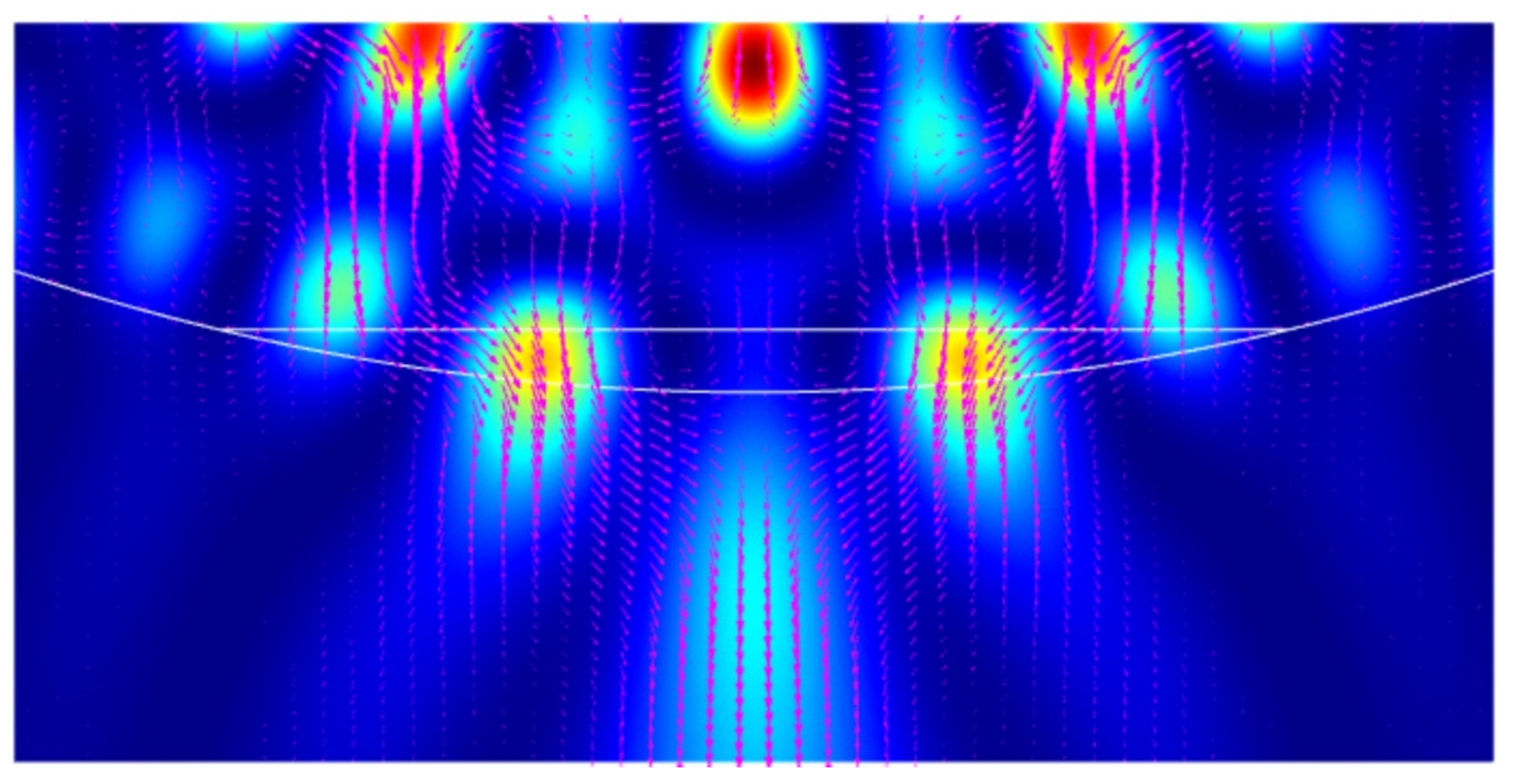
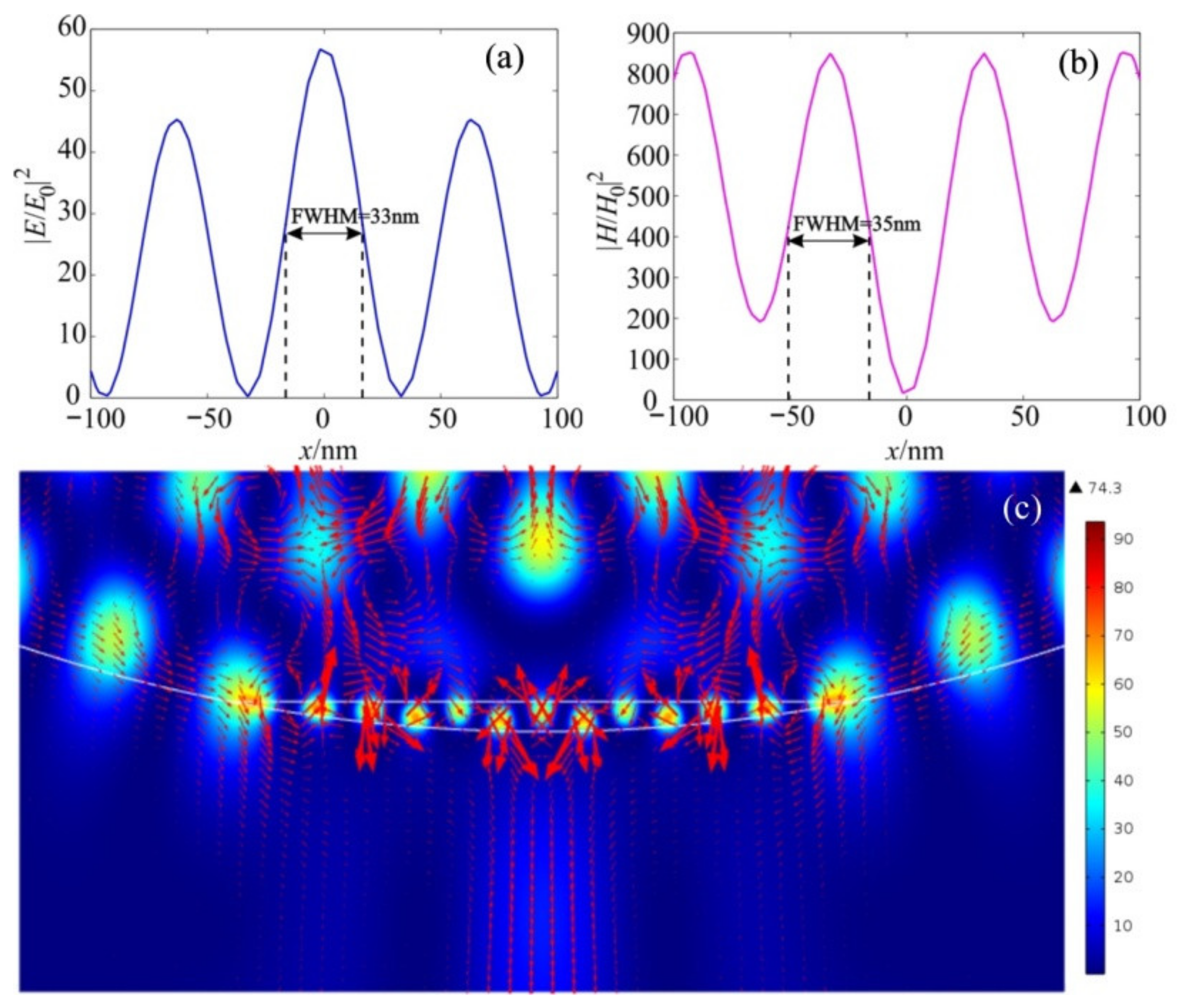
3. Simulation and Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Radziuk, D.; Moehwald, H. Prospects for plasmonic hot spots in single molecule SERS towards the chemical imaging of live cells. Phys. Chem. Chem. Phys. 2015, 17, 21072–21093. [Google Scholar] [CrossRef]
- Nazir, A.; Panaro, S.; Proietti Zaccaria, R.; Liberale, C.; De Angelis, F.; Toma, A. Fano coil-type resonance for magnetic hot-spot generation. Nano Lett. 2014, 14, 3166–3171. [Google Scholar] [CrossRef]
- Pratesi, F.; Burresi, M.; Riboli, F.; Vynck, K.; Wiersma, D. Disordered photonic structures for light harvesting in solar cells. Opt. Express 2013, 21, A460–A468. [Google Scholar] [CrossRef]
- Mohammadi, E.; Tavakoli, A.; Dehkhoda, P.; Jahani, Y.; Tsakmakidis, K.; Tittl, A.; Altug, H. Accessible superchiral near-Fields driven by tailored electric and magnetic resonances in all-dielectric nanostructures. ACS Photonics 2019, 6, 1939–1946. [Google Scholar] [CrossRef]
- Agrawal, T.; Dey, S.; Bhattacharya, S.; Singh, G.; Bisht, P. Numerical investigations on a photonic nanojet coupled plasmonic system for photonic applications. J. Opt. 2022, 24, 044008. [Google Scholar] [CrossRef]
- Chirumamilla, M.; Chirumamilla, A.; Roberts, A.; Zaccaria, R.; De Angelis, F.; Kristensen, P.; Krahne, R.; Bozhevolnyi, S.; Pedersen, K.; Toma, A. Hot-spot engineering in 3D multi-branched nanostructures: Ultrasensitive substrates for surface-enhanced Raman spectroscopy. Adv. Opt. Mater. 2017, 5, 1600836. [Google Scholar] [CrossRef]
- Evlyukhin, A.; Novikov, S.; Zywietz, U.; Eriksen, R.; Reinhardt, C.; Bozhevolnyi, S.; Chichkov, B. Demonstration of magnetic dipole resonances of dielectric nanospheres in the visible region. Nano Lett. 2012, 12, 3749–3755. [Google Scholar] [CrossRef]
- Bakker, R.; Permyakov, D.; Yu, Y.; Markovich, D.; Paniagua-Domínguez, R.; Gonzaga, L.; Samusev, A.; Kivshar, Y.; Luk’yanchuk, B.; Kuznetsov, A.I. Magnetic and electric hotspots with silicon nanodimers. Nano Lett. 2015, 15, 2137–2142. [Google Scholar] [CrossRef]
- Barreda, A.; Saleh, H.; Litman, A.; González, F.; Geffrin, J.; Moreno, F. On the scattering directionality of a dielectric particle dimer of High Refractive Index. Sci. Rep. 2018, 8, 7976. [Google Scholar] [CrossRef]
- Petryayeva, E.; Krull, U.J. Localized surface plasmon resonance: Nanostructures, bioassays and biosensing—A review. Anal. Chim. Acta 2011, 706, 8–24. [Google Scholar] [CrossRef]
- Evlyukhin, A.; Reinhardt, C.; Seidel, A.; Luk’yanchuk, B.; Chichkov, B. Optical response features of Si-nanoparticle arrays. Phys. Rev. B 2010, 82, 45404. [Google Scholar] [CrossRef]
- Hopkins, B.; Filonov, D.; Miroshnichenko, A.; Monticone, F.; Alu, A.; Kivshar, Y. Interplay of magnetic responses in all-dielectric oligomers to realize magnetic Fano resonances. ACS Photonics 2015, 2, 724–729. [Google Scholar] [CrossRef]
- Kuznetsov, A.; Miroshnichenko, A.; Fu, Y.; Zhang, J.; Luk’yanchuk, B. Magnetic light. Sci. Rep. 2012, 2, 492. [Google Scholar] [CrossRef]
- Liu, S.; Sinclair, M.; Mahony, T.; Jun, Y.; Campione, S.; Ginn, J.; Bender, D.; Wendt, J.; Ihlefeld, J.; Clem, P.; et al. Optical magnetic mirrors without metals. Optica 2014, 1, 250–256. [Google Scholar] [CrossRef]
- Luk’yanchuk, B.; Paniagua-Dominguez, R.; Minin, I.; Minin, O.; Wang, Z. Refractive index less than two: Photonic nanojets yesterday, today and tomorrow. Opt. Mater. Express 2017, 7, 1820–1847. [Google Scholar] [CrossRef]
- Tonkaev, P.; Kivshar, Y. All dielectric resonant metaphotonics: Opinion. Opt. Mater. Express 2022, 12, 2879. [Google Scholar] [CrossRef]
- Calandrini, E.; Cerea, A.; De Angelis, F.; Zaccaria, R.; Toma, A. Magnetic hot-spot generation at optical frequencies: From plasmonic metamolecules to all-dielectric nanoclusters. Nanophotonics 2019, 8, 45–62. [Google Scholar] [CrossRef]
- Albella, P.; Poyli, M.; Schmidt, M.; Maier, S.; Moreno, F.; Sáenz, J.; Aizpurua, J. Low-loss electric and magnetic field-enhanced spectroscopy with subwavelength silicon dimers. J. Phys. Chem. C 2013, 117, 13573–13584. [Google Scholar] [CrossRef]
- Gong, T.; Guan, F.; Wei, Z.; Huang, W.; Zhang, X. Tunable magnetic fano resonances on Au nanosphere dimer-dielectric-gold film sandwiched structure. Front. Phys. 2021, 9, 691027. [Google Scholar] [CrossRef]
- Hirohata, A.; Yamada, K.; Nakatani, Y.; Prejbeanu, I.; Diény, B.; Pirro, P.; Hillebrands, B. Review on spintronics: Principles and device applications. J. Magn. Magn. Mater. 2020, 509, 166711. [Google Scholar] [CrossRef]
- Tribelsky, M.; Miroshnichenko, A. Giant in-particle field concentration and Fano resonances at light scattering by high-refractive-index particles. Phys. Rev. A 2016, 93, 053837. [Google Scholar] [CrossRef]
- Hoang, T.; Duan, Y.; Chen, X.; Barbastathis, G. Focusing and imaging in microsphere-based microscopy. Opt. Express 2015, 23, 12337–12353. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Luk’yanchuk, B.; Yue, L.; Yan, B.; Monks, J.; Dhama, R.; Minin, O.V.; Minin, I.V.; Huang, S.; Fedyanin, A. High order Fano resonances and giant magnetic fields in dielectric microspheres. Sci. Rep. 2019, 9, 20293. [Google Scholar] [CrossRef] [PubMed]
- Yue, L.; Wang, Z.; Yan, B.; Monks, J.; Joya, Y.; Dhama, R.; Minin, O.V.; Minin, I.V. Super-enhancement focusing of teflon spheres. Ann. Phys. 2020, 532, 2000373. [Google Scholar] [CrossRef]
- Minin, I.V.; Minin, O.V.; Zhou, S. High-order Fano resonance in a low-index dielectric mesosphere. JETP Lett. 2022, 116, 114. [Google Scholar]
- Minin, O.V.; Minin, I.V. Optical phenomena in mesoscale dielectric particles. Photonics 2021, 8, 591. [Google Scholar] [CrossRef]
- Qiu, J.; Chen, Z.; Chi, M.; Xia, Y. Swelling-induced symmetry breaking: A versatile approach to the scalable production of colloidal particles with a Janus structure. Angew. Chem. Int. Ed. 2021, 60, 12980–12984. [Google Scholar] [CrossRef]
- Minin, O.V.; Minin, I.V. Unusual optical effects in dielectric mesoscale particles. Proc. SPIE 2022, 12193, 121930E. [Google Scholar]
- Minin, I.V.; Minin, O.V.; Cao, Y.; Yan, B.; Wang, Z.; Luk’yanchuk, B. Photonic lenses with whispering gallery waves at Janus particles. Opto-Electron Sci. 2022, 1, 210008. [Google Scholar] [CrossRef]
- Luk’yanchuk, B.S.; Bekirov, A.; Wang, Z.; Minin, I.V.; Minin, O.V.; Fedyanin, A. Optical phenomenon in mesoscale dielectric spheres and immersion lenses based on Janus particles (Review). Phys. Wave Phenom. 2022, 30, 217–241. [Google Scholar] [CrossRef]
- Yu, N.; Genevet, P.; Kats, M.; Aieta, F.; Tetienne, J.; Capasso, F.; Gaburro, Z. Light propagation with phase discontinuities: Generalized laws of reflection and refraction. Science 2011, 334, 333–337. [Google Scholar] [CrossRef] [PubMed]
- Rousseau, E.; Felbacq, D. Concept of a Generalized Law of Refraction: A Phenomenological Model. ACS Photonics 2020, 7, 1649–1654. [Google Scholar] [CrossRef]
- Ghislain, L.; Elings, V.; Crozier, K.; Manalis, S.; Minne, S.; Wilder, K.; Kino, G.; Quate, C. Near-field photolithography with a solid immersion lens. Appl. Phys. Lett. 1999, 74, 501–503. [Google Scholar] [CrossRef]
- Jones, E.; Cohn, S. Surface matching of dielectric lenses. J. Appl. Phys. 1955, 26, 452. [Google Scholar] [CrossRef]
- Polozkov, R.; Shubnic, A.; Shelykh, I.; Iorsh, I. High refractive index and extreme biaxial optical anisotropy of rhenium diselenide for applications in all-dielectric nanophotonics. Nanophotonics 2020, 9, 4737–4742. [Google Scholar]
- Zhu, Y.; Tao, L.; Chen, X.; Ma, Y.; Ning, S.; Zhou, J.; Zhao, X.; Bosman, M.; Liu, Z.; Du, S.; et al. Anisotropic point defects in rhenium diselenide monolayers. iScience 2021, 24, 103456. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Heo, K.; Kang, D.; Shin, C.; Lee, S.; Yu, H.; Park, J. Rhenium Diselenide (ReSe2) Near-Infrared Photodetector: Performance Enhancement by Selective p-Doping Technique. Adv. Sci. 2019, 6, 1901255. [Google Scholar] [CrossRef]
- Minin, I.V.; Minin, O.V.; Luk’yanchuk, B.S. Mesotronic era of dielectric photonics. Proc. SPIE 2022, 12152, 121520D. [Google Scholar]
- Vandersypen, L.M.; Chuang, I.L. NMR techniques for quantum control and computation. Rev. Mod. Phys. 2005, 76, 1037. [Google Scholar] [CrossRef]
- Crescini, N.; Braggio, C.; Carugno, G.; Ortolan, A.; Ruoso, G. Cavity magnon polariton based precision magnetometry. Appl. Phys. Lett. 2020, 117, 144001. [Google Scholar] [CrossRef]
- Oxborrow, M.; Breeze, J.D.; Alford, N.M. Room-temperature solid-state maser. Nature 2012, 488, 353. [Google Scholar] [CrossRef] [PubMed]
- Brunetti, G.; Sasanelli, N.; Armenise, M.N.; Ciminelli, C. Nanoscale Optical Trapping by Means of Dielectric Bowtie. Photonics 2022, 9, 425. [Google Scholar] [CrossRef]
- Scheunert, G.; Cohen, S.R.; Kullock, R.; McCarron, R.; Rechev, K.; Kaplan-Ashiri, I.; Bitton, O.; Dawson, P.; Hecht, B.; Oron, D. Grazing-incidence optical magnetic recording with super-resolution. Beilstein J. Nanotechnol. 2017, 8, 28–37. [Google Scholar] [CrossRef] [PubMed]
- Nie, Z.; Lin, H.; Liu, X.; Zhai, A.; Tian, Y.; Wang, W.; Li, D.; Ding, W.; Zhang, X.; Song, Y.; et al. Three-dimensional super-resolution longitudinal magnetization spot arrays. Light Sci. Appl. 2017, 6, e17032. [Google Scholar] [CrossRef]

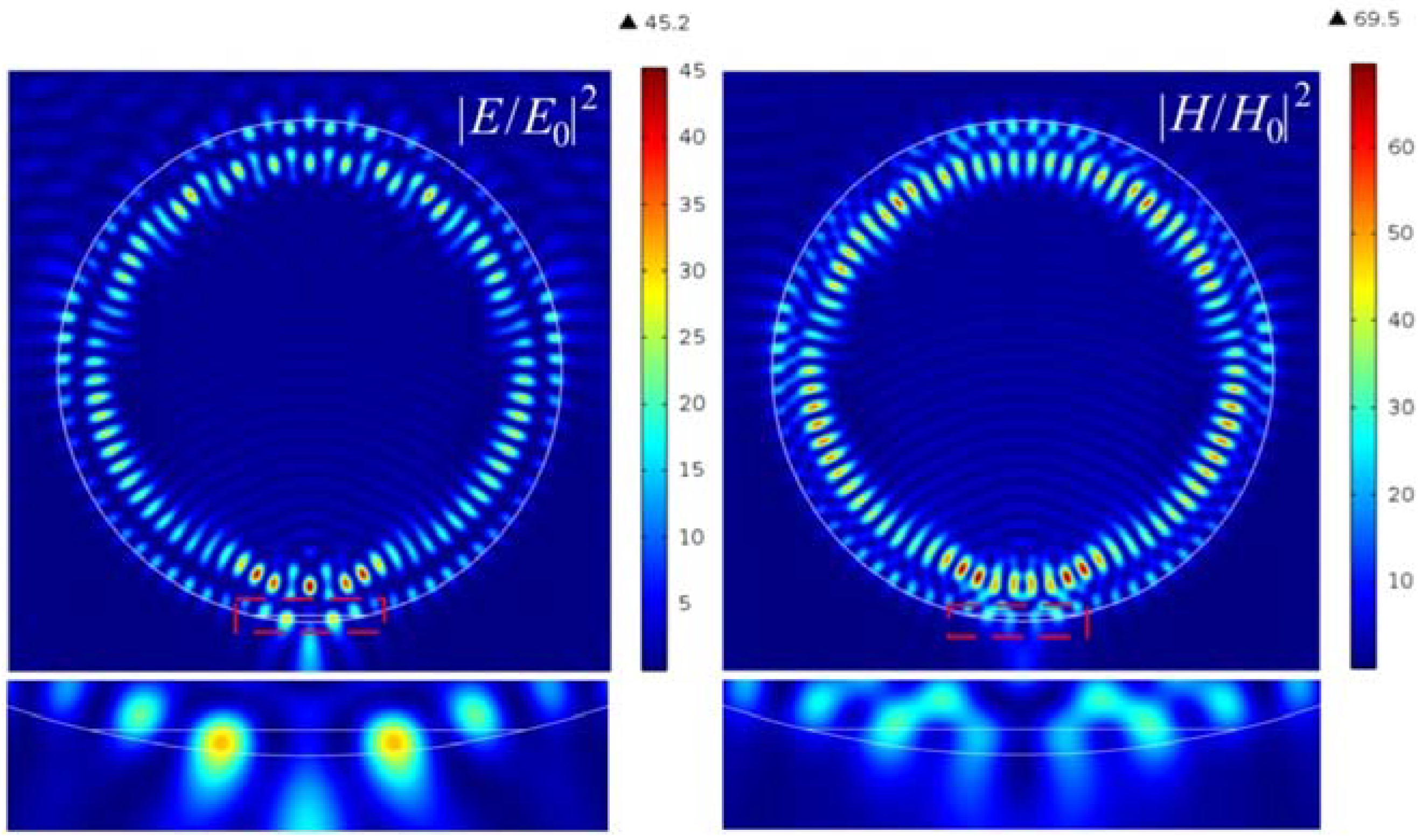
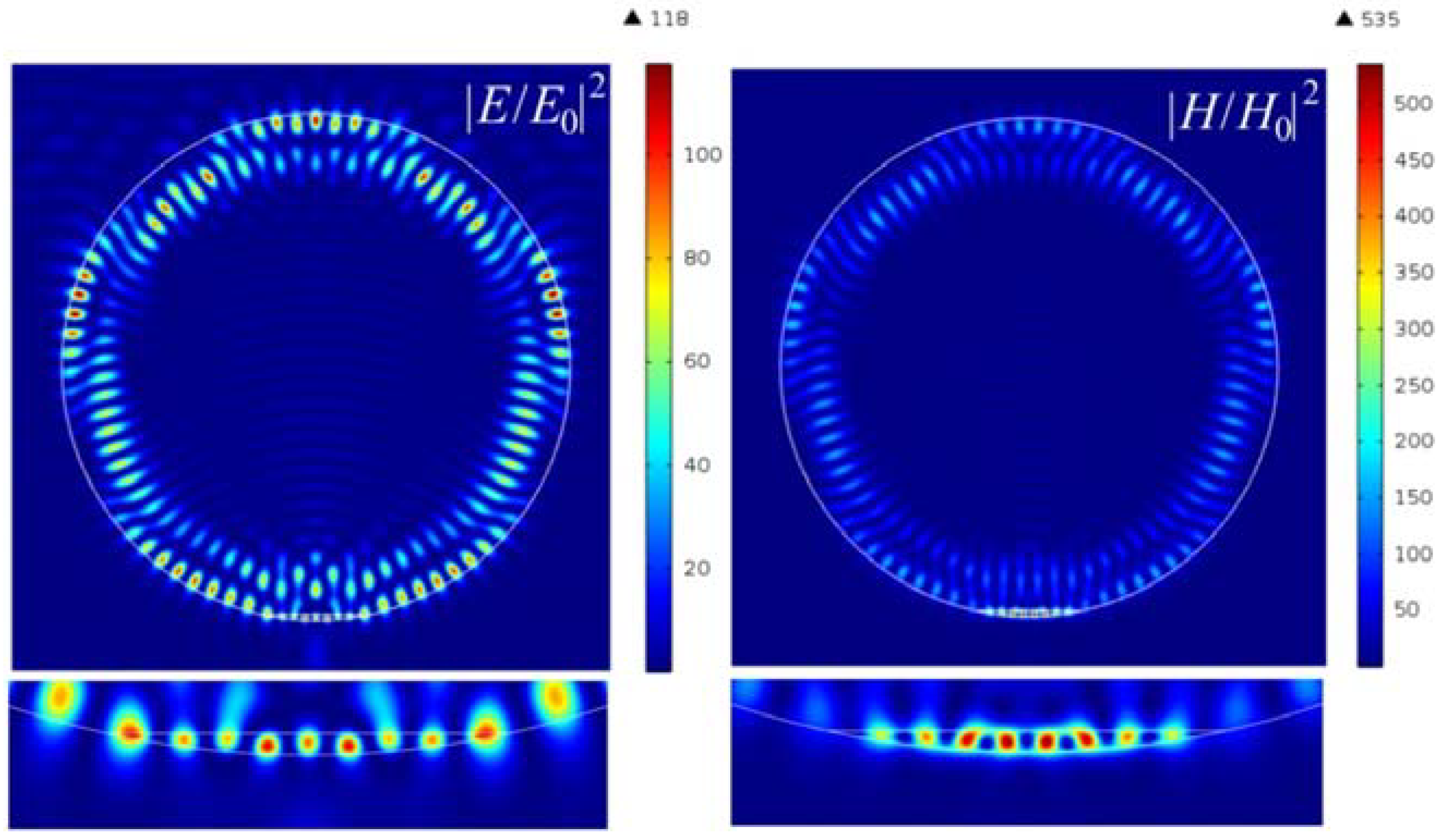
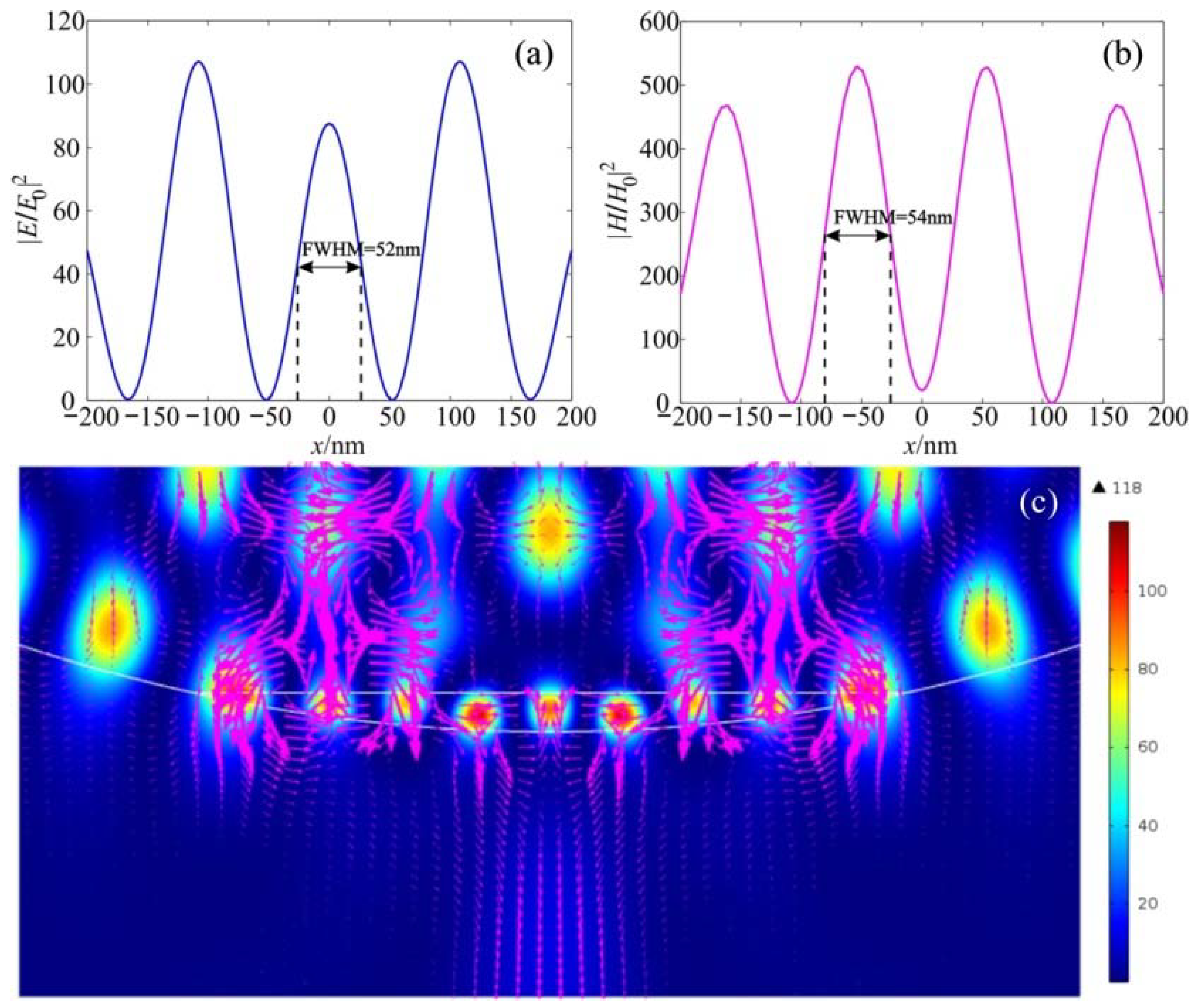

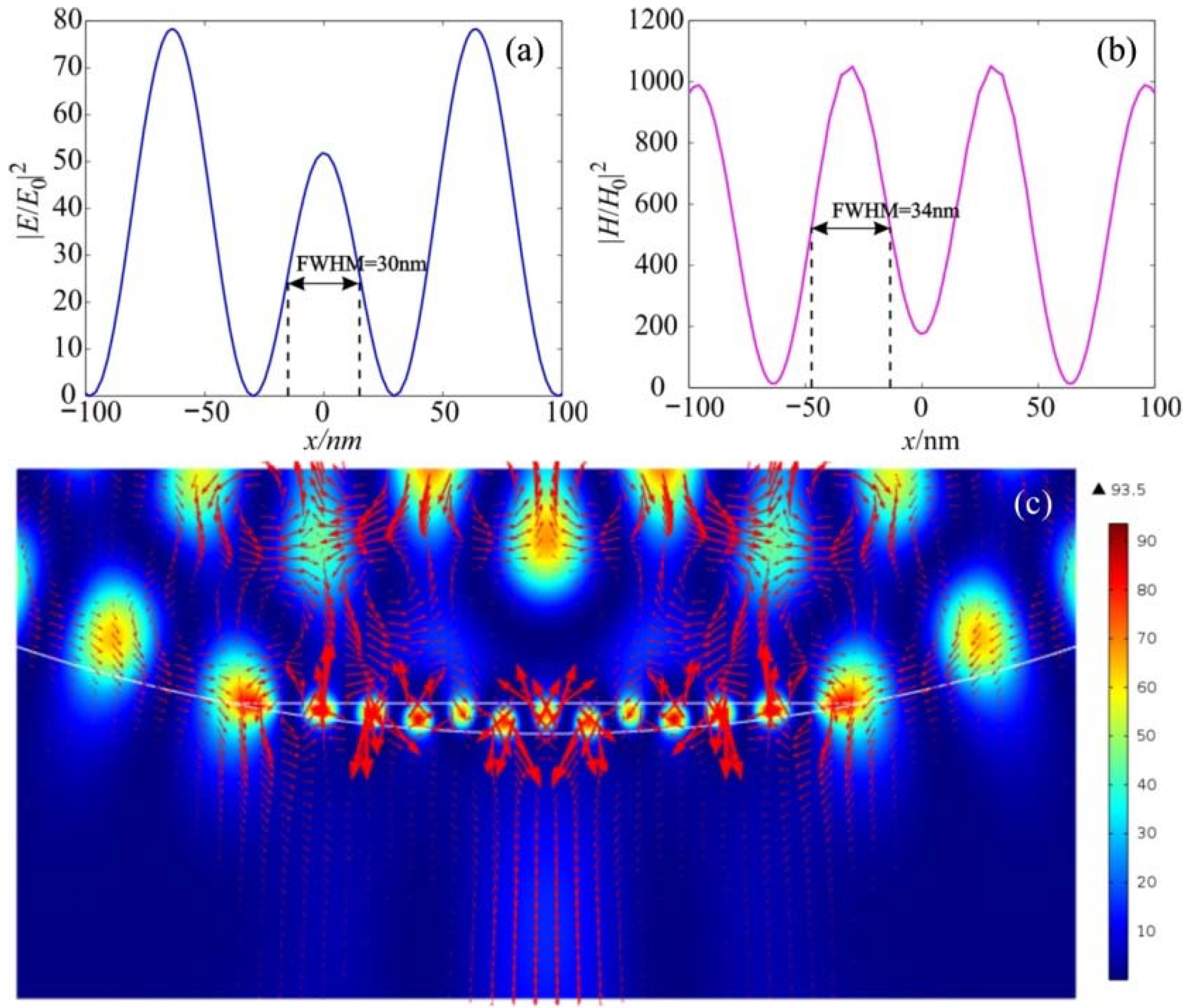
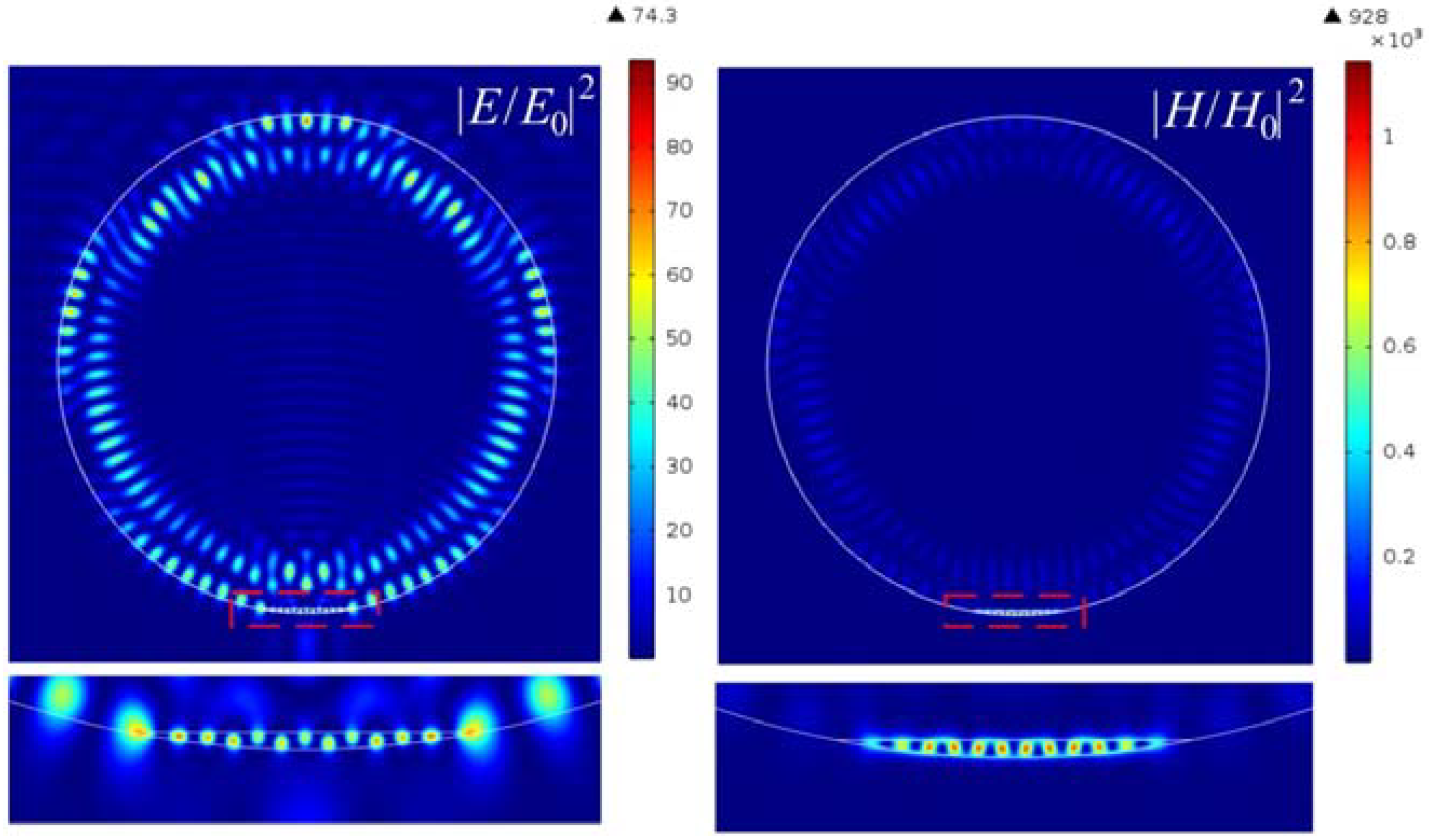
| n | (H/H0)2 | (E/E0)2 | (H/H0)2/(E/E0)2 |
|---|---|---|---|
| 1.5 | 45 | 29 | 1.55 |
| 1.124 | 69 | 45 | 1.53 |
| 0.476 | 535 | 118 | 4.53 |
| 0.3 (k = 0) | 1141 | 93 | 12.27 |
| 0.3 (k = 0.005) | 928 | 74 | 12.54 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Minin, O.V.; Zhou, S.; Liu, C.-Y.; Kong, J.A.N.; Minin, I.V. Magnetic Concentric Hot-Circle Generation at Optical Frequencies in All-Dielectric Mesoscale Janus Particles. Nanomaterials 2022, 12, 3428. https://doi.org/10.3390/nano12193428
Minin OV, Zhou S, Liu C-Y, Kong JAN, Minin IV. Magnetic Concentric Hot-Circle Generation at Optical Frequencies in All-Dielectric Mesoscale Janus Particles. Nanomaterials. 2022; 12(19):3428. https://doi.org/10.3390/nano12193428
Chicago/Turabian StyleMinin, Oleg V., Song Zhou, Cheng-Yang Liu, Jelene Antonicole Ngan Kong, and Igor V. Minin. 2022. "Magnetic Concentric Hot-Circle Generation at Optical Frequencies in All-Dielectric Mesoscale Janus Particles" Nanomaterials 12, no. 19: 3428. https://doi.org/10.3390/nano12193428
APA StyleMinin, O. V., Zhou, S., Liu, C.-Y., Kong, J. A. N., & Minin, I. V. (2022). Magnetic Concentric Hot-Circle Generation at Optical Frequencies in All-Dielectric Mesoscale Janus Particles. Nanomaterials, 12(19), 3428. https://doi.org/10.3390/nano12193428








