Thermal Progress of Unsteady Separated Stagnation Point Flow with Magnetic Field and Heat Generation in Hybrid Ferrofluid
Abstract
:1. Introduction
2. Mathematical Formulation
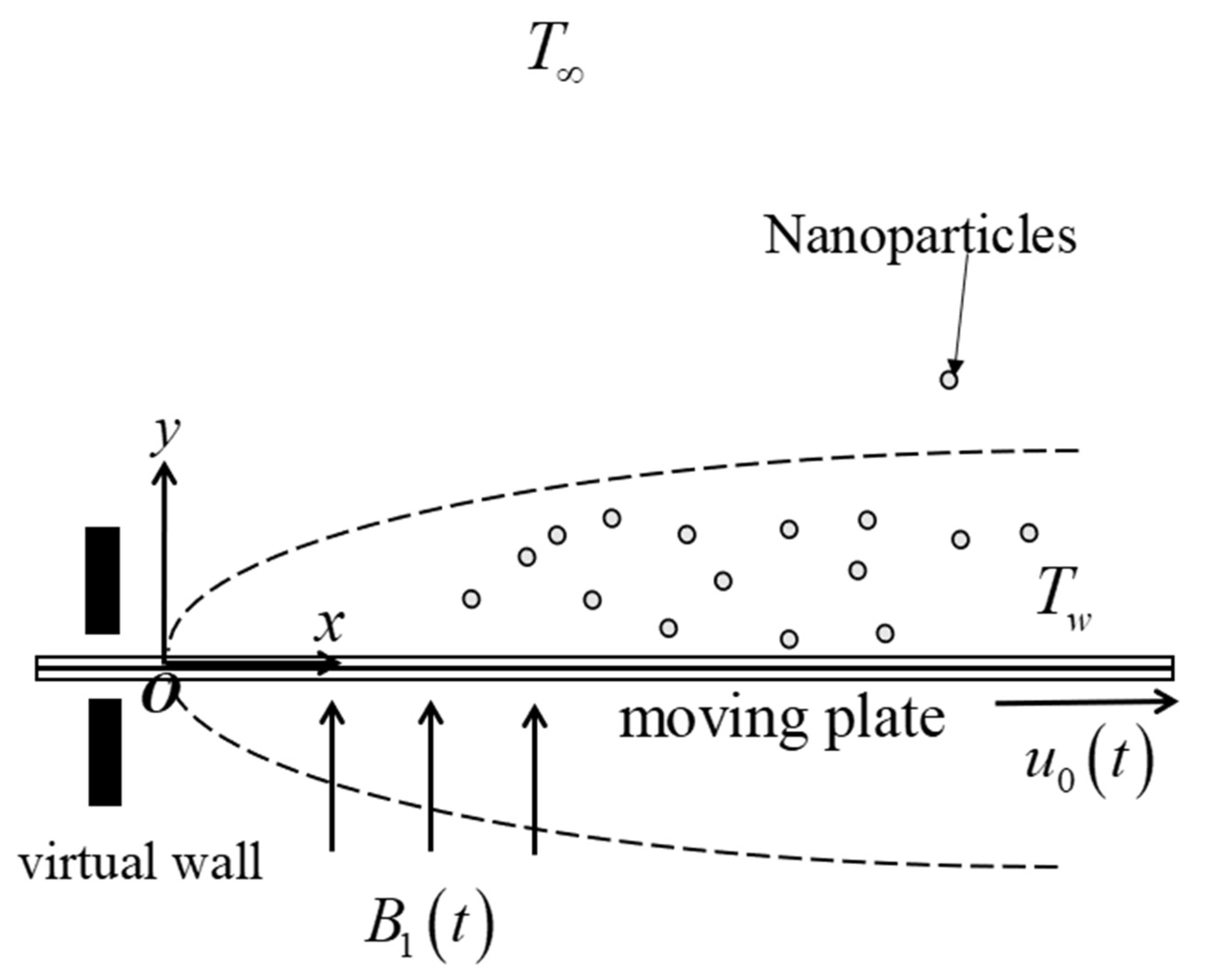
- The free stream velocity (parallel to the plate) is , where and are the constant reference time and time, respectively (see Dholey [43] and Khashi’ie et al. [44]). In addition, refers to the strength of free stream velocity, denoted as the acceleration parameter. This velocity is also located outside the boundary layer region.
- Importantly, is an unsteadiness parameter, where denotes a steady boundary layer flow, while and refer to unsteady accelerating and decelerating parameters, respectively.
- For the heat generation effect, is the variable heat generation factor, where is a constant (see Kumbhakar and Nandi [28]).
- For the magnetic field effect, , where is a constant.
- The temperatures for the wall surface and far-field region are symbolized as and , respectively.
- This model excludes the effect of sedimentation/aggregation since the hybrid nanofluid is assumed to be stably synthesized.
3. Stability Analysis
4. Results and Discussion
5. Conclusions
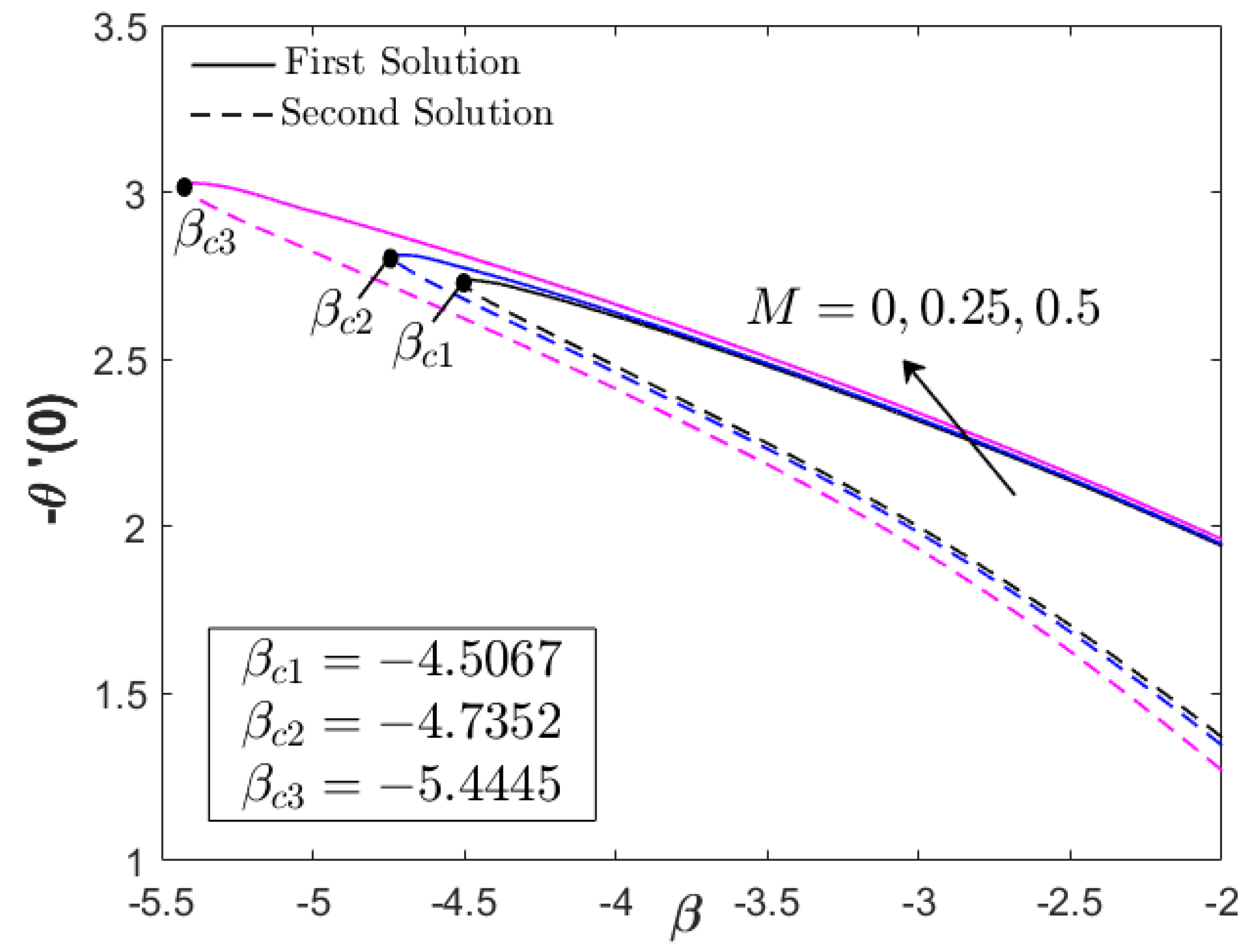
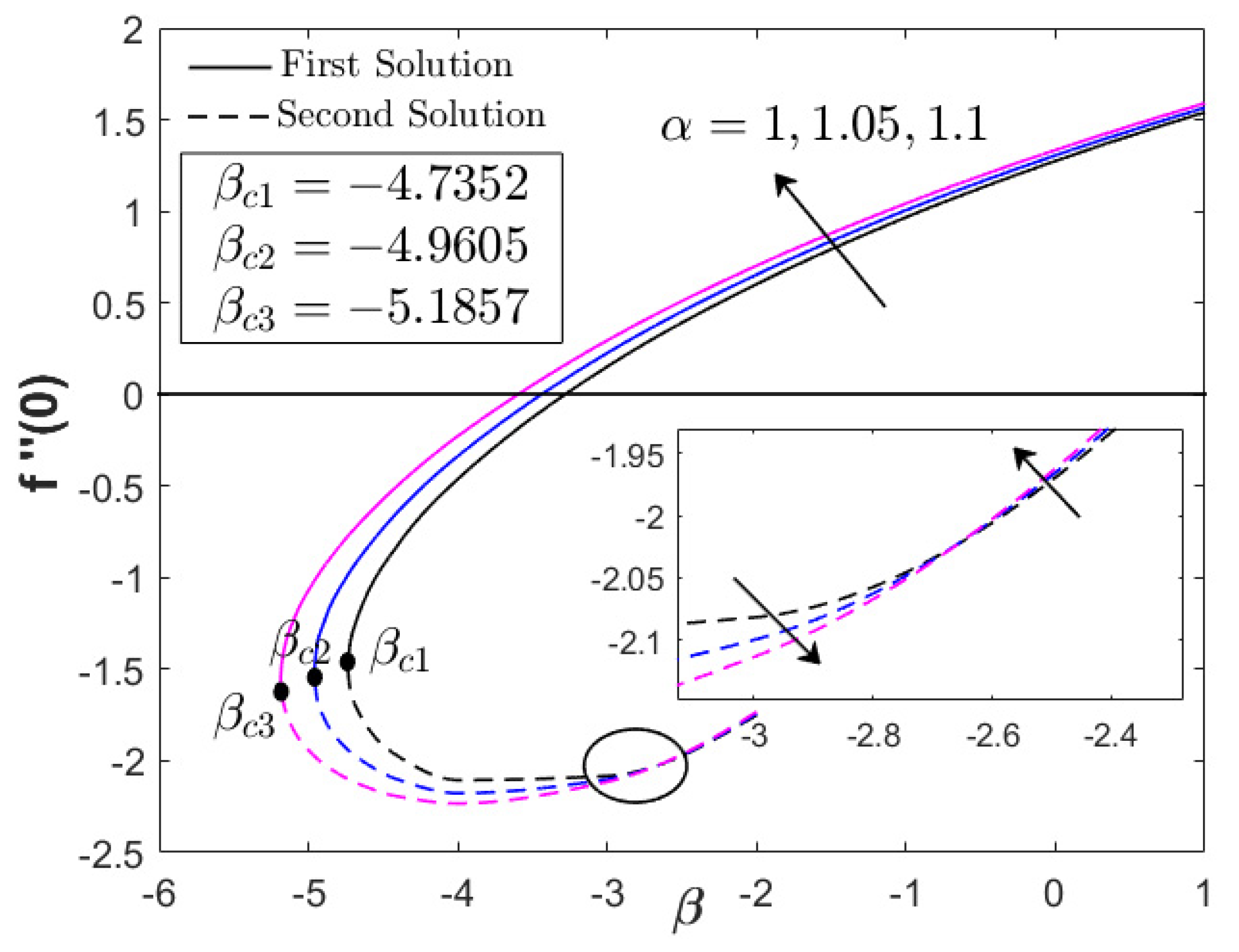
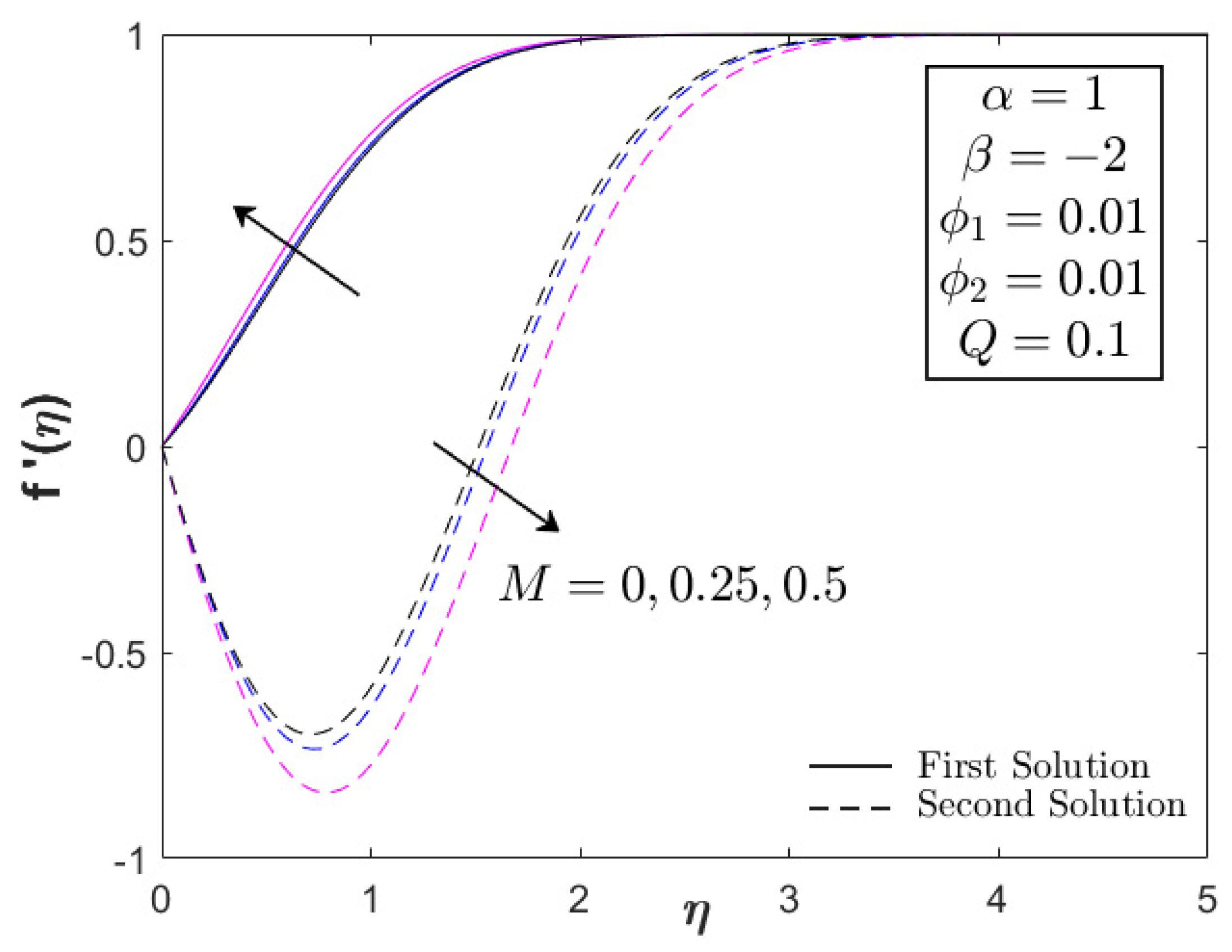
- The magnitude of the skin friction and the heat transfer coefficients is increased for larger magnetic and acceleration parameters.
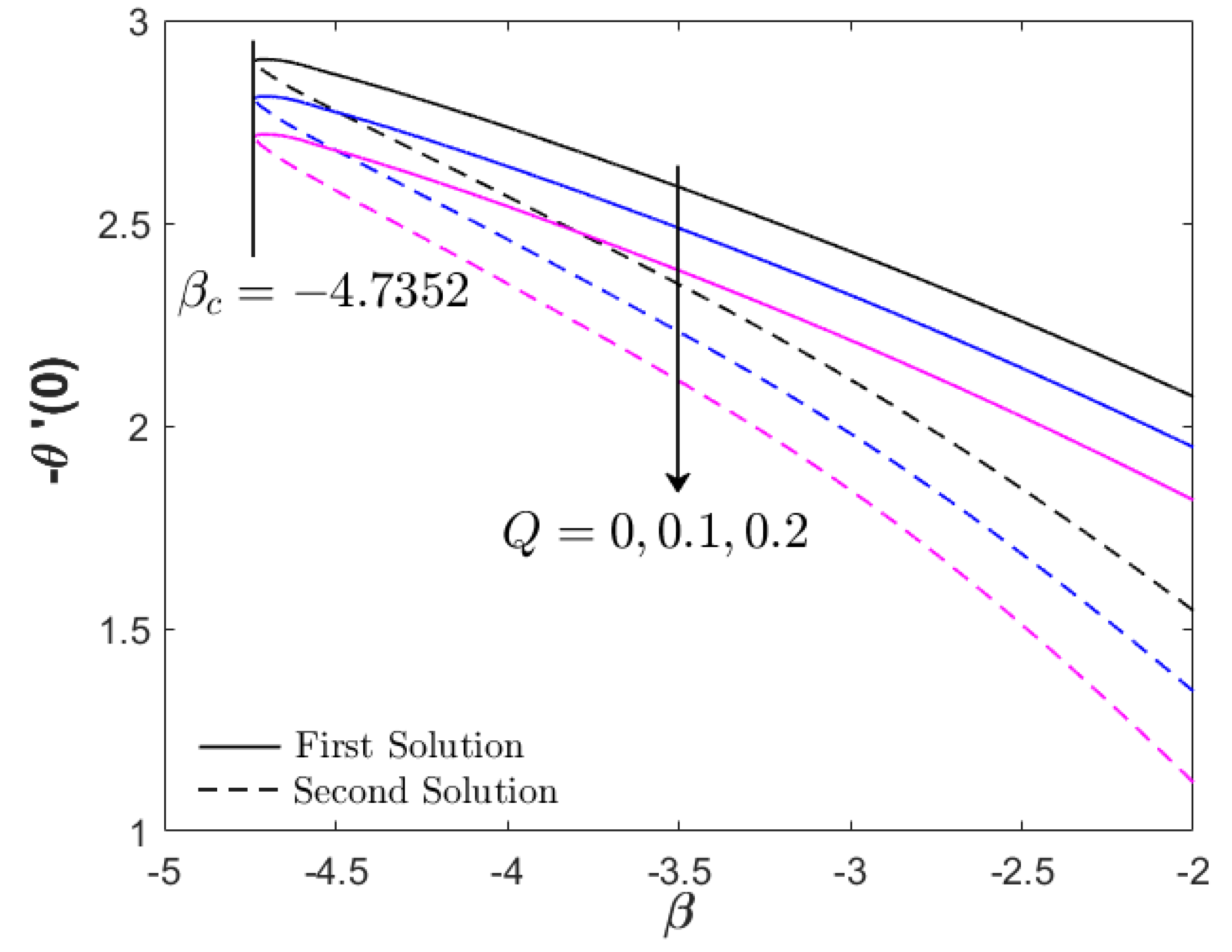
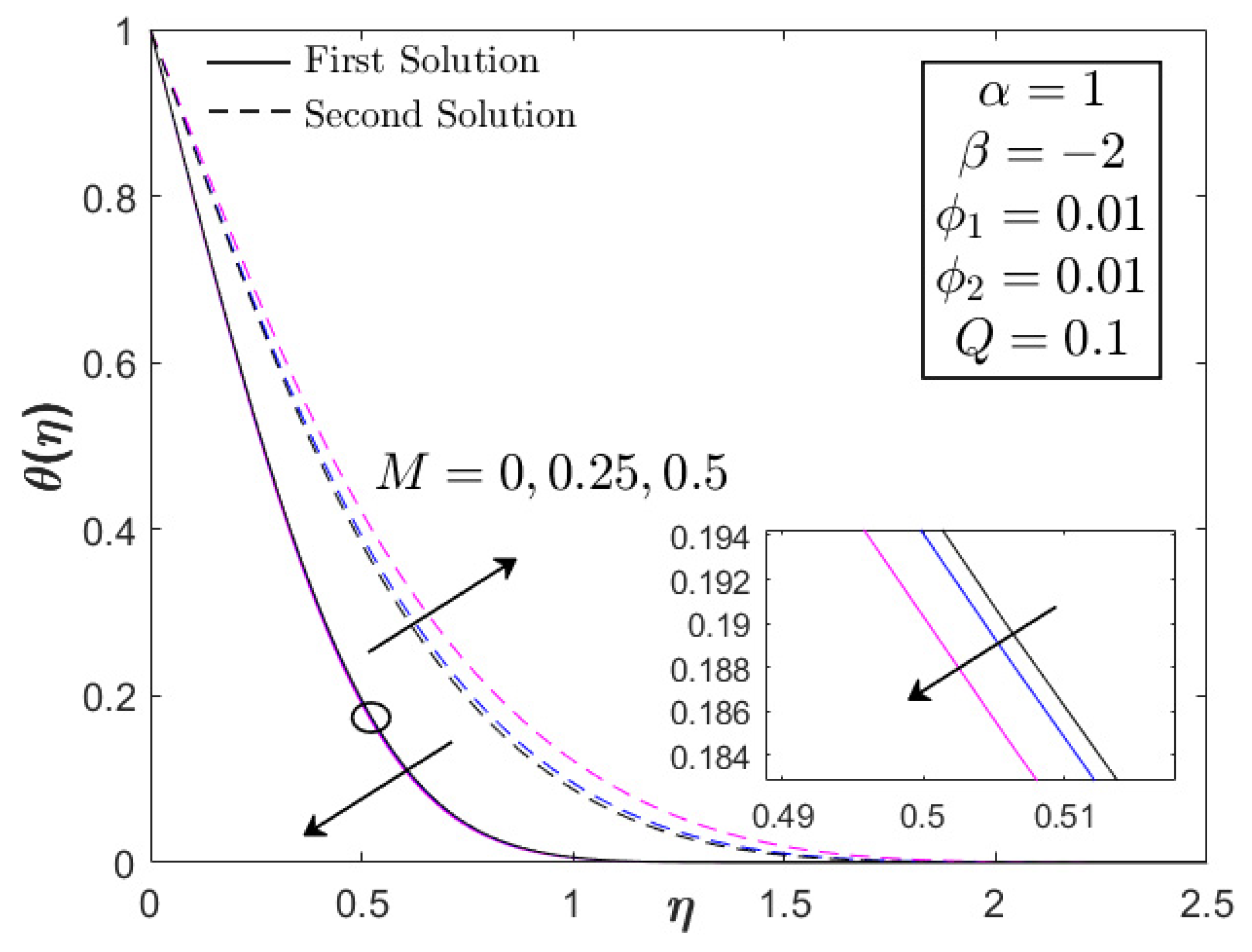
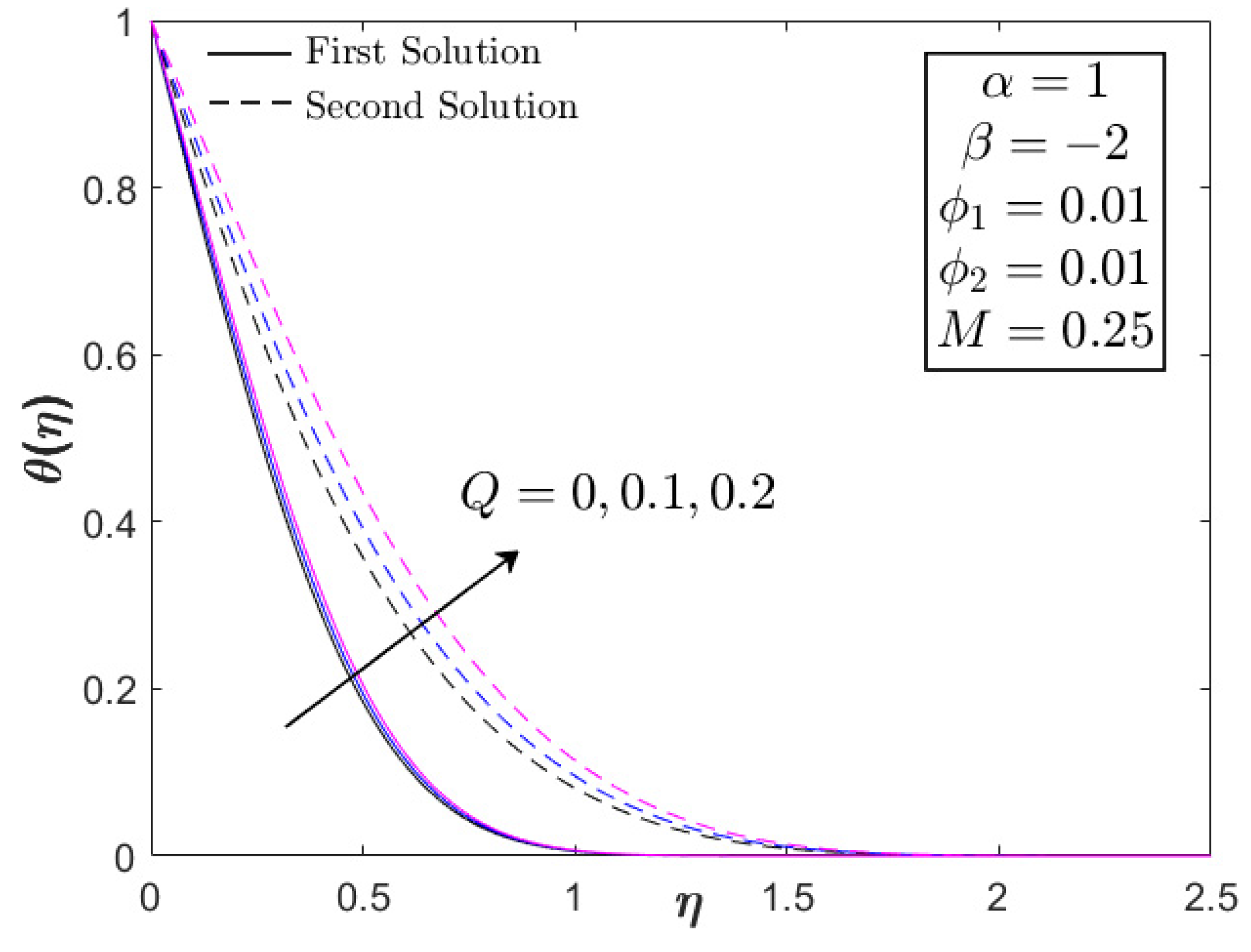
- The heat transfer performance decreases with the imposition of heat generation.
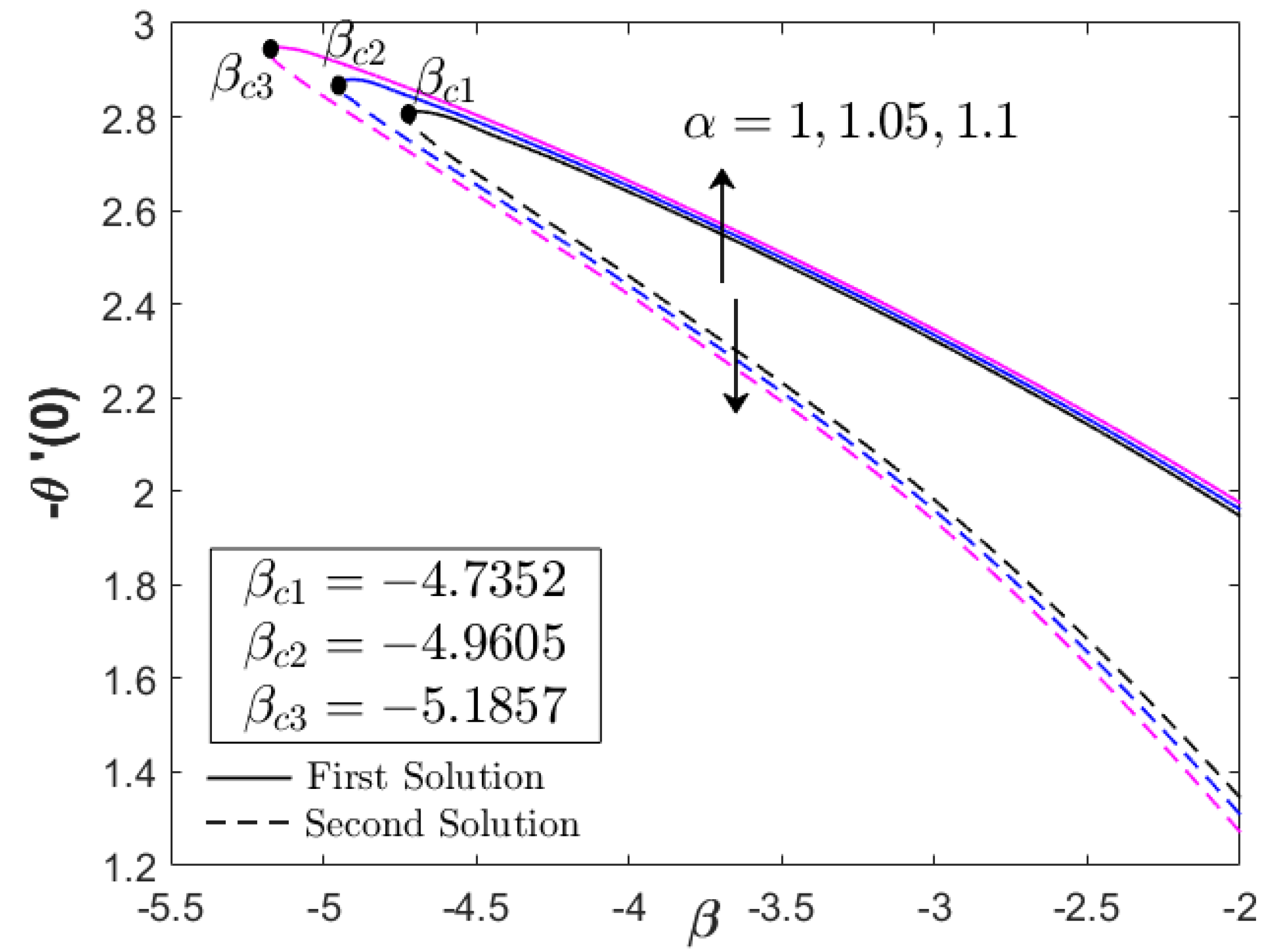
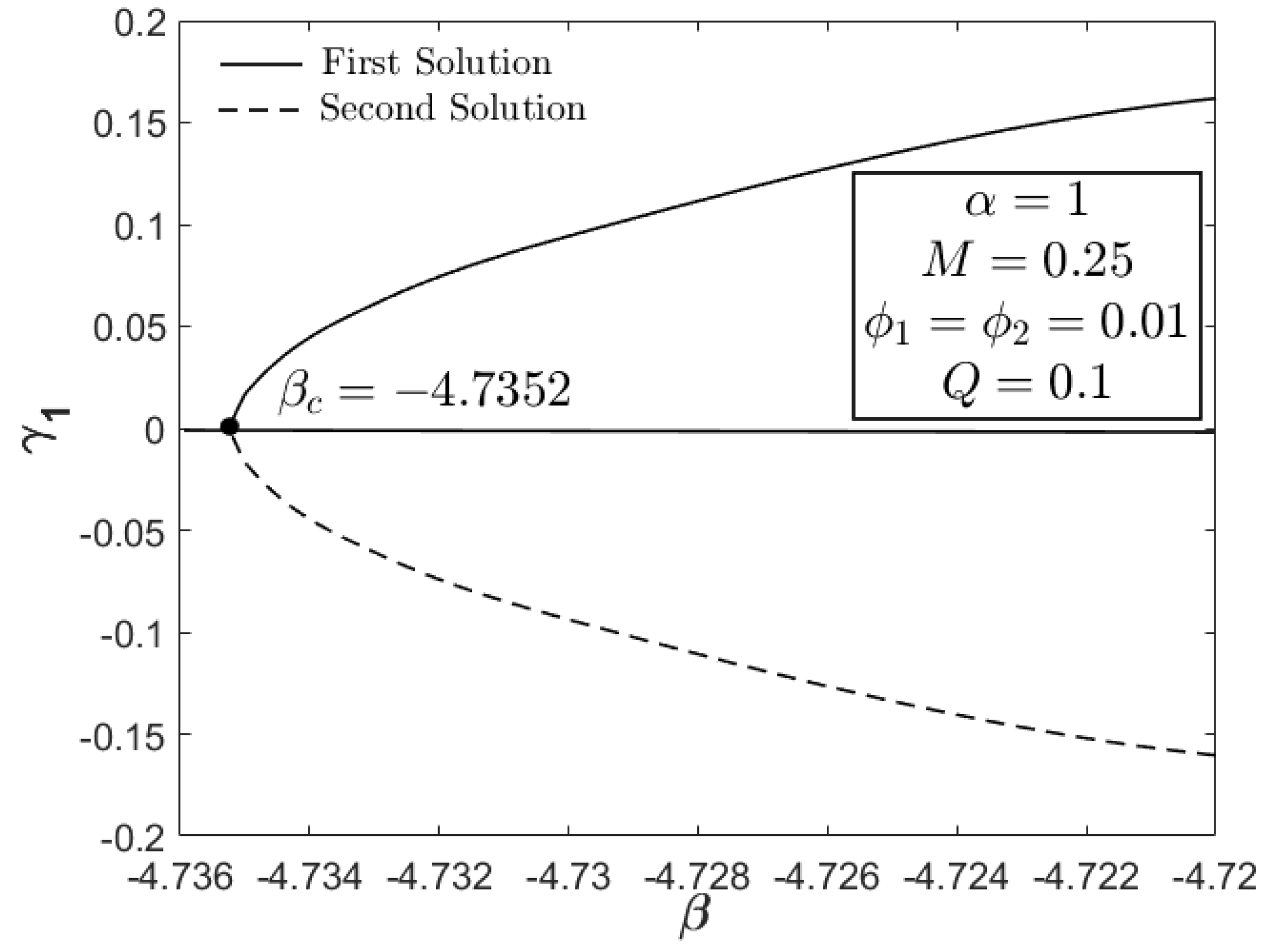
- Larger values of the magnetic and acceleration parameters contribute to an expansion of the domain of the solutions, where they are terminated at certain points of the unsteadiness deceleration parameter.
- The heat generation parameter is not a developing factor in the flow and thermal progress of Fe3O4–CoFe2O4/H2O for the USSP flow case.
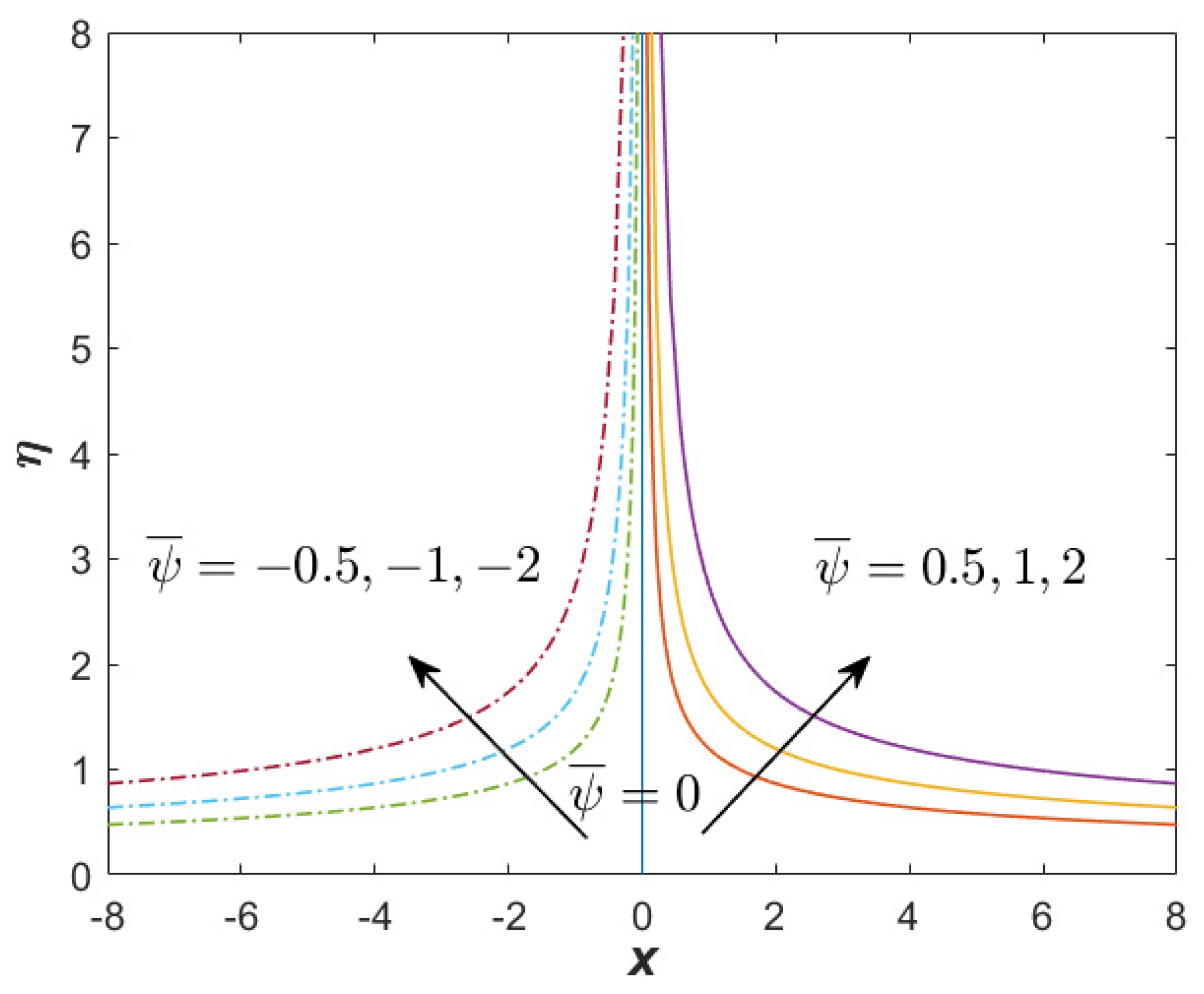
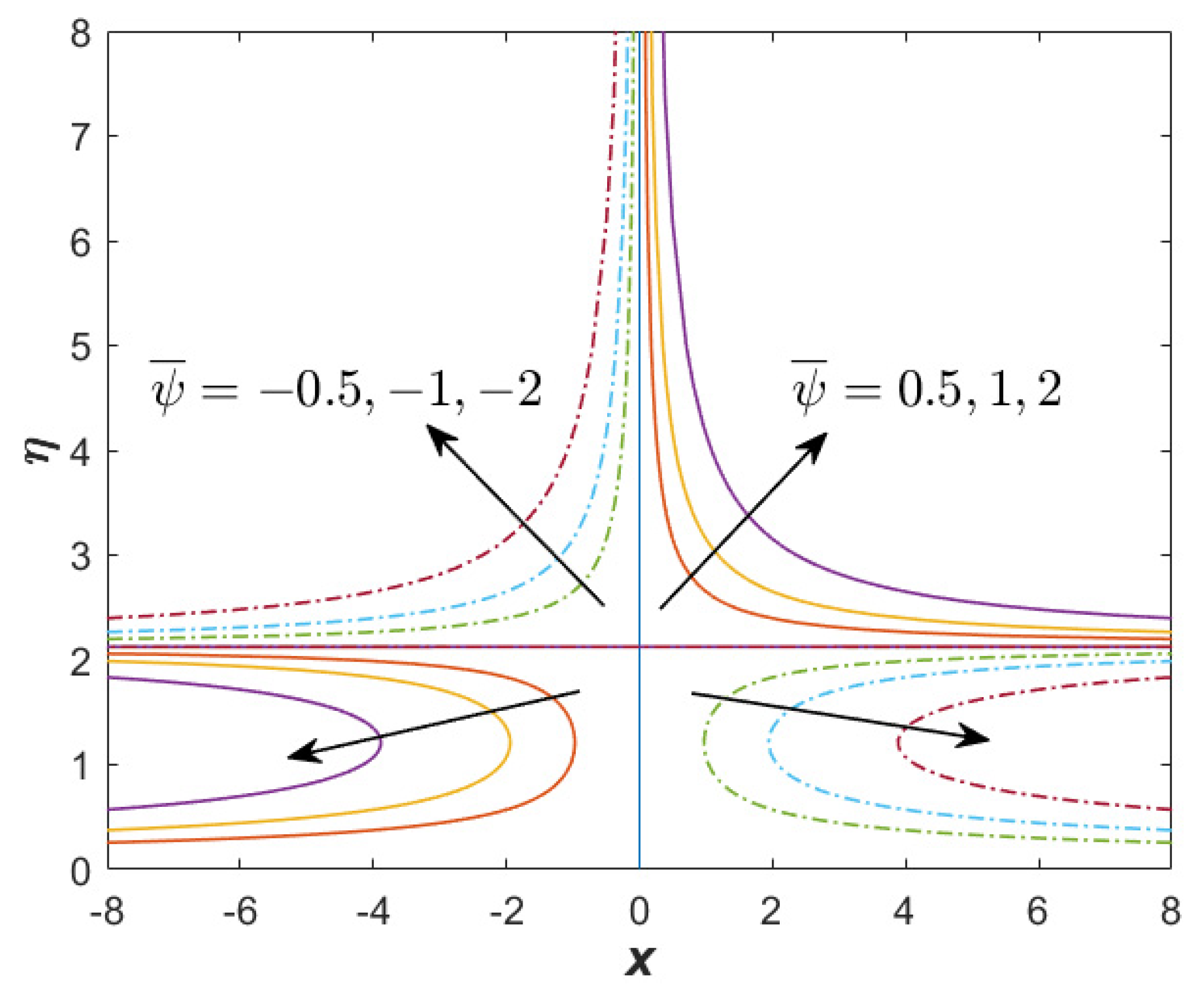
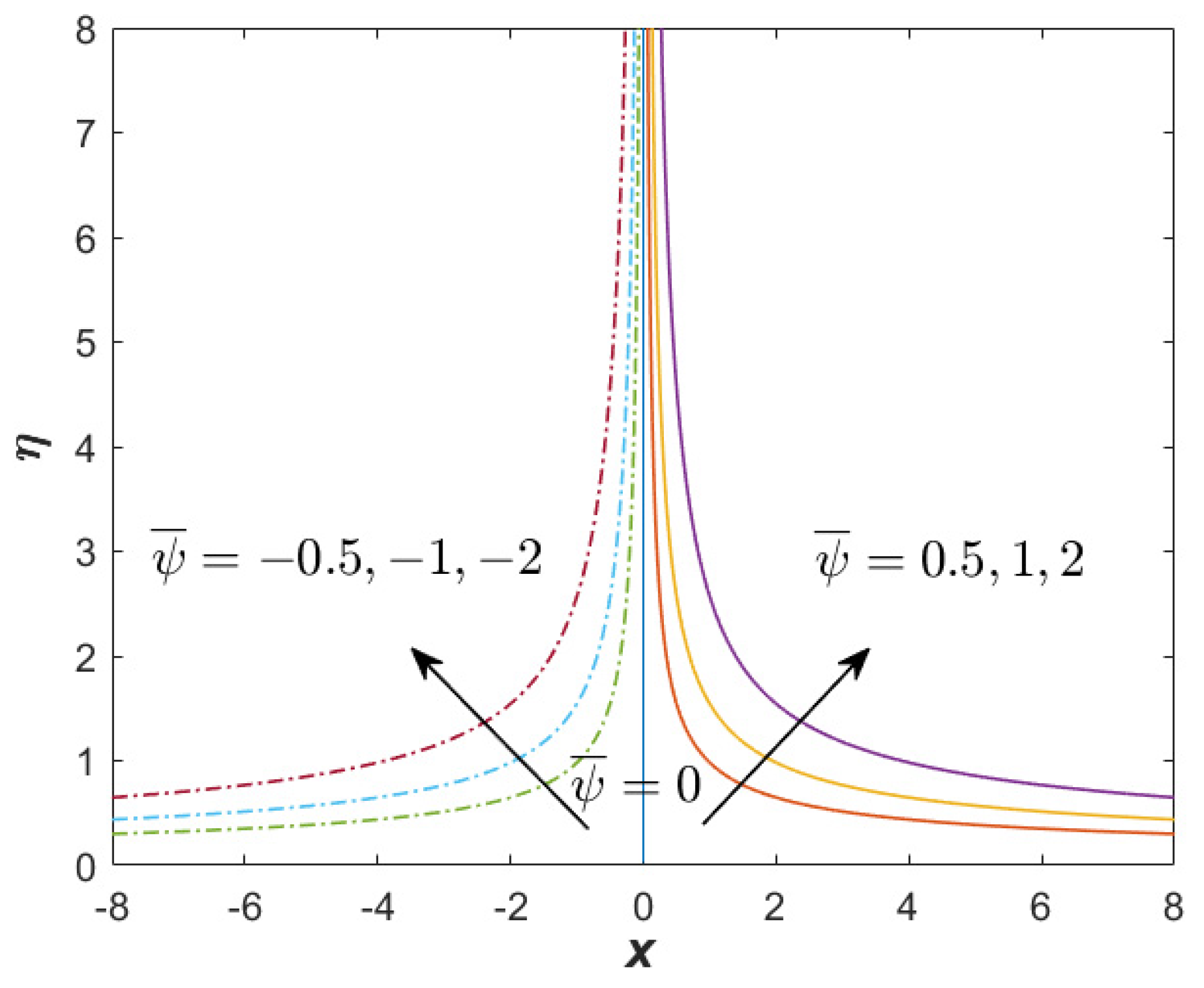
- Streamlines were presented to show the flow pattern, whereby the second solutions were split into two regions, while the first solution presented normal stagnation point flow.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tlili, I.; Mustafa, M.T.; Kumar, K.A.; Sandeep, N. Effect of asymmetrical heat rise/fall on the film flow of magnetohydrodynamic hybrid ferrofluid. Sci. Rep. 2020, 10, 6677. [Google Scholar] [CrossRef] [PubMed]
- Anuar, N.S.; Bachok, N.; Pop, I. Influence of MHD Hybrid Ferrofluid Flow on Exponentially Stretching/Shrinking Surface with Heat Source/Sink under Stagnation Point Region. Mathematics 2021, 9, 2932. [Google Scholar] [CrossRef]
- Saranya, S.; Al-Mdallal, Q.M.; Javed, S. Shifted legendre collocation method for the solution of unsteady viscous-ohmic dissipative hybrid ferrofluid flow over a cylinder. Nanomaterials 2021, 11, 1512. [Google Scholar] [CrossRef] [PubMed]
- Waini, I.; Khashi’ie, N.S.; Kasim, A.R.M.; Zainal, N.A.; Hamzah, K.B.; Arifin, N.M.; Pop, I. Unsteady Magnetohydrodynamics (MHD) Flow of Hybrid Ferrofluid Due to a Rotating Disk. Mathematics 2022, 10, 1658. [Google Scholar] [CrossRef]
- Hamid, R.A.; Nazar, R.; Naganthran, K.; Pop, I. Dusty ferrofluid transport phenomena towards a non-isothermal moving surface with viscous dissipation. Chin. J. Phys. 2022, 75, 139–151. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Camille Issa. Effects of heat generation/absorption and thermophoresis on hydromagnetic flow with heat and mass transfer over a flat surface. Int. J. Numer. Methods Heat Fluid Flow 2000, 10, 432–449. [Google Scholar] [CrossRef]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. Stability analysis of unsteady MHD rear stagnation point flow of hybrid nanofluid. Mathematics 2021, 9, 2428. [Google Scholar] [CrossRef]
- Elbashbeshy, E.M.; Asker, H.G.; Nagy, B. The effects of heat generation absorption on boundary layer flow of a nanofluid containing gyrotactic microorganisms over an inclined stretching cylinder. Ain Shams Eng. J. 2022, 13, 101690. [Google Scholar] [CrossRef]
- Khan, M.R.; Mao, S.; Deebani, W.; Elsiddieg, A.M. Numerical analysis of heat transfer and friction drag relating to the effect of Joule heating, viscous dissipation and heat generation/absorption in aligned MHD slip flow of a nanofluid. Int. Comm. Heat Mass Transf. 2022, 131, 105843. [Google Scholar] [CrossRef]
- Eid, M.R.; Nafe, M.A. Thermal conductivity variation and heat generation effects on magneto-hybrid nanofluid flow in a porous medium with slip condition. Waves Random Complex Media 2022, 32, 1103–1127. [Google Scholar] [CrossRef]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. Heat generation/absorption effect on MHD flow of hybrid nanofluid over bidirectional exponential stretching/shrinking sheet. Chin. J. Phys. 2021, 69, 118–133. [Google Scholar] [CrossRef]
- Wahid, N.S.; Arifin, N.M.; Khashi’ie, N.S.; Pop, I. Hybrid nanofluid slip flow over an exponentially stretching/shrinking permeable sheet with heat generation. Mathematics 2020, 9, 30. [Google Scholar] [CrossRef]
- Bakar, S.A.; Wahid, N.S.; Arifin, N.M.; Khashi’ie, N.S. The flow of hybrid nanofluid past a permeable shrinking sheet in a Darcy–Forchheimer porous medium with second-order velocity slip. Waves Random Complex Media 2022, 1–18. [Google Scholar] [CrossRef]
- Ali, U.; Malik, M.Y.; Alderremy, A.A.; Aly, S.; Rehman, K.U. A generalized findings on thermal radiation and heat generation/absorption in nanofluid flow regime. Phys. A Stat. Mech. Appl. 2020, 553, 124026. [Google Scholar] [CrossRef]
- Hafeez, A.; Khan, M. Flow of Oldroyd-B fluid caused by a rotating disk featuring the Cattaneo-Christov theory with heat generation/absorption. Int. Comm. Heat Mass Transf. 2021, 123, 105179. [Google Scholar] [CrossRef]
- Zaimi, K.; Ishak, A.; Pop, I. Unsteady flow due to a contracting cylinder in a nanofluid using Buongiorno’s model. Int. J. Heat Mass Transf. 2014, 68, 509–513. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Unsteady flow and heat transfer past a stretching/shrinking sheet in a hybrid nanofluid. Int. J. Heat Mass Transf. 2019, 136, 288–297. [Google Scholar] [CrossRef]
- Wang, C.Y. Liquid film on an unsteady stretching sheet. Q. Appl. Math. 1990, 48, 601–610. [Google Scholar] [CrossRef]
- Bhandari, A. Unsteady flow and heat transfer of the ferrofluid between two shrinking disks under the influence of magnetic field. Pramana 2021, 95, 1–12. [Google Scholar] [CrossRef]
- Islam, S.; Zubair, M.; Tassaddiq, A.; Shah, Z.; Alrabaiah, H.; Kumam, P.; Khan, W. Unsteady ferrofluid slip flow in the presence of magnetic dipole with convective boundary conditions. IEEE Access 2020, 8, 138551–138562. [Google Scholar] [CrossRef]
- Hussain, S.; Ahmed, S.E. Unsteady MHD forced convection over a backward facing step including a rotating cylinder utilizing Fe3O4-water ferrofluid. J. Magn. Mag. Mater. 2019, 484, 356–366. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Arifin, N.M.; Pop, I. Unsteady axisymmetric flow and heat transfer of a hybrid nanofluid over a permeable stretching/shrinking disc. Int. J. Numer. Methods Heat Fluid Flow 2021, 31, 2005–2021. [Google Scholar] [CrossRef]
- Khan, M.S.; Mei, S.; Fernandez-Gamiz, U.; Noeiaghdam, S.; Shah, S.A.; Khan, A. Numerical analysis of unsteady hybrid nanofluid flow comprising CNTs-ferrousoxide/water with variable magnetic field. Nanomaterials 2022, 12, 180. [Google Scholar] [CrossRef]
- Mabood, F.; Ashwinkumar, G.P.; Sandeep, N. Simultaneous results for unsteady flow of MHD hybrid nanoliquid above a flat/slendering surface. J. Therm. Anal. Calorim. 2021, 146, 227–239. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Arifin, N.M.; Pop, I. Unsteady axisymmetric radiative Cu-Al2O3/H2O flow over a radially stretching/shrinking surface. Chin. J. Phys. 2022, 78, 169–179. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Waini, I.; Arifin, N.M.; Pop, I. Unsteady squeezing flow of Cu-Al2O3/water hybrid nanofluid in a horizontal channel with magnetic field. Sci. Rep. 2021, 11, 14128. [Google Scholar] [CrossRef]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. Unsteady MHD hybrid nanofluid flow towards a horizontal cylinder. Int. Comm. Heat Mass Transf. 2022, 134, 106020. [Google Scholar] [CrossRef]
- Kumbhakar, B.; Nandi, S. Unsteady MHD radiative-dissipative flow of Cu-Al2O3/H2O hybrid nanofluid past a stretching sheet with slip and convective conditions: A regression analysis. Math. Comput. Simul. 2022, 194, 563–587. [Google Scholar] [CrossRef]
- Lin, J.; Yang, H. A review on the flow instability of nanofluids. Appl. Math. Mech. 2019, 40, 1227–1238. [Google Scholar] [CrossRef]
- Nabavi, M. Steady and unsteady flow analysis in microdiffusers and micropumps: A critical review. Microfluid. Nanofluid. 2019, 7, 599–619. [Google Scholar] [CrossRef]
- Hiemenz, K. Die Grenzschicht an einem in den gleichförmigen Flüssigkeitsstrom eingetauchten geraden Kreiszylinder. Dingler’s Polytech. J. 1911, 326, 321–324. [Google Scholar]
- Homann, F. Der Einfluss grosser Zahigkeit bei der Stromung um den Zylinder und um die Kugel. Z. Angew. Math. Mech. 1936, 16, 153–164. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I.; Baleanu, D.; Nisar, K.S. Dual similarity solutions of MHD stagnation point flow of Casson fluid with effect of thermal radiation and viscous dissipation: Stability analysis. Sci. Rep. 2020, 10, 15405. [Google Scholar] [CrossRef]
- Mahapatra, T.R.; Gupta, A.S. Heat transfer in stagnation-point flow towards a stretching sheet. Heat Mass Transf. 2002, 38, 517–521. [Google Scholar] [CrossRef]
- Mahapatra, T.R.; Gupta, A.S. Stagnation-point flow towards a stretching surface. Can. J. Chem. Eng. 2003, 81, 258–263. [Google Scholar] [CrossRef]
- Wang, C.Y. Stagnation flow towards a shrinking sheet. Int. J. Non. Lin. Mech. 2008, 43, 377–382. [Google Scholar] [CrossRef]
- Lok, Y.Y.; Ishak, A.; Pop, I. MHD stagnation-point flow towards a shrinking sheet. Int. J. Numer. Methods Heat Fluid Flow 2011, 21, 61–72. [Google Scholar] [CrossRef]
- Ishak, A.; Lok, Y.Y.; Pop, I. Stagnation-point flow over a shrinking sheet in a micropolar fluid. Chem. Eng. Comm. 2010, 197, 1417–1427. [Google Scholar] [CrossRef]
- Jusoh, R.; Nazar, R.; Pop, I. Dual solutions of magnetohydrodynamic stagnation point flow and heat transfer of viscoelastic nanofluid over a permeable stretching/shrinking sheet with thermal radiation. J. Phys. Conf. Ser. 2017, 890, 12063. [Google Scholar] [CrossRef]
- Pal, D.; Mandal, G. Magnetohydrodynamic stagnation-point flow of Sisko nanofluid over a stretching sheet with suction. Propuls. Power Res. 2020, 9, 408–422. [Google Scholar] [CrossRef]
- Abbasi, A.; Farooq, W.; Riaz, I. Stagnation point flow of Maxwell nanofluid containing gyrotactic micro-organism impinging obliquely on a convective surface. Heat Transf. 2020, 49, 2977–2999. [Google Scholar] [CrossRef]
- Ghasemi, S.E.; Hatami, M. Solar radiation effects on MHD stagnation point flow and heat transfer of a nanofluid over a stretching sheet. Case Stud. Therm. Eng. 2021, 25, 100898. [Google Scholar] [CrossRef]
- Dholey, S. Magnetohydrodynamic Unsteady Separated Stagnation-Point Flow of a Viscous Fluid over a Moving Plate. Z. Für Angew. Math. Mech. 2016, 96, 707–720. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Wahid, N.S.; Arifin, N.M.; Pop, I. Magnetohydrodynamics Unsteady Separated Stagnation-point (USSP) Flow of a Hybrid Nanofluid on a Moving Plate. Z. Für Angew. Math. Mech. 2022, 102, e202100410. [Google Scholar] [CrossRef]
- Takabi, B.; Salehi, S. Augmentation of the Heat Transfer Performance of a Sinusoidal Corrugated Enclosure by Employing Hybrid Nanofluid. Adv. Mech. Eng. 2015, 6, 147059. [Google Scholar] [CrossRef]
- Roşca, N.C.; Roşca, A.V.; Pop, I. Unsteady Separated Stagnation-Point Flow and Heat Transfer Past a Stretching/Shrinking Sheet in a Copper-Water Nanofluid. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 2588–2605. [Google Scholar] [CrossRef]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. Magnetic Impact on the Unsteady Separated Stagnation-Point Flow of Hybrid Nanofluid with Viscous Dissipation and Joule Heating. Mathematics 2022, 10, 2356. [Google Scholar] [CrossRef]
- Merkin, J.H. On dual solutions occurring in mixed convection in a porous medium. J. Eng. Math. 1986, 20, 171–179. [Google Scholar] [CrossRef]
- Weidman, P.D.; Kubitschek, D.G.; Davis, A.M.J. The effect of transpiration on self-similar boundary layer flow over moving surfaces. Int. J. Eng. Sci. 2006, 44, 730–737. [Google Scholar] [CrossRef]
- Harris, S.D.; Ingham, D.B.; Pop, I. Mixed convection boundary-layer flow near the stagnation point on a vertical surface in a porous medium: Brinkman model with slip. Transp. Porous Media. 2009, 77, 267–285. [Google Scholar] [CrossRef]

| Properties | Water | Magnetite | Cobalt Ferrite |
|---|---|---|---|
| 997.1 | 5180 | 4908 | |
| 4179 | 670 | 700 | |
| 0.613 | 9.8 | 3.6 | |
| 0.05 | 0.74 × 106 | 1.1 × 107 | |
| 6.2 | - | - |
| Properties | Correlations |
|---|---|
| Thermal conductivity | |
| Electrical conductivity | |
| Heat capacity | |
| Density | |
| Dynamic viscosity |
| First Solution | Second Solution | |||||
|---|---|---|---|---|---|---|
| Present Study | [44] | [43] | Present Study | [44] | [43] | |
| 0 | 0.923204 | 0.923204 (0%) | 0.9232 (0.0004%) | −0.985139 | −0.985134 (0.0005%) | −0.9851 (0.0005%) |
| 0.25 | 0.954505 | 0.954505 (0%) | 0.9545 (0.0005%) | −0.961278 | −0.961278 (0%) | −0.9613 (0.0023%) |
| 0.50 | 1.043478 | 1.043478 (0%) | 1.0435 (0.0021%) | −0.851369 | −0.851369 (0%) | −0.8514 (0.0036%) |
| 0.88 | 1.262495 | 1.262495 (0%) | 1.2625 (0.0004%) | 0.038797 | 0.038797 (0%) | 0.0388 (0.0077%) |
| 1 | 1.346660 | 1.346660 (0%) | 1.3467 (0.0030%) | 0.499050 | 0.499050 (0%) | 0.4991 (0.0100%) |
| First Solution | Second Solution | |||||
|---|---|---|---|---|---|---|
| Present Study | [44] | [43] | Present Study | [44] | [43] | |
| 0 | 1.675545 | 1.675545 (0%) | - | 0.502540 | 0.502540 (0%) | - |
| 0.25 | 1.680398 | 1.680398 (0%) | - | 0.425526 | 0.425525 (0.0002%) | - |
| 0.50 | 1.693818 | 1.693818 (0%) | - | 0.188880 | 0.188880 (0%) | - |
| 0.88 | 1.724685 | 1.724685(0%) | - | 0.010937 | 0.010937 (0%) | - |
| 1 | 1.735799 | 1.735799 (0%) | - | 0.206980 | 0.206980 (0%) | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khashi’ie, N.S.; Waini, I.; Zainal, N.A.; Hamzah, K.B.; Kasim, A.R.M.; Arifin, N.M.; Pop, I. Thermal Progress of Unsteady Separated Stagnation Point Flow with Magnetic Field and Heat Generation in Hybrid Ferrofluid. Nanomaterials 2022, 12, 3205. https://doi.org/10.3390/nano12183205
Khashi’ie NS, Waini I, Zainal NA, Hamzah KB, Kasim ARM, Arifin NM, Pop I. Thermal Progress of Unsteady Separated Stagnation Point Flow with Magnetic Field and Heat Generation in Hybrid Ferrofluid. Nanomaterials. 2022; 12(18):3205. https://doi.org/10.3390/nano12183205
Chicago/Turabian StyleKhashi’ie, Najiyah Safwa, Iskandar Waini, Nurul Amira Zainal, Khairum Bin Hamzah, Abdul Rahman Mohd Kasim, Norihan Md Arifin, and Ioan Pop. 2022. "Thermal Progress of Unsteady Separated Stagnation Point Flow with Magnetic Field and Heat Generation in Hybrid Ferrofluid" Nanomaterials 12, no. 18: 3205. https://doi.org/10.3390/nano12183205
APA StyleKhashi’ie, N. S., Waini, I., Zainal, N. A., Hamzah, K. B., Kasim, A. R. M., Arifin, N. M., & Pop, I. (2022). Thermal Progress of Unsteady Separated Stagnation Point Flow with Magnetic Field and Heat Generation in Hybrid Ferrofluid. Nanomaterials, 12(18), 3205. https://doi.org/10.3390/nano12183205









