Effect of Impurity Scattering on Percolation of Bosonic Islands and Superconductivity in Fe Implanted NbN Thin Films
Abstract
1. Introduction
2. Materials and Methods
2.1. Growth and Structure
2.2. Magnetotransport
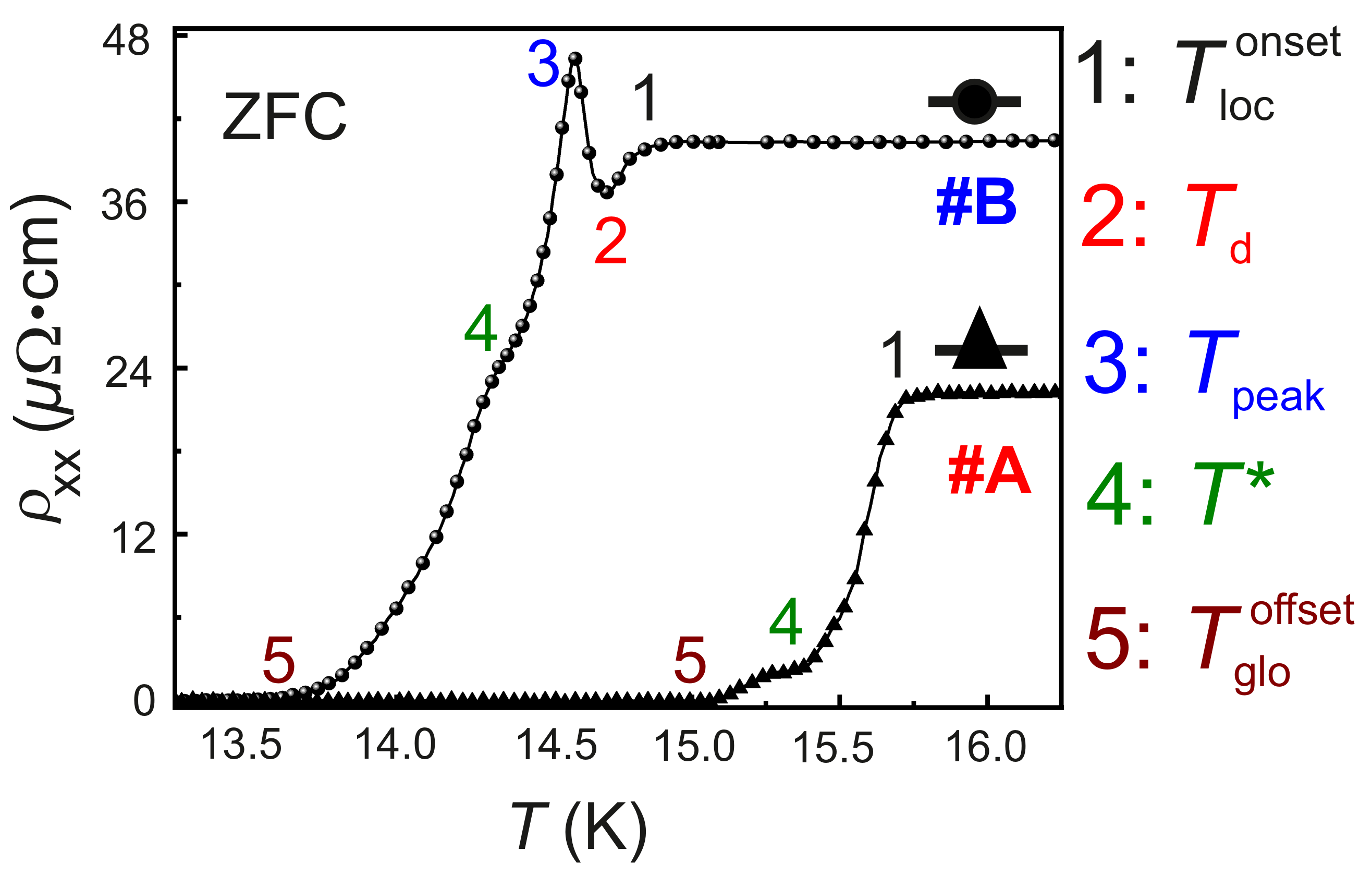
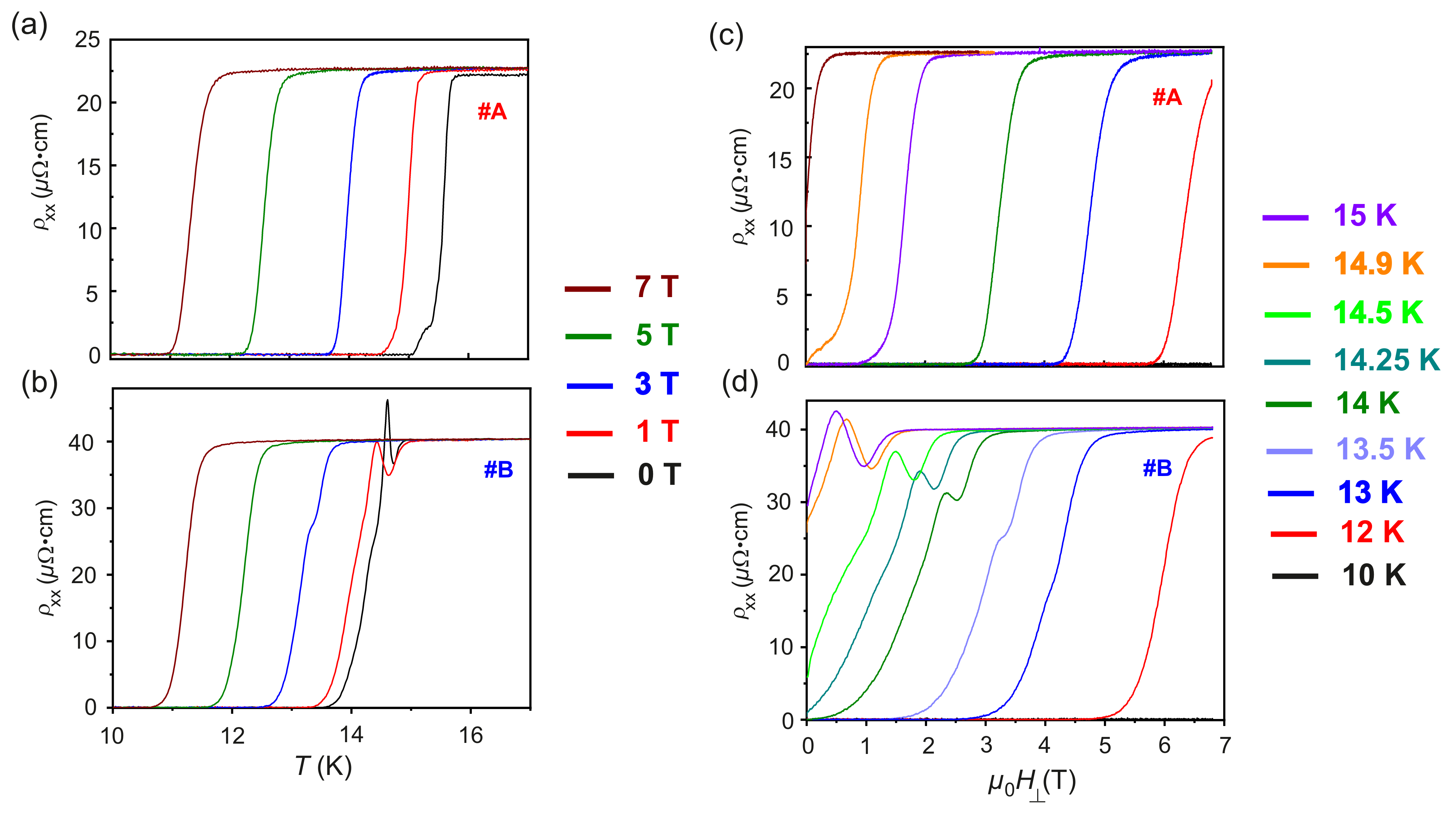
3. Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| YSR | Yu-Shiba-Rusinov |
| FFLO | Fulde-Ferrell-Larkin-Ovchinnikov |
| S | Superconductors |
| F | Ferromagnets |
| BKT | Berezinskii-Kosterlitz-Thouless |
| UHV | Ultrahigh vacuum |
| sccm | Standard cubic centimeters per minute |
| SRIM | Stoppage and range of ions in matter |
| LIA | Lock-in amplifier |
| SMU | Source-measure unit |
| FC | Field cooled |
| ZFC | Zero field cool |
| BI | Bosonic islands |
| HyQUID | Hybrid quantum interference device |
References
- Balatsky, A.V.; Vekhter, I.; Zhu, J.X. Impurity-induced states in conventional and unconventional superconductors. Rev. Mod. Phys. 2006, 78, 373–433. [Google Scholar] [CrossRef]
- Möckli, D.; Haim, M.; Khodas, M. Magnetic impurities in thin films and 2D Ising superconductors. J. Appl. Phys. 2020, 128, 053903. [Google Scholar] [CrossRef]
- Gor’kov, L.P. Theory of Superconducting Alloys. In Superconductivity: Conventional and Unconventional Superconductors; Springer: Berlin/Heidelberg, Germany, 2008; pp. 201–224. [Google Scholar] [CrossRef]
- Anderson, P.W. Theory of dirty superconductors. J. Phys. Chem. Solids 1959, 11, 26–30. [Google Scholar] [CrossRef]
- Abrikosov, A.A.; Gor’kov, L.P. Contribution to the Theory of Superconducting Alloys with Paramagnetic Impurities. Zhur. Eksptl’. Teoret. Fiz. 1960, 39. [Google Scholar]
- Abrikosov, A.A. Magnetic Impurities in Nonmagnetic Metals. Sov. Phys. Usp. 1969, 12, 168–181. [Google Scholar] [CrossRef]
- Zittartz, J.; Müller-Hartmann, E. Theory of magnetic impurities in superconductors. I. Z. Phys. A Hadrons Nucl. 1970, 232, 11–31. [Google Scholar] [CrossRef]
- Müller-Hartmann, E.; Zittartz, J. Theory of magnetic impurities in superconductors. II. Z. Phys. A Hadrons Nucl. 1970, 234, 58–69. [Google Scholar] [CrossRef]
- Zittartz, J. Theory of magnetic impurities in superconductors. III. Z. Phys. A Hadrons Nucl. 1970, 237, 419–426. [Google Scholar] [CrossRef]
- Woolf, M.A.; Reif, F. Effect of Magnetic Impurities on the Density of States of Superconductors. Phys. Rev. 1965, 137, A557–A564. [Google Scholar] [CrossRef]
- Skalski, S.; Betbeder-Matibet, O.; Weiss, P.R. Properties of Superconducting Alloys Containing Paramagnetic Impurities. Phys. Rev. 1964, 136, A1500–A1518. [Google Scholar] [CrossRef]
- Fulde, P.; Maki, K. Theory of Superconductors Containing Magnetic Impurities. Phys. Rev. 1966, 141, 275–280. [Google Scholar] [CrossRef]
- Fulde, P. High field superconductivity in thin films. Adv. Phys. 1973, 22, 667–719. [Google Scholar] [CrossRef]
- Maki, K. Anomalous Scattering by Magnetic Impurities in Superconductors. Phys. Rev. 1967, 153, 428–434. [Google Scholar] [CrossRef]
- Cooper, L.N. Bound Electron Pairs in a Degenerate Fermi Gas. Phys. Rev. 1956, 104, 1189–1190. [Google Scholar] [CrossRef]
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Microscopic Theory of Superconductivity. Phys. Rev. 1957, 106, 162–164. [Google Scholar] [CrossRef]
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Theory of Superconductivity. Phys. Rev. 1957, 108, 1175–1204. [Google Scholar] [CrossRef]
- Pint, W.; Schachinger, E. Superconducting alloys with paramagnetic impurities I: Theory of the upper critical field. Phys. C Supercond. 1989, 159, 33–42. [Google Scholar] [CrossRef]
- Heinrich, B.W.; Pascual, J.I.; Franke, K.J. Single magnetic adsorbates on s-wave superconductors. Prog. Surf. Sci. 2018, 93, 1–19. [Google Scholar] [CrossRef]
- Linder, J.; Robinson, J.W.A. Superconducting spintronics. Nat. Phys. 2015, 11, 307–315. [Google Scholar] [CrossRef]
- Müller, M.; Liensberger, L.; Flacke, L.; Huebl, H.; Kamra, A.; Belzig, W.; Gross, R.; Weiler, M.; Althammer, M. Temperature-Dependent Spin Transport and Current-Induced Torques in Superconductor-Ferromagnet Heterostructures. Phys. Rev. Lett. 2021, 126, 087201. [Google Scholar] [CrossRef]
- Fulde, P.; Ferrell, R.A. Superconductivity in a Strong Spin-Exchange Field. Phys. Rev. 1964, 135, A550–A563. [Google Scholar] [CrossRef]
- Larkin, A.I.; Ovchinnikov, Y.N. Nonuniform state of superconductors. Zh. Eksperim. Teor. Fiz. 1964, 47, 762. [Google Scholar]
- Lenk, D.; Hemmida, M.; Morari, R.; Zdravkov, V.I.; Ullrich, A.; Müller, C.; Sidorenko, A.S.; Horn, S.; Tagirov, L.R.; Loidl, A.; et al. Influence of the FFLO-like state on the upper critical field of a superconductor/ferromagnet bilayer: Angular and temperature dependence. Phys. Rev. B 2016, 93, 184501. [Google Scholar] [CrossRef]
- Buzdin, A.I. Proximity effects in superconductor-ferromagnet heterostructures. Rev. Mod. Phys. 2005, 77, 935–976. [Google Scholar] [CrossRef]
- Chockalingam, S.P.; Chand, M.; Jesudasan, J.; Tripathi, V.; Raychaudhuri, P. Superconducting properties and Hall effect of epitaxial NbN thin films. Phys. Rev. B 2008, 77, 214503. [Google Scholar] [CrossRef]
- Koushik, R.; Kumar, S.; Amin, K.R.; Mondal, M.; Jesudasan, J.; Bid, A.; Raychaudhuri, P.; Ghosh, A. Correlated Conductance Fluctuations Close to the Berezinskii-Kosterlitz-Thouless Transition in Ultrathin NbN Films. Phys. Rev. Lett. 2013, 111, 197001. [Google Scholar] [CrossRef]
- Ganguly, R.; Chaudhuri, D.; Raychaudhuri, P.; Benfatto, L. Slowing down of vortex motion at the Berezinskii-Kosterlitz-Thouless transition in ultrathin NbN films. Phys. Rev. B 2015, 91, 054514. [Google Scholar] [CrossRef]
- Chand, M.; Mishra, A.; Xiong, Y.M.; Kamlapure, A.; Chockalingam, S.P.; Jesudasan, J.; Bagwe, V.; Mondal, M.; Adams, P.W.; Tripathi, V.; et al. Temperature dependence of resistivity and Hall coefficient in strongly disordered NbN thin films. Phys. Rev. B 2009, 80, 134514. [Google Scholar] [CrossRef]
- Chand, M.; Saraswat, G.; Kamlapure, A.; Mondal, M.; Kumar, S.; Jesudasan, J.; Bagwe, V.; Benfatto, L.; Tripathi, V.; Raychaudhuri, P. Phase diagram of the strongly disordered s-wave superconductor NbN close to the metal-insulator transition. Phys. Rev. B 2012, 85, 014508. [Google Scholar] [CrossRef]
- Mondal, M.; Kumar, S.; Chand, M.; Kamlapure, A.; Saraswat, G.; Seibold, G.; Benfatto, L.; Raychaudhuri, P. Role of the Vortex-Core Energy on the Berezinskii-Kosterlitz-Thouless Transition in Thin Films of NbN. Phys. Rev. Lett. 2011, 107, 217003. [Google Scholar] [CrossRef] [PubMed]
- Chockalingam, S.P.; Chand, M.; Kamlapure, A.; Jesudasan, J.; Mishra, A.; Tripathi, V.; Raychaudhuri, P. Tunneling studies in a homogeneously disordered s-wave superconductor: NbN. Phys. Rev. B 2009, 79, 094509. [Google Scholar] [CrossRef]
- Destraz, D.; Ilin, K.; Siegel, M.; Schilling, A.; Chang, J. Superconducting fluctuations in a thin NbN film probed by the Hall effect. Phys. Rev. B 2017, 95, 224501. [Google Scholar] [CrossRef]
- Nikzad, S.; Hoenk, M.; Jewell, A.D.; Hennessy, J.J.; Carver, A.G.; Jones, T.J.; Goodsall, T.M.; Hamden, E.T.; Suvarna, P.; Bulmer, J.; et al. Single Photon Counting UV Solar-Blind Detectors Using Silicon and III-Nitride Materials. Sensors 2016, 16, 927. [Google Scholar] [CrossRef]
- Polakovic, T.; Armstrong, W.; Karapetrov, G.; Meziani, Z.E.; Novosad, V. Unconventional Applications of Superconducting Nanowire Single Photon Detectors. Nanomaterials 2020, 10, 1198. [Google Scholar] [CrossRef]
- Blais, A.; Grimsmo, A.L.; Girvin, S.M.; Wallraff, A. Circuit quantum electrodynamics. Rev. Mod. Phys. 2021, 93, 025005. [Google Scholar] [CrossRef]
- Yong, J.; Lemberger, T.R.; Benfatto, L.; Ilin, K.; Siegel, M. Robustness of the Berezinskii-Kosterlitz-Thouless transition in ultrathin NbN films near the superconductor-insulator transition. Phys. Rev. B 2013, 87, 184505. [Google Scholar] [CrossRef]
- Mondal, M.; Chand, M.; Kamlapure, A.; Jesudasan, J.; Bagwe, V.C.; Kumar, S.; Saraswat, G.; Tripathi, V.; Raychaudhuri, P. Phase Diagram and Upper Critical Field of Homogeneously Disordered Epitaxial 3-Dimensional NbN Films. J Supercond. Nov. Magn. 2011, 24, 341–344. [Google Scholar] [CrossRef][Green Version]
- Sherman, D.; Pracht, U.S.; Gorshunov, B.; Poran, S.; Jesudasan, J.; Chand, M.; Raychaudhuri, P.; Swanson, M.; Trivedi, N.; Auerbach, A.; et al. The Higgs mode in disordered superconductors close to a quantum phase transition. Nat. Phys. 2015, 11, 188–192. [Google Scholar] [CrossRef]
- Tsuji, N.; Nomura, Y. Higgs-mode resonance in third harmonic generation in NbN superconductors: Multiband electron-phonon coupling, impurity scattering, and polarization-angle dependence. Phys. Rev. Res. 2020, 2, 043029. [Google Scholar] [CrossRef]
- Hochberg, Y.; Zhao, Y.; Zurek, K.M. Superconducting Detectors for Superlight Dark Matter. Phys. Rev. Lett. 2016, 116, 011301. [Google Scholar] [CrossRef] [PubMed]
- Krause, S.; Meledin, D.; Desmaris, V.; Pavolotsky, A.; Belitsky, V.; Rudziński, M.; Pippel, E. Epitaxial growth of ultra-thin NbN films on AlxGa1−xN buffer-layers. Supercond. Sci. Technol 2014, 27, 065009. [Google Scholar] [CrossRef][Green Version]
- Sam-Giao, D.; Pouget, S.; Bougerol, C.; Monroy, E.; Grimm, A.; Jebari, S.; Hofheinz, M.; Gérard, J.M.; Zwiller, V. High-quality NbN nanofilms on a GaN/AlN heterostructure. AIP Adv. 2014, 4, 107123. [Google Scholar] [CrossRef]
- Kobayashi, A.; Ueno, K.; Fujioka, H. Coherent epitaxial growth of superconducting NbN ultrathin films on AlN by sputtering. Appl. Phys. Express 2020, 13, 061006. [Google Scholar] [CrossRef]
- Kobayashi, A.; Ueno, K.; Fujioka, H. Autonomous growth of NbN nanostructures on atomically flat AlN surfaces. Appl. Phys. Lett. 2020, 117, 231601. [Google Scholar] [CrossRef]
- Yan, R.; Khalsa, G.; Vishwanath, S.; Han, Y.; Wright, J.; Rouvimov, S.; Katzer, D.S.; Nepal, N.; Downey, B.P.; Muller, D.A.; et al. GaN/NbN epitaxial semiconductor/superconductor heterostructures. Nature 2018, 555, 183–189. [Google Scholar] [CrossRef]
- Hwang, T.J.; Kim, D.H. Variation of superconducting transition temperature by proximity effect in NbN/FeN bilayers. Phys. C Supercond. 2017, 540, 16–19. [Google Scholar] [CrossRef]
- Jha, R.; Jyoti, J.; Awana, V.P.S. Impact of Gd Doping on Morphology and Superconductivity of NbN Sputtered Thin Films. J. Supercond. Nov. Magn. 2013, 26, 3069–3074. [Google Scholar] [CrossRef]
- Vorhauer, J.V. Influence of Fe Implantation on the Superconductivity of NbN. Ph.D. Thesis, Johannes Kepler University, Linz, Austria, 2021. [Google Scholar]
- Zhang, G.; Zeleznik, M.; Vanacken, J.; May, P.W.; Moshchalkov, V.V. Metal–Bosonic Insulator–Superconductor Transition in Boron-Doped Granular Diamond. Phys. Rev. Lett. 2013, 110, 077001. [Google Scholar] [CrossRef]
- Zhang, G.; Samuely, T.; Kačmarčík, J.; Ekimov, E.A.; Li, J.; Vanacken, J.; Szabó, P.; Huang, J.; Pereira, P.J.; Cerbu, D.; et al. Bosonic Anomalies in Boron-Doped Polycrystalline Diamond. Phys. Rev. Appl. 2016, 6, 064011. [Google Scholar] [CrossRef]
- Postolova, S.V.; Mironov, A.Y.; Baklanov, M.R.; Vinokur, V.M.; Baturina, T.I. Reentrant Resistive Behavior and Dimensional Crossover in Disordered Superconducting TiN Films. Sci. Rep. 2017, 7, 1718. [Google Scholar] [CrossRef]
- Sacépé, B.; Seidemann, J.; Ovadia, M.; Tamir, I.; Shahar, D.; Chapelier, C.; Strunk, C.; Piot, B.A. High-field termination of a Cooper-pair insulator. Phys. Rev. B 2015, 91, 220508. [Google Scholar] [CrossRef]
- Peng, Y.; Meng, J.; Mou, D.; He, J.; Zhao, L.; Wu, Y.; Liu, G.; Dong, X.; He, S.; Zhang, J.; et al. Disappearance of nodal gap across the insulator–superconductor transition in a copper-oxide superconductor. Nat. Commun. 2013, 4, 2459. [Google Scholar] [CrossRef]
- Takagi, H.; Batlogg, B.; Kao, H.L.; Kwo, J.; Cava, R.J.; Krajewski, J.J.; Peck, W.F. Systematic evolution of temperature-dependent resistivity in La2−xSrxCuO4. Phys. Rev. Lett. 1992, 69, 2975–2978. [Google Scholar] [CrossRef]
- Ono, S.; Ando, Y.; Murayama, T.; Balakirev, F.F.; Betts, J.B.; Boebinger, G.S. Metal-to-Insulator Crossover in the Low-Temperature Normal State of Bi2Sr2−xLaxCuO6+δ. Phys. Rev. Lett. 2000, 85, 638–641. [Google Scholar] [CrossRef]
- Semba, K.; Matsuda, A. Superconductor-to-Insulator Transition and Transport Properties of Underdoped YBa2Cu3Oy Crystals. Phys. Rev. Lett. 2001, 86, 496–499. [Google Scholar] [CrossRef] [PubMed]
- Komiya, S.; Chen, H.D.; Zhang, S.C.; Ando, Y. Magic Doping Fractions for High-Temperature Superconductors. Phys. Rev. Lett. 2005, 94, 207004. [Google Scholar] [CrossRef]
- Oh, S.; Crane, T.A.; Van Harlingen, D.J.; Eckstein, J.N. Doping Controlled Superconductor-Insulator Transition in Bi2Sr2−xLaxCaCu2O8+δ. Phys. Rev. Lett. 2006, 96, 107003. [Google Scholar] [CrossRef] [PubMed]
- Moshchalkov, V.V.; Vanacken, J.; Trappeniers, L. Phase diagram of high-Tc cuprates: Stripes, pseudogap, and effective dimensionality. Phys. Rev. B 2001, 64, 214504. [Google Scholar] [CrossRef]
- Daou, R.; Doiron-Leyraud, N.; LeBoeuf, D.; Li, S.Y.; Laliberté, F.; Cyr-Choinière, O.; Jo, Y.J.; Balicas, L.; Yan, J.Q.; Zhou, J.S.; et al. Linear temperature dependence of resistivity and change in the Fermi surface at the pseudogap critical point of a high-Tc superconductor. Nat. Phys. 2009, 5, 31–34. [Google Scholar] [CrossRef]
- Zaken, E.; Rosenbaum, R. Superconducting fluctuation conductivity in granular Al-Ge films above the metal-insulator transition. J. Phys. Condens. Matter 1994, 6, 9981–10000. [Google Scholar] [CrossRef]
- Vaglio, R.; Attanasio, C.; Maritato, L.; Ruosi, A. Explanation of the resistance-peak anomaly in nonhomogeneous superconductors. Phys. Rev. B 1993, 47, 15302–15303. [Google Scholar] [CrossRef]
- Lindqvist, P.; Nordström, A.; Rapp, O. New resistance anomaly in the superconducting fluctuation region of disordered Cu-Zr alloys with dilute magnetic impurities. Phys. Rev. Lett. 1990, 64, 2941–2944. [Google Scholar] [CrossRef]
- Nordström, A.; Rapp, O. Resistance-peak anomaly in metallic glasses: Dependence on currents and contact arrangement. Phys. Rev. B 1992, 45, 12577–12579. [Google Scholar] [CrossRef] [PubMed]
- Kalenkov, M.S.; Zaikin, A.D.; Kuzmin, L.S. Theory of a Large Thermoelectric Effect in Superconductors Doped with Magnetic Impurities. Phys. Rev. Lett. 2012, 109, 147004. [Google Scholar] [CrossRef]
- Shelly Connor, D.; Matrozova Ekaterina, A.; Petrashov Victor, T. Resolving thermoelectric “paradox” in superconductors. Sci. Adv. 2016, 2, e1501250. [Google Scholar] [CrossRef] [PubMed]
- Santos, F.L.N.; Perrin, V.; Jamet, F.M.C.; Civelli, M.; Simon, P.; Aguiar, M.C.O.; Miranda, E.; Rozenberg, M.J. Odd-frequency superconductivity in dilute magnetic superconductors. Phys. Rev. Res. 2020, 2, 033229. [Google Scholar] [CrossRef]
- Kornich, V.; Schlawin, F.; Sentef, M.A.; Trauzettel, B. Direct detection of odd-frequency superconductivity via time- and angle-resolved photoelectron fluctuation spectroscopy. Phys. Rev. Res. 2021, 3, L042034. [Google Scholar] [CrossRef]
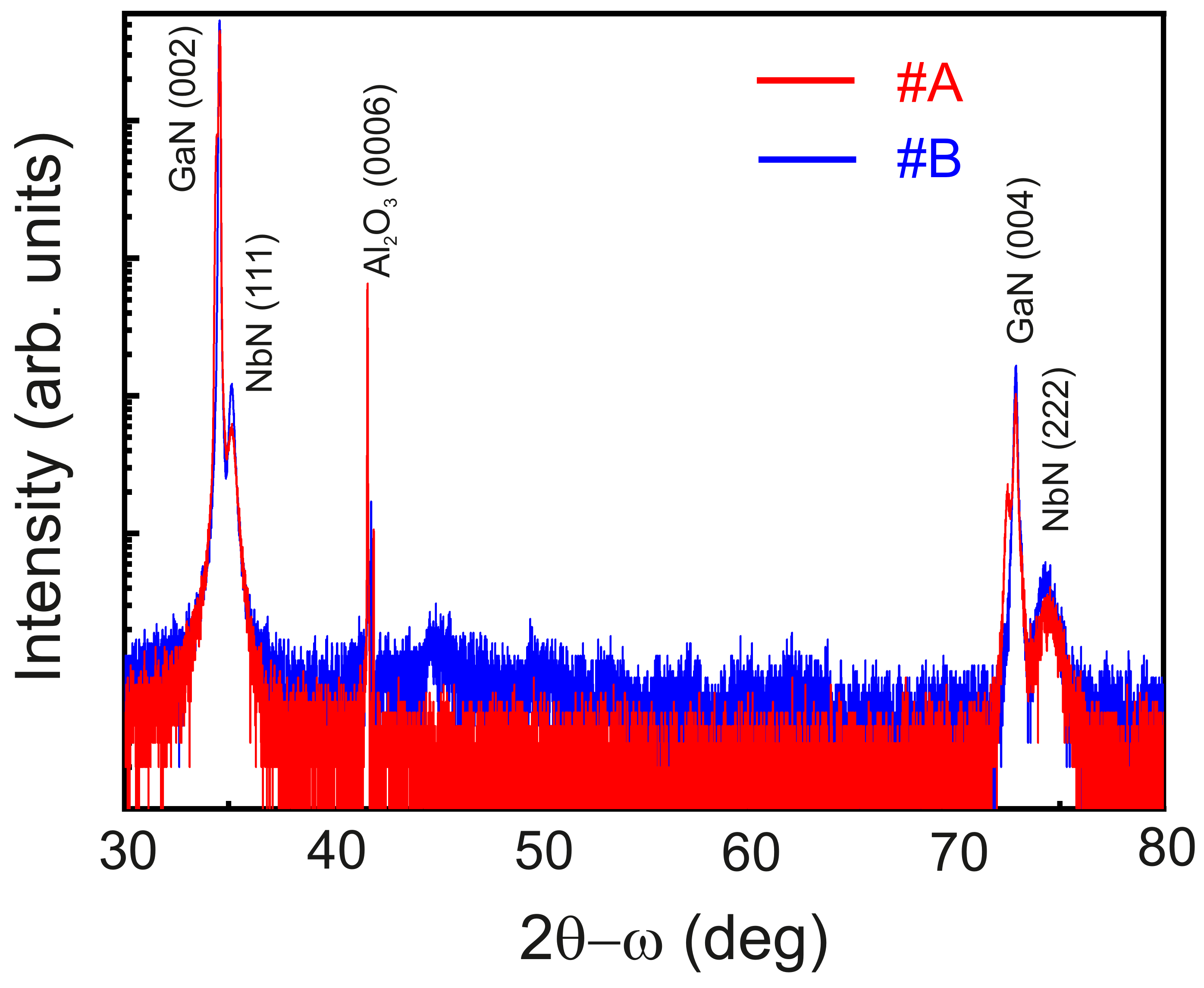



| Sample | Material | Template | Nominal (nm) | Ar:N2 Ratio | P (W) | Tsub (°C) | Implanted Ion | (keV) | Dose (at/cm3) |
|---|---|---|---|---|---|---|---|---|---|
| A | NbN | wz-GaN | 100 | 10:5 | 40 | 500 | - | - | - |
| B | Fe:NbN | wz-GaN | 100 | 10:5 | 40 | 500 | Fe | 35 |
| Sample | (K) | (K) | (K) | (K) | (K) | (K) |
|---|---|---|---|---|---|---|
| A | 15.72 | - | - | 15.27 | 15.05 | 0.67 |
| B | 15.1 | 14.71 | 14.60 | 14.305 | 13.5 | 1.6 |
| (T) | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0 | - | - | 0.0653 | 0.0653 | 0.67 | 0.67 | 1.6 | 1.6 |
| 1 | - | - | 0.1376 | 0.1337 | 0.72 | 0.94 | 1.64 | 1.71 |
| 2 | - | - | 0.0858 | 0.1514 | - | - | 1.5 | 1.34 |
| 3 | - | - | - | 0.1392 | 0.74 | 0.94 | 1.25 | 1.54 |
| 4 | - | - | - | 0.0841 | - | - | 1.23 | 1.25 |
| 5 | - | - | - | - | 0.8 | 0.96 | 1.12 | 1.37 |
| 6 | - | - | - | - | - | - | 1.31 | 1.05 |
| 7 | - | - | - | - | 0.78 | 0.91 | 0.96 | 1.18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adhikari, R.; Faina, B.; Ney, V.; Vorhauer, J.; Sterrer, A.; Ney, A.; Bonanni, A. Effect of Impurity Scattering on Percolation of Bosonic Islands and Superconductivity in Fe Implanted NbN Thin Films. Nanomaterials 2022, 12, 3105. https://doi.org/10.3390/nano12183105
Adhikari R, Faina B, Ney V, Vorhauer J, Sterrer A, Ney A, Bonanni A. Effect of Impurity Scattering on Percolation of Bosonic Islands and Superconductivity in Fe Implanted NbN Thin Films. Nanomaterials. 2022; 12(18):3105. https://doi.org/10.3390/nano12183105
Chicago/Turabian StyleAdhikari, Rajdeep, Bogdan Faina, Verena Ney, Julia Vorhauer, Antonia Sterrer, Andreas Ney, and Alberta Bonanni. 2022. "Effect of Impurity Scattering on Percolation of Bosonic Islands and Superconductivity in Fe Implanted NbN Thin Films" Nanomaterials 12, no. 18: 3105. https://doi.org/10.3390/nano12183105
APA StyleAdhikari, R., Faina, B., Ney, V., Vorhauer, J., Sterrer, A., Ney, A., & Bonanni, A. (2022). Effect of Impurity Scattering on Percolation of Bosonic Islands and Superconductivity in Fe Implanted NbN Thin Films. Nanomaterials, 12(18), 3105. https://doi.org/10.3390/nano12183105





