Pinning Potential of the Self-Assembled Artificial Pinning Centers in Nanostructured YBa2Cu3O7−x Superconducting Films
Abstract
:1. Introduction
2. Materials and Methods
3. Results
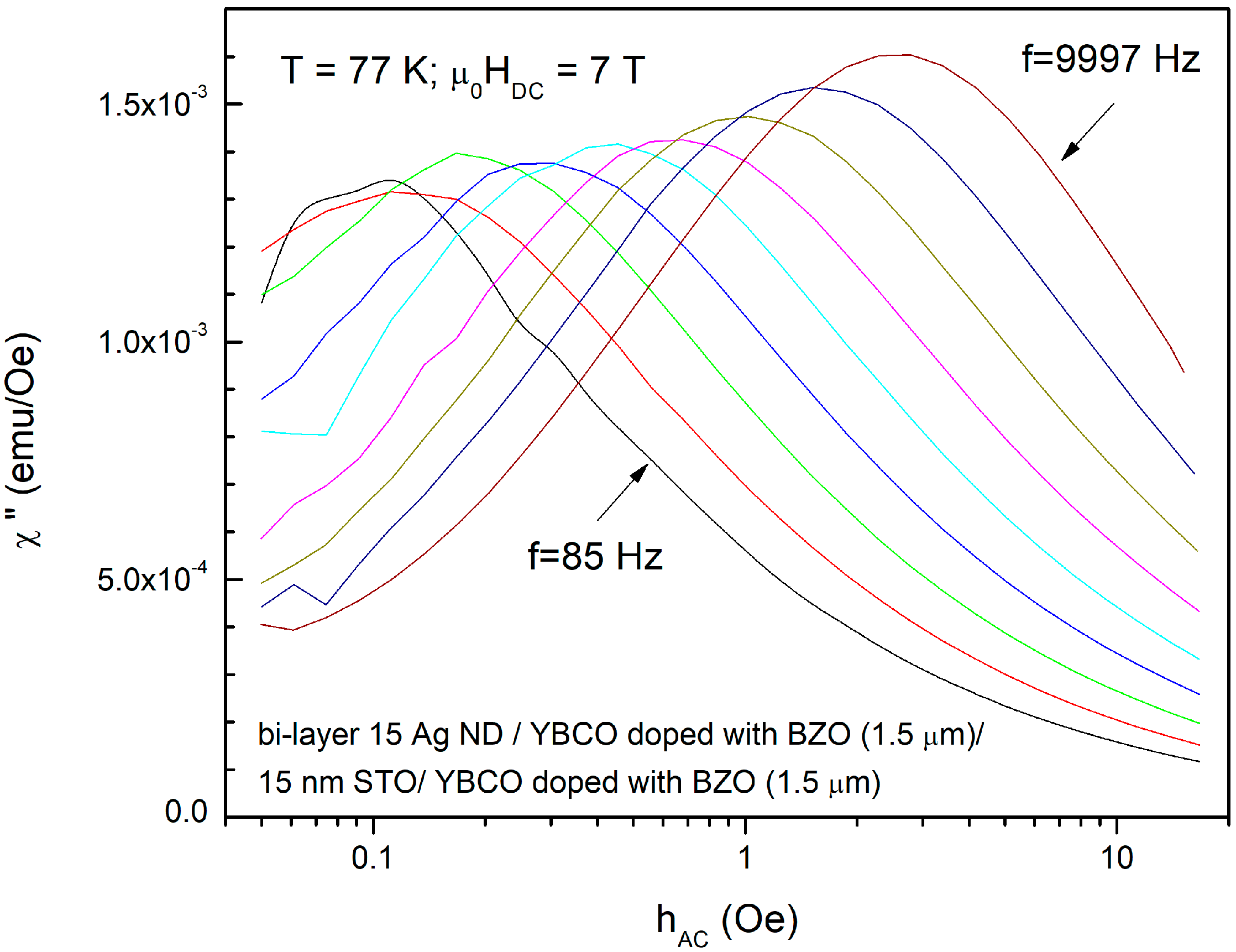
3.1. Frequency-Dependent Out-of-Phase Susceptibility Response
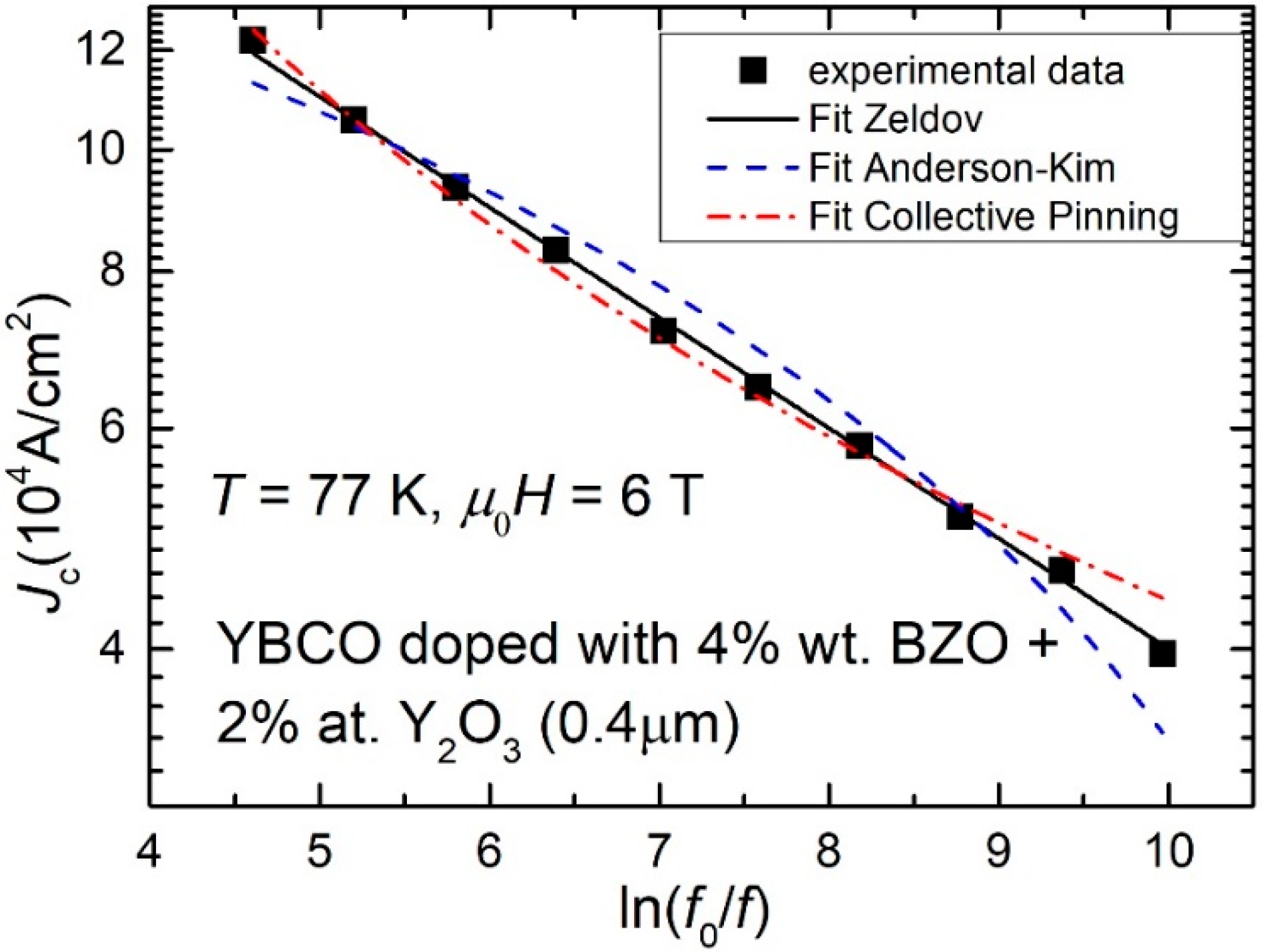
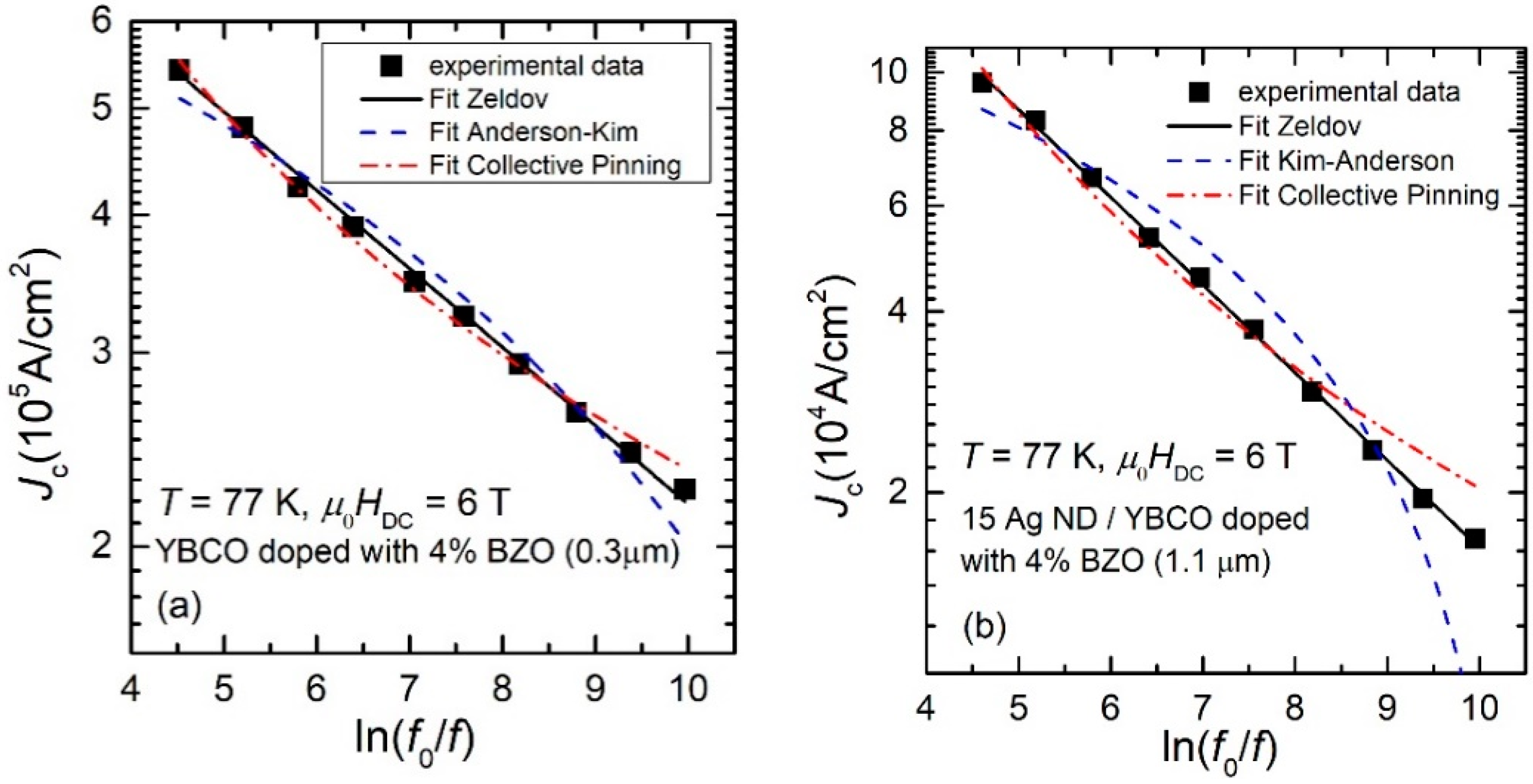
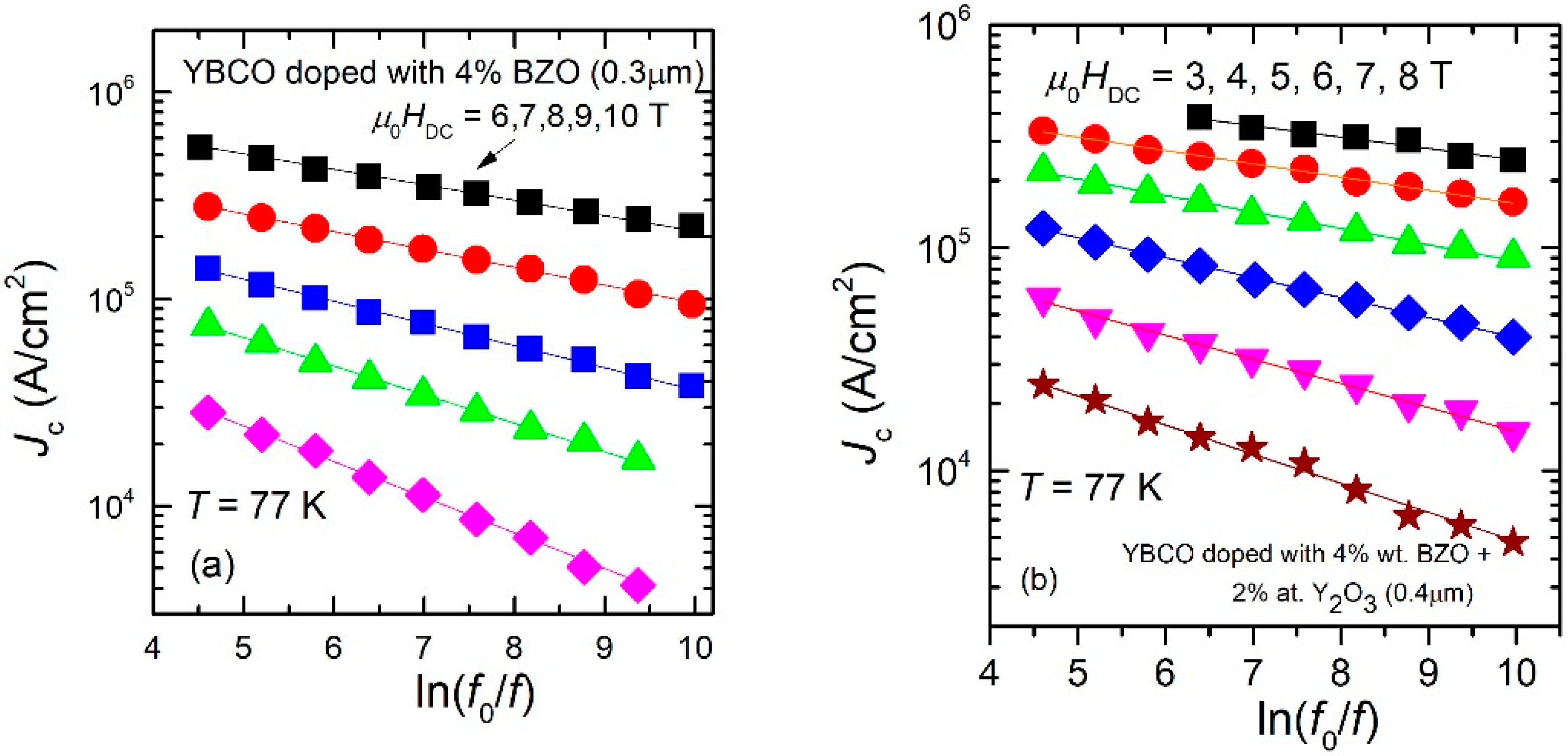
3.2. Frequency-Dependent Critical Current Density: Results and Models
3.3. Pinning Potential from Frequency-Dependent Critical Current Density
3.4. Experimentally-Determined Pinning Potentials
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Foltyn, S.R.; Civale, L.; Jia, Q.X.; Maiorov, B.; Wang, H.; Maley, M. Materials science challenges for high-temperature superconducting wire. Nat. Mater. 2007, 6, 631–642. [Google Scholar] [CrossRef] [PubMed]
- Crisan, A.; Fujiwara, S.; Nie, J.C.; Sundaresan, A.; Ihara, H. Sputtered nanodots: A costless method for inducing effective pinning centers in superconducting thin films. Appl. Phys. Lett. 2001, 79, 4547–4549. [Google Scholar] [CrossRef]
- Crisan, A.; Badica, P.; Fujiwara, S.; Nie, J.C.; Sundaresan, A.; Iyo, A.; Tanaka, Y. Nanodots-induced pinning centers in thin films: Effects on critical current density, activation energy and flux jump rate. IEEE Trans. Appl. Supercond. 2003, 13, 3726–3729. [Google Scholar] [CrossRef]
- Ionescu, M.; Li, A.H.; Zhao, Y.; Liu, H.K.; Crisan, A. Enhancement of critical current density in YBa2Cu3O7−δ thin films grown using PLD on YSZ (001) surface modified with Ag nano-dots. J. Phys. D Appl. Phys. 2004, 37, 1824–1828. [Google Scholar] [CrossRef]
- Macmanus-Driscoll, J.L.; Foltyn, S.R.; Jia, Q.X.; Wang, H.; Serquis, A.; Civale, L.; Maiorov, B.; Hawley, M.E.; Maley, M.P.; Peterson, D.E. Strongly enhanced current densities in superconducting coated conductors of YBa2Cu3O7−x + BaZrO3. Nat. Mater. 2004, 3, 439–443. [Google Scholar] [CrossRef]
- Awang Kechik, M.M.; Mikheenko, P.; Sarkar, A.; Dang, V.S.; Hari Babu, N.; Cardwell, D.A.; Abell, J.S.; Crisan, A. Artificial pinning centres in YBa2Cu3O7−δ thin films by Gd2Ba4CuWOy nanophase inclusions. Supercond. Sci. Technol. 2009, 22, 034020. [Google Scholar] [CrossRef]
- Foltyn, S.R.; Wang, H.; Civale, L.; Jia, Q.X.; Arendt, P.N.; Maiorov, B.; Li, Y.; Maley, M.P.; MacManus-Driscoll, J.L. Overcoming the barrier to 1000 A/cm width superconducting coatings. Appl. Phys. Lett. 2005, 87, 162505. [Google Scholar] [CrossRef]
- Mele, P.; Matsumoto, K.; Horide, T.; Ichinose, A.; Mukaida, M.; Yoshida, Y.; Horii, S.; Kita, R. Incorporation of double artificial pinning centers in YBa2Cu3O7−x films. Phys. C Supercond. Appl. 2008, 468, 1631–1634. [Google Scholar] [CrossRef]
- Zhou, H.; Maiorov, B.; Baily, S.A.; Dowden, P.C.; Kennison, J.A.; Stan, L.; Holesinger, T.G.; Jia, Q.X.; Foltyn, S.R.; Civale, L. Thickness dependence of critical current density in YBa2Cu3O7−δ films with BaZrO3 and Y2O3 addition. Supercond. Sci. Technol. 2009, 22, 085013. [Google Scholar] [CrossRef]
- Ercolano, G.; Bianchetti, M.; Sahonta, S.L.; Kursumovic, A.; Lee, J.H.; Wang, H.; Macmanus-Driscoll, J.L. Strong correlated pinning at high growth rates in YBa2Cu3O7−x thin films with Ba2YNbO6 additions. J. Appl. Phys. 2014, 116, 033915. [Google Scholar] [CrossRef]
- Opherden, L.; Sieger, M.; Pahlke, P.; Huhne, R.; Schultz, L.; Meledin, A.; Van Tendeloo, G.; Nast, R.; Holzapfel, B.; Bianchetti, M.; et al. Large pinning forces and matching effects in YBa2Cu3O7−δ thin films with Ba2Y(Nb/Ta)O6 nano-precipitates. Sci. Rep. 2016, 6, 21188. [Google Scholar] [CrossRef] [PubMed]
- Mikheenko, P.; Sarkar, A.; Dang, V.S.; Tanner, J.L.; Abell, J.S.; Crisan, A. c-Axis correlated extended defects and critical current in YBa2Cu3Ox films grown on Au and Ag-nano dot decorated substrates. Phys. C Supercond. 2009, 469, 798–804. [Google Scholar] [CrossRef]
- Mikheenko, P.; Dang, V.S.; Tse, Y.Y.; Awang Kechik, M.M.; Paturi, P.; Huhtinen, H.; Wang, Y.; Sarkar, A.; Abell, J.S.; Crisan, A. Integrated nanotechnology of pinning centers in YBa2Cu3Ox films. Supercond. Sci. Technol. 2010, 23, 125007. [Google Scholar] [CrossRef]
- Crisan, A.; Dang, V.S.; Mikheenko, P.; Ionescu, A.M.; Ivan, I.; Miu, L. Synergetic pinning centres in BaZrO3 -doped YBa2Cu3O7−x films induced by SrTiO3 nano-layers. Supercond. Sci. Technol. 2017, 30, 045012. [Google Scholar] [CrossRef] [Green Version]
- Develos-Bagarinao, K.; Yamasaki, H.; Ohki, K. Flux pinning properties of YBCO/DyBCO multilayers. J. Appl. Phys. 2008, 104, 063907. [Google Scholar] [CrossRef]
- Mele, P.; Crisan, A.; Adam, M.I. Pinning-Engineered YBa2Cu3Ox Thin Films. In Vortices and Nanostructured Superconductors; Springer: Berlin/Heidelberg, Germany, 2017; pp. 15–63. [Google Scholar]
- MacManus-Driscoll, J.L.; Wimbush, S.C. Processing and application of high-temperature superconducting coated conductors. Nat. Rev. Mater. 2021, 6, 587–604. [Google Scholar] [CrossRef]
- Crisan, A.; Dang, V.S.; Mikheenko, P. Nano-engineered pinning centres in YBCO superconducting films. Phys. C Supercond. 2017, 533, 118–132. [Google Scholar] [CrossRef]
- Bean, C.P. Magnetization of high-field superconductors. Rev. Mod. Phys. 1964, 36, 31–39. [Google Scholar] [CrossRef]
- Brandt, E.H. Thin superconductors in a perpendicular magnetic ac field: General formulation and strip geometry. Phys. Rev. B 1994, 49, 9024–9040. [Google Scholar] [CrossRef]
- Anderson, P.W.; Kim, Y.B. Hard superconductivity: Theory of the motion of abrikosov flux lines. Rev. Mod. Phys. 1964, 36, 39–43. [Google Scholar] [CrossRef]
- Blatter, G.; Feigel’Man, M.V.; Geshkenbein, V.B.; Larkin, A.I.; Vinokur, V.M. Vortices in high-temperature superconductors. Rev. Mod. Phys. 1994, 66, 1125–1388. [Google Scholar] [CrossRef]
- Zeldov, E.; Amer, N.M.; Koren, G.; Gupta, A.; Gambino, R.J.; McElfresh, M.W. Optical and Electrical Enhancement of Flux Creep in YBa2Cu3O7−x Epitaxial Films. Phys. Rev. Lett. 1989, 62, 3093–3096. [Google Scholar] [CrossRef] [PubMed]
- Zeldov, E. Flux creep and vortex potential well structure in high-temperature superconductors. Phys. A Stat. Mech. Appl. 1990, 168, 260–267. [Google Scholar] [CrossRef]
- Tinkham, M. Introduction to Superconductivity, 2nd ed.; McGraw-Hill, Inc.: New York, NY, USA, 1996. [Google Scholar]
- Miu, L.; Mele, P.; Crisan, A.; Ionescu, A.; Miu, D. Evolution of vortex dynamics in YBa2Cu3O7 films with nanorods by adding nanoparticles. Phys. C Supercond. 2014, 500, 40–43. [Google Scholar] [CrossRef]
- Miu, D.; Ivan, I.; Crisan, A.; Mele, P.; Jakob, G.; Miu, L. Inhibition of the detrimental double vortex-kink formation in thick YBa2Cu3O7 films with BaZrO3 nanorods. Supercond. Sci. Technol. 2013, 26, 045008. [Google Scholar] [CrossRef]
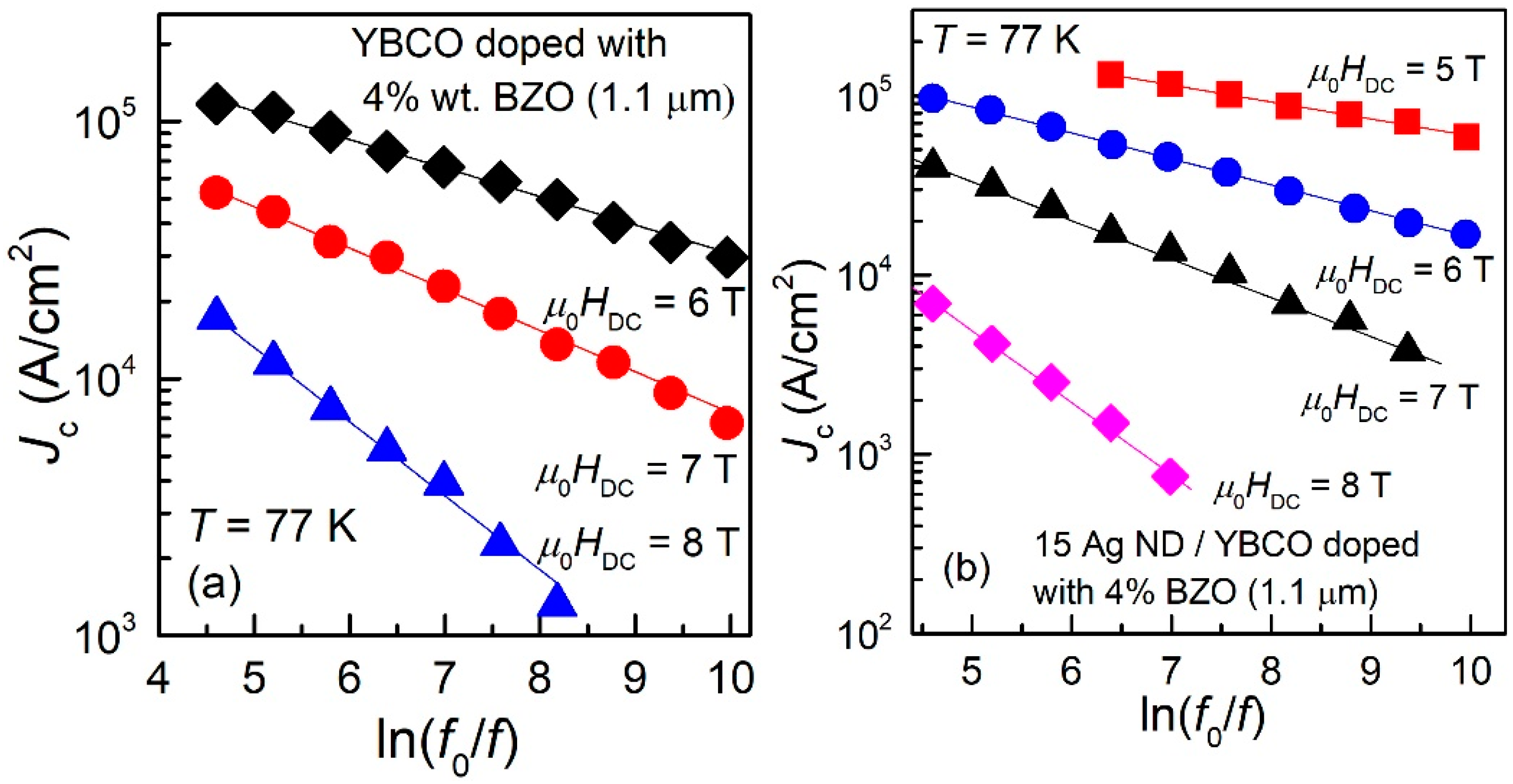
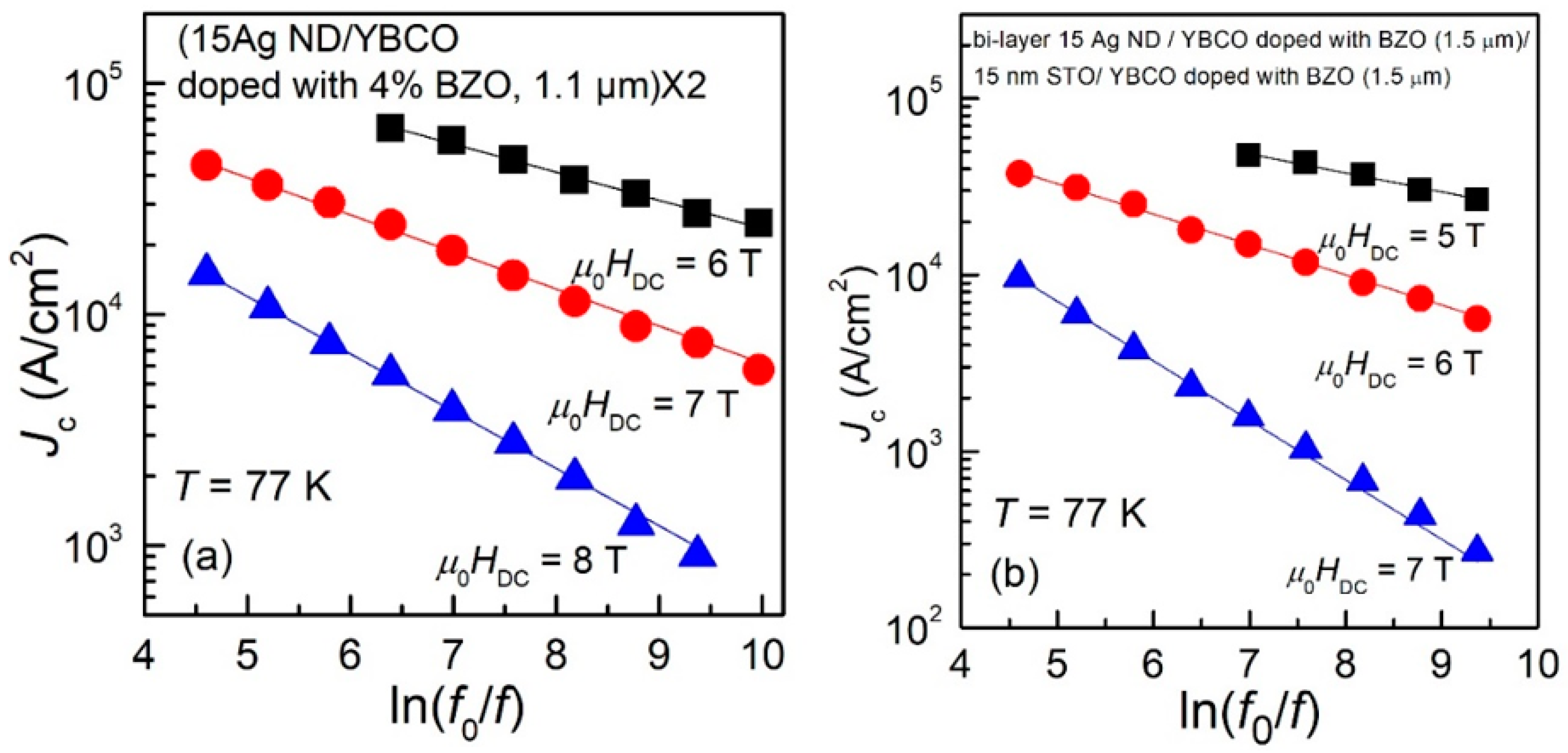
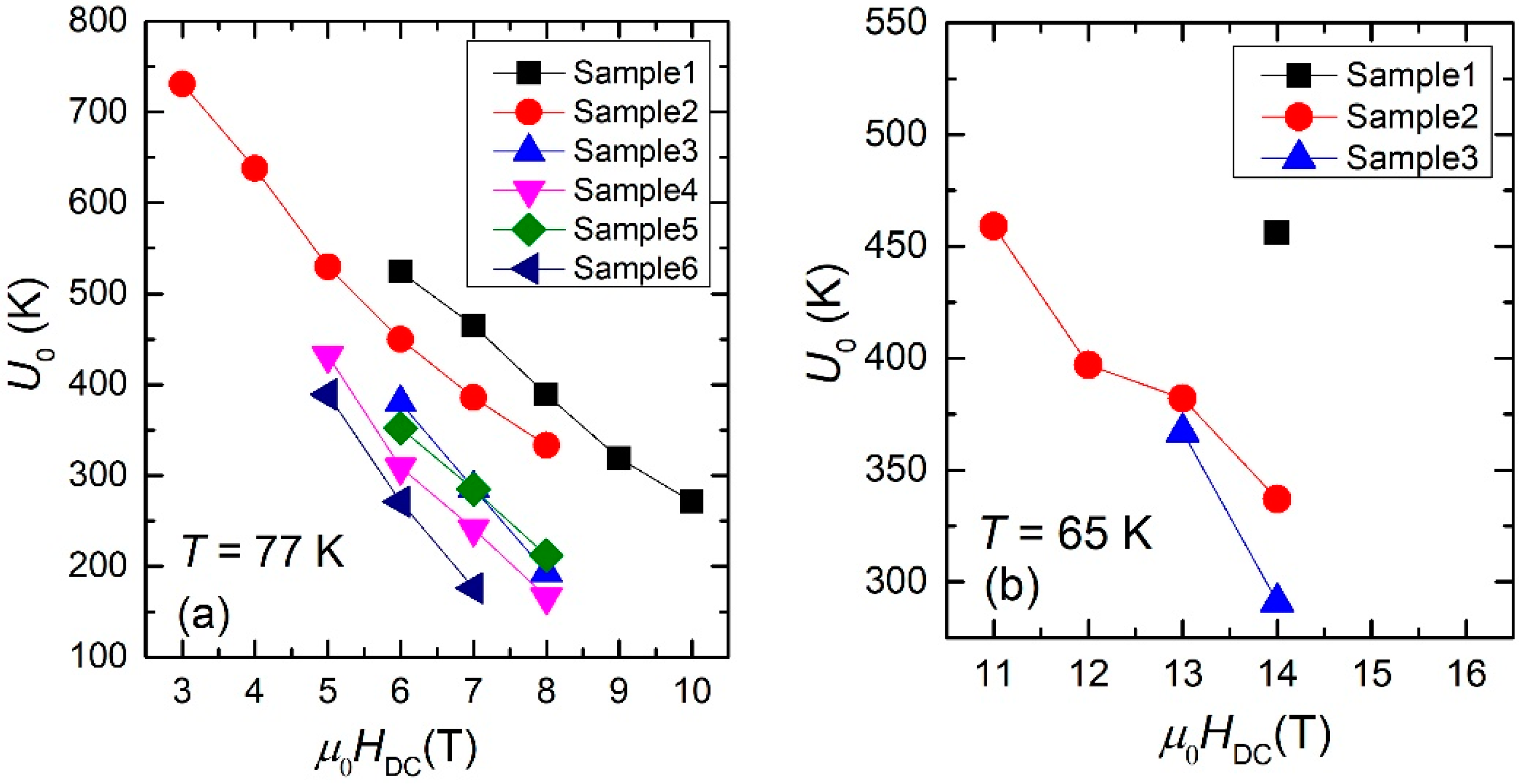
| Sample | DC Field (T) | Uo (K) at T = 77 K |
|---|---|---|
| Sample 1 | 6 | 524 |
| 7 | 465 | |
| 8 | 389 | |
| 9 | 319 | |
| 10 | 271 | |
| Sample 2 | 3 | 731 |
| 4 | 638 | |
| 5 | 530 | |
| 6 | 450 | |
| 7 | 386 | |
| 8 | 333 | |
| Sample 3 | 6 | 380 |
| 7 | 286 | |
| 8 | 193 | |
| Sample 4 | 5 | 432 |
| 6 | 309 | |
| 7 | 241 | |
| 8 | 166 | |
| Sample 5 | 6 | 352 |
| 7 | 285 | |
| 8 | 212 | |
| Sample 6 | 5 | 389 |
| 6 | 271 | |
| 7 | 176 |
| Sample | DC Field (T) | Uo (K) at T = 65 K |
|---|---|---|
| Sample 1 | 14 | 456 |
| Sample 2 | 11 | 459 |
| 12 | 397 | |
| 13 | 382 | |
| 14 | 337 | |
| Sample 3 | 13 | 367 |
| 14 | 291 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ivan, I.; Ionescu, A.M.; Crisan, D.N.; Andrei, A.; Galluzzi, A.; Polichetti, M.; Mosqueira, J.; Crisan, A. Pinning Potential of the Self-Assembled Artificial Pinning Centers in Nanostructured YBa2Cu3O7−x Superconducting Films. Nanomaterials 2022, 12, 1713. https://doi.org/10.3390/nano12101713
Ivan I, Ionescu AM, Crisan DN, Andrei A, Galluzzi A, Polichetti M, Mosqueira J, Crisan A. Pinning Potential of the Self-Assembled Artificial Pinning Centers in Nanostructured YBa2Cu3O7−x Superconducting Films. Nanomaterials. 2022; 12(10):1713. https://doi.org/10.3390/nano12101713
Chicago/Turabian StyleIvan, Ion, Alina M. Ionescu, Daniel N. Crisan, Andreea Andrei, Armando Galluzzi, Massimiliano Polichetti, Jesus Mosqueira, and Adrian Crisan. 2022. "Pinning Potential of the Self-Assembled Artificial Pinning Centers in Nanostructured YBa2Cu3O7−x Superconducting Films" Nanomaterials 12, no. 10: 1713. https://doi.org/10.3390/nano12101713
APA StyleIvan, I., Ionescu, A. M., Crisan, D. N., Andrei, A., Galluzzi, A., Polichetti, M., Mosqueira, J., & Crisan, A. (2022). Pinning Potential of the Self-Assembled Artificial Pinning Centers in Nanostructured YBa2Cu3O7−x Superconducting Films. Nanomaterials, 12(10), 1713. https://doi.org/10.3390/nano12101713








