Abstract
The purpose and novelty of our study include the scrutinization of the unsteady flow and heat characteristics of the unsteady Sutterby nano-fluid flow across an elongated cone using slip boundary conditions. The bioconvection of gyrotactic micro-organisms, Cattaneo–Christov, and thermal radiative fluxes with magnetic fields are significant physical aspects of the study. Anisotropic constraints on the cone surface are taken into account. The leading formulation is transmuted into ordinary differential formate via similarity functions. Five coupled equations with nonlinear terms are resolved numerically through the utilization of a MATLAB code for the Runge–Kutta procedure. The parameters of buoyancy ratio, the porosity of medium, and bioconvection Rayleigh number decrease x-direction velocity. The slip parameter retard y-direction velocity. The temperature for Sutterby fluids is at a hotter level, but its velocity is vividly slower compared to those of nanofluids. The temperature profile improves directly with thermophoresis, v-velocity slip, and random motion of nanoentities.
1. Introduction
In the modern era, many researchers worked on fluid flows that pass through a cone because of its progress in advanced technologies. It have many outstanding applications in industrial and engineering fields such as aeronautical engineering, electronic chips, endoscopy scanning, etc. The effect of chemical reaction on Casson fluid by using cone geometry was analyzed by Deebani et al. [1]. Verma et al. [2] numerically discussed the effects of Soret and Dufour with thermal radiation on MHD flow around a vertical cone. The two-dimensional MHD nanofluid flow passing over a plate or cone was discussed by Ahmad et al. [3]. The investigations of MHD micropolar fluid in the presence of porous medium passing across a cone were studied by Ahmad et al. [4]. Hazarika et al. [5] discussed the effect of variable viscosity of time-dependent micropolar fluid passing over a vertical cone. Dawar et al. [6] used non-isothermal and non-iso-solutal boundary conditions for Williamson nanofluid flow passing through two geometries. Nabwey and Mahdy [7] discussed the impact of non-linear temperature on micropolar fluid flow passing across the cone.
The basic premise of MHD is simple: An electrical conductor fluid, such as seawater, is used to create a unidirectional current. Naseem et al. [8] proposed an analytical treatment for MHD non-Newtonian micro liquid caused by plate stretching in the presence of Brownian motion, concluding that the thermal relaxation parameter has the potential to increase fluid temperature. The magneto hydrodynamic free convective boundary layer flow of a chemically reacting nanofluid from a convectively heated permeable vertical surface was investigated by Uddin et al. [9]. Waqas et al. [10] described a magneto hydrodynamic (MHD) mixed convection flow of micropolar liquid caused by a nonlinear stretched sheet under convective conditions. Srinivas et al. [11] investigated the effect of a chemical reaction on the MHD flow of a nanofluid in a porous pipe that was expanding or contracting in the presence of a heat source/sink. Habib et al. [12] analyzed numerical simulations for slip impacts on MHD nanofluid in the presence of an electromagnetic field and gyrotactic microbes under the influences of activation energy and heat radiation. Refs. [13,14,15,16] scrutinized the aspects of MHD flow of nanofluids.
Choi [17] used the term “nanofluid” in 1995 to describe a novel kind of heat transfer fluid that relies on suspending Nanoscale particles of metallic origin with an average particle size of less than 100 nm inside traditional heat transfer fluids. Nanofluids have been discovered to have improved thermo-physical properties such as thermal conductivity, thermal diffusivity, viscosity, and convective heat transfer coefficients when compared to base fluids such as oil or water in earlier studies. Khan et al. [18] investigated the magnetohydrodynamic thin layer nanofluid applied on a stretching cylinder including heat transfer. Kuznetsov and Nield [19] recently looked at the boundary layer in Newtonian and porous media filled with nanofluid over constant and movable boundaries. Turkyilmazoglu [20] investigated the flow of nanofluid boundary layers across a revolving disc. Hsiao [21] used an applied thermal system for micropolar nanofluid flow past over a stretching sheet. Some other researchers [22,23,24] explored the features of nanofluids.
Bioconvection occurs when the self-propelled kinetic microorganisms increase the density of the normal liquid in a specific direction to a specific direction, where the density gradually moves upward in the moving fluid in the normal fluid. Nayake et al. [25] investigated the velocity of the Casson flow of the electromagnetic sheet exponentially developing when the nanofluid incurs chemical, thermal, isolated, and moving microbial slip effects. Mansour et al. [26] explained bioconvection of magneto-hydrodynamic in the closed-loop cave. Balla et al. [27] analyzed the activity of living microorganisms in the porous square hole. Khan et al. [28] analyzed the bioconvection nanofluidic flow along with the extended former Oldroyd-B walls. Khan et al. [29] discussed the flow of a viscoelastic nanofluid across a moving surface, which is porous, along with the occurrence of microorganisms. Ali et al. [30] investigated the influence of Stefan blowing on Cattaneo–Christov attributes and the bioconvection of self-motivated microorganisms blending in water-based nanoparticles with a leading-edge ablation/accretion.
To the best of the researcher’s knowledge, no analysis of the unsteady Sutterby nano-fluid, heat, and mass characteristics of ordinary nanofluid flow across an elongated cone, keeping in view the conical boundaries in various technological industrial applications, has been performed. Latiff et al. [31] examined theoretically and arithmetically the MHD bioconvective of nanofluid flow near a spinning cone with anisotropic velocity slips, heat slips, density slips, and microbes slips. However, they did not contemplate unsteady Sutterby nanofluid and, due to sedimentation of nanofluids, we use living micro-organisms. The target and novelty of our latest study is to examine the unsteady flow and heat characteristics of the unsteady Sutterby nano-fluid flow across an elongated cone using slip boundary conditions. The physical aspects are improved with bioconvection, applied magnetic force, Cattaneo–Christov diffusion, and anisotropic constraints. The differentiated results are achieved numerically and discussed in detail.
2. Physical Model and Mathematical Formulation
This study contains axisymmetric, unsteady Sutterby nanofluid flow across a rotating cone with self motive micro-organisms. Moreover, rectangular curvilinear coordinate structure is assumed to be stable. The presence of buoyancy forces that are present in the flow depends on mass, temperature, and micro-organism difference. , , and represent velocity components along x, y and z-axis. B (magnetic field of strength) is normal to the rotating cone. The graphical representation of the physical formation is revealed in Figure 1. Here, , T, C, n, and represents fluid temperature at the wall, fluid temperature, nanoparticle volume fraction, and motile micro-organism density. Nanoparticle volume fraction and motile micro-organism density at the wall and , , and are taken away from the wall. With these assumptions, the momentum and mass equations in x and z directions, energy, concentration, and micro-organism conservation, which depends on time, are given below:
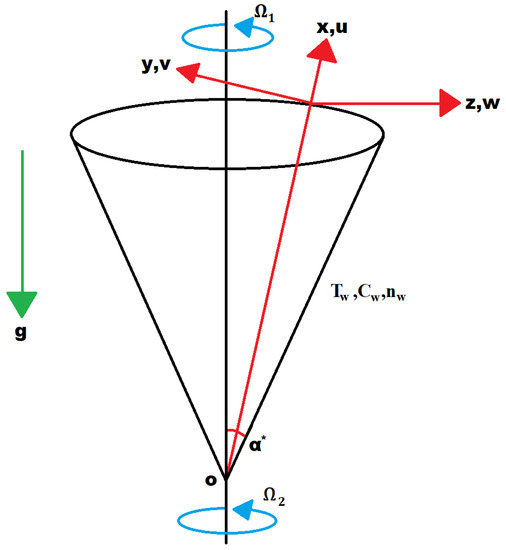
Figure 1.
Flowchart.
Here, t represents time, fluid density is , gravity acceleration is g, fluid viscosity is , deportment index of flow is S, consistency index is , thermal diffusivity is , the thermal expansion coefficient of the base fluid is , the average volume of micro-organism is , micro-organism density is , the ratio of heat capacity of nanofluid to the base fluid is , Brownian motion is , the thermophorsis coefficient is , the chemotaxis constant is , the swimming speed of cell is , and the micro-organism diffusivity coefficient is .
Boundary conditions along with slip conditions are taken into account [32,33]:
where dimensionless angular velocity of the cone is . , , , , and represent velocity, temperature, concentration, and micro-organism density slips.
Introduce the following similarity transformation variables to proceed with the investigation [33].
Equation (1) is satisfied by using Equation (8), and Equations (2)–(6) are reduced into following differential equations.
The non-dimensional parameters in their respective orders are given below:
is the Sutterby Reynolds number, is the Sutterby Deborah number, is the buoyancy ratio, is the bio-convection Rayleigh number, the Prandtl number is , the mixed convection parameter is , is the Grashoff number, is the Rayleigh number, the magnetic field is , denotes Brownian motion, is the thermophoresis parameter, the bioconvection Lewis number is , the bioconvection Peclet number is , is the Schmidt number, is the u-velocity slip, is the v-velocity slip, is the thermal slip, is the solutal slip, and is motile density slip.
The physical quantities are stated as follows.
, , , , and are given below.
, , , , .
, , , ,
Thus, we have the following:
, ,
, , .
where is the local Reynolds number.
3. Numerical Scheme
In this section, there are incorporated numerical outcomes from the nonlinearly accompanying ordinary differential Equations (1)–(6) with boundary conditions in Equation (8), which are combined utilizing the RK-4 technique. To carry out this analytical strategy, governing Equations (1)–(6) are combined into a first-order approach by introducing a distinct variable, as shown below:
along with the following boundary conditions.
, , , ,
, , at ,
, , , , , as .
4. Results and Discussion
For the validation of current outcomes, these are verified in the restricted cases when compared with preceding results (see Table 1). Table 1 provided the outcomes for heat transfer rate , at cone walls for , and when and all other parameters are zero. Among the current and previous findings, adequately sufficient accord is attained.

Table 1.
For and , comparative outputs of .
Graphical outcomes are obtained for different parameters when = 0.1, = 0.1, = 0.1, = 0.1, = 0.1, M = 1.0, S = 0.1, = 6.8, = 0.1, = 0.1, = 5.0, A = 0.1, = 1.0, = 0.1, = 0.1, = 0.5, and = 0.1. Moreover, the suitable ranges of parameters wwere increasing or decreasing behavior becomes smooth are taken as , , , , , , , , , , , , , , , and .
The plots in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7 delineated the distribution of velocities and with a variation of leading parameters for two cases of nanoliquids and Sutterby nanofluids. It is revealed that the speed for Sutterby fluids is significantly slower than ordinary nanofluids. The larger viscous effects for Sutterby fluids impede the flow notably at the face as compared to that of nanofluids. The parabolic curve of rises upward near the boundary due to the stretching cone and then it declines to far-off boundary conditions. Figure 2 portrays the slowing behavior of x-velocity against mounting inputs of unsteadiness and magnetic parameters. In the presence of the magnetic force field, the reactive Lorentz force comes into play and retards the flow (see [31]). In unsteady flow, after the first jerk, the stretch in boundary diminishes and the fluid in the boundary slows down. It is observed that raising the unstable parameter drops the velocity distribution, which is associated by a decrease in the momentum boundary layer thickness in the profile, indicating that the unsteadiness factor declines the fluid velocity due to the spinning cone. From Figure 3, the slowing of fluid velocity is caused by the growing strength of and . The buoyancy effects put forth an adverse reaction to the flow in x-direction; hence, decline. Vivid progress in x-velocity is demonstrated in Figure 4 when mixed convection parameter and u-velocity slip parameter are improved. However, the higher inputs of v-slip velocity and thermal slip decrease the speed , as depicted in Figure 5. A meager decline in y-velocity is revealed against the unsteadiness seen in Figure 5. Moreover, Figure 6 and Figure 7 show the significant decrement of y-velocity when magnetic parameter M, u-velocity slip, and v-velocity slip parameters are made stronger. The sketch for temperature function for nanofluids and Sutterby nanofluids is shown in Figure 8, Figure 9 and Figure 10. It is observed that temperature for Sutterby nano-fluids is higher than that of nanofluids. In addition, Figure 8 indicate that temperature diminishes against the rising inputs of Prandlt number and unsteadiness parameter A. This is due to the notion that enhancing unsteadiness improves heat loss due to the rotating cone, leading to a reduction in temperature distribution. Regardless of the reduction in the rate of heat transmission from the surface to the fluid for larger values of the unstable parameter, the cooling rate is significantly faster than the rate of cooling for the steady flow. However, the larger inputs of the parameter for Brownian motion and thermophoresis improves temperature distribution , as delineated in Figure 9. According to the physical nature of these two slip conditions, the rise in temperature is expected. The fast random motion of nano-particles in the base fluids (higher value of ) and the rapid movement of nanoentities from hotter to colder fluids (higher values of ) are responsible for raising temperature . Figure 10 expose that fluids temperature is reduced against higher values of u-velocity slip and thermal velocity slip , but it rises directly with v-velocity slip . The normalized function of nano-entities’ volume friction is mapped in Figure 11, Figure 12 and Figure 13. Volume friction recedes against , A, and but it becomes enhanced with the increments in , the thermophoretic parameter. Furthermore, u-velocity slip and solutal slip exert a receding impact on , whereas v-velocity slip enhances volume friction . The plots of micro-organism density exhibit decrement in this function against the increment in Peclet number and Lewis number , as shown in Figure 14. Similarly, Figure 15 displays a decreasing trend of against u-velocity slip and unsteadiness parameter A. Figure 16 reveals that micro-organism density increases with v-velocity slip parameter , and it declines rapidly when motile density slip is improved. Table 2 and Table 3 in the respective order presents the enumeration of skin friction factors in x-direction and y-direction. Skin friction along x-direction continues to decrease against parameter A, S, M, , and , but it is enhanced directly with mixed convection parameter . Moreover, parameter A, S, and M incremented with but parameter was reduced significantly. Table 4 enlists the local temperature rate on the cone surface to be reduced against , , and but it increases with A and . From Table 5, it is perceived that increases with A, , but it decreases against and . Results for are registered in Table 6. Parameters A, , and enhance , but it diminishes against .
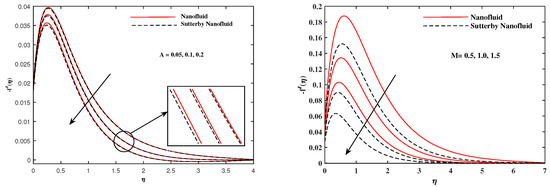
Figure 2.
fluctuate in x-direction with A and M.
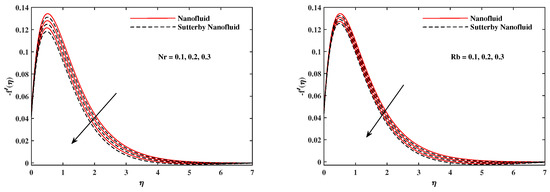
Figure 3.
fluctuate in x-direction with and .
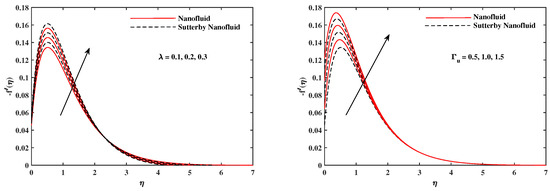
Figure 4.
fluctuate in x-direction with and .
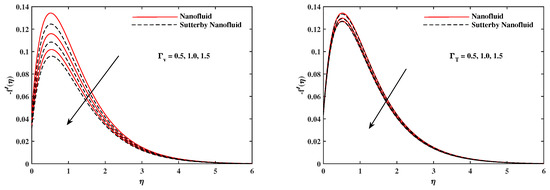
Figure 5.
fluctuate in x-direction with and .
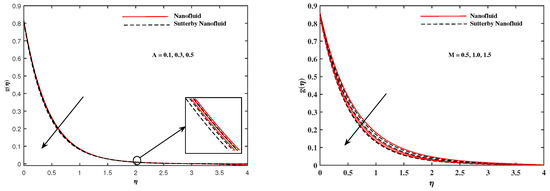
Figure 6.
fluctuate in y-direction with A and M.
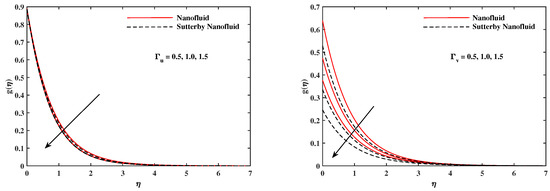
Figure 7.
fluctuate in y-direction with and .
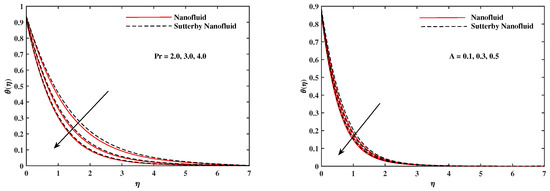
Figure 8.
fluctuate with and A.
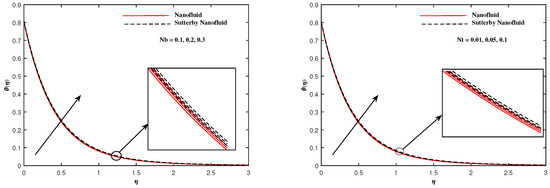
Figure 9.
with and .
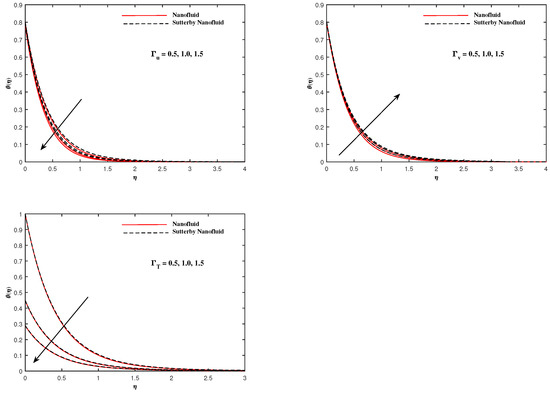
Figure 10.
fluctuate with , , and .
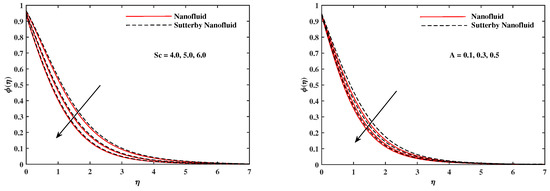
Figure 11.
fluctuate with and A.
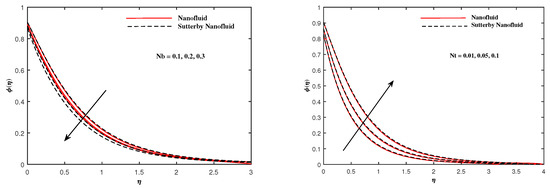
Figure 12.
fluctuate with and .
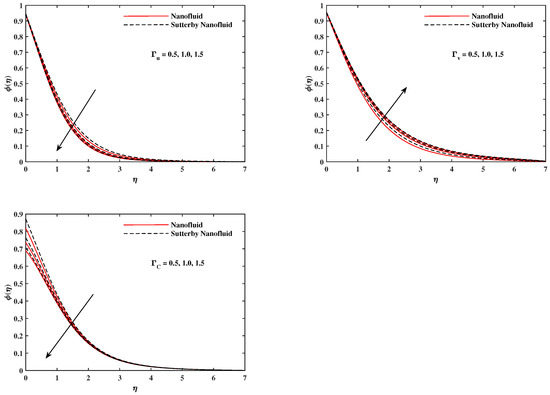
Figure 13.
fluctuate with , , and .
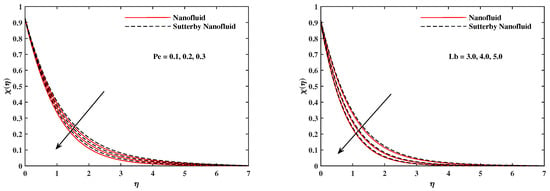
Figure 14.
fluctuate with and .
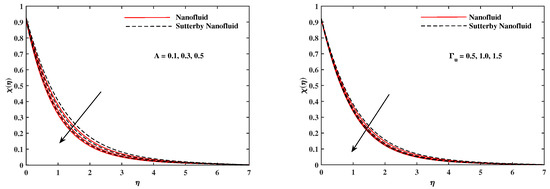
Figure 15.
fluctuate with A and .
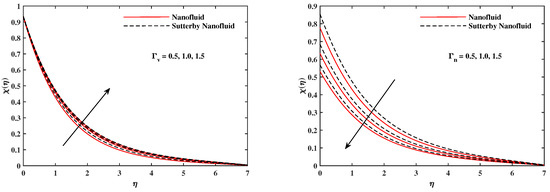
Figure 16.
fluctuate with and .

Table 2.
Results for in x-direction.

Table 3.
Results for in y-direction.

Table 4.
Results for .

Table 5.
Results for .

Table 6.
Results for .
5. Conclusions
The objective and novelty of our manuscript is to explore the unsteady thermal and mass transportation of Sutterby nanofluids along enlarging cone surface where anisotropic boundary conditions are considered. In the presence of a magnetic field acting perpendicular to the axis of the cone’s bioconvection, thermal radiation and non-Fourier flux add to the physical aspects. The RK-4 technique and shooting strategy were used to combine numerical results from nonlinearly accompanying ordinary differential equations with boundary conditions. The impacts of distinct parameters, such as unsteadiness parameter, magnetic field parameter, and slip parameters, are portrayed graphically. Significant findings are stated below:
- In the x-direction, velocity slows down against mounting inputs of A, M, , , , and while it upsurges with and .
- In the y-direction, velocity slows down against mounting inputs of A, M, , and .
- A rising trend is observed in temperature profile when , , and take larger values but it decreases when , A, , and are uplifted.
- Concentration profile decrease when , A, , , and intensifies but the opposite behavior is observed for and .
- Motile density profile decreases when , A, , , and intensifies but the opposite behavior is observed for .
- The skin friction factor along x-direction continues to decrease against A, S, M, , and but it increases directly with mixed convection parameter . Moreover, parameters A, S, and M incremented but parameter was reduced significantly.
- The local temperature rate on the cone surface decreased against , , and but its increased with A and .
- increases directly with A, , and , but it reduces against and .
- Motile density number is directly enhanced with A, , and but it diminishes against .
6. Future Directions
This problem can be extended as hybrid nanofluids by using finite element and finite difference schemes.
Author Contributions
Conceptualization, S.A. (Sohaib Abdal) and I.S.; methodology, S.A. (Saima Afzal) and Z.M.; software, S.A. (Sohaib Abdal); validation, K.M.A. and Z.M.; Formal Analysis, M.M.M.J. and H.M.A.; writing—original draft preparation, S.A. (Sohaib Abdal) and S.A. (Saima Afzal); writing—review and editing, K.M.A. and H.M.A.; supervision, I.S.; funding acquisition, M.M.M.J. and Z.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research have no external funding.
Funding
This research have no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
This research was supported by Taif University, Researchers Supporting Project Number (TURSP-2020/217), Taif University, Taif, Saudi Arabia. Open Access funding provided by the Qatar National Library.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| List of Symbols | |
| Velocity components (m/s) | |
| Cartesian coordinates (m) | |
| t | Time (s) |
| g | Gravity acceleration (m/s) |
| S | Deportment index |
| Consistency index | |
| Prandtl number | |
| Reynolds number | |
| Heat transfer coefficient (W/m) | |
| Brownian motion coefficient (m/s) | |
| Sutterby Deborah number | |
| Buoyancy ratio parameter | |
| Thermophorsis coefficient (m/s) | |
| Micro-organisms diffusivity coefficient (m/s) | |
| Chemotaxis constant (m) | |
| Swimming speed of cell (m/s) | |
| Sutterby Reynolds number | |
| Bioconvection Rayleigh number | |
| Prandtl number | |
| Grashoff number | |
| M | Magnetic field (tesla (symbol T)) |
| Brownian motion parameter | |
| Thermophoresis parameter | |
| Bioconvection Lewis number | |
| Bioconvection Peclet number | |
| Schmidt number | |
| Lewis number | |
| Greek Symbols | |
| u-velocity slip | |
| v-velocity slip | |
| Solutal slip | |
| Motile density slip | |
| Thermal slip | |
| Fluid density (kg/m) | |
| Mixed convection parameter | |
| Thermal diffusivity (m/s) | |
| Average volume of micro-organism | |
| Micro-organism density | |
| Ratio of heat capacity of nanofluid | |
| Subscripts | |
| p | Nanoparticles |
| w | On the wall |
| ∞ | Ambient |
References
- Deebani, W.; Tassaddiq, A.; Shah, Z.; Dawar, A.; Ali, F. Hall effect on radiative Casson fluid flow with chemical reaction on a rotating cone through entropy optimization. Entropy 2020, 22, 480. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Verma, K.; Borgohain, D.; Sharma, B. Soret and Dufour effects on MHD flow about a rotating vertical cone in presence of radiation. J. Math. Comput. Sci. 2021, 11, 3188–3204. [Google Scholar]
- Ahmad, S.; Ali, K.; Saleem, R.; Bashir, H. Thermal analysis of nanofluid flow due to rotating cone/plate—A numerical study. AIP Adv. 2020, 10, 075024. [Google Scholar] [CrossRef]
- Ahmad, S.; Ali, K.; Bashir, H. Interaction of micropolar fluid structure with the porous media in the flow due to a rotating cone. Alex. Eng. J. 2021, 60, 1249–1257. [Google Scholar] [CrossRef]
- Hazarika, G.; Phukan, B.; Ahmed, S. Effect of Variable Viscosity and Thermal Conductivity on Unsteady Free Convective Flow of a Micropolar Fluid Past a Vertical Cone. J. Eng. Phys. Thermophys. 2020, 93, 178–185. [Google Scholar] [CrossRef]
- Dawar, A.; Shah, Z.; Tassaddiq, A.; Kumam, P.; Islam, S.; Khan, W. A convective flow of williamson nanofluid through cone and wedge with non-isothermal and non-isosolutal conditions: A revised buongiorno model. Case Stud. Therm. Eng. 2021, 24, 100869. [Google Scholar] [CrossRef]
- Nabwey, H.A.; Mahdy, A. Numerical approach of micropolar dust-particles natural convection fluid flow due to a permeable cone with nonlinear temperature. Alex. Eng. J. 2021, 60, 1739–1749. [Google Scholar] [CrossRef]
- Naseem, A.; Shafiq, A.; Zhao, L.; Farooq, M. Analytical investigation of third grade nanofluidic flow over a riga plate using Cattaneo-Christov model. Results Phys. 2018, 9, 961–969. [Google Scholar] [CrossRef]
- Uddin, M.; Bég, O.A.; Aziz, A.; Ismail, A. Group analysis of free convection flow of a magnetic nanofluid with chemical reaction. Math. Probl. Eng. 2015, 2015, 621503. [Google Scholar] [CrossRef] [Green Version]
- Waqas, M.; Farooq, M.; Khan, M.I.; Alsaedi, A.; Hayat, T.; Yasmeen, T. Magnetohydrodynamic (MHD) mixed convection flow of micropolar liquid due to nonlinear stretched sheet with convective condition. Int. J. Heat Mass Transf. 2016, 102, 766–772. [Google Scholar] [CrossRef]
- Srinivas, S.; Vijayalakshmi, A.; Reddy, A.S.; Ramamohan, T. MHD flow of a nanofluid in an expanding or contracting porous pipe with chemical reaction and heat source/sink. Propuls. Power Res. 2016, 5, 134–148. [Google Scholar] [CrossRef] [Green Version]
- Habib, D.; Salamat, N.; Abdal, S.; Siddique, I.; Ang, M.C.; Ahmadian, A. On the role of bioconvection and activation energy for time dependent nanofluid slip transpiration due to extending domain in the presence of electric and magnetic fields. Ain Shams Eng. J. 2022, 13, 101519. [Google Scholar] [CrossRef]
- Ali, B.; Naqvi, R.A.; Nie, Y.; Khan, S.A.; Sadiq, M.T.; Rehman, A.U.; Abdal, S. Variable viscosity effects on unsteady MHD an axisymmetric nanofluid flow over a stretching surface with thermo-diffusion: Fem approach. Symmetry 2020, 12, 234. [Google Scholar] [CrossRef] [Green Version]
- Abdal, S.; Alhumade, H.; Siddique, I.; Alam, M.M.; Ahmad, I.; Hussain, S. Radiation and multiple slip effects on magnetohydrodynamic bioconvection flow of micropolar based nanofluid over a stretching surface. Appl. Sci. 2021, 11, 5136. [Google Scholar] [CrossRef]
- Iasiello, M.; Vafai, K.; Andreozzi, A.; Bianco, N. Hypo-and hyperthermia effects on LDL deposition in a curved artery. Comput. Therm. Sci. Int. J. 2019, 11, 95–103. [Google Scholar] [CrossRef]
- Vazifehshenas, F.H.; Bahadori, F. Investigation of Soret effect on drug delivery in a tumor without necrotic core. J. Taiwan Inst. Chem. Eng. 2019, 102, 17–24. [Google Scholar] [CrossRef]
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Technical Report; Argonne National Lab.: Argonne, IL, USA, 1995. [Google Scholar]
- Khan, N.S.; Gul, T.; Islam, S.; Khan, I.; Alqahtani, A.M.; Alshomrani, A.S. Magnetohydrodynamic nanoliquid thin film sprayed on a stretching cylinder with heat transfer. Appl. Sci. 2017, 7, 271. [Google Scholar] [CrossRef]
- Kuznetsov, A.; Nield, D. Natural convective boundary-layer flow of a nanofluid past a vertical plate. Int. J. Therm. Sci. 2010, 49, 243–247. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Nanofluid flow and heat transfer due to a rotating disk. Comput. Fluids 2014, 94, 139–146. [Google Scholar] [CrossRef]
- Hsiao, K.L. Micropolar nanofluid flow with MHD and viscous dissipation effects towards a stretching sheet with multimedia feature. Int. J. Heat Mass Transf. 2017, 112, 983–990. [Google Scholar] [CrossRef]
- Yahya, A.U.; Salamat, N.; Huang, W.H.; Siddique, I.; Abdal, S.; Hussain, S. Thermal charactristics for the flow of Williamson hybrid nanofluid (MoS2+ ZnO) based with engine oil over a streched sheet. Case Stud. Therm. Eng. 2021, 26, 101196. [Google Scholar] [CrossRef]
- Abdal, S.; Hussain, S.; Siddique, I.; Ahmadian, A.; Ferrara, M. On solution existence of MHD Casson nanofluid transportation across an extending cylinder through porous media and evaluation of priori bounds. Sci. Rep. 2021, 11, 7799. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, F.; Abdal, S.; Ayed, H.; Hussain, S.; Salim, S.; Almatroud, A.O. The improved thermal efficiency of Maxwell hybrid nanofluid comprising of graphene oxide plus silver/kerosene oil over stretching sheet. Case Stud. Therm. Eng. 2021, 27, 101257. [Google Scholar] [CrossRef]
- Nayak, M.; Prakash, J.; Tripathi, D.; Pandey, V.; Shaw, S.; Makinde, O. 3D Bioconvective multiple slip flow of chemically reactive Casson nanofluid with gyrotactic micro-organisms. Heat Transf.-Asian Res. 2020, 49, 135–153. [Google Scholar] [CrossRef]
- Mansour, M.A.; Rashad, A.M.; Mallikarjuna, B.; Hussein, A.K.; Aichouni, M.; Kolsi, L. MHD mixed bioconvection in a square porous cavity filled by gyrotactic microorganisms. Int. J. Heat Technol. 2019, 37, 433–445. [Google Scholar] [CrossRef] [Green Version]
- Balla, C.S.; Haritha, C.; Naikoti, K.; Rashad, A. Bioconvection in nanofluid-saturated porous square cavity containing oxytactic microorganisms. Int. J. Numer. Methods Heat Fluid Flow 2019, 2019, 1–37. [Google Scholar] [CrossRef]
- Khan, S.U.; Rauf, A.; Shehzad, S.A.; Abbas, Z.; Javed, T. Study of bioconvection flow in Oldroyd-B nanofluid with motile organisms and effective Prandtl approach. Phys. A Stat. Mech. Its Appl. 2019, 527, 121179. [Google Scholar] [CrossRef]
- Khan, S.; Shehzad, S.A.; Ali, N. Analysis of bioconvection in the suspension of Maxwell nanoparticles with gyrotactic microorganisms: A Prandtl effective approach. Multidiscip. Model. Mater. Struct. 2019, 16, 835–849. [Google Scholar] [CrossRef]
- Ali, B.; Hussain, S.; Abdal, S.; Mehdi, M.M. Impact of Stefan blowing on thermal radiation and Cattaneo–Christov characteristics for nanofluid flow containing microorganisms with ablation/accretion of leading edge: FEM approach. Eur. Phys. J. Plus 2020, 135, 821. [Google Scholar] [CrossRef]
- Abdul, L.N.A.; Uddin, M.J.; Ahmad, I.M. Unsteady MHD bio-nanoconvective anistropic slip flow past a vertical rotating cone. Therm. Sci. 2019, 23, 427–441. [Google Scholar] [CrossRef]
- Uddin, M.J.; Kabir, M.N.; Alginahi, Y.M. Lie group analysis and numerical solution of magnetohydrodynamic free convective slip flow of micropolar fluid over a moving plate with heat transfer. Comput. Math. Appl. 2015, 70, 846–856. [Google Scholar] [CrossRef] [Green Version]
- Saleem, S.; Nadeem, S. Theoretical analysis of slip flow on a rotating cone with viscous dissipation effects. J. Hydrodyn. Ser. B 2015, 27, 616–623. [Google Scholar] [CrossRef]
- Anilkumar, D.; Roy, S. Unsteady mixed convection flow on a rotating cone in a rotating fluid. Appl. Math. Comput. 2004, 155, 545–561. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).